Abstract
A comprehensive understanding of the denitration kinetics of nitrocellulose-based propellants is crucial for optimizing combustion performance and achieving controllable fabrication. However, most existing studies rely on a single kinetic model, which is restricted by formulation composition and grain geometry, limiting their general applicability. In this work, the denitration rate was quantified using the change in explosion heat, introducing an energy-based characterization approach instead of traditional mass-loss measurements. Three kinetic models (the shrinking-core, pseudo-homogeneous, and Avrami models) were employed to identify the rate-controlling step. The shrinking-core model provided the most accurate description of the process. At moderate reagent concentrations (8 wt.% and 12 wt.%) and temperatures (65–75 °C), denitration was primarily reaction-controlled, while at higher temperatures (80 °C), internal diffusion resistance became significant. The apparent activation energy ranged from 69.8 to 73.7 kJ·mol−1, confirming that chemical reaction is the dominant mechanism. This study refines the kinetic understanding of nitrocellulose denitration and provides theoretical guidance for the controlled fabrication of gradient nitrocellulose propellants with tunable progressive-burning behavior.
1. Introduction
As a kind of progressive burning gun propellant, deterrable propellant is generally prepared by coating deterrents with a certain concentration gradient on the surface layer of propellant grains [1,2]. During combustion, the propellant burns gradually from the inhibited surface to the uninhibited core, resulting in a slow initial burning rate followed by a progressive increase [3,4,5]. However, the use of deterrents often leads to excessive muzzle smoke and the release of toxic gases, which are harmful to both operators and the environment [6,7,8,9,10]. Nitrocellulose is the main energetic component of propellants, and its nitrate group content directly determines the energy level of the formulation [11,12,13]. Therefore, adjusting the nitrate group distribution in nitrocellulose offers an effective means to control both the energy release and burning progressivity of propellants. Based on this principle, a gradient denitration strategy has been proposed, in which nitrate groups are gradually removed by a reduction reaction to form a surface-to-core concentration gradient. Compared with traditional deterrable propellants, gradient-denitrated propellants exhibit excellent combustion progressivity, no migration of deterrent components, and lower muzzle smoke and residue [14,15]. Consequently, investigating the evolution law and reaction kinetics of nitrocellulose denitration is of great significance for achieving controllable gradient design of energetic materials.
In the gradient denitration process, hydrazine hydrate reacts with nitrocellulose in a heterogeneous solid–liquid system. The process generally involves liquid-phase diffusion, product-layer diffusion, and surface chemical reaction. Understanding the rate-controlling step is crucial for optimizing process conditions and accurately regulating the gradient distribution of nitrate groups. To describe such heterogeneous reaction behavior, several classical kinetic models have been applied, including the shrinking unreacted-core model [16,17,18,19,20], the pseudo-homogeneous model [21,22,23], and the Avrami model [24,25,26,27,28,29]. These models are all applicable to solid–liquid heterogeneous reactions, but they differ in how they define the reaction front and describe the kinetic parameters. Most existing studies have applied only one of these models for empirical fitting, without comparing their predictive accuracy under different conditions. In addition, the interaction between surface reaction and diffusion resistance at the solid–liquid interface has not been fully clarified, leaving the kinetic mechanism of nitrocellulose denitration insufficiently understood.
Previous studies have established kinetic descriptions of nitrocellulose denitration in different systems. Earlier work on cylindrical single-base propellants proposed a geometric form of the shrinking-core model adapted to that geometry [30], while subsequent research on spherical double-base propellants verified its applicability under various temperatures and reaction times [31]. Although the shrinking-core model was originally developed for spherical particles, its use in propellants with different formulations requires consideration of compositional and structural differences. Single-base and double-base propellants differ in both composition and manufacturing process, leading to distinct reaction behaviors. Moreover, earlier studies characterized the denitration degree by mass change, whereas the present study establishes kinetic modeling through explosion heat, which directly reflects variations in energetic content. This energy-based approach provides a more general and physically meaningful measure for quantifying nitrate-group conversion and allows the model to be applied to different propellant systems.
Therefore, this study selects spherical double-base propellants as the research object to further refine the kinetic description of nitrocellulose denitration. By combining experimental measurements of explosion heat, density, and product-layer thickness, three representative kinetic models (the shrinking unreacted core, pseudo-homogeneous, and Avrami models) are comparatively analyzed. The study aims to identify the most suitable model and establish a universal kinetic framework for understanding the surface denitration process of nitrocellulose-based propellants, providing theoretical support for the controlled preparation of gradient energetic materials.
2. Experiments
2.1. Materials and Chemicals
Double-base spherical propellants were supplied by Luzhou Northern Chemical Industry Co., Ltd. (Luzhou, Sichuan, China). Their composition consisted of 85 wt.% nitrocellulose (13.15 wt.% nitrogen), 10 wt.% nitroglycerin, and 1.5 wt.% centralite II, with the surface coated by graphite. Hydrazine hydrate (N2H4·H2O, >80 wt.%) was purchased from Chengdu Colon Chemical Co., Ltd. (Chengdu, Sichuan, China). All solutions were prepared using deionized water.
2.2. Preparation of Surface-Denitrated Spherical Gun Propellants
The denitration was performed with hydrazine hydrate solution as the active reagent. Typically, 100 g of 8 wt.% solution was placed in a 500 mL three-neck flask, and 50.0 g of spherical propellant was introduced once the solution reached the desired temperature. The reaction was stopped after the specified time, and the solid products were washed in deionized water at 80 °C for 1 h and subsequently dried at 55 °C for 48 h. A set of samples was prepared under different conditions following this protocol, with details provided in Table S1.
2.3. Denitration Mechanism of Spherical Gun Propellant
Since nitrate groups in spherical propellants are mainly derived from nitrocellulose and nitroglycerin [32], the use of hydrazine hydrate as the denitration reagent leads to the following possible reaction pathways.
The reaction pathways of nitrocellulose and hydrazine hydrate are shown as follows:
The reaction pathways of nitroglycerin and hydrazine hydrate are shown as follows:
The denitration of nitrocellulose in spherical propellants proceeds as a heterogeneous solid–liquid reaction. It involves three successive stages: (1) diffusion of hydrazine hydrate through the boundary layer to the outer surface of the propellant particle (external diffusion), (2) penetration of the reagent through the solid product layer to the unreacted core interface (internal diffusion), and (3) chemical reaction of hydrazine hydrate with nitrate groups at that interface. The overall reaction rate is governed by the slowest of these steps, which becomes the rate-controlling stage. The three stages of the denitration process are illustrated in Figure 1.
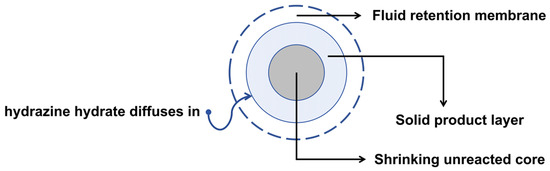
Figure 1.
Schematic illustration of the denitration process of spherical propellants.
2.4. Characterization
Super depth-of-field 3D microscope (VHX-2000C, KEYENCE, Osaka, Japan) with a magnification of 200 times was used to observe the cross-section of the surface-denitrated spherical gun propellant microspheres. The Raman spectrometer (LabRAM Odyssey, HORIBA, Kyoto, Japan) was used to study the molecular structure of samples at distances of 10 μm, 40 μm, 70 μm, and 130 μm from the surface with a laser of 785 nm. Density testing of samples according to the method 401.2 “Density Liquid static weighing method” of GJB 770B-2005 [33]. The oxygen elastic thermometer (RF-C7000, Ruifang Energy Science and Technology Co., Ltd., Changsha, Hunan, China) was used to determine the heat of explosion according to the method 701.1 “Adiabatic method for heat of explosion and burning heat” of GJB 770B-2005.
3. Results and Discussion
3.1. Structural Characterization
Raman spectroscopy was employed to examine the gradient distribution of nitrate groups in the surface-denitrated spherical propellant. As illustrated in Figure 2 for sample 11#, the peaks at 852 cm−1 and 1285 cm−1 are assigned to the O–NO2 stretching and the symmetric –NO2 stretching vibrations, respectively [34], characteristic of nitrate ester groups (–ONO2). The intensity of these signals increased progressively from the outer surface toward the interior, extending to approximately 130 μm. This trend confirms a gradient distribution of nitrate ester groups in double-base spherical propellants, extending from the surface to the core.
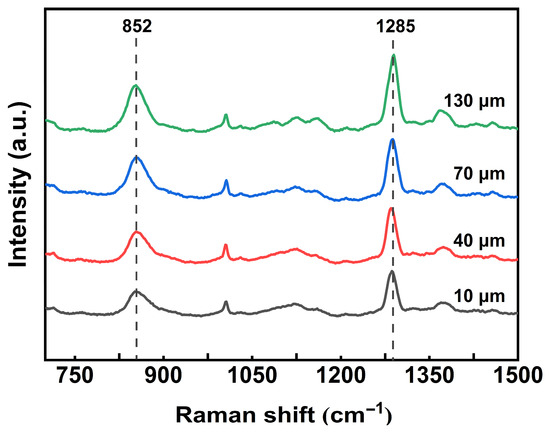
Figure 2.
Raman spectra of sample 11# collected at different depths from the surface.
3.2. Analysis of the Denitration Process of Nitrocellulose in Spherical Gun Propellant
The study assessed how process conditions affect the thickness of the denitrated layer, the density of the product, and the overall denitration rate in spherical propellants.
Among them, the calculation of the denitration rate in the denitration process is based on our previously reported work [30]. The denitration rate (α) of the spherical gun propellant was calculated as follows:
where α is the denitration rate, %; Q0 is the heat of explosion of double-based spherical gun propellants, J·g−1; and Qt is the heat of explosion of surface-denitrated spherical gun propellants, J·g−1.
The influence of reagent concentration on nitrocellulose denitration in surface-modified spherical propellants was examined at 8, 10, 12 and 14 wt.%, under fixed conditions of 70 °C and 60 min. As shown in Figure S1, the denitration products showed an obvious core–shell structure, which is consistent with the Raman results. The thickness of the denitrated layer expanded as concentration increased, whereas sample density generally decreased. This behavior indicates a gradual substitution of surface nitrate groups by hydroxyl groups. Accordingly, Figure 3a demonstrates that the denitration rate also increased, aligning with the observed thickening of the product layer.
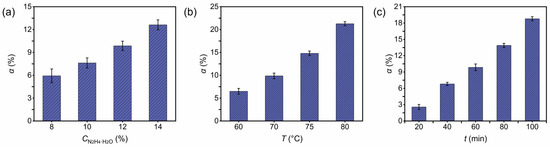
Figure 3.
(a) Effect of denitration agent concentration (8–14 wt.%) on the denitration rate of spherical propellants at 70 °C for 60 min. (b) Effect of reaction temperature (60–80 °C) on the denitration rate at 12 wt.% denitration agent for 60 min. (c) Effect of reaction time (20–100 min) on the denitration rate at 12 wt.% denitration agent and 70 °C.
At a fixed reagent concentration and reaction time, the effect of temperature (65–80 °C) on the denitration of spherical propellants was evaluated. As shown in Figure S2, the product-layer thickness increased from 63.40 μm to 91.50 μm. By contrast, the maximum density reduction was only 0.99% relative to the untreated sample. Furthermore, the denitration rate rose with increasing temperature (shown in Figure 3b), consistent with the observed thickening of the product layer. These results imply that higher temperatures facilitate the conversion of nitrocellulose nitrate groups into hydroxyl groups.
As illustrated in Figure S3, extending the reaction time from 20 to 100 min resulted in an increase in product-layer thickness from 73.85 μm to 91.11 μm. The density change was minimal, with a maximum decrease of 0.96%. Meanwhile, the denitration rate increased from 2.77% to 18.72% (shown in Figure 3c). That is to say that the extension of reaction time had a greater impact on the denitration degree of nitrocellulose in the spherical gun propellant, and a smaller impact on the quality and packing density of the spherical gun propellant.
3.3. Kinetic Analysis
3.3.1. Selection of Kinetic Models
Denitration of nitrocellulose in spherical propellants was treated as a non-catalytic solid–liquid reaction. Rate-time relationships were established at 65–80 °C and at initial concentrations of 8 wt.% and 12 wt.%. The shrinking unreacted core, pseudo-homogeneous, and Avrami models were employed to identify the controlling step, and their descriptive capability was compared.
Based on the three stages of the solid–liquid non-homogeneous reaction process (external diffusion of solute extraction, internal diffusion of solid product layer and chemical reaction), the expressions for the reaction rate of the shrinking unreacted core kinetic model are as follows [16,35]:
When the reaction process is controlled by chemical reaction (SC),
When the reaction process is controlled by external diffusion (SE),
When the reaction process is controlled by internal diffusion of the solid product layer (SI),
where α is the denitration rate of spherical gun propellant; k is the reaction rate constant of the denitration process of the spherical gun propellant, min−1; and t is the reaction time, min.
The pseudo-homogeneous model was suitable for explaining the reaction processes between flowing liquid and fixed solid [21,22,23]. The pseudo-homogeneous model can be divided into three types:
For the zero-order pseudo-homogeneous model (PZ), the rate equation can be expressed as
For the first-order pseudo-homogeneous model (PF), the rate equation can be expressed as
For the second-order pseudo-homogeneous model (PS), the rate equation can be expressed as
where α is the denitration rate of spherical gun propellant; k is the reaction rate constant of the denitration process of the spherical gun propellant, min−1; and t is the reaction time, min.
The Avrami model can also be used to derive rate equations for non-catalytic fluid–solid systems [24,25,26,27,28,29,36]. The logarithmic form of the Avrami model (AV) is as follows:
where α is the denitration rate of spherical gun propellant; k is the reaction rate constant of the denitration process of the spherical gun propellant, min−1; t is the reaction time, min; and n is the Avrami characteristic parameter.
3.3.2. Fitting of Kinetic Models
The denitration rates of nitrocellulose in the spherical gun propellants prepared under different process conditions were fitted into the three models mentioned above; the model parameters are listed in Table 1 and Table 2. The corresponding fitting results are shown in Figures S4 and S5.

Table 1.
Kinetic model parameters at different reaction temperatures for 8 wt.% denitration agent concentration.

Table 2.
Kinetic model parameters at different reaction temperatures for 12 wt.% denitration agent concentration.
As shown in Table 1, when the denitration agent concentration was 8 wt.%, for SC, PZ, PF, PS and AV models, the r2 increased with increasing reaction temperature and reduced simultaneously after 75 °C. Meanwhile, there is a very interesting phenomenon that the r2 of the internal diffusion control model in the shrinking unreacted core model increased dramatically with the increase in reaction temperature. Especially, when the reaction temperature was 80 °C, the r2 reached 0.982, which suggested that the resistance of the internal diffusion increased gradually with increasing temperature. In addition, the characteristic parameter n of the Avrami model exhibited a clear variation with increasing reaction temperature, indicating a transition in the rate-controlling steps. At higher temperatures, the denitration process was jointly governed by chemical reaction and diffusion [37,38], which is consistent with the results obtained from the shrinking unreacted core model.
As summarized in Table 2, at 12 wt.% reagent concentration and lower reaction temperatures, the SC model gave the highest r2 values, suggesting that chemical reaction was the controlling step. With increasing temperature, r2 for this model declined, implying a gradual reduction in chemical-reaction resistance. Conversely, the SI model reached its maximum r2 at 80 °C, indicating that internal diffusion dominated under these conditions. Consistently, the Avrami parameter n was greater than 1 at lower temperatures but dropped below 1 at elevated temperatures. These results indicate that nitrocellulose denitration in spherical propellants was dominated by chemical-reaction control at lower temperatures, whereas at higher temperatures the process shifted to internal diffusion control [39,40,41].
Overall, the SC model yielded the best correlation at 8 wt.% and 12 wt.% concentrations when the temperature was below 80 °C, showing that chemical reaction dominated the denitration of nitrocellulose in spherical propellants. As the temperature rose, internal diffusion within the product layer increasingly limited the process [42,43].
Based on the above discussion, the SC model is more suitable for describing the denitration process of nitrocellulose in the spherical gun propellants. The rate constant k of the denitration process was obtained according to the SC model, which was fitted to the reaction temperature using the Arrhenius equation [44,45,46]. The expression for the Arrhenius equation is shown as follows:
where k is the reaction rate constant, min−1; A0 is the frequency factor, min−1; Ea is the apparent activation energy, kJ·mol−1; R is the ideal gas constant, 8.314 J·mol−1·K−1; and T is the temperature, K.
Figure 4 presents the Arrhenius plots of lnk versus 1000/T at different reagent concentrations. The apparent activation energies were calculated to be 73.7 ± 3.7 and 69.8 ± 4.3 kJ·mol−1, with corresponding pre-exponential factors of 5.38 × 107 and 2.42 × 107, respectively. Thus, the activation energy of the denitration process lies within 69.82–73.71 kJ·mol−1. Since values above 42 kJ·mol−1 indicate chemical reaction control, the results demonstrate that nitrocellulose denitration in spherical propellants is dominated by chemical reaction. Consequently, increasing temperature, reagent concentration, or related parameters can effectively accelerate the process.
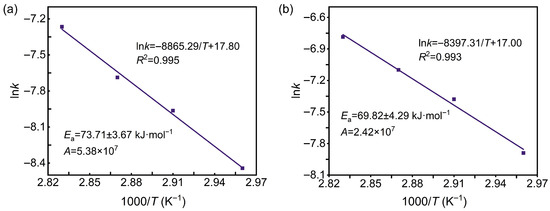
Figure 4.
Arrhenius plots of lnk versus 1000/T at denitration agent concentrations of (a) 8 wt.% and (b) 12 wt.%.
3.3.3. Validation of the Kinetic Model
For spherical propellants, nitrocellulose denitration was found to be governed primarily by the chemical reaction step under different reagent concentrations. Accordingly, a corresponding kinetic model describing this process was established.
When the concentration of denitration agent was 8 wt.%, the kinetic model expression is given by
When the concentration of denitration agent was 12 wt.%, the kinetic model expression is given by
To validate the proposed kinetic models [47,48], the experimental denitration rates under different conditions were substituted into the two equations, and the corresponding fitting curves are presented in Figure 5. The relatively high r2 values confirm that nitrocellulose denitration in spherical propellants was dominated by the chemical reaction step and that the developed models provide reliable accuracy.
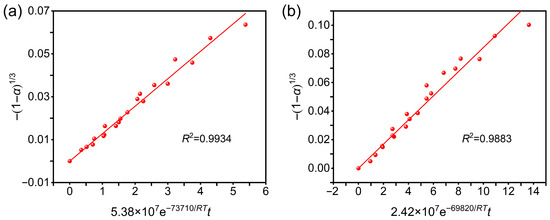
Figure 5.
Validation of the kinetic model at denitration agent concentrations of (a) 8 wt.% and (b) 12 wt.%.
4. Conclusions
In comparison with previous studies, the present findings refine the kinetic understanding of nitrocellulose denitration in spherical double-base propellants. The transition from reaction-controlled behavior at moderate temperatures (65–75 °C) to diffusion-controlled behavior at higher temperatures (80 °C) agrees with earlier reports on spherical propellants, in which the progressive formation of a product layer increased internal diffusion resistance. Compared with prior studies that often characterized conversion by mass change and applied a single-model framework (for example, the shrinking-core model), the current study quantifies conversion via changes in explosion heat, which directly reflect the energetic content of the samples. This energy-based metric is not limited by propellant composition and therefore provides a more physically meaningful basis for comparing kinetic behavior across different systems.
Furthermore, the activation energies obtained (69.8–73.7 kJ·mol−1) are consistent with the range reported for surface-reaction-dominated systems, confirming that chemical reaction is the rate-determining step at moderate temperatures. However, the increasing contribution of internal diffusion with temperature explains the gradual decline in reaction-controlled behavior, which complements and extends earlier conclusions drawn for propellants. Multi-model comparison shows that model selection is governed by the rate-controlling step and system characteristics, offering a theoretical basis for the controlled fabrication of gradient nitrocellulose propellants.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/pr13113668/s1, Table S1: Experimental parameters corresponding to sample numbers; Figure S1: Effect of denitration agent concentration (8, 10, 12, and 14 wt.%) on (a) microstructure, (b) thickness of the denitrated product layer, and (c) sample density at 70 °C for 60 min; Figure S2: Effect of reaction temperature on (a) microstructure, (b) thickness of the denitrated product layer, and (c) sample density with 12 wt.% denitration agent for 60 min; Figure S3: Effect of reaction time on (a) microstructure, (b) thickness of the denitrated product layer, and (c) sample density with 12 wt.% denitration agent at 70 °C; Figure S4: Kinetic model fitting of nitrocellulose denitration in spherical gun propellants at different reaction temperatures (65–80 °C) with 8 wt.% denitration agent. The fitting results for various models are shown: (a) SC, (b) SE, (c) SI, (d) PZ, (e) PF, (f) PS, and (g) AV; Figure S5: Kinetic model fitting of nitrocellulose denitration in spherical gun propellants at reaction temperatures of 65–80 °C with 12 wt.% denitration agent: (a) SC, (b) SE, (c) SI, (d) PZ, (e) PF, (f) PS, and (g) AV.
Author Contributions
Y.L.: writing—original draft, visualization, investigation, formal analysis, data curation. X.W. (Xinyu Wang): investigation, formal analysis, data curation. J.Z.: formal analysis, data curation. H.F.: writing—review & editing, conceptualization, project administration. S.L.: investigation, validation. C.C.: resources. X.W. (Xiaoqing Wu): methodology, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (NSFC) grant (22205111).
Data Availability Statement
Due to ethical restrictions, the raw data cannot be made publicly available. However, deidentified data may be obtained from the corresponding author upon reasonable request.
Acknowledgments
The authors thank the Lu Zhou North Chemical Industries Co., Ltd., for providing the experimental site.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Manning, T.; Wyckoff, J.; Klingaman, K.; Panchal, V.; Rozumov, E.; Bolognini, J.; Young, M.W.; Patel, S. Enhanced propellant performance via environmentally friendly curable surface coating. Def. Technol. 2017, 13, 131–142. [Google Scholar] [CrossRef]
- Liang, H.; Ding, Y.J.; Li, S.Y.; Xiao, Z.L. Combustion performance of spherical propellants deterred by energetic composite deterring agents. ACS Omega 2021, 6, 13024–13032. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhang, J.W.; Meng, D.R.; Cao, X.; Wang, B.B.; Nan, F.Q.; Chen, F.Y.; Du, P.; Liao, X.; He, W.D. Construction of nitrate glycerol ether cellulose/RDX energetic composite in gun propellants and its comprehensive performance. Cellulose 2024, 31, 5725–5745. [Google Scholar] [CrossRef]
- Liu, B.; Ma, F.S.; Bian, X.Y.; Tian, D.Q.; Wang, Q.L.; Lv, H. Research on the Performance of Deterred-coating DIANP Gun Propellant. J. Phys. Conf. Ser. 2023, 2478, 032006. [Google Scholar] [CrossRef]
- Gou, Y.L.; Wei, L.; Yao, Y.J.; Liu, B.; Wang, J.P. Combustion performance of surface-deterred gun propellants with varied deterrent contents. J. Phys. Conf. Ser. 2023, 2478, 032004. [Google Scholar] [CrossRef]
- Moskovchenko, A.; Vantner, M.; Honner, M. Detection of gunshot residue by flash-pulse and long-pulse infrared thermography. Infrared Phys. Technol. 2024, 140, 12. [Google Scholar] [CrossRef]
- Mcneilly, R.J.; Schwanekamp, J.A.; Hyder, L.S.; Hatch, J.P.; Edwards, B.T.; Kirsh, J.A.; Jackson, J.M.; Jaworek, T.; Methner, M.M.; Duran, C.M. Exposure to lead-free frangible firing emissions containing copper and ultrafine particulates leads to increased oxidative stress in firing range instructors. Part. Fibre Toxicol. 2022, 19, 36. [Google Scholar] [CrossRef]
- Ding, Y.J.; Ying, S.J.; Xiao, Z.L.; Wu, W.L.; Li, C.Z.; He, Y. Microcellular Oblate Propellant with Skin-core Structure Deterred by Poly(neopentanediol adipate). Cent. Eur. J. Energ. Mat. 2020, 17, 49–65. [Google Scholar] [CrossRef]
- Li, X.Y.; Wu, R.; Li, Z.C.; Chen, G.; Zhou, H.B.; Zhang, Y.C.; Xiao, Z.G. Study on the erosion reducing mechanisms of microencapsulated hydroxyl silicone oil with a hybrid shell. Mater. Lett. 2025, 401, 139196. [Google Scholar] [CrossRef]
- Wang, D.L.; Liang, H.; Li, H.W.; Chu, Y.K.; Ding, S.X.; Xu, B. Can the gradient distribution and antimigration of deterrents in nitrocellulose-based propellant be balanced?: A strategy for small molecule diffusion followed by UV-induced curing. Cellulose 2025, 32, 2955–2971. [Google Scholar] [CrossRef]
- Saito, Y.; Okada, K.; Endo, T.; Sakakibara, K. Highly surface-selective nitration of cellulose nanofibers under mildly acidic reaction conditions. Cellulose 2023, 30, 10083–10095. [Google Scholar] [CrossRef]
- Aljafree, N.F.A.; Norrrahim, M.N.F.; Samsuri, A.; Yunus, W.M.Z.W. Advancements in nitrated nanocellulose: From structural insights to energetic applications. Cellulose 2025, 32, 8047–8099. [Google Scholar] [CrossRef]
- Boukeciat, H.; Tarchoun, A.F.; Trache, D.; Abdelaziz, A.; Bouhantala, A.; Boustila, C.; Klapötke, T.M.; Thakur, S. Development and characterization of innovative energetic composites based on nitrotriazolone and nanostructured cellulose nitrates. Cellulose 2024, 31, 5479–5498. [Google Scholar] [CrossRef]
- Li, S.Y.; Tao, Z.A.; Ding, Y.J.; Liang, H.; Zhao, X.Z.; Xiao, Z.L.; Li, C.Z.; Ou, J.Y. Gradient denitration strategy eliminates phthalates associated potential hazards during gun propellant production and application. Propellants Explos. Pyrotech. 2020, 45, 1156–1167. [Google Scholar] [CrossRef]
- Li, S.Y.; Li, Y.; Ding, Y.J.; Liang, H.; Xiao, Z.L. One-step green method to prepare progressive burning gun propellant through gradient denitration strategy. Def. Technol. 2021, 22, 135–143. [Google Scholar] [CrossRef]
- Sweygers, N.; Depuydt, D.E.C.; Van Vuure, A.W.; Degrève, J.; Potters, G.; Dewil, R.; Appel, L. Simultaneous production of 5-hydroxymethylfurfural and furfural from bamboo (Phyllostachys nigra “Boryana”) in a biphasic reaction system. Chem. Eng. J. 2020, 386, 123957. [Google Scholar] [CrossRef]
- Wu, W.F.; Wang, C.Y.; Wang, X.R.; Li, H.Q. Removal of V and Fe from spent denitrification catalyst by using oxalic acid: Study of dissolution kinetics and toxicity. Green. Energy Environ. 2021, 6, 660–669. [Google Scholar] [CrossRef]
- Li, S.J.; Zhu, J.X. Leaching kinetics of fluorine during the aluminum removal from spent Li-ion battery cathode materials. J. Environ. Sci. 2024, 138, 312–325. [Google Scholar] [CrossRef]
- Wen, G.D.; Yuan, S.; Liu, J.; Dong, Z.Z.; Han, R.; Ding, H.Y.; Lei, S.L.; Li, Z.H.; Wang, W.Z.; Cao, Y.D. Process optimization for recycling spent lithium iron phosphate batteries based on leaching kinetics and mechanism study. Sep. Purif. Technol. 2025, 370, 133263. [Google Scholar] [CrossRef]
- Chen, S.L.; Wang, X.; Li, H.; Guan, X.T.; Fan, Y.Q.; Yan, Y.C.; Guo, Z.P.; He, H.B.; Long, H.M. Optimizing lithium recovery from artificial β-spodumene slags: A breakthrough in pyrometallurgical processing of spent lithium-ion batteries. J. Environ. Chem. Eng. 2025, 13, 117291. [Google Scholar] [CrossRef]
- Dickinson, C.F.; Heal, G.R. Solid–liquid diffusion controlled rate equations. Thermochim. Acta 1999, 340, 89–103. [Google Scholar] [CrossRef]
- Zainol, M.M.; Asmadi, M.; Amin, N.A.S. Bio-fuel additive synthesized from levulinic acid using ionic liquid-furfural based carbon catalyst: Kinetic, thermodynamic and mechanism studies. Chem. Eng. Sci. 2022, 247, 117079. [Google Scholar] [CrossRef]
- Rouquette, L.M.J.; Altenschmidt, L.; Culina, M.; Brant, W.R.; Ebin, B.; Petranikova, M. Kinetics study of the dissolution of black mass material using oxalic acid as a leaching agent. J. Hazard. Mater. Adv. 2025, 18, 100750. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Wang, M.D.; Zhang, Y.J.; Zhan, F.K.; Qiu, Y.J.; Chen, T.; Zhao, L.M. Kinetic analysis of PA4 thermal degradation: Thermal stability with respect to crystallinity. Polym. Degrad. Stab. 2024, 227, 110880. [Google Scholar] [CrossRef]
- Aslan, B.G.; Aslan, C.; Iihan, S. Hydrometallurgical Recovery of Valuable Metals from Hazardous Petrochemical Industry Waste and Kinetic Investigation. J. Sustain. Metall. 2023, 9, 1535–1549. [Google Scholar] [CrossRef]
- Shi, M.Q.; Min, X.B.; Shen, C.; Chai, L.Y.; Ke, Y.; Yan, X.; Liang, Y.J. Separation and recovery of copper in Cu-As-bearing copper electrorefining black slime by oxidation acid leaching and sulfide precipitation. Trans. Nonferrous Met. Soc. China 2021, 31, 1103–1112. [Google Scholar] [CrossRef]
- Liu, S.F.; Song, S.C.; Tang, K.; Ye, L.G. Efficient separation and recovery of cobalt from grinding waste of cemented carbide using a sulfuric acid-sodium persulfate mixed solution. Hydrometallurgy 2025, 231, 106419. [Google Scholar] [CrossRef]
- Yang, D.E.; Zhang, Z.Y.; Zhang, F.S. The recycling of subway tunnel muck: A low alkalinity cementitious material for ecological concrete preparation. Waste Dispos. Sustain. Energy 2025, 7, 243–257. [Google Scholar] [CrossRef]
- Cui, F.; Fan, H.L.; Li, S.Y.; Wu, X.Q.; Li, C.Z.; Xiao, Z.L. Kinetic model for denitration reaction process of cylindrical single-base gun propellant. ACS Omega 2023, 8, 46197–46204. [Google Scholar] [CrossRef]
- Li, S.Y.; Li, Y.; Ding, Y.J.; Xiao, Z.L.; Shi, Y.D.; Yuan, Y. Reaction Kinetics Model of Surface-Denitrated Spherical Gun Propellant. Propell. Explos. Pyrotech. 2023, 48, 202200210. [Google Scholar] [CrossRef]
- Xiong, J.; Feng, S.; Peng, R.F.; Jin, B. Effect of aziridino[60]fullerenes on thermal stability of nitrocellulose. Cellulose 2024, 31, 235–246. [Google Scholar] [CrossRef]
- GB 770B-2005; Test Method of Propellant. Armament Standard Publication Department of COSTIND: Beijing, China, 2005.
- Sun, Y.; Pan, A.F.; Ma, Y.Z.; Zhang, J.W.; Chang, J.; Wang, Z. Kinetics of kaolinite dissolution and hydrosodalite precipitation during alkali leaching of diasporic bauxite. Appl. Clay Sci. 2024, 260, 107537. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Xiao, J.; Wu, M.R.; Dong, Z.Y.; Li, Y.T.; Shun, W.; Yang, Y. Synthesis of γ-Al2O3 for fluoride removal from spent Lithium-Ion battery leaching solution: Performance and mechanism. Sep. Purif. Technol. 2025, 378, 134822. [Google Scholar] [CrossRef]
- Gu, K.H.; Li, W.H.; Han, J.W.; Liu, W.; Qin, W.Q.; Cai, L.B. Arsenic removal from lead-zinc smelter ash by NaOH-H2O2 leaching. Sep. Purif. Technol. 2019, 209, 128–135. [Google Scholar] [CrossRef]
- Esquerdo, V.M.; Quintana, T.M.; Dotto, G.L.; Pinto, L.A.A. Kinetics and mass transfer aspects about the adsorption of tartrazine by a porous chitosan sponge. React. Kinet. Mech. Catal. 2015, 116, 105–117. [Google Scholar] [CrossRef]
- Sun, B.B.; Hu, Y.N.; Cheng, H.F.; Tao, S. Releases of Brominated Flame Retardants (BFRs) from Microplastics in Aqueous Medium: Kinetics and Molecular-size Dependence of Diffusion. Water Res. 2018, 151, 215–225. [Google Scholar] [CrossRef] [PubMed]
- Mosoarca, G.; Popa, S.; Vancea, C.; Dan, M.; Boran, S. Removal of Methylene Blue from Aqueous Solutions Using a New Natural Lignocellulosic Adsorbent—Raspberry (Rubus idaeus) Leaves Powder. Polymers 2022, 14, 1966. [Google Scholar] [CrossRef]
- Marinović, S.; Mudrinić, T.; Milovanović, B.; Jović-Jovičić, N.; Ajduković, M.; Banković, P.; Milutinović-Nikolić, A. The influence of cobalt loading in cobalt-supported aluminum pillared montmorillonite on the kinetic of Oxone® activated oxidative degradation of tartrazine. React. Kinet. Mech. Catal. 2023, 136, 1157–1168. [Google Scholar] [CrossRef]
- Farouq, R. Coupling Adsorption-Photocatalytic Degradation of Methylene Blue and Maxilon Red. J. Fluoresc. 2022, 32, 1381–1388. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, L.; Lucas, D.P.; Ueslei, G.F.; Ruan, D.O.l.A.; Iara, R.P.; Renato, R.P.; Luciano, D.M.G.; Luciene, P.R.P.; Demetrius, P. Adsorptive Removal of Aromatic Amine from Aqueous Solutions Using Carbon Black as Adsorbent. Chem. Eng. Commun. 2022, 210, 1108–1117. [Google Scholar] [CrossRef]
- Senouci, B.Z.; Houcine, B. Enhancing Methylene Blue Sorption on Spotted Golden Thistle Stalks by Soft Chemical Pretreatments. Chem. Eng. Commun. 2021, 209, 365–377. [Google Scholar] [CrossRef]
- Shi, G.C.; Liao, Y.L.; Su, B.W.; Zhang, Y. Kinetics of copper extraction from copper smelting slag by pressure oxidative leaching with sulfuric acid. Sep. Purif. Technol. 2020, 241, 116699. [Google Scholar] [CrossRef]
- Jian, X.W.; Jing, H.; Cai, Z.L.; Zhang, Y.M.; Liu, T.; Liu, H. Effect of alkaline fusion on muscovite decomposition and the vanadium release mechanism from vanadium shale. R. Soc. Open Sci. 2018, 5, 180700. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, K.; Wang, Y.P.; Long, T.; Wan, H.; Li, H.; Wang, Q. Dissolution of gold in chalcopyrite-containing cyanide solutions. J. Cent. South Univ. 2020, 27, 1495–1502. [Google Scholar] [CrossRef]
- Ajiboye, E.A.; Panda, P.K.; Adebayo, A.O.; Ajayi, O.O.; Tripathy, B.C.; Ghosh, M.K.; Basu, S. Leaching kinetics of Cu, Ni and Zn from waste silica rich integrated circuits using mild nitric acid. Hydrometallurgy 2019, 188, 161–168. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).