Dynamic Escape Path Optimization Model Study Based on Spatio-Temporal Evolution of Coal Mine Water Inrush
Abstract
1. Introduction
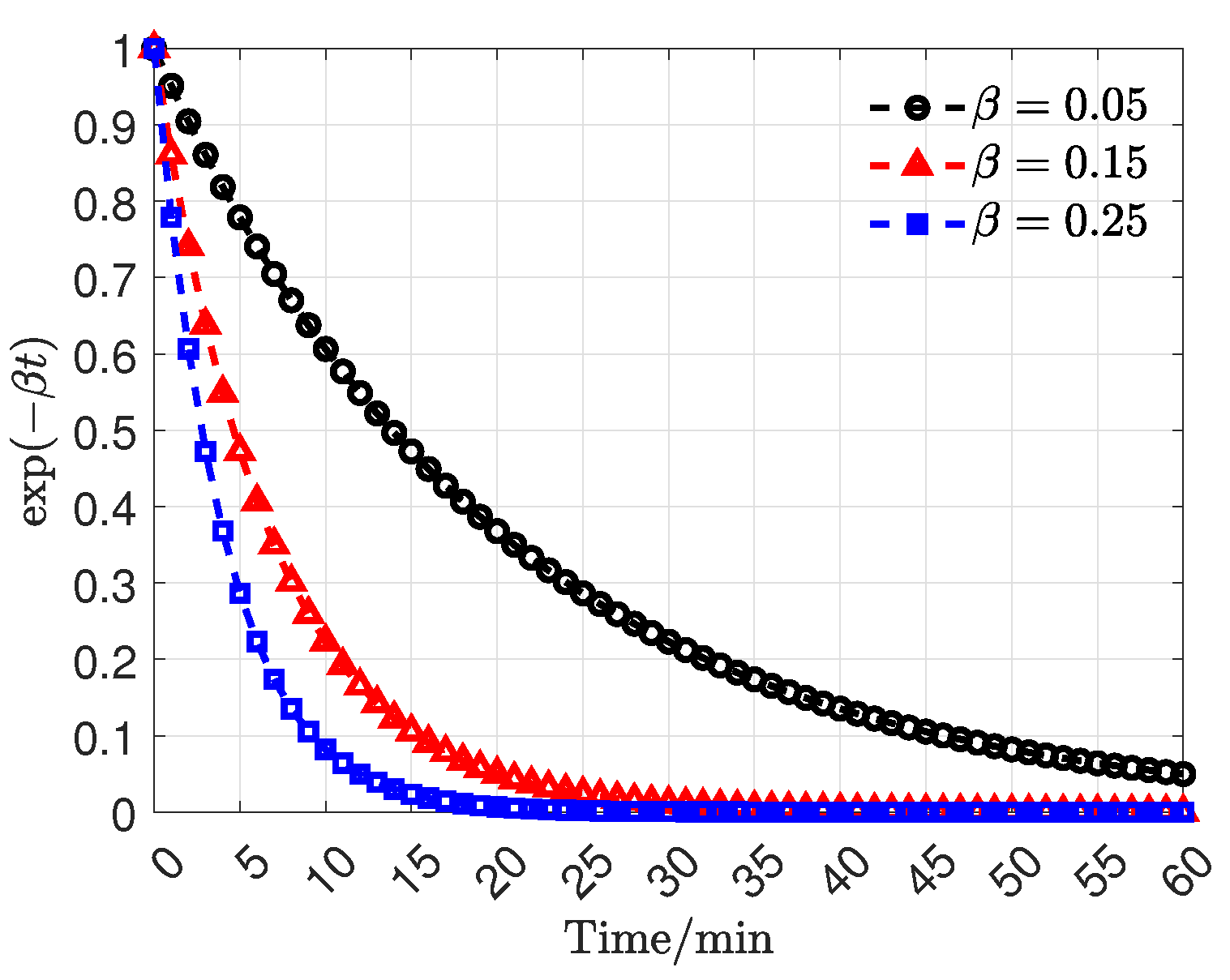
2. Spatio-Temporal Evolution of Coal Mine Water Inrush
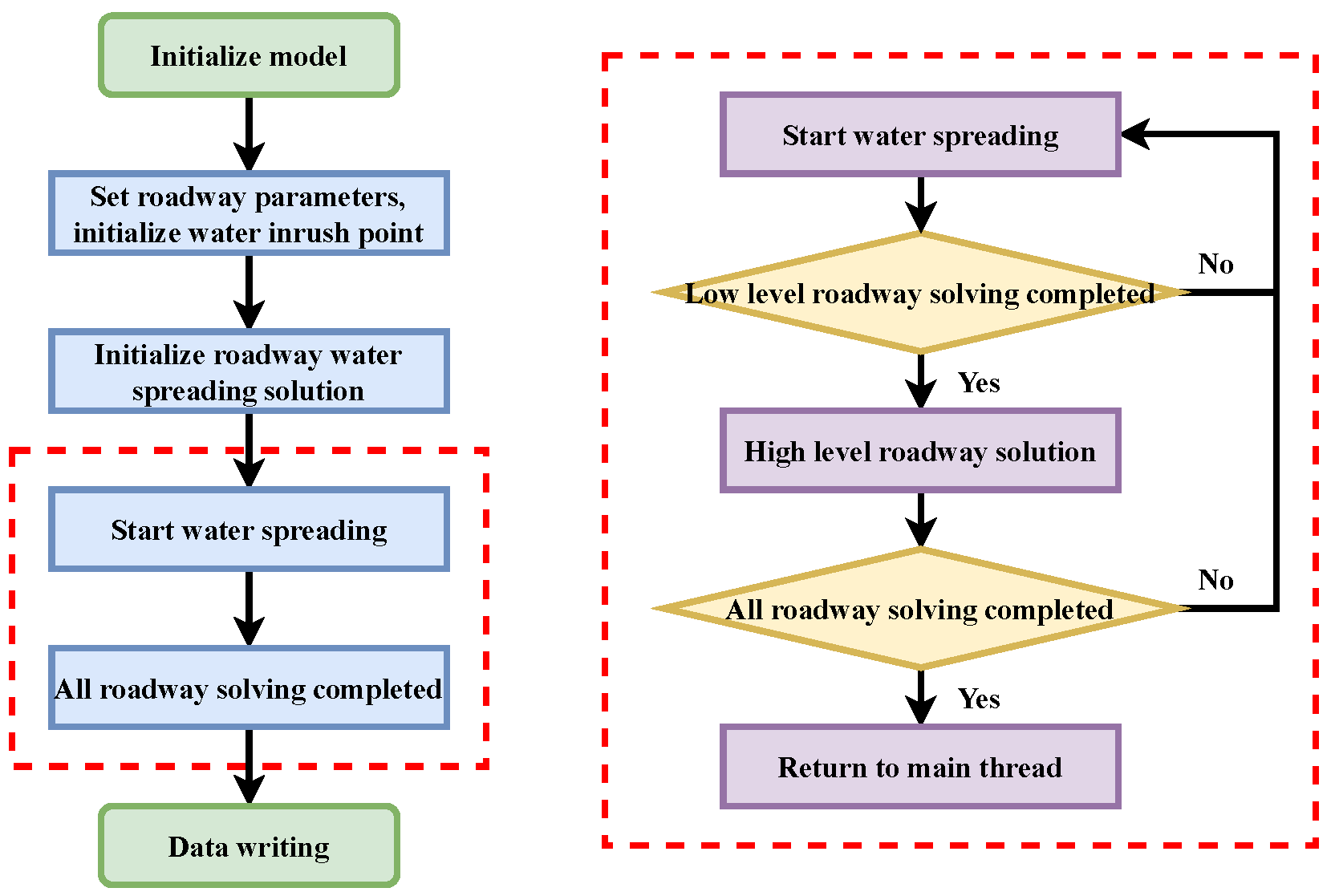
3. Dynamic Escape Path Optimization
4. Model Validation
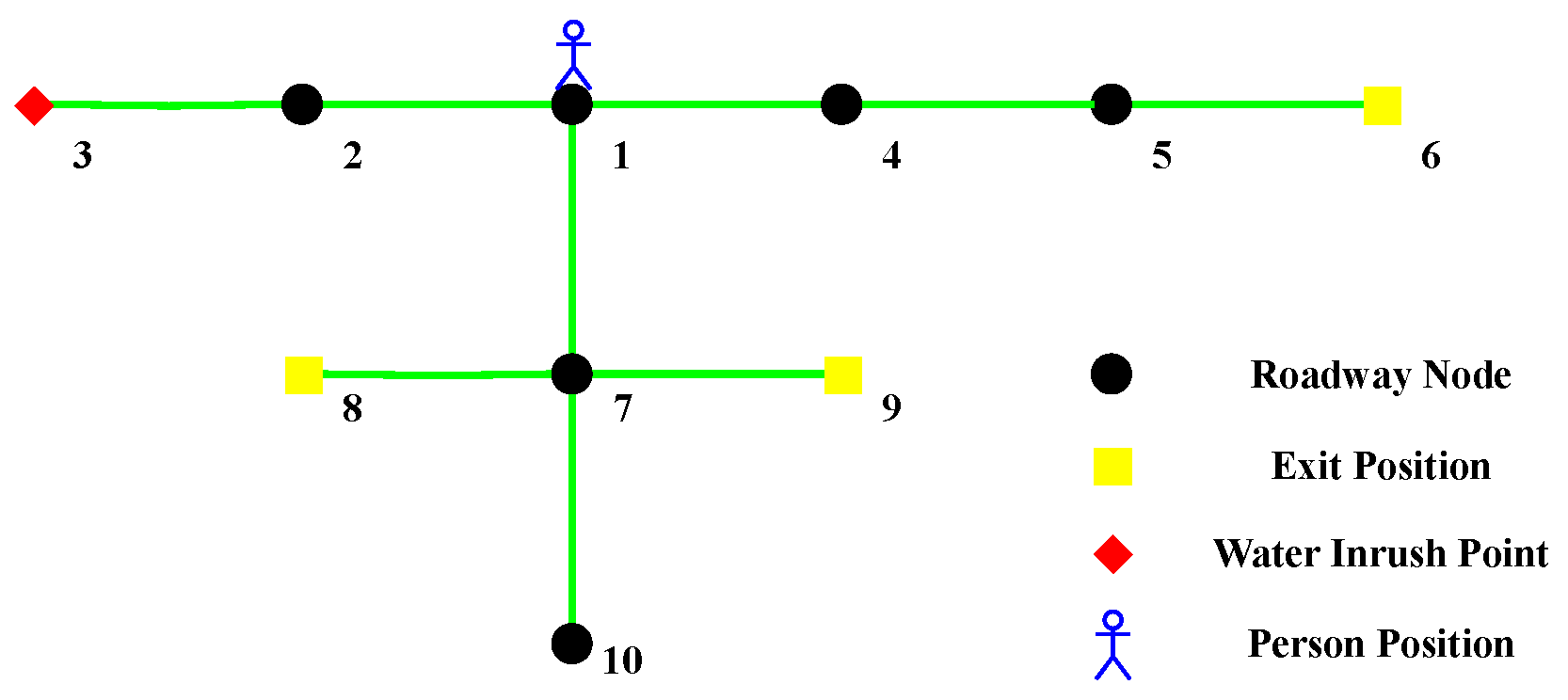
4.1. Single Water Inrush Point and Single Person
4.2. Multiple Water Inrush Points and Multiple Persons
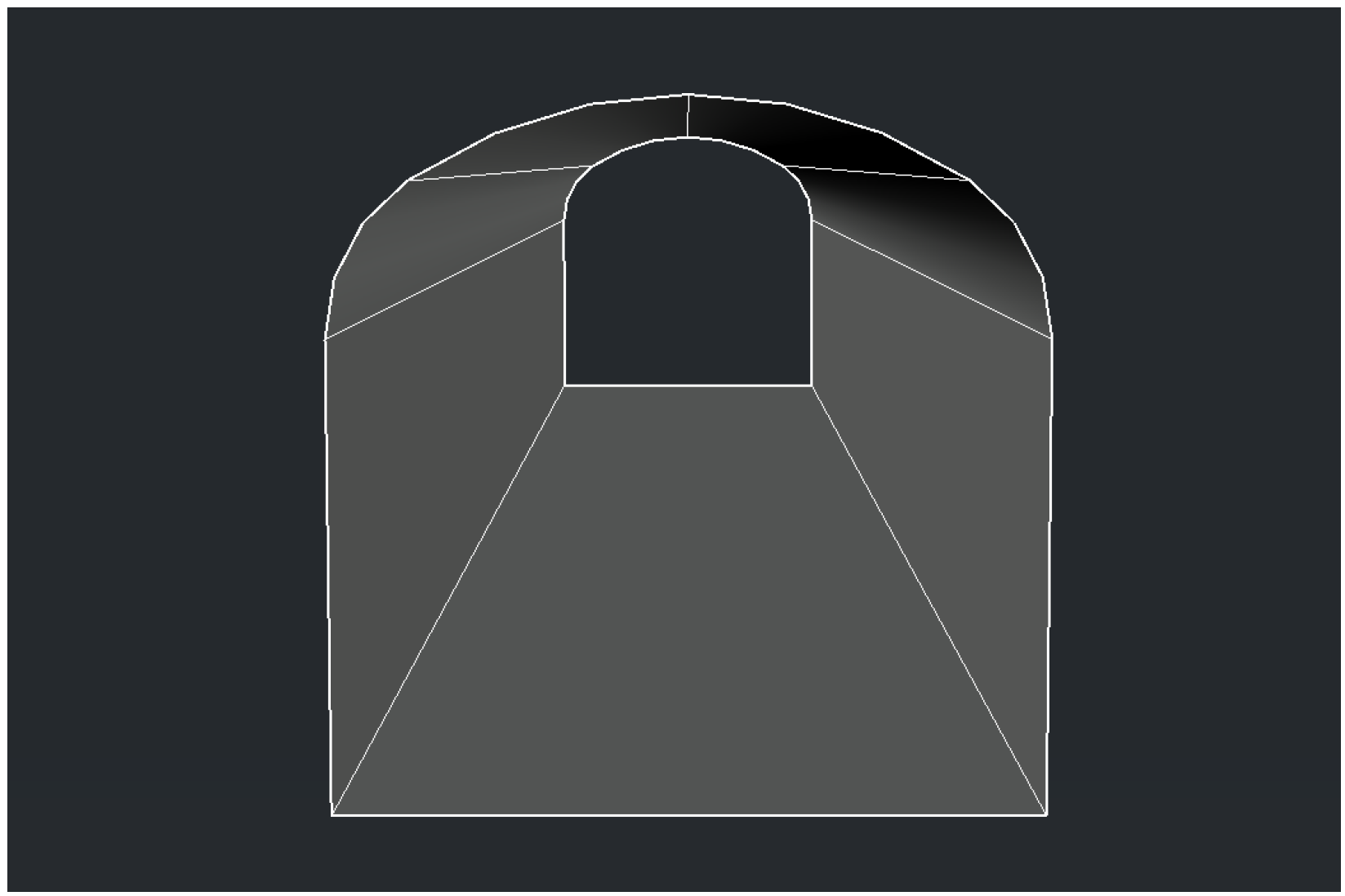
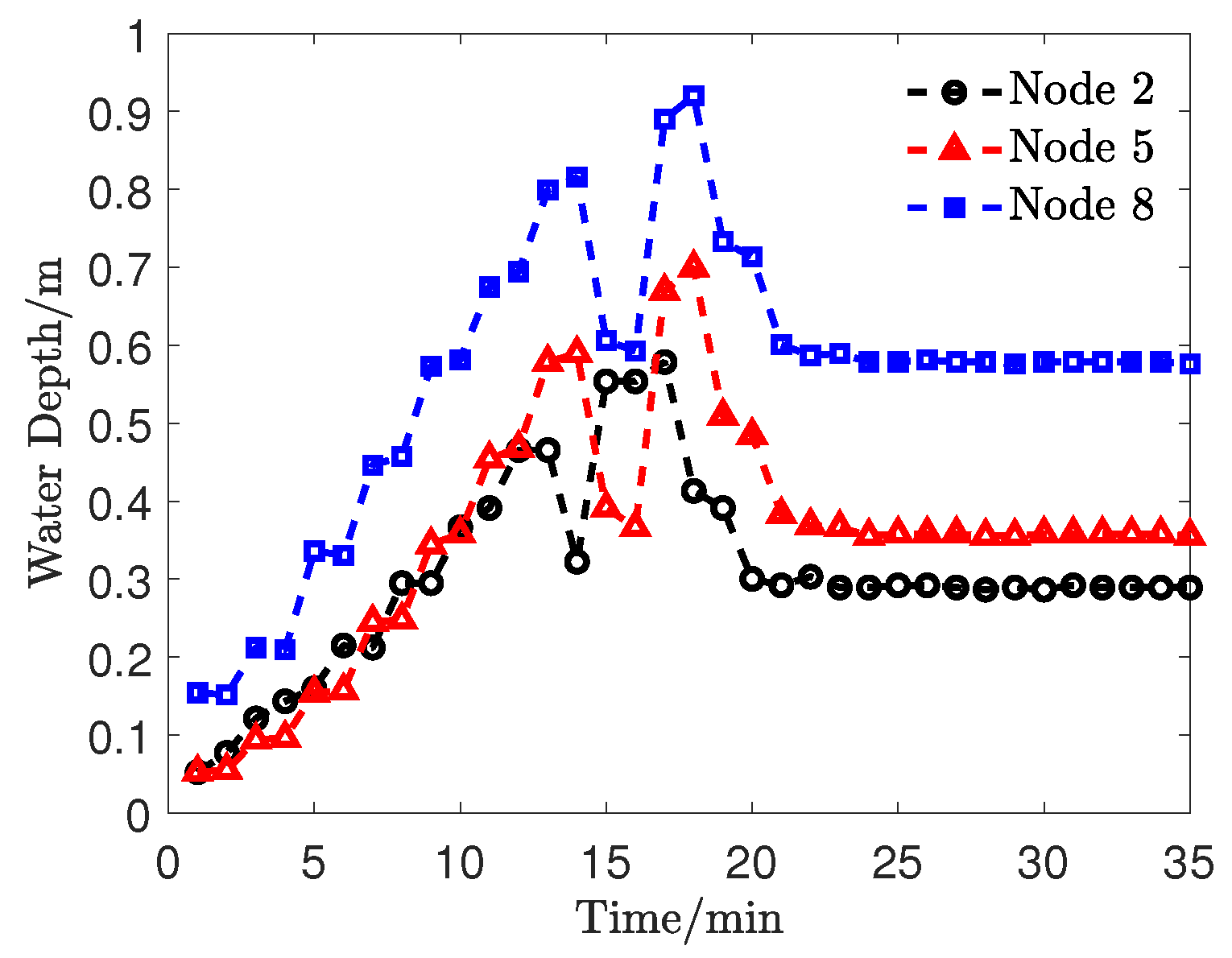
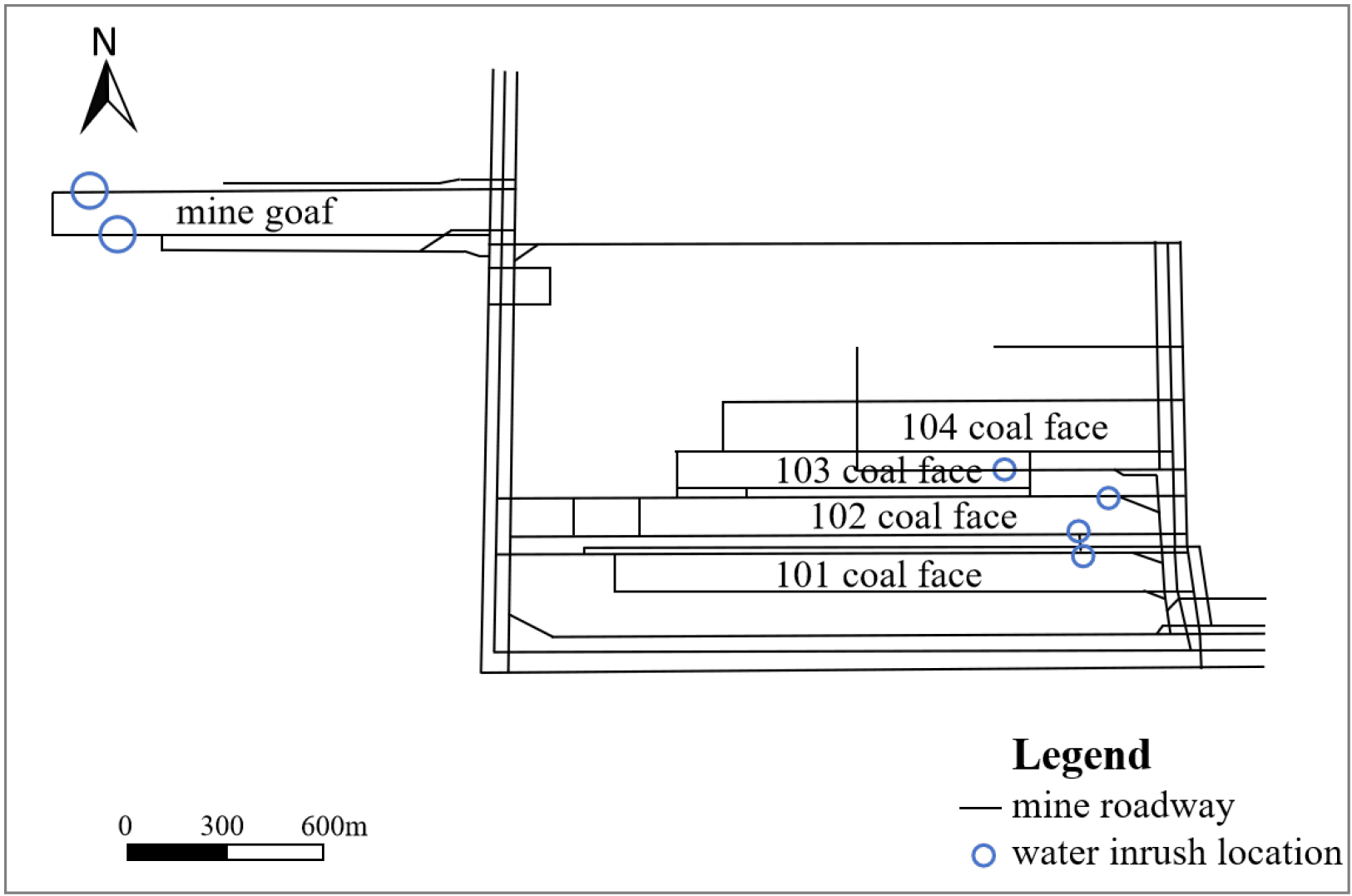
4.3. Actual Coal Mine with Multiple Water Inrush Points
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, G.; Pei, Z.; Shi, T. Unveiling unprecedented methane hotspots in China’s leading coal production hub: A satellite mapping revelation. Geophys. Res. Lett. 2024, 51, e2024GL109065. [Google Scholar] [CrossRef]
- Qian, Q.; Tian, Y.; Lin, L. Modelling the socio-economic impacts of coal production reduction: A macro provincial analysis of China. Energy Rep. 2024, 12, 4306. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, Y.; Liu, Z. Study on the characteristics of compound dust source pollution and foam dust suppression technology in coal mine anchor excavation production. Process Saf. Environ. Prot. 2024, 186, 593. [Google Scholar] [CrossRef]
- Liu, Q.; Shang, J.; Wang, J. Research on the evaluation of the operating effectiveness of the safety double prevention mechanism of coal mine enterprises based on matter-element extension. Process Saf. Environ. Prot. 2024, 185, 899. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, Q.; Xu, S. Early Warning of Coal Mine Production Environment Safety Risks Based on Multi-Source Information Feature Fusion. Sustainability 2025, 17, 2085. [Google Scholar] [CrossRef]
- Jia, L.; Wang, L.; Cheng, Y. Enhancing mine safety and mitigating greenhouse gas emissions: A comprehensive analysis of fluid migration dynamics in coalbed methane co-production. Process Saf. Environ. Prot. 2025, 196, 106933. [Google Scholar] [CrossRef]
- Wu, Q. Research progress, issues, and prospects of mine water prevention and control and resource utilization in China. J. China Coal Soc. 2014, 39, 795. [Google Scholar]
- Wang, X.; Xu, Z.; Sun, Y. Construction of multi-factor identification model for real-time monitoring and early warning of mine water inrush. Int. J. Min. Sci. Technol. 2021, 31, 853. [Google Scholar] [CrossRef]
- Zhang, Y.; Shu, P.; Zhai, F. Preparation and properties of hydrotalcite microcapsules for coal spontaneous combustion prevention. Process Saf. Environ. Prot. 2021, 152, 536. [Google Scholar] [CrossRef]
- Zhu, T.; Li, W.; Chen, W. Risk assessment of cretaceous water inrush in the Ordos basin based on the FAHP-EM. Water Policy 2021, 23, 1249. [Google Scholar] [CrossRef]
- Huang, C.; Dong, W.; Cao, Z. Water inrush mechanism of fault zone in Karst tunnel under fluid-solid coupling field considering effective stress. Geofluids 2022, 2022, 4205174. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Wang, X. Evaluation on the risk of water inrush due to roof bed separation based on improved set pair analysis-variable fuzzy sets. ACS Omega 2022, 7, 9430. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, J. A state-of-the-art review on rock seepage mechanism of water inrush disaster in coal mines. Int. J. Coal Sci. Technol. 2022, 9, 1. [Google Scholar] [CrossRef]
- Xiao, L.; Li, F.; Niu, C. Evaluation of water inrush hazard in coal seam roof based on the AHP-CRITIC composite weighted method. Energies 2022, 16, 114. [Google Scholar] [CrossRef]
- Yang, B.; Shi, W.; Yang, X. Nonlinear seepage erosion model of water inrush considering particle size distribution of Karst collapse column and its engineering applications. Sci. Rep. 2022, 12, 17078. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Wang, H.; Song, D. Analysis of the catastrophe mechanism and treatment countermeasures of a sudden water inrush disaster in a long and deeply buried tunnel in the Karst area. J. Perform. Constr. Facil. 2023, 37, 4349. [Google Scholar] [CrossRef]
- Gu, Q.; Huang, Z.; Li, S. An approach for water-inrush risk assessment of deep coal seam mining: A case study in Xinlongzhuang coal mine. Environ. Sci. Pollut. Res. Int. 2020, 27, 43163. [Google Scholar] [CrossRef]
- Hou, E.; Yao, X.; Che, X. Evaluation of the risk of water gushing (inrush) in aquifer of coal seam roof based on three diagram method: A case study in Hujiahe coal mine, China. Preprint 2020. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Yang, B. Assessing water and sand inrushes hazard reductions due to backfill mining by combining gis and entropy methods. Mine Water Environ. 2021, 40, 956. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, W.; Qian, J. Potential of hydraulic tomography in exploring the preferential flowpaths of water inrush in coal mine areas. J. Hydrol. 2021, 602, 126830. [Google Scholar] [CrossRef]
- Cai, M.; Zhu, X.; Liu, D. Mine water inrush rescue model based on optimized SPFA algorithm. Coal Geol. Explor. 2019, 47, 14. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Ye, Z. Development of a mixed reality assisted escape system for underground mine based on the mine water-inrush accident background. Tunn. Undergr. Space Technol. 2024, 143, 105471. [Google Scholar] [CrossRef]
- Xie, B.; Zhu, D.; Li, B. Research on optimal emergency evacuation path for mine water inrush based on dynamic D-K algorithm. Saf. Coal Mines 2024, 55, 192. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, B.; Xu, M. Design and implementation of an escape route planning system for deep mine water inrush based on graph structure. China Min. Mag. 2025, 34, 126. [Google Scholar] [CrossRef]
- Sun, J.; Zou, L.; Govender, N. Coupling SPH-DEM method for simulating the dynamic response of breakwater structures under severe free surface flow. Powder Technol. 2024, 441, 119805. [Google Scholar] [CrossRef]
- Luo, P.; Zhang, J. An immersed boundary method coupled non-hydrostatic model for free surface flow. Comput. Fluids 2024, 275, 106241. [Google Scholar] [CrossRef]
- Tao, Y.; Wright, D.; Lokhandwala, A. Impacts of rainfall spatiotemporal variability on pressurized flow conditions in urban drainage systems. J. Hydrol. 2025, 662, 133874. [Google Scholar] [CrossRef]
- Liu, X. Analysis and mitigation of post-bore noises in modeling mixed flows in closed conduits. Phys. Fluids 2025, 37, 4. [Google Scholar] [CrossRef]
- Lallem, P.; Luo, L.; Krafczyk, M. The lattice Boltzmann method for nearly incompressible flows. J. Comput. Phys. 2021, 431, 109713. [Google Scholar] [CrossRef]
- Mahdi, A.; Ali, S.; Amin, A. Analysis of radiative heat transfer in two-dimensional irregular geometries by developed immersed boundary-lattice Boltzmann method. J. Quant. Spectrosc. Radiat. Transf. 2022, 280, 108086. [Google Scholar] [CrossRef]
- Karimnejad, S.; Amiri, D.; He, F. Coupling immersed boundary and lattice Boltzmann method for modeling multi-body interactions subjected to pulsatile flow. Math. Methods Appl. Sci. 2023, 46, 6767. [Google Scholar] [CrossRef]
- Lin, R.; Lan, S.; Wu, X. Effect of perforated cracks on liquid water in microporous layers by lattice Boltzmann method. Renew. Energy 2024, 222, 119900. [Google Scholar] [CrossRef]
- Lee, H.; Hong, W.; Lee, Y. Experimental study on the influence of water depth on the evacuation speed of elderly people in flood conditions. Int. J. Disaster Risk Reduct. 2019, 39, 101198. [Google Scholar] [CrossRef]
- Wu, Q.; Du, Y.; Xu, H. Finding the earliest arrival path through a time-varying network for evacuation planning of mine water inrush. Saf. Sci. 2020, 130, 104836. [Google Scholar] [CrossRef]
- Mathilde, V.; Maciej, D.; Yoann, P. A theoretical and experimental study of a new algorithm for minimum cost flow in dynamic graphs. Discret. Appl. Math. 2021, 296, 203. [Google Scholar] [CrossRef]
- Li, X.; Yu, H.; Song, W. Investigation of pedestrian speed in formation evacuating in two specific water depths. Saf. Sci. 2024, 169, 106333. [Google Scholar] [CrossRef]
- Zhang, J. The Model-Calculus Subsystem of Short Track Speed Skating Tactical Simulation System. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2011. [Google Scholar]
- Jiang, Z. Artificial intelligence athlete training simulation system. Inf. Technol. 2022, 2, 95. [Google Scholar]
- Ibrahim, A.; Nnaji, C.; Namian, M. Investigating the impact of physical fatigue on construction workers’ situational awareness. Saf. Sci. 2023, 163, 106103. [Google Scholar] [CrossRef]
- Umer, W.; Yu, Y.; Afari, M. Towards automated physical fatigue monitoring and prediction among construction workers using physiological signals: An on-site study. Saf. Sci. 2023, 166, 106242. [Google Scholar] [CrossRef]
- Deng, K.; Hu, X.; Li, M. An extended social force model considering the psychological impact of the hazard source and its behavioural manifestation. Phys. A Stat. Mech. Its Appl. 2023, 627, 129127. [Google Scholar] [CrossRef]
- Ding, N.; Zhu, Y.; Liu, X. A modified social force model for crowd evacuation considering collision predicting behaviors. Appl. Math. Comput. 2024, 466, 128448. [Google Scholar] [CrossRef]





| Structure | 1-D Simu. | 3-D Simu. | Time Cost ↓ | Max. Error | Ave. Error |
|---|---|---|---|---|---|
| Roadway curve | 0.7 min | 125 min | 99.4% | 15.3% | 10.2% |
| Roadway junction | 1.5 min | 215 min | 99.3% | 14.7% | 8.34% |
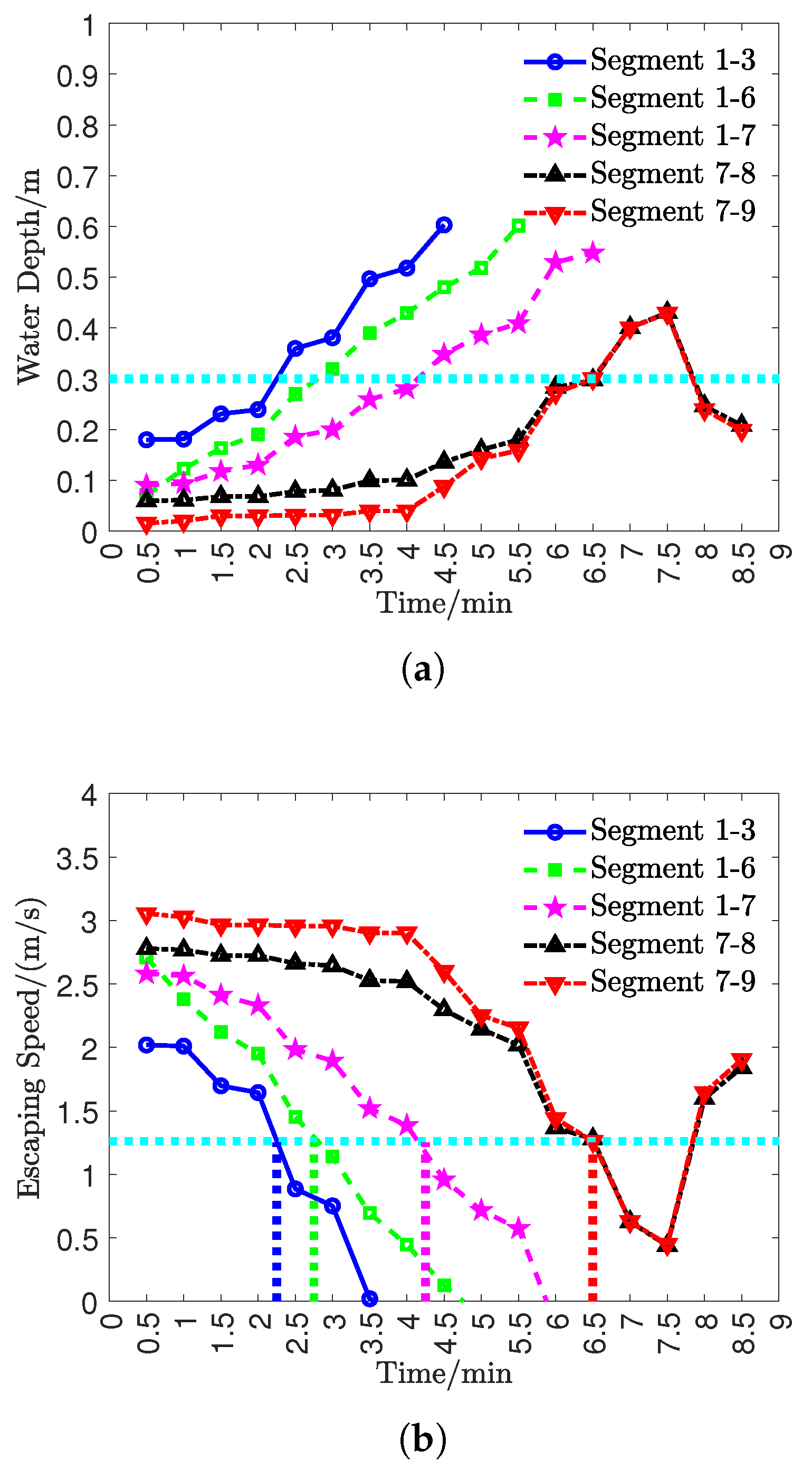
| Roadway | Length/m | Window Escape Time/min | Escape Time/min | Risk Score |
|---|---|---|---|---|
| 1-3 | 174 | 2.25 | 1.76 | 0.78 |
| 1-6 | 335 | 2.75 | 2.81 | 1.02 |
| 1-7 | 133 | 4.25 | 1.15 | 0.27 |
| 7-8 | 159 | 6.50 | 1.31 | 0.20 |
| 7-9 | 187 | 6.50 | 1.44 | 0.22 |
| Roadway | Length | Escape Time | Risk Score | Escape Speed | Rescue Priority |
|---|---|---|---|---|---|
| 1-2 | 2557 m | 29.9 min | 0.95 | 85.5 m/min | #9 |
| 1-4 | 4350 m | 50.1 min | 0.65 | 86.8 m/min | #11 |
| 2-5 | 3927 m | 45.7 min | 0.76 | 85.9 m/min | #10 |
| 4-5 | 3682 m | 44.9 min | 0.95 | 82.0 m/min | #8 |
| 4-7 | 89 m | 1.45 min | 0.12 | 61.3 m/min | #7 |
| 5-6 | 110 m | 2.35 min | 0.28 | 46.8 m/min | #3 |
| 5-8 | 143 m | 4.95 min | 0.83 | 28.8 m/min | #2 |
| 6-9 | 47 m | 2.60 min | 0.62 | 18.0 m/min | #1 |
| 7-8 | 55 m | 1.10 min | 0.39 | 50.0 m/min | #6 |
| 8-9 | 133 m | 2.76 min | 0.52 | 48.1 m/min | #4 |
| 9-13 | 64 m | 1.33 min | 0.43 | 48.1 m/min | #4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, L.; Liu, Z.; Wang, X.; Liu, W.; Wang, S.; Ma, L.; Fan, T.; Chen, W.; Hu, J. Dynamic Escape Path Optimization Model Study Based on Spatio-Temporal Evolution of Coal Mine Water Inrush. Processes 2025, 13, 3666. https://doi.org/10.3390/pr13113666
An L, Liu Z, Wang X, Liu W, Wang S, Ma L, Fan T, Chen W, Hu J. Dynamic Escape Path Optimization Model Study Based on Spatio-Temporal Evolution of Coal Mine Water Inrush. Processes. 2025; 13(11):3666. https://doi.org/10.3390/pr13113666
Chicago/Turabian StyleAn, Lin, Zaibing Liu, Xinmiao Wang, Wenming Liu, Shaolong Wang, Liang Ma, Tao Fan, Weiming Chen, and Junjie Hu. 2025. "Dynamic Escape Path Optimization Model Study Based on Spatio-Temporal Evolution of Coal Mine Water Inrush" Processes 13, no. 11: 3666. https://doi.org/10.3390/pr13113666
APA StyleAn, L., Liu, Z., Wang, X., Liu, W., Wang, S., Ma, L., Fan, T., Chen, W., & Hu, J. (2025). Dynamic Escape Path Optimization Model Study Based on Spatio-Temporal Evolution of Coal Mine Water Inrush. Processes, 13(11), 3666. https://doi.org/10.3390/pr13113666






