An Extended Rayleigh Equation for the Uniform Inviscid Plane Flow with Gas Bubble Crossflow
Abstract
1. Introduction
2. Equations of the Present Model
2.1. General Equations
2.2. Basic Equations for the Inviscid Bubbly Plane Flow
3. Formulation of Linear Stability Analysis
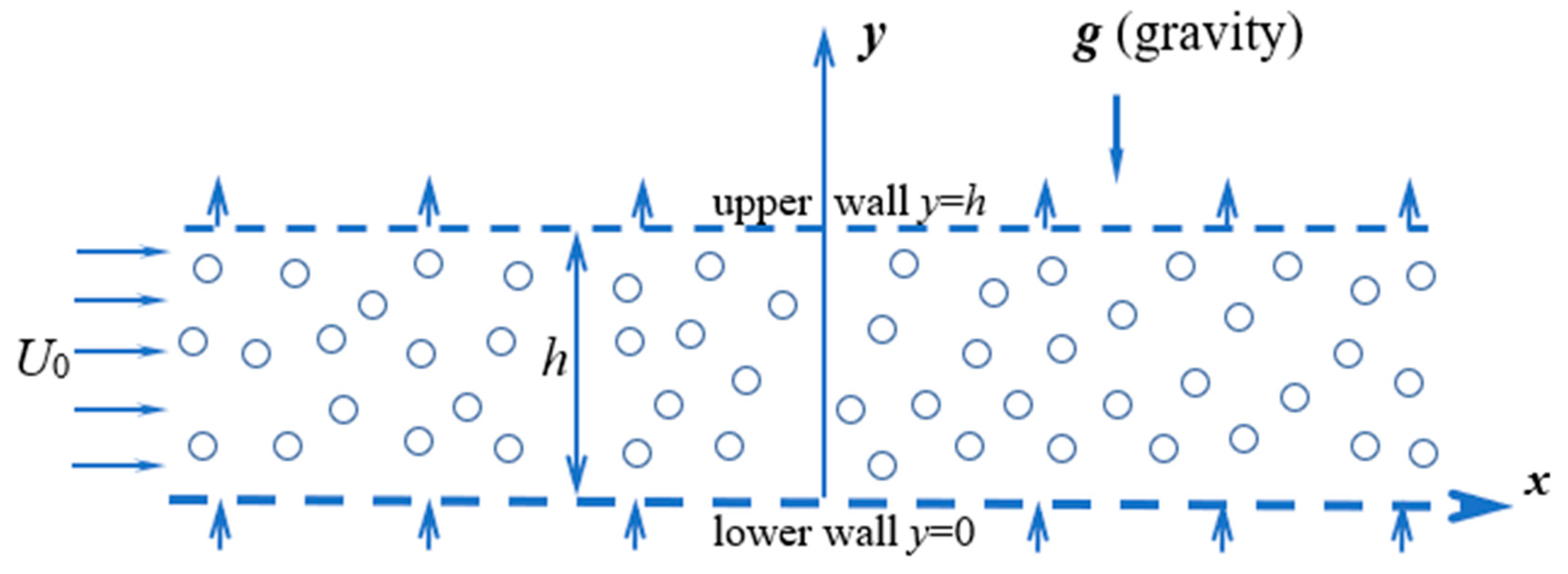
3.1. The Uniform Base Flow with Bubble Crossflow
3.2. An Extended Rayleigh Equation
4. Stability of the Bubble Crossflow-Driven Uniform Flow
4.1. The Case Without the Lift Force (CL = 0)
4.2. The Case with the Lift Force (CL > 0)
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Equations (1)–(5)
Appendix B. Derivation of Equation (20)
References
- Berman, A.S. Laminar Flow in Channel with Porous Walls. J. Appl. Phys. 1953, 24, 1232–1235. [Google Scholar] [CrossRef]
- Taylor, G. Fluid flow in regions bounded by porous surfaces. Proc. Royal. Soc. 1956, A234, 456–475. [Google Scholar]
- Hains, F.D. Stability of plane Couette-Poiseuille flow with uniform crossflow. Phys. Fluids 1971, 14, 1620–1623. [Google Scholar] [CrossRef]
- Sheppard, D.M. Hydrodynamic stability of the flow between parallel porous walls. Phys. Fluids 1972, 15, 241–244. [Google Scholar] [CrossRef]
- Dokoza, T.; Hennings de Lara, J.V.; Oberlack, M. Invariant scaling laws for plane Couette flow with wall-transpiration. Phys. Fluids 2024, 36, 035138. [Google Scholar] [CrossRef]
- Abdullah, M.; Park, G.I. Revisiting crossflow-based stabilization in channel flow. Phys. Rev. Fluids 2024, 9, 113901. [Google Scholar] [CrossRef]
- Sun, W.; Yalcin, A.; Oberlack, M. Stability of plane Couette flow with constant wall transpiration. Phys. Rev. Fluids 2024, 9, 053906. [Google Scholar] [CrossRef]
- Cuthbert, J.; Walton, A. Nonlinear coherent structures in 2D plane Couette flow with constant throughflow. J. Fluid Mech. 2025, 1002, A30. [Google Scholar] [CrossRef]
- Prakhar, S.; Prosperetti, A. Linear theory of particulate Rayleigh-Benard instability. Phys. Rev. Fluids 2021, 6, 083901. [Google Scholar] [CrossRef]
- Raza, S.; Feritas, R.B.; Alves, L.S.B.; Calzavarini, E.; Hirata, S.C. Stabilization of the Rayleigh-Benard system by injection of thermal inertial particles and bubbles. Phys. Fluids 2024, 36, 124141. [Google Scholar] [CrossRef]
- Raza, S.; Hirata, S.C.; Calzavarini, E. Impact of particle injection velocity on the stability of the particulate Rayleigh-Benard system. J. Fluid Mech. 2025, 1015, R2. [Google Scholar] [CrossRef]
- Dong, P.; Lu, B.; Gong, S.; Cheng, D. Experimental study of submerged gas jets in liquid cross flow. Exp. Therm. Fluid Sci. 2020, 112, 109998. [Google Scholar] [CrossRef]
- Li, W.; Meng, Z.; Sun, J.; Cai, W.; Hou, Y. Air horizontal jets into quiescent water. Nuclear Engng. Tech. 2023, 55, 2011–2017. [Google Scholar] [CrossRef]
- Wang, H.; Xu, Y.; Li, S.Y. Effects of orifice height and gas flow rate on underwater bubbles dynamics in crossflow. Int. J. Multiph. Flow 2025, 184, 105127. [Google Scholar] [CrossRef]
- Climent, E.; Magnaudet, J. Large-scale simulations of bubble-induced convection in a liquid layer. Phys. Rev. Let. 1999, 82, 4827–4830. [Google Scholar] [CrossRef]
- Ruzicka, M.C.; Thomas, N.H. Buoyancy-driven instability of bubbly layers: Analogy with thermal convection. Int. J. Multiph. Flow 2003, 29, 249–270. [Google Scholar] [CrossRef]
- Nakamura, K.; Yoshikawa, H.N.; Tasaka, Y.; Murai, Y. Linear stability analysis of bubble-induced convection in a horizontal liquid layer. Phys. Rev. E 2020, 102, 053102. [Google Scholar] [CrossRef]
- Nakamura, K.; Yoshikawa, H.N.; Tasaka, Y.; Murai, Y. Bifurcation analysis of bubble-induced convection in a horizontal liquid layer: Role of forces on bubbles. J. Fluid Mech. 2021, 923, R4. [Google Scholar] [CrossRef]
- Ru, C.Q. Particulate flow of a viscous fluid driven by a torsionally oscillating disk. J. Fluid Engng. (ASME) 2025, 147, 041302. [Google Scholar] [CrossRef]
- Ru, C.Q. On particle-modified velocity fields of particulate Taylor-Couette flow. Phys. Fluids 2024, 36, 093340. [Google Scholar] [CrossRef]
- Ru, C.Q. Steady radial diverging flow of a particle-laden fluid with particle migration. Fluids 2025, 10, 200. [Google Scholar] [CrossRef]
- Magnaudet, J.; Eames, I. The motion of high-Reynolds-Number bubbles. Annu. Rev. Fluid Mech. 2000, 32, 659–708. [Google Scholar] [CrossRef]
- Legendre, D.; Zenit, R. Gas bubble dynamics. Rev. Modern Phys. 2025, 97, 025001. [Google Scholar] [CrossRef]
- Saffman, P.G. On the stability of laminar flow of a dusty gas. J. Fluid Mech. 1962, 13, 120–128. [Google Scholar] [CrossRef]
- Michael, D.H. Kelvin-Helmholtz instability of a dusty gas. Proc. Camb. Phil. Soc. 1965, 61, 569–571. [Google Scholar] [CrossRef]
- Dimas, A.A.; Kiger, K.T. Linear instability of a particle-laden mixing layer with dynamic dispersed phase. Phys. Fluids 1998, 10, 253957. [Google Scholar] [CrossRef]
- Senatore, G.; Davis, S.; Jacobs, G. The effect of non-uniform mass loading on the linear, temporal development of particle-laden shear layers. Phys. Fluids 2015, 27, 033302. [Google Scholar] [CrossRef]
- Drazin, P.G.; Howard, L.N. Hydrodynamic stability of parallel flow of inviscid fluid. Adv. Appl. Mech. 1966, 9, 1–89. [Google Scholar]
- Legendre, D.; Magnaudet, J. The lift force on s spherical bubble in a viscous linear shear flow. J. Fluid Mech. 1998, 368, 81–126. [Google Scholar] [CrossRef]
- Tomiyama, A.; Tamai, H.; Zun, I.; Hosokawa, S. Transverse migration of single bubbles in simple shear flows. Chem. Engng. Sci. 2002, 57, 1849–1858. [Google Scholar] [CrossRef]
- Lucus, D.; Prasser, H.M.; Manera, P.A. Influence of the lift force on the stability of a bubble column. Chem. Engng. Sci. 2005, 60, 3609–3619. [Google Scholar] [CrossRef]
- Hidman, N.; Strom, H.; Sasic, S.; Sardina, G. The lift force on deformable and freely moving bubbles in linear shear flows. J. Fluid Mech. 2022, 952, A34. [Google Scholar] [CrossRef]
- Shi, P.; Climent, E.; Legendre, D. Lift force on a spherical droplet in a viscous linear shear flow. J. Fluid Mech. 2024, 1000, A88. [Google Scholar] [CrossRef]
- Mohammadi, M.H.; Sotiropoulos, F.; Brinkerhoff, J.R. Eulerian-Eulerian large eddy simulation of two-phase dilute bubbly flows. Chem. Engng. Sci. 2019, 208, 115156. [Google Scholar] [CrossRef]
- Beaumont, F.; Liger-Belair, G.; Polidori, G. Computational fluid dynamics (CFD) as a tool for investigating self-organized ascending bubble-driven flow patterns in champagne glasses. Foods 2020, 9, 972. [Google Scholar] [CrossRef] [PubMed]
- Fard, M.G.; Vernet, A.; Stiriba, Y.; Grau, X. Transient large-scale two-phase flow structures in a 3D bubble column reactor. Int. J. Multiphase Flow 2020, 127, 103236. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, W. Numerical simulation of bubbly jets in crossflow using OpenForm. Phys. Fluids 2022, 34, 123305. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Klinkenberg, J.; de Lange, H.C.; Brandt, L. Linear stability of particle laden flows: The influence of added mass, fluid acceleration and Basset history force. Mechanica 2014, 49, 811–827. [Google Scholar] [CrossRef]
- Boronin, S.A.; Osiptsov, A.N. Stability of a vertical Couette flow in the presence of settling particles. Phys. Fluids 2020, 32, 024104. [Google Scholar] [CrossRef]
- Li, H.; Ku, X.; Lin, J. Eulerian-Lagrangian simulation of inertial migration of particles in circular Couette flow. Phys. Fluids 2020, 32, 073308. [Google Scholar] [CrossRef]
- Ru, C.Q. Stability of plane parallel flow revisited for particle-fluid suspensions. J. Appl. Mech. (ASME) 2024, 91, 111005. [Google Scholar] [CrossRef]
- Ru, C.Q. On Kelvin-Helmholtz instability of particulate two-fluid flow. Acta Mech. Sin. 2025, 41, 324143. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ru, C.Q. An Extended Rayleigh Equation for the Uniform Inviscid Plane Flow with Gas Bubble Crossflow. Processes 2025, 13, 3665. https://doi.org/10.3390/pr13113665
Ru CQ. An Extended Rayleigh Equation for the Uniform Inviscid Plane Flow with Gas Bubble Crossflow. Processes. 2025; 13(11):3665. https://doi.org/10.3390/pr13113665
Chicago/Turabian StyleRu, C. Q. 2025. "An Extended Rayleigh Equation for the Uniform Inviscid Plane Flow with Gas Bubble Crossflow" Processes 13, no. 11: 3665. https://doi.org/10.3390/pr13113665
APA StyleRu, C. Q. (2025). An Extended Rayleigh Equation for the Uniform Inviscid Plane Flow with Gas Bubble Crossflow. Processes, 13(11), 3665. https://doi.org/10.3390/pr13113665





