An Extended Rayleigh Equation for the Uniform Inviscid Plane Flow with Gas Bubble Crossflow

Abstract

The classic second-order Rayleigh equation governs the linear stability of single-phase inviscid plane flows, and its extension to two-phase inviscid plane flows with a crossflow of another fluid remains to be investigated. The present work studies the linear stability of steady uniform inviscid two-phase flow in a horizontal channel with gas bubbles injected from the lower wall and removed from the upper wall. An extended fourth-order Rayleigh equation with constant coefficients is derived for the linear stability of the two-phase uniform inviscid plane flow with the bubble crossflow injected at the bubble terminal velocity. Our analytical results show that the uniform inviscid plane flow driven by the bubble crossflow is linearly unstable with rapidly growing disturbances in the absence of the lift force. On the other hand, when the positive lift force coefficient is nearly equal to the added mass coefficient, the uniform inviscid plane flow driven by the bubble crossflow is linearly stable to the admissible disturbances consistent with the bubble-injection boundary conditions. These analytical results reveal the destabilizing effect of the bubble crossflow and confirm the stabilizing effect of the positive lift force on the inviscid plane flows, which could stimulate further research interest in the qualitatively different roles of the bubble crossflow and the lift force in the stability of inviscid plane flows as compared to viscous plane flows.

1. Introduction

Fluid flow in a channel of permeable porous walls is a topic of fundamental and practical significance [1,2]. Extensive research effort has been continuously made to investigate the effect of a uniform crossflow on the stability of plane flow in a channel with two parallel porous walls, see e.g., the earlier works [3,4] and recent works [5,6,7,8]. Remarkably, these studies have led to an elegant modified Orr–Sommerfeld equation for the single-phase plane Poiseuille/Couette flow due to a uniform crossflow of the same fluid. However, such a modified Orr–Sommerfeld equation cannot be extended to two-phase viscous plane flows in the presence of the crossflow of another fluid.

Recently, the effect of solid–particle crossflow on the stability of two-phase particulate flow has been studied in the literature. For example, Prakhar and Prosperetti [9] studied the effect of solid–particle crossflow on the particulate Rayleigh–Bénard (pRB) flow stability of a fluid layer in which heavier particles are injected from the upper plane at the particle terminal velocity (determined by the force balance between the Stokes drag and the buoyancy) and removed from the lower plane. Interestingly, their results showed that the heavier particles injected at their terminal velocity have a stabilizing effect on the pRB flow as compared to the particle-free system. Raza et al. [10] further studied the pRB flow with the lighter particles injected from the lower plane at the particle terminal velocity and removed from the upper plane, and confirmed that the lighter particles injected at their terminal velocity have a stabilizing effect on the pRB flow. Furthermore, Raza et al. [11] showed that the heavier (lighter) particles injected from above (below) at an injection velocity lower than their terminal velocity stabilize (destabilize) the pRB flow of the horizontal fluid layer.

Gas crossflow is commonly involved in many industrial two-phase gas–liquid flow problems [12,13,14], and the buoyancy-driven gas bubble crossflow in a quiescent liquid has been investigated in recent literature [15,16,17,18]. To mention a few, for instance, a large-scale simulation of bubble-induced pRB flow instability in a quiescent liquid layer was conducted by Climent & Magnaudet [15]. More recently, Nakamura et al. [17] studied the stability of the non-uniform flow in a quiescent fluid layer between two horizontal planes driven by the bubbles injected from the lower plane at an injection velocity lower than the bubble terminal velocity. Consistent with the results of Raza et al. [11] on the destabilizing effect on the pRB flow instability of lighter particles injected at the sub-terminal velocity, Nakamura et al. [17] showed that the bubble crossflow injected at the sub-terminal velocity triggers the instability of the non-uniform bubbly flow of the quiescent liquid layer.

Almost all of the above-mentioned studies (including Raza et al. [10,11] and Nakamura et al. [17,18], by which the present work is inspired) have focused on the crossflow-driven viscous particulate or bubbly flows, and extensive numerical computation is always required for the related flow stability analysis. In particular, explicit analytical results, such as a modified Orr–Sommerfeld equation for the two-phase viscous plane flows with a crossflow of another fluid, cannot be achieved. To the best of our knowledge, explicit mathematical analysis on the stability of the crossflow-driven two-phase particulate or bubbly inviscid flow is rarely reported in the literature. More specifically, even for the simplest uniform inviscid plane flow, the influence of a uniform gas bubble crossflow on the Rayleigh equation, which governs the linear stability of inviscid plane flows, is to be clarified.

In view of the fundamental role of the Rayleigh equation in the linear stability of inviscid plane flows, the present work aims at developing an extended Rayleigh equation for the linear stability of the uniform inviscid plane flow in a horizontal channel driven by a uniform gas bubble crossflow injected from the lower wall at the bubble terminal velocity. The equations of the present model are formulated in Section 2, and the uniform base flow driven by the bubble crossflow and its linear stability are formulated in Section 3. An extended fourth-order Rayleigh equation with constant coefficient is derived for the linear stability of the uniform two-phase inviscid plane flow driven by the bubble crossflow injected at the bubble terminal velocity, and detailed analytical results are given in Section 4 with an emphasis on the stabilizing effect of the positive lift force on the flow stability. Finally, the main results are summarized in Section 5.

2. Equations of the Present Model

In the present work, the linear stability of the uniform inviscid plane flow driven by bubble crossflow injected from the lower wall will be studied using the two-phase model developed in the author’s recent works (see the Stokes drag-based model [19], and the upgraded models with the added mass and the lift force [20,21], respectively), as explained in Appendix A.

2.1. General Equations

As illustrated in Appendix A, for a viscous liquid with small non-deformable spherical gas bubbles, because the liquid-to-gas density ratio $\left({\rho }_{\mathrm{f}}/{\rho }_{\mathrm{S}}\right)\propto {10}^3$ and the mass of bubbles is ignored compared to the liquid, it follows from Equation (A3) of Appendix A that the hydrodynamics of an incompressible gas–liquid suspension is governed by the modified form of Navier–Stokes equations.

$$\rho {\displaystyle \frac{\mathrm{d}{\mathit{v}}_{\mathrm{m}}}{\mathrm{d}t}}=\rho \left[{\displaystyle \frac{\partial {\mathit{v}}_{\mathrm{m}}}{\partial t}}+\left({\mathit{v}}_{\mathrm{m}}·\nabla \right){\mathit{v}}_{\mathrm{m}}\right]=-\nabla p+\nabla ·\left(\mu \left[\nabla \mathit{v}+{\left(\nabla \mathit{v}\right)}^{\mathrm{T}}\right]\right)+{\rho }_{\mathrm{f}}\left(1-\delta \right)\mathit{g},$$

(1)

$$\mathrm{d}\mathrm{i}\mathrm{v}\mathit{v}=0,$$

(2)

$${\displaystyle \frac{\partial }{\partial t}}\rho +\mathrm{d}\mathrm{i}\mathrm{v}\left[\rho {\mathit{v}}_{\mathrm{m}}\right]=0.$$

(3)

Here ρ_f and ρ_S are the densities of the liquid and spherical bubbles, x and t are the vectorial spatial coordinates and time, p(x, t) is the pressure field of the suspension, v(x, t) is the volume-averaged velocity field of the suspension given by $\mathit{v}=\delta {\mathit{v}}_{\mathrm{S}}+{\mathit{v}}_{\mathrm{f}}\left(1-\delta \right)$, v_m(x, t) is the mass-averaged velocity field of the suspension defined by $\rho {\mathit{v}}_{\mathrm{m}}=\delta {\rho }_{\mathrm{S}}{\mathit{v}}_{\mathrm{S}}+{\rho }_{\mathrm{f}}\left(1-\delta \right){\mathit{v}}_{\mathrm{f}}$ with (A4) in Appendix A, where v_S(x, t) and v_f(x, t) are the velocity field of spherical bubbles and the liquid, respectively, the effective density ρ (per unit volume) of the suspension is given by $\rho ={\rho }_{\mathrm{S}}\delta +{\rho }_{\mathrm{f}}(1-\delta )$ with (A2) in Appendix A. Here, δ is the volume fraction of bubbles, μ is the effective viscosity of the suspension, which can be estimated by the formula $\mu ={\mu }_{\mathrm{f}}\left(1+k\delta \right)$ in the dilute limit with the constant k and the viscosity μ_f of the fluid, and $\nabla$ and ${\nabla }^2$ are the gradient and Laplacian operators.

For a gas–liquid suspension with $\left({\rho }_{\mathrm{f}}/{\rho }_{\mathrm{S}}\right)\propto {10}^3$, with the ignored mass of bubbles, (A10) gives

$${\mathit{v}}_{\mathrm{m}}+a{\displaystyle \frac{\mathrm{d}{\mathit{v}}_{\mathrm{m}}}{\mathrm{d}t}}+C_L{\displaystyle \frac{2{\rho r}_{\mathrm{S}}^2}{9\mu }}\left[{\mathit{v}}_{\mathrm{m}}\times \left(\nabla \times \mathit{v}\right)\right]=\mathit{v}+b{\displaystyle \frac{\mathrm{d}\mathit{v}}{\mathrm{d}t}}+C_L{\displaystyle \frac{2\rho r_{\mathrm{S}}^2}{9\mu }}\mathit{v}\times \left(\nabla \times \mathit{v}\right)+{\displaystyle \frac{2\delta {\rho }_{\mathrm{f}}{r}_{\mathrm{S}}^2}{9\mu }}\mathit{g},$$

(4)

It follows from (A11) that

$$a=C_a{\displaystyle \frac{2\rho r_{\mathrm{S}}^2}{9\mu }},b=a\left(1-{\displaystyle \frac{\delta }{C_a(1-\delta )}}\right),\rho =\left(1-\delta \right){\rho }_{\mathrm{f}}.$$

(5)

Here, C_a and C_L are the added mass coefficient and the lift force coefficient, respectively, d/dt denotes the material derivative of the associated velocity field along its own streamlines, r_S is the radius of the spherical bubbles, the coefficients a and b are derived by considering the Stokes drag, the forces due to added mass and flow acceleration, the lift force and the buoyancy, as explained in Appendix A, which are applicable to gas bubbles (see e.g., Equation (11) in Magnaudet & Eames [22], or Equations (92)–(95) in Legendre & Zenit [23]).

Here, it should be stated that the Stokes drag-based models (μ ≠ 0 included in Equation (5) but not in the Navier–Stokes equations Equation (1)) of particle-laden inviscid fluids have been widely adopted to study linear stability of inviscid particulate flows [24,25,26,27]. For instance, the inviscid version of the Stokes drag-based Saffman model [24] was used by Michael [25] to study Kelvin-Helmholtz instability of particle-laden inviscid flows. Although the fluid viscosity can play an essential role in many flow stability problems, as highlighted in the now-classic reference [28], the study of inviscid flow stability is of fundamental and practical relevance, particularly for the flows away from the solid walls. Therefore, as stated above, it is of specific interest to investigate the influence of a uniform bubble crossflow on the Rayleigh equation, which governs the linear stability of plane inviscid flows.

2.2. Basic Equations for the Inviscid Bubbly Plane Flow

For the 2D inviscid plane flow in the x-y plane with μ = 0 in Equation (1), Equations (1)–(3) give

$${\displaystyle \frac{\partial u_{\mathrm{m}}}{\partial t}}+u_{\mathrm{m}}{\displaystyle \frac{\partial u_{\mathrm{m}}}{\partial x}}+v_{\mathrm{m}}{\displaystyle \frac{\partial u_{\mathrm{m}}}{\partial y}}=-\left({\displaystyle \frac{1}{\rho }}\right){\displaystyle \frac{\partial p}{\partial x}},$$

(6a)

$${{\displaystyle \frac{\partial v_{\mathrm{m}}}{\partial t}}+u}_{\mathrm{m}}{\displaystyle \frac{\partial v_{\mathrm{m}}}{\partial x}}+v_{\mathrm{m}}{\displaystyle \frac{\partial v_{\mathrm{m}}}{\partial y}}=-\left({\displaystyle \frac{1}{\rho }}\right){\displaystyle \frac{\partial p}{\partial y}}-g,$$

(6b)

$${\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}=0,$$

(6c)

$${\displaystyle \frac{\partial \rho }{\partial t}}+u_{\mathrm{m}}{\displaystyle \frac{\partial \rho }{\partial x}}+v_{\mathrm{m}}{\displaystyle \frac{\partial \rho }{\partial y}}+\rho \left({\displaystyle \frac{\partial u_{\mathrm{m}}}{\partial x}}+{\displaystyle \frac{\partial v_{\mathrm{m}}}{\partial y}}\right)=0.$$

(6d)

Here (u_m, v_m) are the x- and y-components of the velocity field v_m(x, t), while (u, v) are the x- and y-components of the velocity field v(x, t). Please note that

$$\left(\nabla \times \mathit{v}\right)=\left[\begin{array}{c}0\\ 0\\ v_{,x}-u_{,y}\end{array}\right],\mathit{v}\times \left(\nabla \times \mathit{v}\right)=\left[\begin{array}{c}v\left(v_{,x}-u_{,y}\right)\\ -u\left(v_{,x}-u_{,y}\right)\\ 0\end{array}\right],{\mathit{v}}_{\mathrm{m}}\times \left(\nabla \times \mathit{v}\right)=\left[\begin{array}{c}{v}_{\mathrm{m}}\left(v_{,x}-u_{,y}\right)\\ -u_{\mathrm{m}}\left(v_{,x}-u_{,y}\right)\\ 0\end{array}\right],$$

(7)

the v_m-v relations (4) give

$$\begin{gathered} u_{\mathrm{m}}+a\left({\displaystyle \frac{\partial u_{\mathrm{m}}}{\partial t}}+u_{\mathrm{m}}{\displaystyle \frac{\partial u_{\mathrm{m}}}{\partial x}}+v_{\mathrm{m}}{\displaystyle \frac{\partial u_{\mathrm{m}}}{\partial y}}\right)+C_L{\displaystyle \frac{2\rho r_{\mathrm{S}}^2}{9\mu }}{v}_{\mathrm{m}}\left(v_{,x}-u_{,y}\right) \\ =u+b\left({\displaystyle \frac{\partial u}{\partial t}}+u{\displaystyle \frac{\partial u}{\partial x}}+v{\displaystyle \frac{\partial u}{\partial y}}\right)+C_L{\displaystyle \frac{2\rho r_{\mathrm{S}}^2}{9\mu }}v\left(v_{,x}-u_{,y}\right), \end{gathered}$$

(8a)

$$\begin{gathered} v_{\mathrm{m}}+a\left({{\displaystyle \frac{\partial v_{\mathrm{m}}}{\partial t}}+u}_{\mathrm{m}}{\displaystyle \frac{\partial v_{\mathrm{m}}}{\partial x}}+v_{\mathrm{m}}{\displaystyle \frac{\partial v_{\mathrm{m}}}{\partial y}}\right)-C_L{\displaystyle \frac{2\rho r_{\mathrm{S}}^2}{9\mu }}{u}_{\mathrm{m}}\left(v_{,x}-u_{,y}\right) \\ =v+b\left({\displaystyle \frac{\partial v}{\partial t}}+u{\displaystyle \frac{\partial v}{\partial x}}+v{\displaystyle \frac{\partial v}{\partial y}}\right)-C_L{\displaystyle \frac{2\rho r_{\mathrm{S}}^2}{9\mu }}u\left(v_{,x}-u_{,y}\right)-{\displaystyle \frac{2\delta {\rho }_{\mathrm{f}}{r}_{\mathrm{S}}^2}{9\mu }}g, \end{gathered}$$

(8b)

where the comma denotes the partial derivative.

3. Formulation of Linear Stability Analysis

Let us focus on the uniform inviscid plane flow in a horizontal channel driven by the bubbles injected from the permeable lower wall at the bubble terminal velocity and removed from the upper permeable wall, as shown in Figure 1 below, where U₀ is the constant velocity in the horizontal x-direction.

Similar to some known related works (see e.g., [17]), the present problem is defined by three independent injection conditions at the bottom y = 0: two injection velocities (v_inS = v_∞, v_inf = 0) of the spherical bubbles and the liquid, respectively, and the volume fraction δ_in = ε of the injected bubbles at y = 0, where the bubble terminal velocity v_∞ is defined by (10) below. In particular, the present work considers the gas bubble injection alone, and therefore, the liquid injection velocity is assumed to be zero (v_inf = 0).

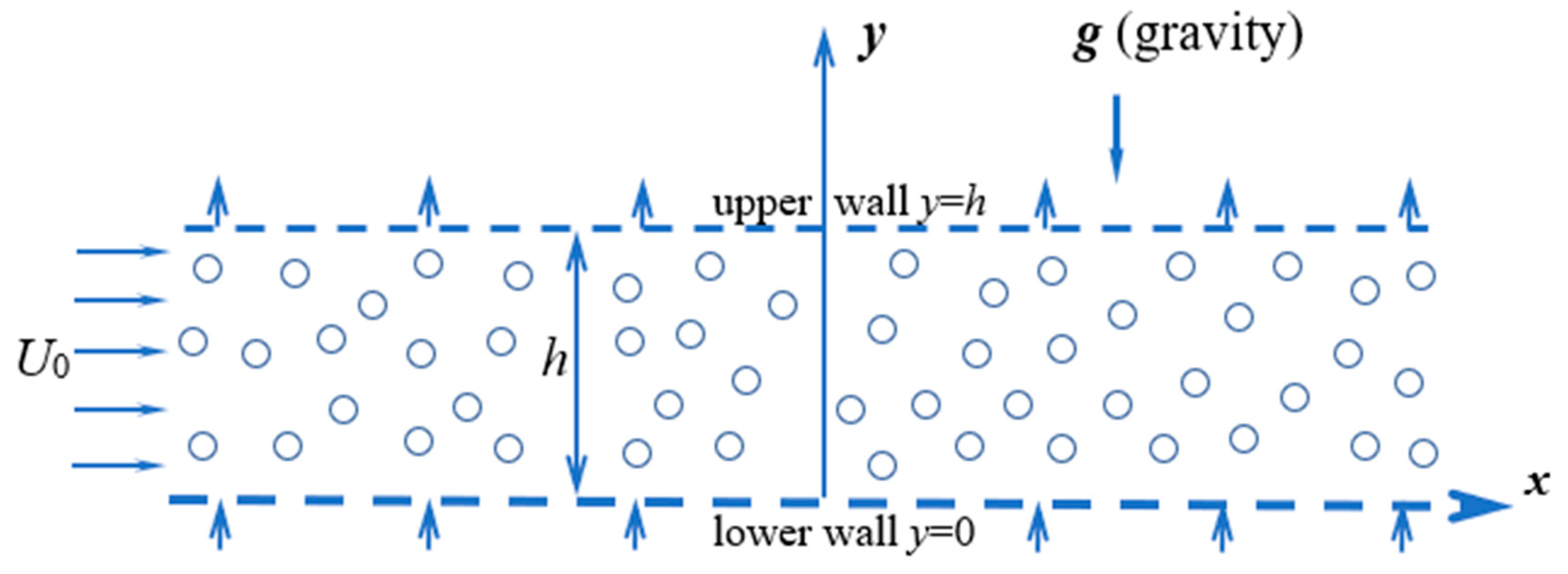
3.1. The Uniform Base Flow with Bubble Crossflow

It is easily verified that the uniform base flow given below meets all Equations (6a–d) and (8a,b)

$$u=u_{\mathrm{m}}=U_0,v=v_0=\epsilon v_{\mathrm{\infty }},v_{\mathrm{m}}=0,\delta =\epsilon ,p=p_0+p_0\left(y\right).$$

(9)

In particular,

$$v_0={\displaystyle \frac{2\epsilon {\rho }_{\mathrm{f}}{r}_{\mathrm{S}}^2}{9{\mu }_0}}g,{v_{\mathrm{S}}=v_{\infty },v}_{\mathrm{S}}-v={\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}g,v_{\infty }\equiv {\displaystyle \frac{2{\rho }_{\mathrm{f}}{r}_{\mathrm{S}}^2}{9{\mu }_0}}g,$$

(10)

where vs is the actual velocity of spherical bubbles, and

$${\rho }_0={\rho }_{\mathrm{f}}\left(1-\epsilon \right),{\mu }_0={\mu }_{\mathrm{f}}\left(1+k\epsilon \right),p_0\left(y\right)=-{\rho }_{\mathrm{f}}\left(1-\epsilon \right)gy,a_0=C_a{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}},b_0=a_0\left(1-{\displaystyle \frac{\epsilon }{C_a(1-\epsilon )}}\right).$$

(11)

Specifically, the actual velocity of bubbles of the uniform base flow is $v_{\infty }={\displaystyle \frac{2{\rho }_{\mathrm{f}}{r}_{\mathrm{S}}^2}{9{\mu }_0}}g$, while the relative velocity (v_S-v) of bubbles with respect to the suspension (moving at the velocity v₀) is ${\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}g$, where ρ = (1 − δ)ρ_f is the suspension’s effective density, as explained in (A7) of the Appendix A.

3.2. An Extended Rayleigh Equation

Let us apply the present model with Equations (6a–d) and (8a,b) to study the linear stability of the uniform inviscid flow (9). Similar to some known related works [9,10,17], let us consider 2D disturbances of the form shown below

$$\begin{gathered} \mathit{v}=\left[\begin{array}{c}u\\ v\\ 0\end{array}\right]=\mathit{U}+\mathrm{R}\mathrm{e}\left[\mathit{u}{e}^{i\alpha \left(x-ct\right)}\right],{\mathit{v}}_m=\left[\begin{array}{c}{u}_{\mathrm{m}}\\ v_{\mathrm{m}}\\ 0\end{array}\right]={\mathit{U}}_{\mathrm{m}}+\mathrm{R}\mathrm{e}\left[\mathit{w}{e}^{i\alpha \left(x-ct\right)}\right], \\ p=p_0+{\rho }_0\left(\mathrm{y}\right)+\mathrm{R}\mathrm{e}\left[p\left(y\right)e^{i\alpha \left(x-ct\right)}\right],\delta =\epsilon +\mathrm{R}\mathrm{e}\left[\delta \left(y\right)e^{i\alpha \left(x-ct\right)}\right], \end{gathered}$$

(12)

where (u, w) are complex-valued and associated with the disturbed velocity fields v(x, t) and v_m(x, t), respectively, p(y) and δ(y) are complex-valued and associated with the disturbed pressure field and the bubble volumne fraction, respectively, α is the (non-negative) wave-number, and c is the (complex) wave-speed, and (u, w, U, U_m) are of the form

$$\mathit{u}=\left[\begin{array}{c}{u}_1\left(\mathrm{y}\right)\\ u_2\left(\mathrm{y}\right)\\ 0\end{array}\right],\mathit{w}=\left[\begin{array}{c}{w}_1\left(\mathrm{y}\right)\\ w_2\left(\mathrm{y}\right)\\ 0\end{array}\right],\mathit{U}\left(\mathrm{y}\right)=\left[\begin{array}{c}{U}_0\\ v_0\\ 0\end{array}\right],{\mathit{U}}_{\mathrm{m}}\left(\mathrm{y}\right)=\left[\begin{array}{c}{U}_0\\ 0\\ 0\end{array}\right].$$

(13)

It is seen from (12) that the product (-iαc) determines the growth rate of the disturbances. Here, it is stated that the growth rate (-iαc) should be understood as a parameter independent of the wave-number α. For instance, the growth rate (-iαc) can be non-zero even when α approaches zero.

It is verified from (6a,b) that the linearized equations for infinitesimal disturbances u and w, and p are

$${\rho }_0\left[i\alpha w_1\left(U_0-c\right)\right]=-i\alpha p,{\rho }_0\left[i\alpha w_2\left(U_0-c\right)\right]=-p_{,y},$$

(14)

Eliminating p(y) in (14), we have

$$w_{1,y}=i\alpha w_2.$$

(15)

And the linearized equations for infinitesimal disturbances u and w of (8a,b) give

$$w_1+a_0\left[i\alpha w_1\left(U_0-c\right)\right]=u_1+b_0\left[i\alpha u_1\left(U_0-c\right)+{v_{0}u}_{1,y}\right]+C_L{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}{v}_0\left(i\alpha u_2-u_{1,y}\right),$$

(16a)

$$w_2+a_0\left[i\alpha w_2\left(U_0-c\right)\right]=u_2+b_0\left[i\alpha u_2\left(U_0-c\right)+{v_{0}u}_{2,y}\right]-{\displaystyle \frac{2\delta {\rho }_{\mathrm{f}}{r}_{\mathrm{S}}^2}{9{\mu }_0}}g.$$

(16b)

It follows from (16a,b) that

$$w_2={\displaystyle \frac{\left[1+b_0\alpha i\left(U_0-c\right)\right]u_2}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}}+{\displaystyle \frac{b_0{v_{0}u}_{2,y}}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}}-{\displaystyle \frac{v_{\infty }\delta \left(y\right)}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}},$$

(17a)

$$w_1={\displaystyle \frac{{v_{0}u}_{1,y}}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}}\left(b_0-C_L{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}\right)+{\displaystyle \frac{\left[1+b_0\alpha i\left(U_0-c\right)\right]u_1}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}}+{i\alpha C}_L{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0\left[1+a_0\alpha i\left(U_0-c\right)\right]}}{v}_0{u}_2.$$

(17b)

Furthermore, it follows from (6c,d) that

$$i\alpha u_1=-u_{2,y}.$$

(18)

$$\left(c-U_0\right)\left(i\alpha \delta \right){\rho }_{\mathrm{f}}+{\rho }_0\left(i\alpha w_1+w_{2,y}\right)=0.$$

(19)

Thus, we have five Equations (15), (17a,b), (18), and (19) for the five unknown functions (w₁, w₂, u₁, u₂, δ) of the coordinate y.

Using (15,17b,18,19) to substitute (w₁, w₂, u₁, δ) into (17a), an extended 4th-order Rayleigh equation with constant coefficients for u₂(y) is obtained (the detailed derivation is given in Appendix B)

$$\left[\begin{array}{c}\left({\displaystyle \frac{2r_{\mathrm{S}}^{2}g{\rho }_0}{9{\mu }_0}}\right){\displaystyle \frac{v_0}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}}\left(b_0-C_L{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}\right){\displaystyle \frac{d^2}{d{y}^2}}\\ +\left(i\alpha v_0\left(U_0-c\right)\left(b_0-C_L{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}\right)+{\displaystyle \frac{2r_{\mathrm{S}}^{2}g{\rho }_0}{9{\mu }_0}}{\displaystyle \frac{\left[1+b_0\alpha i\left(U_0-c\right)\right]}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}}\right){\displaystyle \frac{d}{dy}}\\ +i\alpha \left(U_0-c\right)\left[1+b_0\alpha i\left(U_0-c\right)\right]+{\alpha }^2{\displaystyle \frac{2r_{\mathrm{S}}^{2}g{\rho }_0}{9{\mu }_0}}\left(C_L{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}\right){\displaystyle \frac{v_0}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}}\end{array}\right]\left(u_{2,yy}-{\alpha }^2{u}_2\right)=0.$$

(20)

Clearly, in the absence of the bubble injection, Equation (20) reduces to the classical second-order Rayleigh equation for the special case of constant mean velocity U₀ [28].

For the present bubble crossflow problem, the admissible disturbances should be consistent with the given injection conditions, and therefore, they will not change the three boundary conditions of bubble injection for the normal velocities of the bubbles and the liquid and the volume fraction of the bubbles at the lower wall y = 0. Thus, the disturbed normal velocities of the bubbles and the liquid associated with the disturbances must vanish at y = 0, and also the disturbed volume fraction of bubbles must vanish at y = 0 too. In view of (A2) and (A4) of Appendix A, we have

$${\left.u_2\right|}_{y=0}=0,{\left.w_2\right|}_{y=0}=0,{\left.\delta \right|}_{y=0}=0,$$

(21)

In addition, for the present inviscid flow problem with gas-permeable walls, the normal component of the disturbed velocity field of the suspension or the liquid must be zero, and consequently, the normal component u₂ or w₂ should be assumed to be zero at the upper wall y = h, which gives

$${\left.u_2\right|}_{y=h}=0\mathrm{o}\mathrm{r} {\left.w_2\right|}_{y=h}=0.$$

(22)

Thus, the growth rate (-iαc) of the disturbances is determined by Equation (20) with the four homogeneous boundary conditions (21), (22), and the linear stability of the uniform base flow is determined by the sign of the real part of (-iαc). The base flow is linearly unstable when and only when the real part of (-iαc) becomes positive.

4. Stability of the Bubble Crossflow-Driven Uniform Flow

Let us now study the linear stability of the uniform base flow (9) driven by the bubble crossflow injected at the bubble terminal velocity. To highlight the role of the lift force in the flow stability, we shall study the two cases without and with the lift force, respectively.

4.1. The Case Without the Lift Force (C_L = 0)

The lift force on gas bubbles in a liquid is extremely sensitive to the size and deformability of gas bubbles and various flow conditions, and the lift coefficient C_L can change its sign from positive to negative [29,30,31,32,33]. In view of the uncertainty of the lift coefficient C_L, some authors have assumed C_L = 0 in some specific gas–liquid flows [34,35,36,37]. In this section, we shall first study the linear stability of the uniform inviscid base flow (9) without considering the lift force.

When the lift force is absent with C_L = 0, it is verified from (20) that the four eigenvalues of (20) are (±α) and (λ₁, λ₂) given by

$${\lambda }_1={\displaystyle \frac{-\left[1+b_0\alpha i\left(U_0-c\right)\right]}{v_0{b}_0}},{\lambda }_2={\displaystyle \frac{-i\alpha \left(U_0-c\right)\left[1+a_0\alpha i\left(U_0-c\right)\right]}{\left(\frac{2{{\rho }_{0}r}_{\mathrm{S}}^{2}g}{9{\mu }_0}\right)}}.$$

(23)

In the general cases of four distinct eigen-roots (±α, λ₁, λ₂), the general solution of (20) is

$$u_2\left(y\right)=A\left(e^{\alpha y}+e^{-\alpha y}\right)+B\left(e^{\alpha y}-e^{-\alpha y}\right)+C{e}^{{\lambda }_{1}y}+D{e}^{{\lambda }_{2}y},$$

(24)

with the four complex coefficients A, B, C, and D.

It is seen from (17a) that, with u₂ = w₂ = 0 at y = 0, ${\left.\delta \right|}_{y=0}=0\stackrel{yields}{\to }{\left.u_{2,y}\right|}_{y=0}=0.$ Thus, it follows from u₂ = 0 and u_2,y = 0 at y = 0 that we have $2A=-\left(C+D\right),$ $2\alpha B=-\left({\lambda }_{1}C+{\lambda }_{2}D\right)$, and u₂(y) given by (24) is given in terms of the coefficients C and D as

$$\begin{gathered} {2\alpha u}_2\left(y\right)=\left[{2\alpha e}^{{\lambda }_{1}y}-\alpha \left(e^{\alpha y}+e^{-\alpha y}\right)-{\lambda }_1\left(e^{\alpha y}-e^{-\alpha y}\right)\right]C \\ +\left[{2\alpha e}^{{\lambda }_{2}y}-\alpha \left(e^{\alpha y}+e^{-\alpha y}\right)-{\lambda }_2\left(e^{\alpha y}-e^{-\alpha y}\right)\right]D. \end{gathered}$$

(25)

Next, it follows from (15), (17b), (18) that the condition w₂ = 0 at y = 0 gives w_1,y = 0 at y = 0, which gives

$$\left[v_0{b}_0{\lambda }_1+1+b_0\alpha i\left(U_0-c\right)\right]\left({\lambda }_1^2-{\alpha }^2\right)C+\left[v_0{b}_0{\lambda }_2+1+b_0\alpha i\left(U_0-c\right)\right]\left({\lambda }_2^2-{\alpha }^2\right)D=0.$$

(26)

It is readily seen from (23) that

$$\left[v_0{b}_0{\lambda }_1+1+b_0\alpha i\left(U_0-c\right)\right]=0.$$

(27)

Therefore, for the condition (26) to hold for two independent arbitrary coefficients C and D, the growth rate is determined by

$$\left[v_0{b}_0{\lambda }_2+1+b_0\alpha i\left(U_0-c\right)\right]=0.$$

(28)

It is verified from (23) that the growth rate of the disturbances determined by condition (28) gives

$$a_0\alpha i\left(U_0-c\right)={\displaystyle \frac{\left(\frac{2{\rho }_0{r}_{\mathrm{S}}^{2}g}{9{\mu }_0{v}_0}-1\right)\pm \sqrt{{\left(\frac{2{\rho }_0{r}_{\mathrm{S}}^{2}g}{9{\mu }_0{v}_0}-1\right)}^2+4\frac{a_0}{b_0}\left(\frac{2{\rho }_0{r}_{\mathrm{S}}^{2}g}{9{\mu }_0{v}_0}\right)}}{2}}.$$

(29)

Clearly, the disturbance u₂(y) given by (25), with two independent arbitrary coefficients C and D and the growth rate Re(-iαc) determined by (29), meets the condition (26) (w₂ = 0 at y = 0). Thus, the non-zero disturbances u₂(y) given by (25) with two independent arbitrary coefficients C and D are guaranteed to satisfy the 4th boundary condition, either u₂(h) = 0 or w₂(h) = 0 of (22), at the upper wall of the horizontal channel.

Since ${\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^{2}g}{9{\mu }_0{v}_0}}$ is of the order (1/ε) >> 1 in the dilute bubbly fluids, it is seen from (29) that the disturbances given by (25) with the sign “+” in (29) grow rapidly, a few order of magnitude faster than the time scale of the modified relaxation time of gas bubbles estimated by the parameter a₀ [23]. Therefore, it is concluded that, in the absence of the lift force, the uniform flow of a uniformly moving inviscid liquid layer driven by the bubble crossflow injected at the bubble terminal velocity is linearly unstable to the rapidly growing disturbances with the boundary conditions (21) and (22). To the best of our knowledge, a comparison of this result with known results cannot be made here due to the lack of available related data with C_L = 0.

4.2. The Case with the Lift Force (C_L > 0)

As stated by some previous authors (see e.g., [31]) that the lift force with a positive coefficient C_L > 0 could have a stabilizing effect on bubbly flow. In addition, some authors have adopted the relation C_L = Ca = 0.5 for gas–liquid bubbly flows [9,15,17]. Thus, b₀ is expected to be nearly equal to $C_L{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}$ for gas–liquid inviscid flows in the dilute limit. For the mathematical simplicity, let us consider the case when

$$C_L{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}=b_0=\left(1-{\displaystyle \frac{\epsilon }{C_a(1-\epsilon )}}\right)C_a{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^2}{9{\mu }_0}}.$$

(30)

Thus, the 4th-order Equation (20) reduces to the following 3rd-order equation

$$\left[\begin{array}{c}\left({\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^{2}g}{9{\mu }_0}}\right){\displaystyle \frac{\left[1+b_0\alpha i\left(U_0-c\right)\right]}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}}{\displaystyle \frac{d}{dy}}\\ +i\alpha \left(U_0-c\right)\left[1+b_0\alpha i\left(U_0-c\right)\right]+{\alpha }^2{\displaystyle \frac{2{\rho }_0{r}_{\mathrm{S}}^{2}g}{9{\mu }_0}}{\displaystyle \frac{b_0{v}_0}{\left[1+a_0\alpha i\left(U_0-c\right)\right]}}\end{array}\right]\left(u_{2,yy}-{\alpha }^2{u}_2\right)=0.$$

(31)

Thus, in the general cases of three distinct eigen-roots (±α, λ₀), the general solution of (31) is given by

$$u_2\left(y\right)=E\left(e^{\alpha y}+e^{-\alpha y}\right)+F\left(e^{\alpha y}-e^{-\alpha y}\right)+G{e}^{{\lambda }_{0}y},$$

(32)

with the 3 complex coefficients E, F, and G, and λ₀ is the third eigen-root of Equation (31).

As explained above, if the admissible disturbances do not change the three boundary conditions of bubble injection at the lower wall y = 0, we have ${\left.u_2\right|}_{y=0}=0,{\left.w_2\right|}_{y=0}=0,{\left.\delta \right|}_{y=0}=0.$ Thus, with u₂ = w₂ = 0 at y = 0, ${\left.\delta \right|}_{y=0}=0\stackrel{yields}{\to }{\left.u_{2,y}\right|}_{y=0}=0$, and it follows from u₂ = 0 and u_2,y = 0 at y = 0 that u₂(y) given by (32) is of the form

$$2\alpha u_2\left(y\right)=\left[-\alpha \left(e^{\alpha y}+e^{-\alpha y}\right)-{\lambda }_0\left(e^{\alpha y}-e^{-\alpha y}\right)+2\alpha e^{{\lambda }_{0}y}\right]G.$$

(33)

It is easily verified from (15), (17b), (18) with (30) that the condition w₂ = 0 at y = 0 gives u_2,yy = 0 at y = 0, which requests that u₂(y) given by (33) to meet the condition

$${\alpha }^2={\lambda }_0^2.$$

(34)

Therefore, for the admissible disturbances not to change the three injection conditions at y = 0, the three eigenvalues of (31) must include a double eigenvalue (α) or (−α).

For example, if the eigen-Equation (31) has the double root (−α) and then λ₀ = −α, instead of (32), the general solution of (31) is of the form

$$u_2\left(y\right)=L\left(e^{\alpha y}+e^{-\alpha y}\right)+M\left(e^{\alpha y}-e^{-\alpha y}\right)+Ny{e}^{-\alpha y},$$

(35)

with the 3 complex coefficients L, M, N. Thus, it follows from u₂ = 0 and u_2,y = 0 at y = 0 that we have L = 0 and 2αM = (−N), and u₂(y) given by (35) is of the form

$$u_2\left(y\right)=\left[\left(e^{\alpha y}-e^{-\alpha y}\right)-2\alpha y{e}^{-\alpha y}\right]M.$$

(36)

Again, for u₂(y) given by (36), it follows from (15), (17b), (18) that the condition w₂ = 0 at y = 0 gives u_2,yy = 0 at y = 0, which requests

$$\left[1+b_0\alpha i\left(U_0-c\right)\right]4{\alpha }^{2}M=0.$$

(37)

It is seen from (31) that the required condition (37) contradicts the assumption λ₀ = −α. A similar contradiction appears if the eigen-Equation (31) is assumed to have the double root (+α).

Thus, it is concluded that, when the positive lift coefficient C_L is nearly equal to the added mass coefficient C_a and meets the condition (30), the disturbances satisfying (31) with the three bubble-injection boundary conditions (${\left.u_2\right|}_{y=0}=0,{\left.w_2\right|}_{y=0}=0,{\left.\delta \right|}_{y=0}=0$) cannot exist, and therefore the uniform inviscid flow driven by the bubble crossflow injected at the bubble terminal velocity is linearly stable. This result agrees with Lucas et al. [31], who confirmed the stabilizing effect of the positive lift force on the bubbly flow; it is also in qualitative agreement with Raza et al. [10], where it was shown that the lighter particles injected from the lower plane at the particle terminal velocity have a stabilizing effect on the pRB flow.

5. Conclusions

Inspired by recent literature on the bubble crossflow-induced flow instability, the present work focuses on the influence of a uniform gas bubble crossflow on the Rayleigh equation, which governs the linear stability of inviscid plane flows. For the first time in the literature, an extended fourth-order Rayleigh equation with constant coefficients is derived for the uniform inviscid plane flow driven by the gas bubble crossflow injected at the bubble terminal velocity. When the lift force is ignored, our analytical results show that the uniform inviscid plane flow driven by the bubble crossflow is linearly unstable with the rapidly growing disturbances, which grow a few orders of magnitude faster than the time scale of the modified relaxation time of gas bubbles. However, if the positive lift force is nearly equal to the added mass force (as suggested by some previous authors on the gas–liquid two-phase flows), the uniform inviscid plane flow driven by the bubble crossflow is linearly stable to the admissible disturbances consistent with the given bubble-injection boundary conditions.

Compared to some known results reported in recent literature on the viscous flow instability driven by gas bubble injection, the present results highlight some qualitatively different effects of the bubble crossflow and the lift force on the stability of inviscid bubbly flows. On the other hand, the present work is limited to the uniform inviscid plane flow with a gas crossflow injected at the bubble terminal velocity. The influence of a gas bubble crossflow on the stability of a non-uniform inviscid plane flow driven by gas bubbles injected at a velocity different from the bubble terminal velocity raises a challenging research subject for further work.