Empowering the Potential of Nearshoring in Mexico: Addressing Energy Challenges with a Fuzzy-CES Framework

Abstract

Nearshoring in Mexico is expanding rapidly, yet chronic volatility in the national power grid threatens the reliability and cost-competitiveness of relocated manufacturing lines. To inform strategic mitigation, this study presents a hybrid Fuzzy–CES decision-support framework that embeds the Constant-Elasticity-of-Substitution (CES) production function within a Mamdani Fuzzy-Inference Engine, implemented in both Type-1 and Interval Type-2 variants, to evaluate and optimize production adaptability in energy-constrained environments. Using sector-wide data from Mexico’s automotive industry, key input variables (energy reliability, capital intensity, and labor availability) are objectively quantified and normalized to reflect the realities of regional plant operations. The system linguistically classifies each facility’s production elasticity as low, moderate, or high, and generates actionable recommendations for resource allocation, such as targeted investments in renewable microgrids or workforce strategies. Implemented in MATLAB, simulation results confirm that, while high capital and labor inputs are essential, energy reliability remains the primary bottleneck limiting adaptability; only states with all three strong factors achieve maximum resilience. The Type-2 fuzzy approach demonstrates superior robustness to input uncertainty, enhancing managerial decision-making under volatile grid conditions. In addition, a case study regarding the automotive industry is presented to illustrate how the proposed framework is implemented. The same structure can be used to deploy it in another industry. This research offers a transparent, data-driven tool to inform both firm-level investment and regional policy, directly supporting Mexico’s efforts to sustain competitiveness and resilience in the global shift toward nearshoring.

1. Introduction

Nearshoring has become a pivotal paradigm in contemporary global trade, characterized by the relocation of production facilities closer to target markets. Scholars highlight three principal benefits of this strategy: enhanced operational efficiency, diminished logistical and geopolitical risks, and greater agility in meeting evolving consumer demands [1]. By shortening supply chains, firms can reduce lead times and buffer themselves against international disruptions, thereby strengthening their overall resilience.

For Mexico, nearshoring presents a strategic opportunity to deepen its integration into global commerce. Its proximity to the United States, the world’s largest consumer market, affords unparalleled advantages in transit speed and cost. Coupled with competitive labor costs, this geographic leverage makes Mexico a prime locale for firms seeking to optimize their value chains [1].

Beyond location-driven benefits, Mexico’s diversified industrial base underpins its attractiveness. The nation boasts established clusters in automotive, electronics, aerospace, and food processing, which together form a dynamic ecosystem capable of supporting end-to-end manufacturing processes [2]. A young, technically proficient workforce further enhances this profile, enabling firms to maintain high productivity levels while also ensuring cost competitiveness.

Finally, Mexico’s participation in multilateral trade agreements amplifies its nearshoring appeal. Under the United States–Mexico–Canada Agreement (USMCA), Mexican exports gain preferential access to over 46 countries, strengthening its position as a nearshoring hub and incentivizing foreign direct investment [3]. Figure 1 illustrates the distribution of automotive manufacturing firms across the country. It was adapted from [4].

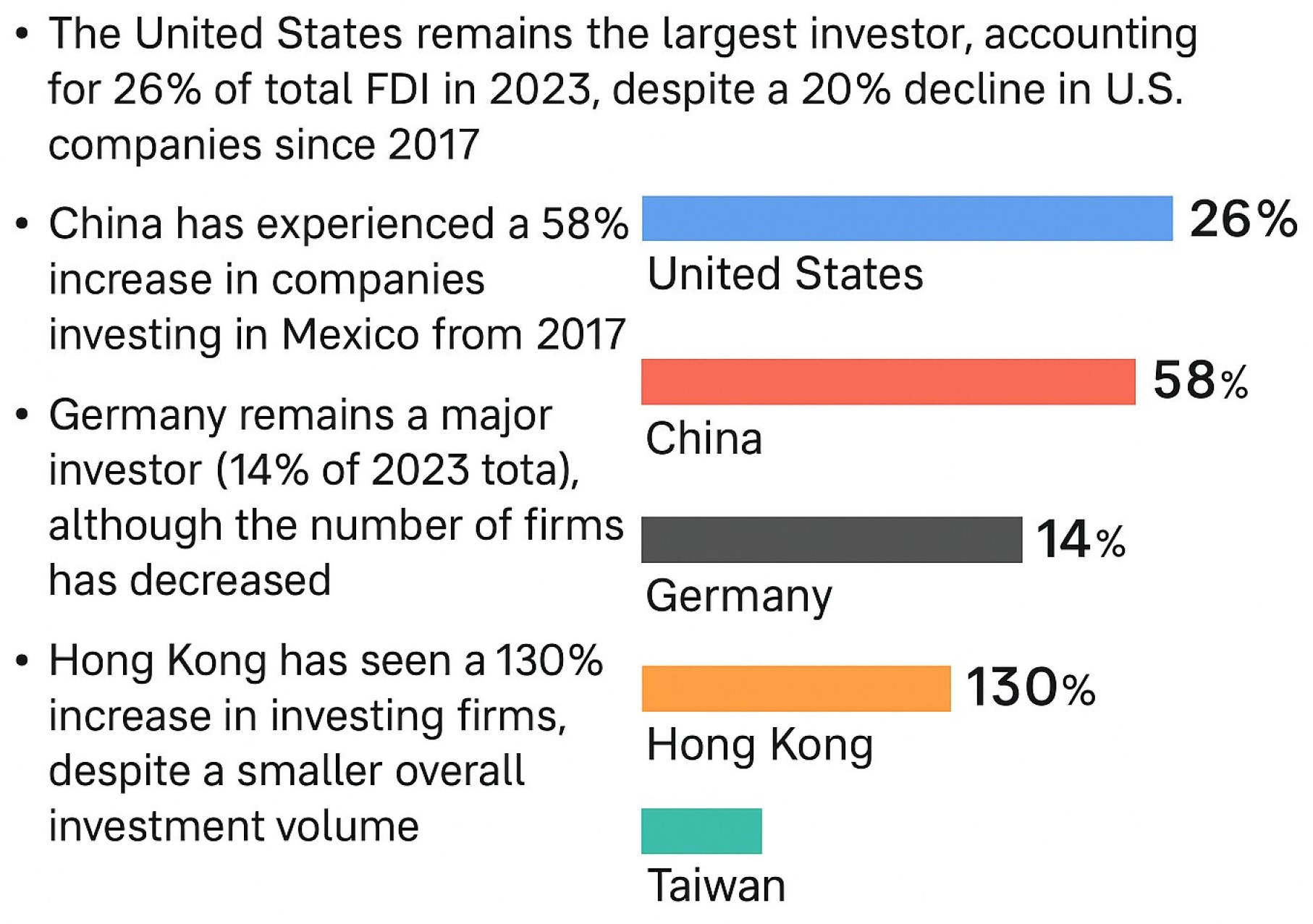
Mexico’s surge in nearshoring-driven industrialization has placed acute pressure on its electricity grid. In northern manufacturing hubs, surging demand often outstrips generation capacity, leading to power outages that halt production lines and erode investor confidence. This vulnerability is compounded by the country’s heavy dependence on fossil fuels, which not only elevates energy prices but also amplifies the environmental footprint of new facilities. Regulatory ambiguity, particularly around granting permits for renewable projects and a shortfall in clean-energy investments, has further delayed Mexico’s shift toward a more resilient, low-carbon grid [2]. Concurrently, foreign direct investment trends mirror the global reorientation toward nearshoring. Between 2017 and 2023, Taiwan’s investment volume and number of entrants in Mexico experienced a modest decline. In contrast, Hong Kong-based firms expanded their presence by approximately 130%, despite accounting for only a small share of total FDI flows. These shifts highlight both the competitive landscape for nearshoring destinations and the strategic recalibrations undertaken by source economies in response to supply chain realignments [5]. Figure 2 shows FDI in Mexico.

The rise in total investment, from $14.1 billion in 2022 to $22.3 billion in 2023, underscores Mexico’s growing prominence as a global manufacturing hub, mainly driven by its proximity to the U.S. and favorable trade agreements [5].

Additionally, Mexico’s automotive sector is expanding rapidly through nearshoring; however, energy reliability has emerged as a critical bottleneck. Industry surveys and experts report that many new projects have been stalled by uncertainty in securing sufficient power from the grid, as companies “hoped to increase their electricity consumption but had faced setbacks due to CFE” (the state utility) [6,7]. 67% of firms in Nuevo León (a major automotive hub) seeking to grow operations recently encountered power supply constraints [6]. The automotive sector alone accounts for about 2.8% of Mexico’s national electricity demand [7], so even regional grid instabilities can disrupt production lines. Researchers have quantified the stakes: manufacturing output in Mexico is susceptible to electricity costs and outages, with an average elasticity estimate of −0.28 and a maximum of −0.51 for the auto industry [8]. This means that unreliable or expensive power has a disproportionately large impact on automotive production output, underscoring the need for adaptive strategies.

To address these challenges, manufacturers and policymakers are turning to on-site generation and smart energy management. Distributed generation (DG) solutions, such as solar photovoltaic (PV) systems combined with battery storage, are gaining traction as a direct response to grid shortfalls [7]. By integrating PV and Battery Energy Storage (BESS) at factories, firms can buffer against grid outages and even form self-sustaining microgrids. For example, Quartux and other energy service providers report that solar-battery installations of up to 0.5 MW (the threshold for exempt distributed generation in Mexico) have already helped automotive suppliers secure reliable power in the face of utility limitations [7]. Such solar and storage microgrids allow a plant to run critical processes during blackouts, effectively decoupling production from grid instability. A Mexican industrial project deployed a 3.72 MWh liquid-cooled BESS with a high-voltage solar array, creating a resilient power system that maintains operations throughout outages [9].

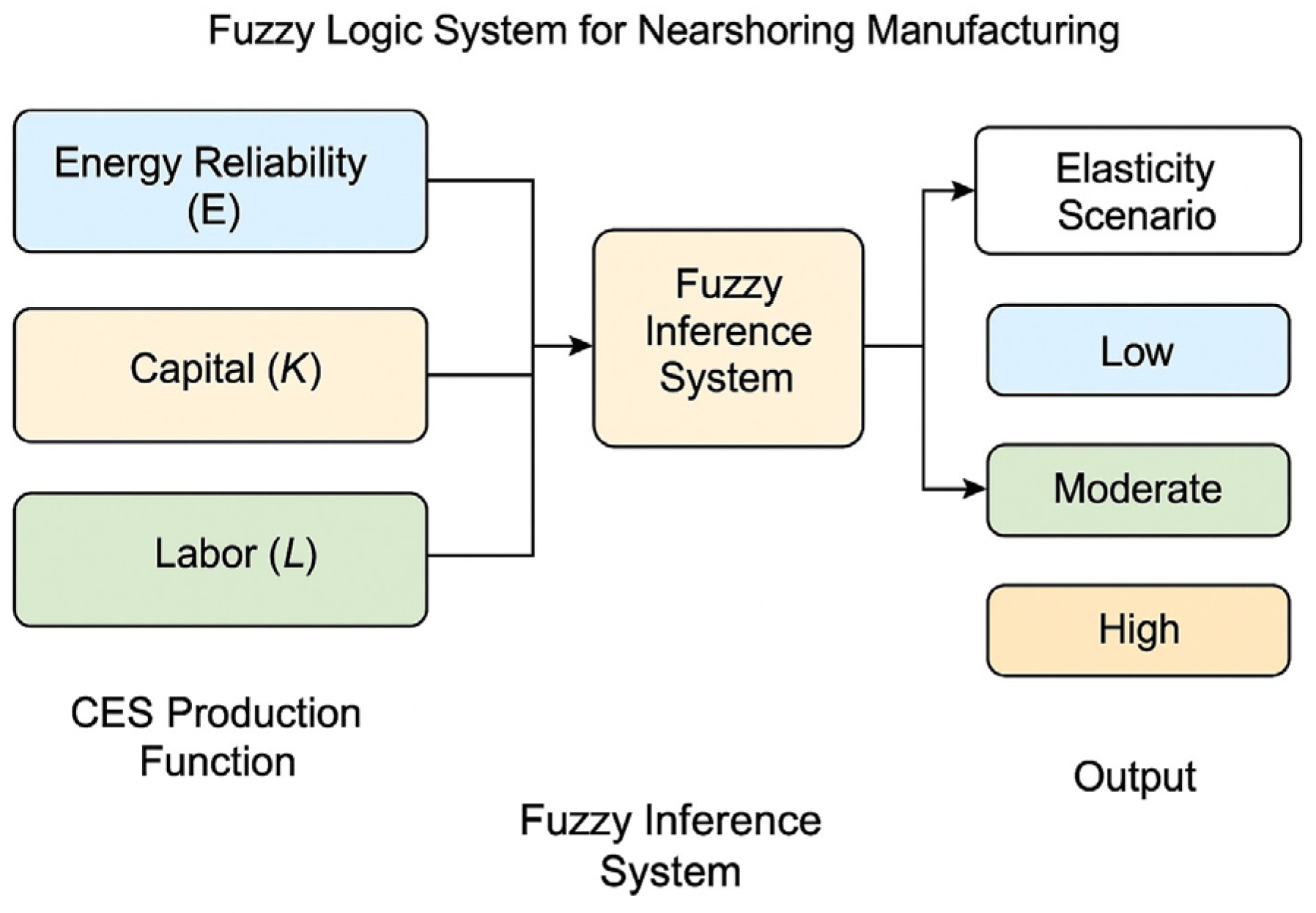
This paper proposes a fuzzy logic–based decision-making framework to overcome Mexico’s energy-related nearshoring barriers. By combining a rule-based inference engine with the Constant-Elasticity-of-Substitution (CES) production function [10,11,12], the framework quantifies how capital and labor can substitute for unreliable energy inputs. In doing so, it fills a critical methodological gap: existing optimization tools (e.g., mixed-integer linear programming [13], stochastic programming [14]) assume perfect probabilistic knowledge of future energy availability and treat electricity as an immutable constraint, while pure fuzzy systems lack an endogenous economic model to guide resource reallocation under grid instability.

Central to our approach is the integration of the CES function into the fuzzy inference engine. By casting the substitution elasticity (ρ) as a linguistic variable, the Fuzzy–CES framework retains fuzzy logic’s interpretability and real-time responsiveness, yet grounds each rule in economic theory. Decision-makers can simulate scenarios—such as prolonged outages or fluctuating renewable outputs—to identify optimal strategies, including microgrid deployment, renewable infrastructure investment, or adoption of energy-efficient technologies. This capability is especially pertinent in northern industrial hubs, such as Nuevo León and Chihuahua, where recurring power shortages imperil nearshoring operations [5].

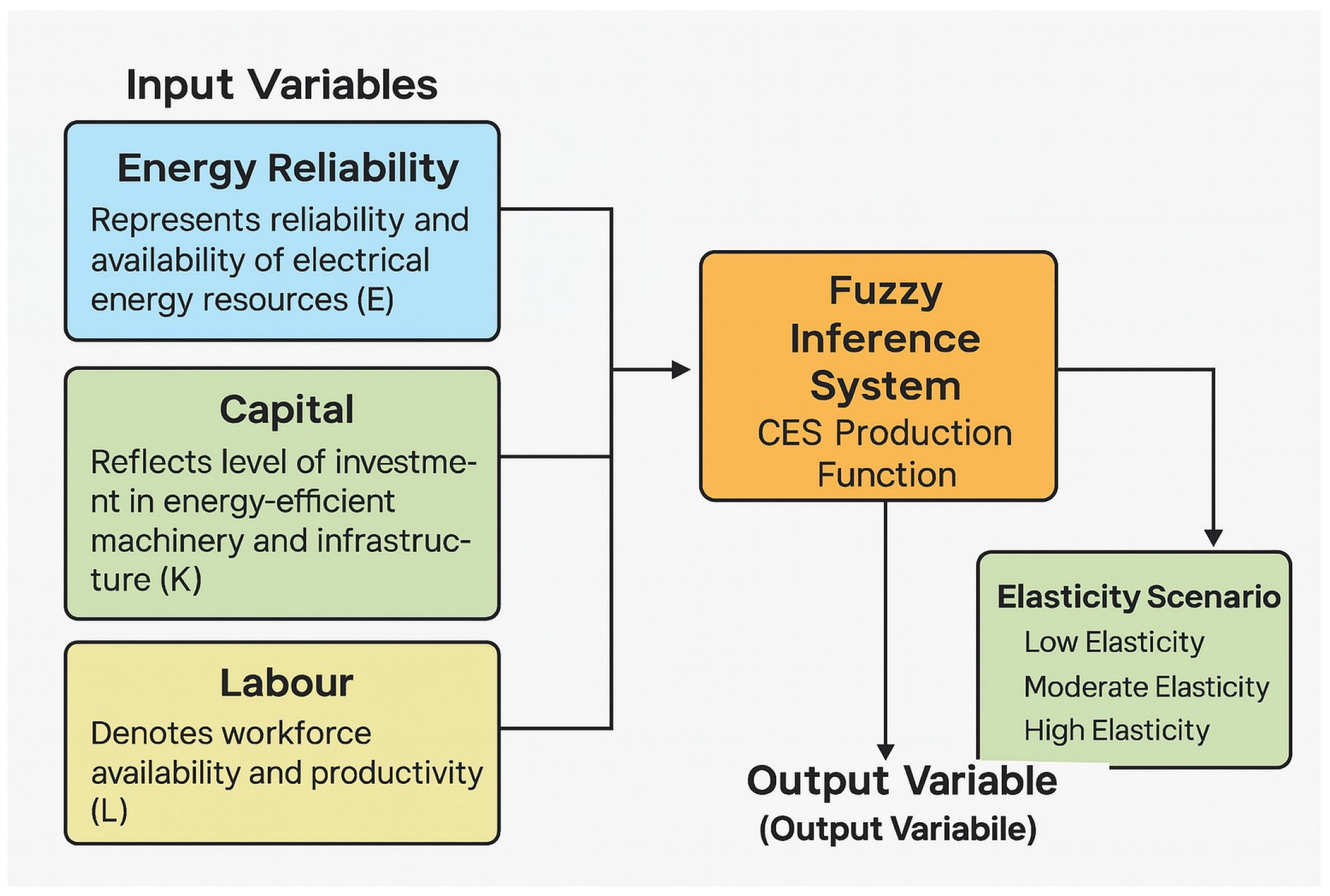
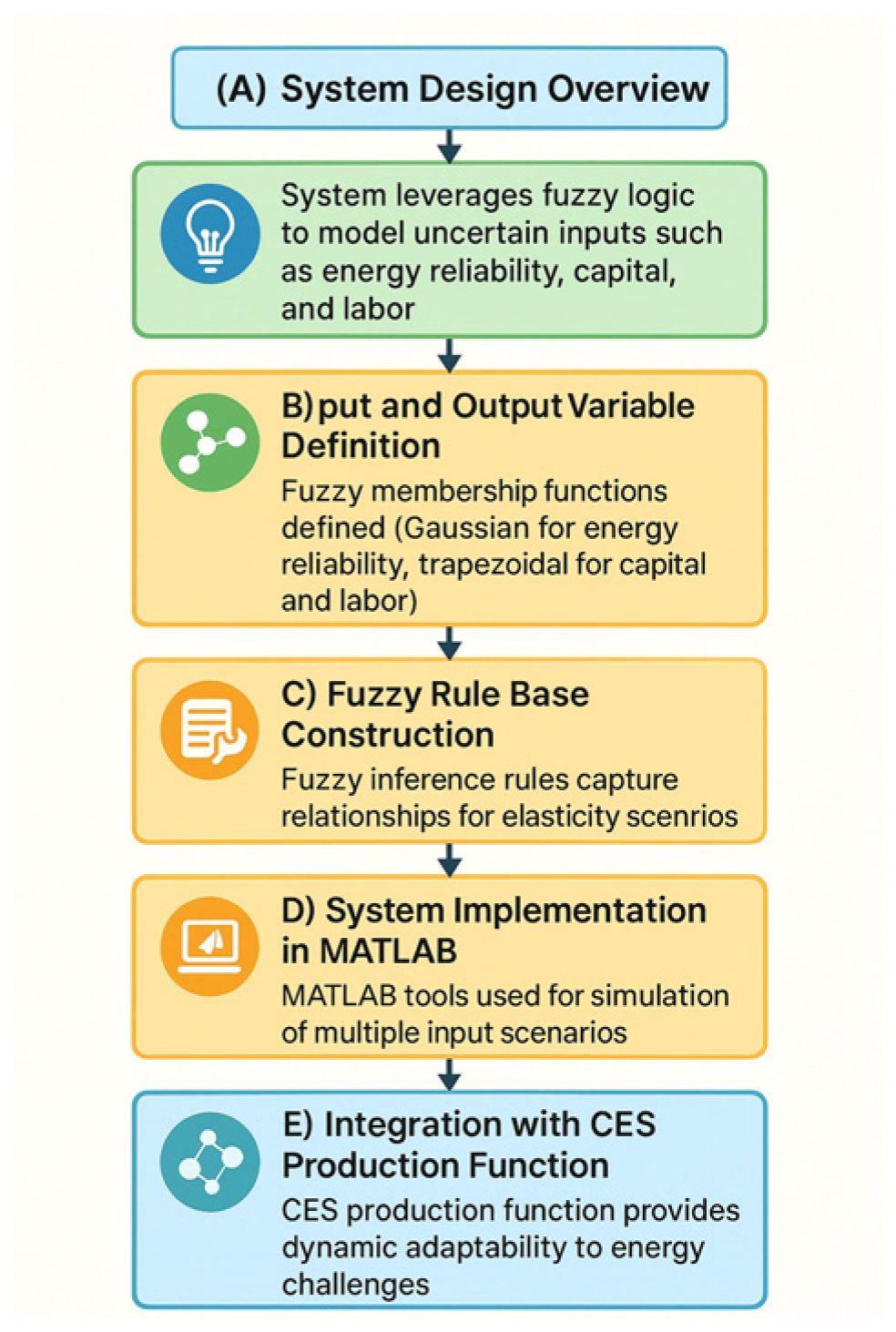
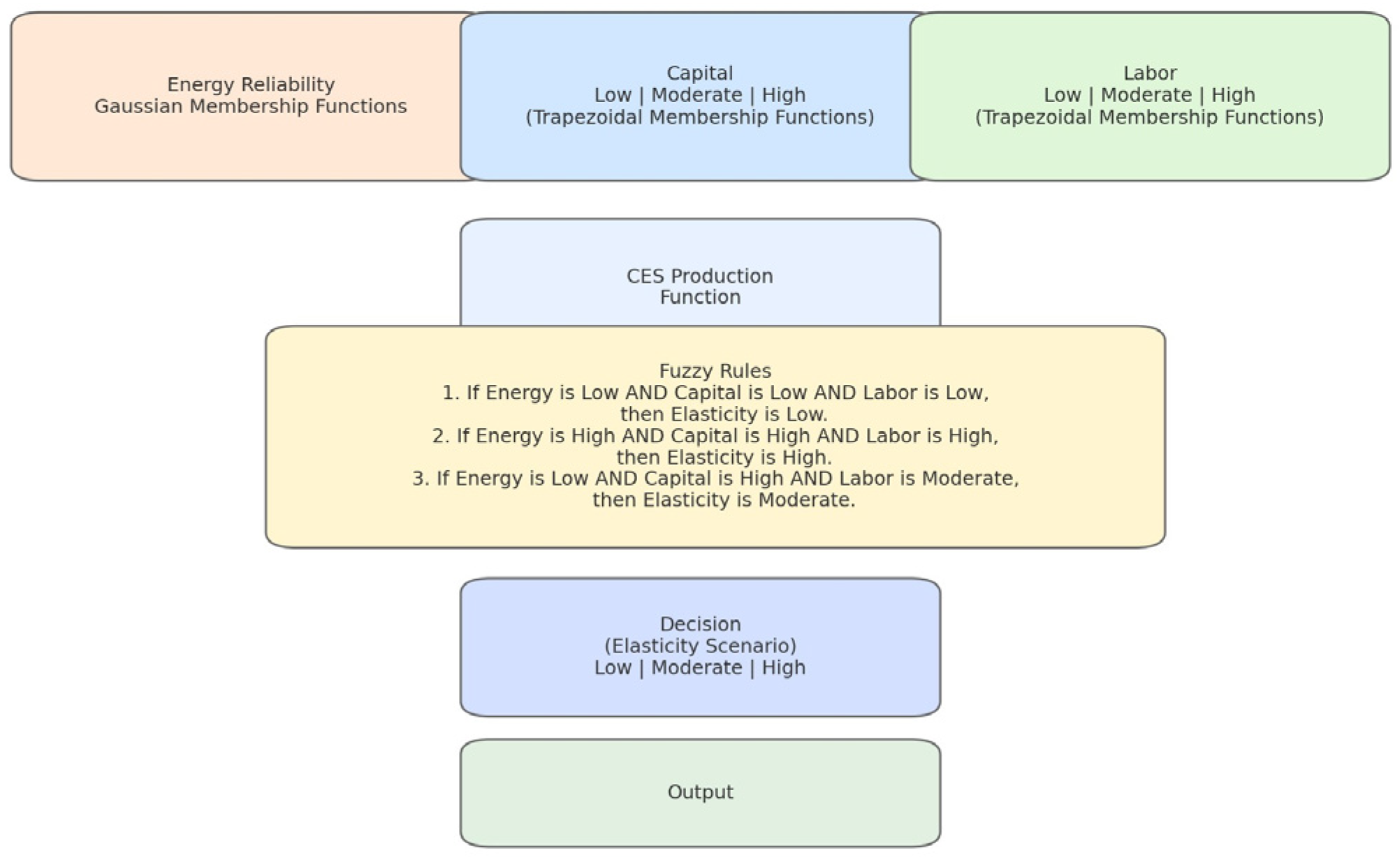
Despite its seemingly simple architecture—three inputs (Energy Reliability, Labor, Capital) and one output (Elasticity)—the proposed Fuzzy–CES engine delivers a host of critical innovations and practical advantages:

• Fuzzified economic theory. In traditional production-theory applications, the CES parameter appears as a fixed scalar; here, it is reimagined as a fuzzified linguistic variable. Decision-makers express “low,” “medium,” or “high” substitutability directly within the rule base, uniting economic substitution theory with uncertainty handling in a single, interpretable inference surface.
• Compact, transparent rule base. To prevent rule-based proliferation while maintaining real-time performance, the system employs only twelve carefully selected IF–THEN rules. Two membership-function types—Gaussian for Energy Reliability and Labor, and trapezoidal for Capital and the Elasticity output—were selected based on a sensitivity analysis of historical nearshoring plant data, which distilled all significant decision boundaries without redundancy.
• Minimal calibration effort. The 3:1 design drastically reduces data requirements: plant engineers normalize only three key KPIs to a familiar 0–10 scale, define three linguistic categories per input, and thereafter need only edit a handful of rules to accommodate new conditions.
• Methodological robustness and reproducibility. Implementation in MATLAB R2024a’s Fuzzy Logic Toolbox leverages built-in Karnik–Mendel type-reduction algorithms and an interactive membership-function design environment, ensuring each elasticity recommendation can be traced back to clear, domain-relevant IF–THEN logic with minimal custom coding.

Mexico’s grid still derives over 70 percent of its electricity from fossil fuels [10], and the adoption of smart grids or distributed renewable energy remains sluggish. Regulatory uncertainty and underinvestment exacerbate this bottleneck. Our framework directly addresses these challenges by embedding infrastructure limitations and operational variability into scenario planning. Moreover, it complements broader structural improvements—such as upgrading transportation and logistics networks, streamlining bureaucracy, bolstering regional security, and expanding the advanced manufacturing workforce—thus strengthening the overall nearshoring ecosystem.

The contributions of this work are threefold:

• Methodological innovation. The Fuzzy–CES paradigm unifies economic substitution theory with rule-based AI, enabling rapid, interpretable decisions that account for both energy reliability and input substitutability.
• Practical relevance. By simulating diverse energy–labor–capital scenarios, the framework yields data-driven recommendations—ranging from microgrids to efficiency retrofits—that directly address grid instability in strategic states [5].
• Strategic guidance. Our analysis underscores the need for targeted investments in renewable energy, smart-grid technology, and public–private collaboration, while highlighting how fuzzy logic can extend beyond energy management to workforce planning and logistics optimization in nearshoring contexts.

This paper advances both academic discourse and industrial practice by offering a coherent and computationally tractable tool for navigating Mexico’s energy sector constraints. By integrating CES-based modeling within a transparent fuzzy inference system, the proposed framework enhances the resilience, sustainability, and competitiveness of Mexico’s evolving nearshoring landscape. Additionally, a comprehensive case study of the automotive industry is presented to illustrate the implementation of the proposed framework. In terms of energy and manufacturing, this proposal deals with a hybrid Fuzzy–CES decision framework that translates conditions of energy reliability (E), capital (K), and labor (L) into an interpretable elasticity signal before detailed optimization, thereby complementing the growing body of energy-aware scheduling and flexibility tools. In additive manufacturing specifically, recent work has moved beyond single-machine heuristics to process–schedule co-design, learning power-demand patterns under alternative process parameters and co-optimizing them with job sequencing against time-varying tariffs and demand charges; validated on FDM with operational data, this demonstrates that peaks and total energy cost can be proactively shaped without throughput loss [15]. At a higher level, a PRISMA-guided review integrates disparate notions of demand response, multi-energy integration, and digital enablers (ML, RL, predictive control, digital twins, blockchain) into a Climate-Resilient Industrial Flexibility Framework that links concepts, sectoral practice, and policy/market design—precisely the scaffold into which plant-level tools should plug [16]. System adequacy and on-site reliability also hinge on which flexibility assets are financed: interval Type-2 trapezoidal fuzzy sets with PROMETHEE-II expand storage investment screening to include land intensity and resource footprints, typically elevating pumped hydro overall while favoring wind-to-hydrogen in economic/green/social priorities, evidence that portfolio choices upstream shape the reliability envelope within which factory operations unfold [17]. On the supply side, AI has become the digital backbone of PV-rich systems, MPPT optimization, forecasting, parameter estimation, and fault diagnostics dominate a rapidly expanding literature using ANN, Type-2 fuzzy logic, CNN/LSTM, SVM, trees/forests, k-NN, and PSO; a MATLAB Type-2 selector even maps problem types to methods, improving the quality of inputs that later drive industrial scheduling and procurement [18]. These micro-level currents are consistent with macro signals: scenario meta-analyses for 2024–2025 show demand rising faster than expected (+2200 TWh by 2035), a shrinking Net-Zero premium (19% → 15%), and a capital pivot away from gas toward grids, storage, and hydrogen, marking a shift in the system’s pressure point from generation to flexibility under the combined stresses of AI data centers, heatwaves, and transport electrification [19]. Within this landscape, hybrid scheduling exemplars illustrate multiple routes to robustness under uncertainty and tariffs, event-triggered blends of off-line and on-line re-optimization that reduce rescheduling cost in PV–storage–turbine–grid settings [20], remanufacturing models that jointly solve process planning and shop scheduling with speed-switching and RL-PSO to outperform on/off heuristics [21], deep-learning-assisted multi-objective schedulers that co-optimize energy, cost, and makespan with discrete-event simulation for deployability [22], process-aware demand-response scheduling that re-times polysilicon production to time-of-use price signals via state–task networks [23], and AM-specific matheuristics (SLM) that jointly decide nesting, batch assignment, and orientation to minimize machine energy at realistic scales [24]. Relative to these “optimizer-first” approaches, this proposal contributes an upstream, uncertainty-robust classification layer—embedding CES substitutability inside a Type-1/Interval Type-2 fuzzy engine, so that noisy E–K–L realities are converted into a crisp elasticity score/class; this output can gate, weight, or parameterize any of the downstream optimizers in [15,20,21,22,23,24], while aligning plant choices with the flexibility framework in [16], the storage portfolio logic in [17], the PV/AI intelligence in [18], and the system-wide capital reallocation imperative in [19], thereby positioning the work as a bridge from macro flexibility needs to executable, plant-level decisions in energy-constrained nearshoring.

2. Background and Motivation

2.1. The Role of the CES Production Function in Nearshoring and Electrical Energy Adaptation

Research on economic growth theory can be transformed into studies on the production function, which mathematically represents the dependent relationship between input factors of production and output. Economists have proposed various forms of production function, with the one introduced by Professor Solow of the Massachusetts Institute of Technology, who received the Nobel Prize in Economics and had the most significant impact. This production function can be adapted for the context of nearshoring in Mexico, where it could play a central role in enhancing operational efficiency, optimizing resource allocation, and improving manufacturing resilience. As global businesses shift supply chains closer to major consumer markets, such as the United States, adaptive and robust production models become increasingly essential. One of the most relevant tools in this context is the Constant Elasticity of Substitution (CES) production function [11,12,25,26], which provides a flexible framework for modeling input substitutability within the constraints of energy use and operational limitations.

2.1.1. CES Function and Electrical Energy Adaptability

Nearshoring operations are susceptible to energy and infrastructure-related variables, particularly fluctuations in electricity availability. The CES production function addresses these concerns by enabling substitutability between key inputs, capital (K), labor (L), and electrical energy factors (E), to sustain output levels under varying conditions. The conventional CES function could be adjusted in terms of energy so that it can be expressed as shown in Equation (1) [11,12,27]:

Y = A (αKρ + βLρ + γEρ) (1/ρ),

(1)

where

Y is the output;

A is a constant representing the total factor productivity;

K is the capital input;

L is the labor input;

E is the electrical energy factor;

α; β; and γ are the distribution parameters (which represent the relative importance of capital; labor; and the energy factor in the production process);

ρ is the substitution parameter that determines the elasticity of substitution between the inputs.

In Equation (1), ρ is related to the elasticity of substitution (σ) between the inputs by the following relationship in Equation (2).

σ = 1/(1 − ρ),

(2)

In this paper, the following criteria will be applied: the limit as ρ → 0, the CES function converges to the Cobb–Douglas form, implying unit elasticity of substitution (σ = 1).

Inadmissible region (ρ > 1).

For ρ > 1, Equation (2) yields a negative σ, which is economically meaningless; such parameter values are, therefore, inadmissible.

Complementarity condition.

If ρ < 0 (so 0 < σ < 1), capital, labor, and energy act as complements; if 0 < ρ < 1 (σ > 1), they are substitutes.

To illustrate the model that integrates energy, consider a small factory in Mexico whose baseline inputs are as follows (K, L, E are dimensionless):

• Capital K = 100;
• Labor L = 50;
• Electrical Energy E = 80.

Assume A = 1, α = β = 0.4, γ = 0.2 (constant returns to scale).

Table 1. Elasticity of Substitution Scenarios.

ρ	σ = 1/(1 − ρ)	Classification	Output Y
−0.50	0.66	strong complements	70.70
0	1.00	Cobb–Douglas	72.47
0.30	1.429	moderate substitutes	73.54
0.50	2.00	strong substitutes	74.25
0.90	10.0	near-perfect substitutes	75.65

shows the implied elasticity of substitution and resulting output for several representative values of ρ. In an operational setting, the CES weights α, β, γ are ordinarily calibrated from a firm’s accounting and metering records rather than assigned a priori. A standard procedure begins by extracting three annual cost streams from audited financial statements or activity-based cost reports: capital services (depreciation plus the user cost of fixed assets), direct-labor compensation, and purchased electricity. The procedure then divides each stream by the sum of the three to yield empirically grounded expenditure shares that satisfy α + β + γ = 1. Where plant-level records are sparse, the same ratios can be approximated from national input–output tables or from a stratified survey of comparable factories and then refined through expert elicitation to reflect local operating realities such as overtime prevalence or self-generation of power. Baseline quantities K, L, E are obtained by normalizing physical indicator machine-hour capacity, direct-labor hours, and metered kilowatt-hours, so that the median capital value across the sample is set to 100 and all other inputs are scaled proportionally; this preserves their relative magnitudes while keeping the numerical range convenient for simulation. In this paper, the values α = β = 0.4, γ = 0.2, and K = 100, L = 50, E = 80 serve purely as illustrative placeholders, chosen to match typical cost ranges reported by mid-sized maquiladoras. They should be recalibrated using the procedure above before the model is deployed in any specific factory. Table 1 illustrates how the σ–ρ link enables managers to precisely quantify the additional capital or overtime labor required to maintain throughput when the local grid falters, precisely the sort of adaptability nearshoring firms need in energy-constrained regions such as Nuevo León and Baja California in Mexico.

In this scenario, where capital, labor, and electrical energy, respectively, account for 40%, 40%, and 20% of production cost (α = β = 0.4, γ = 0.2), the Constant-Elasticity-of-Substitution (CES) function reveals a strictly increasing relationship between the substitution parameter ρ and total output Y. When ρ = −0.5, the three inputs behave as strong complements (σ ≈ 0.6); the plant’s simulated throughput is constrained at Y ≈ 70.7. As ρ approaches zero, the technology converges to the Cobb–Douglas (σ = 1) form, thereby increasing output to Y ≈ 72.4. Further increases to ρ = 0.30 (moderate substitutes, σ ≈ 1.4) and ρ = 0.50 (strong substitutes, σ = 2) continue this upward trajectory, culminating in Y ≈ 75.6 when ρ = 0.9, a near-perfect-substitution regime (σ = 10).

Quantitatively, the factory gains roughly five percentage points of throughput, an increase in more than 7% relative to the strong-complement baseline, simply by moving along the substitution spectrum from ρ = −0.5 to ρ = 0.9. This monotonic lift substantiates the framework’s managerial insight: firms that invest in technologies or work practices that raise the mutual substitutability of capital, labor, and energy (e.g., energy-efficient machinery, cross-trained operators, on-site renewables) can buffer production against intermittent grid failures. In energy-constrained nearshoring hubs such as Nuevo León and Baja California, enhancing σ becomes a quantifiable lever for sustaining output under volatile electricity supply conditions (See Figure 3).

With ρ = −0.50, the low σ indicates that capital, labor, and energy must rise together to lift output; saving on electricity while adding robots, for instance, would decrease productivity. Each factor’s marginal product depends proportionally on its share near the Cobb–Douglas case, in the limit ρ → 0. Usually, Cobb–Douglas is a limit case, not precisely at ρ = 0 in the strict CES equation. As ρ increases to 0.3 or 0.5, the factory can cope with a 10% drop in electricity by raising capital 5% with only a marginal fall in output. This illustrates CES’s flexibility and resilience in addressing energy reliability problems in northern Mexican states. This flexibility is crucial for manufacturing operations in Mexico, where industrial hubs such as Nuevo León and Baja California frequently experience energy reliability issues due to high demand and strained grid infrastructure. The CES function enables manufacturers to assess the adaptability of their production processes to energy-related challenges and to develop strategies for resilience and optimization.

2.1.2. Proposed Elasticity Scenarios in Nearshoring

The CES production function introduces elasticity of substitution as a parameterized measure of how responsive a production system is to shifts in input conditions. In Mexico’s ongoing energy challenges, evaluating production through high, low, or intermediate elasticity scenarios allows for informed decision-making in nearshoring operations.

(1)

High Elasticity of Substitution: When the substitution parameter satisfies (implying an elasticity of substitution σ > 1), the CES production function describes high substitutability among inputs [28,29,30]. In practice, this means a factory can offset an unexpected reduction in energy factor E by reallocating resources toward capital K or labor L with only a marginal loss in output.

• Operational implications: Flexible response to power disruptions.

  ○

  If grid instability lowers the available electricity, managers can:

  ▪

  Increase capital investment in energy-efficient or dual-input machinery, or

  ▪

  Schedule temporary overtime or add extra shifts to increase effective labor input. Either strategy maintains throughput as long as the energy constraint persists.

• Reactive investment focus: Nearshoring facilities in energy-volatile regions (e.g., Nuevo León, Chihuahua) should keep a reactive capital budget earmarked for equipment that performs efficiently under variable voltage or can switch seamlessly to backup generation. Such machinery amplifies the substitutability advantage granted by a high σ.
• Dynamic labor deployment: Shifting production to periods of stable energy supply by extending shift lengths or staggering crews lets plants exploit excess labor capacity when electricity is plentiful and throttle back when power is scarce.
• Resilience without large output shocks: Because σ > 1 flattens the isoquants of the production function, a 10% shortfall in energy can often be neutralized by roughly a 5% rise in capital or a similar labor adjustment, keeping the drop in output essentially negligible.
• High elasticity equips nearshoring manufacturers with a built-in buffer against Mexico’s uneven grid performance. By deliberately cultivating substitutable capital (energy-smart machinery) and maintaining flexible labor policies, plants can navigate electricity volatility while sustaining delivery commitments to U.S. markets, turning an energy vulnerability into a competitive edge.

(2)

Low Elasticity of Substitution: In this low-elasticity regime, capital (K), labor (L), and energy (E) act as complements rather than substitutes: a reduction in one input cannot be cheaply offset by expanding the others. Unreliable grid power or sharp increases in electricity prices translate almost directly into lower output.

• Operational implications: Even a modest energy shortfall, a ten-percent drop caused by rolling brownouts, will reduce throughput by nearly the same percentage. Hiring extra workers or adding robots provides little relief because the additional inputs sit idle whenever energy remains the bottleneck. To remain viable under these conditions, a factory must prioritize energy security as a core capital investment.

  ○

  The first action is stabilizing on-site supply through renewable generation (rooftop solar, small-scale wind, or hybrid combinations) and battery storage that can ride through brief outages. High-efficiency diesel or natural-gas generators can serve as a last-resort backup, but they should be sized and automated so that they start within seconds of a voltage sag.

• Reactive investment focus: At the grid interface, factories benefit from negotiating firm capacity contracts with local utilities and installing power-conditioning equipment, uninterruptible power systems, voltage regulators, and harmonic filters to protect sensitive drives and controls.
• Dynamic labor deployment: Inside the factory, tight preventive maintenance schedules keep motors, inverters, and PLCs within specification so that transient voltage drops do not trigger cascading shutdowns. Monitoring of bearings, cooling fans, and insulation temperatures flags incipient faults that would magnify the impact of any energy disruption.
• Management should regard advocacy for regional grid upgrades as a strategic, not peripheral, activity. Coordinating with state and federal authorities to modernize substations, reinforce transmission lines, and streamline interconnections is essential if Mexico’s nearshoring expansion is to reach its full potential.
• Until those structural upgrades materialize, production planning must assume that energy shocks will disproportionately affect output and, therefore, front-load investments in on-site generation, storage, and robust power electronics to preserve supply chain reliability.

(3)

Intermediate Elasticity: When the CES parameter lies between zero and one, the resulting elasticity of substitution is greater than one but not extreme. In this intermediate-elasticity regime, capital (K), labor (L), and energy (E) can replace one another only partially: a moderate shortfall in electricity can be cushioned by modest additions of capital or labor, yet complete offset is impossible without addressing the underlying energy constraint.

• Short-duration outages, seasonal rate spikes, or brief grid instability episodes may reduce effective energy input by five to ten percent. A factory with intermediate elasticity can recover most of the lost output by upgrading a subset of machines to energy-efficient drives (raising K) or extending select shifts during off-peak hours (raising L).
• Unlike high-elasticity factories that rely mainly on automation or low-elasticity factories that prioritize large-scale power projects, intermediate-elasticity facilities benefit from hybrid solutions. Typical measures include installing a modest rooftop solar array paired with a small battery for peak shaving, upgrading the most energy-intensive motors, and implementing load-shifting schedules to keep production from tariff peaks.

2.2. Strategic Actions

Targeted energy upgrades rather than full-scale micro-grid builds, for example. A 200 kW solar array with 1 MWh of storage can smooth mid-afternoon price spikes without the upfront cost of a multi-megawatt system. Selective machinery replacement focused on high-duty-cycle equipment. Replacing only the worst performers yields the most energy savings while keeping capital expenditures manageable. Rotate shifts to concentrate production in hours of stable voltage. In thermally stressed regions, overtime is offered during cooler nights, reducing HVAC load.

2.2.1. Data-Driven Energy Management

Install sub-metering and predictive analytics to forecast demand peaks, then pre-heat, pre-cool, or pre-charge equipment during low-tariff windows. For example, a plastics extruder in Chihuahua faces mid-summer power curtailments driven by regional cooling demand. CES modeling shows that installing a 250 kW rooftop PV system, along with a 0.5 MWh battery, enables the factory to absorb a five percent energy cut with only a two percent decline in output, provided the factory also lengthens its night shift by one hour [31,32,33]. The combined capital- and labor-tweak maintains customer deliveries without the expense of a full generator farm. Intermediate-elasticity strategies dovetail with Mexico’s incremental grid improvements and decarbonization goals. They provide manufacturers with a cost-effective bridge: robust enough to handle today’s intermittent reliability, yet flexible enough to scale down reliance on fossil fuel backup as the national grid and renewable energy sources improve. In short, a moderate elasticity of substitution suggests a balanced toolkit, comprising part energy-efficiency investment, part renewable increment, and part intelligent scheduling. That mix is ideal for nearshoring factories in regions where the grid is steadily strengthening but not yet fully dependable [31,32,33].

2.2.2. Extreme Deterioration of Electrical Energy Conditions

When electrical conditions deteriorate to the point of prolonged blackouts or crippling price spikes, the effective energy input, E, collapses, and routine adjustments in capital, K, or labor, L, no longer maintain a stable throughput. A factory facing this level of stress must transition from incremental fixes to a structural transformation. The first imperative is energy autonomy: installing a micro-grid or a combined heat-and-power (CHP) system secures a dedicated, controllable supply that decouples production schedules from grid volatility. In parallel, deep automation, robotics, AI-driven controls, and remote-operation software reduce the factory’s dependence on manual labor during outages and permit an immediate, precise ramp-up once power returns. Integrating large-scale renewables such as wind or solar, backed by sizable battery storage, cushions the facility against price shocks and supply interruptions while advancing decarbonization goals. If, after implementing these measures, energy volatility remains intolerable, management must weigh the long-term costs of relocating critical production stages to a region with more stable infrastructure. Although relocation is disruptive, it can be the decisive step for safeguarding contractual commitments and preserving the factory’s economic viability when external power conditions have deteriorated beyond where traditional capital–labor substitutions are effective.

2.3. Research-Driven Insight

On the other hand, recent studies support the integration of energy considerations into production models. Simulation-based methods have demonstrated that optimizing operational states in response to energy supply inconsistencies can enhance manufacturing performance and reduce downtime [11,30]. Similarly, incorporating energy consumption into production scheduling has improved productivity while minimizing costs and environmental impact [12]. These findings reaffirm the relevance of CES-based modeling in energy-constrained manufacturing contexts, particularly for Mexico’s nearshoring strategy. The CES production function offers a dynamic and adaptable framework for modeling the interplay between capital, labor, and energy in nearshoring environments. Its use allows manufacturers to simulate and prepare for energy-related disruptions by evaluating input substitutability and aligning strategies with infrastructure capabilities. As global supply chains continue to shift toward regionalization, CES-based decision support tools will be instrumental in helping Mexico consolidate its position as a competitive, energy-resilient manufacturing hub.

2.4. Decision-Making Based on ρ and E

The elasticity of substitution (ρ) offers key insights for nearshoring operations in Mexico to anticipate and address electrical energy challenges:

• High ρ (High Substitutability): Factories should focus on reactive strategies, such as investing in flexible technologies and increasing labor inputs during energy disruptions.
• Low ρ (Low Substitutability): Consistent production requires stabilizing energy availability through renewable infrastructure investments, preventive maintenance, and energy storage solutions.
• Moderate ρ: A mixed approach combining energy-efficient technologies with partial energy controls provides the most cost-effective strategy for regions with moderate energy challenges.
• Extreme Conditions: Prolonged or extreme energy challenges necessitate long-term structural investments, such as renewable energy systems, automation, or even relocation to regions with more stable energy conditions.

The CES production function, including energy as a critical factor, provides nearshoring manufacturers with a valuable tool for evaluating resilience and guiding decision-making. By incorporating electrical energy reliability into operational strategies, factories can ensure sustainable productivity and adaptability to Mexico’s dynamic energy landscape. This approach positions nearshoring operations to overcome electrical energy challenges while capitalizing on Mexico’s growing role in global supply chains.

2.5. Fuzzy Logic Principles

Fuzzy set theory provides a structured framework for reasoning with linguistic or partially observed data. Conventional—or Type-1—fuzzy systems assign a single, crisp membership grade μ ∈ [0,1] to every input, so the underlying membership functions (e.g., Gaussian or trapezoidal) are fully specified and uncertainty is ignored [34,35,36]. While this assumption is acceptable when sensor readings are precise and linguistic judgments are unambiguous, it becomes restrictive in manufacturing environments, such as the Mexican nearshoring factories analyzed in this study, where grid conditions fluctuate. Human assessments of capital or labor availability are inherently vague.

Type 2 fuzzy logic generalizes the Type 1 paradigm by treating the membership grade as a fuzzy set. Each primary membership function is wrapped by a secondary membership function that captures the epistemic uncertainty surrounding μ. Collecting all such secondary grades forms the Footprint of Uncertainty (FOU), which delimits the admissible range of μ for every input value [37,38]. By embedding this additional degree of freedom directly in the membership layer, Type 2 systems model the “noise” that arises from intermittent power quality sensors, variable labor shift patterns, and expert-elicited capital indices—circumstances that typify energy-constrained nearshoring operations.

Several performance implications follow. First, a Type-2 rule base can remain compact because uncertainty is absorbed by the FOUs rather than by proliferating antecedent clauses; empirical studies report sharper rule-base compression and lower tuning effort than comparable Type-1 designs [34,35,39]. Second, the defuzzified output of a Type-2 Mamdani engine is much less sensitive to small perturbations in input data, yielding more stable elasticity estimates when kilowatt-hour readings or overtime inventories fluctuate within acceptable error bands [34,35]. Finally, Type-2 models demonstrate superior generalization in decision-support tasks where factory managers must extrapolate from sparse data, precisely the setting of the Fuzzy–CES proposed here.

The present work employs a dual implementation: a baseline Type-1 Mamdani system and its interval Type-2 extension [37,39]. The comparative results confirm the theoretical expectation: the Type 2 variant delivers more reliable elasticity scenarios under noisy energy-reliability inputs, enabling nearshoring factories to adjust resource allocations with greater confidence in the face of Mexico’s volatile grid. Thus, adopting Type-2 is not a cosmetic refinement but a necessary methodological advance for handling the multifaceted uncertainty characterizing modern energy-aware manufacturing [38,40].

2.6. A Fuzzy Logic-Based Decision-Making System for Nearshoring and Energy Challenges

This proposal introduces a fuzzy logic system designed to address the critical challenges faced by manufacturers engaged in nearshoring operations, particularly in terms of energy reliability and resource allocation. The system leverages the Constant Elasticity of Substitution (CES) production function, incorporating three key inputs, energy reliability (E), capital (K), and labor (L), to evaluate and optimize production decisions under varying conditions. The primary objective of this system is to provide a structured, data-driven method for assessing the adaptability of production processes in response to energy reliability challenges. Energy reliability, modeled as the stability and availability of energy resources, is combined with inputs for capital investment (machinery, infrastructure, and equipment) and labor availability or productivity. The system’s output, called the elasticity scenario, categorizes production adaptability into three levels: low, moderate, and high. This classification guides manufacturers in determining whether their production processes can withstand energy fluctuations and resource constraints (See Figure 4).

3. Methodology

This section outlines the development and implementation methodology of the fuzzy logic-based decision-making system designed to support energy-resilient nearshoring operations in Mexico. The system integrates the Constant Elasticity of Substitution (CES) production function with fuzzy inference logic to assess the adaptability of manufacturing processes under varying levels of energy reliability, labor availability, and capital investment.

3.1. System Design Overview

The proposed system aims to evaluate production adaptability, referred to as the “elasticity scenario,” based on three critical input variables: energy reliability (E), capital (K), and labor (L). Due to their inherently uncertain and variable nature in real-world manufacturing environments, these inputs are modeled using fuzzy logic. The CES production function informs the system’s structure by modeling how these inputs contribute to output and how substitutable they are in maintaining productivity (See Figure 5). This section defines a Mamdani-type fuzzy inference engine with three normalized inputs: Energy Reliability (E), Capital (K), and Labor (L), each mapped from 0 to 10 and fuzzified into Low, Medium, and High categories (Gaussian for E and L, and trapezoidal for K). A twelve-rule IF–THEN base evaluates all principal E–K–L combinations to produce an Elasticity Scenario output (Conservative, Moderate, Aggressive), which is likewise trapezoidal and defuzzified via the centroid method to yield a crisp 0–10 elasticity score. Optionally, an Interval Type-2 extension encapsulates each membership function in upper and lower uncertainty bounds.

3.1.1. Input and Output Variable Definition

Three input variables were defined:

• Energy Reliability (E): Represents the stability and availability of electrical energy resources.
• Capital (K): Reflects the level of investment in energy-efficient machinery and infrastructure.
• Labor (L): Denotes workforce availability and productivity.

Each input variable is normalized within the range [0,10] and modeled using fuzzy membership functions. Gaussian membership functions are employed for energy reliability to handle smooth transitions, while trapezoidal functions are used for capital and labor to reflect investment thresholds and workforce levels.

The system’s output variable is the Elasticity Scenario, categorized into the following:

• Low Elasticity: Rigid production systems with limited adaptability.
• Moderate Elasticity: Systems with partial adaptability.
• High Elasticity: Highly flexible and energy-resilient production systems.

Triangular membership functions define the output fuzzy set due to their simplicity and effectiveness in modeling discrete outcomes.

3.1.2. Fuzzy Rule Base Construction

A total of 12 fuzzy inference rules were formulated to capture the relationships between input conditions and the resulting elasticity scenario. The rules were constructed based on expert heuristics, empirical logic, and the behavior of CES functions regarding substitutability. The following stand as examples:

• If Energy Reliability is low, Capital is low, AND Labor is low, then Elasticity is low.
• If Energy Reliability is high, Capital is high, AND Labor is high, THEN Elasticity is high.

These rules reflect the system’s ability to infer compensation mechanisms, such as labor or capital investment offsetting energy instability.

3.1.3. System Implementation in MATLAB

The fuzzy inference system (FIS) was implemented using the MATLAB Fuzzy Logic Toolbox [41]. The following steps were as follows:

• Define FIS structure and variables (input/output): Assign appropriate membership functions to each input/output. The membership type of each input is shown in

  Table 2. Description of linguistic variables.

  Variable	Linguistic Terms	Membership-Function Type
  E (Energy)	Low, Moderate, High	Gaussian
  K (Capital)	Low, High	Trapezoidal
  L (Labor)	Low, High	Trapezoidal

  . Two trapezoidal terms were used for (K) and (L) to reflect a threshold-like adequate vs. inadequate availability with diminishing returns once a minimum level is met, which sharply simplifies the rule base without losing discriminatory power for these inputs. In contrast, Energy reliability (E) shows graded effects around the mid-range in our sensitivity scans, so it kept three (Low/Moderate/High) Gaussian terms to resolve those transitions.

2.

Three Gaussian MFs for Energy (E): Models smooth, continuous fluctuations in grid reliability (e.g., voltage sags, transient outages) with bell-shaped curves rather than hard thresholds. Uses three overlapping levels (Low, Moderate, High) to discriminate small yet critical changes in energy availability.

3.

Two Trapezoidal MFs for Capital (K) and Labor (L): Captures step-like “adequacy” behavior. Once a minimum resource level is reached, it further increases yield, diminishing returns via flat-topped functions with linear shoulders. Additionally, it simplifies the rule base by only distinguishing between “Low” and “High,” thereby keeping expert elicitation and computation manageable.

The grid ensures every (E, K, L) combination triggers at least one rule, with no gaps in factory-adaptability assessment. Gaussian and trapezoidal shapes extend naturally to Interval Type-2 (by adding Footprints of Uncertainty), supporting noise modeling and linguistic vagueness without wholesale redesign.

• Encode the rule base using Mamdani inference logic.
• Apply fuzzy aggregation and defuzzification (using the centroid method).
• Simulate multiple input scenarios and visualize results using 3D surface plots.

Additionally, two versions of the system were developed:

• A Type-1 FIS, suitable for systems with low input uncertainty.
• A Type-2 FIS is used to model higher uncertainty in energy, labor, or capital estimates using secondary membership functions and the footprint of uncertainty (FOU).

This paper demonstrates that the twelve Mamdani rules in the proposed knowledge base span the entire input hypercube. Consequently, every crisp triplet (E,K,L) possesses strictly positive membership in the antecedent of at least one rule, guaranteeing that the fuzzy-inference engine always returns a valid output. The three input variables, energy reliability (E), capital intensity (K), and labor availability (L), are described by overlapping membership functions, so each numeric value belongs to at least one linguistic term on every axis. Because the linguistic design employs three terms for E (Low, Moderate, High) and two terms each for K and L (Low, High), the canonical combinatorial space contains 12 distinct antecedent triples. The accompanying coverage table assigns each of these 12 triples to exactly one rule; where adjacent fuzzy sets intersect, a numeric point may activate more than one rule, but no point is ever left without coverage. Given that (i) every numeric input excites at least one linguistic term per variable and (ii) every linguistic combination appears as a rule antecedent, the max–min composition inherent in Mamdani reasoning ensures that at least one rule fires with non-zero strength for every (E,K,L) ∈ Ω. The 12-rule base is therefore exhaustive, eliminating dead zones in the fuzzy logic’s operating envelope. This comprehensive coverage ensures that the Fuzzy–CES module generates a well-defined elasticity scenario for any combination of energy reliability, capital utilization, and labor availability, a crucial prerequisite for real-time decision support in nearshoring factories facing volatile grid conditions. The complete twelve-rule knowledge base is presented below.

• R1 IF EnergyReliability is Low AND Capital is Low AND Labor is Low THEN ElasticityScenario is Low
• R2 IF EnergyReliability is Low AND Capital is Low AND Labor is High THEN ElasticityScenario is Low
• R3 IF EnergyReliability is Low AND Capital is High AND Labor is Low THEN ElasticityScenario is Moderate
• R4 IF EnergyReliability is Low AND Capital is High AND Labor is High THEN ElasticityScenario is Moderate
• R5 IF EnergyReliability is Moderate AND Capital is Low AND Labor is Low THEN ElasticityScenario is Low
• R6 IF EnergyReliability is Moderate AND Capital is Low AND Labor is High THEN ElasticityScenario is Moderate
• R7 IF EnergyReliability is Moderate AND Capital is High AND Labor is Low THEN ElasticityScenario is Moderate
• R8 IF EnergyReliability is Moderate AND Capital is High AND Labor is High THEN ElasticityScenario is High
• R9 IF EnergyReliability is High AND Capital is Low AND Labor is Low THEN ElasticityScenario is Moderate
• R10 IF EnergyReliability is High AND Capital is Low AND Labor is High THEN ElasticityScenario is Moderate
• R11 IF EnergyReliability is High AND Capital is High AND Labor is Low THEN ElasticityScenario is High
• R12 IF EnergyReliability is High AND Capital is High AND Labor is High THEN ElasticityScenario is High

3.2. Integration with CES Production Function

The Constant-Elasticity-of-Substitution (CES) production function furnishes the theoretical foundation for the fuzzy-logic decision framework by formalizing the joint contribution of capital K, labor L and energy reliability E to aggregate output. Crucially, the fuzzy system does not attempt to solve the CES equation numerically in real time; instead, it treats the substitution parameter ρ as a conceptual input that shapes rule construction and simulation-scenario design. Practically, each elasticity band derived from ρ (low, moderate, high) dictates the membership functions’ geometry and the rule base’s logical structure. This design choice enables the inference engine to simulate how deterioration in E propagates through the production process and how the substitutability of K and L can compensate for energy shortages.

Variable selection follows directly from CES theory: because K, L and E are the only leverage points in the production function, they are adopted as the exclusive inputs of the fuzzy system, while total-factor productivity A could be held constant and therefore omitted from the rule base. Membership-function tuning then mirrors the elasticity regime implied by ρ. In low-elasticity contexts, narrow and steep sets ensure that even modest drops in energy reliability quickly push the system into a state of low adaptability. Conversely, high-elasticity contexts employ broader, overlapping sets that reflect the wider latitude for factor substitution documented by CES theory. Rule antecedents and consequents are crafted to replicate the slopes of CES isoquants. A rule such as “IF Energy Reliability is Low AND Capital is High AND Labor is High THEN Elasticity Scenario is Moderate” operationalizes the theoretical proposition that abundant K and L can partially, though not fully, offset an energy deficit. The analyst designates a target elasticity band during simulation and injects representative (E, K, L) triplets into the fuzzy inference system. Because the rule base has been pre-calibrated to the selected ρ, the engine instantaneously returns an elasticity classification of low, moderate, or high, thereby conveying, without numerically solving the CES expression, how variations in energy reliability affect output and how capital–labor adjustments may restore production. In this way, the CES function informs variable interpretation and rule design. Figure 6 shows the flow diagram of the framework. At the same time, the fuzzy-logic layer delivers computational economy and real-time applicability for nearshoring operations in energy-volatile regions of Mexico. A compact pseudocode is presented below (Algorithm 1).

Algorithm 1 Type-1 and Type-2 Fuzzy Inference Procedure
1:	Require: S: scenario grid over (E, K, L)
2:	Require: Membership functions (MFs):
3:	E: 3 Gaussian functions {Low, Moderate, High}
4:	K: 2 trapezoidal functions {Low, High}
5:	L: 2 trapezoidal functions {Low, High}
6:	Require: Rule base: 12 Mamdani IF–THEN rules (R1 − R12)
7:	Require: Inference: Mamdani min–max
8:	Require: Defuzzification:
9:	Type-1: centroid
10:	Type-2: Karnik–Mendel (KM) type-reduction → centroid
11:	Require: Noise/FOU parameters (Type-2 only):
12:	Ehat ∼ N (E, σε)
13:	Khat = K + U (−δK, +δK)
14:	Lhat = L + U (−δL, +δL)
15:	Build footprint of uncertainty (FOU):
16:	Increase σE → σE (1 + ρE)
17:	Widen trapezoidal shoulders by (δK, δL).
18:	Apply Mamdani min–max inference on extended MFs. Perform type-reduction via KM algorithm.
19:	Compute final crisp output via centroid defuzzification.
20:	Ensure: Defuzzified Type-1 and Type-2 results for all scenarios in

Scenario Simulation and Analysis

Multiple simulated input conditions were tested to assess the system’s adaptability under different energy availability profiles. Results from the fuzzy inference engine were analyzed to the following:

• Evaluate system recommendations under varying (E, K, L) combinations.
• Identify thresholds where energy reliability becomes the limiting factor.
• Compare adaptability under Type-1 and Type-2 fuzzy logic environments.

These simulations support strategic decision-making by identifying necessary investments or workforce adjustments to achieve high production resilience in energy-constrained contexts.

3.3. Fuzzy Logic-Based Decision-Making System

This fuzzy logic-based decision-making system evaluates elasticity scenarios in nearshoring operations and addresses energy challenges. Figure 7 depicts the general description of the Fuzzy Logic Inference System using the Constant Elasticity of Substitution (CES) Production Function. The system uses the CES production function to model the relationships between three key inputs: energy reliability, capital, and labor. Energy reliability refers to the availability and stability of energy resources, with low reliability indicating unstable conditions, moderate reliability representing occasional disruptions, and high reliability indicating consistent energy availability. Capital captures investment levels in machinery, equipment, and infrastructure, ranging from low investment, which limits production capabilities, to high investment, which enhances flexibility. Labor models workforce availability and productivity, where low labor reflects limited capacity and high labor indicates a skilled and efficient workforce.

The system’s output, the decision or elasticity scenario, determines the production process’s adaptability to variations in these inputs. Elasticity is classified into three categories: low elasticity indicates rigidity in the production process with limited adaptability; moderate elasticity reflects a system that is somewhat flexible but constrained; and high elasticity demonstrates robust adaptability to input variations.

The system defines the inputs and outputs using fuzzy membership functions. Energy reliability is modeled with Gaussian functions, allowing smooth transitions between low, moderate, and high states. Capital and labor are modeled with trapezoidal membership functions, which capture their levels. The output decision is classified using triangular membership functions, simplifying the determination of whether the elasticity scenario is low, moderate, or high. Figure 5 illustrates the input and output relationship in the fuzzy logic system. 12 fuzzy rules govern the relationship between inputs and outputs. These rules define how energy reliability, capital, and labor combinations influence the elasticity scenario. For example, when energy reliability, capital, and labor are all low, the system determines the elasticity to be low, reflecting the limited capacity for adaptability. In contrast, if energy reliability, capital, and labor are all high, the system predicts high elasticity, demonstrating a production process that is highly adaptable to changes. Rules account for combinations of inputs and their ability to compensate for deficiencies in one area, such as how high capital and labor levels can mitigate the impact of low energy reliability. The fuzzy logic system dynamically evaluates the relationship between inputs and outputs to provide actionable insights. For instance, low energy reliability typically leads to low elasticity unless offset by high capital or labor levels. Balanced inputs, where energy reliability, capital, and labor are all moderate or high, result in mild or high elasticity, signifying a more adaptable production system.

4. Proposed Framework for Energy Reliability in the Automotive Industry for Nearshoring

The system enables manufacturers to simulate scenarios and visualize the elasticity of production under different conditions. It supports scenario planning, allowing users to test strategies such as increasing capital investment, improving energy reliability, or optimizing labor productivity. By identifying which inputs to adjust, manufacturers can enhance production adaptability and mitigate risks associated with energy disruptions.

To ensure the robustness and generalizability of the proposed Fuzzy–CES framework, input variables for capital (K), labor availability (L), and energy reliability (E) were derived from authoritative, sector-wide data sources, rather than relying solely on a single-factory case (e.g., BMW San Luis Potosí [42,43] or Audi [44]). This approach enables the simulation and validation of elasticity scenarios that reflect the broader landscape of Mexican automotive manufacturing, making the framework more applicable for policymakers and industry practitioners.

Figure 8 provides a geographic overview of Mexico’s major automotive manufacturing sites, including plant locations, aggregate annual vehicle production capacity, and total sector employment, illustrating the spatial distribution and scale of the input variables used in the analysis [45]. The network comprises three types of plants. Vehicle plants comprise a total of 20 facilities, with an annual production capacity of 5,056,148 units and a workforce of 83,967 employees. The engine plants comprise a total of 10 facilities, capable of producing 5,682,180 engines annually and employing 11,534 people. Transmission plants comprise seven facilities, with an annual output of 2,373,800 transmissions and employ 8400 staff [45].

Energy Reliability (E) represents the stability and sufficiency of the electrical supply for automotive manufacturing. Because production in this sector is highly sensitive to power interruptions, resulting in downtime, equipment risk, and supply chain delays, a robust, quantitative reliability metric is essential for both operational and strategic analysis. The Customer Average Interruption Duration Index (CAIDI) is the industry-standard metric for reliability in electric utilities, measuring the average outage duration experienced per user annually (in minutes per year). A lower CAIDI value indicates a more reliable energy supply, and vice versa.

Energy reliability was quantified using the CAIDI reported by CRE for 2023 [46]. CAIDI measures the average annual duration of electrical interruptions experienced per user in each grid division. For comparability, CAIDI values were normalized to a 0–10 scale using the regulatory threshold (CAIDI_DTotal = 70.93 min/year) as the maximum and the best observed regional value (31.47 min/year for Valle de México Centro) as the minimum:

For each state (or plant), the number of employees L_norm was calculated as

E_norm = 10 × (CAIDI_DTotal − CAIDI_region/CAIDI_DTotal − CAIDI_min),

(3)

where

CAIDI_DTotal = 70.93 is the regulatory reference.

CAIDI_min = 31.47 is the best CAIDI among all regions.

CAIDI_region = CAID for each region.

According to CRE [46],

Table 3. Energy reliability expressed in CAIDI and its normalized E. Data source: CRE [46].

Region	Key States Covered	CAIDI [36]	Normalized E
Baja California	Baja California, Baja California Sur	37.12	8.6
Noroeste	Sonora, Sinaloa	41.73	7.4
Norte	Chihuahua, Coahuila, Durango	42.3	7.3
Golfo Norte	Tamaulipas, Nuevo León	49.76	5.4
Golfo Centro	Veracruz	59.57	2.9
Bajío	Guanajuato, Querétaro, Aguascalientes, San Luis Potosí	52.4	4.7
Jalisco	Jalisco	43.59	6.9
Centro Occidente	Zacatecas, Michoacán	50.77	5.1
Centro Sur	Morelos, Puebla	38.84	8.1
Centro Oriente	Hidalgo, Tlaxcala	38.59	8.2
Oriente	Mexico State (East)	70.08	0.2
Sureste	Tabasco, Chiapas, Oaxaca	57.48	3.4
Peninsular	Yucatán, Quintana Roo, Campeche	36.41	8.7
Valle de México Norte	Mexico State (North)	37.01	8.6
Valle de México Centro	CDMX, Mexico State (Center)	31.47	10
Valle de México Sur	Mexico State (South)	34.34	9.3

presents the regional energy reliability in Mexico’s electric grid, CAID and normalized energy reliability € for each distribution division and its main states.

In this research, the K input reflects the scale and technological capability of automotive manufacturing infrastructure. Because direct investment data (plant value, machinery costs) are typically confidential and not consistently reported across states or firms, annual vehicle production capacity serves as a transparent, sectorally valid proxy for deployed capital.

• High production capacity = greater capital investment (larger, more automated, and modern plants).
• This method is widely accepted in industrial engineering and economics for cross-sectional benchmarking.
• For each state (or plant), capital intensity K_norm was calculated as follows:

K_norm = 10 × (K_plant − K_min/K_max − K_min),

(4)

where

K_plant = Annual vehicle production capacity for the state/plant.

K_min, K_max = The minimum and maximum annual production capacities among all plants/states in the national dataset.

According to AMIA [45],

Table 4. Annual vehicle production capacity and normalized capital intensity (K) for Mexican states with automotive assembly plants. Data source: AMIA [45].

State	Vehicle Production Capacity [45]	Normalized K
Aguascalientes	766,708	8.4
Baja California	137,780	0
Coahuila	564,400	5.7
Guanajuato	888,100	10
Jalisco	218,290	1.1
Mexico State	517,920	5.1
Morelos	232,400	1.3
Nuevo Leon	249,000	1.5
Puebla	622,500	6.5
San Luis Potosi	444,050	4.1
Sonora	415,000	3.7

presents the vehicle production capacity and the normalized value. K is expressed on a 0–10 scale, where 0 represents the state with the lowest production capacity (Baja California, 137,780) and 10 corresponds to the highest (Guanajuato, 888,100).

Labor Availability (L) is a key driver of operational flexibility and resilience in the automotive manufacturing industry. It reflects the total workforce available for production, which impacts not only output but also the plant’s ability to adapt to supply or labor shocks.

In a sectoral context, when confidential wage or detailed HR data are not available, the total number of plant employees is a widely accepted and transparent proxy for labor availability. Normalizing this across all plants/states allows for direct benchmarking and integration into your fuzzy inference system [45].

For each state (or plant), the number of employees L_norm was calculated as

L_norm = 10 × (L_plant − L_min/L_max − L_min),

(5)

where

L_plant = Number of employees for each state/plant.

L_min, L_max = The minimum and maximum number of employees among all plants/states.

According to AMIA [45],

Table 5. Total automotive manufacturing employment by state and normalized labor availability (L) on a 0–10 scale. Data source: AMIA [45].

State	Number of Employees [45]	Normalized L
Aguascalientes	13,900	8.2
Baja California	1600	0
Coahuila	9836	5.5
Guanajuato	14,038	8.3
Jalisco	2000	0.3
Mexico State	5953	2.9
Morelos	5183	2.4
Nuevo Leon	3000	0.9
Puebla	16,546	10
San Luis Potosi	7800	4.1
Sonora	4111	1.7

presents the number of employees required for vehicle production capacity and the corresponding normalized value. L is expressed on a 0–10 scale, where 0 represents the state with the lowest number of employees (Baja California, with 1600), and 10 corresponds to the highest (Puebla, with 16,546).

Once the input variables, E, K, and L, have been objectively quantified and normalized on a sectoral scale, the fuzzy inference system can be used to assess real-world production adaptability in Mexican automotive plants.

Therefore, each plant or region can be characterized by its unique E, K, and L profile, calculated using the presented normalization procedures and public sector data.

Table 6. Normalized input variables (E, K, and L) for the fuzzy inference framework for each major automotive-producing Mexican state.

State	E	K	L
Aguascalientes	4.7	8.4	8.2
Baja California	8.6	0	0
Coahuila	7.3	5.7	5.5
Guanajuato	4.7	10	8.3
Jalisco	6.9	1.1	0.3
Mexico State	0.2 (East), 8.6 (North), 10 (Center), 9.3 (South)	5.1	2.9
Morelos	8.1	1.3	2.4
Nuevo Leon	5.4	1.5	0.9
Puebla	8.1	6.5	10
San Luis Potosi	4.7	4.1	4.1
Sonora	7.4	3.7	1.7

presents the normalized input variables of the automotive assembly parts. For example, a plant in San Luis Potosí (Bajío region) may have E = 4.7, K = 4.1 and L = 4.1. These normalized values are then directly entered as the three inputs to the fuzzy logic system, triggering a set of inference rules. Regarding Mexico States, the E value is shown for each major electrical distribution subregion.

The following depicts in detail how varying E, K, and L, either individually or in combination, impact the decision surface and adaptability classification of the production system. By running these scenarios, the framework provides:

• Quantitative assessment of production elasticity (adaptability) under current conditions.
• Actionable recommendations—for instance, identifying whether improvements in grid reliability, upskilling of labor, or capital investment would most enhance resilience.
• Comparative benchmarking: Plants or regions can be compared on a standardized scale, supporting both local optimization and national-level policy.

The results of this fuzzy logic system include clear insights into production flexibility, actionable guidance for resource allocation, and improved decision-making for nearshoring operations. For example, using the fuzzy rules, the normalized E, K, and L values from Table 6 allow for a precise interpretation of production elasticity for each state.

This fuzzy logic system provides manufacturers with a comprehensive tool to evaluate and optimize production adaptability in the face of energy and operational challenges. By capturing the complexities of real-world scenarios and offering data-driven insights, the system empowers stakeholders to make informed decisions that enhance resilience, efficiency, and sustainability in their nearshoring operations.

The surface of the proposed Type-1 fuzzy system (see Figure 9a) visually demonstrates the relationship between capital investment, energy reliability, and the resulting elasticity of production. The Decision surface attains its minimum when both capital and energy reliability are near the origin of their scales, corresponding to states such as Baja California (K, L = 0, E = 8.6), where capital is very low, even if energy reliability is high. According to the fuzzy rules (specifically Rule 9), these conditions result in only moderate elasticity, underscoring the limited adaptability in the absence of sufficient capital and labor resources—even when grid conditions are excellent.

Conversely, states like Puebla (K = 6.5, E = 8.1, L = 10) occupy the far upper corner of the surface, where both capital and energy reliability are high. Here, the system achieves its global maximum, consistent with Rule 12, which classifies this configuration as high elasticity. These conditions reflect a robust production environment, well-positioned to accommodate the fluctuations and uncertainties typical of nearshoring operations.

The surface is not strictly monotonic. Along the capital axis, when energy reliability is very low (E near 0), increasing capital from low to moderate values may initially lower the decision score before a gradual recovery, illustrating that greater investment alone does not automatically confer adaptability if the grid remains unstable. This is evident in regions where either capital or labor is high, but energy reliability remains low, highlighting the necessity of a balanced resource profile for optimal adaptability.

For states like San Luis Potosí (E = 4.7, K = 4.1, L = 4.1), all three inputs are moderate. These points lie along the surface ridge where marginal gains in adaptability become apparent as either capital or energy reliability improves. The system, as per the rule base, identifies such configurations as moderate to high elasticity, but also signals that targeted improvements in any input could push the system toward maximum adaptability.

Hence, the idea that capital expansion alone can offset poor grid conditions must be tempered; any compensation is partial and cannot match the performance achievable with reliable power. A pronounced ridge appears where Energy Reliability is moderate (around 4–6) and Capital is at least moderate (4 or higher); here, improvements in either input reinforce each other. However, beyond this ridge, the marginal gains taper off, reflecting saturation in the fuzzy rule base.

Overall, the surface confirms the study’s central argument: Capital deepening alone will not provide the elasticity needed for Mexican nearshoring factories to withstand grid volatility, unless it is accompanied by investment in local energy security, such as microgrids or on-site renewables. This finding is particularly salient in the Mexican context, where automotive vehicle assembly plants are concentrated in just 11 out of 32 states, and the distribution of energy reliability (E) is far from uniform across regions. As seen in Table 3, states such as Baja California (E = 8.6), Puebla (E = 8.1), and Mexico State (North, Center, South; E = 8.6–10) exhibit high energy reliability. In contrast, key automotive states such as Guanajuato, San Luis Potosí, and Aguascalientes, all in the Bajío region, have only moderate energy reliability (E ≈ 4.7). The situation is even more acute in Nuevo León (E = 5.4) and Coahuila (E = 7.3), both of which are central to automotive production, yet face grid conditions that cannot be classified as optimal.

Overall, the surface confirms the study’s central argument. Unless firms invest in local energy security, such as microgrids or on-site renewables, capital deepening will not provide the elasticity needed for Mexican nearshoring factories to withstand grid volatility.

The surface of the proposed fuzzy type 2 is presented in Figure 9b, and it is recommended for use when high uncertainty is present in the system. It depicts the Type-2 fuzzy surface for the Decision score as a joint function of Capital and Energy-Reliability. The minimum Decision values arise near the origin, where both inputs are small; under these conditions, the production system cannot compensate for supply interruptions. Raising Capital while holding Energy Reliability near its lower bound gradually lifts the surface, confirming that investment in factories or energy-saving technologies can confer limited resilience even when the grid remains unstable. Nevertheless, the effect is bounded: the Decision score reaches only moderate levels until Energy-Reliability improves.

Once Energy-Reliability enters a mid-range band, roughly the central third of its scale, the surface exhibits a pronounced upward slope, and additional capital investment yields much steeper gains in the Decision metric. Beyond this ridge, the surface begins to level off, indicating diminishing marginal returns as the rule base saturates. The global maximum lies in the far corner where Capital and Energy-Reliability approach their maxima; here, the system is highly adaptable, accommodating load fluctuations without compromising throughput. The Type-2 surface is noticeably smoother than its Type-1 counterpart, particularly along the transition between low and moderate Energy-Reliability. This smoothing reflects the Footprint of Uncertainty embedded in the Type-2 membership functions. By explicitly modeling measurement noise and linguistic vagueness, the Type-2 engine dampens abrupt changes in the decision score that small input perturbations would otherwise trigger. Consequently, the Type-2 system offers more stable guidance when grid conditions or capital estimates fluctuate within realistic error bounds, a desirable property for nearshoring factories operating under Mexico’s volatile power network.

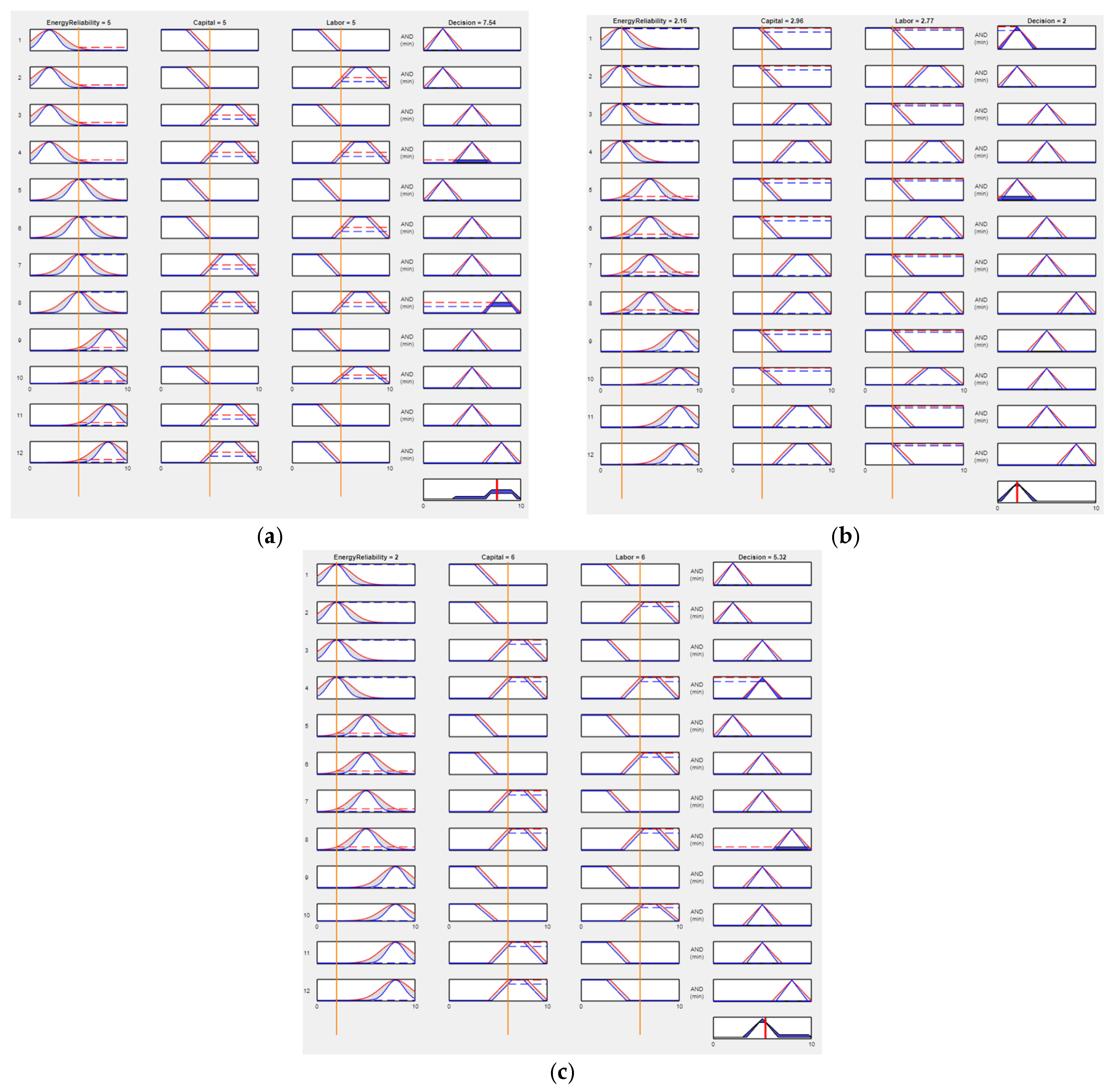
Figure 10a depicts an inference plot for the Type-1 when the factory operates at Energy-Reliability = 5, Capital = 5, and Labor = 5. At these mid-range conditions, the input for Energy-Reliability lies near the center of the “Moderate” membership function and still retains partial grade in “High”; the Capital and Labor share approximately equal membership in “Low” and “High.” As a result, several of the twelve rules fire simultaneously. Each rule’s firing strength is obtained through the standard Mamdani conjunction—minimum across the three antecedent grades, so the aggregated output, shown in the right-hand column, is the union of clipped consequents weighted by those minimum values. Defuzzification by centroid yields an overall Decision score of 7.28, a value in the upper segment of the 0–10 scale. The inference pattern, therefore, confirms that when all three resources are available at moderate-to-high levels, the fuzzy inference system classifies the system as highly adaptable; conversely, a genuinely low-adaptability outcome would require falling predominantly in the lower portions of the input ranges, which is not the case here.

Figure 10b presents a single-step inference of the interval Type-1 Mamdani fuzzy system for the input vector (E,K,L) = (2.16, 2.96, 2.77). The vertical line in the three left-hand columns represents their respective membership functions activated. Energy-Reliability falls deep within the “Low” Gaussian set and acquires only a negligible grade in “Moderate.” Capital and Labor intersect the midpoint of their trapezoidal “Low” sets while retaining a small but non-zero grade in “High,” an overlap intrinsic to the two-term partitions for these variables.

Given that the dominant membership grades correspond to “Low” on every axis, the rules whose antecedents comprise the Low–Low–Low triple fire have the highest strength. The fourth column shows their consequences after clipping; the union of these truncated output sets forms a composite fuzzy region concentrated in the first quartile of the decision universe. Centroid defuzzification of this region yields a Decision score of approximately 2.0. This numerical result places the operating point firmly within the low-elasticity regime defined earlier. Practically, a factory running at these resource levels would possess limited flexibility to reallocate inputs if external power quality were to deteriorate. The inference plot, therefore, corroborates the broader conclusion drawn from the surface analyses. Without additional capital reserves or a more reliable energy supply, the production system remains insufficiently adaptable for robust nearshoring operations. Figure 10c illustrates the inference step for the input vector (Energy-Reliability = 2.0, Capital = 6.0, Labor = 6.0). The Energy-Reliability falls almost entirely within the “Low” membership function; its grade in “Moderate” is negligible. Capital and Labor intersect the upper half of their “High” trapezoids while retaining a small grade in “Low,” as intended by the overlapping design.

Because the dominant grades correspond to Low–High–High, the rules with that antecedent fire most strongly. Their clipped consequences aggregate into an output region centered in the middle segment of the decision universe. Centroid defuzzification produces a Decision value of 5.67. This numerical result places the operating point in the intermediate-elasticity regime: substantial capital and labor mitigate, but do not fully overcome, the limitation imposed by low energy reliability. The outcome confirms that meaningful resilience requires improvements in resource investment and grid stability.

Figure 11a shows a single inference step of the interval Type-2 Mamdani system for the balanced input vector (E,K,L) = (5, 5, 5). Each of the three input intersects its corresponding “Moderate” membership function at full grade and retains a non-negligible grade in the neighboring “High” set. The upper and lower bounds of every Type-2 membership function are displayed as paired curves, illustrating the footprint of uncertainty that distinguishes the Type-2 representation from its Type-1 counterpart.

Because substantial membership is present in both “Moderate” and “High” terms, several rules fire with comparable strength, chiefly those that contain the Moderate–Moderate–Moderate and High–High–High antecedent triples. After the usual minimum-operator conjunction, their clipped consequents aggregate into an output region centered in the upper third of the decision universe. Centroid defuzzification of this region yields a Decision value of 7.54.

This result places the operating point in the high-elasticity regime, confirming that when energy reliability, capital, and labor are all held at mid-to-upper values, the fuzzy system classifies the production system as strongly adaptable. The visibly smoother transition between the contributing rules, an effect of the interval Type-2 footprint, demonstrates the enhanced robustness of the Type-2 approach; small perturbations in the input would shift both the upper and lower membership bounds rather than altering a single crisp grade, thereby stabilizing the defuzzified output. Figure 11b describes an inference step of the interval Type-2 Mamdani fuzzy system for the input vector (E,K,L) = (2.16, 2.96, 2.77). The vertical guideline in the three input panels marks the value relative to its two-level membership functions (upper and lower bounds shown as paired curves). Energy-Reliability is almost wholly contained in the “Low” set, while Capital and Labor lie near the center of their “Low” trapezoids and contribute only a marginal grade to “High.”

Because the dominant memberships correspond to the Low–Low–Low antecedent, the rule block associated with that combination fires with greatest strength. The clipped consequences merge into an output region confined to the lowest quarter of the decision universe. Centroid defuzzification of the aggregated set returns a Decision score of 2.0.

This value places the operating point in the low-elasticity regime: the factory could not reallocate resources if external power quality deteriorated. Figure 11c reinforces the earlier surface analysis, demonstrating that without reliable energy and additional capital, the fuzzy inference system judges the production system insufficiently adaptable for robust nearshoring operations. Also, it presents the Type-2 Mamdani inference for the operating point (E,K,L) = (2, 6, 6). Energy-Reliability lies almost entirely within its “Low” membership set. Capital and Labor intersect the upper half of their “High” trapezoids while sharing a small grade with “Low,” reflecting the intended overlap between neighboring sets. The paired upper- and lower-boundary curves shown for every membership function visualize the footprint of uncertainty characteristic of the Type-2 formulation.

The rules combine low energy with high capital and labor, fire most strongly; their consequences dominate the aggregated output centered in the middle portion of the decision scale. Centroid defuzzification yields a Decision value of 5.32.

This result situates the factory in an intermediate-elasticity regime. Significant capital resources and labor availability provide some capacity to adapt. Still, persistently low energy reliability prevents the system from reaching the high-adaptability range documented under more favorable grid conditions. Figure 11c reinforces the earlier conclusion that capital deepening can only partially offset the performance penalties imposed by an unstable energy supply.

Figure 12 illustrates the general representation of the proposed fuzzy logic systems, types 1 (a) and 2 (b). The memberships are also presented.

Contribution to Nearshoring and Energy Challenges Using a Fuzzy Logic Strategy

The proposed fuzzy logic system could directly address the energy challenges faced by nearshoring operations by offering manufacturers a structured method to evaluate and adapt their production strategies [47]. It enables companies to assess the impact of energy reliability on production processes and develop strategies to stabilize energy inputs, such as implementing renewable energy systems, investing in energy-efficient technologies, or enhancing storage capabilities. For example, the system advises long-term solutions in regions with low energy reliability, such as deploying microgrids or renewable energy infrastructure. In high elasticity scenarios, it emphasizes short-term strategies, such as increasing labor or capital investments, to sustain production.

The system provides actionable insights for investment decisions by enabling manufacturers to determine whether additional capital or labor can compensate for energy deficits. By simulating varying scenarios of energy reliability, capital, and labor availability, the system guides manufacturers in balancing resource allocation to maximize productivity. This approach is especially critical in industrial hubs with high energy demand, such as northern Mexico, as it ensures production continuity and operational efficiency.

This system’s significant contribution lies in its ability to optimize resource allocation by analyzing how inputs (energy, capital, and labor) interact under different energy conditions. It helps manufacturers prioritize renewable energy integration and energy-efficient technologies, ensuring that production processes are resilient and sustainable. The fuzzy logic system reduces reliance on trial-and-error methods, saving time and resources while enabling data-driven decisions that address specific energy challenges in nearshoring contexts.

The proposed system aligns with the goals of nearshoring by providing manufacturers with a tool to enhance their competitiveness and sustainability. It allows companies to anticipate energy-related risks, adapt their production processes accordingly, and make informed decisions that support long-term operational success. By integrating advanced computational techniques, this system enhances Mexico’s position as a leading nearshoring destination, enabling manufacturers to overcome energy challenges while maintaining high levels of productivity and adaptability.

This paper demonstrates the transformative potential of fuzzy logic systems in modern manufacturing. Combining advanced decision-making capabilities with practical applications provides a scalable and efficient solution to nearshoring and energy reliability challenges. The system’s ability to simulate real-world scenarios and generate actionable insights makes it an invaluable tool for navigating the complexities of energy challenges in global supply chain realignments.

Fuzzy Logic Type-1 employs fixed membership functions with precise parameters for inputs such as Energy Reliability, Capital, and Labor. These inputs have a single value representing their degree of membership, which works well when the inputs are stable and well-defined. However, this approach may become less adaptable in uncertain environments, as even slight changes in input values can lead to substantial changes in the output.

On the other hand, Fuzzy Logic Type 2 represents membership functions as ranges rather than fixed values. This “cloud” of possible membership values allows Type 2 fuzzy logic to handle better input uncertainty and variability, such as fluctuating energy reliability or labor availability in nearshoring operations. Accounting for uncertainty directly offers greater flexibility and robustness. The system can adapt to changes in conditions, ensuring that decision-making remains stable and accurate even when input data is imprecise or fluctuating. One key advantage of Type 2 over Type 1 is its ability to handle uncertainty more effectively. It allows the system to accommodate fluctuating inputs accurately, such as energy reliability. Type 2 also offers improved robustness because it remains stable when input data is uncertain or imprecise. Additionally, since uncertainty is inherently represented within the membership functions, Type 2 typically requires fewer rules, which enhances computational efficiency. The flexibility of Type 2 allows it to dynamically adjust to changing conditions, making it more adaptable to real-world situations. Type 2 is more suited to environments where input data fluctuates or is uncertain. It provides more robust, flexible, and adaptable decision-making tools than Type 1, making it especially valuable for addressing manufacturers’ energy challenges, particularly in nearshoring operations. Its ability to model uncertainty and variation within the membership functions gives it a significant advantage in optimizing production adaptability under varying conditions.

5. Discussion

The findings of this study underscore the pivotal role of energy reliability in determining the production elasticity and overall adaptability of nearshoring operations in Mexico’s automotive sector. As shown by recent surveys and analyses [6,7,8], manufacturing output in Mexico remains highly sensitive to both energy price fluctuations and grid disruptions, with elasticity estimates for the auto sector ranging from −0.28 to −0.51, substantially larger in magnitude than those reported in other industrial contexts. Our simulation results reinforce these observations: even in states with robust capital and labor inputs, such as Guanajuato and San Luis Potosí, only moderate levels of energy reliability limit the achievable production elasticity, confirming previous research that identifies energy as a primary constraint on manufacturing resilience [7,8].

Unlike conventional optimization frameworks, such as mixed-integer linear programming and stochastic programming, which require detailed probabilistic knowledge of future energy states and often fail to adapt to real-time variability [13,14], the fuzzy logic-based approach presented here offers greater interpretability and responsiveness to practical uncertainties. The integration of the Constant Elasticity of Substitution (CES) function within the fuzzy inference system distinguishes this framework from earlier models by embedding an explicit economic rationale for factor substitution, as advocated by CES theory [11,12,25,26]. This hybrid methodology advances recent calls for decision-support systems that account for the joint effects of capital, labor, and energy in dynamic industrial settings [30].

The case studies analyzed provide further nuance to the theoretical implications of the model. In Puebla, where all three normalized inputs, energy reliability, capital, and labor, are high, the fuzzy-CES system predicts high elasticity, in line with actual plant performance and recent investment trends [45]. Conversely, in Baja California, despite high energy reliability, the absence of sufficient capital and labor yields only moderate elasticity, illustrating the limitations of capital deepening as a standalone strategy. This finding aligns with empirical research highlighting the diminishing returns of single-factor investments in the absence of systemic grid improvements [7,9].

Moreover, the introduction of Type-2 fuzzy logic provides increased robustness under conditions of input uncertainty, as suggested by earlier work on interval type-2 systems [34,35,37,38]. The system’s enhanced stability in the face of fluctuating energy and labor inputs is especially relevant in Mexico’s northern industrial hubs, where supply chain volatility and labor market dynamics frequently challenge deterministic planning. These results are based on simulation studies showing that uncertainty-aware models yield improved performance in energy-constrained environments [30,39].

Importantly, the framework’s practical value extends beyond operational decision-making. By providing actionable, state-level recommendations, for example, prioritizing microgrid deployment in Guanajuato or capital investment in Baja California, the system supports both firm-level strategy and regional policy development. Such recommendations echo the growing emphasis in the recent literature on targeted, data-driven interventions to enhance energy resilience and manufacturing competitiveness [7,9]. The methodology also aligns with Mexico’s broader policy objectives regarding grid modernization, renewable integration, and industrial decarbonization [7,10].

This hybridization advances earlier on energy-aware production scheduling by offering a more interpretable and adaptable model. Unlike purely statistical or black-box AI approaches, the fuzzy-CES framework retains transparency in how decisions are derived, facilitating better stakeholder trust and operational integration. The implications of this system are significant for both operational and strategic levels. On the operational side, manufacturers can use the system to evaluate investment trade-offs and prioritize resource reallocation in response to energy instability. For example, in scenarios where increasing labor is impractical due to skill shortages, the model helps identify whether capital investments, such as energy-efficient equipment, could be effective substitutes.

Strategically, the system enables long-term planning by identifying thresholds where infrastructure investment (e.g., microgrids or renewable energy deployment) becomes essential. In this way, the framework supports policy-aligned industrial strategies aimed at reducing dependency on fossil fuels while enhancing the resilience of manufacturing supply chains. Moreover, this research aligns with Mexico’s national decarbonization and energy modernization goals. The ability to evaluate production resilience in energy-constrained contexts complements broader sustainability targets and positions Mexican nearshoring hubs to attract more resilient, energy-responsible manufacturing operations.

While the system offers valuable insights, several limitations merit further investigation. First, the current fuzzy rule base is manually designed, relying on expert heuristics. Integrating machine learning techniques for rule induction could enhance scalability and precision as complexity increases. Second, the model does not currently incorporate real-time energy pricing or demand-response signals, which are increasingly important in dynamic energy markets. Future enhancements should include temporal variables and adaptive rule updating mechanisms. Additionally, although the system uses synthetic scenarios, its validation in a live industrial environment remains an important next step. Collaborations with manufacturers operating in energy-variable regions would provide real-world data for fine-tuning membership functions, improving defuzzification accuracy, and demonstrating commercial feasibility.

6. Conclusions

This paper presents a fuzzy logic-based decision-making framework that effectively addresses the pressing energy reliability challenges facing nearshoring operations in Mexico. By integrating the Constant Elasticity of Substitution (CES) production function into a fuzzy inference system, the model provides a robust, data-driven approach for assessing production adaptability under varying input conditions, namely, energy reliability, capital investment, and labor availability. The proposed system distinguishes itself through its ability to classify production adaptability into distinct elasticity scenarios (low, moderate, and high), offering actionable insights that manufacturers can use to mitigate risks and optimize operational resilience. These elasticity scenarios serve as a strategic guide to identify when capital and labor investments can compensate for limited energy availability, and when more structural interventions, such as integrating renewable energy or deploying microgrids, are required.

Empirical analysis of Mexico’s automotive sector demonstrates that production elasticity is highly sensitive to the weakest link among energy reliability, capital investment, and labor availability. The study shows that even world-class plants with leading capital and labor metrics are constrained by only moderate energy reliability—a scenario common in central Mexican manufacturing hubs. Conversely, where all three factors are strong, factories achieve maximum adaptability and resilience, confirming the framework’s predictive utility. By applying Fuzzy Logic Type-1 and Type-2, the system captures varying degrees of uncertainty in real-world manufacturing environments. While Type-1 performs well under defined conditions, the Type-2 variant enhances adaptability and stability in uncertain or rapidly changing scenarios, such as those common in energy-volatile regions of northern Mexico. Simulation results reinforce the system’s practical utility. When tested under diverse combinations of input values, the fuzzy logic engine provided consistent and interpretable output decisions that align with the underlying CES production theory.

These insights enable manufacturers to evaluate potential disruptions preemptively, adapt their strategies, and make informed decisions about resource allocation, thereby improving productivity and reducing vulnerability to energy constraints. From a broader perspective, this work contributes to the literature on energy-aware manufacturing and industrial adaptability by demonstrating how fuzzy logic systems can be operationalized to support strategic planning in nearshoring contexts. It also bridges theoretical economic models (CES functions) with applied AI techniques, reinforcing the value of hybrid models for industrial decision support. In practical terms, this research recommends a dual strategy for Mexico’s nearshoring sector: sustained investment in both traditional production factors (capital and labor) and targeted improvements in energy infrastructure, especially through distributed and renewable solutions. This approach is essential for maintaining competitiveness and fulfilling the promise of nearshoring in an increasingly volatile global landscape. Moreover, the presented case study of the automotive industry describes how the proposed framework is implemented. As a result, this framework can be implemented in several industries.

Future work should expand the framework’s application to other sectors and integrate real-time energy and market data. Collaborations with industry stakeholders will be vital for refining the tool and ensuring its relevance and impact on Mexico’s and the region’s industrial resilience. Finally, our future work will involve a systematic elicitation and analysis of practitioner feedback to validate and refine the proposed fuzzy CES framework. Although interviews with plant managers can yield valuable insights into real-world applicability and usability, conducting and rigorously coding these discussions fall outside the scope of the present manuscript, which is devoted to developing and demonstrating the core model architecture and its simulation results. Consequently, we will pursue a dedicated qualitative study, informed by thematic coding and triangulated against quantitative performance metrics, in a subsequent publication to ensure that practitioner perspectives meaningfully inform framework enhancements.