Numerical Simulation of Gas–Water Two-Phase Seepage During Coalbed Methane Development in ZhengZhuang Block: A Case Study of Well Z29
Abstract
1. Introduction
2. Model Construction
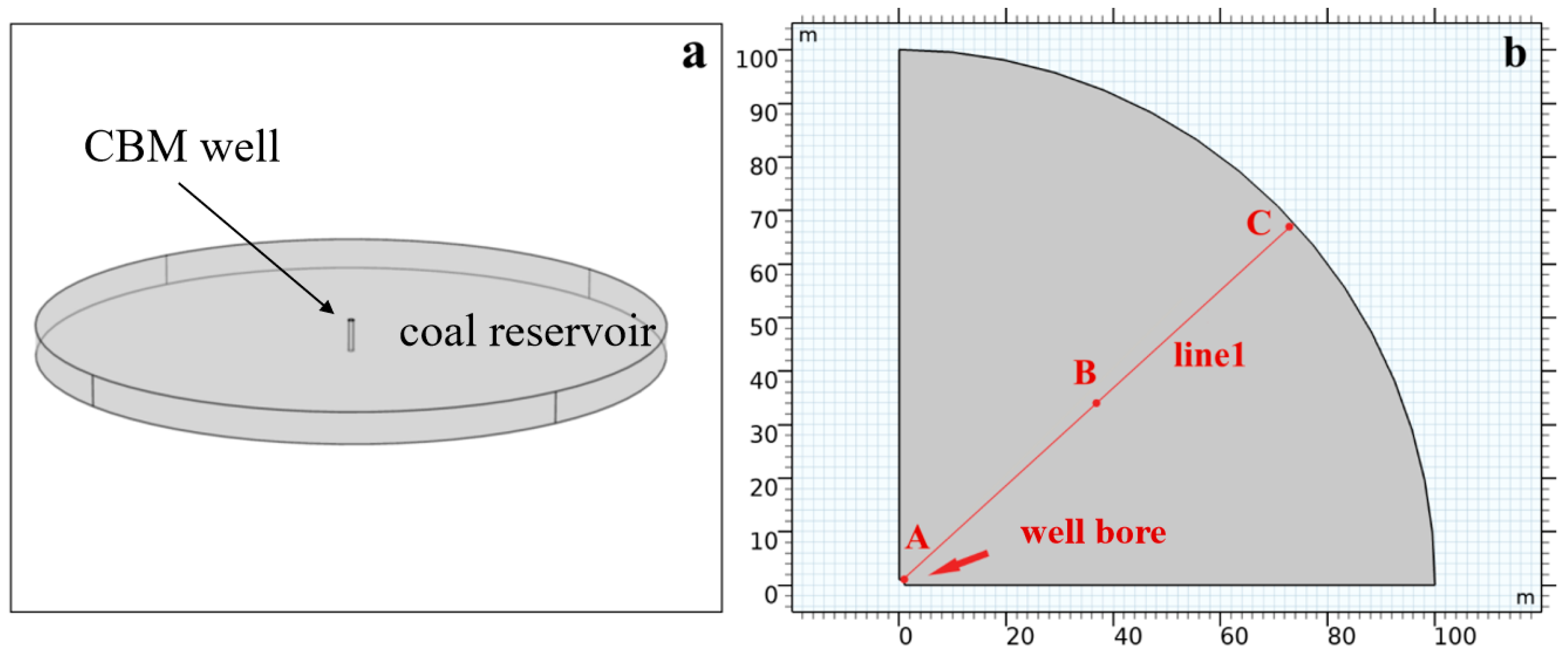
2.1. Establishment and Assumptions of Geometric Model
- (1)
- There are only two types of fluids in the coal reservoir: water and methane.
- (2)
- The deformation of coal reservoirs is relatively small during CBM development.
- (3)
- During the development of CBM, the temperature is kept constant. The fluid viscosity in pores and fractures remains unchanged, and the influence of gravity is not considered.
- (4)
- The compressibility of water is negligible, and methane is an ideal gas.
- (5)
- The fluid flow in the pores and fractures of coal reservoirs conforms to Darcy’s law.
- (6)
- The adsorption/desorption of CBM in coal reservoirs conforms to the Langmuir isotherm equation.
2.2. Construction of Numerical Model and Problem Description
2.3. Model Governing Equations and Boundary Conditions
2.3.1. Dynamic Permeability Change Model
2.3.2. Fluid–Solid Coupling Equations
2.3.3. Production Calculation Equation
2.3.4. Initial and Boundary Conditions
3. Model Validation
4. Results and Discussion
4.1. Influence of Young’s Modulus on the CBM Production
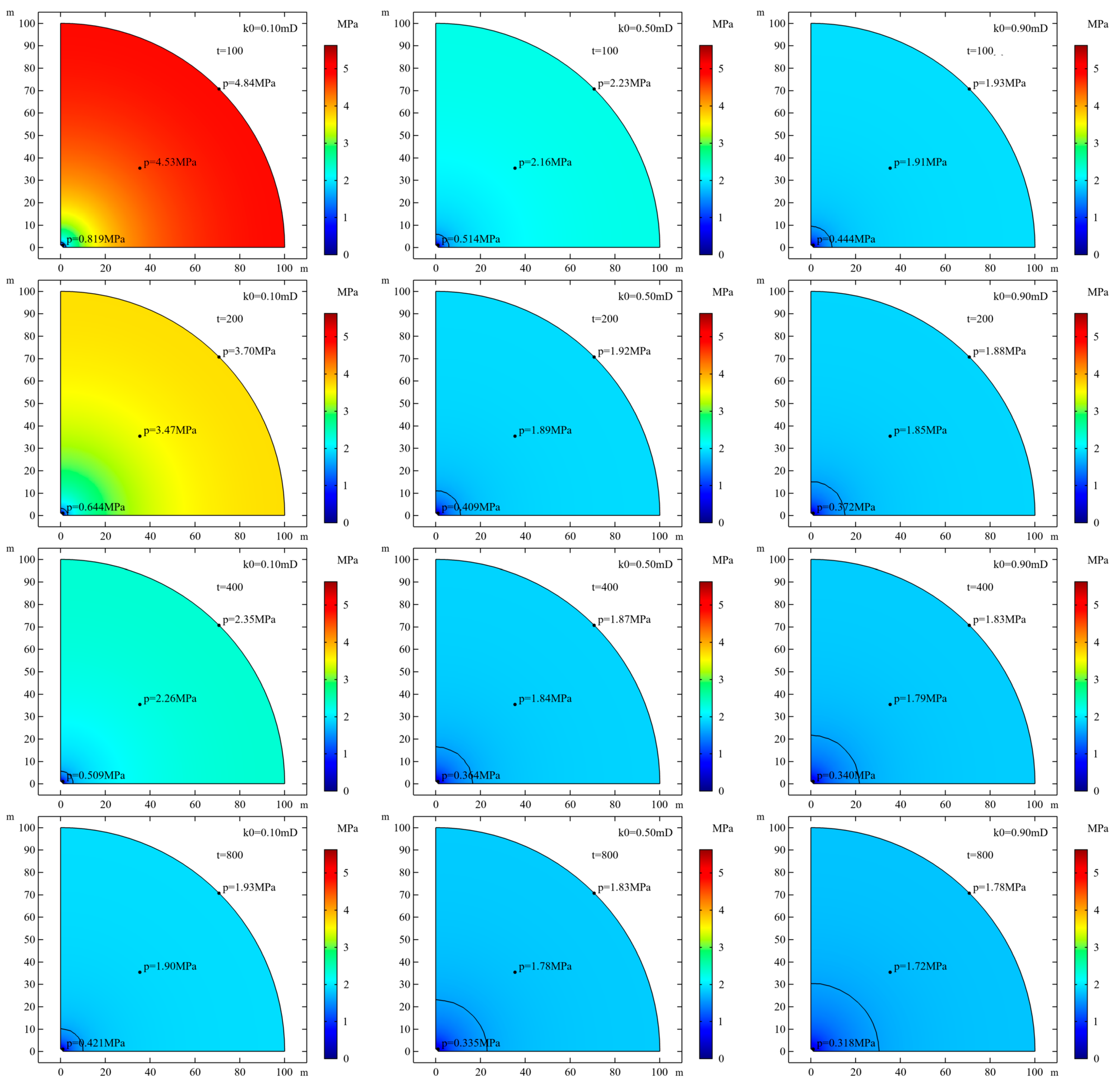
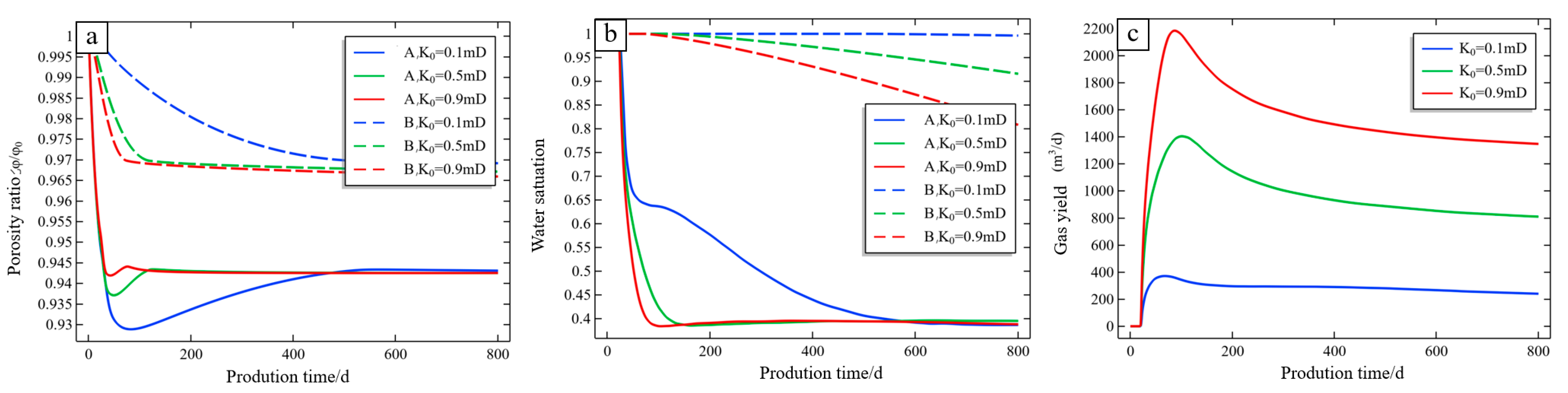
4.2. Influence of Initial Permeability on Gas Production
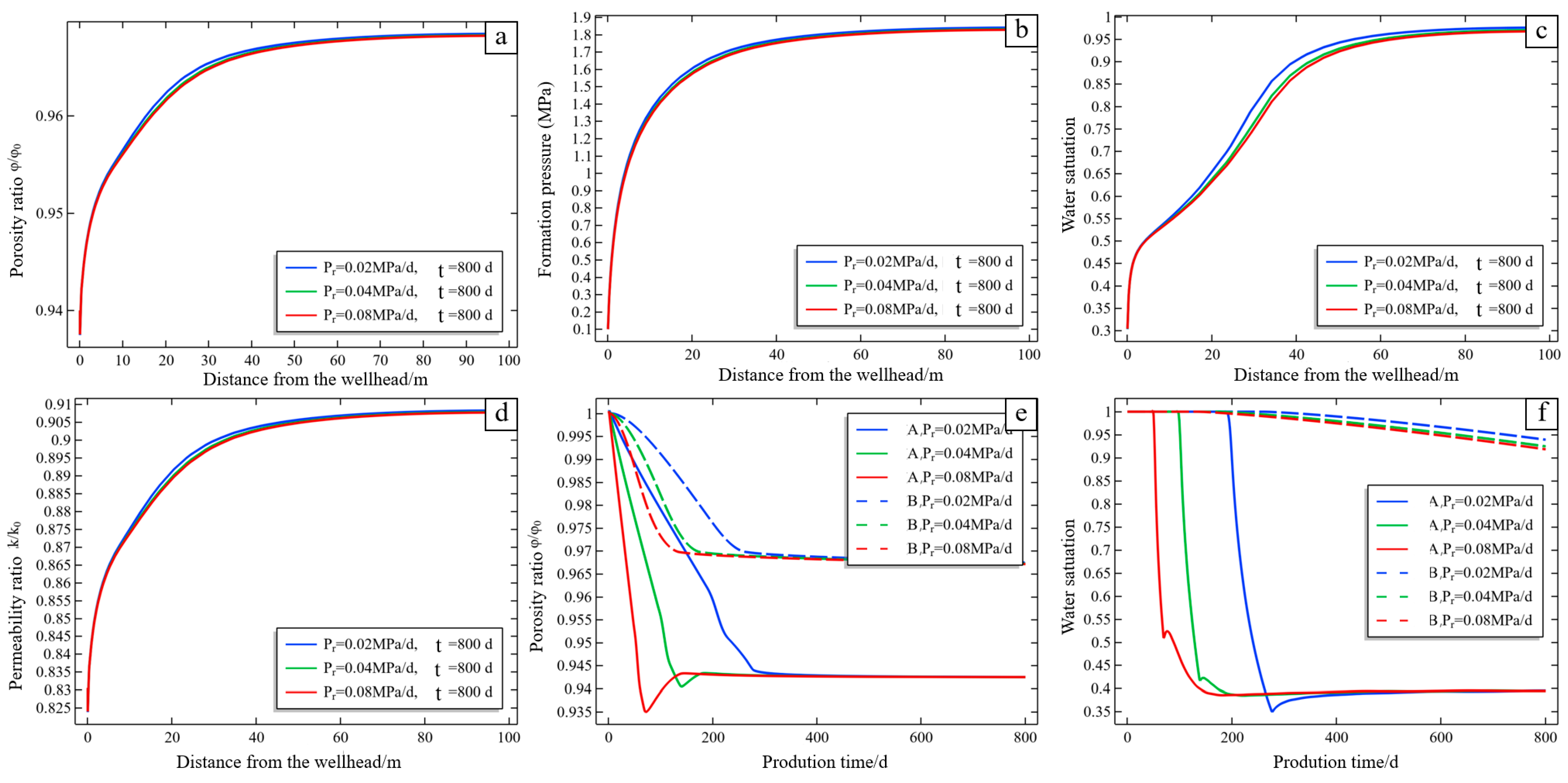
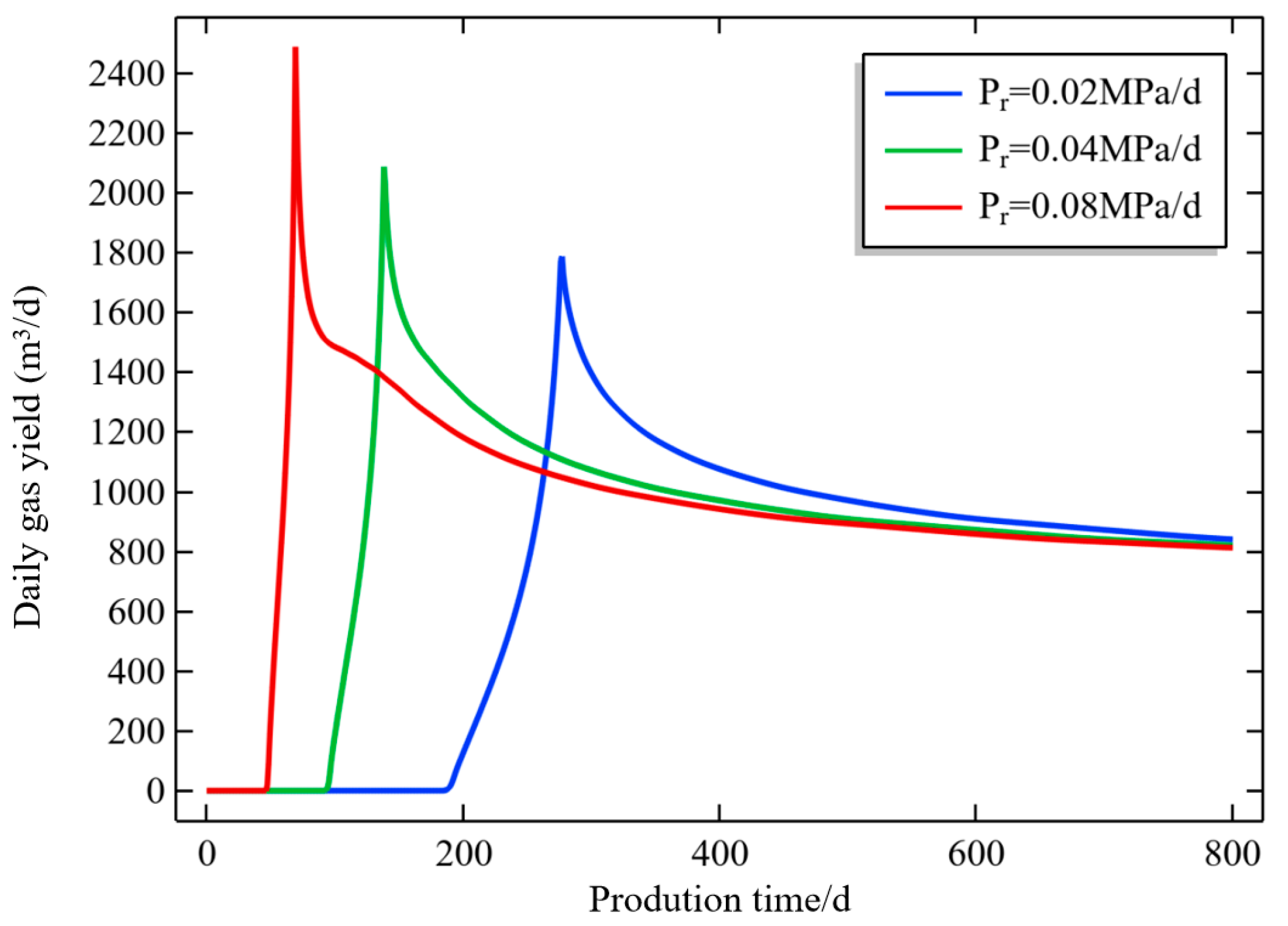
4.3. Influence of Drainage System on CBM Production
5. Conclusions
- (1)
- A higher Young’s modulus in coal reservoirs can make the porosity decline slowly in the zone away from the well bore by preventing a decline in fluid pressure and the deformation of the coal reservoir, which has a positive effect on CBM production. The maximum daily gas production for the coal reservoir with 2.7 GPa is 1402 m3/d, while that with 1.5 GPa is only 1125 m3/d.
- (2)
- The initial permeability of coal reservoirs is a major factor affecting CBM production. A high-permeability reservoir environment can quickly balance the effective stress and matrix shrinkage effect, while a low-permeability reservoir will inhibit the desorption of CBM, thereby affecting coal matrix shrinkage.
- (3)
- Although the faster the pressure reduction rate, the higher the CBM production in the early stage of drainage, formation framework deformation caused by a high pressure drop rate will lead to a decrease in reservoir porosity and permeability, and such a production system is not conducive to the efficient production of CBM. In the actual production process, sudden changes in bottom-hole flowing pressure should be avoided as much as possible to prolong the stable gas production period and achieve sustainable production with high daily gas output.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, X.X.; Wang, H.; Du, F.F.; Yao, Y.B.; Liu, D.M.; Liu, Z. CBM enrichment mechanisms in the Southern Qinshui Basin: A synergistic role of tectonic-lithological-hydrodynamic coupling. Int. J. Coal Geol. 2025, 309, 104861. [Google Scholar] [CrossRef]
- Joussineau, G.D. The impact of multiscale cleat geometry on coal’s petrophysical properties in the Lorraine basin, NE France: Implications for coalbed methane (CBM) production and CO2 storage. J. Struct. Geol. 2025, 191, 105346. [Google Scholar] [CrossRef]
- Min, C.; Wen, G.Q.; Gou, L.J.; Li, X.G.; Yang, Z.Z. Interpretability and causal discovery of the machine learning models to predict the production of CBM wells after hydraulic fracturing. Energy 2023, 285, 129211. [Google Scholar] [CrossRef]
- Wang, K.; Guo, L.; Xu, C.; Wang, W.J.; Yang, T.; Lin, S.S.; Cai, Y.B. Multiscale characteristics of pore-fracture structures in coal reservoirs and their influence on coalbed methane (CBM) transport: A review. Geoenergy Sci. Eng. 2024, 242, 213181. [Google Scholar] [CrossRef]
- Li, G.; Qin, Y.; Wang, B.Y.; Zhang, M.; Lin, Y.B.; Song, X.J.; Mi, W.T. Fluid seepage mechanism and permeability prediction model of multi-seam interbed coal measures. Fuel 2024, 356, 129556. [Google Scholar] [CrossRef]
- Mazumder, M.; Tripathy, A.; Bal, A.; Liu, S.Q.; Singh, T.N.; Pan, Z.J. Multi-proxy assessment of thermal and microstructural evolution in sub-bituminous coal affected by igneous Intrusion: Implications for CBM storage and transport. Fuel 2026, 405, 136414. [Google Scholar] [CrossRef]
- Xu, B.X.; Li, X.F.; Ren, W.N.; Chen, D.; Chen, L.; Bai, Y.H. Dewatering rate optimization for coal-bed methane well based on the characteristics of pressure propagation. Fuel 2017, 188, 11–18. [Google Scholar] [CrossRef]
- Liu, Z.S.; Liu, D.M.; Cai, Y.D.; Pan, Z.J. The impacts of flow velocity on permeability and porosity of coals by core flooding and nuclear magnetic resonance: Implications for coalbed methane production. J. Pet. Sci. Eng. 2018, 171, 938–950. [Google Scholar] [CrossRef]
- Liu, Z.; Han, J.; Yang, H.; Lv, J.L.; Dong, S. A new model for coal gas seepage based on fracture-pore fractal structure characteristics. Int. J. Rock Mech. Min. Sci. 2024, 173, 105626. [Google Scholar] [CrossRef]
- Chen, Y.L.; Ren, T.L.; Zhang, X.Q. Flow characteristics in porous media based on fractional order and multiple relaxation time lattice Boltzmann method and improver Ghost Fluid Method boundary processing mode. Int. Commun. Heat Mass Transf. 2025, 169, 109705. [Google Scholar] [CrossRef]
- Dang, Z.; Wang, X.M.; Bie, S.Z.; Su, X.B.; Hou, S.H. Experimental study of water occurrence in coal under different negative pressure conditions: Implication for CBM productivity during negative pressure drainage. Energy 2024, 303, 131989. [Google Scholar] [CrossRef]
- Li, G.Q.; Meng, Z.P.; Wang, B.Y. Diffusion and seepage mechanisms of high rank coal-bed methane reservoir and its numerical simulation at early drainage rate. J. China Coal Soc. 2014, 39, 1919–1926, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Zhang, J.M.; Hou, X.W.; Liu, S.M.; Zhu, Y.M.; Liu, A.; Fan, L.; Wang, Y.J.; Zhang, H. Quantifying and modeling of coal permeability spatiotemporal response: Implications for gas recovery and CO2 sequestration. Fuel 2025, 388, 134561. [Google Scholar] [CrossRef]
- Liu, T.; Liu, S.M.; Lin, B.Q.; Fu, X.H.; Zhu, C.J.; Yang, W.; Zhao, Y. Stress response during in-situ gas depletion and its impact on permeability and stability of CBM reservoir. Fuel 2020, 266, 117083. [Google Scholar] [CrossRef]
- Sun, F.R.; Liu, D.M.; Cai, Y.D.; Qiu, Y.K. A micro-macro coupled permeability model for gas transport in coalbed methane reservoirs. Energy 2023, 284, 128604. [Google Scholar] [CrossRef]
- Xiao, Z.Y.; Wang, G.; Liu, J.; Deng, H.F.; Jiang, Y.J.; Jiang, F.; Zheng, C.C. Experimental study and model improvement on coal permeability: The influence of effective stress, slip effect, and water content. Int. J. Rock Mech. Min. Sci. 2025, 185, 105972. [Google Scholar] [CrossRef]
- Aghighi, M.A.; Cui, T.; Schoning, G.; Espinoza, D.N.; Pandey, S. Subsidence associated with dewatering and gas extraction from coal seams: Contribution of desorption-induced coal shrinkage. J. Hydrol. 2024, 637, 131355. [Google Scholar] [CrossRef]
- Gao, R.; Bai, D.; Yu, B.; Tai, Y.; Meng, X.B.; Zhang, W.Y. Ground fracturing of multi-strata for strong ground pressure control in extra-thick coal seams with hard roofs: Numerical simulation and case study. Eng. Fract. Mech. 2024, 303, 110129. [Google Scholar] [CrossRef]
- Liu, C.; Yu, B.C.; Zhao, H.G.; Hong, Z.Q.; Tian, Z.C.; Zhang, D.M.; Liu, Y.X. Effective stress effect and slippage effect of gas migration in deep coal reservoirs. Int. J. Rock Mech. Min. Sci. 2022, 155, 105142. [Google Scholar] [CrossRef]
- Meng, Y.; Li, Z.P.; Lai, F.P. Influence of effective stress on gas slippage effect of different rank coals. Fuel 2021, 285, 119207. [Google Scholar] [CrossRef]
- Cao, Z.Z.; Xiong, Y.; Xue, Y.; Du, F.; Li, Z.H.; Huang, C.H.; Wang, S.R.; Yu, Y.Q.; Wang, W.Q.; Zhai, M.L.; et al. Diffusion evolution rules of grouting slurry in mining-induced cracks in overlying strata. Rock Mech. Rock Eng. 2025, 58, 6493–6512. [Google Scholar] [CrossRef]
- Teng, T.; Xue, Y.; Zhang, C. Modeling and simulation on heat-injection enhanced coal seam gas recovery with experimentally validated non-Darcy gas flow. J. Pet. Sci. Eng. 2019, 177, 734–744. [Google Scholar] [CrossRef]
- Rui, Z.H.; Deng, H.Y.; Hu, T.; Sheng, G.L.; Wilson, M.; Dindoruk, B.; Patil, S. Coupling mechanism analysis of CO2 non-Darcy flow in multi-scale reservoirs: A case study of the life-cycle process of fracturing-development in shale oil reservoirs. Pet. Sci. 2025, 22, 1171–1199. [Google Scholar] [CrossRef]
- Li, X.L.; Huan, H.H.; Lin, H.X.; Li, Z.H.; Du, F.; Cao, Z.Z.; Fan, X.; Ren, H. Determination method of rational position for working face entries in coordinated mining of section coal pillars and lower sub-layer. Sci. Rep. 2025, 15, 29440. [Google Scholar] [CrossRef]
- Geng, J.B.; Zeng, G.X.; Liu, C.Y.; Li, X.S.; Zhang, D.M. Development and application of triaxial seepage test system for gas-water two-phase in coal rock. Energy 2023, 277, 127439. [Google Scholar] [CrossRef]
- Ma, S.Q.; Lin, B.Q.; Zhao, J.J.; Zhang, X.L.; Liu, Q.; Liu, T. Two-phase flow characteristics of high-temperature CO2 and water and dynamic wettability variations in nano-scale coal pores with different sizes and shapes. Fuel 2026, 404, 136406. [Google Scholar] [CrossRef]
- Han, J.; Liu, Z.; Yang, H.; Zhou, Z.; Gu, Q.B. Modeling of water-injected coal with fracture-pore structure and experimental study of gas-water two-phase transport characteristics. Int. J. Rock Mech. Min. Sci. 2025, 195, 106272. [Google Scholar] [CrossRef]
- Wang, Q.; Su, X.B.; Feng, Y.L.; Wang, H.; Song, J.X. Experimental study of gas-water two-phase flow patterns in fracture: Implication for enhancing coalbed methane production. J. Pet. Sci. Eng. 2021, 207, 109168. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, J.T.; Wang, K.; Miao, T.N.; Zhang, T.; Feng, D.; Sun, F.R.; Wang, S.; Han, S.; Li, X.F. The gas-water two phase flow behavior in low-permeability CBM reservoirs with multiple mechanisms coupling. J. Nat. Gas Sci. Eng. 2018, 52, 82–93. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, J.T.; Zhang, T.; Wu, K.L.; Feng, D.; Sun, F.R.; Huang, L.; Hou, C.H.; Li, X.F. A fully-coupled semi-analytical model for effective gas/water phase permeability during coal-bed methane production. Fuel 2018, 223, 44–52. [Google Scholar] [CrossRef]
- Shu, L.Y.; Ma, Y.K.; Liu, Z.S.; Li, H.Y. Study and application of a continuous inversion model of coal seam gas pressure in front area of heading face. Int. J. Coal Sci. Technol. 2023, 10, 80. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, J.T.; Wu, K.L.; Ma, H.Y.; Li, S.M.; Zhang, T.; Feng, D.; Liu, W.Y.; Liu, Y.S.; Wang, S.R.; et al. Novel optimization method for production strategy of coal-bed methane well: Implication from gas-water two-phase version productivity equations. J. Pet. Sci. Eng. 2019, 176, 632–639. [Google Scholar] [CrossRef]
- Li, Z.B.; Ren, T.; Li, X.C.; Cheng, Y.P.; He, X.Q.; Qiao, M.; Yang, X.H. Full-scale pore structure characterization of different rank coals and its impact on gas adsorption capacity: A theoretical model and experimental study. Energy 2023, 277, 127621. [Google Scholar] [CrossRef]
- Kong, X.G.; Wang, E.Y.; Liu, Q.L.; Li, Z.H.; Li, D.X.; Cao, Z.Y.; Niu, Y. Dynamic permeability and porosity evolution of coal seam rich in CBM based on the flow-solid coupling theory. J. Nat. Gas Sci. Eng. 2017, 40, 61–71. [Google Scholar] [CrossRef]
- Liu, D.M.; Yao, Y.B.; Chang, Y.H. Measurement of adsorption phase densities with respect to different pressure: Potential application for determination of free and adsorbed methane in CBM reservoir. Chem. Eng. J. 2022, 446, 137103. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, D.M.; Cai, Y.D.; Sun, F.R.; Zhou, Y.F. Pathways and challenges of the application of geophysical techniques to multifaceted CBM reservoir characterization. Gondwana Res. 2025, 147, 164–183. [Google Scholar] [CrossRef]
- Su, X.F.; Liu, Y.; Cui, Z.Q.; Zhang, J.G.; Yu, L.; Wang, K. Influence of depressurization rate on gas production capacity of high-rank coal in the south of Qinshui Basin, China. Pet. Explor. Dev. 2019, 46, 642–650. [Google Scholar] [CrossRef]
- Reisabadi, M.Z.; Haghighi, M.; Sayyafzadeh, M.; Khaksar, A. Effect of matrix shrinkage on wellbore stresses in coal seam gas: An example from Bowen Basin, east Australia. J. Nat. Gas Sci. Eng. 2020, 77, 103280. [Google Scholar] [CrossRef]





| Parameter | Meaning | Value | Unit |
|---|---|---|---|
| ρc | Apparent density of the coal reservoir | 1460 | kg/m3 |
| E | Young’s modulus | 2.7 | GPa |
| v | Poisson’s ratio | 0.30 | / |
| T | Temperature | 300 | K |
| VL | Langmuir volume | 44.36 | cm3/g |
| PL | Langmuir pressure | 3.14 | MPa |
| Pd | Critical desorption pressure | 1.6 | MPa |
| τ | Adsorption time constant | 9.5 | d |
| φ0 | Initial porosity | 0.06 | / |
| k0 | Initial permeability | 0.5 | mD |
| ρw | Density of water | 1000 | kg/m3 |
| ρair | Density of gas under standard conditions | 0.716 | kg/m3 |
| μw | Viscosity of water | 1 | mPa·s |
| μg | Viscosity of CBM | 0.019 | mPa·s |
| pcoal | Coal reservoir pressure | 5.63 | MPa |
| bk | Slip coefficient | 0.1 | MPa |
| α | Effective stress coefficient | 1 | / |
| Number of Scheme | Scheme | Variable Parameter |
|---|---|---|
| 1 | Influence of Young’s modulus | E = 1.5 GPa |
| E = 2.1 GPa | ||
| E = 2.7 GPa | ||
| 2 | Influence of initial permeability | k0 = 0.1 mD |
| k0 = 0.5 mD | ||
| k0 = 0.9 mD | ||
| 3 | Influence of drainage system | Pr = 0.02 MPa/d |
| Pr = 0.04 MPa/d | ||
| Pr = 0.08 MPa/d |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Li, Y.; Cui, C.; Yan, Z. Numerical Simulation of Gas–Water Two-Phase Seepage During Coalbed Methane Development in ZhengZhuang Block: A Case Study of Well Z29. Processes 2025, 13, 3593. https://doi.org/10.3390/pr13113593
Liu Z, Li Y, Cui C, Yan Z. Numerical Simulation of Gas–Water Two-Phase Seepage During Coalbed Methane Development in ZhengZhuang Block: A Case Study of Well Z29. Processes. 2025; 13(11):3593. https://doi.org/10.3390/pr13113593
Chicago/Turabian StyleLiu, Zhengshuai, Yang Li, Cong Cui, and Zhendong Yan. 2025. "Numerical Simulation of Gas–Water Two-Phase Seepage During Coalbed Methane Development in ZhengZhuang Block: A Case Study of Well Z29" Processes 13, no. 11: 3593. https://doi.org/10.3390/pr13113593
APA StyleLiu, Z., Li, Y., Cui, C., & Yan, Z. (2025). Numerical Simulation of Gas–Water Two-Phase Seepage During Coalbed Methane Development in ZhengZhuang Block: A Case Study of Well Z29. Processes, 13(11), 3593. https://doi.org/10.3390/pr13113593





