1. Introduction
The growing global demand for sustainable energy solutions has driven the development of technologies capable of increasing efficiency and reducing the environmental impact of thermal systems, particularly in residential and commercial applications. In this context, solar-assisted heat pumps (SAHPs) have emerged as a promising alternative for water heating [
1,
2,
3,
4]. Among them, direct expansion systems (DX-SAHPs) offer advantages such as structural simplicity, lower thermal losses, and higher coefficients of performance (COP) [
5,
6,
7].
In parallel, the choice of refrigerant plays a crucial role in the efficiency and sustainability of heat pump systems. In recent years, propane (R290) has gained increasing attention as a natural refrigerant for heat pump applications. It combines favorable thermodynamic properties, such as high latent heat of vaporization and excellent heat transfer performance, with a very low global warming potential (GWP ≈ 3) and zero ozone depletion potential (ODP). Compared to synthetic refrigerants, R290 allows higher energy efficiency and can operate effectively in compact systems such as DX-SAHPs [
5,
6,
7].
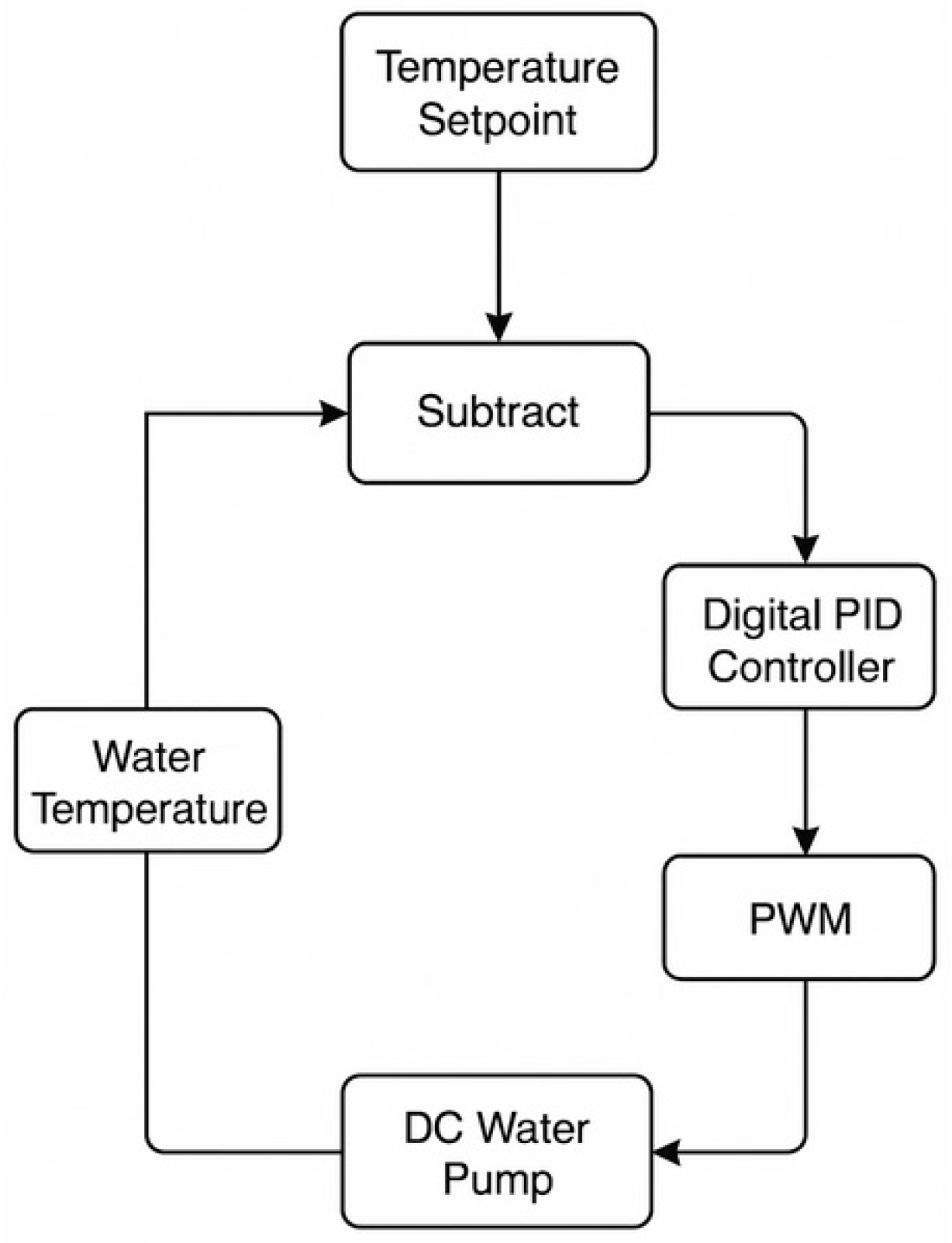
However, the performance of these systems depends strongly on the accurate regulation of the water outlet temperature at the condenser, especially under variable operating and climatic conditions. A distinctive feature of direct-expansion solar-assisted heat pumps is that the thermal input at the evaporator is directly dependent on solar irradiance, which inherently fluctuates with weather conditions. This variability significantly affects the system’s thermal balance and makes precise temperature control even more challenging. Manual control, although technically feasible, requires constant monitoring and frequent corrective actions, making it unsuitable for practical applications [
8]. Therefore, the implementation of automatic control systems is essential to ensure thermal stability, energy efficiency, and user comfort.
The field of dynamic system control has contributed significantly to thermal engineering by enabling the manipulation of input variables to achieve optimal output behavior [
9]. Several studies have focused on the development of control strategies for refrigeration and heating systems. Rasmussen and Larsen [
10] developed a nonlinear adaptive method for superheat and capacity regulation in refrigeration systems. Choi [
11] evaluated different strategies for water outlet temperature regulation, identifying water flow rate adjustment as one of the most effective approaches. Maia et al. [
12,
13] proposed adaptive control strategies for superheat regulation based on experimentally validated mathematical models. In the specific context of DX-SAHP systems, Alvarez [
8] applied a PID controller tuned using the ITAE criterion, achieving excellent thermal regulation using carbon dioxide as the refrigerant, and Paulino [
14] developed and tested a low-cost control system to regulate the water temperature in a CO
2 DX-SAHP and investigated the effect of the expansion valve opening on the system’s performance. The results showed that a static expansion valve can be suitable for stable operation, but an electronic valve is more efficient in responding quickly to sudden variations in solar radiation.
More recent efforts include model predictive control (MPC) [
15], variable setpoint strategies, and energy optimization techniques [
16,
17] for enhancing system performance under diverse operating conditions. Among conventional techniques, proportional–integral–derivative (PID) control remains the most widely adopted solution in industrial applications due to its simplicity, reliability, and ease of digital implementation [
18]. The effectiveness of PID control depends on accurate tuning of its parameters. Tuning methods can be empirical, such as Ziegler–Nichols and Cohen–Coon [
19], or model-based, such as direct synthesis [
20,
21], which allows the design of robust controllers that are adapted to the process dynamics.
Although several studies have explored control strategies for DX-SAHP systems, few have addressed the specific challenges imposed by the variable solar input inherent to these systems, especially when natural refrigerants such as R290 are used. This variability significantly influences the system dynamics. Therefore, there remains a clear need for experimentally validated, low-cost, and robust control solutions capable of maintaining stable operation and high efficiency under real residential conditions.
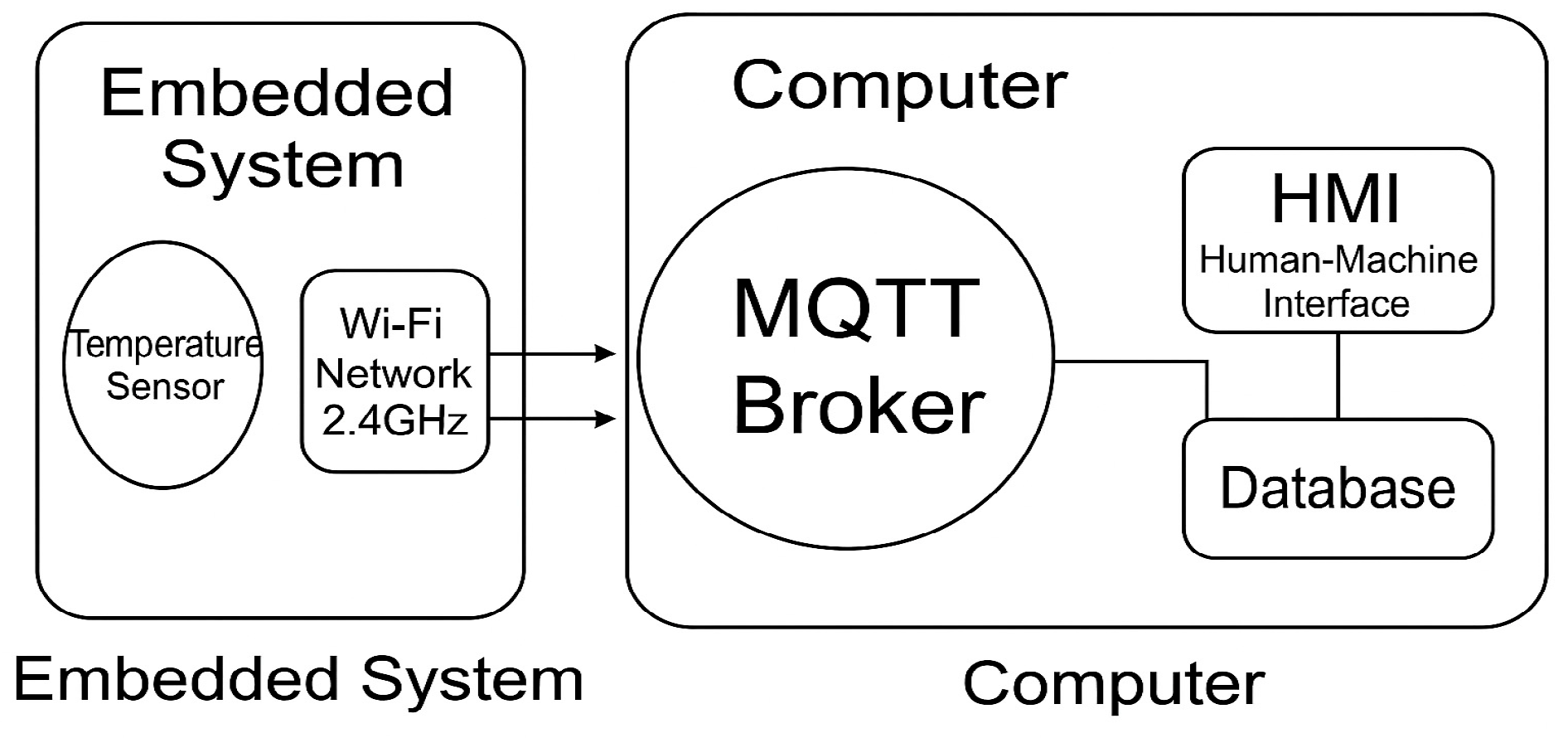
This study presents the design, modeling, embedded implementation, and experimental validation of a digital PID controller for regulating the water outlet temperature in a DX-SAHP system using R290 as the working fluid. The tuning was performed using the direct synthesis method, based on a first-order model identified experimentally. Compared with conventional PID and MPC strategies, the proposed controller provides a simple, reliable, and computationally efficient solution that can be easily implemented in low-cost embedded hardware while maintaining accurate and stable temperature control under variable solar conditions. The proposed work proposes an innovative and cost-effective embedded solution for accurate water temperature control in residential applications. The main innovation of this work lies in the development of a fully embedded and low-cost digital control solution for outlet water temperature regulation in a DX-SAHP using R290, experimentally validated to ensure accuracy, robustness, and applicability to real residential systems.
Although R290 was selected in this study due to its favorable thermodynamic and environmental properties, the proposed control methodology is general and can be adapted to DX-SAHP systems operating with other refrigerants, as long as their dynamic parameters are experimentally identified.
3. Results
3.1. Experimental Validation of the Identified Model
The resulting model was a first-order linear system, described by Equation (4).
where
y(
t) is the water temperature at time step
t,
y(
t − 1) is the previous temperature, and
u(
t) is the control input (water flow rate).
The discrete-time transfer function in the z-domain is presented in Equation (5).
The corresponding continuous-time transfer function, obtained via the bilinear (Tustin) approximation, is given by Equation (6).
where
G(
s) is the system transfer function,
s is the Laplace variable. The model exhibits a negative static gain, indicating that an increase in water flow leads to a decrease in water temperature—a behavior expected for this type of heat exchange system.
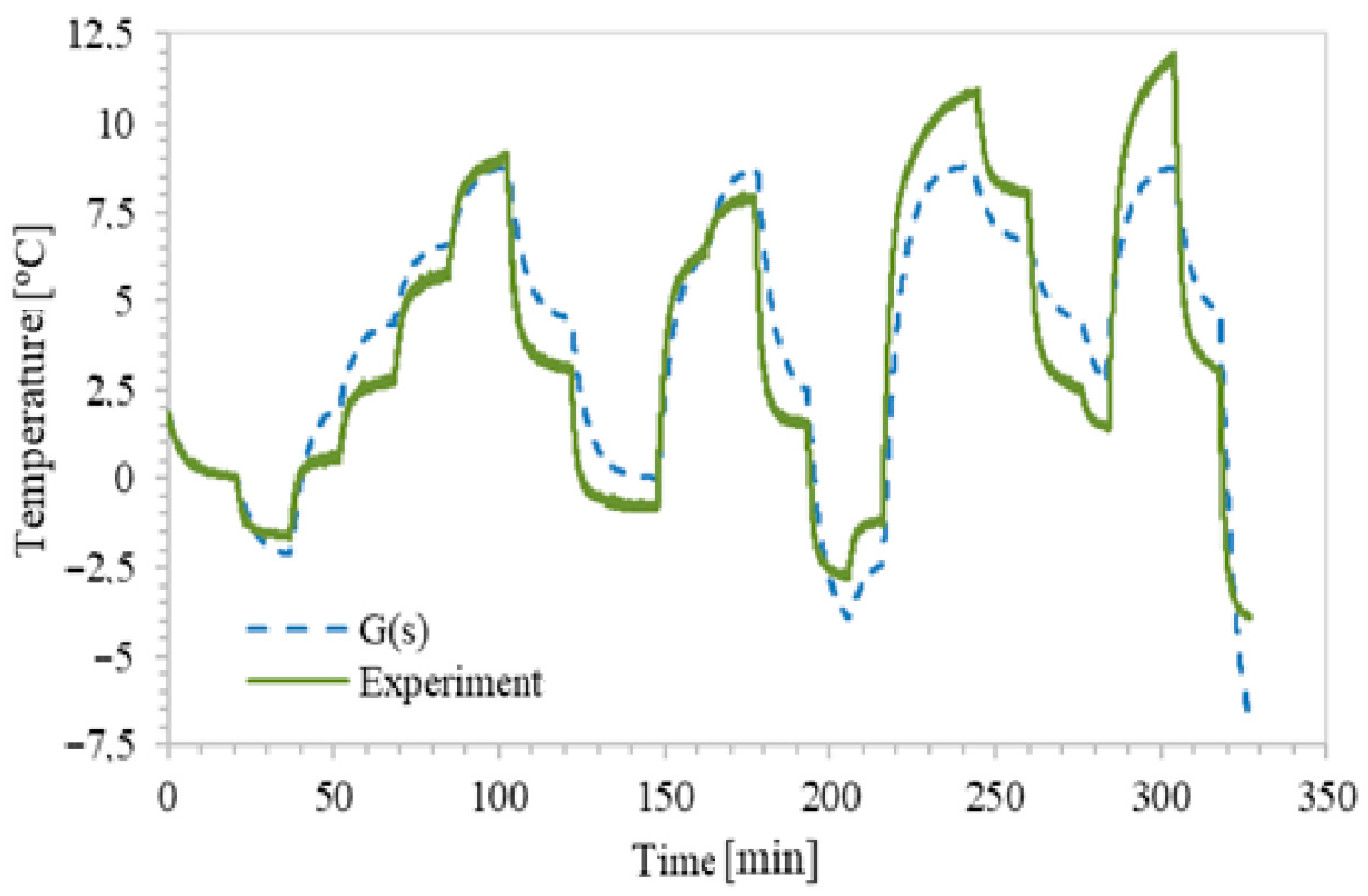
Model validation was evaluated by comparing its output with the experimental data.
Figure 9 shows that the ARX model accurately reproduces the system behavior.
The model accuracy was quantified using performance indices such as the Root Mean Squared Error (RMSE) and the Normalized Dimensionless Error Index (NDEI). The RMSE was 1.34 °C and the NDEI was 0.32, indicating good agreement between the model and measured data.
In addition, the prediction errors for the water temperature were analyzed. The minimum error was 2.6 × 10−5 °C, the maximum error was 3.8 °C, the mean error was 1.1 °C, and the standard deviation was 1.5 °C. With a 95% confidence interval, the results indicate that the model provides accurate predictions near the operating point of 47.5 °C.
3.2. Digital Controller Implementation
Based on the transfer function obtained in Equation (6), the system’s time constant was determined to be 283 s. For first-order systems, the settling time is typically estimated as four times the time constant [
21], which corresponds to approximately 19 min for the system to reach steady-state conditions.
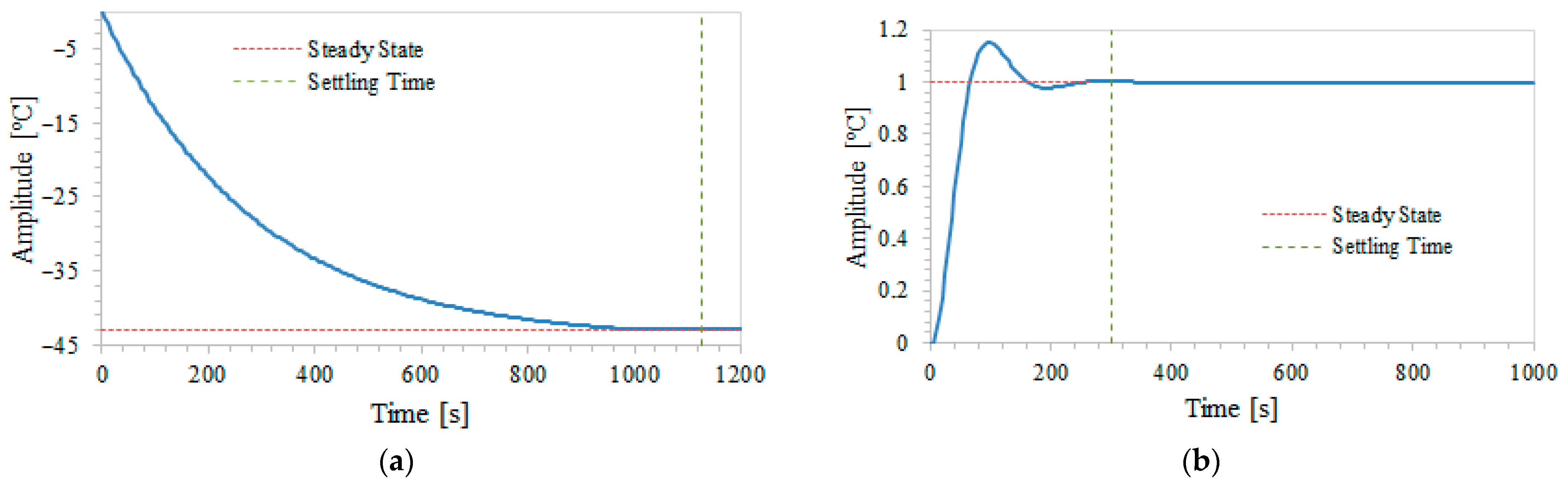
However, as the open-loop response was found to be slow and inadequate for the desired performance requirements, a closed-loop underdamped behavior was adopted to improve the system dynamics. The objective was to enable faster convergence to the steady-state without compromising system stability.
The desired settling time was set to 300 s, which represents a compromise between fast thermal regulation and the limitations of the system. To meet this specification, a damping ratio of
= 0.6 was selected, characterizing an underdamped second-order response. With these parameters, the natural frequency
ωn was calculated, and the desired closed-loop transfer function was obtained, as expressed in Equation (7).
Figure 10 illustrates a comparison between the open-loop and the desired closed-loop step responses. The open-loop response is clearly slower and fails to meet the performance criteria, taking excessive time to reach steady-state. In contrast, the designed closed-loop response, with a settling time of 300 s, exhibits significantly faster stabilization and efficiently reaches the final value, demonstrating improved performance. This comparison highlights that adopting an underdamped closed-loop configuration significantly enhanced the dynamic behavior of the system.
Using the desired closed-loop transfer function and the system model, the direct synthesis method was applied to compute a controller that ensures the desired output dynamics, as given in Equation (8).
Since the control algorithm was implemented on an embedded system, the controller had to operate in discrete time. Therefore, the continuous-time transfer function was discretized using the Tustin method, with a sampling time of
Ts = 7.5 s. This value was chosen to provide approximately 10 samples per time constant, which is recommended to preserve the system dynamics in the digital domain [
20].
The discrete-time controller transfer function is shown in Equation (9).
This transfer function was converted into a set of difference equations, allowing implementation directly in the embedded system. The control law computes the current control signal based on present and past error values, as well as previous control efforts. Given that the transfer function is of second order, the implementation requires storing two past values of both the error and control signals in memory buffers.
The resulting controller was rewritten in the form of a parallel PID structure, and the PID parameters were computed as follows: s, and s.
After obtaining the discrete-time transfer function of the controller, it was applied to the system model to simulate the step response of the closed-loop system. The simulation results, shown in
Figure 11, illustrate the improved performance of the system under PID control.
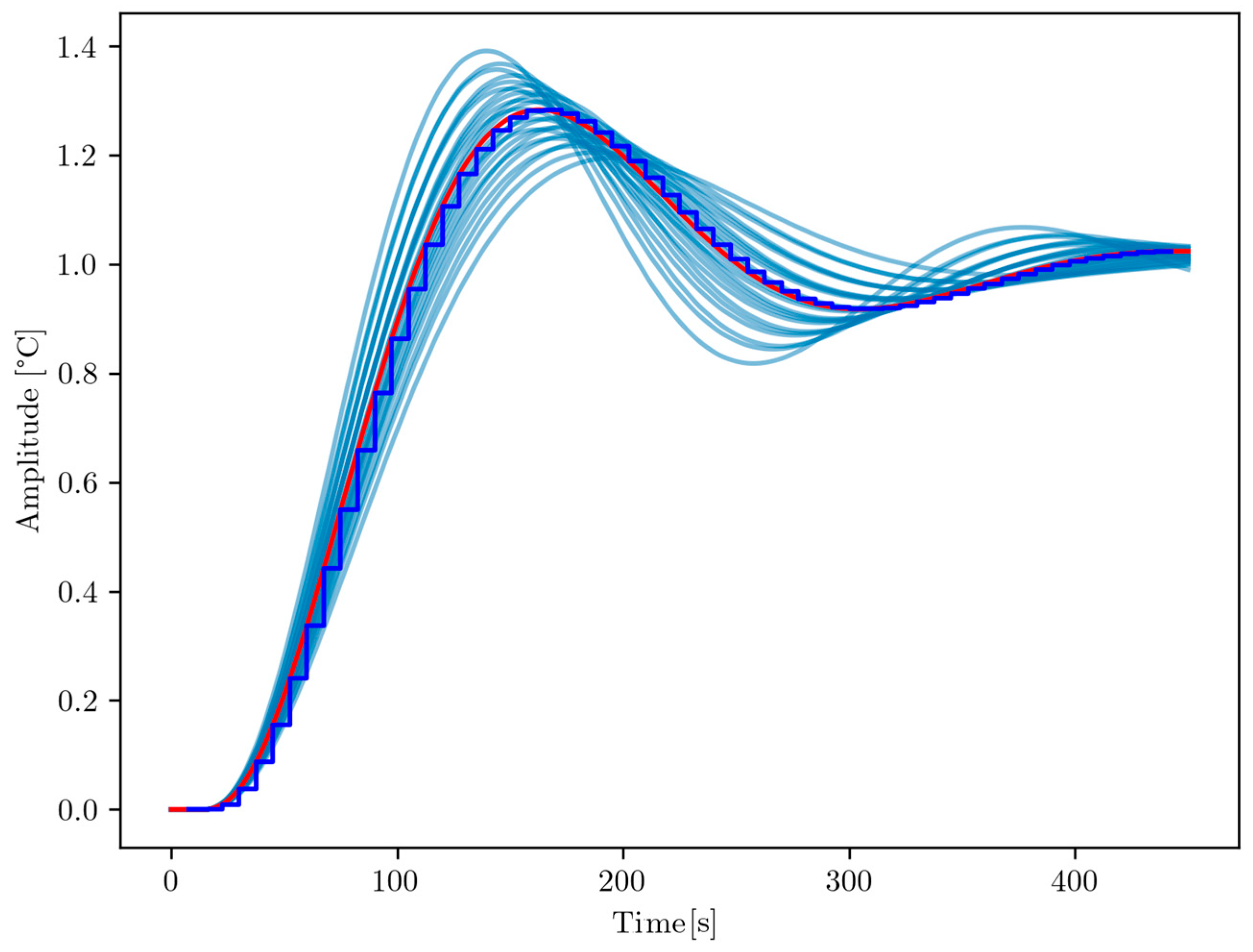
3.3. Robustness Assessment
The robustness analysis showed that, even under model uncertainties (±15% variation in system parameters), the controller maintained stability and exhibited performance close to that of the nominal system. Step responses were simulated for both the nominal system and perturbed models, as shown in
Figure 12.
Despite parameter variations, the system’s response with uncertainties (blue lines) closely matched the nominal response (red line), indicating that the controller is sufficiently robust to handle uncertainties without significantly compromising performance or stability.
3.4. Simulation Results
The computational simulations were carried out using the dynamic mathematical model developed by [
8], who studied the same DX-SAHP system investigated in this work, with the aim of evaluating the performance of the proposed controller. For this purpose, the controller was assumed to operate around the system equilibrium point. Accordingly, the system output signal was offset by subtracting the equilibrium temperature, while the control signal was adjusted by adding the corresponding equilibrium value.
The objective of the simulations was to assess the response of the system under two distinct conditions: a disturbance in the reference signal and a disturbance in the output signal. The first simulation involved a perturbation in the reference input, as illustrated in
Figure 13. In this scenario, the system reference was altered, and the controller was responsible for compensating for the variation to maintain the temperature within the desired range. The controller demonstrated effective disturbance rejection, keeping the system temperature stable.
The second simulation considered a disturbance in the output signal, which corresponds to the controlled variable (temperature), as shown in
Figure 14. In this case, the controller had to respond to unexpected changes in the system temperature and restore it to the desired reference value. Once again, the controller exhibited an efficient response, with the temperature promptly corrected back to the setpoint.
3.5. Experimental Performance Evaluation
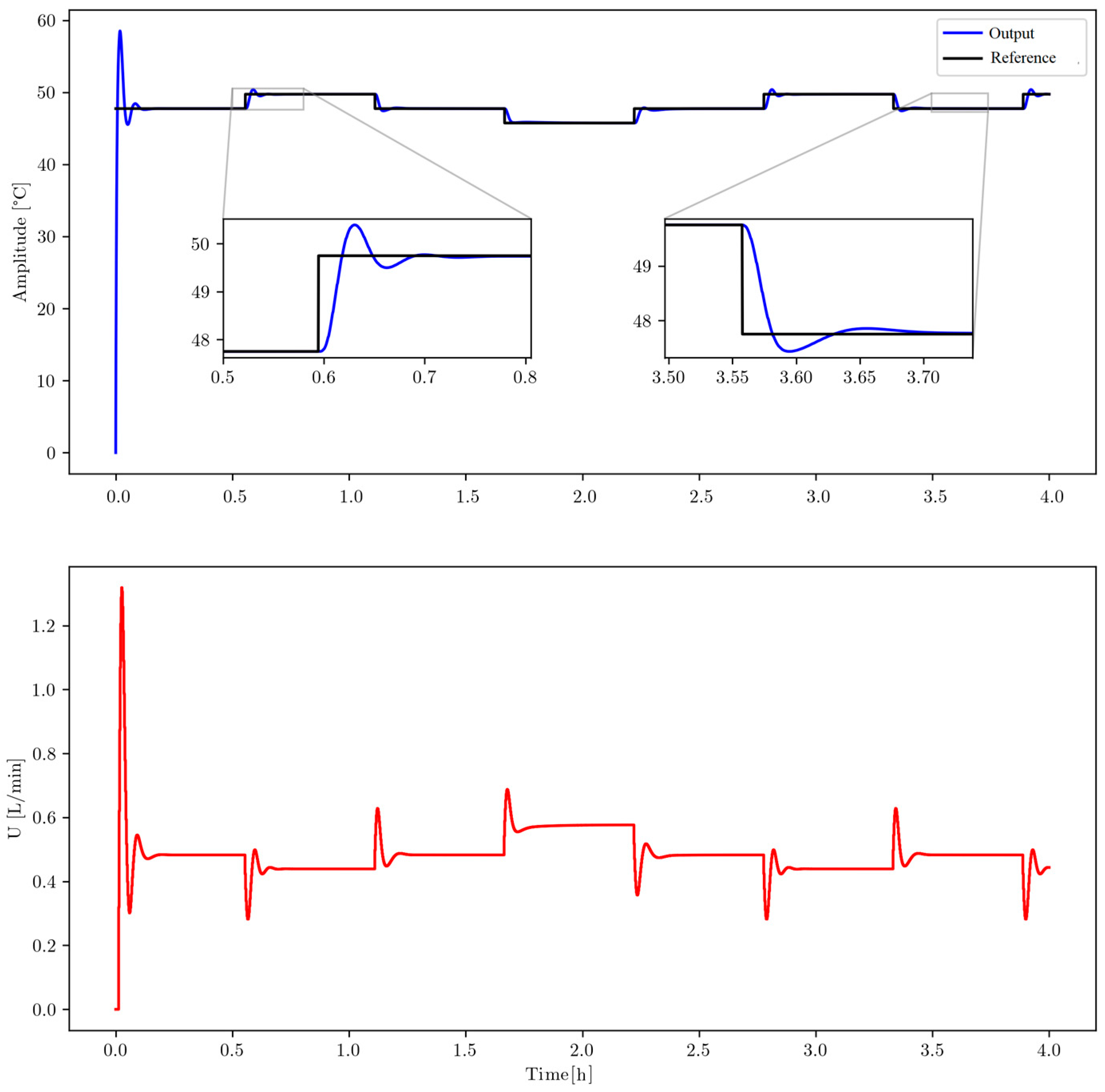
To further assess the performance of the developed controller, experimental tests were conducted on the actual system. The reference temperature was set at 47.5 °C, and the experiments aimed to evaluate the system’s ability to reject external disturbances while maintaining the outlet water temperature close to the setpoint.
In the first experiment, the system’s response to inlet water temperature variations was tested using an electric resistor controlled by a variac to induce disturbances. This setup allowed for controlled perturbations at the condenser water inlet. As shown in
Figure 15, the controller effectively compensated for these disturbances, maintaining a nearly constant outlet temperature and demonstrating strong disturbance rejection capability.
It is important to note that when the inlet water temperature exceeds the setpoint, the DX-SAHP system does not switch to cooling mode, as it is designed solely for heating. In such cases, the controller reduces or temporarily suspends the compressor and expansion valve actions to prevent overheating, keeping the outlet temperature close to the setpoint, as illustrated in
Figure 15.
The second test, illustrated in
Figure 16, was conducted under clear-sky conditions with high solar radiation stability. Step disturbances in the incident solar radiation were deliberately introduced using shading devices to simulate sudden changes in irradiance. Despite these abrupt changes, the controller dynamically adjusted the water flow rate, keeping the outlet temperature close to the reference.
In the third experiment, the system was evaluated under adverse weather conditions, with high variability in solar irradiance due to cloud cover. In addition to natural fluctuations, controlled disturbances were also applied using shading devices. As presented in
Figure 17, the controller remained robust and effective, adjusting the water flow as needed to maintain the outlet temperature near the setpoint, even under highly unstable conditions.
It should be noted that
Figure 15 illustrates the system response to inlet water temperature variations only, without the influence of solar radiation, whereas
Figure 16 and
Figure 17 show the response under varying solar irradiance conditions.
The three experiments confirmed the effectiveness of the proposed controller under different types of disturbances. The ability to maintain a stable outlet water temperature despite significant variations in input conditions (both inlet water temperature and solar irradiance) highlights the good performance, robustness, and practical applicability of the control system in solar-assisted heat pump water heating applications.
4. Discussion
The results presented in this study demonstrate the successful development and validation of a control system for the DX-SAHP water heating process, grounded on a first-order linear model identified from experimental data. The ARX model accurately captured the system dynamics near the operating point, as evidenced by low root mean squared error and normalized dimensionless error index values, and small prediction errors. This confirms the model’s adequacy as a reliable basis for controller design.
The identified system exhibited a slow open-loop response with a time constant of approximately 283 s, leading to an unsatisfactory settling time for practical applications. By adopting an underdamped closed-loop configuration with a damping ratio of 0.6 and a target settling time of 300 s, the controller effectively accelerated system response without compromising stability. This design choice aligns with established control theory principles and improves the transient response significantly, as shown by the comparative step response analysis.
Robustness analysis further highlighted the controller’s resilience to parameter uncertainties of ±15%, with performance degradation minimal and stability preserved. This robustness is essential given the inherent variability in solar irradiance and water inlet conditions typical in real-world solar-assisted heat pump systems.
Simulation results reinforced the controller’s ability to reject disturbances both at the reference input and at the output, consistently restoring system temperature to the setpoint despite perturbations. These findings were substantiated by experimental tests, which confirmed the controller’s practical efficacy under varying inlet water temperatures and highly dynamic solar irradiance conditions—ranging from stable clear-sky days to rapidly fluctuating cloudy periods.
The experimental outcomes demonstrate that the controller maintains the outlet water temperature remarkably close to the reference despite significant external disturbances, confirming robustness and applicability in real operating environments. This robustness and accuracy endorse the proposed control approach as a promising solution for enhancing the performance and reliability of solar-assisted heat pump water heating systems.
Future research may extend this work by investigating adaptive or predictive control strategies to further enhance disturbance rejection capabilities under more extreme or rapidly varying environmental conditions. Integration with energy management systems and longer-term field tests will also be valuable to evaluate real-world operational benefits and energy savings.
5. Conclusions
This work developed and validated a model-based controller for a solar-assisted heat pump water heating system. The proposed solution was implemented as a fully embedded and low-cost digital controller, demonstrating that effective water temperature regulation can be achieved without the need for expensive hardware or complex architectures. The control strategy was based on manipulating the water circulation pump, which proved to be an effective and practical choice compared to alternative options such as expansion valve control. Experimental validation confirmed not only the improvement in response time and robustness to disturbances, but also the ability of the system to maintain stable outlet water temperature even under significant solar irradiance fluctuations.
These results highlight the practical contribution of this work, demonstrating that the proposed embedded control approach is both technically effective and economically viable for residential applications, enhancing system performance and energy efficiency. Furthermore, the proposed embedded PID control system shows strong potential for real-world implementation in residential DX-SAHP units. Its modular and low-cost design facilitates scalability to systems with higher capacities or multiple parallel units. Because the controller is fully digital and based on open-source hardware, it offers potential for integration with smart-grid platforms and home energy management systems, enabling demand-side control and optimizing electricity usage according to dynamic pricing or renewable generation availability. Overall, the use of low-cost components provides an attractive cost–benefit balance for residential or commercial deployment while maintaining precise and stable water temperature regulation.