Research on Electrical Properties of the Cutting Zone in Cutting Metal/Insulation Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement of Triboelectrification Electrostatic Potential in Turning
2.2. Measurement of Charged Particles Emission Intensity in Turning
3. Results and Discussion
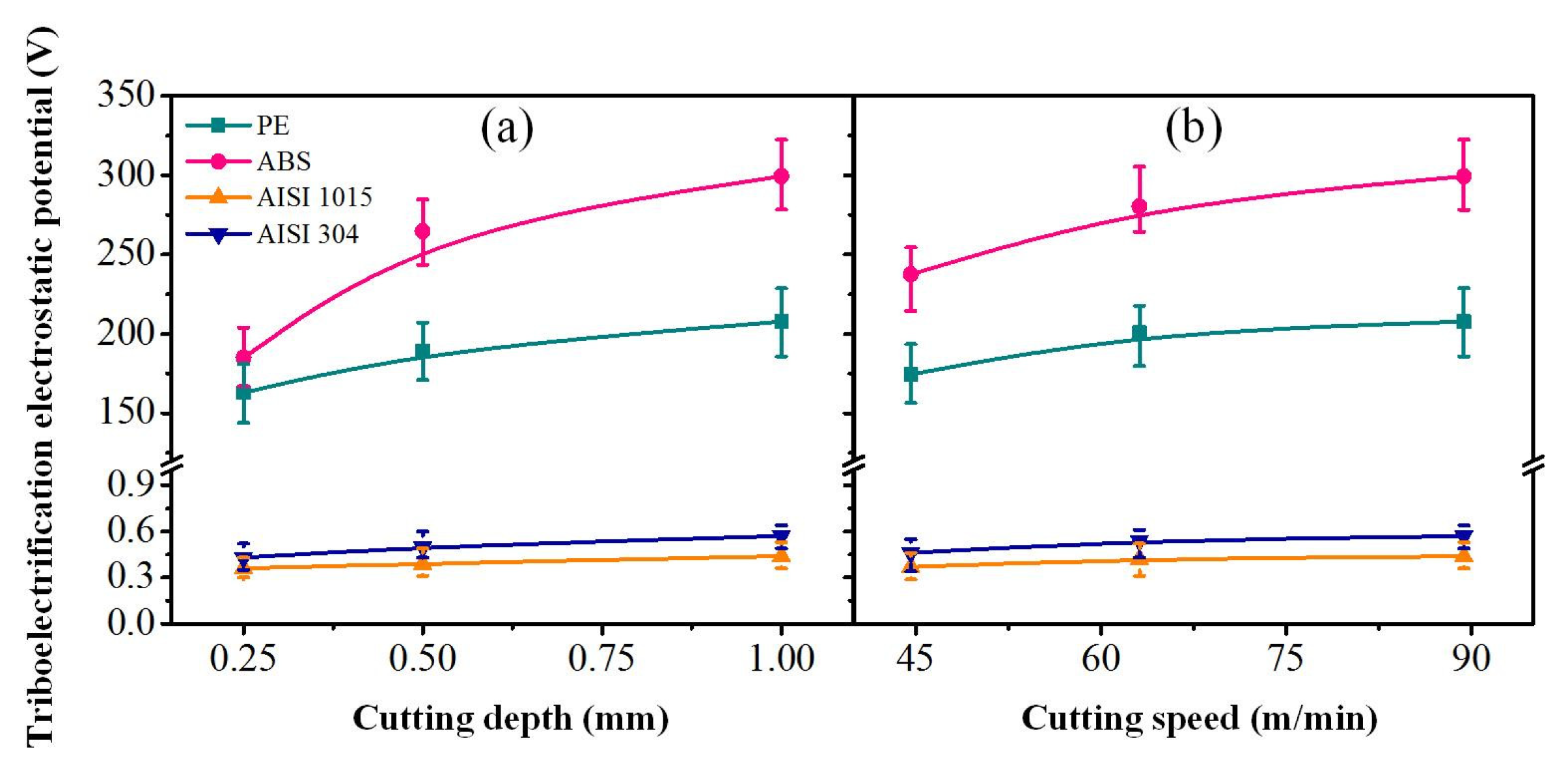
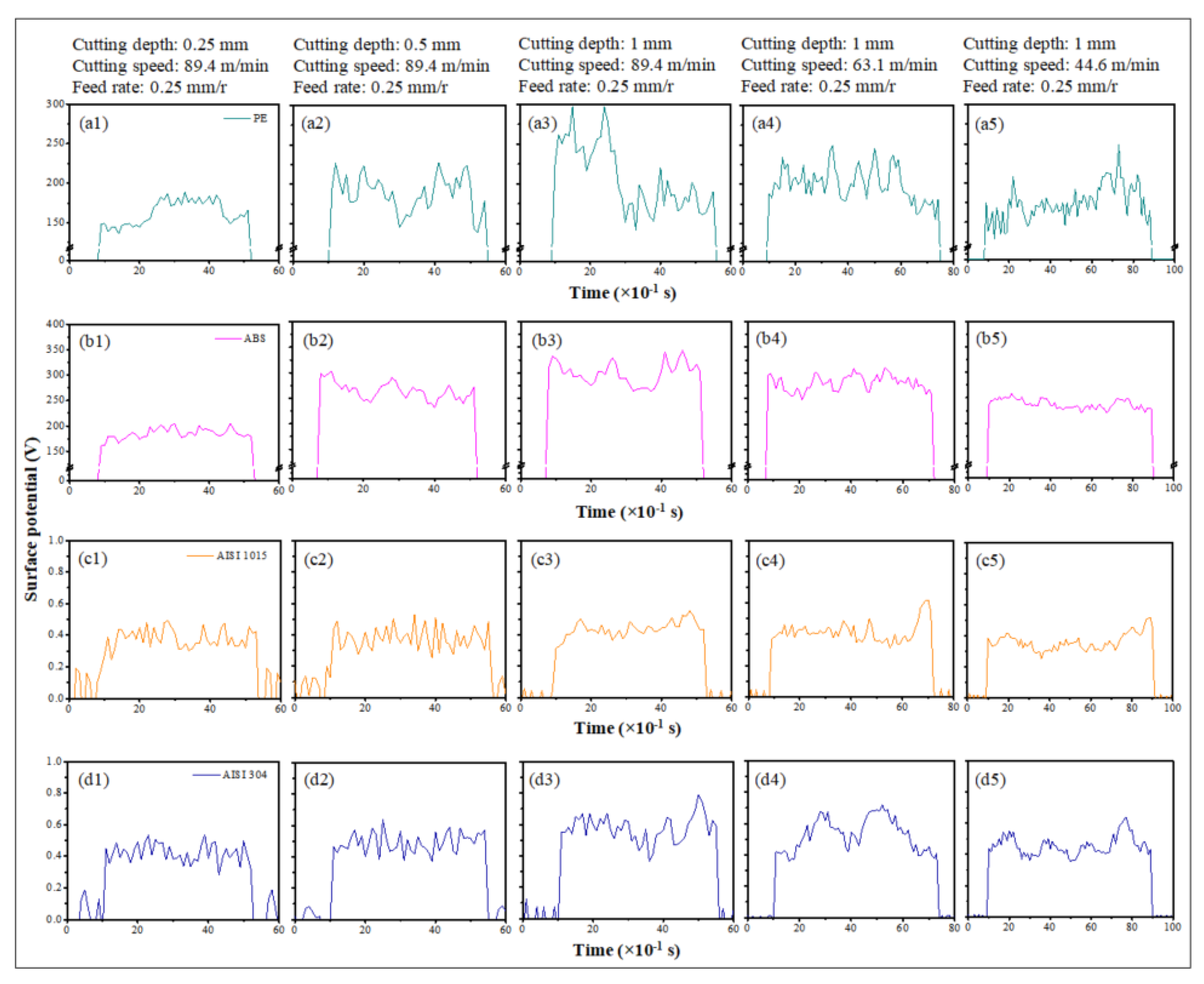
3.1. Measurement of Triboelectrification Electrostatic Potential
3.2. The Measurement of Emission Intensity of Charged Particles and the Calculation of Self-Excited Axial Electric Field Intensity
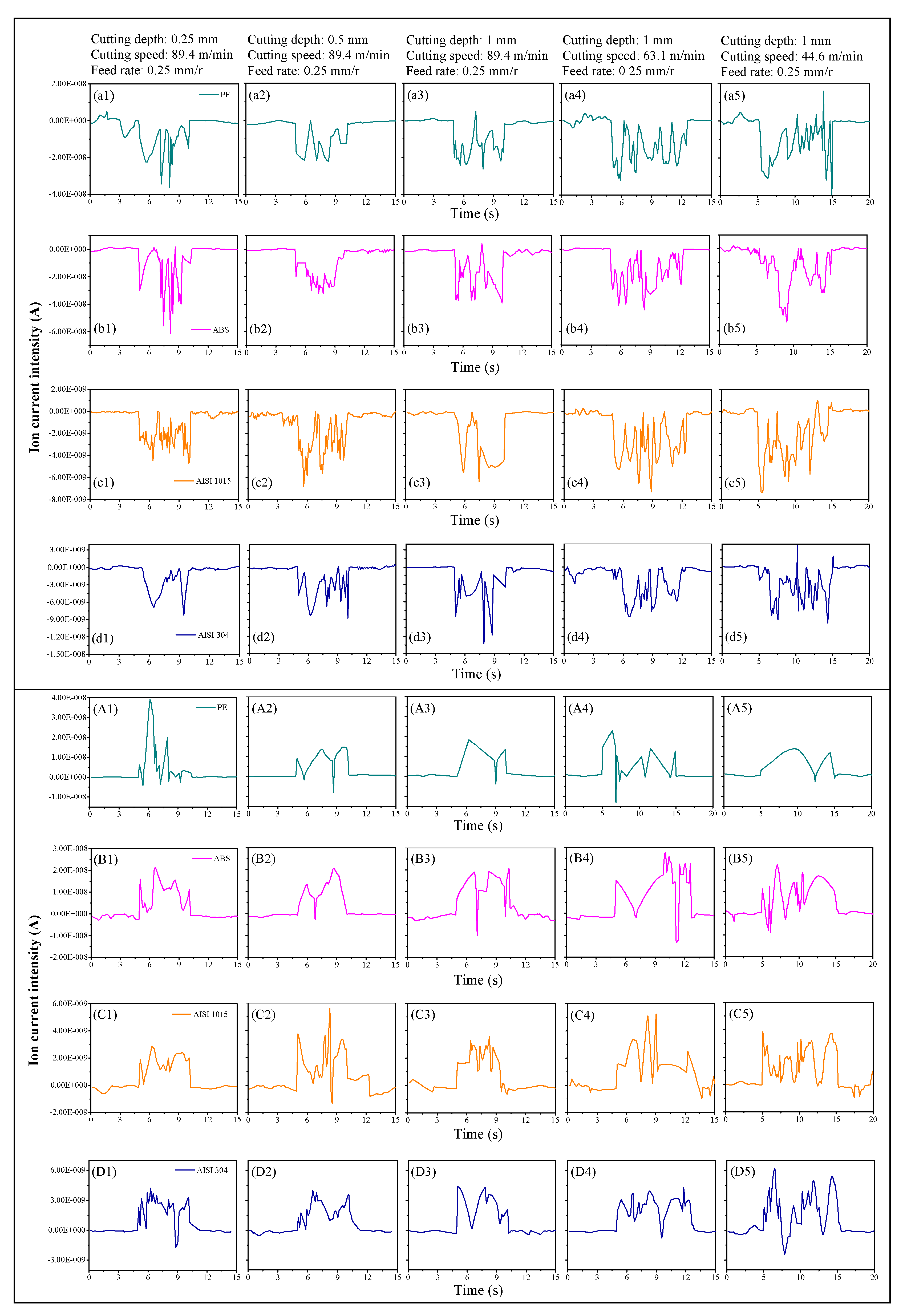
3.2.1. Measurement of Emission Intensity of Charged Particles
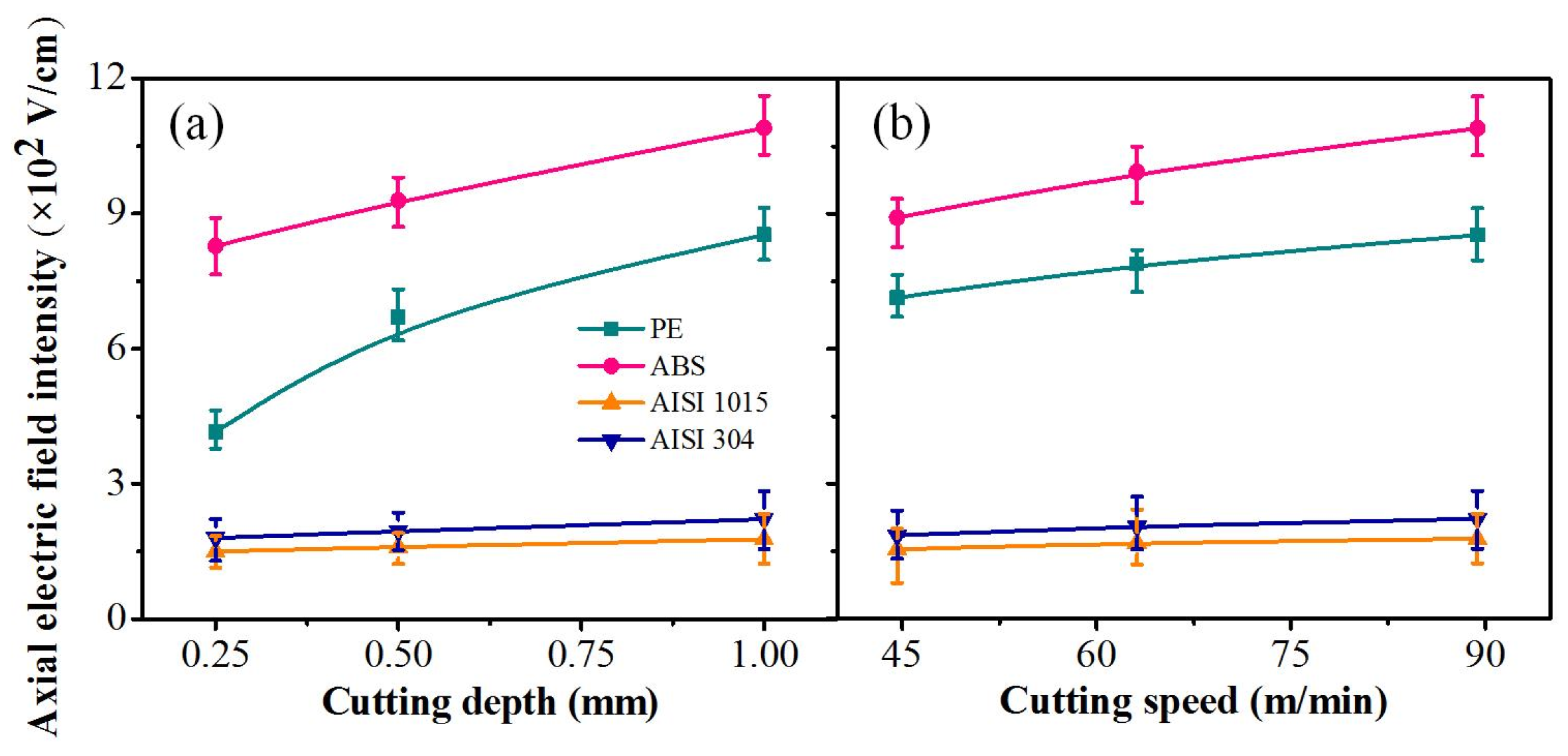
3.2.2. Self-Excited Axial Electric Field Formed by the Charged Particle Emission in the Capillary
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, B.; Luan, Z.; Zhang, R.; Xia, Y.; Yao, W.; Liu, J.; Ma, Y.; Hu, X.; Xu, X. Effect of electroosmosis on lubricant penetration at the tool–chip interface. J. Mater. Process. Technol. 2022, 307, 117653. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Shao, T.M. A method of charge measurement for contact electrification. J. Electrostat. 2013, 71, 712–716. [Google Scholar] [CrossRef]
- Nakayama, K. Contact geometry and distribution of plasma generated in the vicinity of sliding contact. Jpn. J. Appl. Phys. 2007, 46, 6007–6014. [Google Scholar] [CrossRef]
- Jian, L.Q.; Ning, L.P.; Yang, S.R.; Wang, J.M.; Hua, M.Q. Triboelectrification Electrostatic Potential of MC Nylon 6 under Point Contact Dry Sliding. Tribol. Lett. 2009, 36, 199–208. [Google Scholar] [CrossRef]
- Sow, M.; Lacks, D.J.; Sankaran, R.M. Effects of material strain on triboelectric charging: Influence of material properties. J. Electrostat. 2013, 71, 396–399. [Google Scholar] [CrossRef]
- Tang, J.; He, L.; Jin, Z.H.; Lu, J.D. Material tribo-electrification potential changing during wear. Mater. Des. 2003, 24, 223–226. [Google Scholar] [CrossRef]
- Nakayama, K.; Martin, J.M. Tribochemical reactions at and in the vicinity of a sliding contact. Wear 2006, 261, 235–240. [Google Scholar] [CrossRef]
- Nakayama, K.; Leiva, J.A.; Enomoto, Y. Chemi-emission of electrons from metal surfaces in the cutting process due to metal/gas interactions. Tribol. Int. 1995, 28, 507–515. [Google Scholar] [CrossRef]
- Nakayama, K. Triboemission of electrons, ions, and photons from diamondlike carbon films and generation of tribomicroplasma. Surf. Coat. Technol. 2004, 188, 599–604. [Google Scholar] [CrossRef]
- Nakayama, K. The plasma generated and photons emitted in an oil-lubricated sliding contact. J. Phys. D Appl. Phys. 2007, 40, 1103–1107. [Google Scholar] [CrossRef]
- Ning, L.P.; Jian, L.Q.; Yang, S.R.; Wang, J.Q.; Ren, J.F.; Wang, J.M. Effect of carbon black on triboelectrification electrostatic potential of MC nylon composites. Tribol. Int. 2010, 43, 568–576. [Google Scholar] [CrossRef]
- Nakayama, K. Mechanism of Triboplasma Generation in Oil. Tribol. Lett. 2011, 41, 345–351. [Google Scholar] [CrossRef]
- Nakayama, K.; Tanaka, M. Simulation analysis of triboplasma generation using the particle-in-cell/Monte Carlo collision (PIC/MCC) method. J. Phys. D Appl. Phys. 2012, 45, 49. [Google Scholar] [CrossRef]
- Nakayama, K. Triboemission of Charged Particles from Various Solids Under Boundary Lubrication Conditions. Wear 1994, 178, 61–67. [Google Scholar] [CrossRef]
- Scudiero, L.; Dickinson, J.T.; Enomoto, Y. The electrification of flowing gases by mechanical abrasion of mineral surfaces. Phys. Chem. Miner. 1998, 25, 566–573. [Google Scholar] [CrossRef]
- Wang, Z.L.; Wang, A.C. On the origin of contact-electrification. Mater. Today 2019, 30, 34–51. [Google Scholar] [CrossRef]
- Nakayama, K.; Fujimoto, T. The energy of electrons emitted from wearing solid surfaces. Tribol. Lett. 2004, 17, 75–81. [Google Scholar] [CrossRef]
- Govindaraj, J.; Subbiah, S. Charged-Particle Emissions During Material Deformation, Failure and Tribological Interactions of Machining. J. Tribol. 2019, 141, 031101. [Google Scholar] [CrossRef]
- Nakayama, K. Effect of Normal Force on the Triboplasma Generation Under Oil Lubrication. Tribol. Lett. 2014, 53, 449–456. [Google Scholar] [CrossRef]
- You, P. Generation and harm of static electricity. Phys. Technol. 1992, 29–31. [Google Scholar]
- Olufayo, O.A.; Abou-El-Hossein, K.; Kadernani, M.M. Tribo-electric Charging in the Ultra-high Precision Machining of Contact lens Polymers. Procedia Mater. Sci. 2014, 6, 194–201. [Google Scholar] [CrossRef]
- Dickinson, J.T. Fracto-emission: The role of charge separation. J. Vac. Sci. Technol. A Vac. Surf. Film. 1984, 2, 1112. [Google Scholar] [CrossRef]
- Ciniero, A.; Le Rouzic, J.; Baikie, I.; Reddyhoff, T. The origins of triboemission—Correlating wear damage with electron emission. Wear 2017, 374, 113–119. [Google Scholar] [CrossRef]
- Nakayama, K.; Hashimoto, H. Triboemission From Various Materials In Atmosphere. Wear 1991, 147, 335–343. [Google Scholar] [CrossRef]
- Smith, T.; Naerheim, Y.; Lan, M.S. Theoretical analysis of cutting fluid interaction in machining. Tribol. Int. 1988, 21, 239–247. [Google Scholar] [CrossRef]
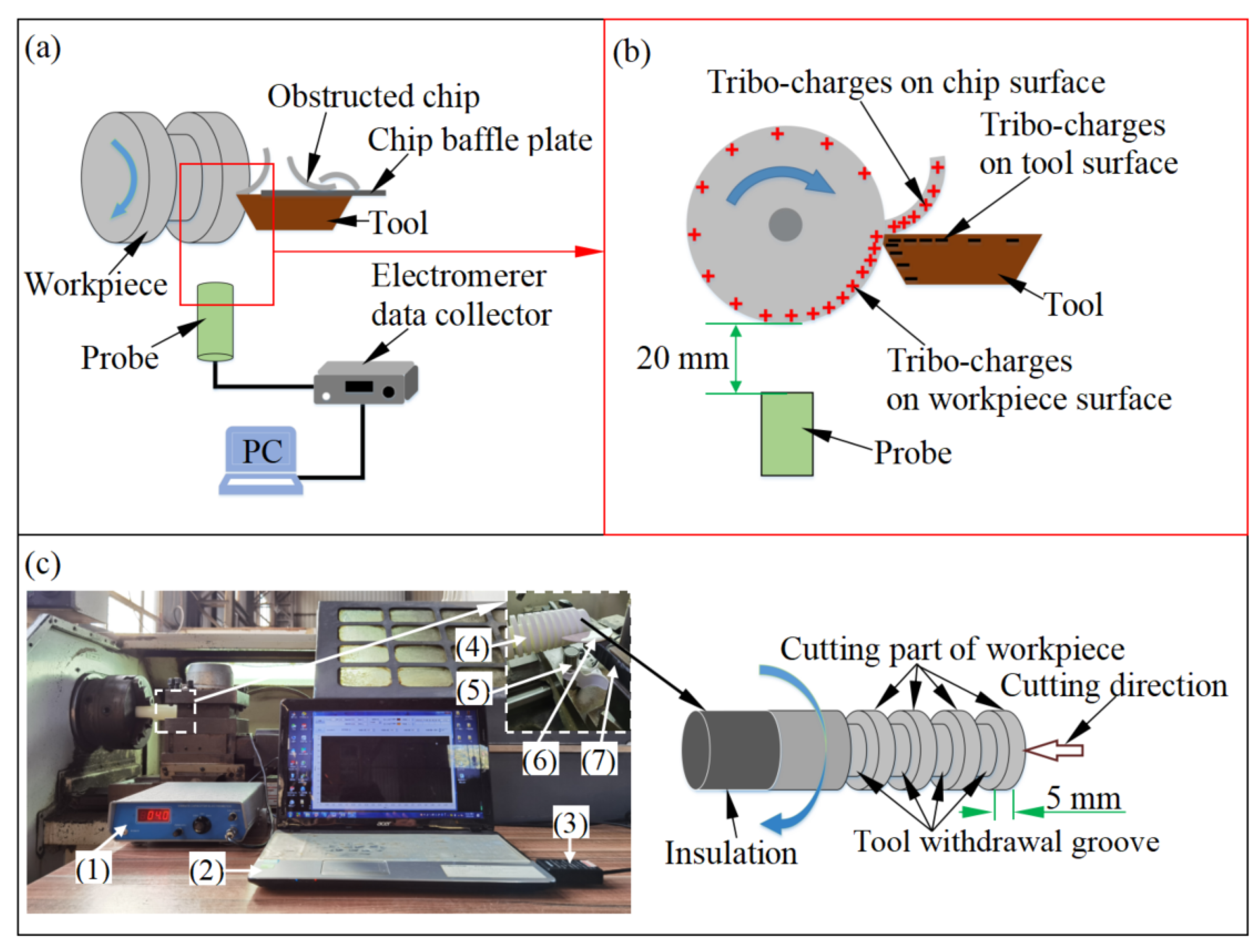




| Machine Tool | CAK6150D Precision Lathe |
|---|---|
| Cutting tool | Coated cemented carbide, PVD-TiAlN, CCMT09T304N-SU, Sumitomo Co., Ltd., Fukuoka, Japan |
| Tool holder | SCLCR2020KO9C |
| Workpiece materials | Mild steel (AISI 1015); Stainless steel (AISI 304); Polyethylene (PE); Acrylonitrile Butadiene Styrene (ABS). |
| Cutting parameters | Cutting speed: 44.6, 63.1, and 89.4 m/min; Depth of cut: 0.25, 0.5, and 1 mm; Feed rate: 0.25 mm/r; Cutting length: 5 mm. |
| Environment | Dry |
| Triboelectrification electrostatic potential detector | Vibratory capacitance electrometer (EST102, Beijing Hua Jinghui Technology Ltd., Beijing, China) |
| Material | Electrical Resistivity (nΩ·m) | Hardness | Ultimate Strength (MPa) | Yield Strength (MPa) |
|---|---|---|---|---|
| Mild steel (AISI 1015) | 159 | 111 (HB) | 385 | 325 |
| Stainless steel (AISI 304) | 720 | 201 (HB) | 515 | 215 |
| Tungsten carbide (YG6) as tool material | 800 | 90 (HRA) | 344 | |
| Polyethylene (PE) | ≥1 × 1019 | 45 (Ball Indentation Hardness) | 28 | |
| Acrylonitrile Butadiene Styrene (ABS) | ≥1 × 1019 | 93.2 (Ball Indentation Hardness) | 38 | 45.1 |
| Material | AISI 1015 | AISI 304 | YG6 | PE | ABS |
|---|---|---|---|---|---|
| Conductivity (S/m) | 6.3 × 106 | 1.4 × 106 | 1.25 × 106 | ≤1 × 10−10 | ≤1 × 10−10 |
| (s) | <2.3 × 10−18 | <1.05 × 10−17 | <1.17 × 10−17 | ≥0.147 | ≥0.201 |
| 2~10 | 80~100 | 10~20 | 2.3~3.4 | 2.4~4.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, B.; Yang, C.; Zhou, Q.; Guo, X.; Shamsullo, Q.S.; Zheng, G.; Tong, Z.; Xu, X. Research on Electrical Properties of the Cutting Zone in Cutting Metal/Insulation Materials. Processes 2025, 13, 3587. https://doi.org/10.3390/pr13113587
Feng B, Yang C, Zhou Q, Guo X, Shamsullo QS, Zheng G, Tong Z, Xu X. Research on Electrical Properties of the Cutting Zone in Cutting Metal/Insulation Materials. Processes. 2025; 13(11):3587. https://doi.org/10.3390/pr13113587
Chicago/Turabian StyleFeng, Bohua, Chen Yang, Qianying Zhou, Xiaomei Guo, Qurbonalizoda Saidabdullo Shamsullo, Gaoan Zheng, Zeqi Tong, and Xuefeng Xu. 2025. "Research on Electrical Properties of the Cutting Zone in Cutting Metal/Insulation Materials" Processes 13, no. 11: 3587. https://doi.org/10.3390/pr13113587
APA StyleFeng, B., Yang, C., Zhou, Q., Guo, X., Shamsullo, Q. S., Zheng, G., Tong, Z., & Xu, X. (2025). Research on Electrical Properties of the Cutting Zone in Cutting Metal/Insulation Materials. Processes, 13(11), 3587. https://doi.org/10.3390/pr13113587






