Exploration of a Novel Technology for Waterless Fracturing in Shale Reservoirs Based on Microwave Heating

Abstract

Chinese shale reservoirs are typically deep, clay-rich, and highly water-sensitive, which severely limits the effectiveness of conventional hydraulic fracturing. To address this challenge, we propose a microwave-assisted waterless fracturing method and investigate its feasibility through laboratory experiments on core samples from the Gulong shale and tight sandstone formations in the Daqing Oilfield. A coupled model integrating microwave power dissipation, pore water heating, and thermal stress evolution is developed to interpret the underlying mechanisms. Experimental results show that, under microwave irradiation (200 W, 40 s) and initial pore water content of 2.1–6%, fracturing is successfully induced without external fluid injection. The tensile failure of the rock coincides with the peak internal pore pressure generated by rapid vaporization and thermal expansion of pore water, as confirmed by a modified tensile strength measurement method. Fracture patterns observed in SEM and post-treatment imaging align with model predictions, demonstrating that microwave energy absorption by pore water is the primary driver of rock failure. The technique eliminates water-related formation damage and is inherently suitable for deep, water-sensitive reservoirs. This study provides experimental evidence and mechanistic insight supporting microwave-based waterless fracturing as a viable approach for challenging shale formations.

1. Introduction

Petroleum exploration results indicate [1,2,3] that the total amount of shale oil potentially generated through in situ upgrading from medium- and low-maturity shale oil resources in China is approximately 101.62 billion tons. With an estimated recovery factor of 65%, the total recoverable resources of medium- to low-maturity shale oil in China could reach as high as 66.04 billion tons, revealing enormous resource potential. However, due to the complex geological conditions and significant extraction challenges, the overall production performance of shale oil in China remains poor to date, with recovery rates reaching only 1–3% [4], indicating a substantial gap in oil recovery technologies. Clearly, developing innovative extraction methods tailored to the specific characteristics of China’s medium- and low-maturity shale oil reservoirs and further improving recovery rates represent a highly significant and meaningful endeavor. Shale oil (or other tight oil) reservoirs have extremely low permeability, making hydraulic fracturing essential for commercial production. However, unlike marine shales in North America, Chinese continental shales contain high-viscosity, low-GOR, poorly flowing oil, and are characterized by high clay content and strong water sensitivity [5,6,7], leading to poor fracturing performance. For example, in Daqing Oilfield, challenges include great burial depth (1500–3000 m), low porosity (3–8%), ultra-low permeability (<0.1 mD), high clay content (20–40%) causing severe water sensitivity and fluid leak-off, and serious proppant embedment due to low Young’s modulus (<20 GPa). These conditions result in even worse fracturing efficiency, demanding urgent solutions.

Since the 1980s, microwave heating has attracted significant attention in petroleum engineering for its ability to modify and fracture oil-bearing reservoirs. In 1984, Chen et al. [8] investigated the selective heating of different rock minerals by microwaves and their wave transmission properties, showing experimentally that certain minerals are nearly transparent to microwaves, while sulfides, arsenides, and water in reservoirs can be rapidly heated to high temperatures within seconds. Bridges and Taflove [9], studying overseas shale oil reservoirs, proposed that thermal gradients induced by microwave’s selective heating of minerals could generate fractures in oil shale, alongside their research on in situ kerogen conversion. A recent experimental study [10] demonstrated that high-power (15 kW), short-pulse (3 s) microwave irradiation can induce fractures in coal under isotropic stress, with fracture apertures increasing as heating duration extends. Chen et al. [5,11,12,13] applied microwaves to basalt and conducted uniaxial compression tests, finding that microwave-treated samples exhibited rougher fracture surfaces and more developed microcracks compared to untreated ones. Similar results were observed in granite through both experiments and numerical simulations. Overall, existing studies confirm that microwave heating can induce fracturing in shale reservoirs [14]. On the one hand, different minerals exhibit varying microwave absorption and thermal conductivity, resulting in large localized temperature gradients and high thermal stresses. On the other hand, microwave irradiation vaporizes pore fluids, generating high internal vapor pressure. The combined effect of excessive thermal stress and internal pressure can exceed the rock’s tensile strength, causing fracture formation. However, most current studies are limited to laboratory experiments with qualitative descriptions; quantitative mechanistic analyses remain scarce. To date, no research has been reported on developing waterless fracturing technologies for water-sensitive shale reservoirs based on microwave-induced fracturing mechanisms. On the one hand, different minerals exhibit varying microwave absorption and thermal conductivity, resulting in large localized temperature gradients and high thermal stresses. On the other hand, microwave irradiation vaporizes pore fluids, generating high internal vapor pressure. The combined effect of excessive thermal stress and internal pressure can exceed the rock’s tensile strength, causing fracture formation. However, most current studies are limited to laboratory experiments with qualitative descriptions; quantitative mechanistic analyses remain scarce. In light of the limitations of conventional hydraulic fracturing in deep, clay-rich, and water-sensitive continental shale reservoirs—such as those in Daqing Oilfield—this study proposes a microwave-based waterless fracturing approach. Building on existing models of microwave–rock interactions, we derive a new analytical expression for the transient temperature field induced by microwave irradiation in heterogeneous shale, explicitly incorporating mineral-dependent dielectric properties, thermal conductivity, and heat loss mechanisms. This model is rigorously validated against controlled laboratory experiments under reservoir-relevant conditions, establishing a quantitative relationship between microwave operating parameters (e.g., power and exposure time) and thermal response. The resulting integrated theoretical–experimental framework not only advances the mechanistic understanding of microwave-induced thermal fracturing but also enables predictive, physics-informed design for field-scale implementation in water-sensitive shale plays.

2. Principle of Waterless Fracturing Technology for Shale Reservoirs

This paper proposes a novel reservoir fracturing method—waterless fracturing technology—in which subsurface reservoirs are heated via surface-based microwave radiation to induce rock fracturing and crack formation through thermal effects, as an alternative to conventional hydraulic fracturing that relies on injecting high-pressure fluids (e.g., water) from the surface. This approach is supported by substantial experimental evidence [5,7,8,9,10,11,12,13,14]. Studies show that when microwave radiation is applied to underground shale reservoirs, pore water within confined spaces (such as water-filled pores in tight shale) is selectively heated. Due to spatial confinement, the heated water cannot expand freely, leading to a rapid increase in pore pressure. Moreover, pore water exhibits higher dielectric loss and thermal expansion coefficients compared to other mineral components, making it more efficient at absorbing microwave energy and rapidly increasing in temperature. This process generates significant thermal stress. When the combined effect of elevated pore pressure and thermal stress exceeds the tensile strength of the rock, fracture initiation or fragmentation occurs, thereby achieving effective crack formation.

The proposed waterless fracturing method is fundamentally based on two physical mechanisms: (1) differential microwave absorption among reservoir minerals, and (2) heterogeneous thermal expansion properties. Microwaves can efficiently heat certain components within the shale matrix—such as pore water—but are less effective in heating other mineral phases, resulting in non-uniform energy distribution. Additionally, different minerals exhibit varying thermal expansion coefficients. Consequently, under microwave irradiation, individual components experience differing degrees of temperature rise and volumetric expansion, generating localized thermal stresses within the rock. These differential thermal effects ultimately lead to the initiation and propagation of microcracks.

According to the definition of the thermal expansion coefficient $\zeta$, the following formula is obtained:

$$\zeta ={\displaystyle \frac{1}{V}}{({\displaystyle \frac{\partial V}{\partial T}})}_P$$

(1)

where $V$ denotes rock volume, and $T$ and $P$ represent temperature and pressure, respectively.

Table 1. Thermal Expansion coefficient of typical minerals found in shales. The data are at 293 °K (or 20 °C) unless noted.

Rock Type	Thermal Expansion Coeff., (K−1)
Berea Sandstone (Dry)	1.5 × 10−6
Boom Clay (wet)	3.3 × 10−6
Calcite	13.1 × 10−6
Water	6.6 × 10−5
Pyrite	9.7 × 10−6 (40 °C)

lists the thermal expansion properties of several typical reservoir minerals and water [15,16,17]. It can be seen from the table that the thermal expansion coefficients of different substances vary significantly, resulting in distinct thermal expansion behaviors (or volumetric expansion). The thermal expansion coefficient of water is much higher than that of other rock-forming minerals, with its expansion capacity being approximately 20 times that of clay minerals. This indicates that under microwave irradiation, the mismatch in thermal expansion and contraction between pore water and the surrounding rock matrix generates substantial thermal stress, which can lead to fracture initiation within the reservoir rock.

3. Mathematical Model for Shale Reservoir Fracturing Based on Microwave Heating

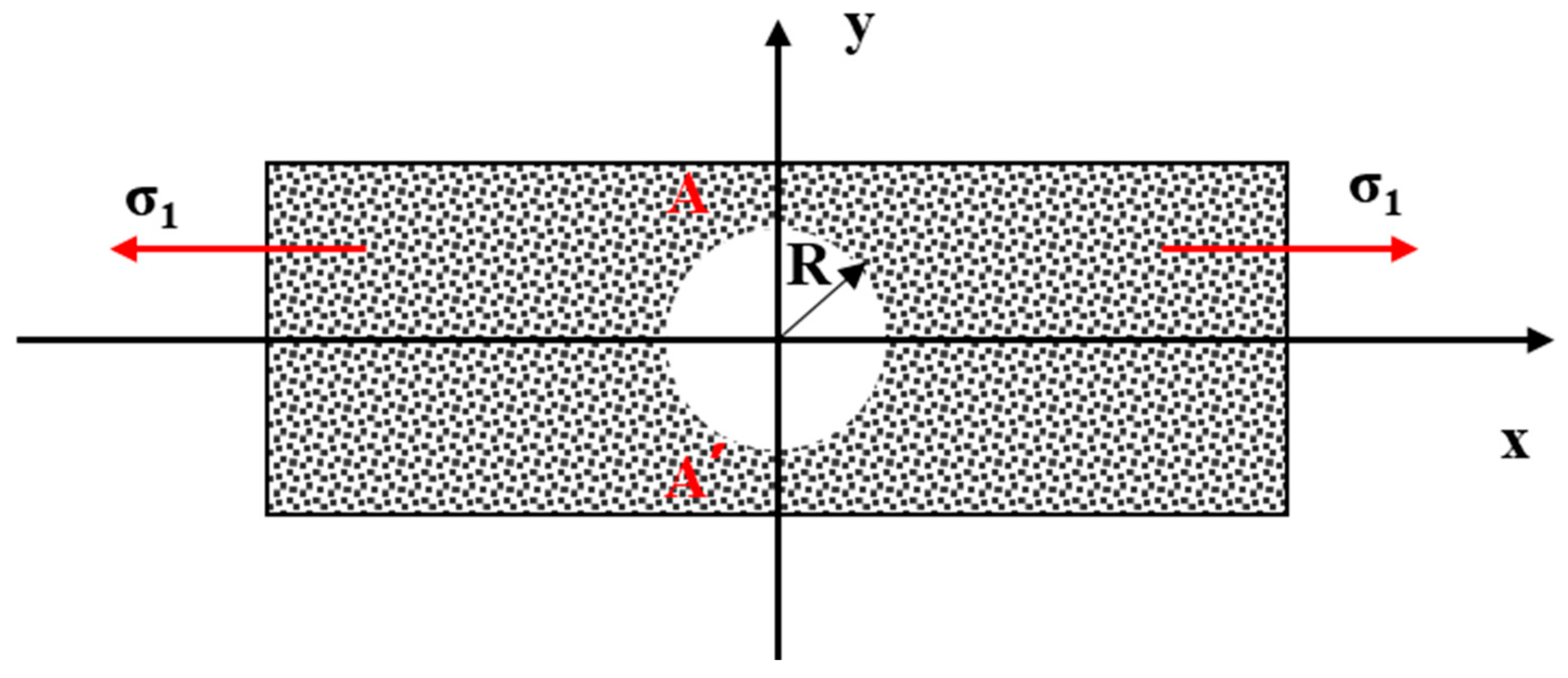
3.1. Temperature Field Model of Pore Water in Shale Reservoirs

When microwave radiation is applied to heat underground shale reservoir rock, derived from analysis of Maxwell’s equations [18], the microwave power dissipated per unit volume of the reservoir medium (or the heat generated per unit time per unit volume of the reservoir medium) can be expressed by the following equation:

$$P_{av}={\displaystyle \frac{1}{2}}\omega {\epsilon }_0{\epsilon }_r^{"}{\displaystyle \underset{V}{\int }E\cdot E^{*}dV}$$

(2)

where $P_{av}$ denotes the average dissipated power; $\omega$ represents the microwave angular frequency, with $\omega =2\pi f$; and $f$ being the microwave frequency; $E$ is the electric field strength, and $E^{*}$ denotes the conjugate vector of the electric field; ${\epsilon }_0$ is the permittivity of free space, 8.85 × 10⁻¹² F/m; ${\epsilon }_r^{"}$ is the relative dielectric loss factor of the heated medium, which is the imaginary part of the relative complex permittivity ${\epsilon }_r^{*}$ of an isotropic material, expressed as:

$${\epsilon }_r^{*}={\epsilon }_r^{\prime }-j{\epsilon }_r^{"}$$

(3)

In Equation (3), ${\epsilon }_r^{\prime }$ denotes the real part of the relative permittivity of the heated medium.

Equation (2) is integrated over the entire volume of the reservoir rock subjected to microwave irradiation. If the reservoir contains several different rock minerals and water with varying microwave absorption capabilities, the total energy absorbed by the rock (or the microwave dissipation power) must account for all constituent components. If the volume fractions of the minerals and their respective dielectric loss constants are known, Equation (2) can be rewritten as:

$$P_{av}={\displaystyle \frac{1}{2}}\omega {\epsilon }_0({\displaystyle \underset{V}{\int }E\cdot E^{*}dV)}{\displaystyle \sum _i{\epsilon }_{r,i}^{"}}$$

(4)

In Equation (4), the index i represents the summation over all mineral and fluid components present in the reservoir, accounting for their respective dielectric loss constants.

Since the wavelength of the electromagnetic waves used in microwave heating is approximately 12 cm (corresponding to a frequency of 2450 MHz), which is much larger than the grain size of minerals and pore diameters, the electric field $E$ can be considered uniform across all components within the spatial volume $V$. Therefore, when integrating Equation (3) over the volume $V$, the electric field $E$ is treated as identical for all rock constituents, significantly simplifying the calculation.

Table 2. Relative dielectric constants of typical minerals in shale. The number listed in the parenthesis in the first column is the frequency the measurement was conducted.

Rock/Mineral	Dielectric Const. (εr′)	Dielectric Loss (εr″)
20 Ω salt water (1.1 GHz)	79	5.6
1 Ω salt water (1.1 GHz)	77	21
0.1 Ω salt water (1.1 GHz)	59	167
Dolomite (1 GHz)	7.41	1.80 × 10−3
Calcite (1 GHz)	8.94	4.20 × 10−4
Quartz (1 GHz)	3.89	5.33 × 10−4
Pyrite (2.45 GHz)	83	17

lists the dielectric constants of typical substances commonly found in oil-bearing reservoir rocks [19]. It is evident from the table that the relative dielectric loss factor ${\epsilon }_r^{"}$ of pore water with varying salinity is thousands of times greater than that of other media. Therefore, pore water (including fresh and saline water) in the rock matrix dominates the microwave power dissipation in the reservoir, while the contributions from other reservoir components are negligible and can be ignored—a common simplification also adopted in industrial microwave heating applications. Accordingly, Equation (4) can be simplified to:

$$P_{av}\approx {\displaystyle \frac{1}{2}}\omega {\epsilon }_0{\epsilon }_{r,w}^{"}{\displaystyle \underset{V}{\int }E\cdot E^{*}dV}$$

(5)

In general, the electric field within the integration volume V is not constant but varies spatially; therefore, the electric field $E$ in Equation (5) must remain inside the integral. However, when high precision is not required, the electric field $E$ can be approximated as uniform throughout the volume. In this case, it can be estimated using the relation $E\cdot E^{*}=E^2$, leading to:

$$P_{av}\approx \omega {\epsilon }_0{\epsilon }_{r,w}^{"}{E}_{rms}^{2}V$$

(6)

In Equation (6), ${\epsilon }_{r,w}^{"}$ denotes the relative dielectric loss factor of pore water in the reservoir rock, $E_{rms}$ represents the root-mean-square (RMS) value of the electric field strength, and all other symbols have the same physical meanings as previously defined.

The root-mean-square (RMS) value of the electric field strength, $E_{rms}$ can be approximately estimated using the following equation [20]:

$$E_{rms}={\displaystyle \frac{\sqrt{377P_1}}{D_P}}$$

(7)

$$P_1=P_0{e}^{-2{\alpha }_{c}L}$$

(8)

$$D_P={\displaystyle \frac{{\lambda }_0}{2\pi \sqrt{{\epsilon }_r^{\prime }}tg\delta }}$$

(9)

$$tg\delta ={\displaystyle \frac{{\epsilon }_r^{"}}{{\epsilon }_r^{\prime }}}$$

(10)

where $P_0$ denotes the input power of the microwave source; ${\alpha }_c$ is the attenuation coefficient due to the waveguide wall; $L$ represents the well depth; ${\lambda }_0$ is the wavelength in free space; and $D_P$ denotes the power penetration depth. Equation (6) is used in this paper to calculate the average power dissipation in the reservoir.

After the microwave-absorbing material (e.g., pore water) in the reservoir rock absorbs microwave energy, its rate of temperature rise depends on a series of relevant physical parameters. According to thermodynamic theory, the power required to raise the temperature of a mass $M$ from $T_w^0$ °C to $T_w^t$ °C within a time $t$ is given by the following equation:

$$P_{av}={\displaystyle \frac{M{C}_p(T_w^t-T_w^0)}{t}}$$

(11)

By combining Equations (6) and (11), the mathematical model describing the temperature variation in pore water in the reservoir under microwave irradiation can be derived as:

$$T_w^t=T_w^0+{\displaystyle \frac{\omega {\epsilon }_0{\epsilon }_{r,w}^{"}{E}_{rms}^2}{{\rho }_w{C}_p}}t$$

(12)

In Equation (12), ${\rho }_w$ denotes the density of pore water (in kg/m³); $C_p$ represents the specific heat capacity of pore water (in J/(kg·°C)); $t$ is the microwave irradiation heating time (in seconds). All other symbols have the same physical meanings as defined previously.

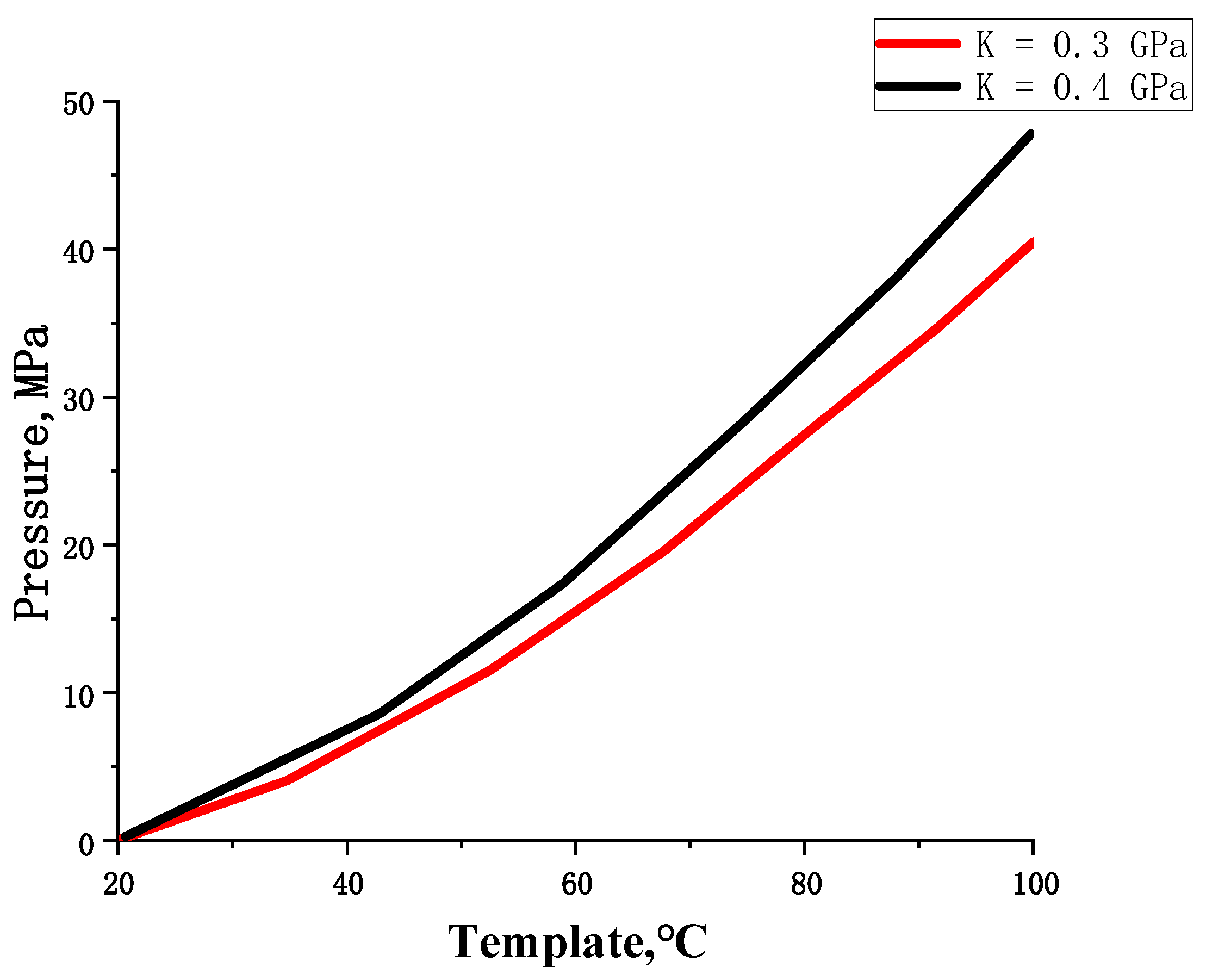
3.2. Pressure Field Model of Pore Water in Shale Reservoirs

The pressure variation in pore water in a shale reservoir induced by microwave heating can be analyzed using a fluid equation of state (EOS). The EOS for water within the pores (hereinafter referred to as “pore water”) can be expressed as:

$$z={\displaystyle \frac{P_w}{R{T}_w{\rho }_w}}$$

(13)

In Equation (13), R is the specific gas constant for pure water [21], 0.461526 kJ·kg⁻¹·°C⁻¹; $T_w$ is the temperature, °C; $P_w$ is the pressure, kPa; $V_w$ is the volume of water, m³, ${\rho }_w$ is the density of pore water, kg/m³, and $z$ is the compressibility factor.

Based on experimental data published by the International Association for the Properties of Water and Steam (IAPWS), the applicable temperature and pressure range of Equation (13) can be corrected using Equation (14):

$$\begin{array}{l}{P}_w\le 100\mathrm{MPa}\begin{array}{cc}& \end{array}(0°\mathrm{C}\le T\le 800°\mathrm{C})\\ P_w\le 50\mathrm{MPa}\begin{array}{cc}& \end{array}(800°\mathrm{C}\le T\le 2000°\mathrm{C})\end{array}$$

(14)

The above temperature and pressure range covers all operational conditions considered in this study as well as the predicted parameter range for laboratory experiments.

Equations (12) and (13) are coupled, and a MATLAB R2023a computational program is developed using the method proposed by Holmgren et al. [22] to calculate the physical properties of water within the range defined by Equation (14), enabling prediction of pore pressure evolution in shale reservoir rocks under microwave irradiation. The analysis and calculations are carried out for three distinct cases as follows.

(1) Pressure variation in water in pores of an incompressible rock

First, an idealized scenario is considered: the reservoir rock is sufficiently rigid and impermeable, remaining incompressible and undeformed even under high pore water pressure. Under this assumption, the volume of pore water remains constant, and its density stays unchanged. The net effect of temperature increase is thus solely a rise in pore water pressure. This temperature-dependent pressure change can be directly obtained from the equation of state for water under constant density conditions. The calculated results are shown in Figure 1.

It can be seen that pore water pressure is a function of temperature. Starting from an initial condition of 1 atm and 20 °C, the pressure increases rapidly with rising temperature. Given that the tensile strength of shale is approximately 10 MPa [23], Figure 1 indicates that a temperature increase of only about 10 °C is sufficient to reach this threshold, potentially initiating rock fracturing. Furthermore, it is noted that, under constant pore water density, as long as the pores are fully water-saturated, the rate of pressure increase is essentially independent of the volume of water within the rock.

(2) Pressure variation in water in pores of a compressible rock

Now, a more realistic scenario is considered: the reservoir rock is assumed to be compressible under conditions of microwave heating of pore water and the resulting pressure increase. This case is equivalent to allowing the pore water to expand in volume during microwave irradiation. It can be reasonably inferred that the coupled effect of rock compressibility and thermal expansion of pore water will reduce the magnitude of pore water pressure rise induced by microwave heating.

The shale reservoir rocks considered in this study are typically dense, fine-grained, and characterized by small pore sizes. Due to the presence of water-saturated pores, their disturbance to the in situ stress field is confined within a few pore radii. Consequently, the overall macroscopic volume change in the rock matrix caused by increased pore water pressure is negligible. Under this condition, the volumetric deformation of the rock matrix due to thermo-compression effects should equal the volume expansion of the pore water:

$$d{V}_m=-d{V}_w$$

(15)

In Equation (15), ΔV denotes the volume change; $d{V}_m$ and $d{V}_w$ represent the volumes change in the rock matrix (solid phase) and pore water, respectively.

The pressure applied to the rock matrix $P_m$ is equal to the pore water pressure $P_w$, and its incremental form can be expressed as:

$$d{P}_m=d{P}_w$$

(16)

Under the action of pore water pressure, the volume change in the rock matrix depends on the bulk modulus $K_m$ of the rock matrix (or solid phase):

$$K_m=-V_m^0{\displaystyle \frac{d{P}_m}{d{V}_m}}$$

(17)

In Equation (17), $V_m^0$ denotes the initial volume of the rock matrix, i.e., the volume of the rock matrix (solid phase) at the initial time when microwave irradiation begins (t = 0). Combining Equations (15)–(17), we obtain:

$$d{P}_w={\displaystyle \frac{K_m}{V_m^0}}d{V}_w$$

(18)

And:

$$\left\{\begin{array}{l}{V}_w^0=x_w{V}_r^0\\ V_m^0=(1-x_w)V_r^0\end{array}\right.$$

(19)

In Equation (19), $x_w$ denotes the water content, defined as the volume fraction of pore water in the total reservoir rock volume, and $V_r^0$ represents the initial volume of the rock matrix (solid phase). Therefore, Equation (18) can be rewritten as:

$$d{P}_w={\displaystyle \frac{K_m}{(1-x_w)V_r^0}}d{V}_w$$

(20)

The following relationship can be further applied:

$$\left\{\begin{array}{l}d{P}_w=P_w^t-P_w^0\\ d{V}_w=V_w^t-V_w^0\end{array}\right.$$

(21)

In Equation (21), the variables $P_w^t$ and $P_w^0$ denote the fluid pressure at an arbitrary time and at the initial time, respectively. With this notation, Equation (20) can be rewritten as:

$$P_w^t=P_w^0+{\displaystyle \frac{K_m{x}_w}{(1-x_w)}}({\displaystyle \frac{V_w^t}{V_w^0}}-1)$$

(22)

By converting the pore water volume into density, Equation (22) can be expressed as follows:

$$P_w^t=P_w^0+{\displaystyle \frac{K_m{x}_w}{(1-x_w)}}({\displaystyle \frac{{\rho }_w^0}{{\rho }_w^t}}-1)$$

(23)

Equation (23) indicates that the pressure of heated pore water depends on the change in water density, the water volume fraction, and the bulk modulus of the rock matrix. According to the equation of state (EOS) of water, the density of pore water is a function of temperature and pressure. Therefore, given the rock matrix bulk modulus and water content, the pore water pressure at a specified temperature can be determined by simultaneously solving Equation (23) and the water EOS [24]. In this study, within the prescribed temperature range, the bisection method is employed to solve Equations (13) and (23) simultaneously, with the calculation tolerance set within 0.01 MPa. The resulting computed values are shown in Figure 2.

As shown in Figure 3, under initial conditions of 1 atmosphere and 20 °C, the increase in pore water pressure within a reservoir rock containing 10% pore water varies under different bulk modulus conditions. Figure 3 indicates that the rate of increase in pore water pressure is primarily determined by the rock’s bulk modulus. A smaller bulk modulus results in a greater volumetric expansion of the pore water, leading to relatively smaller pressure increases as temperatures rise. Figure 3 illustrates the changes in the density of the pore water. If pore water accounts for only 10% of the total rock volume, a 4% change in water density would cause an approximate 0.4% change in the volume of the rock matrix (the solid phase). This highlights the significant impact that even minor changes in pore water properties can have on the overall structure of the rock.

(3) Changes in Pore Water Pressure under Reservoir Conditions

Figure 2 illustrates the changes in pore water pressure during microwave heating under laboratory conditions. However, in actual underground reservoirs, factors such as well depth result in significantly higher initial temperatures and pressures for the pore water in reservoir rocks compared to laboratory settings. Consequently, the initial density of pore water in Equation (23) will differ from its initial value under laboratory conditions. Additionally, under substantial overburden stress, the bulk modulus of the rock matrix is greater than that under laboratory conditions [16,24]. These factors will inevitably alter the rate of pressure increase in pore water during microwave irradiation.

Figure 4 shows the calculated increase in pore water pressure due to temperature rise, under initial conditions of 20 °C and 62 MPa. These conditions correspond to a reservoir depth of approximately 2800 m, with an overburden stress of about 62 MPa. Under such pressure conditions, the typical bulk modulus of shale reservoir rock is measured to be around 30 GPa [24]. The results indicate that when pore water is heated to 40 °C, the pore pressure increases to between approximately 62 MPa and 72 MPa.

3.3. Tensile Strength Criterion for Fracturing in Shale Reservoirs

In unconventional shale reservoir rocks, water-saturated pores occupy a small volume fraction; therefore, it is reasonable to neglect interactions between pores when analyzing the stress distribution around a pore. Furthermore, for simplicity, the two-dimensional problem of a single pore is idealized as a circular hole of radius R, as illustrated in Figure 5.

For the case shown in Figure 5, the maximum tensile stress occurs along the y-axis. Therefore, we focus only on the tensile stress distribution along the y-axis, which, according to Jaeger et al. [15], can be expressed as:

$${\sigma }_x={\sigma }_1\left[1+{\displaystyle \frac{1}{2}}{({\displaystyle \frac{R}{y}})}^2+{\displaystyle \frac{3}{2}}{({\displaystyle \frac{R}{y}})}^4\right]+P_w{({\displaystyle \frac{R}{y}})}^2$$

(24)

Equation (24) is applicable in the region where y ≥ R. It is evident from Equation (24) that the maximum tensile stress occurs at point A (x = 0, y = R) and point A′ (x = 0, y = −R) in Figure 5, and the maximum tensile stress is given by:

$${\sigma }_x^{\max }=3{\sigma }_1+P_w$$

(25)

When the maximum tensile stress exceeds the tensile strength of the rock, the rock fails. The failure stress ${\sigma }_c$ of the rock at this point is given by:

$${\sigma }_x^{\max }={\sigma }_c$$

(26)

Equation (26) describes an intrinsic material property of the reservoir rock matrix (solid phase) at the point of fracture, and thus can serve as a criterion for hydraulic fracturing.

It is well known that the “Brazilian test” is traditionally used to determine the tensile strength of rock [22]. This method measures the tensile strength $S_{tr}$ under conditions of zero pore pressure ($P_w=0$), where ${\sigma }_1$ is defined as the tensile stress at which the rock sample fails. Therefore, combining Equations (25) and (26), the tensile strength obtained from the Brazilian test is given by:

$$S_{tr}={\displaystyle \frac{1}{3}}{\sigma }_c$$

(27)

In the case of rock tensile strength testing using the microwave irradiation heating method, the measured tensile strength can be denoted as $S_{mw}$. Notably, this method involves no externally applied mechanical stress (${\sigma }_1=0$). According to Equation (25), the measured strength should equal the pore water pressure $P_w$ at the point of rock failure. Therefore, combining Equations (25) and (26), we obtain:

$$S_{mw}={\sigma }_c$$

(28)

From Equations (27) and (28), it follows that:

$${\displaystyle \frac{S_{mw}}{S_{tr}}}=3$$

(29)

From Equations (27) and (28), it follows theoretically that the tensile strength of rock measured using the microwave irradiation heating method is three times the value obtained from the conventional Brazilian test. Analysis shows that the tensile strength derived from increasing pore pressure via microwave heating equals the pore pressure at rock failure. This allows direct assessment of whether fracturing occurs in the reservoir rock during microwave irradiation, without relying on the traditional Brazilian test criterion.

According to Jaeger et al. [15], when the pores in the rock are three-dimensional and spherical, the factor 3 in Equations (25) and (29) should be replaced by 4, indicating a fourfold relationship between the two methods under such geometrical conditions.

4. Laboratory Experiments and Discussion of Results

4.1. Experimental Samples and Sample Preparation

The rock samples used in the waterless fracturing laboratory experiments include two tight sandstone cores from the Daqing oilfield, two shale core plugs from the Gulong oilfield, and two self-prepared clay slabs. All core samples were obtained from the same intact rock interval and showed no discernible cracks under SEM observation, ensuring the reliability of the experimental results.

Prior to microwave irradiation heating experiments, the samples were prepared as follows:

(1) Tight sandstone samples: The dried sandstone core plugs were evacuated under vacuum for more than 40 h, followed by saturation with 2% potassium chloride (KCl) solution under vacuum conditions;

(2) Shale core samples: The shale core plugs were immersed in brine solution for one week to ensure full pore water equilibration;

(3) Clay slab samples: Artificial clay plates were fabricated by compacting a mixture of montmorillonite and kaolinite clay powders under a pressure of 0.5 GPa.

4.2. Experimental Procedures

4.2.1. Measurement of Water Content in Rock Samples

The water content of the rock samples was measured using a nuclear magnetic resonance (NMR) spectrometer (Bruker, Billerica, MA, USA) operating at frequencies ranging from 2 MHz to 13 MHz. The water content was determined by comparing the NMR signal intensity of the samples with that of reference samples of known water content. The NMR signals were acquired using the spin echo method [25].

4.2.2. Microwave Irradiation Heating Experiments

The majority of the microwave irradiation experiments were conducted using a GX2-N microwave instrument (China University of Petroleum, Beijing, China), with a small number carried out using a Monowave-300 microwave reactor (Anton Paar GmbH, Graz, Austria). During the experiments, microwave radiation was applied at a constant output power of 200 W, with a maximum irradiation duration of 40 s. The microwave heating was immediately terminated upon visual detection of cracking or sudden fracturing of the rock sample. The temperature evolution of the samples was monitored in real time using an infrared thermometer.

4.2.3. Brazilian Tensile Strength Test

To compare with the theoretical analysis and experimental results of microwave-induced fracturing in reservoir rocks, the Brazilian tensile strength test was performed on the samples according to the standard ASTM D3967–16: Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens (ASTM International, West Conshohocken, PA, USA, 2016) [26].

4.3. Experimental Results and Discussion

4.3.1. Microwave Heating of Tight Sandstone from the Daqing Oilfield

Figure 6 shows the tight sandstone samples from the Daqing oilfield before and after microwave irradiation. Scanning electron microscopy (SEM) images (see Figure 7) reveal grain sizes of approximately 60–70 µm. Visual and microscopic observations confirm that the samples are highly compact with minimal pore development. Immediately after microwave irradiation, the surface temperature of the sample was measured using an infrared thermometer and found to be 51 °C. X-ray diffraction (XRD) analysis indicates that the rock matrix consists of 97.4% quartz, with minor amounts of muscovite and clay minerals. The bulk modulus of the sandstone matrix ranges from 2.8 GPa to 4.1 GPa.

Using the measured matrix elastic moduli, a water content of 6% determined by NMR, and an initial ambient pressure of 0.1 MPa, the evolution of pore pressure was modeled over a temperature range from 20 °C to 100 °C, as shown in Figure 8. The analysis indicates that when the temperature reaches 51 °C, the pore water pressure increases to between 10.0 MPa and 12.0 MPa. This pressure range is interpreted as the effective tensile strength of the core sample, corresponding to the critical pore pressure at which rock failure initiates under microwave-induced thermal stressing.

As previously described, Brazilian tensile strength tests were also conducted on the same type of sandstone samples, yielding a measured tensile strength of 3 MPa. Using Equation (28) derived earlier, the equivalent tensile strength of the sandstone under microwave irradiation heating is theoretically estimated to be in the range of 9–12 MPa. This predicted range is in good agreement with the critical pore pressure range (10.0–12.0 MPa) observed in the microwave-induced fracturing experiments shown in Figure 8.

The close consistency between the results of the two experimental methods not only validates the reliability of the measurements but also supports the validity of the theoretical analysis presented in this study. Therefore, it is concluded that Equation (28) can be reliably used as a criterion for assessing the success of waterless fracturing in reservoir rocks under microwave irradiation heating.

4.3.2. Microwave Heating of Shale and Clay Slabs

The shale core samples used in this experiment are primarily composed of quartz or carbonate minerals, clay, and organic matter, with only a small amount of pyrite (approximately 1 wt%). Figure 9 presents the experimental results: on the left is the original shale core plug from the Gulong oilfield in Daqing, and on the right is the same core after 35 s of microwave irradiation. The water content of this core sample is 3.3%. As shown in Figure 9, the core was completely destroyed after microwave heating, exhibiting severe fragmentation.

Figure 10 shows the results of microwave irradiation on another shale core plug, which had a water content of 2.2%. After heating, only minor cracking was observed. Subsequently, nuclear magnetic resonance (NMR) testing was performed on this partially fractured core, and no detectable water signal was found. This result is significant, as it further supports the proposed mechanism: the increase in pore water pressure induced by microwave heating is the primary cause of fracturing in shale reservoirs. In the absence of pore water, effective fracturing is unlikely to occur.

Figure 11 shows the experimental results of microwave irradiation on a clay slab pressed from montmorillonite powder. This clay slab contained 6 wt% water. In the P100N30AP-F4 microwave heating apparatus, the slab fractured after approximately 9 s of microwave exposure. Additionally, a similar experiment was conducted on a clay slab made from kaolinite, which was subjected to 30 s of microwave radiation. The results indicated that the fracturing behavior of the kaolinite slab was comparable to that of the montmorillonite slab, with no significant differences observed.

Analysis of microwave irradiation-induced fracturing experiments on tight sandstone and shale reveals that the increase in pore water pressure is the fundamental mechanism responsible for effective fracturing and fragmentation of these low-permeability rocks. In principle, this mechanism can be extended to fracturing applications in subsurface reservoirs.

As shown in the calculations in Figure 4, raising the temperature of pore water by several tens of degrees Celsius can easily increase the pore pressure. Equation (22) further indicates that the rate of pore pressure increase is directly proportional to the bulk modulus of the rock matrix. Consequently, for harder rocks or those located in deeper formations, the pore pressure rises more rapidly. Therefore, microwave-induced heating of pore water represents a promising and worthy-of-further-investigation fracturing technique.

5. Summary and Discussion

Compared to conventional hydraulic fracturing, electromagnetic wave-based methods (including microwave and other radio-frequency radiation) offer several distinct advantages:

(1) This approach is a “waterless” fracturing technique that requires no surface water injection, thereby eliminating the risk of water sensitivity in shales—particularly beneficial for water-sensitive, clay-rich reservoirs.

(2) The high pore pressures generated by microwave heating can fracture or even pulverize deep, tight rock formations, facilitating the release of oil trapped in nanoscale pores and significantly enhancing oil recovery.

(3) By eliminating the need for fracturing fluids, this method avoids formation damage caused by fluid leak-off. Furthermore, no chemical additives are required, eliminating the risk of chemical contamination.

(4) Through optimization of electromagnetic wavelength and power dissipation profiles, control over the fracturing process based on electromagnetic field theory offers superior spatial targeting and energy focusing, enabling more precise and predictable stimulation compared to hydraulic fracturing.

(5) By adjusting heating duration and power input, the temperature of pore water can be further elevated, enhancing thermally induced stresses. This enables the technique to overcome the higher overburden pressures associated with greater depths, making waterless fracturing feasible for deep and hard rock reservoirs.

In conclusion, microwave irradiation-based fracturing is an environmentally benign, mechanistically sound, and highly promising reservoir stimulation technology with broad application potential. Beyond enhancing shale oil recovery, the underlying thermal–mechanical mechanisms—particularly the generation of controlled microcracks through thermal stress and pore pressure buildup—may also inform strategies for geohazard mitigation in underground engineering [27]. For instance, the ability to pre-weaken high-stress rock zones via targeted microwave heating could offer a novel approach to mitigating rockburst risk, a catastrophic failure mode driven by brittle fracture under high confinement. Moreover, the evolution of pore structure during microwave heating—such as microcrack nucleation, enhanced connectivity, and fluid redistribution—holds promise as a source of precursory signals for impending failure [28,29]. While this study primarily employs NMR imaging to visualize fracture networks, future work will leverage quantitative NMR relaxation data in conjunction with acoustic emission monitoring to develop a multi-parameter early-warning framework. Such an integrated approach could not only optimize stimulation efficiency in reservoirs but also enhance safety in high-stress underground operations, bridging energy recovery and geotechnical risk management through a unified thermal–fracture paradigm.