An Intelligent Choquet Fuzzy Integral-Based Framework for Risk Assessment in Seismic Acquisition Processes
Abstract
1. Introduction
1.1. Safety Risk Evaluation Is Characterized by Pervasive Interdependencies Among Factors
1.2. Recent Advances in Intelligent Risk Assessment
- Theoretically, this work advances fuzzy integral theory by tailoring it to model interdependent risks in seismic acquisition.
- Methodologically, it introduces an intelligent mechanism to convert qualitative expert judgments into quantitative fuzzy measures [19].
- Practically, it provides a computationally efficient and empirically validated decision-support tool. Customized for Sinopec’s operational safety framework, the tool is designed to ensure a tangible real-world impact.
2. Choquet Fuzzy Integral
3. Methodology
3.1. Overview of the Proposed Framework
3.2. Algorithmic Steps for Risk Aggregation
3.2.1. Theoretical Framework and Computational Sequence
Computational Workflow for Risk Aggregation
Fuzzy Weight Aggregation
- Defuzzification Procedure: The relative distance method converts fuzzy weights into crisp values, establishing a reproducible mapping between linguistic terms.
- Expert evaluations are consolidated using the geometric mean operator. This approach preserves the triangular fuzzy structure while minimizing the influence of outlier judgments.
- Fuzzy Density Assignment: Resulting crisp values are assigned as fuzzy densities, forming the basis for interaction parameter calculation [28].
Computational Implementation
3.2.2. Mathematical Formalization
- Fuzzy Weight Aggregation
- B.
- Comprehensive Defuzzification Framework
- C.
- Fuzzy Density Assignment: The resulting crisp values are assigned as fuzzy densities. This forms the basis for calculating the interaction parameter.
3.2.3. Numerical Implementation
3.2.4. Static Nature and Dynamic Extension Potential
3.2.5. Computational Efficiency Analysis
3.2.6. Comparative Analysis and Selection of the Choquet Integral
4. Intelligent Model for Safety Risk Assessment in Seismic Acquisition Project
5. Identification of Safety Risk Factors in Seismic Acquisition Projects
- Theft, hijacking, or loss of civil explosives during transportation: These incidents pose severe safety threats. Contributing factors include inadequate guarding, improper well sealing, and mishandling of misfires. Robust security protocols and strict handling procedures are required to mitigate such risks and ensure the safe transport of hazardous materials.
- Traffic injury risk: Arises from the extensive use of vehicles for transporting personnel and materials. Key causes include driver error, vehicle malfunction, and adverse weather conditions.
- Damage to above and below ground facilities: Construction activities may endanger nearby structures and infrastructure due to insufficient site surveys, poorly located wells, inadequate safety distances, or operational errors.
- Drowning risk: Operations conducted near rivers, canals, reservoirs, or aquaculture ponds, such as underwater cable deployment or air gun operations without adequate protection, present drowning hazards. Major contributing factors include failure to wear life-saving equipment, vessel malfunction, and severe weather.
- Accidental explosion of civil explosives: Unintended detonations during transport may result from illegal parking, unqualified transportation practices, use of radio frequency devices, detonation line short circuits, or adverse environmental conditions.
- Fire risk: Collective accommodations and high fuel consumption during project execution heighten fire hazards. Contributing factors include unsafe fuel storage, unauthorized electrical use, and open flame heating practices on site.
- Electrocution risk: Electrical hazards may arise from equipment use, construction operations, or shared accommodations. Major risks include contact between detonation lines and wells, improper wiring, unsafe proximity to power lines, high voltage operations, and lightning strikes.
- Mechanical injury risk: The operation of heavy machinery introduces hazards related to improper operation, lack of protective gear, and mechanical failures.
- Sudden illness risk: The high physical demands of seismic acquisition work can lead to acute medical incidents, especially under extreme environmental or workload conditions.
6. Case Analyses and Model Validation
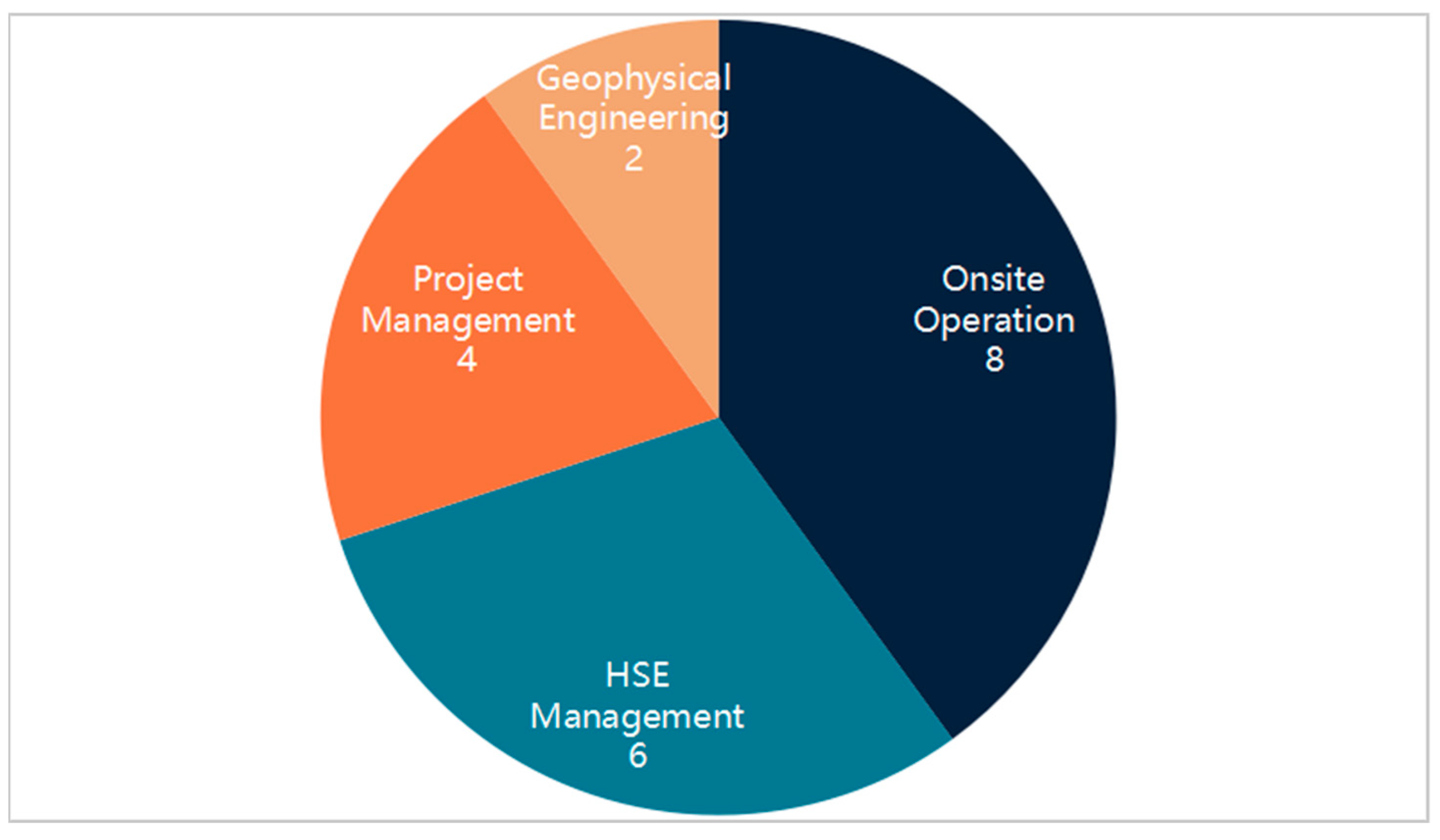
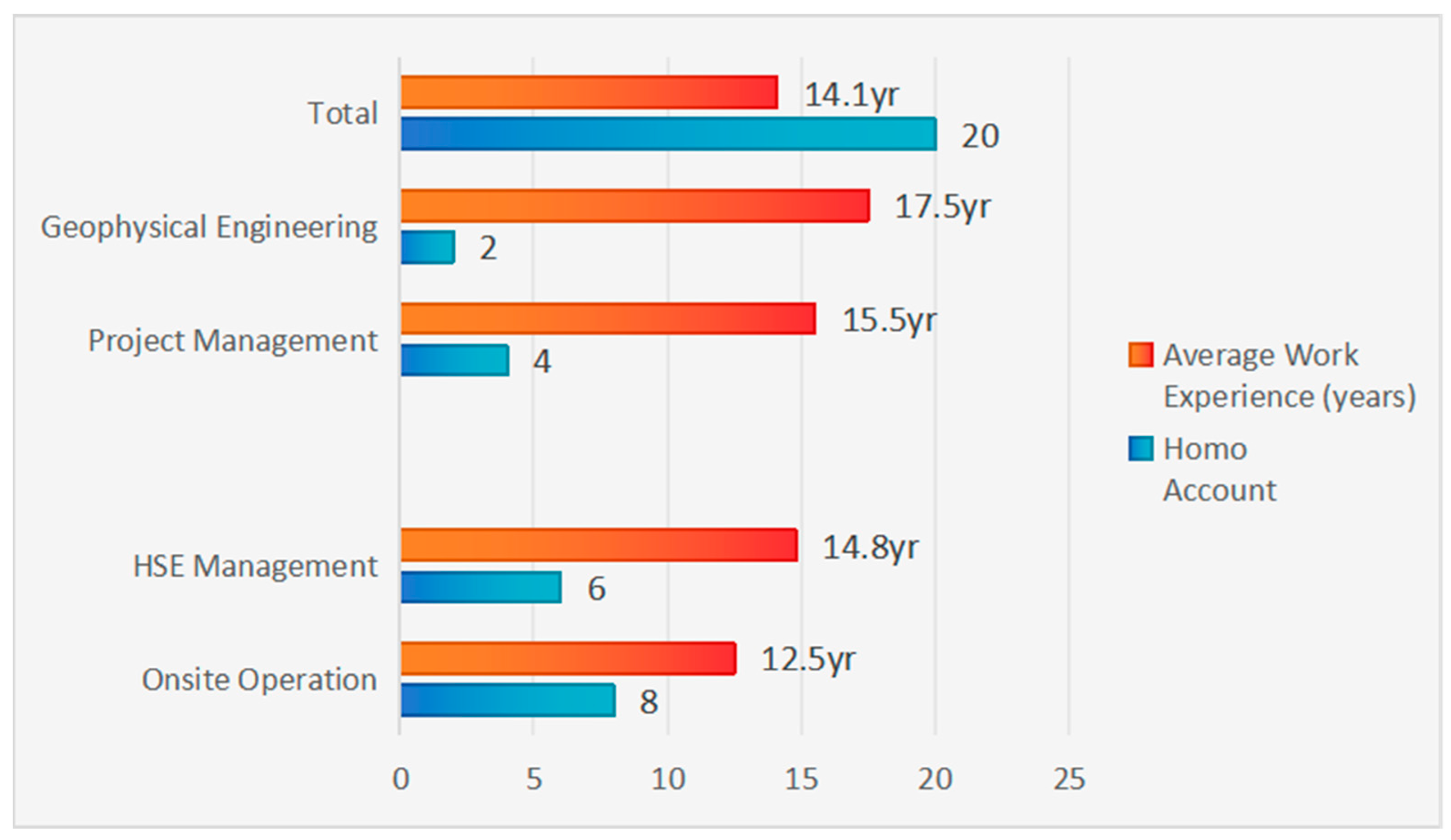
- Professional expertise in seismic acquisition safety, including domains such as health, safety, and environment (HSE) management, field operations, geophysical engineering, and risk assessment.
- Industry experience of no less than ten years in the oil and gas sector, with at least five years specifically devoted to seismic acquisition projects [31].
- Institutional diversity, ensuring representation from Sinopec, academic institutions, and independent safety consulting organizations to minimize potential evaluation bias.
- HB Project Actual Incident Rate: 0.34%
- SC Project Actual Incident Rate: 0.41%
6.1. Delphi Process Implementation
6.1.1. Expert Elicitation and Consensus Building
6.1.2. Process Termination and Consensus Validation
6.1.3. Quantification of Factor Interdependencies
6.1.4. Experimental Validation Framework
6.2. Experimental Setup and Baseline Models
- (1)
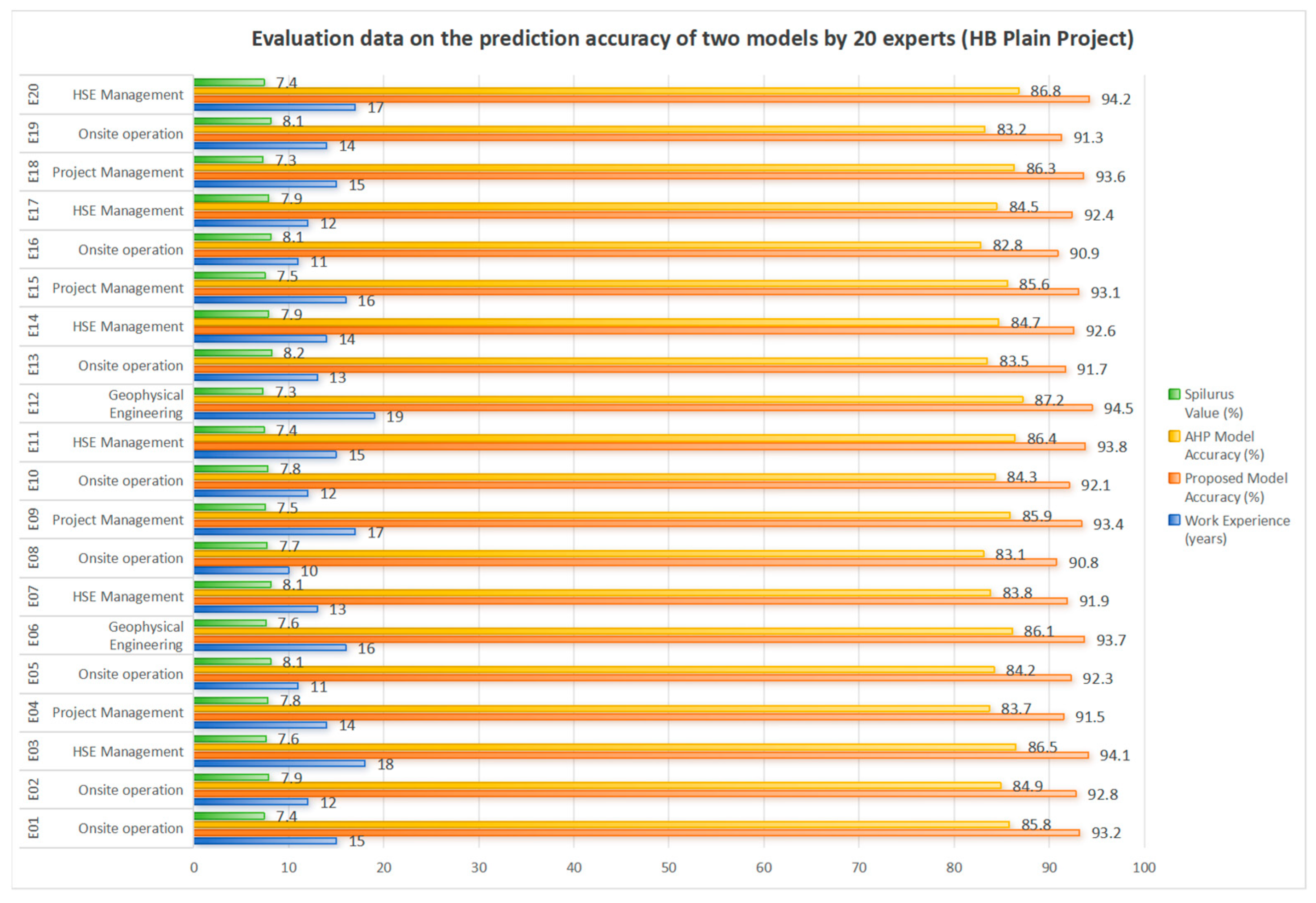
- HB Project: Conducted in a water networked plain region characterized by complex hydrological conditions.
- (2)
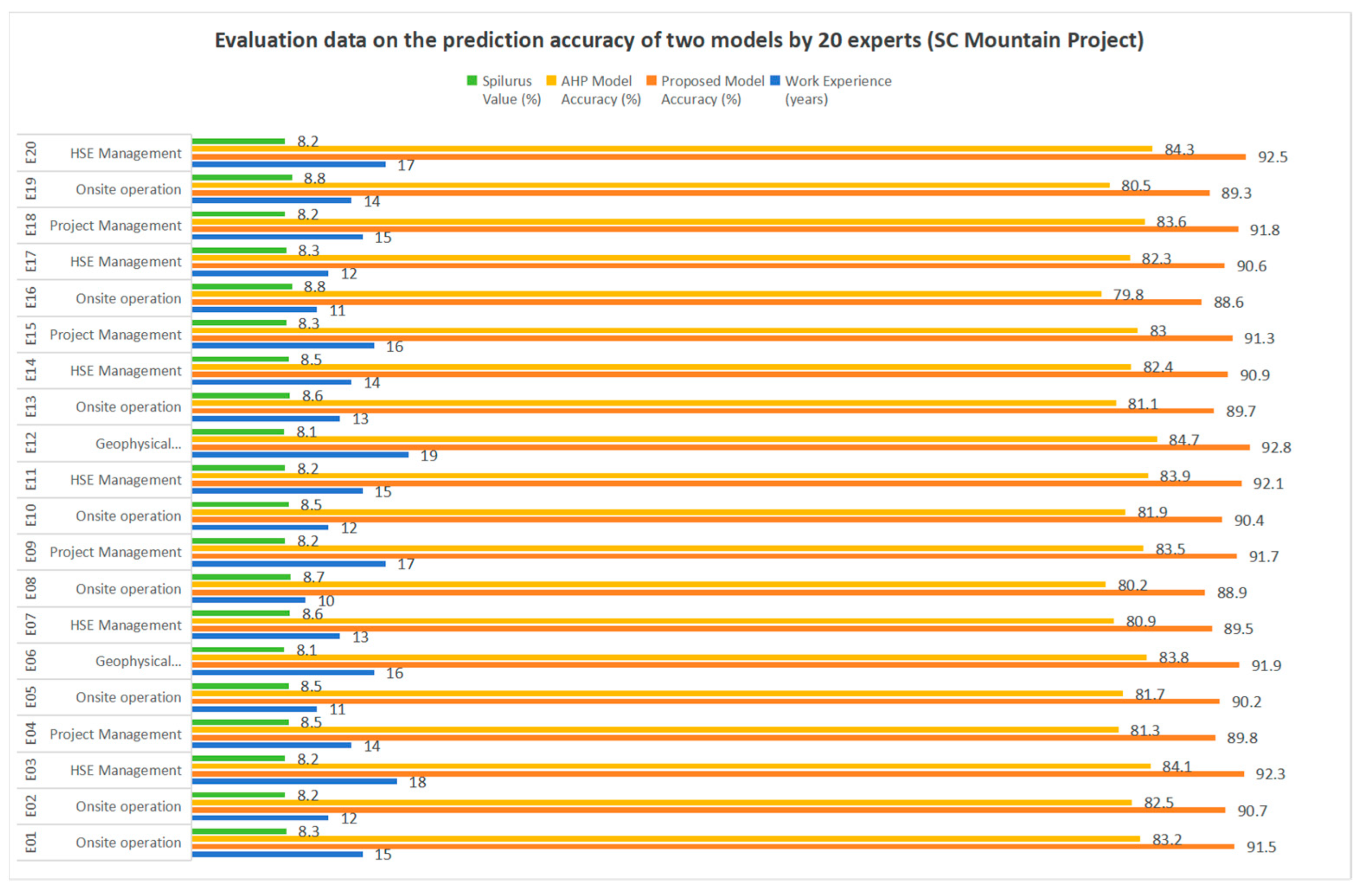
- SC Project: Conducted in a mountainous area with rugged terrain and variable weather conditions.
6.2.1. Risk Quantification and Classification Framework
- Risk Quantification Procedure:
- b.
- Risk Classification Mechanism
6.2.2. Risk Indicator Analysis
6.3. Case Study 2: SC Project in a Mountainous Region
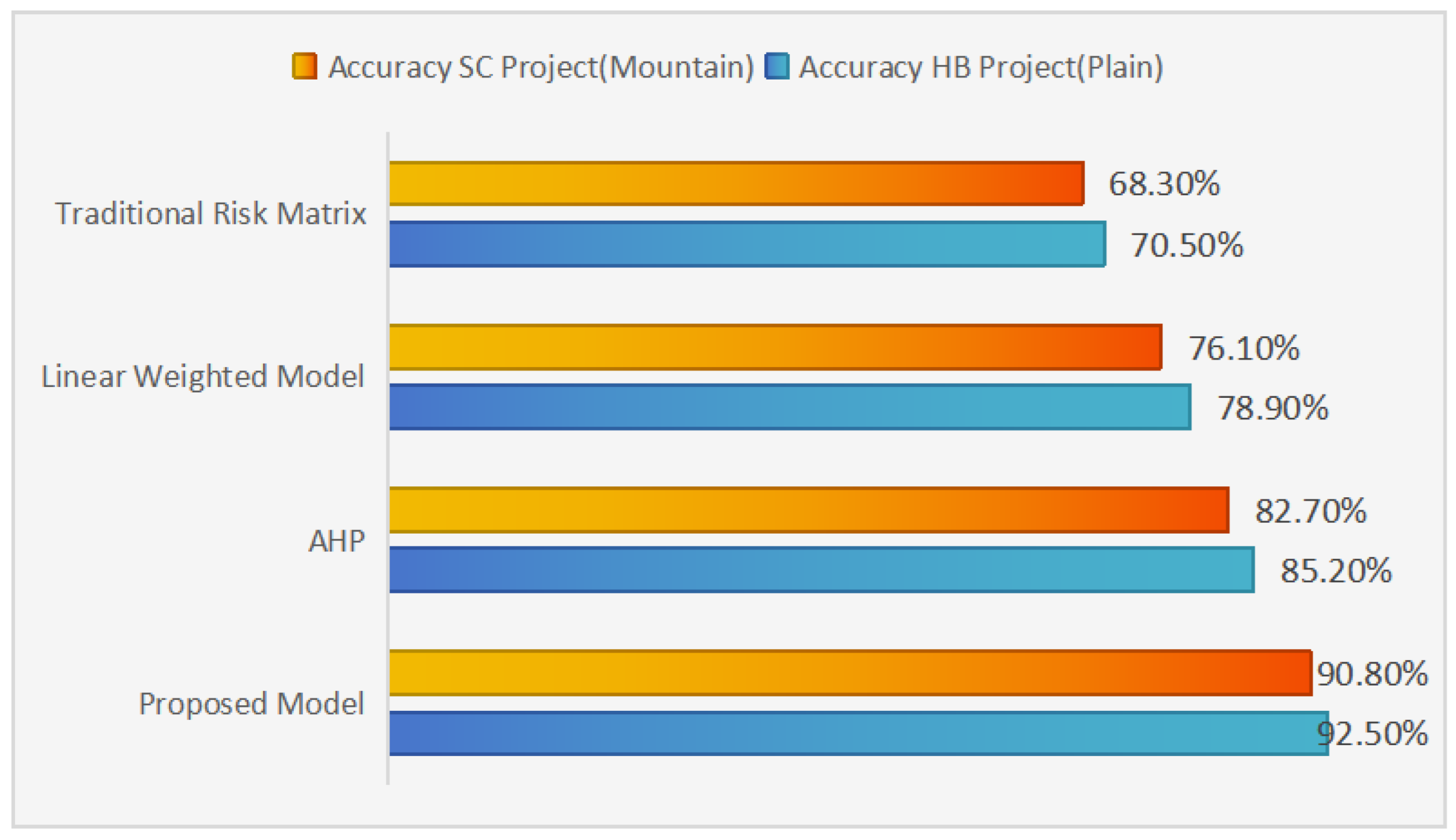
6.4. Comparative Analysis of Results
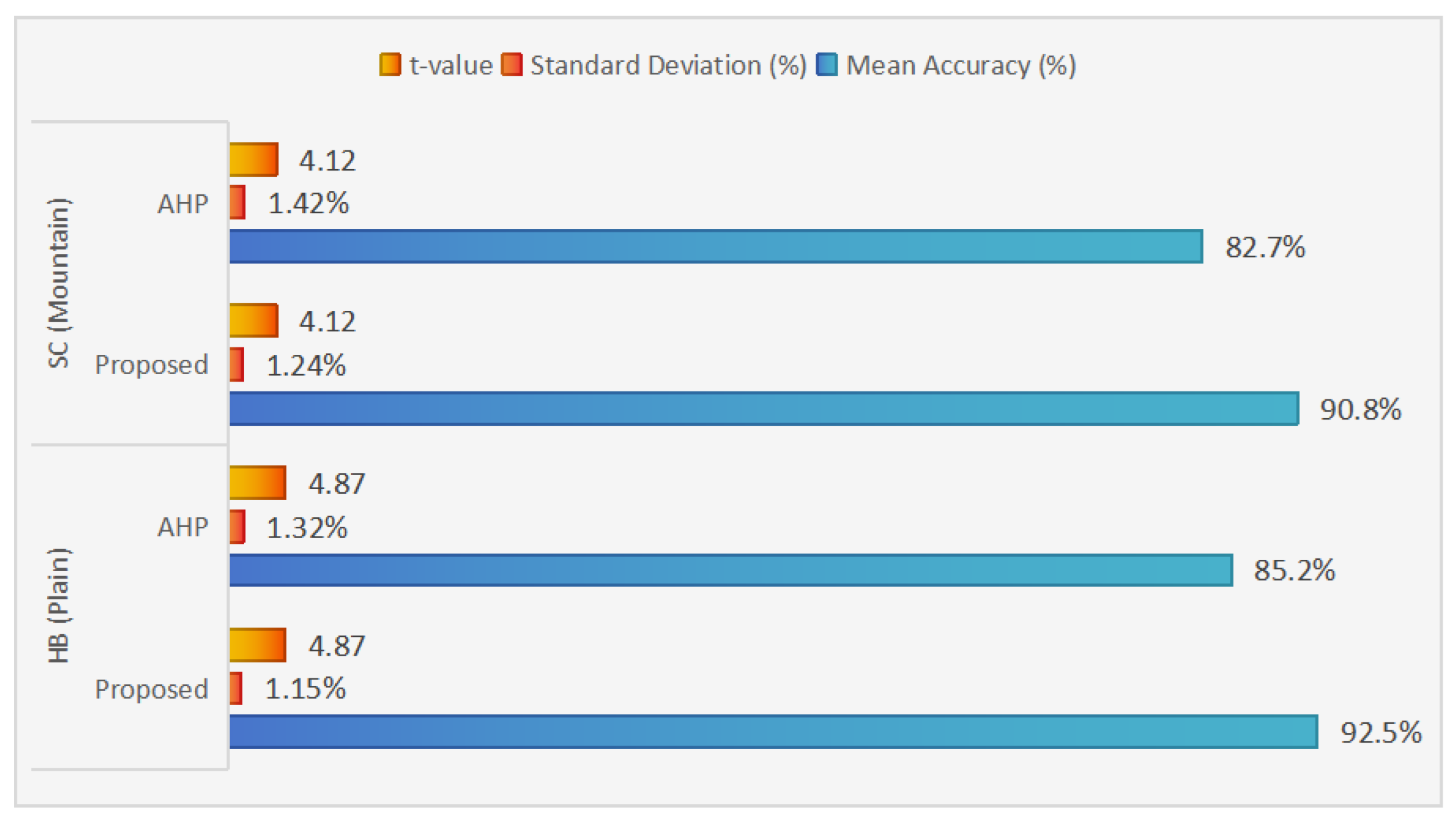
6.5. Performance Superiority and Statistical Validation
6.6. In Depth Case Analysis
6.6.1. HB Project Analysis
6.6.2. SC Project Analysis
6.6.3. Cohen’s D Effect Size Calculation and Analysis
- AHP model standard deviation: SD2 = 2.8%
- Sample Capacity: n1 = n2 = 20
6.7. Sensitivity Analysis
7. Discussion
8. Conclusions
Generalizability and Future Work
- (1)
- Integrating Bayesian fuzzy methods and machine learning techniques to dynamically update fuzzy measures from operational data, thereby reducing reliance on static expert judgments and mitigating bias;
- (2)
- Developing a dynamic, phase specific risk assessment capability that captures temporal fluctuations in risk throughout a project’s lifecycle;
- (3)
- Validating the framework’s efficacy and adaptability through extensive case studies in diverse industrial settings.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sugeno, M. Theory of Fuzzy Integrals and Its Applications. Ph.D. Thesis, Tokyo Institute of Technology, Tokyo, Japan, 1974. Available online: https://t2r2.star.titech.ac.jp/rrws/file/CTT100595242/ATD100000413/ (accessed on 8 March 2021).
- Peng, B.; Zheng, C.; Wei, G.; Zhao, X.; Wan, A. Risk Assessment Method on Haze Networks Public Opinion Based on Intuitionistic Fuzzy Choquet Integral. Int. J. Fuzzy Syst. 2022, 24, 2858–2872. [Google Scholar] [CrossRef]
- Epuh, E.E.; Joshua, E.O. Modeling of Porosity and Permeability for Hydrocarbon Exploration: A Case Study of Gongola Arm of the Upper Benue Trough. J. Afr. Earth Sci. 2019, 162, 103646. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Q.; Guo, J.; Adumene, S.; Goleiji, E.; Yazdi, M. A Risk-Based Review of Dangerous Goods Storage and Handling at a Manufacturing Facility. Int. J. Adv. Manuf. Technol. 2025, 138, 4313–4336. [Google Scholar] [CrossRef]
- Vora, M.; Sanni, S.; Flage, R. An Environmental Risk Assessment Framework for Enhanced Oil Recovery Solutions from Offshore Oil and Gas Industry. Environ. Impact Assess. Rev. 2021, 88, 106512. [Google Scholar] [CrossRef]
- Alao, J.O. The Emerging Roles of 3D and 4D Geophysical and Geological Modelling in Evaluating Seismic Risks: A Critical Review. Earthq. Res. Adv. 2025, in press. [Google Scholar] [CrossRef]
- Pritika; Shanmugam, B.; Azam, S. Risk Evaluation and Attack Detection in Heterogeneous IoMT Devices Using Hybrid Fuzzy Logic Analytical Approach. Sensors 2024, 24, 3223. [Google Scholar] [CrossRef] [PubMed]
- Arrow, K.J. A Difficulty in the Concept of Social Welfare. J. Political Econ. 1950, 58, 328–346. [Google Scholar] [CrossRef]
- Gao, B.; Ma, Z.; Gu, J.; Han, X.; Xiang, P.; Lv, X. Fusing Multi-Source Quality Statistical Data for Construction Risk Assessment and Warning Based on Deep Learning. Knowl.-Based Syst. 2024, 284, 111223. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Luo, H.; He, J.; Cheung, R.W.M. AI-powered Landslide Susceptibility Assessment in Hong Kong. Eng. Geol. 2021, 288, 106103. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Yang, X.; Yin, S.; Chen, J. Rural Social-Ecological Systems Vulnerability Evolution and Spatial-Temporal Heterogeneity in Arid Environmental Change Region: A Case Study of Minqin Oasis, Northwestern China. Appl. Geogr. 2022, 145, 102747. [Google Scholar] [CrossRef]
- Sinopec Group. Production Safety Risk Management Regulations (Trial). Safety Document No. [2016] 625, 30(3): petgeo2023-113.2016. Available online: http://sipc.sinopec.com/sipc/en/hsse/manage_sys/default.shtml (accessed on 8 March 2021).
- Kulikowski, D.; Robson, A.G. Exploring for Unswept Gas: Integrating Reservoir Models, Production Data, and Fault Seal Analysis in the Northern Carnarvon Basin, Australia. AAPG Bull. 2024, 108, 1653–1686. [Google Scholar] [CrossRef]
- Becerra-Bayona, C.A.; Mora, A. Integrated Geological and Geophysical Workflow for Structural Modelling: Case Study from the Contractional Foothills Zone of the Colombian Eastern Cordillera. Pet. Geosci. 2024, 30, petgeo2023-113. [Google Scholar] [CrossRef]
- Helwig, N. EU Strategic Autonomy after the Russian Invasion of Ukraine: Europe’s Capacity to Act in Times of War. J. Common Mark. Stud. 2023, 61, 57–67. [Google Scholar] [CrossRef]
- Tüysüz, F.; Kahraman, C. A novel fuzzy analytic network process approach for evaluating digital transformation strategies. J. Intell. Fuzzy Syst. 2022, 43, 121–134. [Google Scholar] [CrossRef]
- Cooper, L. Heuristic Methods for Location-Allocation Problems. SIAM Rev. 1964, 6, 37–53. [Google Scholar] [CrossRef]
- Jayaraman, V.; Klassen, R.; Linton, J.D. Supply Chain Management in A Sustainable Environment. J. Oper. Manag. 2007, 25, 1071–1074. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Chang, V.; Hawash, H.; Chakrabortty, R.K.; Ryan, M. Deep-IFS: Intrusion Detection Approach for Industrial Internet of Things Traffic in Fog Environment. IEEE Trans. Ind. Inform. 2021, 17, 7704–7715. [Google Scholar] [CrossRef]
- Wu, J.Z.; Beliakov, G. Marginal Contribution Representation of Capacity-based Multicriteria Decision Making. Int. J. Intell. Syst. 2020, 35, 373–400. [Google Scholar] [CrossRef]
- Beliakov, G.; James, S. Choquet Integral-based Measures of Economic Welfare and Species Diversity. Int. J. Intell. Syst. 2022, 37, 2849–2867. [Google Scholar] [CrossRef]
- Kalhori, M.R.N.; Beliakov, G. A Fuzzy Measure and Choquet Integral-Based Approach in the Predictive Knowledge-Based Systems: Application to the Electricity Demand Forecasting. IEEE Trans. Fuzzy Syst. 2025, 33, 1379–1390. [Google Scholar] [CrossRef]
- Sinopec Group. Safety and Environmental Risk Management Guidelines. Document No. [2018] 38, 2018. Available online: http://www.sinopec.com/listco/en/000/000/041/41782.shtml (accessed on 8 March 2021).
- Marlina, E.; Hidayanto, A.N.; Purwandari, B. Towards a Model of Research Data Management Readiness in Indonesian Context: An Investigation of Factors and Indicators Through the Fuzzy Delphi Method. Libr. Inf. Sci. Res. 2022, 44, 101141. [Google Scholar] [CrossRef]
- Sirbiladze, G.; Kacprzyk, J.; Midodashvili, B.; Khachidze, M.; Midodashvili, L.; Parshutkin, I. Possibilistic Simulation Based Interactive Fuzzy MAGDM under Discrimination Q-Rung Picture Linguistic Information. Application in Educational Programs Efficiency Evaluation. Eng. Appl. Artif. Intell. 2023, 123 Pt A, 106278. [Google Scholar] [CrossRef]
- Xia, H.; Hu, Y.; Li, Z.; Lan, H.; Zhang, J. Electron Spin Polarization in Rechargeable Batteries: Theoretical Foundation and Practical Applications. Adv. Funct. Mater. 2024, 35, 2413491. [Google Scholar] [CrossRef]
- Zhang, K.; Zheng, W.; Liao, Z.; Xie, H.; Zhou, C.; Chen, S.; Zhu, J. Risk Assessment of Ground Collapse along Tunnels in Karst Terrain by Using an Improved Extension Evaluation Method. Tunn. Undergr. Space Technol. 2022, 129, 104669. [Google Scholar] [CrossRef]
- Meng, X.; Chang, J.; Wang, X.; Wang, Y.; Wang, Z. Flood Control Operation Coupled with Risk Assessment for Cascade Reservoirs. J. Hydrol. 2019, 572, 543–555. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.; Guo, Y.; Li, D.; Bohlooli, N. Modeling Optimal Energy Exchange Operation of Microgrids Considering Renewable Energy Resources, Risk-based Strategies, and Reliability Aspect Using Multi-objective Adolescent Identity Search Algorithm. Sustain. Cities Soc. 2023, 91, 104380. [Google Scholar] [CrossRef]
- Qin, Y.; Qi, Q.; Scott, P.J.; Jiang, X. An Additive Manufacturing Process Selection Approach Based on Fuzzy Archimedean Weighted Power Bonferroni Aggregation Operators. Robot. Comput.-Integr. Manuf. 2020, 64, 101926. [Google Scholar] [CrossRef]
- Lin, Y.; Zhuang, G.; Xia, J.; Chen, G.; Zhang, H.; Lu, J. Asynchronous Dynamic Output Feedback Control for Delayed Fuzzy Stochastic Markov Jump Systems Based on HMM Strategy. Int. J. Fuzzy Syst. 2022, 24, 2302–2317. [Google Scholar] [CrossRef]
- Balabel, A.; Faizan, M.; Alzaed, A. Towards a Computational Fluid Dynamics-Based Fuzzy Logic Controller of the Optimum Windcatcher Internal Design for Efficient Natural Ventilation in Buildings. Math. Probl. Eng. 2021, 2021, 9936178. [Google Scholar] [CrossRef]
- Rodhi, N.N.; Anwar, N.; Wiguna, I.P.A. A Review on Risk Factors in the Project of Oil and Gas Industry. IPTEK J. Technol. Sci. 2017, 28, 63–67. [Google Scholar] [CrossRef][Green Version]
- Olawoyin, R. Exploration of the Spatial-Composite Risk Index (CRI) for the Characterization of Toxicokinetics in Petrochemical Active Areas. Chemosphere 2013, 92, 1207–1213. [Google Scholar] [CrossRef]
- Schmidt, C.W. Genetically Modified Foods: Breeding Uncertainty. Environ. Health Perspect. 2005, 113, A526–A533. [Google Scholar] [CrossRef] [PubMed]
- Iraj Esmaeili, Hamed Kashani. Managing Cost Risks in Oil and Gas Construction Projects: Root Causes of Cost Overruns. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 8, 1193. [Google Scholar] [CrossRef]
- Dickson, T.J.; Trathen, S.; Waddington, G.; Terwiel, F.A.; Baltis, D. A Human Factors Approach to Snowsport Safety: Novel Research on Pediatric Participants’ Behaviors and Head Injury Risk. Appl. Ergon. 2015, 53 Pt A, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Dhalmahapatra, K.; Garg, A.; Singh, K.; Xavier, N.F.; Maiti, J. An Integrated RFUCOM—RTOPSIS Approach for Failure Modes and Effects Analysis: A Case of Manufacturing Industry. Reliab. Eng. Syst. Saf. 2022, 221, 108333. [Google Scholar] [CrossRef]
- Sutherland, K.; Yeung, W.; Mak, Y.; Levesque, J.F.; NSW Health Clinical Analytics Working Group. Envisioning the Future of Clinical Analytics: A Modified Delphi Process in New South Wales, Australia. BMC Med. Inform. Decis. Mak. 2020, 20, 210. [Google Scholar] [CrossRef]
- Tamarozzi, F.; Mazzi, C.; Antinori, S.; Arsuaga, M.; Becker, S.L.; Bottieau, E.; Camprubi-Ferrer, D.; Caumes, E.; Duvignaud, A.; Grobusch, M.P.; et al. Consensus Definitions in Imported Human Schistosomiasis: A GeoSentinel and TropNet Delphi Study. Lancet Infect. Dis. 2024, 24, e627–e637. [Google Scholar] [CrossRef]
- Gaganis, C.; Papadimitri, P.; Tasiou, M. A Multicriteria Decision Support Tool for Modelling Bank Credit Ratings. Ann. Oper. Res. 2020, 306, 27–56. [Google Scholar] [CrossRef]
- Lauritsen, S.M.; Thiesson, B.; Jørgensen, M.J.; Riis, A.H.; Espelund, U.S.; Weile, J.B.; Lange, J. The Framing of Machine Learning Risk Prediction Models Illustrated by Evaluation of Sepsis in General Wards. NPJ Digit. Med. 2021, 4, 158. [Google Scholar] [CrossRef]
- Singh, R. Performance Comparison of Fuzzy and Choquet Fuzzy Integral Control for Line of Sight Stabilization Application. Middle-East J. Sci. Res. 2013, 13, 1501–1509. [Google Scholar] [CrossRef]
- Rubio-Hervas, J.; Gupta, A.; Ong, Y.S. Data-driven Risk Assessment and Multicriteria Optimization of UAV Operations. Aerosp. Sci. Technol. 2018, 77, 510–523. [Google Scholar] [CrossRef]
- Mahmoudian, M.S.; Shiri, Y.; Vaezian, A. Estimating the Safe Mud Weight Window for Drilling Operations Through Pre-Stack Seismic Inversion, a Case Study in One of the Southwestern Iran Oil Fields. J. Pet. Explor. Prod. Technol. 2025, 15, 24. [Google Scholar] [CrossRef]



| Fuzzy Semantic Evaluation Level (for Risk) | Fuzzy Weight Semantic Evaluation Level (for Importance) | Standardized Normal Triangular Fuzzy Number |
|---|---|---|
| Highly Hazardous | Extremely Important | (0.75, 1.00, 1.00) |
| hazardous | Important | (0.50, 0.75, 1.00) |
| Moderate | Moderate | (0.25, 0.50, 0.75) |
| Safe | Negligible | (0.00, 0.25, 0.50) |
| High Safe | Non-critical | (0.00, 0.00, 0.25) |
| Expert | Linguistic Assessment | Triangular Fuzzy Number |
|---|---|---|
| E1 | Extremely Important | (0.75, 1.00, 1.00) |
| E2 | Important | (0.50, 0.75, 1.00) |
| E3 | Extremely Important | (0.75, 1.00, 1.00) |
| Risk Level | Residual Risk Value RI (Risk Index) | Risk Level | Minimum Security Requirements | Proposed Risk Control Responsible Department |
|---|---|---|---|---|
| Low Risk (Blue) | RI < 10 | Widely acceptable risk | Implement existing management procedures and maintain the integrity and effectiveness of current safety measures to prevent further escalation of risks. | Base-level units |
| Moderate (Yellow) | 10 ≤ RI < 15 | Widely acceptable risk | Risk can be further reduced by establishing reliable monitoring and alarm systems or high-quality management procedures. | Secondary-level units |
| 15 ≤ RI < 20 | Widely acceptable risk | Risk can be further reduced by setting a risk reduction factor equivalent to the protection layer of SIL1. | Secondary-level units | |
| Hazardous (Orange) | 20 ≤ RI < 40 | High risk, intolerable risk | Risk should be further reduced by setting a risk reduction factor equivalent to the protection layers of SIL2 or SIL3. New installations should reduce risk during the design phase; for existing installations, measures should be taken to reduce risk. | Enterprise supervisory authority |
| Highly Hazardous (Red) | 40 ≤ RI < 60 | Extremely high risk, intolerable risk | Risk must be reduced by implementing a risk reduction factor equivalent to the protection layer of SIL3. New installations should reduce risk during the design phase, while existing installations must immediately implement measures to mitigate risk. | Enterprise leadership |
| No. | Qualitative Description | Quantitative Description | Frequency Weight Value “L” (0.1–1) |
|---|---|---|---|
| Frequency of Occurrence | |||
| F (Time/yr) | |||
| 1 | No comparable occurrences have been recorded in Seismic Acquisition Project operations. Empirical evidence indicates an effectively negligible probability of such events. | <10−6 | 0.03 |
| 2 | No comparable occurrences have been recorded during Seismic Acquisition Project operations. | 10−5 > F ≥ 10−6 | 0.056 |
| 3 | Similar events may occur during seismic acquisition projects. | 10−4 > F ≥ 10−5 | 0.083 |
| 4 | Similar incidents have been observed in the Seismic Acquisition Project. | 10−3 > F ≥ 10−4 | 0.11 |
| 5 | Comparable incidents have been documented or may manifest during service life in analogous equipment and facilities. | 10−2 > F ≥ 10−3 | 0.139 |
| 6 | Exhibits an estimated recurrence rate of 1–2 instances throughout the service life of technical systems. | 10−1 > F ≥ 10−2 | 0.17 |
| 7 | Recurrence remains probable throughout the service life of technical systems. | 1 > F ≥ 10−1 | 0.194 |
| 8 | This phenomenon exhibits recurrent annual incidence across technical assets with established operational histories. | F ≥ 1 | 0.222 |
| Severity Level | Health and Safety Impacts (Human Personnel Impairment) | Property Damage Impact | Non-Financial Impacts and Social Impacts |
|---|---|---|---|
| A | Minor health/safety incidents: 1. First aid or medical treatment is required, but hospitalization is not needed, and no workdays are lost due to the injury caused by the incident. 2. Short-term exposure exceeding safety standards, causing temporary discomfort, but without long-term health effects. | The direct economic loss from the incident is below 100,000 yuan. | It may cause short-term dissatisfaction, complaints, or grievances among a small number of residents in the surrounding community (e.g., complaints about facility noise exceeding standards). |
| B | Moderate impact health/safety incidents: 1. Loss of workdays due to accident-related injuries; 2. 1–2 Homo sapiens with minor injuries. | The direct economic loss is between 100,000 yuan and 500,000 yuan, with partial equipment downtime. | 1. Short-term coverage by local media; 2. Disruption to the daily operation of local public facilities (e.g., causing a road to be impassable for 24 h). |
| C | Major impact health/safety incidents: 1. More than 3 individuals with minor injuries, 1–2 individuals with serious injuries (including acute industrial poisoning, and similar cases); 2. Exceeding exposure limits, leading to long-term health effects or causing severe occupational-related diseases. | The direct economic loss is between 500,000 yuan and 2 million yuan, with 1–2 sets of equipment experiencing downtime. | 1. Compliance issues are present, but they do not result in serious safety consequences or lead to enforcement actions by local government regulatory authorities; 2. Long-term coverage by local media; 3. Adverse social impact in the local area, causing significant disruption to the daily operation of local public facilities. |
| D | Major safety incidents resulting in fatalities or serious injuries: 1. 1–2 fatalities and 3–9 serious injuries within the boundary area; 2. 1–2 serious injuries outside the boundary area. | The direct economic loss is between 2 million yuan and 10 million yuan, with 3 or more sets of equipment experiencing downtime, and localized fires or explosions occurring. | Direct economic losses exceeding 2 million yuan but less than 10 million yuan; shutdown of 3 or more sets of equipment; occurrence of localized fire and explosion incidents. |
| E | Severe safety incidents: 1. 3–9 fatalities and 10–49 serious injuries within the boundary area; 2. 1–2 fatalities and 3–9 serious injuries outside the boundary area. | The direct economic loss from the accident is between 10 million yuan and 50 million yuan, with an uncontrolled fire or explosion occurring. | 1. Causing long-term negative attention from domestic or international media; 2. Resulting in adverse social impact at the provincial level and causing significant disruption to the daily operation of provincial public facilities; 3. Leading to enforcement actions by relevant provincial government departments; 4. Resulting in the loss of production, operational, and sales licenses in the local market. |
| F | Catastrophic safety incidents resulting in multiple fatalities or injuries both within and outside the plant boundary: 1. 10 or more fatalities and fewer than 30 fatalities within the boundary area; 50 or more and fewer than 100 serious injuries within the boundary area; 2. 3–9 fatalities and 10 or more, but fewer than 50 serious injuries outside the boundary area. | The direct economic loss from the accident is between 50 million yuan and 100 million yuan. | 1. Leading to enforcement actions by relevant national authorities; 2. Causing severe social impact on a national scale; 3. Attracting focused coverage or a series of reports by domestic and international media. |
| Safety Risk Matrix | Likelihood Levels—From Rare to Frequent | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Accident Severity Levels “R” (from minor to severe) | Safety Risk Matrix “S” | Similar incidents have not occurred in Seismic Acquisition Project and the likelihood of such events is extremely low | Similar incidents have not occurred in Seismic Acquisition Project | Similar incidents have occurred in the Seismic Acquisition Project | Similar incidents have occurred in A company | Similar incidents have occurred or are likely to occur during the service life of multiple comparable equipment and facilities | May occur once or twice during the service life of the equipment and facilities | Multiple occurrences may happen during the service life of the equipment and facilities | Frequent occurrences (at least once a year) take place in the equipment and facilities |
| A | 1 | 1 | 2 | 3 | 5 | 7 | 10 | 15 | |
| B | 2 | 2 | 3 | 5 | 7 | 10 | 15 | 23 | |
| C | 2 | 3 | 5 | 7 | 11 | 16 | 23 | 35 | |
| D | 5 | 8 | 12 | 17 | 25 | 37 | 0 | 0 | |
| E | 7 | 10 | 15 | 22 | 32 | 0 | 0 | 0 | |
| F | 10 | 15 | 20 | 30 | 0 | 0 | 0 | 0 | |
| Frequency weight value ”L” | 0.03 | 0.056 | 0.083 | 0.11 | 0.139 | 0.17 | 0.194 | 0.222 | |
| Risk Assessment for the Plain and Lake Region Seismic Data Acquisition Project A | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Evaluation Criteria | Evaluation Criteria | Weight Semantic Evaluation | Triangular Fuzzy Numbers | Weight Value | Equipment Factors | Human Factors | ||||
| Semantics | Triangular Fuzzy Numbers | Evaluation Value | Semantic Evaluation | Triangular Fuzzy Numbers | Evaluation Value | |||||
| B1: Risk of theft or loss of civil explosive materials | C1: Improper security measures | Hazardous | (0.5, 0.75, 1) | 0.78 | Important | (0.5, 0.75, 1) | 0.79 | Moderate | (0.25, 0.5, 0.75) | 0.3 |
| C2: Inadequate guarding | Moderate | (0.25, 0.5, 0.75) | Moderate | (0.25, 0.5, 0.75) | Negligible | (0, 0.25, 0.5) | ||||
| C3: Improper well sealing | Hazardous | (0.5, 0.75, 1) | Important | (0.5, 0.75, 1) | Moderate | (0.25, 0.5, 0.75) | ||||
| C4: Issues during misfire handling | Hazardous | (0.5, 0.75, 1) | Important | (0.5, 0.75, 1) | Negligible | (0, 0.25, 0.5) | ||||
| B2: Traffic injury risk | C5: Driver errors | Highly Hazardous | (0.75, 1, 1) | 0.5 | Extremely Important | (0.75, 1, 1) | 0.84 | Extremely Important | (0.75, 1, 1) | 0.73 |
| C6: Vehicle malfunctions | Moderate | (0.25, 0.5, 0.75) | Moderate | (0.25, 0.5, 0.75) | Moderate | (0.25, 0.5, 0.75) | ||||
| C7: Adverse weather | Moderate | (0.25, 0.5, 0.75) | Important | (0.5, 0.75, 1) | Moderate | (0.25, 0.5, 0.75) | ||||
| B3: Risk of damage to above-ground/under-ground facilities | C8: Insufficient site surveys | Safe | (0, 0.25, 0.25) | 0.24 | Moderate | (0.25, 0.5, 0.75) | 0.25 | Negligible | (0, 0.25, 0.5) | 0.17 |
| C9: Unreasonable well locations | Highly Hazardous | (0.75, 1, 1) | Important | (0.5, 0.75, 1) | Important | (0.5, 0.75, 1) | ||||
| C10: Inadequate safety distance | Safe | (0, 0.25, 0.25) | Non-critical | (0, 0, 0.25) | Non-critical | (0, 0, 0.25) | ||||
| C11: Operational errors | Safe | (0, 0.25, 0.25) | Non-critical | (0, 0, 0.25) | Non-critical | (0, 0, 0.25) | ||||
| B4: Drowning risk | C12: Failure to wear life-saving equipment | Safe | (0, 0.25, 0.25) | 0.35 | Negligible | (0, 0.25, 0.5) | 0.27 | Non-critical | (0, 0, 0.25) | 0.1 |
| C13: Vessel issues | Highly Hazardous | (0.75, 1, 1) | Important | (0.5, 0.75, 1) | Moderate | (0.25, 0.5, 0.75) | ||||
| C14: Severe weather | Safe | (0, 0.25, 0.25) | Non-critical | (0, 0, 0.25) | Non-critical | (0, 0, 0.25) | ||||
| B5: Risk of accidental explosion of civil explosives | C15: Illegal vehicle parking | Hazardous | (0.5, 0.75, 1) | 0.77 | Important | (0.5, 0.75, 1) | 0.83 | Important | (0.5, 0.75, 1) | 0.88 |
| C16: Non-professional transport | Hazardous | (0.5, 0.75, 1) | Important | (0.5, 0.75, 1) | Important | (0.5, 0.75, 1) | ||||
| C17: Use of radio-frequency devices | Hazardous | (0.5, 0.75, 1) | Extremely Important | (0.75, 1, 1) | Extremely Important | (0.75, 1, 1) | ||||
| C18: Short-circuiting of detonation lines | Highly Hazardous | (0.75, 1, 1) | Extremely Important | (0.75, 1, 1) | Extremely Important | (0.75, 1, 1) | ||||
| C19: Adverse weather | Safe | (0, 0.25, 0.25) | Negligible | (0, 0.25, 0.5) | Moderate | (0.25, 0.5, 0.75) | ||||
| B6: Fire risk | C20: Fuel storage hazards | Highly Hazardous | (0.75, 1, 1) | 0.74 | Extremely Important | (0.75, 1, 1) | 0.98 | Negligible | (0, 0.25, 0.5) | 0.16 |
| C21: Unauthorized electrical use | Highly Hazardous | (0.75, 1, 1) | Extremely Important | (0.75, 1, 1) | Moderate | (0.25, 0.5, 0.75) | ||||
| C22: Open-flame heating in the field | Highly Safe | (0, 0, 0.25) | Extremely Important | (0.75, 1, 1) | Non-critical | (0, 0, 0.25) | ||||
| B7: Electrocution risk | C23: Detonation lines contacting wells | Highly Hazardous | (0.75, 1, 1) | 0.91 | Important | (0.5, 0.75, 1) | 0.72 | Extremely Important | (0.75, 1, 1) | 0.59 |
| C24: Improper wiring | Highly Hazardous | (0.75, 1, 1) | Moderate | (0.25, 0.5, 0.75) | Moderate | (0.25, 0.5, 0.75) | ||||
| C25: unsafe proximity to power lines | Hazardous | (0.5, 0.75, 1) | Extremely Important | (0.75, 1, 1) | Important | (0.5, 0.75, 1) | ||||
| C26: High-voltage zone operations | Highly Hazardous | (0.75, 1, 1) | Important | (0.5, 0.75, 1) | Moderate | (0.25, 0.5, 0.75) | ||||
| C27: Lightning strikes | Moderate | (0.25, 0.5, 0.75) | Negligible | (0, 0.25, 0.5) | Non-critical | (0, 0, 0.25) | ||||
| B8: Mechanical injury risk | C28: Improper operation | Hazardous | (0.5, 0.75, 1) | 0.95 | Important | (0.5, 0.75, 1) | 0.84 | Important | (0.5, 0.75, 1) | 0.84 |
| C29: Lack of protective gear | Highly Hazardous | (0.75, 1, 1) | Extremely Important | (0.75, 1, 1) | Extremely Important | (0.75, 1, 1) | ||||
| C30: Operating faulty machinery | Highly Hazardous | (0.75, 1, 1) | Moderate | (0.25, 0.5, 0.75) | Moderate | (0.25, 0.5, 0.75) | ||||
| B9: Risk of sudden illness | C31: Excessive labor intensity | Hazardous | (0.5, 0.75, 1) | 0.76 | Negligible | (0, 0.25, 0.5) | 0.16 | Moderate | (0.25, 0.5, 0.75) | 0.84 |
| C32: Occupational disease hazards | Moderate | (0.25, 0.5, 0.75) | Moderate | (0.25, 0.5, 0.75) | Important | (0.5, 0.75, 1) | ||||
| C33: Abnormal health conditions | Hazardous | (0.5, 0.75, 1) | Non-critical | (0, 0, 0.25) | Extremely Important | (0.75, 1, 1) | ||||
| Effect Size (d) | Magnitude | Meaning Explanation |
|---|---|---|
| 0.2 | Small | Differences exist, but they may be small and difficult to detect in complex systems. |
| 0.5 | Medium | The differences are of moderate importance and have some practical significance. |
| 0.8 | Large | The differences are great and have obvious practical significance and importance. |
| Model | HB Project (Plain) | SC Project (Mountain) | Effect Size (d) | Time (min) |
|---|---|---|---|---|
| Time (min) | Accuracy | |||
| Proposed Model | 125 | 0.925 | - | 138 |
| AHP | 163 | 0.852 | 1.45 | 175 |
| Linear Weighted Model | 145 | 0.789 | 2.13 | 162 |
| Traditional Risk Matrix | 195 | 0.705 | 2.87 | 210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Mao, N.; Cheng, L.; Du, G. An Intelligent Choquet Fuzzy Integral-Based Framework for Risk Assessment in Seismic Acquisition Processes. Processes 2025, 13, 3558. https://doi.org/10.3390/pr13113558
He C, Mao N, Cheng L, Du G. An Intelligent Choquet Fuzzy Integral-Based Framework for Risk Assessment in Seismic Acquisition Processes. Processes. 2025; 13(11):3558. https://doi.org/10.3390/pr13113558
Chicago/Turabian StyleHe, Chuan, Ningbo Mao, Leli Cheng, and Guangbin Du. 2025. "An Intelligent Choquet Fuzzy Integral-Based Framework for Risk Assessment in Seismic Acquisition Processes" Processes 13, no. 11: 3558. https://doi.org/10.3390/pr13113558
APA StyleHe, C., Mao, N., Cheng, L., & Du, G. (2025). An Intelligent Choquet Fuzzy Integral-Based Framework for Risk Assessment in Seismic Acquisition Processes. Processes, 13(11), 3558. https://doi.org/10.3390/pr13113558







