A Proposed Systematic Problem Solving Methodology Within Six Sigma Projects Applied for Continuous Improvement of Textile Dyeing Processes
Abstract
1. Introduction
1.1. Literature Review
1.2. Research Gap and Objectives
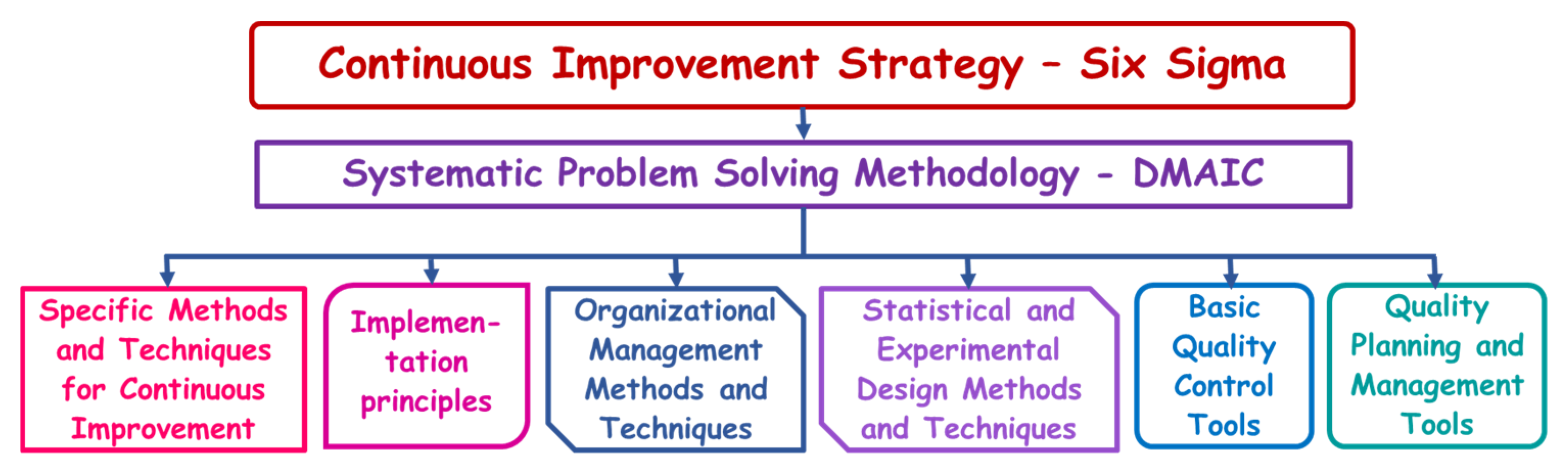
1.3. Contribution of DISMO Methodology
- Exclusive statistical orientation: DISMO provides a systematic and prescriptive approach that relies predominantly on advanced statistical methods—particularly DOE—for problem-solving, unlike DMAIC, which uses only optional DOE, in one or two of its phases, and also incorporates various non-statistical tools;
- Standardization and predictability: DISMO structures the Six Sigma project into a sequence of five fixed and logical steps, creating a simpler and more predictable workflow compared to the high flexibility of tool selection within DMAIC phases;
- Focus on experimental design: DISMO directly and mandatorily integrates statistical techniques in its Identify and Select stages, as well as DOE and Response Surface Methodology (RSM) in its final stages (Model and Optimize), ensuring the statistically supported choice of project targets, the data-based selection of influence factors, the development of a mathematical model, and the determination of optimal process settings;
- Prescriptiveness: The DISMO methodology is prescriptive—it specifies exactly which statistical tools must be used in each phase (e.g., Rank Correlation in phase I, ANOVA in S, and DOE/RSM in M and O), thus eliminating the ambiguity present in DMAIC.
2. Materials and Methods
2.1. Textiles Direct Dyeing
2.1.1. Raw Materials
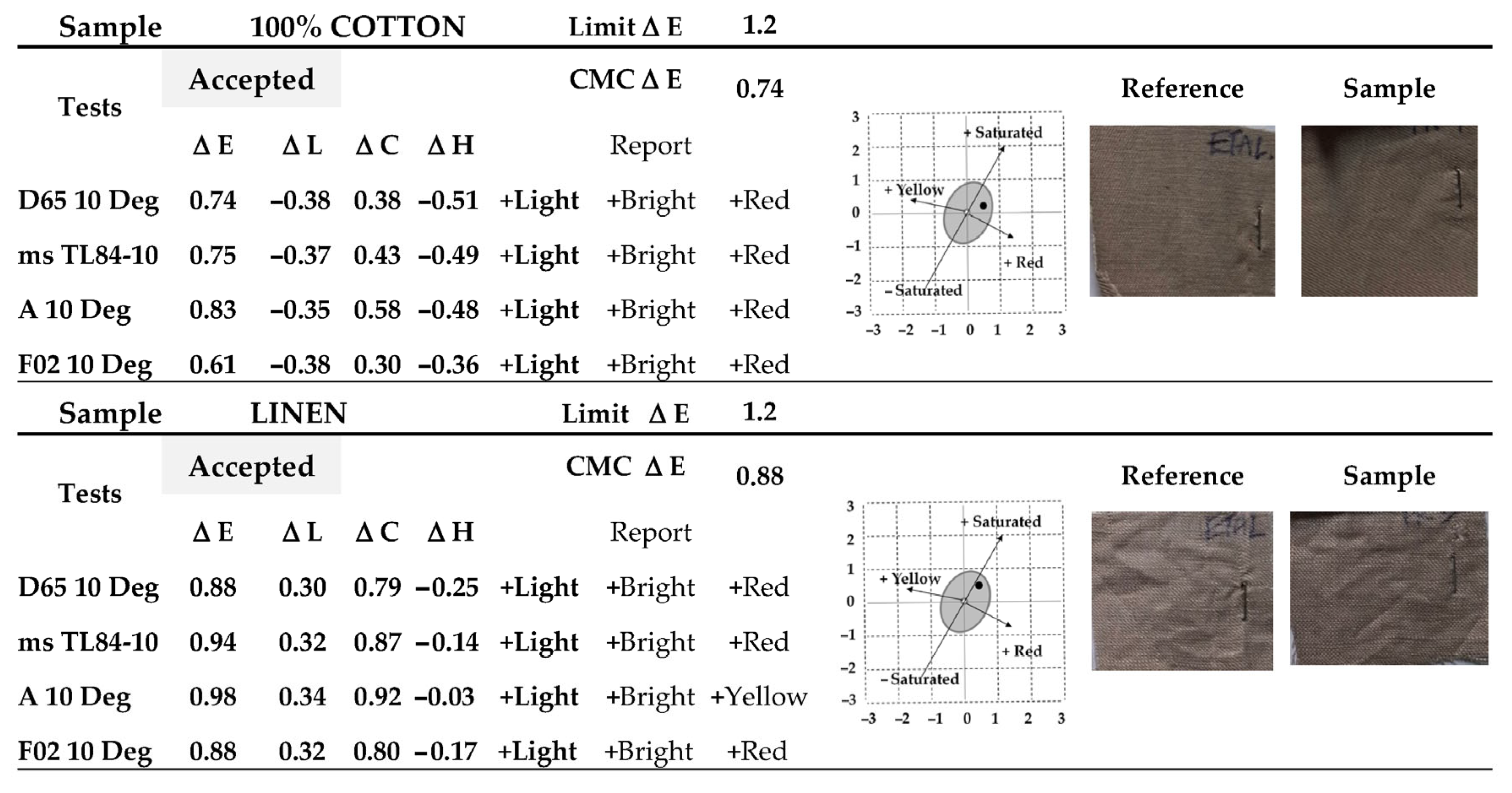
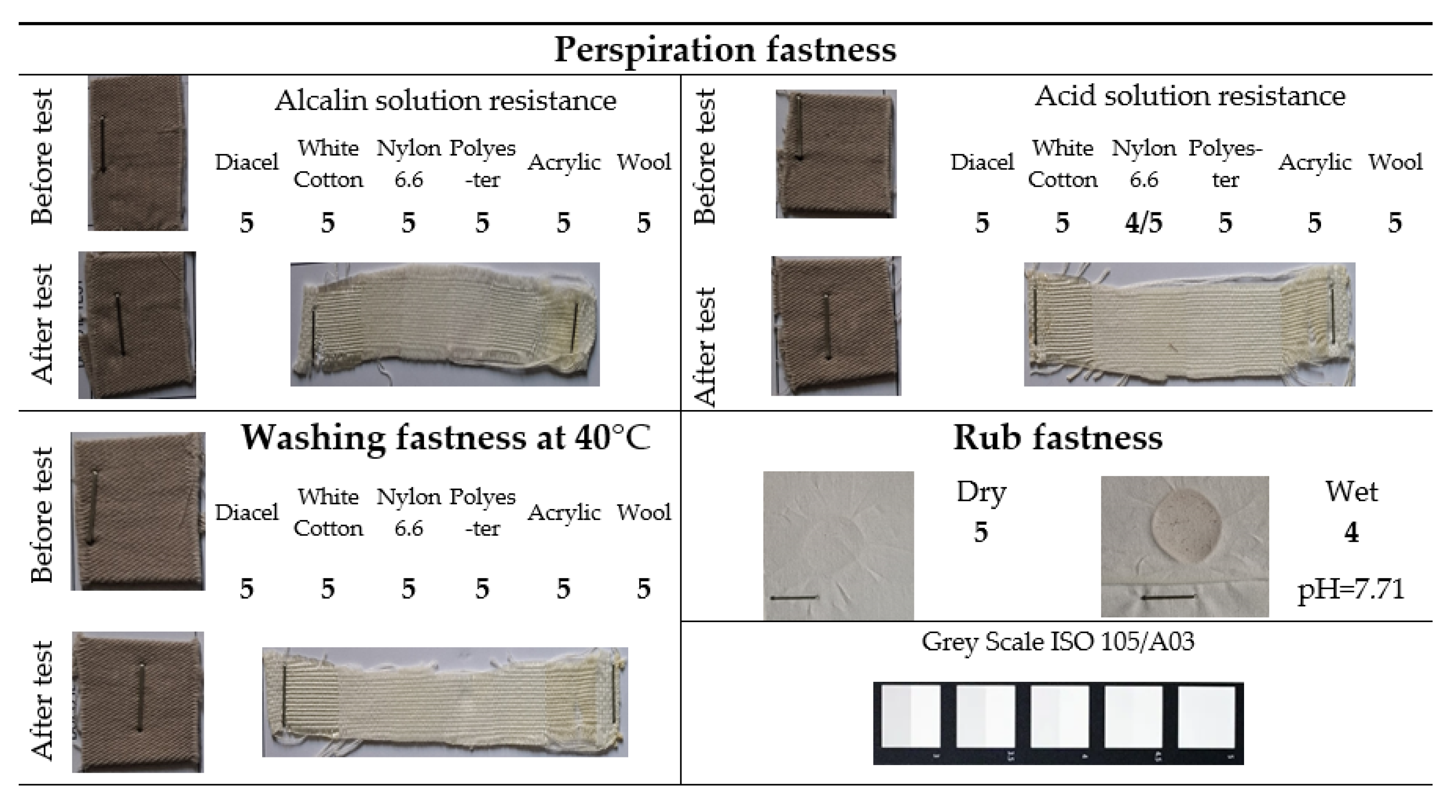
2.1.2. Key Performance Indicators (KPIs) Testing
- ΔL*, ΔC*, ΔH* are the differences in luminance, chroma, and hue between the two colors;
- l and c are the adjustment factors for luminance and chroma, usually l = 2, c = 1;
- SL, SC, SH are weighting functions (tolerances) that scale the differences ΔL*, ΔC*, and ΔH* according to the color reference values.
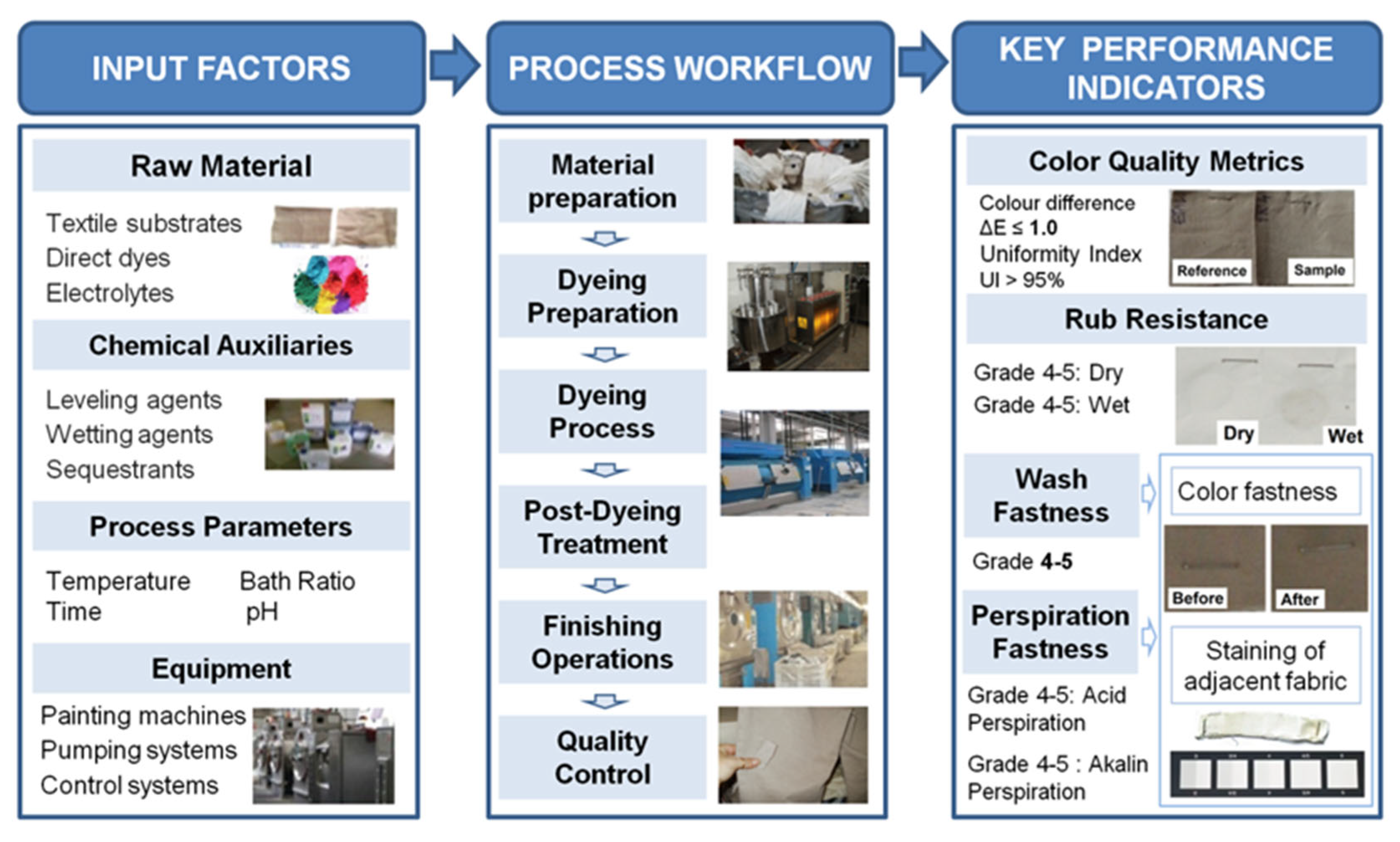
- identification of the target CIEHLC cylindrical coordinates of the color standard provided by the customer, using the spectrophotometer;
- calculating the dyeing recipe (Figure 3) by identifying the combination of three dyes, found in the database available in stock, and their share in the composition of the dye set, in order to reproduce the target color of the standard;
- preparation of both cotton and linen fabric samples, of the same size and shape, with uniform and defect-free surfaces for the test batch dyeing;
- preparing the dyeing solution by dissolving the direct dye base, in the quantities indicated in the dyeing recipe, in an aqueous solution with neutral pH (Figure 4a);
- introducing the samples and the dyeing solution into the cylindrical containers of the mechanical stirrer, after it has been previously brought to a temperature of 30 °C (Figure 4b);
- raising the temperature to 40 °C and adding the neutral electrolyte (salt) in the desired concentrations to the dyeing solution for each individual sample;
- rapidly increasing temperature, so as to reach the temperature indicated for each experimental test, in less than 10 min;
- establishing the test time (30 min) from the moment the container is closed;
- extracting the samples at the end of the test time, for rinsing in two separate water baths, with detergent at 40 °C and cold water, respectively;
- squeezing and placing the samples in an oven for drying (Figure 4c);
- comparative reading of sample results against the color standard using a spectrophotometer and automatic calculation of the ΔE value according to the CMC (2:1) formula, used for color assessment in the field of textile materials.
2.2. New Proposed Systematic Problem Solving Methodology in Six Sigma Framework—DISMO
2.2.1. Describe Interconnections Between Process Variables—D
2.2.2. Identify the Objective Function—I
- Designing the survey form, by clearly listing the k selected OFs, and the method of assigning ranks, distributing and completing them individually, without mutual influences, by each of the m stakeholders;
- Tabular recording of the ranks aij, associated with the characteristics Yj and analyzed by each stakeholder i in the individual forms, and calculation of the sum of the ranks for each factor (by columns) Aj:and assigning, based on these, the global ranks, Rj;
- Correction of the initial ranks aij, for stakeholders who assigned identical ranks for at least two factors, in order to establish the real position in the ordered hierarchy, tabular recalculation of the new sum of ranks for each factor, Ajc, and assignment, based on them, of the corrected global ranks, Rjc;
- Checking the adequacy of the data in the initial table with those in the corrected table, by calculating the correlation coefficient:The new ranking is considered consistent with the initial one, if the calculated value of the rs coefficient is close to 1.
- Verifying the concordance between the points of view expressed by stakeholders, using the consensus coefficient:wheretj representing the number of identical ranks assigned by stakeholder i;
- Testing the statistical significance of the consensus coefficient with the chi-square criterion, since k > 7:If the calculated value of the criterion is greater than or equal to the critical one:then the agreement between the opinions of the stakeholders is significant, with the confidence level P = 1 − α;
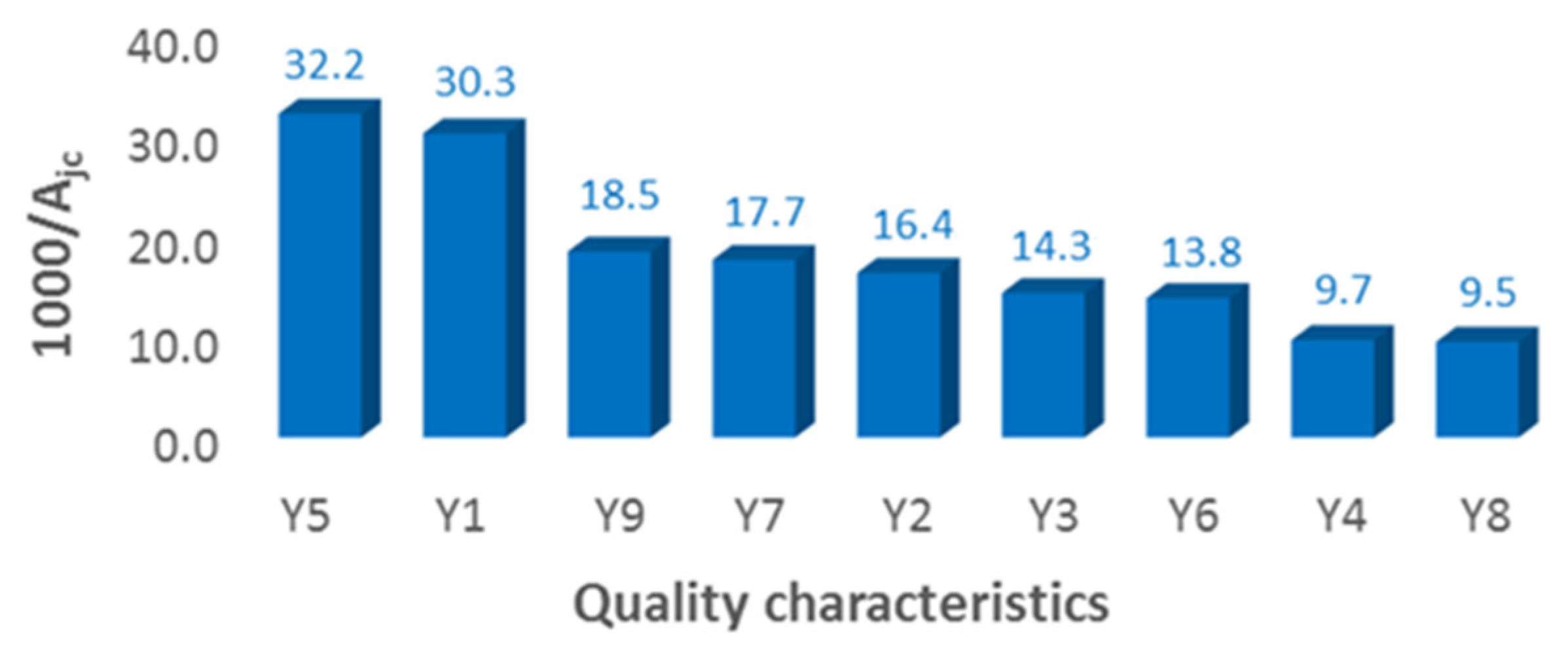
- Graphical representation of the results of the ranking by a column chart, choosing as the axis of values a/Ajc, where a is a scale factor.
2.2.3. Select the Experimental Influence Factors—S
- Random balance, RB, which is a supersaturated factorial experiment, carried out with the aim of ordering a number of k factors according to the effect generated on an OF, whose program matrix is constructed by randomly distributing the factor levels, provided that each level assigned to any factor appears the same number of times [51,52].
- Calculating sums of squares
- ○
- Total sum of squares:where is the general average of all observations.
- ○
- Sum of squares for factor A:where is the OF average value at the level i of factor A.
- ○
- Sum of squares for factor B:where is the OF average value at the level j of factor B.
- ○
- Sum of squares for interaction AB:where is the OF average value at the combination ij of factors levels.
- ○
- Sum of squares for error (residuals):The fundamental relation of the total variability decomposition is:
- Establishing the corresponding number of degrees of freedom:The basic relationship of degrees of freedom:
- Calculus of the mean of squaresMean square are calculated by dividing the sums of squares by their corresponding degrees of freedom. They represent estimates of the variance attributed to each factor.
- ○
- Mean squares for factor A:
- ○
- Mean squares for factor B:
- ○
- Mean squares for interaction AB:
- ○
- Mean squares error:
- Determining Fisher ratios
- ○
- Fisher ratio for factor A:
- ○
- Fisher ratio for factor B:
- ○
- Fisher ratio for interaction AB:
- Testing the statistical significance of the influence of factors and interactions.If the calculated Fisher ratio is greater than or equal to the critical one:then factor A, factor B, or interaction AB is significant with a confidence level .Next, it is possible to continue the examination of a factor’s influence by applying a multiple range test, which allows one to compare pairs of factors’ levels to assess if there is a significant difference between the corresponding calculated means. To this end, an appropriate test is selected, such as Fisher LSD, Duncan, Tukey HSD, Bonferroni, or Scheffé, taking into account the particular objectives and resources of the research: number of treatments, sensitivity, costs generated by false positive or false negative results.
2.2.4. Model the Investigated Process—M
- Design and implementation of the experimental program, after identifying the customers’ interest on different OFs and selecting the “vital few” IFs with their ranges of influence;Within the experiment, each factor selected as relevant is assigned only two levels, upper and lower, coded +1 and –1, and the trials consisting of all possible combinations of the levels of these independent variables. The purpose of coding the levels of IFs is to facilitate and generalize the writing of program matrices of FFEs, performed using the rule of alternating the signs of the k factors involved, at each attempt, according to the powers of 2j−1, j = 1…k.
- Model fitting by estimating regression coefficients of factors, bj, and interactions, bju:where is the average of measured OF values at i trial;
- Establishing the statistical significance of regression coefficients, using Student’s t-test [51] or multifactorial ANOVA [50,52];Nonsignificant effects or interactions should be excluded from the empirical model found.
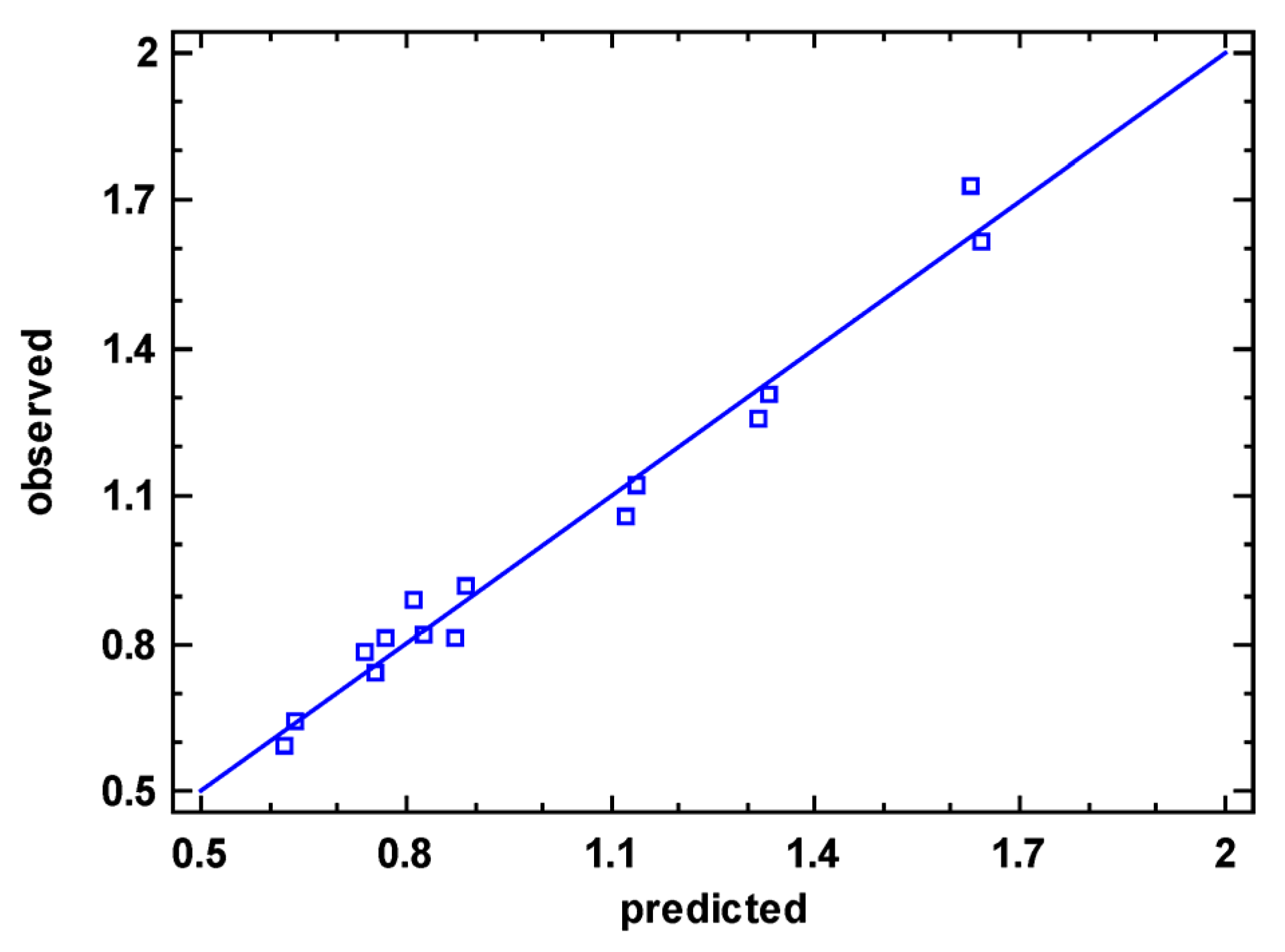
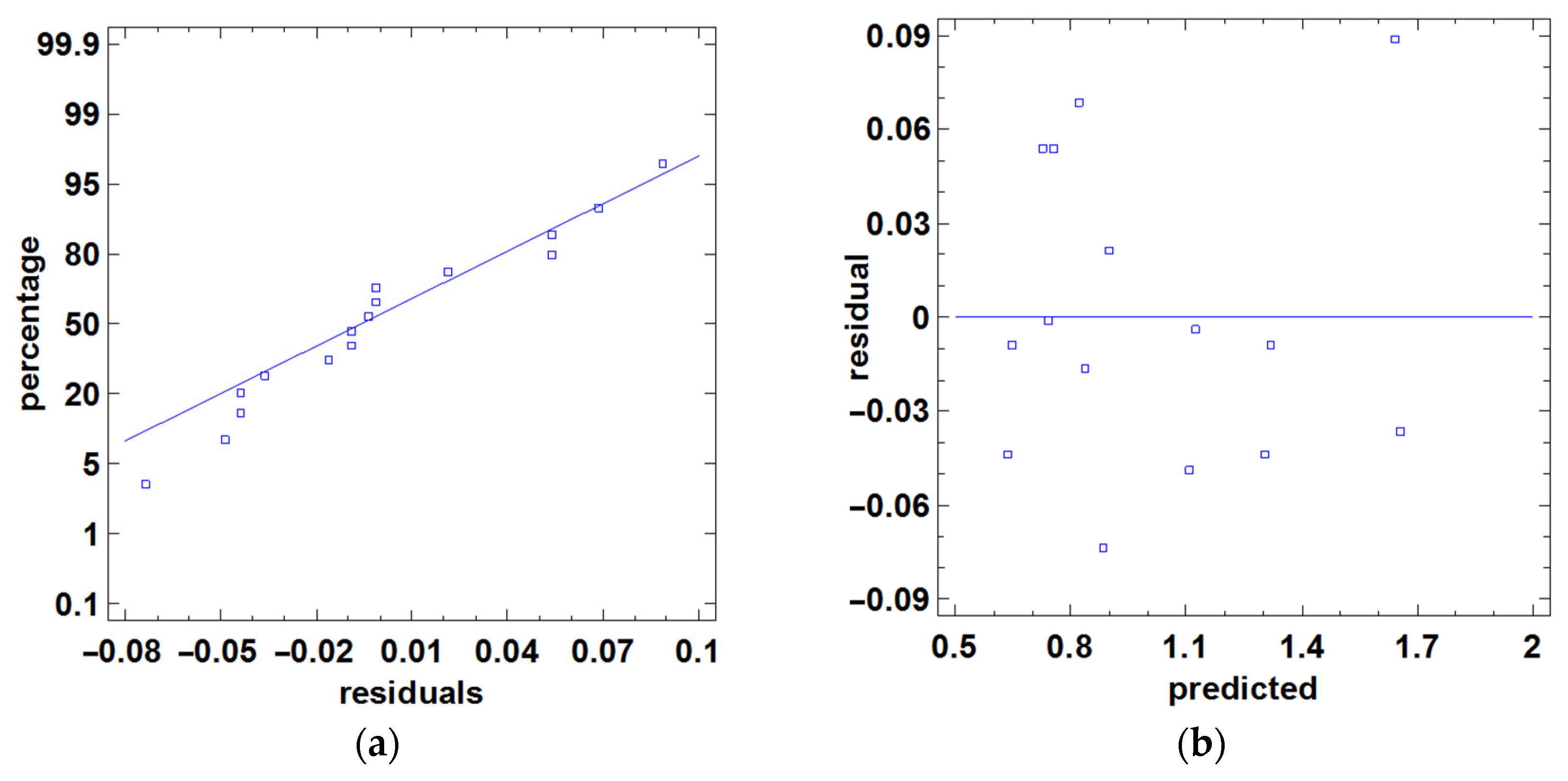
- Model adequacy check and decisions regarding further research;In order to determine whether or not the fitted model is adequate, a residuals analysis must be performed using a Fisher test [51] or examining the residuals plot [50]. The conclusion of this analysis will be used for the substantiated establishment of subsequent decisions to be applied in the next stage of the proposed problem solving methodology.
2.2.5. Optimize the Process—O
2.2.6. DISMO Characteristics
3. Results
3.1. D—Describe Interconnections Between Process Variables
3.2. I—Identify the Objective Function
- Y1—color uniformity, meaning the absence of variations in the color characteristic parameters used in dyeing practice (hue, brightness, intensity) over the entire surface of the dyed article, which is conditioned by the migration capacity of the dyes, the dyeing speed, the temperature, the leveling auxiliaries with affinity for the fiber or dyes;
- Y2—color fastness to household and industrial washing, i.e., the behavior of the color and resistance to change its characteristics over time under the action of repeated washing;
- Y3—finishing characteristics, depending on the operations performed manually on the dyed product to give it a higher value or quality;
- Y4—color fastness to perspiration, namely the stability of color characteristics over time when exposed to alkaline and acidic chemicals;
- Y5—color difference, defined as the geometric distance between two color locations, in a color space, sensory equidistant;
- Y6—color fastness to light, defined as the ability of the fabric to retain its original color when exposed both to UV radiation and natural or artificial light, by comparing its discoloration with a Blue Wool reference scale (1–8);
- Y7—color fastness to water, meaning color stability in contact with pure water (humidity, rain, accidental washing);
- Y8—rubbing resistance, described as the durability over time of color characteristics under repeated action of mechanical forces, tested both dry and wet;
- Y9—delivery time, namely the deadlines established by commercial agreements for the delivery of products, after they have been subjected to the technological dyeing process.
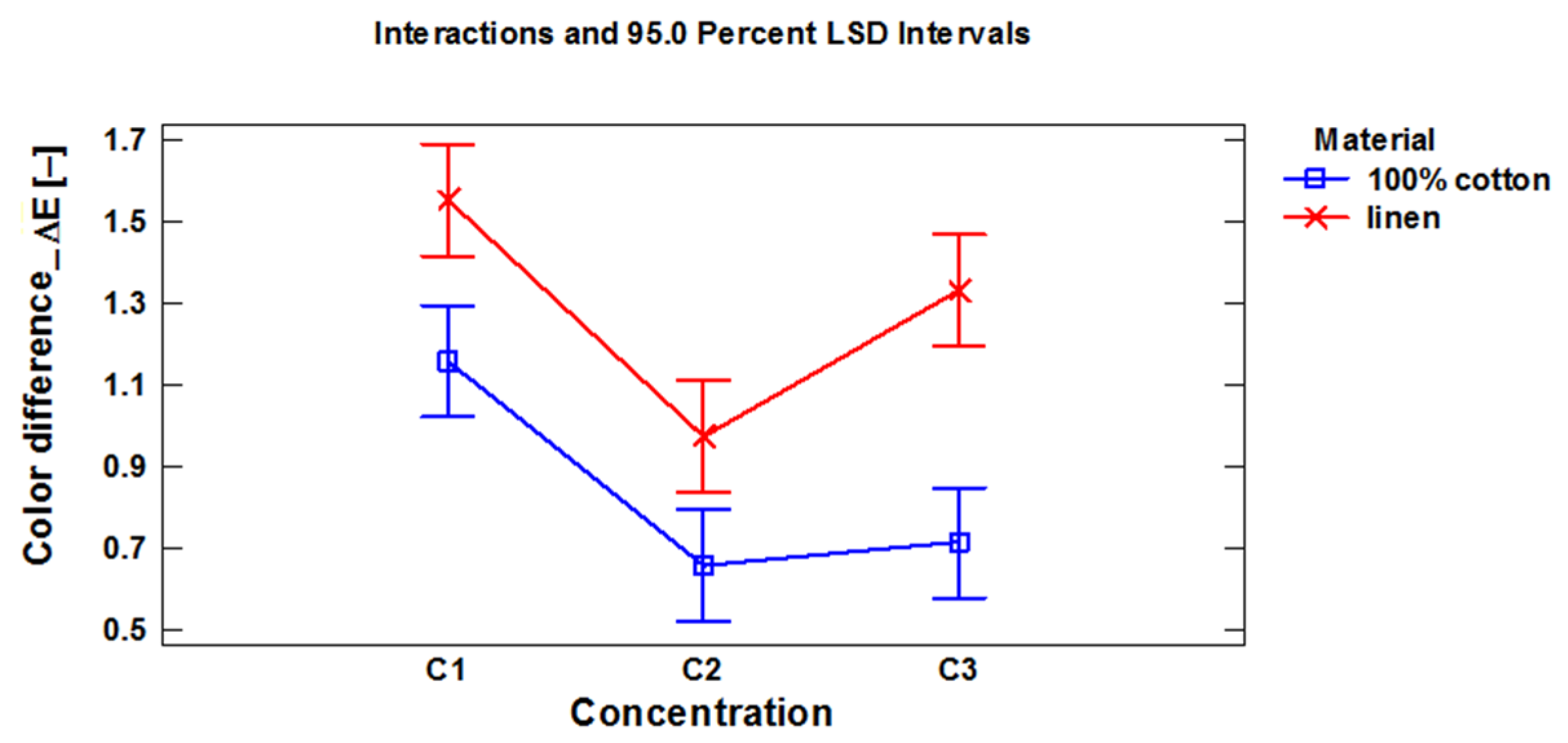
3.3. S—Select the Experimental Influence Factors
3.4. M—Model the Investigated Process
- neutral electrolyte concentration, C [g/L];
- dyeing temperature, T [°C];
- support material, M.
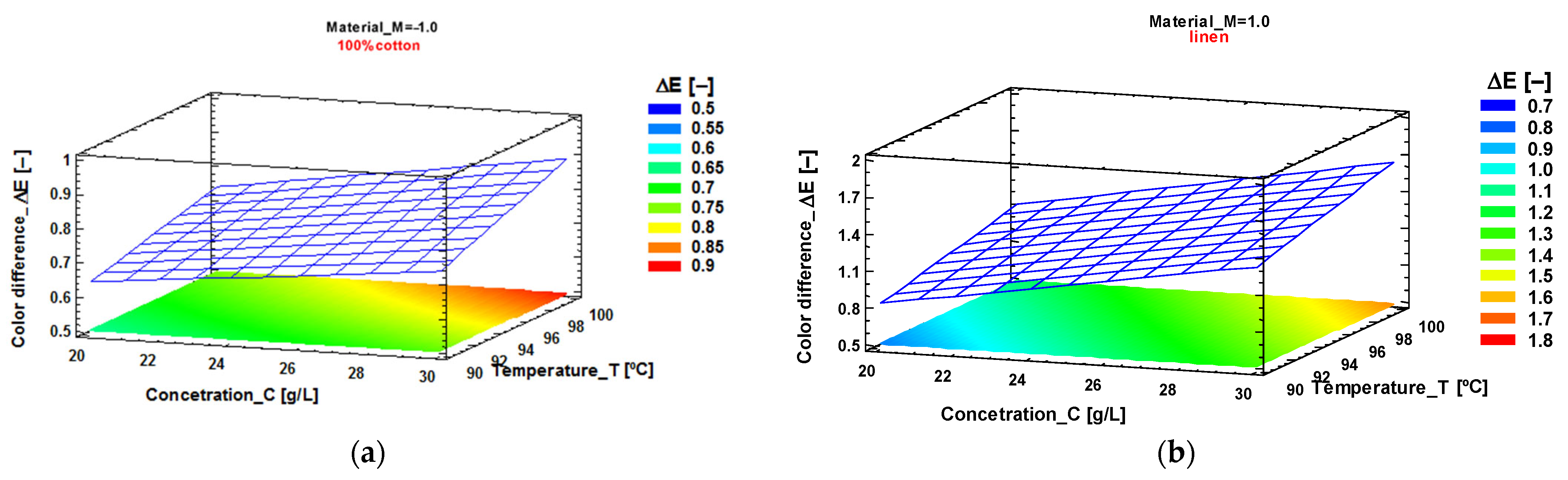
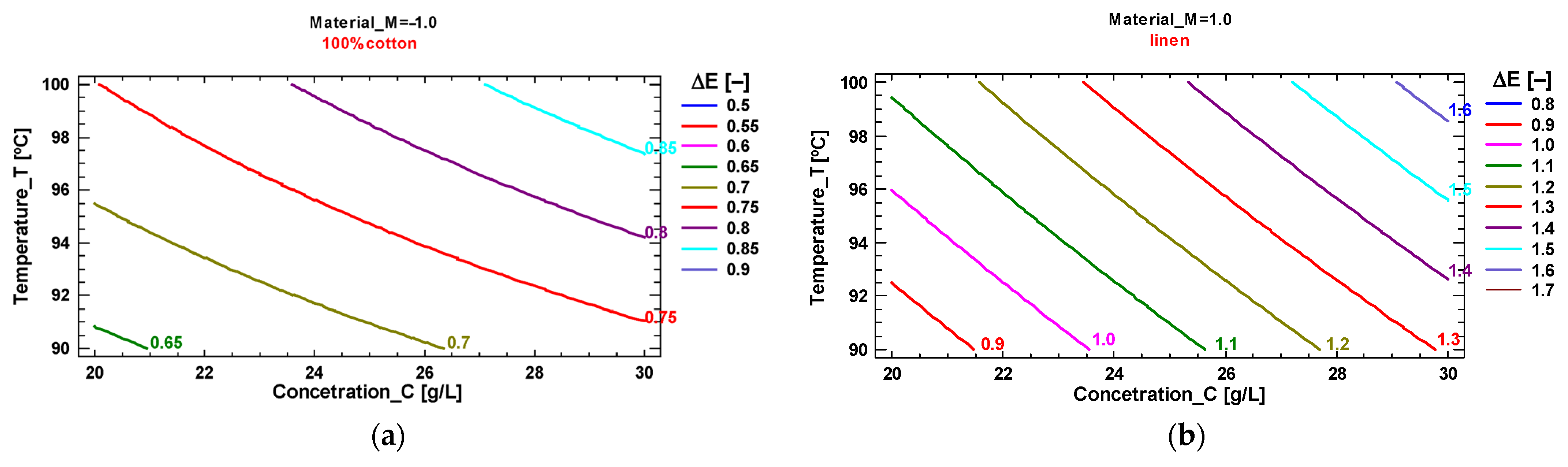
3.5. O—Optimize the Process
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CI | Continuous Improvement |
| DMAIC | Define–Measure–Analyze–Improve–Control |
| OEE | Overall Equipment Effectiveness |
| KPI | Key Performance Indicator |
| DOE | Design of Experiments |
| DISMO | Describe–Identify–Select–Model–Optimize |
| IV | Input Variable |
| OV | Output Variable |
| OF | Objective Function |
| IF | Influence Factor |
| VOE | Voice of Employees |
| VOC | Voice of Customer |
| VOP | Voice of Process |
| VOB | Voice of Business |
| SA | Systemic Analysis |
| RCA | Root-Cause Analysis |
| RC | Rank Correlation |
| ANOVA | Analysis of Variance |
| RB | Random Balance |
| FFE | Full Factorial Experiment |
| CCFE | Central Composite Factorial Experiment |
| RSM | Response Surface Methodology |
References
- Pande, P.S.; Neuman, R.P.; Cavanagh, R.R. Six Sigma; All: Bucharest, Romania, 2008; p. 25. [Google Scholar]
- George, M.L.; Rowlands, D.; Price, M.; Maxey, J. Using DMAIC to Improve, Speed, Quality, and Cost. In The Lean Six Sigma Pocket Toolbox; McGraw Hill: New York, NY, USA, 2005; pp. 1–26. [Google Scholar]
- Gaikwad, L.M.; Sunnapwar, V.K.; Teli, S.N.; Parab, A.B. Application of DMAIC and SPC to Improve Operational Performance of Manufacturing Industry: A Case Study. J. Inst. Eng. India Ser. C 2017, 100, 229–238. [Google Scholar] [CrossRef]
- Jou, Y.-T.; Silitonga, R.M.; Lin, M.-C.; Sukwadi, R.; Rivaldo, J. Application of Six Sigma Methodology in an Automotive Manufacturing Company: A Case Study. Sustainability 2022, 14, 14497. [Google Scholar] [CrossRef]
- Hung, H.C.; Sung, M.H. Applying six sigma to manufacturing processes in the food industry to reduce quality cost. Sci. Res. Essays 2015, 6, 580–591. [Google Scholar]
- Adeodu, A.; Maladzhi, R.; Kana-Kana Katumba, M.G.; Daniyan, I. Development of an improvement framework for warehouse processes using lean six sigma (DMAIC) approach. A case of third party logistics (3PL) services. Heliyon 2023, 9, e14621. [Google Scholar] [CrossRef] [PubMed]
- Monday, L.M. Define, Measure, Analyze, Improve, Control (DMAIC) Methodology as a Roadmap in Quality Improvement. Glob. J. Qual. Saf. Healthc. 2022, 5, 44–46. [Google Scholar] [CrossRef]
- Imansuri, F.; Chayatunnufus, T.; Safril, S.; Sumasto, F.; Purwojatmiko, B.H.; Salati, D. Reducing Defects using DMAIC Methodology in an Automotive Industry. Spektrum Ind. 2024, 22, 1–13. [Google Scholar] [CrossRef]
- Kusumawardani, R.; Ana; Singgih, M.L. Achieving Manufacturing Excellence Using Lean DMAIC. Eng. Proc. 2025, 84, 7. [Google Scholar] [CrossRef]
- Mittal, A.; Gupta, P.; Kumar, V.; Al Owad, A.; Mahlawat, S.; Singh, S. The performance improvement analysis using Six Sigma DMAIC methodology: A case study on Indian manufacturing company. Heliyon 2023, 9, e14625. [Google Scholar] [CrossRef]
- Mncwango, B.; Mdunge, Z.L. Unraveling the Root Causes of Low Overall Equipment Effectiveness in the Kit Packing Department: A Define–Measure–Analyze–Improve–Control Approach. Processes 2025, 13, 757. [Google Scholar] [CrossRef]
- Rodriguez Delgadillo, R.; Medini, K.; Wuest, T. A DMAIC Framework to Improve Quality and Sustainability in Additive Manufacturing—A Case Study. Sustainability 2022, 14, 581. [Google Scholar] [CrossRef]
- Boyles, D.R.A. DOE: The Power Tool of the Analyze and Improve Phases. 2010. Available online: https://www.isixsigma.com/design-of-experiments-doe/doe-power-tool-analyze-and-improve-phases/ (accessed on 12 October 2025).
- Srebrenkoska, S.; Kochov, A.; Minovski, R. Six Sigma and design of experiments for improving the production of composite pipes. J. Technol. Plast. 2016, 41, 11–18. [Google Scholar]
- Kumaravadivel, A.; Natarajan, U. Application of Six-Sigma DMAIC methodology to sand-casting process with response surface methodology. Int. J. Adv. Manuf. Technol. 2013, 69, 1403–1420. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Zhang, H.; Li, Y.; Wang, R.; Qiu, Z. Six sigma robust design optimization for thermal protection system of hypersonic vehicles based on successive response surface method. Chin. J. Aeronaut. 2019, 32, 2095–2108. [Google Scholar] [CrossRef]
- McDermott, O.; Tansh, J.S.; Trubetskaya, A.; Rosa, A.; Moran, R. Digital marketing process enhancement in an online store utilising a combination of design of experiments and Lean Six Sigma. Int. J. Lean Six Sigma 2025. [Google Scholar] [CrossRef]
- Hussain, T.; Jamshaid, H.; Sohail, A. Reducing defects in textile weaving by applying Six Sigma methodology: A case study. Int. J. Six Sigma Compet. Advant. 2014, 8, 95–104. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.R.; Ray, S. Reduction of Yarn Packing Defects Using Six Sigma Methods: A Case Study. Qual. Eng. 2006, 18, 189–206. [Google Scholar] [CrossRef]
- Das, P.; Roy, S.; Antony, J. An Application of Six Sigma Methodology to Reduce lot-to-lot Shade Variation of Linen Fabrics. J. Ind. Text. 2007, 36, 227–251. [Google Scholar] [CrossRef]
- Pacheco-Bonilla, M.; Cespedes-Blanco, C.; Raymundo, C.; Mamani-Macedo, N.; Dominguez, F. Quality Management Model Based on Lean Six Sigma for Reducing Returns of Defective Clothing Articles in SMEs from the Clothing Industry. In Advances in Human Factors, Business Management and Leadership; Al-Emad, S., Liyanage, G.R.S., Salman, B.Y.E., Eds.; Springer Nature: New York, NY, USA, 2020; Volume 1209, pp. 470–477. [Google Scholar] [CrossRef]
- Alarcón, F.J.; Calero, M.; Martín-Lara, M.Á.; Pérez-Huertas, S. An integrated Lean and Six Sigma framework for improving productivity performance: A case study in a Spanish chemicals manufacturer. Appl. Sci. 2024, 14, 10894. [Google Scholar] [CrossRef]
- Kaka, S.; Maryam, M.; Wassan, R.K.; Sarwar, U.; Akbar, A.; Ansari, J. Reducing Outgoing Quality Level (OQL) in Textile Manufacturing Through Six Sigma Methodology: A Case Study. Text. Leather Rev. 2024, 7, 1252–1272. [Google Scholar] [CrossRef]
- Phruksaphanrat, B.; Tipmanee, N. Six sigma DMAIC for machine efficiency improvement in a carpet factory. Songklanakarin J. Sci. Technol. 2019, 41, 887–898. [Google Scholar] [CrossRef]
- Suwanich, T.; Chutima, P. Process improvement of reactive dye synthesis using Six Sigma concept. IOP Conf. Ser. 2017, 215, 012006. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Y.K.; Lo, K.C.; Kan, C. Intelligent techniques and optimization algorithms in textile colour management: A systematic review of applications and prediction accuracy. Fash. Text. 2024, 11, 13. [Google Scholar] [CrossRef]
- El Khaoudi, M.; El Bakkali, M.; Messnaoui, R.; Cherkaoui, O.; Soulhi, A. Literature review on artificial intelligence in dyeing and finishing processes. Data Metadata 2024, 3, 360. [Google Scholar] [CrossRef]
- Fazeli, F.; Tavanai, H.; Hamadani, A.Z. Application of Taguchi and Full Factorial Experimental Design to Model the Color Yield of Cotton Fabric Dyed with Six Selected Direct Dyes. J. Eng. Fibers Fabr. 2012, 7, 34–42. [Google Scholar] [CrossRef]
- Pervez, M.N.; Yeo, W.S.; Lin, L.; Xiong, X.; Naddeo, V.; Cai, Y. Optimization and prediction of the cotton fabric dyeing process using Taguchi design-integrated machine learning approach. Sci. Rep. 2023, 13, 12363. [Google Scholar] [CrossRef]
- Moula, G.; Hosen, D.; Siddiquee, A.B.; Momin, A.; Kaisar, Z.; Al Mamun, A.; Islam, A. Effect of dye bath pH in dyeing of cotton knitted fabric with reactive dye (Remazol Yellow RR) in exhaust method: Impact on color strength, chromatic values and fastness properties. Heliyon 2022, 8, e11246. [Google Scholar] [CrossRef] [PubMed]
- Antony, J. Six Sigma vs. Lean: Some perspectives from leading academics and practitioners. Int. J. Product. Perform. Manag. 2011, 60, 185–190. [Google Scholar] [CrossRef]
- Chakravorty, S.S. Six Sigma programs: An implementation model. Int. J. Prod. Econ. 2009, 119, 1–16. [Google Scholar] [CrossRef]
- Kumar, M.; Antony, J.; Tiwari, M.K. Six Sigma implementation framework for SMEs—A roadmap to manage and sustain the change. Int. J. Prod. Res. 2011, 49, 5449–5467. [Google Scholar] [CrossRef]
- Burkinshaw, S.M. Physico-Chemical Aspects of Textile Coloration; John Wiley & Sons: New York, NY, USA, 2015; pp. 153–200. [Google Scholar] [CrossRef]
- Kiron, M. Classification, Application and Aftertreatment of Direct Dyes. Available online: https://textilelearner.net/direct-dye-classification/ (accessed on 7 December 2024).
- Dobrovăț, M.; Grigoriu, A.; Alexandrescu, I.; Bidalach, R.; Cernat, M.; Muscă, M.; Nagy, G.; Petraru, M.; Popescu, M. Îndrumar Teoretic și Practic Pentru Vopsirea Materialelor Textile; CERTEX: Bucharest, Romania, 1994; pp. 29–40. [Google Scholar]
- Archive for the ‘Direct Dyes’ Category. Available online: https://www.worlddyevariety.com/direct-dyes (accessed on 7 December 2024).
- Kuehni, R.G. Quality Control: Color Difference Perception and Calculation. In Color Vision and Technology; AATCC: Durham, NC, USA, 2008; pp. 200–222. [Google Scholar]
- Nguyen, T.A. Effect of Biodegradable and Metallic Mordants on Dyeing Cotton Fabric with Spent Coffee Grounds. In Proceedings of the 6th International Conference on Green Technology and Sustainable Development (GTSD), Nha Trang, Vietnam, 29–30 July 2022. [Google Scholar]
- ISO 105-J03; Textiles—Tests for Colour Fastness—Part J03: Calculation of Colour Differences. International Organization for Standardization (ISO): Geneva, Switzerland, 2009.
- Datacolor 650™ User Guide. Available online: https://www.datacolor.com/wp-content/uploads/2022/04/Datacolor-650-600-400-Users-Guide-4230-0395M-Rev1.pdf (accessed on 7 December 2024).
- ISO 105-E04; Textiles—Tests for Colour Fastness—Part E04: Colour Fastness to Perspiration. International Organization for Standardization (ISO): Geneva, Switzerland, 2013.
- ISO 105-A02; Textiles—Tests for Colour Fastness—Part A02: Grey Scale for Assessing Change in Colour. International Organization for Standardization (ISO): Geneva, Switzerland, 1993.
- ISO 105-A03; Textiles—Tests for Colour Fastness—Part A03: Grey Scale for Assessing Staining. International Organization for Standardization (ISO): Geneva, Switzerland, 1993.
- ISO 105-C06; Textiles—Tests for Colour Fastness—Part C06: Colour Fastness to Domestic and Commercial Laundering. International Organization for Standardization (ISO): Geneva, Switzerland, 2010.
- ISO 105-X12; Textiles—Tests for Colour Fastness—Part X12: Colour Fastness to Rubbing. International Organization for Standardization (ISO): Geneva, Switzerland, 2004.
- Lean Six Sigma DMAIC Process Explained with Example and Case Study. Available online: https://www.reddit.com/r/OperationExcellence/comments/ov7hsx/lean_six_sigma_dmaic_process_explained_with/ (accessed on 4 September 2020).
- Šibalija, T.V.; Majstorović, V.D. Integrating Lean with/within Six Sigma. Int. J. Total Qual. Manag. Excell. 2010, 38x, 4. [Google Scholar]
- Six Sigma Tools for DMAIC Phases. Available online: https://www.sprintzeal.com/blog/dmaic-tools (accessed on 4 September 2020).
- Gubencu, D.V. Îmbunătățirea Continuă a Proceselor Tehnologice; Politehnica: Timișoara, Romania, 2023; pp. 154–173+232–246+355–382. [Google Scholar]
- Taloi, D. Optimizarea Proceselor Tehnologice, 2nd ed.; Academiei RSR: Bucharest, Romania, 1987; pp. 101–129+170–179. [Google Scholar]
- Hinkelmann, K.; Kempthorne, O. Advanced Experimental Design. In Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 2, pp. 241–278+596–607. [Google Scholar]
- Berenson, M.L.; Levine, D.M. The Analysis of Variance. In Basic Statistics for Business Concepts and Applications, 4th ed.; Prentice-Hall: Hoboken, NJ, USA, 1989; pp. 478–492. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 5th ed.; John Wiley and Sons: New York, NY, USA, 2001; pp. 218–276. [Google Scholar]
- Anthony, J. Design of Experiments for Engineers and Scientists, 2nd ed.; Elsevier: London, UK, 2014; pp. 95–124. [Google Scholar]
- Hinkelmann, K.; Kempthorne, O. Response Surface Design. In Design and Analysis of Experiments, Volume 1. Introduction to Experimental Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 1, pp. 497–531. [Google Scholar]
- Dean, A.; Voss, B. Response Surface Methodology. In Design and Analysis of Experiments; Springer: New York, NY, USA, 1999; pp. 547–592. [Google Scholar]
- John, P.W.M. Response Surfaces. In Statistical Design and Analysis of Experiments; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998; pp. 193–219. [Google Scholar]
- F Distribution Probability Calculator. Available online: https://stattrek.com/online-calculator/f-distribution (accessed on 4 April 2025).
- Wolela, A.D. Effect and Role of Salt in Cellulosic Fabric Dyeing. Adv. Res. Text. Eng. 2021, 6, 1061. [Google Scholar] [CrossRef]
- Luan, F.; Xuan Xu, X.; Liu, H.; Dias Soeiro Cordeiro, M.N. Review of quantitative structure-activity/property relationship studies of dyes: Recent advances and perspectives. Color. Technol. 2013, 129, 173–186. [Google Scholar] [CrossRef]










| Color Index No. | Chemical Name | Commercial Name | Molecular Formula |
|---|---|---|---|
| 40291 | Direct Orange 39 | Direct Orange 2GL 120% | C46H28N8Na4O12S4 |
| 30145 | Direct Brown 95 | Direct Brown FRL/C | C31H20N6Na2O9S |
| 36250 | Direct Black 112 | Direct Gray GLL 200% | C58H34N15Na7O24S4 |
| Symbol | Phase Name | Phase Objective | Perspective/Lens | Methods | Result | Decisions |
|---|---|---|---|---|---|---|
| D | Describe | Mapping potential causal connections between IVs and OVs of the process | VOE | SA RCA | Input–output cybernetic model Cause–effect diagram | List of potential OFs and IFs |
| I | Identify | OFs ranking | VOC | RC | OFs hierarchy | Prioritization of OFs to be investigated |
| S | Select | IFs statistical significance testing | VOP | ANOVA RB | Statistical significance of IFs and interactions IFs hierarchy | Selection of experimental IFs and of assigned variation ranges |
| M | Model | IFs ranking | VOP | FFE | Fitted model Statistical significance of regression coefficients Model adequacy Model validation | Estimating OFs values by interpolation Exploring the multifactorial space through iterative methods |
| O | Optimize | Modeling the action of IFs on OF | VOB | CCFE RSM | Fitted 2nd order model Model analysis and validation Response surfaces Contour plots | Optimal settings of IFs Managerial and production decisions |
| Stakeholder | Quality Characteristics | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CRi | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y8 | Y9 |
| CR1 | 1 | 5 | 6 | 7 | 2 | 8 | 4 | 9 | 3 |
| CR2 | 1 | 3 | 4 | 5 | 2 | 3 | 6 | 4 | 5 |
| CR3 | 1 | 3 | 7 | 8 | 2 | 6 | 4 | 5 | 4 |
| CR4 | 5 | 4 | 7 | 9 | 3 | 1 | 2 | 8 | 6 |
| CR5 | 2 | 6 | 3 | 6 | 1 | 4 | 3 | 5 | 1 |
| CR6 | 1 | 2 | 3 | 9 | 5 | 6 | 7 | 8 | 4 |
| CR7 | 2 | 5 | 3 | 6 | 1 | 4 | 3 | 6 | 1 |
| CR8 | 3 | 8 | 6 | 7 | 1 | 5 | 4 | 9 | 2 |
| CR9 | 2 | 7 | 5 | 8 | 1 | 6 | 4 | 9 | 3 |
| CR10 | 6 | 3 | 2 | 4 | 1 | 1 | 1 | 5 | 4 |
| CR11 | 1 | 2 | 6 | 8 | 3 | 7 | 4 | 9 | 5 |
| CR12 | 2 | 1 | 4 | 7 | 5 | 6 | 3 | 8 | 6 |
| CR13 | 1 | 5 | 6 | 7 | 2 | 8 | 4 | 9 | 3 |
| Aj | 28 | 54 | 62 | 91 | 29 | 65 | 49 | 94 | 47 |
| Rj | 1 | 5 | 6 | 8 | 2 | 7 | 4 | 9 | 3 |
| Stakeholder | Quality Characteristics | Ti | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CRi | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y8 | Y9 | |
| CR1 | 1 | 5 | 6 | 7 | 2 | 8 | 4 | 9 | 3 | 0 |
| CR2 | 1 | 3.5 | 5.5 | 7.5 | 2 | 3.5 | 9 | 5.5 | 7.5 | 18 |
| CR3 | 1 | 3 | 8 | 9 | 2 | 7 | 4.5 | 6 | 4.5 | 6 |
| CR4 | 5 | 4 | 7 | 9 | 3 | 1 | 2 | 8 | 6 | 0 |
| CR5 | 3 | 8.5 | 4.5 | 8.5 | 1.5 | 6 | 4.5 | 7 | 1.5 | 18 |
| CR6 | 1 | 2 | 3 | 9 | 5 | 6 | 7 | 8 | 4 | 0 |
| CR7 | 3 | 7 | 4.5 | 8.5 | 1.5 | 6 | 4.5 | 8.5 | 1.5 | 18 |
| CR8 | 3 | 8 | 6 | 7 | 1 | 5 | 4 | 9 | 2 | 0 |
| CR9 | 2 | 7 | 5 | 8 | 1 | 6 | 4 | 9 | 3 | 0 |
| CR10 | 9 | 5 | 4 | 6.5 | 2 | 2 | 2 | 8 | 6.5 | 30 |
| CR11 | 1 | 2 | 6 | 8 | 3 | 7 | 4 | 9 | 5 | 0 |
| CR12 | 2 | 1 | 4 | 8 | 5 | 6.5 | 3 | 9 | 6.5 | 6 |
| CR13 | 1 | 5 | 6 | 7 | 2 | 8 | 4 | 9 | 3 | 0 |
| Ajc | 33 | 61 | 69.5 | 103 | 31 | 72 | 56.5 | 105 | 54 | ∑Ti = 96 |
| Rjc | 2 | 5 | 6 | 8 | 1 | 7 | 4 | 9 | 3 | - |
| Δj2 | 1024 | 19 | 20.25 | 1444 | 1156 | 49 | 72.25 | 1600 | 121 | ∑Δj2 = 5502.5 |
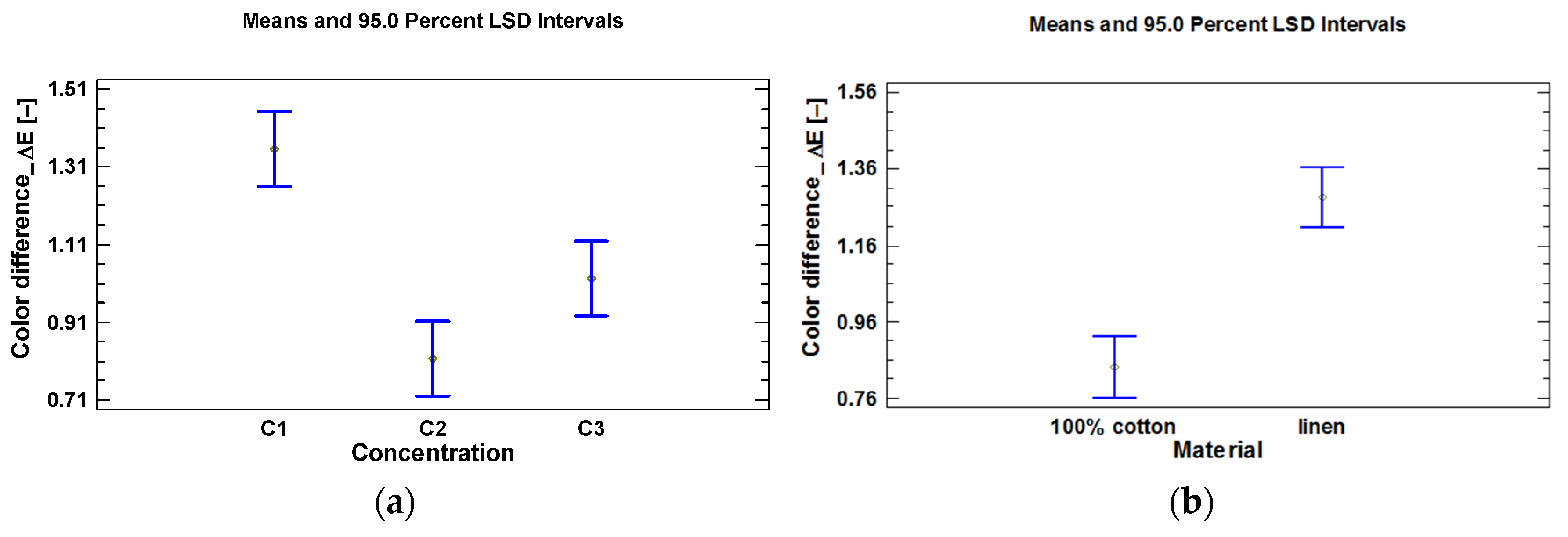
| Run No. | Concentration | Material | ΔE (−) | Run No. | Concentration | Material | ΔE (−) |
|---|---|---|---|---|---|---|---|
| 1 | C1 | cotton | 0.98 | 10 | C1 | linen | 1.45 |
| 2 | C1 | cotton | 1.31 | 11 | C1 | linen | 1.68 |
| 3 | C1 | cotton | 1.18 | 12 | C1 | linen | 1.53 |
| 4 | C2 | cotton | 0.74 | 13 | C2 | linen | 1.15 |
| 5 | C2 | cotton | 0.52 | 14 | C2 | linen | 0.88 |
| 6 | C2 | cotton | 0.71 | 15 | C2 | linen | 0.89 |
| 7 | C3 | cotton | 0.73 | 16 | C3 | linen | 1.16 |
| 8 | C3 | cotton | 0.52 | 17 | C3 | linen | 1.34 |
| 9 | C3 | cotton | 0.89 | 18 | C3 | linen | 1.49 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | Fisher Ratio | p-Value |
|---|---|---|---|---|---|
| A: Concentration | SSA = 0.890844 | dfA = 2 | MSA = 0.445422 | FA = 19.00 | 0.0002 |
| B: Material | SSB = 0.88445 | dfB = 1 | MSB = 0.88445 | FB = 37.73 | 0.0001 |
| AB | SSAB = 0.0724 | dfAB = 2 | MSAB = 0.0362 | FAB = 1.54 | 0.2531 |
| Residual | SSe = 0.281333 | dfe = 12 | MSe = 0.0234444 | ||
| Total (corr.) | SST = 2.12903 | dfT = 17 |
| Contrast | Significance | Mean Difference | +/− Limits |
|---|---|---|---|
| C1-C2 | yes | 0.54 | 0.192611 |
| C1-C3 | yes | 0.333333 | 0.192611 |
| C2-C3 | yes | −0.206667 | 0.192611 |
| Run No. | A: C | B: T | C: M | Yi: ΔE (−) | ||||
|---|---|---|---|---|---|---|---|---|
| Coded | (g/L) | Coded | (°C) | Coded | (−) | Yi1 | Yi2 | |
| 1. | −1 | 20 | −1 | 90 | −1 | cotton | 0.64 | 0.59 |
| 2. | +1 | 30 | −1 | 90 | −1 | cotton | 0.74 | 0.78 |
| 3. | −1 | 20 | +1 | 100 | −1 | cotton | 0.81 | 0.74 |
| 4. | +1 | 30 | +1 | 100 | −1 | cotton | 0.92 | 0.81 |
| 5. | −1 | 20 | −1 | 90 | +1 | linen | 0.82 | 0.89 |
| 6. | +1 | 30 | −1 | 90 | +1 | linen | 1.31 | 1.26 |
| 7. | −1 | 20 | +1 | 100 | +1 | linen | 1.12 | 1.06 |
| 8. | +1 | 30 | +1 | 100 | +1 | linen | 1.62 | 1.73 |
| Coeff. | Value | Coeff. | Value | Coeff. | Value | Coeff. | Value |
|---|---|---|---|---|---|---|---|
| b0 | 0.99 | b2 | 0.11125 | b12 | 0.0125 | b23 | 0.045 |
| b1 | 0.15625 | b3 | 0.23625 | b13 | 0.0975 | - | - |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | Fisher Ratio | p-Value |
|---|---|---|---|---|---|
| A: C | 0.390625 | 1 | 0.390625 | 96.97 | 0.0000 |
| B: T | 0.198025 | 1 | 0.198025 | 49.16 | 0.0001 |
| C: M | 0.893025 | 1 | 0.893025 | 221.70 | 0.0000 |
| AB | 0.0025 | 1 | 0.0025 | 0.62 | 0.4535 |
| AC | 0.1521 | 1 | 0.1521 | 37.76 | 0.0003 |
| BC | 0.0324 | 1 | 0.0324 | 8.04 | 0.0219 |
| blocks | 0.0009 | 1 | 0.0009 | 0.22 | 0.6491 |
| Total error | 0.032225 | 8 | 0.00402812 | ||
| Total (corr.) | 1.7018 | 15 |
| Run No. | A: C (g/L) | B: T (°C) | C: M (−) | Yi: ΔEobs (−) | : ΔEpred (−) | (−) | (−) |
|---|---|---|---|---|---|---|---|
| 1 | 20 | 95 | cotton | 0.92 | 0.965 | −0.045 | 0.002025 |
| 2 | 20 | 95 | linen | 0.95 | 0.9725 | −0.0225 | 0.00050625 |
| 3 | 25 | 95 | cotton | 0.79 | 0.75375 | 0.03625 | 0.001314063 |
| 4 | 25 | 95 | linen | 1.27 | 1.22625 | 0.04375 | 0.001914063 |
| 0.037945273 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gubencu, D.-V.; Ușurelu, R.A.; Han, A.-A. A Proposed Systematic Problem Solving Methodology Within Six Sigma Projects Applied for Continuous Improvement of Textile Dyeing Processes. Processes 2025, 13, 3546. https://doi.org/10.3390/pr13113546
Gubencu D-V, Ușurelu RA, Han A-A. A Proposed Systematic Problem Solving Methodology Within Six Sigma Projects Applied for Continuous Improvement of Textile Dyeing Processes. Processes. 2025; 13(11):3546. https://doi.org/10.3390/pr13113546
Chicago/Turabian StyleGubencu, Dinu-Valentin, Ruxandra Andreea Ușurelu, and Adelina-Alina Han. 2025. "A Proposed Systematic Problem Solving Methodology Within Six Sigma Projects Applied for Continuous Improvement of Textile Dyeing Processes" Processes 13, no. 11: 3546. https://doi.org/10.3390/pr13113546
APA StyleGubencu, D.-V., Ușurelu, R. A., & Han, A.-A. (2025). A Proposed Systematic Problem Solving Methodology Within Six Sigma Projects Applied for Continuous Improvement of Textile Dyeing Processes. Processes, 13(11), 3546. https://doi.org/10.3390/pr13113546






