Influence of Step Size and Temperature Sensor Placement on Cascade Control Tuning for a Multi-Reaction Tubular Reactor Process
Abstract
1. Introduction
2. Materials and Methods
2.1. Process Simulation
2.2. Process Characterization and Tuning of the Control System
2.3. Evaluation of the Control Structure
2.4. Fractal Analysis
3. Discussion and Results
3.1. Analysis of Control Design Parameters
3.2. Control System Evaluation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Ai | Pre-exponential factor of the i-th simultaneous reaction |
| cs | Coefficient relating the molar flow to the heat capacity of the solid phase |
| Ei | Activation energy of the i-th simultaneous reaction |
| FMA | Molar flow of maleic anhydride |
| FB | Molar flow of benzene |
| IAE | Integral Absolute Error |
| ki | Reaction rate of the i-th simultaneous reaction |
| K | Gain |
| FOPDTM | First-Order Plus Dead Time Model |
| P | Proportional |
| PI | Proportional–Integral |
| R | Universal gas constant |
| t | Time |
| TC | Jacket temperature |
| TS | Solid phase temperature |
| TF | Fluid temperature |
| Us-f | Liquid film heat transfer coefficient for the jacket |
| Uf-c | Liquid film heat transfer coefficient for the jacket |
| z | Reactor length |
| ∆m | Step change magnitude |
| ∆Hi | Heat of the i-th reaction, i = 1, 2, 3 |
| θ | Time delay |
| τ | Integral time constant |
Appendix A
| Zone | Step | Parameter | 3.04 m (95%) | 1.92 m (60%) | 0.64 m (20%) | 0.16 m (5%) |
|---|---|---|---|---|---|---|
| Zone 1 | 10% | TR (K) | 738.50673 | 773.15722 | 933.46012 | 796.95867 |
| Tc (K) | 704.51586 | 704.51586 | 704.51586 | 704.51586 | ||
| Yield (%) | 22.37844 | 22.37844 | 22.37844 | 22.37844 | ||
| Selectivity (%) | 24.09332 | 24.09332 | 24.09332 | 24.09332 | ||
| IAE | 0.04689 | 0.04758 | 0.04999 | 0.05004 | ||
| 9% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046667 | 0.047497 | 0.049225 | 0.048951 | ||
| 8% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046527 | 0.047567 | 0.048579 | 0.048125 | ||
| 7% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046438 | 0.047652 | 0.048250 | 0.047706 | ||
| 6% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046411 | 0.047761 | 0.047920 | 0.047327 | ||
| Zone 2 | 5% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046383 | 0.047745 | 0.047722 | 0.047107 | ||
| 4% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046409 | 0.047676 | 0.047535 | 0.046918 | ||
| 3% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046443 | 0.047533 | 0.047410 | 0.046799 | ||
| 2% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046447 | 0.047363 | 0.047330 | 0.046730 | ||
| 1% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046421 | 0.047226 | 0.047238 | 0.046219 | ||
| Zone 3 | −1% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046477 | 0.047720 | 0.047749 | 0. 047288 | ||
| −2% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24. 093324 | ||
| IAE | 0.046590 | 0.050018 | 0.049949 | 0.049854 | ||
| −3% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.046018 | 0.048373 | 0.049113 | 0.048980 | ||
| −4% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.045904 | 0.048060 | 0.049026 | 0.048871 | ||
| −5% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.045871 | 0.047967 | 0.049026 | 0.048865 | ||
| Zone 4 | −6% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0. 045848 | 0.047941 | 0.049010 | 0.048864 | ||
| −7% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.045833 | 0.047920 | 0.049003 | 0.048875 | ||
| −8% | TR (K) | 738.506731 | 773.157216 | 933.460125 | 796.958668 | |
| Tc (K) | 704.515859 | 704.515859 | 704.515859 | 704.515859 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.093324 | 24.093324 | 24.093324 | 24.093324 | ||
| IAE | 0.045815 | 0.047903 | 0.04898 | 0.048881 | ||
| −9% | TR (K) | 675.204051 | 682.115014 | 690.653198 | 648.224513 | |
| Tc (K) | 636.196168 | 636.196168 | 636.196168 | 636.595215 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 50.426878 | 50.426878 | 50.426878 | 50.692474 | ||
| IAE | 0.044199 | 0.044151 | 0.044283 | 0.044622 | ||
| −10% | TR (K) | 675.204051 | 682.115014 | 690.653198 | 668.830166 | |
| Tc (K) | 636.196168 | 636.196168 | 636.196168 | 636.196168 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 50.426878 | 50.426878 | 50.426878 | 50.426878 | ||
| IAE | 0.044761 | 0.044721 | 0.045071 | 0.045130 |
| Zone | Step | Parameter | 3.04 m (95%) | 1.92 m (60%) | 0.64 m (20%) | 0.16 m (5%) |
|---|---|---|---|---|---|---|
| Zone 1 | 10% | TR (K) | 731.209117 | 761.123611 | 865.91278 | 810.3801 |
| Tc (K) | 695.358144 | 695.358144 | 695.35814 | 695.35814 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.61628 | 24.61628 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.74381 | 27.74381 | ||
| IAE | 0.046085 | 0.045471 | 0.04922 | 0.04992 | ||
| 9% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045799 | 0.045160 | 0.048421 | 0.048870 | ||
| 8% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045574 | 0.044951 | 0.047723 | 0.048071 | ||
| 7% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045420 | 0.044846 | 0.047355 | 0.047666 | ||
| 6% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045306 | 0.044784 | 0.046966 | 0.047301 | ||
| Zone 2 | 5% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045213 | 0.044764 | 0.046724 | 0.047090 | ||
| 4% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045163 | 0.044778 | 0.046476 | 0.046908 | ||
| 3% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045143 | 0.044835 | 0.046296 | 0.046795 | ||
| 2% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045132 | 0.044934 | 0.046176 | 0.046731 | ||
| 1% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045148 | 0.045106 | 0.046072 | 0.045868 | ||
| Zone 3 | −1% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24. 616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045463 | 0.046151 | 0.046731 | 0.047264 | ||
| −2% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045904 | 0.048750 | 0.049197 | 0.049762 | ||
| −3% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045348 | 0.047385 | 0.048338 | 0.048932 | ||
| −4% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045232 | 0.047109 | 0.048246 | 0.048829 | ||
| −5% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045197 | 0.047027 | 0.048245 | 0.048822 | ||
| Zone 4 | −6% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045172 | 0.047004 | 0.048229 | 0.048820 | ||
| −7% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045155 | 0.046985 | 0.048222 | 0.048833 | ||
| −8% | TR (K) | 731.209117 | 761.123611 | 865.912781 | 810.380104 | |
| Tc (K) | 695.358144 | 695.358144 | 695.358144 | 695.358144 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 27.743812 | 27.743812 | 27.743812 | 27.743812 | ||
| IAE | 0.045136 | 0.046970 | 0.048208 | 0.048839 | ||
| −9% | TR (K) | 685.777153 | 695.131626 | 708.726068 | 710.565877 | |
| Tc (K) | 646.698892 | 646.698892 | 646.698892 | 646.698892 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 46.191636 | 46.191636 | 46.191636 | 46.191636 | ||
| IAE | 0.043709 | 0.043781 | 0.043908 | 0.044211 | ||
| −10% | TR (K) | 685.777153 | 695.131626 | 708.726068 | 710.565877 | |
| Tc (K) | 646.698892 | 646.698892 | 646.698892 | 646.698892 | ||
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | ||
| Selectivity (%) | 46.191636 | 46.191636 | 46.191636 | 46.191636 | ||
| IAE | 0.044223 | 0.044306 | 0.044697 | 0.045049 |
| Zone | Step | Parameter | 3.04 m (95%) | 1.92 m (60%) | 0.64 m (20%) | 0.16 m (5%) |
|---|---|---|---|---|---|---|
| Zone 1 | 10% | TR (K) | 736.90046 | 769.99242 | 928.02369 | 836.19874 |
| Tc (K) | 703.1152 | 703.1152 | 703.1152 | 703.1152 | ||
| Yield (%) | 22.37844 | 22.37844 | 22.37844 | 22.37844 | ||
| Selectivity (%) | 24.15366 | 24.15366 | 24.15366 | 24.15366 | ||
| IAE | 0.04657 | 0.04641 | 0.04983 | 0.05181 | ||
| 9% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046693 | 0.047702 | 0.049231 | 0.049816 | ||
| 8% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046557 | 0.047812 | 0.048586 | 0.049073 | ||
| 7% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046471 | 0.047917 | 0.048257 | 0.048714 | ||
| 6% | TR (K) | 739.695790 | 775.55565 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046449 | 0.048045 | 0.047927 | 0.048424 | ||
| Zone 2 | 5% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046424 | 0.048027 | 0.047729 | 0.048264 | ||
| 4% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046454 | 0.047946 | 0.047542 | 0.048158 | ||
| 3% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046491 | 0.047777 | 0.047418 | 0.048109 | ||
| 2% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046495 | 0.047575 | 0.047338 | 0.048084 | ||
| 1% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046467 | 0.047397 | 0.047245 | 0.047133 | ||
| Zone 3 | −1% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046511 | 0.047823 | 0.047755 | 0.048404 | ||
| −2% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046609 | 0.050083 | 0.049954 | 0.050615 | ||
| −3% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.046038 | 0.048426 | 0.049118 | 0.049752 | ||
| −4% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.045924 | 0.048111 | 0.049032 | 0.049648 | ||
| −5% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.045891 | 0.048017 | 0.049031 | 0.049640 | ||
| Zone 4 | −6% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.045868 | 0.047991 | 0.049016 | 0.049639 | ||
| −7% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.045853 | 0.047970 | 0.049008 | 0.049653 | ||
| −8% | TR (K) | 739.695790 | 775.555659 | 937.242681 | 763.897356 | |
| Tc (K) | 705.571136 | 705.571136 | 705.571136 | 705.571136 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 24.047055 | 24.047055 | 24.047055 | 24.047055 | ||
| IAE | 0.045835 | 0.047953 | 0.048994 | 0.049659 | ||
| −9% | TR (K) | 676.109678 | 683.196717 | 691.465401 | 648.224513 | |
| Tc (K) | 636.595215 | 636.595215 | 636.595215 | 636.595215 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 50.692474 | 50.692474 | 50.692474 | 50.692474 | ||
| IAE | 0.044200 | 0.044153 | 0.044283 | 0.044622 | ||
| −10% | TR (K) | 676.109678 | 683.196717 | 691.465401 | 648.224513 | |
| Tc (K) | 636.595215 | 636.595215 | 636.595215 | 636.595215 | ||
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | ||
| Selectivity (%) | 50.692474 | 50.692474 | 50.692474 | 50.692474 | ||
| IAE | 0.044763 | 0.044722 | 0.045071 | 0.045458 |
References
- Nise, N.S. Control Systems Engineering, 8th ed.; Wiley: Hoboken, NJ, USA, 2019; pp. 4–6. [Google Scholar]
- Burns, R. Advanced Control Engineering; Elsevier Science: Oxford, UK, 2001; pp. 1–3. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 13th ed.; Pearson: Hoboken, NJ, USA, 2016. [Google Scholar]
- Cheng, Z.; Li, L.; Zhong, C.; Wang, J.; Bai, X.; Liu, J. Adaptive Nonlinear Active Disturbance Rejection Current Controller for Distributed Generation System Considering Uncertain Ripples. IEEE Trans. Power Electron. 2025, 40, 4984–4996. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Chen, X.; Li, Z.; Su, C.-Y. Adaptive Pseudoinverse Control for Constrained Hysteretic Nonlinear Systems and Its Application on Dielectric Elastomer Actuator. IEEE/ASME Trans. Mechatron. 2023, 28, 2142–2154. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Y.; Lu, J.; Tan, C. Improved Active Disturbance Rejection Control for Electro-Hydrostatic Actuators via Actor–Critic Reinforcement Learning. Eng. Appl. Artif. Intell. 2025, 158, 111485. [Google Scholar] [CrossRef]
- Trivedi, B.C.; Culbertson, B.M. Maleic Anhydride; Plenum Press: New York, NY, USA, 1982; pp. 1–40. [Google Scholar]
- McMullen, R.L. Maleic Anhydride Applications in Personal Care. In Handbook of Maleic Anhydride Based Materials; Musa, O., Ed.; Springer: Cham, Switzerland, 2016; pp. 441–507. [Google Scholar] [CrossRef]
- Hood, D.K.; Musa, O.M. Application of Maleic Anhydride in Coatings, Adhesives and Printing. In Handbook of Maleic Anhydride Based Materials; Musa, O., Ed.; Springer: Cham, Switzerland, 2016; pp. 509–575. [Google Scholar] [CrossRef]
- Cortes-Barreda, J.; Hernandez-Espinosa, J.; Urrea-García, G.R.; Luna-Solano, G.; Cantu-Lozano, D. Implementation of Software for the Determination of Modeling Error in a Tubular Reactor. In New Perspectives in Software Engineering. CIMPS 2020; Mejia, J., Muñoz, M., Rocha, Á., Quiñonez, Y., Eds.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2021; Volume 1297. [Google Scholar] [CrossRef]
- Urrea-García, G.R.; Reséndiz-Camacho, S.; Álvarez-Ramírez, J.; Luna-Solano, G. Variable Cascade Control Structure for Tubular Reactors. Chem. Eng. Technol. 2015, 38, 521–529. [Google Scholar] [CrossRef]
- Van den Berg, F.W.J.; Hoefsloot, H.C.J.; Boelens, H.F.M.; Smilde, A.K. Selection of optimal sensor position in a tubular reactor using robust degree of observability criteria. Chem. Eng. Sci. 2000, 55, 827–837. [Google Scholar] [CrossRef]
- Smith, C.A.; Corripio, A.B. Control Automático de Procesos, Teoría y Práctica, 2nd ed.; Limusa/Wiley: Mexico City, Mexico, 2014. [Google Scholar]
- Skogestad, S.; Grimholt, C. The SIMC Method for Smooth PID Controller Tuning. In PID Control in the Third Millennium; Vilanova, R., Visioli, A., Eds.; Springer: London, UK, 2012; pp. 147–174. [Google Scholar] [CrossRef]
- Hernández-Espinosa, J.; Urrea-García, G.R.; Luna-Solano, G. Estructura de Control Variable en Cascada para Compensar Variaciones en Parámetros en un Reactor Tubular. In Proceedings of the Congreso Nacional de Control Automático 2017, Monterrey, Nuevo León, México, 4–6 October 2017; Tecnológico Nacional de México, Instituto Tecnológico de Orizaba: Orizaba, Mexico, 2018. [Google Scholar]
- Wu, W.; Huang, M.-Y. Nonlinear Inferential Control for an Exothermic Packed-Bed Reactor: Geometric Approaches. Chem. Eng. Sci. 2003, 58, 2023–2034. [Google Scholar] [CrossRef]
- Ramirez-Castelan, C.E.; Moguel-Castañeda, J.; Puebla, H.; Hernandez-Martinez, E. A study of temperature sensor location based on fractal analysis for cascade control schemes in tubular reactors. Chem. Eng. Sci. 2016, 141, 195–204. [Google Scholar] [CrossRef][Green Version]
- Urrea, R.; Alvarez, J.; Alvarez-Ramirez, J. Linear PI Temperature-Concentration Cascade Control for Tubular Reactors. Chem. Eng. Commun. 2008, 195, 803–820. [Google Scholar] [CrossRef]
- Uraz, C.; Atalay, S. Oxidation of Benzene to Maleic Anhydride in a Fluidized Bed Reactor. Chem. Eng. Technol. 2007, 30, 1708–1715. [Google Scholar] [CrossRef]
- Phung Quach, T.Q.; Rouleau, D.; Chavarze, C.; Laguerze, C. Catalytic Oxidation of Benzene to Maleic Anhydride in a Continuous Stirred Tank Reactor. Can. J. Chem. Eng. 1978, 56, 72–78. [Google Scholar] [CrossRef]
- Dmuchovsky, B.; Freerks, M.C.; Pierron, E.D.; Munch, R.H.; Zienty, F.B. A study of the catalytic oxidation of benzene to maleic anhydride. J. Catal. 1965, 4, 291–300. [Google Scholar] [CrossRef]
- Uraz, C.; Atalay, S. Comparison between the performances of a fluidized-bed reactor and a fixed-bed reactor for the oxidation of benzene to maleic anhydride. Turk. J. Eng. Env. Sci. 2012, 36, 59–71. [Google Scholar] [CrossRef]
- Bielański, A.; Piwowarczyk, J.; Poźniczek, J. Catalytic Activity of Vanadium Oxides in the Oxidation of Benzene. J. Catal. 1988, 113, 334–340. [Google Scholar] [CrossRef]
- Tufan, G.; Akgerman, A. Kinetics of benzene oxidation over a vanadium oxide (V2O5) catalyst. Ind. Eng. Chem. Proc. Des. Dev. 1981, 20, 604–608. [Google Scholar] [CrossRef]
- Schowengerdt, R.A. Data Models. In Remote Sensing: Models and Methods for Image Processing, 3rd ed.; Schowengerdt, R.A., Ed.; Academic Press: Cambridge, MA, USA, 2007; pp. 127–182. [Google Scholar] [CrossRef]
- Yaffe, M.J.; Boyd, N.F. Quantitative Image Analysis for Estimation of Breast Cancer Risk. In Handbook of Medical Image Processing and Analysis, 2nd ed.; Bankman, I.N., Ed.; Academic Press: Cambridge, MA, USA, 2009; pp. 381–398. [Google Scholar] [CrossRef]


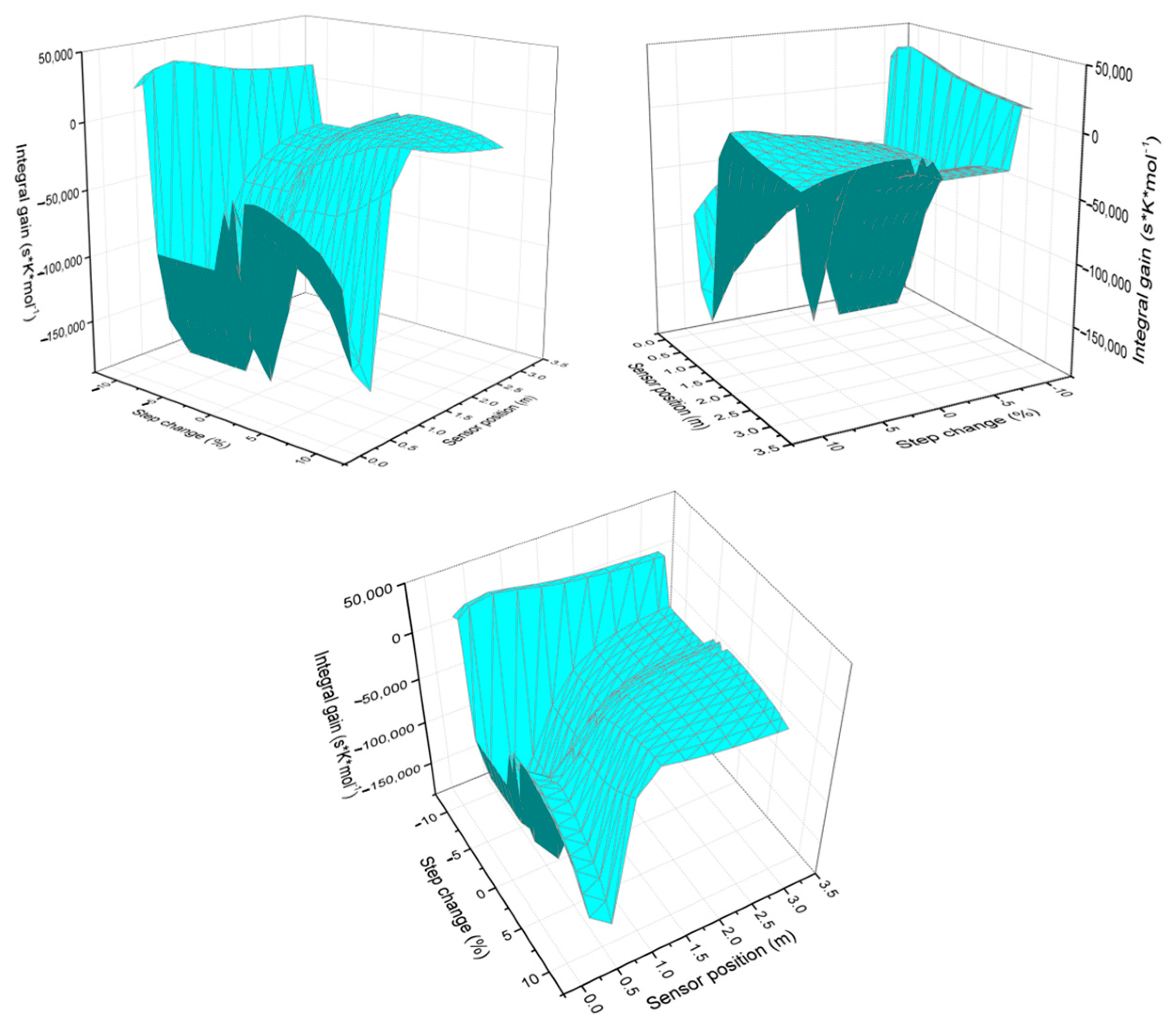

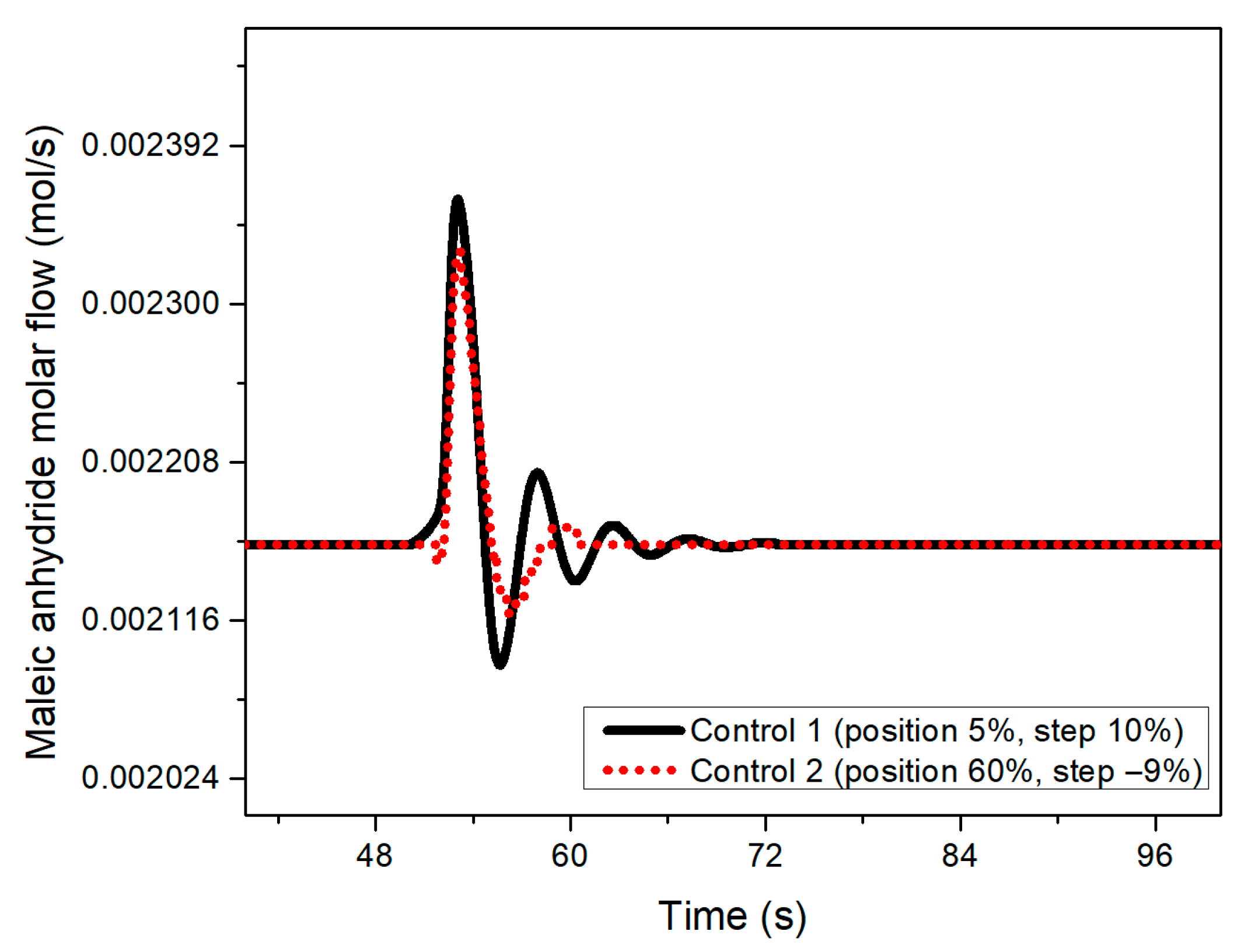


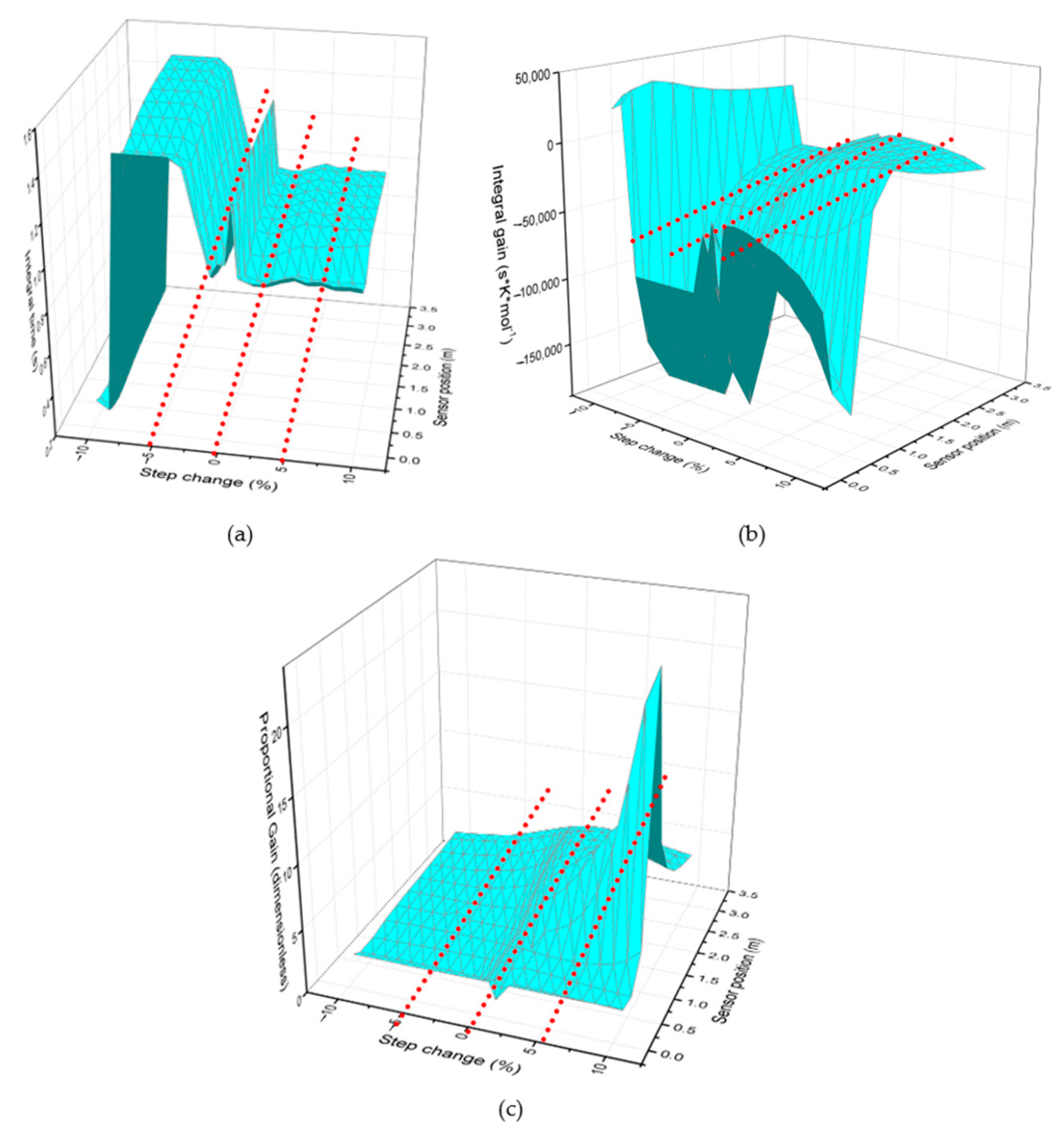
| Step Change | Parameters | 3.04 m (95%) | 1.92 m (60%) | 0.64 m (20%) | 0.16 m (5%) |
|---|---|---|---|---|---|
| Sequence 1: 10% disturbance in feed composition | |||||
| 10% | TR (K) | 738.50673 | 773.15722 | 933.46012 | 796.95867 |
| TC (K) | 704.51586 | 704.51586 | 704.51586 | 704.51586 | |
| Yield (%) | 22.37844 | 22.37844 | 22.37844 | 22.37844 | |
| Selectivity (%) | 24.09332 | 24.09332 | 24.09332 | 24.09332 | |
| IAE | 0.04689 | 0.04758 | 0.04999 | 0.05004 | |
| −9% | TR (K) | 675.204051 | 682.115014 | 690.653198 | 648.224513 |
| TC (K) | 636.196168 | 636.196168 | 636.196168 | 636.595215 | |
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | |
| Selectivity (%) | 50.426878 | 50.426878 | 50.426878 | 50.692474 | |
| IAE | 0.044199 | 0.044151 | 0.044283 | 0.044622 | |
| Sequence 2: 10% disturbance in feed temperature | |||||
| 10% | TR (K) | 731.209117 | 761.123611 | 865.91278 | 810.3801 |
| TC (K) | 695.358144 | 695.358144 | 695.35814 | 695.35814 | |
| Yield (%) | 24.616283 | 24.616283 | 24.61628 | 24.61628 | |
| Selectivity (%) | 27.743812 | 27.743812 | 27.74381 | 27.74381 | |
| IAE | 0.046085 | 0.045471 | 0.04922 | 0.04992 | |
| −9% | TR (K) | 685.777153 | 695.131626 | 708.726068 | 710.565877 |
| TC (K) | 646.698892 | 646.698892 | 646.698892 | 646.698892 | |
| Yield (%) | 24.616283 | 24.616283 | 24.616283 | 24.616283 | |
| Selectivity (%) | 46.191636 | 46.191636 | 46.191636 | 46.191636 | |
| IAE | 0.043709 | 0.043781 | 0.043908 | 0.044211 | |
| Sequence 3: 10% disturbance in composition and −10% disturbance in feed temperature | |||||
| 10% | TR (K) | 736.90046 | 775.555659 | 937.24268 | 763.89736 |
| TC (K) | 705.571136 | 705.571136 | 705.57114 | 705.57114 | |
| Yield (%) | 22.378439 | 22.378439 | 22.37844 | 22.37844 | |
| Selectivity (%) | 24.047055 | 24.047055 | 24.04706 | 24.04706 | |
| IAE | 0.046913 | 0.047754 | 0.04999 | 0.05086 | |
| −9% | TR (K) | 676.109678 | 683.196717 | 691.465401 | 648.224513 |
| TC (K) | 636.595215 | 636.595215 | 636.595215 | 636.595215 | |
| Yield (%) | 22.378439 | 22.378439 | 22.378439 | 22.378439 | |
| Selectivity (%) | 50.692474 | 50.692474 | 50.692474 | 50.692474 | |
| IAE | 0.044200 | 0.044153 | 0.044283 | 0.044622 | |
| Proportional Gain | Integral Gain | Integral Time | |
|---|---|---|---|
| Global fractality | 1.6170 | 1.75 | 1.9597 |
| Fractality zone 1 (10 to 5%) | 1.5164 | 1.5860 | 1.6955 |
| Fractality zone 2 (5 to 0%) | 1.5237 | 1.6603 | 1.9165 |
| Fractality zone 3 (0 to −5%) | 1.6695 | 1.6611 | 1.8293 |
| Fractality zone 4 (−5 to −10%) | 1.6469 | 1.6782 | 1.8103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manica Jauregui, M.; Garcia Rojas, I.; Luna Solano, G.; Sánchez Ramírez, C.; Urrea García, G.R. Influence of Step Size and Temperature Sensor Placement on Cascade Control Tuning for a Multi-Reaction Tubular Reactor Process. Processes 2025, 13, 3530. https://doi.org/10.3390/pr13113530
Manica Jauregui M, Garcia Rojas I, Luna Solano G, Sánchez Ramírez C, Urrea García GR. Influence of Step Size and Temperature Sensor Placement on Cascade Control Tuning for a Multi-Reaction Tubular Reactor Process. Processes. 2025; 13(11):3530. https://doi.org/10.3390/pr13113530
Chicago/Turabian StyleManica Jauregui, Magdalena, Isai Garcia Rojas, Guadalupe Luna Solano, Cuauhtémoc Sánchez Ramírez, and Galo Rafael Urrea García. 2025. "Influence of Step Size and Temperature Sensor Placement on Cascade Control Tuning for a Multi-Reaction Tubular Reactor Process" Processes 13, no. 11: 3530. https://doi.org/10.3390/pr13113530
APA StyleManica Jauregui, M., Garcia Rojas, I., Luna Solano, G., Sánchez Ramírez, C., & Urrea García, G. R. (2025). Influence of Step Size and Temperature Sensor Placement on Cascade Control Tuning for a Multi-Reaction Tubular Reactor Process. Processes, 13(11), 3530. https://doi.org/10.3390/pr13113530







