A Comprehensive Review of Discrete Element Method Studies of Granular Flow in Static Mixers
Abstract
1. Introduction
| Aspect | Details | References |
|---|---|---|
| Industrial relevance | Granular materials are essential in pharmaceuticals, food, mining, chemical engineering, agriculture, and construction; mixing ensures product uniformity and process performance. | [1,2,9] |
| Static mixer advantages | No moving parts, low energy consumption, continuous operation in confined geometries, reduced maintenance, enhanced reliability. | [3,10,11] |
| Challenges of granular flow | Non-linear, segregating behaviour; influenced by particle shape, size, density, cohesion, friction; issues like channelling, dead zones, radial segregation. | [4,13,15,16] |
| Experimental approaches | Provide insights into flow regimes, particle distribution, mixing quality; limited by resolution and difficulty in visualizing opaque granular media. | [5,20] |
| DEM principle and interactions | DEM simulates discrete particles by solving Newton’s laws for translational/rotational dynamics with time-stepping; contact forces (elastic, damping, frictional) typically modelled with spring-dashpot or Hertz-Mindlin laws. | [27,28,29,30,31] |
| Particle-scale details | Captures particle size, shape, roughness, cohesion, adhesion, and explicitly defined boundaries (walls, blades, mixers). | [9,32,33] |
| Dynamic phenomena | Segregation, clogging, arching, compaction, mixing efficiency captured at particle scale. | [33] |
| Time integration & computation | Explicit schemes (velocity-Verlet, Euler-Cromer) require small time steps (10–30% of contact time); simulations are computationally demanding, often needing millions of steps. | [29,34,35,36,37] |
| Computational strategies | Efficiency improved by parallel computing (multi-core CPUs, GPUs, HPC), neighbour list optimization (linked-cell, Verlet), or simplified contact models. | [38,39,40,41,42] |
| Applications in static mixers | DEM predicts particle trajectories, residence time, segregation, flow regimes; supports geometry optimization, design calibration, and scale-up studies. | [5,6,7,21,22,24,43,44] |
| Contact models | Hertzian (nonlinear, accurate, heavy); linear spring-dashpot (simpler, widely used); tangential models include Coulomb friction, rolling/torsional resistance, and cohesion for powders. | [5,8,44,45,46,47,48,49] |
| DEM advantages | High fidelity; can couple with CFD for multiphase flows; enables virtual prototyping, sensitivity analyses, and scalability studies. | [23,25,26] |
| Design & optimization challenges | Achieving uniform mixing without segregation; scale-up difficulties; absence of standardized design rules; requires careful geometry tailoring. | [10,17,18,19] |
| Future directions | Enhanced experimental validation, multi-scale and hybrid modelling, integration with machine learning, improved contact models, better parameter calibration. | [21,26] |
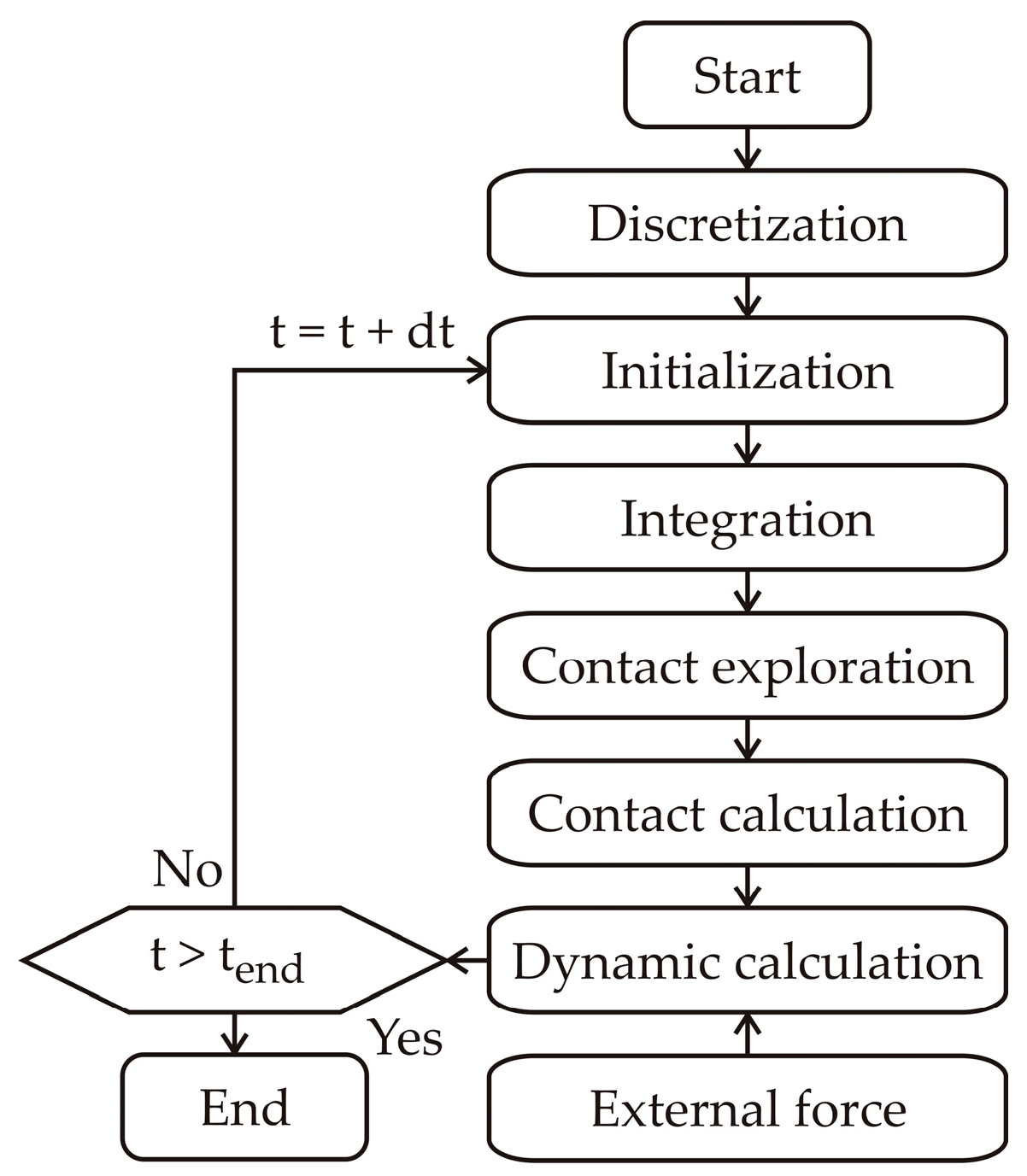
2. Fundamentals of DEM for Granular Flow
3. DEM Implementation in Static Mixers
- Multiphase coupling, where DEM is integrated with CFD to model gas–solid or liquid–solid flows in static mixers used for fluidized or wetted granular systems.
- Non-spherical particle modelling enhances the realism of simulations for elongated, angular, or irregularly shaped particles commonly found in agricultural and pharmaceutical applications.
- Thermal and reactive modelling, where temperature profiles or chemical transformations are coupled to the mechanical mixing process.
- Batch systems involve placing a fixed number of particles into the domain and allowing them to settle under gravity before initiating the flow.
- Continuous systems, where particles are continuously inserted at the inlet with specified velocities or mass flow rates and exit the system through an outlet.
- Quasi-steady-state setups, where a small representative volume is used with periodic inlets and outlets to maintain a constant particle population.
- Wetted or paste-like granular flows, where the presence of a liquid modifies cohesion and flowability.
- Gas–solid systems, such as pneumatic conveying or aerated mixing.
- Liquid–solid mixing, where high-viscosity fluids or slurries are processed in static mixer geometries.
- Heat and mass transfer analysis, where fluids serve as heat carriers or solute dispersants interacting with solid particulates.
- One-way coupling, where the fluid affects particle motion (e.g., drag forces), but particles do not influence the fluid flow-suitable for dilute systems.
- Two-way coupling, where particle motion also alters the local fluid velocity and pressure fields-appropriate for denser flows where particle–fluid interactions are strong.
- Four-way coupling, which additionally includes inter-particle collisions and turbulence–particle interactions, is often used in highly dynamic multiphase environments.
4. Performance Evaluation and Validation
- Lacey’s mixing index, which compares the variance of a sample’s composition to the variance in a fully segregated and ideally mixed state.
- Relative Standard Deviation (RSD), which expresses the variability of sample composition as the standard deviation relative to the mean concentration.
- Intensity of segregation (I), defined as the normalized variance of component concentration over time or space.
- Entropy-based indices, which interpret mixing as a measure of disorder in the system.
5. Strengths, Limitations and Challenges of DEM
- Parallel computing on multi-core CPUs, GPUs, or HPC clusters distributes workload, reducing simulation time.
- Domain decomposition partitions the simulation space for concurrent processing, enabling larger systems.
- Model simplifications—spherical particles, fewer particles, or coarse-graining—lower computational load but may reduce fidelity.
- Adaptive time stepping and event-driven algorithms refine resolution during collisions, improving efficiency without losing accuracy.
6. Future Directions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Suresh, P.; Sreedhar, I.; Vaidhiswaran, R.; Venugopal, A. A comprehensive review on process and engineering aspects of pharmaceutical wet granulation. Chem. Eng. J. 2017, 328, 785–815. [Google Scholar] [CrossRef]
- Rangel-Gil, R.S.; Nasrala-Álvarez, J.M.; Romañach, R.J.; Méndez, R. Blend uniformity monitoring in a continuous manufacturing mixing process for a low-dosage formulation using a stream sampler and near infrared spectroscopy. Int. J. Pharm. 2024, 661, 124478. [Google Scholar] [CrossRef]
- Bennour, E.; Kezrane, C.; Kaid, N.; Alqahtani, S.; Alshehery, S.; Menni, Y. Improving mixing efficiency in laminar-flow static mixers with baffle inserts and vortex generators: A three-dimensional numerical investigation using corrugated tubes. Chem. Eng. Process. Process Intensif. 2023, 193, 109530. [Google Scholar] [CrossRef]
- Meier, S.W.; Lueptow, R.M.; Ottino, J.M. A dynamical systems approach to mixing and segregation of granular materials in tumblers. Adv. Phys. 2007, 56, 757–827. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. A comprehensive review of the application of DEM in the investigation of batch solid mixers. Rev. Chem. Eng. 2023, 39, 729–764. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, F.; Furtney, J.; Damjanac, B. A review of methods, applications and limitations for incorporating fluid flow in the discrete element method. J. Rock. Mech. Geotech. Eng. 2022, 14, 1005–1024. [Google Scholar] [CrossRef]
- Hou, Q.F.; Kuang, S.B.; Yu, A.B. A DEM-based approach for analyzing energy transitions in granular and particle-fluid flows. Chem. Eng. Sci. 2017, 161, 67–79. [Google Scholar] [CrossRef]
- Göbel, F.; Golshan, S.; Norouzi, H.R.; Zarghami, R.; Mostoufi, N. Simulation of granular mixing in a static mixer by the discrete element method. Powder Technol. 2019, 346, 171–179. [Google Scholar] [CrossRef]
- Bridgwater, J. Mixing of powders and granular materials by mechanical means—A perspective. Particuology 2012, 10, 397–427. [Google Scholar] [CrossRef]
- Ghanem, A.; Lemenand, T.; Della Valle, D.; Peerhossaini, H. Static mixers: Mechanisms, applications, and characterization methods—A review. Chem. Eng. Res. Des. 2014, 92, 205–228. [Google Scholar] [CrossRef]
- Hosni, M.; Hammoudi, M.H.; Si-Ahmed, E.K.; Legrand, J.; Douib, L. Single and two-phase flows in a horizontal pipe with a Kenics static mixer: Effect of pressure drop on mixing. Can. J. Chem. Eng. 2023, 101, 828–844. [Google Scholar] [CrossRef]
- Ribeiro, A.; Montes, F.; Sousa, J.; Pais, A. Comminution technologies in the pharmaceutical industry: A comprehensive review with recent advances. Rev. Chem. Eng. 2025, 41, 69–100. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, S.; Luding, S. The role of particle shape in computational modelling of granular matter. Nat. Rev. Phys. 2023, 5, 505–525. [Google Scholar] [CrossRef]
- Pezo, M.; Pezo, L.; Jovanović, A.; Lončar, B.; Čolović, R. DEM/CFD approach for modeling granular flow in the revolving static mixer. Chem. Eng. Res. Des. 2016, 109, 317–326. [Google Scholar] [CrossRef]
- Xie, X.; Liu, X.; Ding, F.; Zhang, L. Characteristics and mechanism of the particle migration subject to the shear flow of concrete flow under pressure. J. Build. Eng. 2023, 79, 107693. [Google Scholar] [CrossRef]
- Shah, U.V.; Karde, V.; Ghoroi, C.; Heng, J.Y. Influence of particle properties on powder bulk behaviour and processability. Int. J. Pharm. 2017, 518, 138–154. [Google Scholar] [CrossRef] [PubMed]
- Tang, P.; Puri, V.M. Methods for minimizing segregation: A review. Part. Sci. Technol. 2004, 22, 321–337. [Google Scholar] [CrossRef]
- Ottino, J.M.; Khakhar, D.V. Mixing and segregation of granular materials. Annu. Rev. Fluid. Mech. 2000, 32, 55–91. [Google Scholar] [CrossRef]
- Bowler, A.L.; Bakalis, S.; Watson, N.J. A review of in-line and on-line measurement techniques to monitor industrial mixing processes. Chem. Eng. Res. Des. 2020, 153, 463–495. [Google Scholar] [CrossRef]
- Delannay, R.; Valance, A.; Mangeney, A.; Roche, O.; Richard, P. Granular and particle-laden flows: From laboratory experiments to field observations. J. Phys. D Appl. Phys. 2017, 50, 053001. [Google Scholar] [CrossRef]
- El-Emam, M.A.; Zhou, L.; Shi, W.; Han, C.; Bai, L.; Agarwal, R. Theories and applications of CFD-DEM coupling approach for granular flow: A review. Arch. Comput. Methods Eng. 2021, 28, 4979–5020. [Google Scholar] [CrossRef]
- Boac, J.M.; Ambrose, R.K.; Casada, M.E.; Maghirang, R.G.; Maier, D.E. Applications of discrete element method in modeling of grain postharvest operations. Food Eng. Rev. 2014, 6, 128–149. [Google Scholar] [CrossRef]
- Umbanhowar, P.B.; Lueptow, R.M.; Ottino, J.M. Modeling segregation in granular flows. Annu. Rev. Chem. Biomol. Eng. 2019, 10, 129–153. [Google Scholar] [CrossRef]
- Kafashan, J.; Wiącek, J.; Abd Rahman, N.; Gan, J. Two-dimensional particle shapes modelling for DEM simulations in engineering: A review. Granul. Matter 2019, 21, 80. [Google Scholar] [CrossRef]
- Wang, S.; Shen, Y. CFD-DEM-VOF-phase diagram modelling of multi-phase flow with phase changes. Chem. Eng. Sci. 2023, 273, 118651. [Google Scholar] [CrossRef]
- Salloum, N.; Brinz, T.; Atxutegi, A.; Heinrich, S. Design and optimization of stirrer and mixer design for the correct mixing of pharmaceutical powders through DEM. Powder Technol. 2025, 449, 120413. [Google Scholar] [CrossRef]
- Paulick, M.; Morgeneyer, M.; Kwade, A. Review on the influence of elastic particle properties on DEM simulation results. Powder Technol. 2015, 283, 66–76. [Google Scholar] [CrossRef]
- Campello, E.M. A description of rotations for DEM models of particle systems. Comput. Part. Mech. 2015, 2, 109–125. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Sturm, M.; Wirtz, S.; Scherer, V. Selection of an appropriate time integration scheme for the discrete element method (DEM). Comput. Chem. Eng. 2008, 32, 2263–2279. [Google Scholar] [CrossRef]
- Benvenuti, L.; Kloss, C.; Pirker, S. Identification of DEM simulation parameters by Artificial Neural Networks and bulk experiments. Powder Technol. 2016, 291, 456–465. [Google Scholar] [CrossRef]
- Thornton, C.; Cummins, S.J.; Cleary, P.W. An investigation of the comparative behaviour of alternative contact force models during elastic collisions. Powder Technol. 2011, 210, 189–197. [Google Scholar] [CrossRef]
- Zheng, Q.J.; Yang, R.Y.; Zeng, Q.H.; Zhu, H.P.; Dong, K.J.; Yu, A.B. Interparticle forces and their effects in particulate systems. Powder Technol. 2024, 436, 119445. [Google Scholar] [CrossRef]
- Shahzad, K.; Aeken, W.V.; Mottaghi, M.; Kamyab, V.K.; Kuhn, S. Aggregation and clogging phenomena of rigid microparticles in microfluidics: Comparison of a discrete element method (DEM); CFD-DEM coupling method. Microfluid. Nanofluid. 2018, 22, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Regueiro, R.A. A comprehensive study of MPI parallelism in three-dimensional discrete element method (DEM) simulation of complex-shaped granular particles. Comput. Part. Mech. 2018, 5, 553–577. [Google Scholar] [CrossRef]
- Liang, S.; Ji, S. Coordinated time-stepping method for coupled DEM-FEM-MBD algorithm. Int. J. Comput. Methods 2022, 19, 2150067. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Trucano, T.G.; Hirsch, C. Verification, validation,; predictive capability in computational engineering and physics. Appl. Mech. Rev. 2004, 57, 345–384. [Google Scholar] [CrossRef]
- Burns, S.J.; Piiroinen, P.T.; Hanley, K.J. Critical time step for DEM simulations of dynamic systems using a Hertzian contact model. Int. J. Numer. Methods Eng. 2019, 119, 432–451. [Google Scholar] [CrossRef]
- Navarro, C.A.; Hitschfeld-Kahler, N.; Mateu, L. A survey on parallel computing and its applications in data-parallel problems using GPU architectures. Commun. Comput. Phys. 2014, 15, 285–329. [Google Scholar] [CrossRef]
- Grandison, A.; Cavanagh, Y.; Lawrence, P.J.; Galea, E.R. Increasing the simulation performance of large-scale evacuations using parallel computing techniques based on domain decomposition. Fire Technol. 2017, 53, 1399–1438. [Google Scholar] [CrossRef]
- Duan, T.; Dinavahi, V. Adaptive time-stepping universal line and machine models for real time and faster-than-real-time hardware emulation. IEEE Trans. Ind. Electron. 2019, 67, 6173–6182. [Google Scholar] [CrossRef]
- Firoj, M.; Maheshwari, B.K. A new nonlinear spring-dashpot model of CPRF of NPP structure based on coupled BEM-FEM approach. Earthquake Eng. Struct. Dyn. 2023, 52, 932–955. [Google Scholar] [CrossRef]
- Gujjala, Y.K.; Kim, H.M.; Ryu, D.W. GPGPU-based parallel computation using discrete elements in geotechnics: A state-of-art review. Arch. Comput. Methods Eng. 2023, 30, 1601–1622. [Google Scholar] [CrossRef]
- Jovanović, A.; Pezo, M.; Pezo, L.; Lević, L. DEM/CFD analysis of granular flow in static mixers. Powder Technol. 2014, 266, 240–248. [Google Scholar] [CrossRef]
- Frungieri, G.; Boccardo, G.; Buffo, A.; Karimi-Varzaneh, H.A.; Vanni, M. CFD-DEM characterization and population balance modelling of a dispersive mixing process. Chem. Eng. Sci. 2022, 260, 117859. [Google Scholar] [CrossRef]
- Zhou, L.; Elemam, M.A.; Agarwal, R.K.; Shi, W. Discrete Element Method (DEM). In Discrete Element Method for Multiphase Flows with Biogenic Particles: Agriculture Applications; Springer Nature: Cham, Switzerland, 2024; pp. 83–102. [Google Scholar]
- Ai, J.; Chen, J.F.; Rotter, J.M.; Ooi, J.Y. Assessment of rolling resistance models in discrete element simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- Schmelzle, S.; Asylbekov, E.; Radel, B.; Nirschl, H. Modelling of partially wet particles in DEM simulations of a solid mixing process. Powder Technol. 2018, 338, 354–364. [Google Scholar] [CrossRef]
- Alizadeh, E.; Bertrand, F.; Chaouki, J. Development of a granular normal contact force model based on a non-Newtonian liquid filled dashpot. Powder Technol. 2013, 237, 202–212. [Google Scholar] [CrossRef]
- Wensrich, C.M.; Katterfeld, A. Rolling friction as a technique for modelling particle shape in DEM. Powder Technol. 2012, 217, 409–417. [Google Scholar] [CrossRef]
- Coetzee, C.J.; Els, D.N.J. Calibration of granular material parameters for DEM modelling and numerical verification by blade-granular material interaction. J. Terramech. 2009, 46, 15–26. [Google Scholar] [CrossRef]
- Yeom, S.B.; Ha, E.S.; Kim, M.S.; Jeong, S.H.; Hwang, S.J.; Choi, D.H. Application of the discrete element method for manufacturing process simulation in the pharmaceutical industry. Pharmaceutics 2019, 11, 414. [Google Scholar] [CrossRef]
- Navarro, H.A.; de Souza Braun, M.P. Determination of the normal spring stiffness coefficient in the linear spring–dashpot contact model of discrete element method. Powder Technol. 2013, 246, 707–722. [Google Scholar] [CrossRef]
- Al-Hababi, T.; Cao, M.; Saleh, B.; Alkayem, N.F.; Xu, H. A critical review of nonlinear damping identification in structural dynamics, Methods, applications, and challenges. Sensors 2020, 20, 7303. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, L.; Liu, Z.; Chen, M.; Xia, X.; Zhao, Y. A review of recent development for the CFD-DEM investigations of non-spherical particles. Powder Technol. 2022, 412, 117972. [Google Scholar] [CrossRef]
- Tomas, J.; Kleinschmidt, S. Improvement of flowability of fine cohesive powders by flow additives. Chem. Eng. Technol. 2009, 32, 1470–1483. [Google Scholar] [CrossRef]
- Cheung, G.; O’Sullivan, C. Effective simulation of flexible lateral boundaries in two-and three-dimensional DEM simulations. Particuology 2008, 6, 483–500. [Google Scholar]
- Xu, J.; Liu, X.; Hu, S.; Ge, W. Virtual process engineering on a three-dimensional circulating fluidized bed with multiscale parallel computation. J. Adv. Manuf. Process. 2019, 1, e10014. [Google Scholar] [CrossRef]
- Kritikos, A.; Singh, R.; Tsilomelekis, G.; Muzzio, F.J. A Novel CFD Model of SMX Static Mixer Used in Advanced Continuous Manufacturing of Active Pharmaceutical Ingredients (API). J. Pharm. Innov. 2024, 19, 14. [Google Scholar] [CrossRef]
- Pezo, M.; Pezo, L.; Lončar, B.; Kojić, P.; Ilić, M.; Jovanović, A. Granular flow in screw conveyors: A review of experiments and discrete element method (DEM) studies. Powder Technol. 2025, 459, 121040. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.D. Assessing mixing characteristics of particle-mixing and granulation devices. Particuology 2008, 6, 419–444. [Google Scholar] [CrossRef]
- Kresta, S.M.; Etchells, A.W., III; Dickey, D.S.; Atiemo-Obeng, V.A. (Eds.) Advances in Industrial Mixing: A Companion to the Handbook of Industrial Mixing; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Habchi, C.; Ghanem, A.; Lemenand, T.; Della Valle, D.; Peerhossaini, H. Mixing performance in split-and-recombine milli-static mixers—A numerical analysis. Chem. Eng. Res. Des. 2019, 142, 298–306. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Kuang, S.B.; Chu, K.W.; Yu, A. Discrete particle simulation of particle-fluid flow: Model formulations and their applicability. J. Fluid. Mech. 2010, 661, 482–510. [Google Scholar] [CrossRef]
- Hou, Q.; Dianyu, E.; Kuang, S.; Li, Z.; Yu, A.B. DEM-based virtual experimental blast furnace: A quasi-steady state model. Powder Technol. 2017, 314, 557–566. [Google Scholar] [CrossRef]
- Hajisharifi, A.; Romano, F.; Girfoglio, M.; Beccari, A.; Bonanni, D.; Rozza, G. A non-intrusive data-driven reduced order model for parametrized CFD-DEM numerical simulations. J. Comput. Phys. 2023, 491, 112355. [Google Scholar] [CrossRef]
- Kuo, H.P.; Knight, P.C.; Parker, D.J.; Tsuji, Y.; Adams, M.J.; Seville, J.P.K. The influence of DEM simulation parameters on the particle behaviour in a V-mixer. Chem. Eng. Sci. 2002, 57, 3621–3638. [Google Scholar] [CrossRef]
- Khan, D.; Plopski, A.; Fujimoto, Y.; Kanbara, M.; Jabeen, G.; Zhang, Y.J.; Zhang, X.; Kato, H. Surface remeshing: A systematic literature review of methods and research directions. IEEE Trans. Visual Comput. Graphics 2020, 28, 1680–1713. [Google Scholar] [CrossRef]
- Dai, L.; Chan, Y.R.; Vastola, G.; Zhang, Y.W. Discrete element simulation of powder flow in revolution powder analyser: Effects of shape factor, friction and adhesion. Powder Technol. 2022, 408, 117790. [Google Scholar] [CrossRef]
- Cornejo, A.; Mataix, V.; Zárate, F.; Oñate, E. Combination of an adaptive remeshing technique with a coupled FEM-DEM approach for analysis of crack propagation problems. Comput. Part. Mech. 2020, 7, 735–752. [Google Scholar] [CrossRef]
- Chandratilleke, G.R.; Jin, X.; Shen, Y.S. DEM study of effects of particle size and density on mixing behaviour in a ribbon mixer. Powder Technol. 2021, 392, 93–107. [Google Scholar] [CrossRef]
- Yu, A.B.; Standish, N. A study of particle size distributions. Powder Technol. 1990, 62, 101–118. [Google Scholar] [CrossRef]
- Börzsönyi, T.; Stannarius, R. Granular materials composed of shape-anisotropic grains. Soft Matter 2013, 9, 7401–7418. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Y. Multi-super-ellipsoid model for non-spherical particles in DEM simulation. Powder Technol. 2020, 361, 190–202. [Google Scholar] [CrossRef]
- Duriez, J.; Bonelli, S. Precision and computational costs of Level Set-Discrete Element Method (LS-DEM) with respect to DEM. Comput. Geotech. 2021, 134, 104033. [Google Scholar] [CrossRef]
- Marques, F.; Flores, P.; Claro, J.P.; Lankarani, H.M. Modeling and analysis of friction including rolling effects in multibody dynamics: A review. Multibody Sys. Dyn. 2019, 45, 223–244. [Google Scholar] [CrossRef]
- Hassanzadeh, V.; Wensrich, C.M.; Moreno-Atanasio, R. Elucidation of the role of cohesion in the macroscopic behaviour of coarse particulate systems using DEM. Powder Technol. 2020, 361, 374–388. [Google Scholar] [CrossRef]
- Bridgwater, J. Fundamental powder mixing mechanisms. Powder Technol. 1976, 15, 215–236. [Google Scholar] [CrossRef]
- Jin, G.; Zhou, Z.; Liu, Y.; Gao, C.; Ma, H.; Yang, Z.; Jing, Y.; Tu, H. A novel coarse-grained discrete element method for simulating failure process of strongly bonded particle materials. Powder Technol. 2025, 464, 121212. [Google Scholar] [CrossRef]
- Cabiscol, R.; Finke, J.H.; Kwade, A. Assessment of particle rearrangement and anisotropy in high-load tableting with a DEM-based elasto-plastic cohesive model. Granul. Matter 2019, 21, 98. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Yin, Z.Y.; Liang, Z. DEM modeling of large-scale triaxial test of rock clasts considering realistic particle shapes and flexible membrane boundary. Eng. Geol. 2020, 279, 105871. [Google Scholar] [CrossRef]
- Rahmani, R.K.; Keith, T.G.; Ayasoufi, A. Numerical simulation of turbulent flow in an industrial helical static mixer. Int. J. Numer. Methods Heat. Fluid. Flow. 2008, 18, 675–696. [Google Scholar] [CrossRef]
- Wu, J.; Yin, Q.; Jing, H. Surface roughness and boundary load effect on nonlinear flow behavior of fluid in real rock fractures. Bull. Eng. Geol. Environ. 2020, 79, 4917–4932. [Google Scholar] [CrossRef]
- Rahmani, R.K.; Keith, T.G.; Ayasoufi, A. Three-dimensional numerical simulation and performance study of an industrial helical static mixer. J. Fluids Eng. 2005, 127, 467–483. [Google Scholar] [CrossRef]
- Anirudh, R.; Archibald, R.; Asif, M.S.; Becker, M.M.; Benkadda, S.; Bremer, P.T.; Bude, R.H.; Chang, C.S.; Chen, L.; Churchill, R.M.; et al. 2022 review of data-driven plasma science. IEEE Trans. Plasma Sci. 2023, 51, 1750–1838. [Google Scholar] [CrossRef]
- Toson, P.; Doshi, P.; Matic, M.; Siegmann, E.; Blackwood, D.; Jain, A.; Brandon, J.; Lee, K.; Wilsdon, D.; Kimber, J.; et al. Continuous mixing technology: Validation of a DEM model. Int. J. Pharm. 2021, 608, 121065. [Google Scholar] [CrossRef]
- Barrios, G.K.; Tavares, L.M. A preliminary model of high pressure roll grinding using the discrete element method and multi-body dynamics coupling. Int. J. Miner. Process. 2016, 156, 32–42. [Google Scholar] [CrossRef]
- Xu, J.; Wang, F.; Abegaz, R. State of the Art of CFD-DEM Coupled Modeling and Its Application in Turbulent Flow-Induced Soil Erosion. Geosciences 2025, 15, 21. [Google Scholar] [CrossRef]
- Mäkiharju, S.A.; Dewanckele, J.; Boone, M.; Wagner, C.; Griesser, A. Tomographic X-ray particle tracking velocimetry: Proof-of-concept in a creeping flow. Exp. Fluids 2022, 63, 16. [Google Scholar] [CrossRef]
- Govender, N.; Wilke, D.N.; Wu, C.Y.; Rajamani, R.; Khinast, J.; Glasser, B.J. Large-scale GPU based DEM modeling of mixing using irregularly shaped particles. Adv. Powder Technol. 2018, 29, 2476–2490. [Google Scholar] [CrossRef]
- Gu, Z.; Chen, J.J.J. A probabilistic analysis of some selected mixing indices. Chem. Eng. Res. Des. 2015, 93, 293–303. [Google Scholar] [CrossRef]
- Szpicer, A.; Bińkowska, W.; Stelmasiak, A.; Wojtasik-Kalinowska, I.; Czajkowska, A.; Mierzejewska, S.; Domiszewski, Z.; Rydzkowski, T.; Piepiórka-Stepuk, J.; Pó?torak, A. Advances in Computational Fluid Dynamics of Mechanical Processes in Food Engineering: Mixing, Extrusion, Drying and Process Optimization. Appl. Sci. 2025, 15, 8752. [Google Scholar] [CrossRef]
- Song, Y.; Zhou, T.; Bai, R.; Zhang, M.; Yang, H. Review of CFD-DEM modeling of wet fluidized bed granulation and coating processes. Processes 2023, 11, 382. [Google Scholar] [CrossRef]
- Goh, W.P.; Ghadiri, M. DEM simulation of particle attrition in mechanofusion device. Powder Technol. 2025, 456, 120822. [Google Scholar] [CrossRef]
- Yan, Z.; Wilkinson, S.K.; Stitt, E.H.; Marigo, M.J.C.P.M. Discrete element modelling (DEM) input parameters: Understanding their impact on model predictions using statistical analysis. Comput. Part. Mech. 2015, 2, 283–299. [Google Scholar] [CrossRef]
- Wen, Y.; Liu, M.; Liu, B.; Shao, Y. Comparative study on the characterization method of particle mixing index using DEM method. Procedia Eng. 2015, 102, 1630–1642. [Google Scholar] [CrossRef]
- Lee, H.W.; Park, D. Understanding and development of residence time distribution (RTD) model in continuous manufacturing. J. Pharm. Invest. 2025, 55, 481–495. [Google Scholar] [CrossRef]
- Kashid, M.N.; Renken, A.; Kiwi-Minsker, L. (Eds.) Real Reactors and Residence Time Distribution (RTD). In Microstructured Devices for Chemical Processing; Wiley-VCH: Weinheim, Germany, 2015; pp. 89–128. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Zhu, T.; Han, K. Size effect on contact behavior in DEM simple shear tests. Sci. Rep. 2021, 11, 19914. [Google Scholar] [CrossRef]
- Hadi, A.; Roeplal, R.; Pang, Y.; Schott, D.L. DEM modelling of segregation in granular materials: A review. Kona Powder Part. J. 2024, 41, 78–107. [Google Scholar] [CrossRef]
- Mori, Y.; Sakai, M. Advanced DEM simulation on powder mixing for ellipsoidal particles in an industrial mixer. Chem. Eng. J. 2022, 429, 132415. [Google Scholar] [CrossRef]
- Mirabolghasemi, M.; Prodanović, M.; DiCarlo, D.; Ji, H. Prediction of empirical properties using direct pore-scale simulation of straining through 3D microtomography images of porous media. J. Hydrol. 2015, 529, 768–778. [Google Scholar] [CrossRef]
- Coetzee, C.; Katterfeld, A. Calibration of DEM parameters. In Simulations in Bulk Solids Handling: Applications of DEM and Other Methods; McGlinchey, D., Ed.; Wiley-VCH: Weinheim, Germany, 2023; pp. 1–40. [Google Scholar] [CrossRef]
- Ghommem, M.; Abbad, M.; Aidagulov, G.; Dyer, S.; Brady, D. Modeling of fiber bridging in fluid flow for well stimulation applications. Pet. Sci. 2020, 17, 671–686. [Google Scholar] [CrossRef]
- Saeed, M.K.; Siraj, M.S. Mixing study of non-spherical particles using DEM. Powder Technol. 2019, 344, 617–627. [Google Scholar] [CrossRef]
- Grima, A.P.; Wypych, P.W. Investigation into calibration of discrete element model parameters for scale-up and validation of particle-structure interactions under impact conditions. Powder Technol. 2011, 212, 198–209. [Google Scholar] [CrossRef]
- Shafaie, V.; Movahedi Rad, M. Multi-objective genetic algorithm calibration of colored self-compacting concrete using DEM: An integrated parallel approach. Sci. Rep. 2024, 14, 4126. [Google Scholar] [CrossRef]
- Roos, P.R.; Rijnberg, F.M.; Westenberg, J.J.; Lamb, H.J. Particle tracing based on 4D flow magnetic resonance imaging: A systematic review into methods, applications,; current developments. J. Magn. Reson. Imaging 2023, 57, 1320–1339. [Google Scholar] [CrossRef] [PubMed]
- Coetzee, C.J.; Scheffler, O.C. The calibration of dem parameters for the bulk modelling of cohesive materials. Processes 2022, 11, 5. [Google Scholar] [CrossRef]
- Ge, W.; Wang, L.; Xu, J.; Chen, F.; Zhou, G.; Lu, L.; Chang, Q.; Li, J. Discrete simulation of granular and particle-fluid flows: From fundamental study to engineering application. Rev. Chem. Eng. 2017, 33, 551–623. [Google Scholar] [CrossRef]
- Maiti, R.; Roy, A.K. Discrete element model of low-velocity projectile penetration and impact crater on granular bed. Powder Technol. 2024, 448, 120350. [Google Scholar] [CrossRef]
- Behjani, M.A.; Motlagh, Y.G.; Bayly, A.E.; Hassanpour, A. Assessment of blending performance of pharmaceutical powder mixtures in a continuous mixer using Discrete Element Method (DEM). Powder Technol. 2020, 366, 73–81. [Google Scholar] [CrossRef]
- Wang, T.F.; Huang, A.N.; Hsu, W.Y.; Kuo, H.P. Recent Progress in Radiation-Based Investigation Techniques for Understanding Particle Motion—A Review. Kona Powder Part. J. 2025, 2026002. [Google Scholar] [CrossRef]
- Santos, D.A.; Barrozo, M.A.; Duarte, C.R.; Weigler, F.; Mellmann, J. Investigation of particle dynamics in a rotary drum by means of experiments and numerical simulations using DEM. Adv. Powder Technol. 2016, 27, 692–703. [Google Scholar] [CrossRef]
- Bernhardt, M.L.; Biscontin, G. Experimental validation study of 3D direct simple shear DEM simulations. Soils Found. 2016, 56, 336–347. [Google Scholar] [CrossRef]
- Lu, Y.; Agrawal, M. A computational-fluid-dynamics-based Eulerian-granular approach for characterization of sand erosion in multiphase-flow systems. SPE J. 2014, 19, 586–597. [Google Scholar] [CrossRef]
- Lu, L.; Benyahia, S.; Li, T. An efficient and reliable predictive method for fluidized bed simulation. AlChE J. 2017, 63, 5320–5334. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhou, L.; Bai, L.; Wang, B.; Agarwal, R. Recent advances and perspectives of CFD-DEM simulation in fluidized bed. Arch. Comput. Methods Eng. 2024, 31, 871–918. [Google Scholar] [CrossRef]
- Guo, Y.; Curtis, J.S. Discrete element method simulations for complex granular flows. Annu. Rev. Fluid. Mech. 2015, 47, 21–46. [Google Scholar] [CrossRef]
- Li, X.F.; Zhang, Q.B.; Li, H.B.; Zhao, J. Grain-based discrete element method (GB-DEM) modelling of multi-scale fracturing in rocks under dynamic loading. Rock. Mech. Rock. Eng. 2018, 51, 3785–3817. [Google Scholar] [CrossRef]
- Ramezanzad, A.; Jaradat, K.; Abdelaziz, S. Coupled CFD-DEM Simulations: A Review of Applications and Modeling Limitations. In Proceedings of the International Foundations Congress and Equipment Expo 2024 (IFCEE 2024), Dallas, TX, USA, 7–10 May 2024; pp. 216–226. [Google Scholar] [CrossRef]
- Xiao, J.; Tozato, K.; Nomura, R.; Otake, Y.; Terada, K.; Moriguchi, S. Sensitivity analysis on critical combinations of input parameters in DEM granular flow analysis. Acta Geotech. 2025, 20, 387–412. [Google Scholar] [CrossRef]
- Li, L.; Hu, C.; Yuan, Y.; He, X.; Wu, Z. Efficient optimization parameter calibration method-based DEM simulation for compacted loess slope under dry-wet cycling. Sci. Rep. 2024, 14, 17418. [Google Scholar] [CrossRef]
- Soltanbeigi, B.; Podlozhnyuk, A.; Papanicolopulos, S.A.; Kloss, C.; Pirker, S.; Ooi, J.Y. DEM study of mechanical characteristics of multi-spherical and superquadric particles at micro and macro scales. Powder Technol. 2018, 329, 288–303. [Google Scholar] [CrossRef]
- Choi, S.H.; Chan, A.M.M. A virtual prototyping system for rapid product development. Comput.-Aided Des. 2004, 36, 401–412. [Google Scholar] [CrossRef]
- Ge, M.; Chen, J.; Zhao, L.; Zheng, G. Mixing transport mechanism of three-phase particle flow based on CFD-DEM coupling. Processes 2023, 11, 1619. [Google Scholar] [CrossRef]
- Radl, S.; Kalvoda, E.; Glasser, B.J.; Khinast, J.G. Mixing characteristics of wet granular matter in a bladed mixer. Powder Technol. 2010, 200, 171–189. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, Y.; Jia, Y.; Bian, H.; Bur, N.; Zhu, J.; Colliat, J.B. Impact of particle shape on crushing Behaviour of Rock particles using X-ray Micro-CT testing and DEM modelling. Rock. Mech. Rock. Eng. 2024, 57, 7813–7834. [Google Scholar] [CrossRef]
- Fries, L. Modeling food particle systems: A review of current progress and challenges. Annu. Rev. Chem. Biomol. Eng. 2021, 12, 97–113. [Google Scholar] [CrossRef]
- Marigo, M.; Stitt, E.H. Discrete element method (DEM) for industrial applications: Comments on calibration and validation for the modelling of cylindrical pellets. Kona Powder Part. J. 2015, 32, 236–252. [Google Scholar] [CrossRef]
- Roessler, T.; Richter, C.; Katterfeld, A.; Will, F. Development of a standard calibration procedure for the DEM parameters of cohesionless bulk materials-part I: Solving the problem of ambiguous parameter combinations. Powder Technol. 2019, 343, 803–812. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhen-Yu, Y.I.N.; He, G.F.; Zhang, P.; Jiang, M. The potential of a multi-fidelity residual neural network based optimizer to calibrate DEM parameters of rock-like bonded granular materials. Comput. Geotech. 2024, 168, 106137. [Google Scholar] [CrossRef]
- Suleiman, N.; Murtaza, Y. Scaling microservices for enterprise applications: Comprehensive strategies for achieving high availability, performance optimization, resilience,; seamless integration in large-scale distributed systems and complex cloud environments. Appl. Res. Artif. Intell. Cloud Comput. 2024, 7, 46–82. [Google Scholar]
- Leube, P.C.; De Barros, F.P.; Nowak, W.; Rajagopal, R. Towards optimal allocation of computer resources: Trade-offs between uncertainty quantification, discretization and model reduction. Environ. Modell. Software 2013, 50, 97–107. [Google Scholar] [CrossRef]
- Liu, G.Y.; Xu, W.J.; Zhou, Q. DEM contact model for spherical and polyhedral particles based on energy conservation. Comput. Geotech. 2023, 153, 105072. [Google Scholar] [CrossRef]
- Angelidakis, V.; Nadimi, S.; Otsubo, M.; Utili, S. CLUMP: A code library to generate universal multi-sphere particles. SoftwareX 2021, 15, 100735. [Google Scholar] [CrossRef]
- Lai, Z.; Zhao, S.; Zhao, J.; Huang, L. Signed distance field framework for unified DEM modeling of granular media with arbitrary particle shapes. Comput. Mech. 2022, 70, 763–783. [Google Scholar] [CrossRef]
- Jaradat, K.A.; Abdelaziz, S.L. Simplifying the physico-chemical contacts in cohesive soils for efficient DEM simulations. Comput. Geotech. 2023, 154, 105155. [Google Scholar] [CrossRef]
- Shi, L.; Ren, Z.; Zhou, C.; Shen, L.; Bai, H.; Huang, Z. Numerical simulation of an entangled wire-silicone rubber continuous interpenetration structure based on domain meshing superposition method. Composites Part. B 2023, 256, 110648. [Google Scholar] [CrossRef]
- Perera, C. Optimizing Performance in Parallel and Distributed Computing Systems for Large-Scale Applications. J. Adv. Comput. Syst. 2024, 4, 35–44. [Google Scholar]
- Giannis, K.; Kwade, A.; Finke, J.H.; Schilde, C. The effect of particle shape on the compaction of realistic non-spherical particles-a multi-contact dem study. Pharmaceutics 2023, 15, 909. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Zhao, J.; Li, Z.; Wang, H. Numerical simulation of multiphase multi-physics flow in underground reservoirs: Frontiers and challenges. Capillarity 2024, 12, 72–79. [Google Scholar] [CrossRef]
- Misener, R.; Biegler, L. Formulating data-driven surrogate models for process optimization. Comput. Chem. Eng. 2023, 179, 108411. [Google Scholar] [CrossRef]
- Kemp, I.C. Developments in scale-up procedures for industrial dryers. Drying Technol. 2024, 42, 1964–1985. [Google Scholar] [CrossRef]
- Zhou, Q.; Xu, W.J.; Liu, G.Y. A contact detection algorithm for triangle boundary in GPU-based DEM and its application in a large-scale landslide. Comput. Geotech. 2021, 138, 104371. [Google Scholar] [CrossRef]
- Longwei, L.; Jian, L.; Shichang, L.; Zhangjun, D.; Shanxiong, C.; Xiaoyang, W. A hybrid scaling coarse-graining method based on a computational fluid dynamics-discrete element method. Comput. Part. Mech. 2025, 12, 1099–1113. [Google Scholar] [CrossRef]
- Sitaraman, H.; Vaidhynathan, D.; Grout, R.; Hauser, T.; Hrenya, C.M.; Musser, J. An error-controlled adaptive time-stepping method for particle advancement in coupled CFD-DEM simulations. Powder Technol. 2021, 379, 203–216. [Google Scholar] [CrossRef]
- Azanaw, G.M. Blending Data-Driven Surrogates with Physics-Based Topology Optimization: A Critical Review of Machine Learning-Accelerated Design in Fibre-Reinforced Polymer and Concrete Structures. Am. J. Sci. 2025, 10, 80–93. [Google Scholar] [CrossRef]
- Zhang, S.W.; Shang, L.Y.; Zhou, L.; Lv, Z.B. Hydrate deposition model and flow assurance technology in gas-dominant pipeline transportation systems: A review. Energy Fuels 2022, 36, 1747–1775. [Google Scholar] [CrossRef]
- Cremonesi, M.; Franci, A.; Idelsohn, S.; Oñate, E. A state of the art review of the particle finite element method (PFEM). Arch. Comput. Methods Eng. 2020, 27, 1709–1735. [Google Scholar] [CrossRef]
- Yang, G.C.; Yang, S.C.; Jing, L.; Kwok, C.Y.; Sobral, Y.D. Efficient lattice Boltzmann simulation of free-surface granular flows with μ (I)-rheology. J. Comput. Phys. 2023, 479, 111956. [Google Scholar] [CrossRef]
- Otto, E.; Ajalova, A.; Buück, A.; Tsotsas, E.; Kienle, A. Population balance modeling of particle size and porosity in fluidized bed spray agglomeration. Ind. Eng. Chem. Res. 2024, 63, 17545–17556. [Google Scholar] [CrossRef]
- Marquardt, J.E.; Krause, M.J. A review of the homogenized lattice boltzmann method for particulate flow simulations: From fundamentals to applications. Powders 2024, 3, 500–530. [Google Scholar] [CrossRef]
- Guo, N.; Zhao, J. A coupled FEM/DEM approach for hierarchical multiscale modelling of granular media. Int. J. Numer. Methods Eng. 2014, 99, 789–818. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A.; Neveu, A.; Francqui, F. Analysis of cohesive mannitol particle mixing: A comparative study of machine learning methods. Chem. Eng. Res. Des. 2025, 214, 188–201. [Google Scholar] [CrossRef]
- Zhang, S.; Tekeste, M.Z.; Li, Y.; Gaul, A.; Zhu, D.; Liao, J. Scaled-up rice grain modelling for DEM calibration and the validation of hopper flow. Biosyst. Eng. 2020, 194, 196–212. [Google Scholar] [CrossRef]




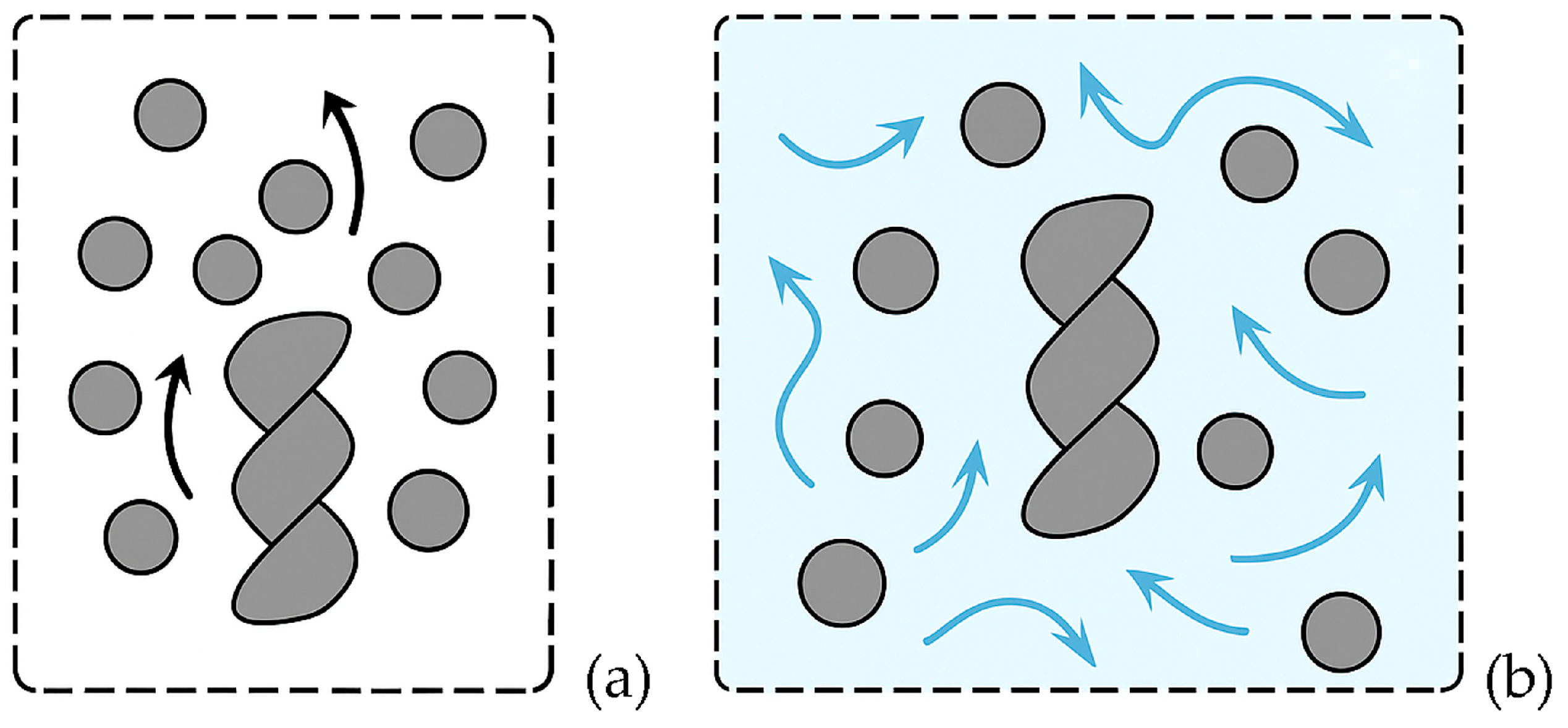
| Term | Definition | Typical Cause/Context |
|---|---|---|
| Dead zones | Regions within the mixer where particle motion is minimal or stagnant, leading to poor mixing efficiency. | Low shear regions, poor geometry design, or excessive friction near walls. |
| Channelling | Preferential flow of particles along specific low-resistance paths, bypassing other regions of the mixer. | Uneven flow distribution, high feed rates, or geometry-induced flow asymmetry. |
| Clogging (arching) | Formation of stable particle bridges or arches that obstruct flow through the mixer channels. | High cohesion, irregular particle shape, or narrow flow passages. |
| Segregation | Spatial separation of particles differing in size, density, or shape, reducing mixture homogeneity. | Differences in particle properties, vibration, or gravitational settling during flow. |
| Contact Model/Interaction | Governing Equation | Physical Interpretation | Practical Implications for Static Mixers | Computational Considerations | Calibration and Sensitivity | Typical Applications | Ref. |
|---|---|---|---|---|---|---|---|
| Hertzian (nonlinear) | Nonlinear elastic contact; models particle deformation accurately | Captures realistic collision behaviour; important for deformable particles and high-fidelity simulations | High computational cost; small time steps needed for stability | Sensitive to stiffness; requires careful experimental or inverse calibration; sensitive to particle shape | Simulations requiring accurate deformation, energy dissipation, or contact stress analysis | [27,39] | |
| Linear spring–dashpot | Linear elastic contact with energy dissipation | Efficient for large-scale simulations; suitable for rigid or nearly elastic particles; controls restitution | Computationally cheaper; may produce unrealistic overlaps if stiffness is too low | Easier calibration; damping strongly affects energy loss; less sensitive to particle shape | Industrial-scale mixers, fast screening of process parameters, coarse-grained simulations | [52] | |
| Tangential (elastic-damped Coulomb friction) | Tangential resistance and friction; accounts for rolling/sliding | Influences energy dissipation, particle interlocking, and segregation; critical for predicting mixing efficiency | Moderate computational cost; stability depends on time step and stiffness selection | Parameters require calibration; sensitive to surface roughness and particle shape | Predicting particle segregation, flow uniformity, and residence time distributions | [53] | |
| Rolling resistance/torque | Models energy loss due to particle rotation and rolling | Reduces unrealistic rolling; affects segregation and mixing patterns | Adds modest computational cost | Rolling friction coefficient must be calibrated; depends on particle shape | Systems with non-spherical particles or elongated shapes; controlling axial mixing | [54] | |
| Cohesive interactions (van der Waals/liquid bridges) | Models attractive forces between particles | Critical for high-moisture or fine powders; affects agglomeration, arching, and flow blockage | Increases computational complexity; smaller time steps may be needed | Difficult to measure directly; often fitted to experimental bulk behaviour | Wet or fine granular systems; silage, powders, high-moisture feedstock’s | [55] | |
| Boundary/wall interactions | Interaction between particles and mixer walls | Influences dead zones, particle segregation, and flow uniformity | Computational cost depends on wall discretization and contact model | Wall friction calibration critical for accurate flow | All static mixer designs; particularly important for narrow or complex geometries | [56] |
| No. | Mixer Type/Geometry | Material or System Studied | Methodology | Key Findings | Reference |
|---|---|---|---|---|---|
| 1 | Laminar static mixer with baffles and vortex generators | Liquid–liquid mixing under laminar conditions | CFD (3D RANS) | Demonstrated that optimized vortex-generator geometries significantly enhance mixing efficiency while reducing pressure drop. | [3]. |
| 2 | Static mixer (cross-blade type) | Granular solids | DEM simulation | Quantified granular mixing patterns and residence time distributions; validated DEM predictions against experiments. | [8] |
| 3 | Various static mixer designs | Liquids and suspensions | Review (CFD, experimental) | Comprehensive review of mixing mechanisms, design correlations, and performance metrics in static mixers. | [10] |
| 4 | Kenics static mixer | Single- and two-phase flows | CFD and experimental validation | Quantified the effect of pitch angle and element number on pressure drop and mixing uniformity. | [11] |
| 5 | Revolving static mixer (FixMix type) | Granular materials | DEM–CFD hybrid model | Demonstrated that rotation combined with static elements improves particle homogeneity and reduces segregation. | [14] |
| 6 | Helical static mixer (Komax type) | Granular and particulate systems | DEM–CFD coupling | Provided quantitative insight into local shear and particle dispersion mechanisms within static mixing zones. | [43] |
| 7 | SMX-type static mixer | Active pharmaceutical ingredients (API) | CFD modeling | Developed a validated CFD model for static mixer flow; used for process scale-up in continuous pharmaceutical manufacturing. | [58] |
| 8 | Milli-scale split-and-recombine mixer | Microreactor applications | CFD | Evaluated micromixing and residence time uniformity; identified optimized geometrical ratios for efficient micro-scale mixing. | [62] |
| 9 | Helical static mixer | Turbulent liquid flow | CFD (k–ε model) | Showed flow enhancement and reduced axial dispersion through helical insert geometries. | [81] |
| 10 | Industrial helical static mixer | Single-phase turbulent flow | CFD (3D Navier–Stokes) | Predicted pressure loss and flow development; validated simulation with industrial-scale data. | [83] |
| 11 | Pipeline static mixers (Kenics, Sulzer SMX, etc.) | Various industrial fluids | Experimental and industrial review | Provided design guidelines and performance maps for industrial static mixing applications across scales. | [27] |
| Section | Category | Details | References |
|---|---|---|---|
| Granular Flow | Industrial relevance | Granular materials are essential in pharmaceuticals, food, mining, chemical engineering, agriculture, and construction; mixing ensures product uniformity and process performance. | [1,2,9] |
| Challenges | Non-linear, segregating behaviour; influenced by particle shape, size, density, cohesion, friction; issues like channeling, dead zones, radial segregation. | [4,13,15,16] | |
| Experimental approaches | Insights into flow regimes, particle distribution, and mixing quality; limited by resolution and difficulty in visualizing opaque granular media. | [5,20] | |
| Static Mixers | Advantages | No moving parts, low energy consumption, continuous operation, reduced maintenance, enhanced reliability. | [3,10,11] |
| Types and geometry | Kenics®, Sulzer SMX/SMXL®, helical, SAR, and novel AM designs; geometry represented by analytical primitives or CAD meshes; adaptive meshing and periodic geometries balance accuracy and computational cost. | [21,45,61,62,66,67,69] | |
| Design and optimization challenges | Achieving uniform mixing without segregation; scale-up difficulties; absence of standardized design rules; requires careful geometry tailoring. | [10,17,18,19] | |
| DEM Modelling | Purpose and applications | Investigates particle-scale mechanisms (transport, shear, dispersion, segregation); supports design optimization, virtual prototyping, predictive analysis, and scale-up. | [5,27,28,29,30,31,44,45,60,89,94,95] |
| Material and boundary properties | Particle size, shape, friction, cohesion, density, elastic modulus, restitution coefficient; rigid walls; batch, continuous, or quasi-steady simulations; inlet/outlet conditions; ramp-up injection avoids artefacts. | [5,43,66,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86] | |
| Outputs and flow phenomena | RTD, mixing quality indices (Lacey’s, Danckwerts, entropy-based), velocity fields, dispersion, dead zones, segregation, channeling, particle–particle/wall interactions, shear/stress fields, flow visualization. | [14,44,63,64,66,87,88,89,90,91,95,96,97,98,99,100] | |
| Contact models | Hertzian (nonlinear, accurate, heavy) and linear spring-dashpot (simpler, widely used); tangential models include Coulomb friction, rolling/torsional resistance, cohesion. | [5,8,44,46,47,48,49] | |
| Advanced modelling and comparison | Multiphase coupling (DEM–CFD, reactive/thermal systems); one-/two-/four-way strategies; drag, lift, turbulence, capillarity; DEM vs. CFD/FEM; hybrid models combine strengths. | [21,86,87,88,115,116,117,118,119,120] | |
| Sensitivity, calibration and validation | Input parameters tuned via experiments (shear cell, angle of repose); validated against tracer studies, PIV, MRI, PEPT, X-ray tomography. | [5,85,101,102,107,108,109,110,111,112,113,114,121,122] | |
| Strengths and limitations | High particle-level realism; supports optimization and scale-up. Limitations: high computational cost; industrial-scale DEM often requires hybrid or reduced-order approaches. | [5,65] | |
| Future directions | Enhanced measurement techniques, multi-scale and hybrid modelling, machine learning integration, improved contact models, better parameter calibration. | [21,26] |
| Aspect | Description | References |
|---|---|---|
| Particle-scale resolution | Tracks individual particle motions, collisions, rotations, and interactions; resolves microscale phenomena (force chains, contact dynamics, segregation). | [24,123,125] |
| Mixing behaviour analysis | Quantifies residence time distributions, velocity fields, shear rates, mixing indices; identifies dead zones, preferential pathways, clustering. | [109,126] |
| Material property influence | Captures effects of particle size, shape, density, friction, cohesion, surface roughness on flow and mixing behaviour. | [123,127] |
| Geometry and boundary modelling | Flexibility to represent irregular geometries, mixer internals, and complex boundary conditions. | [109] |
| Virtual prototyping and parametric studies | Enables systematic evaluation of design variations, operating conditions, and material properties. | [124] |
| Process visualization | Provides advanced visualization of flow fields, stress maps, and particle trajectories for performance diagnosis and optimization. | [125] |
| Expanded applications | Supports modelling of breakage, attrition, agglomeration, and coating processes beyond simple mixing. | [128] |
| Computational cost | DEM requires tracking millions of particles with small time steps → high memory and CPU demand; industrial-scale simulations remain challenging. | [21,74,92,132,133] |
| Simplifications and scaling | Often relies on spherical particles, reduced counts, or scaled-down mixers → may reduce accuracy and generalizability. | [5,134] |
| Contact model limitations | Uses empirical contact laws (friction, restitution, stiffness, cohesion) that are difficult to measure and calibrate accurately. | [14,27,94] |
| Parameter calibration | Requires iterative, multi-parameter tuning; influenced by particle variability, environmental conditions, and lack of standard protocols. | [94,129,130,131] |
| Fluid-phase coupling | DEM alone cannot capture fluid dynamics; DEM–CFD or DEM–FEM coupling needed for multiphase systems, but increases cost/complexity. | [21] |
| Shape modelling | Advanced models (clumped spheres, polyhedral, superquadric, voxel/mesh) improve realism but raise computational demands. | [24,134,136] |
| Cohesive forces | Cohesion models (JKR, liquid bridge, adhesive laws) capture van der Waals, capillary, or electrostatic effects but add complexity and calibration challenges. | [137,138] |
| Research Area | DEM Advantages/Focus | Comparison/Appropriate Scenarios | References |
|---|---|---|---|
| Computational efficiency and scalability | Advanced algorithms (parallelization, GPU acceleration, adaptive resolution) enable larger particle simulations | Hybrid methods can reduce cost in less critical regions | [5,34,92,139,144,145,146] |
| Particle shape and material modelling | Realistic particle geometries, friction, cohesion, deformability | CFD/FEM treat particles as continuum; less detail | [5,24,99,134,140] |
| Multi-physics coupling | Integration with CFD, FEM, LBM, PBM, thermal/chemical models | Hybrid models capture coupled phenomena efficiently | [5,21,43,141,148,149,150,151,152,153] |
| Machine learning and data-driven methods | Parameter calibration, surrogate modelling, predictive acceleration | Applicable across all simulation types | [142,147] |
| Experimental validation and data acquisition | DEM provides detailed particle-scale insights to validate experiments | CFD/FEM rely more on macroscopic measurements | [21] |
| Scale-up strategies | Links lab-scale DEM results with full-scale mixer performance | Hybrid or continuum models used for large-scale predictions | [92,129,143,155] |
| Advanced contact models | Captures adhesion, cohesion, plastic/viscoelastic deformation | Continuum models cannot represent individual particle contacts | [43] |
| Hybrid and multiscale modelling | Combines DEM detail with continuum efficiency | Ideal for industrial-scale simulations | [145,151] |
| Industrial applications and design innovation | Virtual prototyping, optimization, troubleshooting, novel materials | Supports design decisions without extensive experiments | [92,99,154,155] |
| Digital twins and process monitoring | Real-time DEM coupling with sensor data for adaptive control | Enhances predictive maintenance and process optimization | [154] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pezo, M.; Pezo, L.; Lončar, B.; Kojić, P.; Jovanović, A.A. A Comprehensive Review of Discrete Element Method Studies of Granular Flow in Static Mixers. Processes 2025, 13, 3522. https://doi.org/10.3390/pr13113522
Pezo M, Pezo L, Lončar B, Kojić P, Jovanović AA. A Comprehensive Review of Discrete Element Method Studies of Granular Flow in Static Mixers. Processes. 2025; 13(11):3522. https://doi.org/10.3390/pr13113522
Chicago/Turabian StylePezo, Milada, Lato Pezo, Biljana Lončar, Predrag Kojić, and Aleksandar Aca Jovanović. 2025. "A Comprehensive Review of Discrete Element Method Studies of Granular Flow in Static Mixers" Processes 13, no. 11: 3522. https://doi.org/10.3390/pr13113522
APA StylePezo, M., Pezo, L., Lončar, B., Kojić, P., & Jovanović, A. A. (2025). A Comprehensive Review of Discrete Element Method Studies of Granular Flow in Static Mixers. Processes, 13(11), 3522. https://doi.org/10.3390/pr13113522








