Mechanism of Pressure Fluctuations and Flow Patterns Under Steady Operating Conditions of a Variable Speed Pump-Turbine
Abstract
1. Introduction
2. Numerical Methods
2.1. Computational Domain and Main Parameters of the Pump-Turbine
2.2. Three-Dimensional CFD Setup
3. The Simulation Results and Analysis
3.1. The Results in the Turbine Mode
3.1.1. Variations of Macro-Parameters in the Turbine Mode
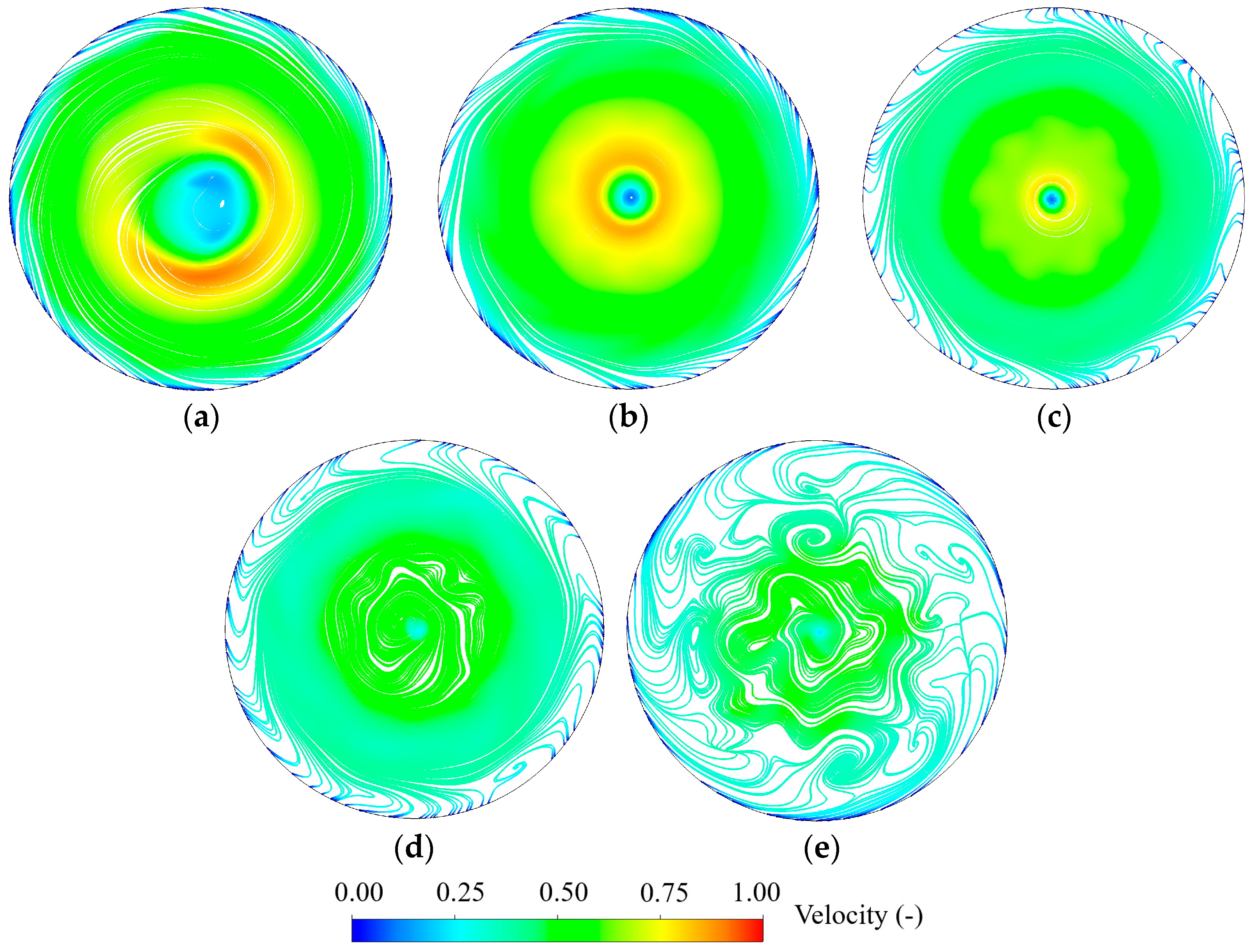
3.1.2. Evolutions of Flow Patterns in the Turbine Mode
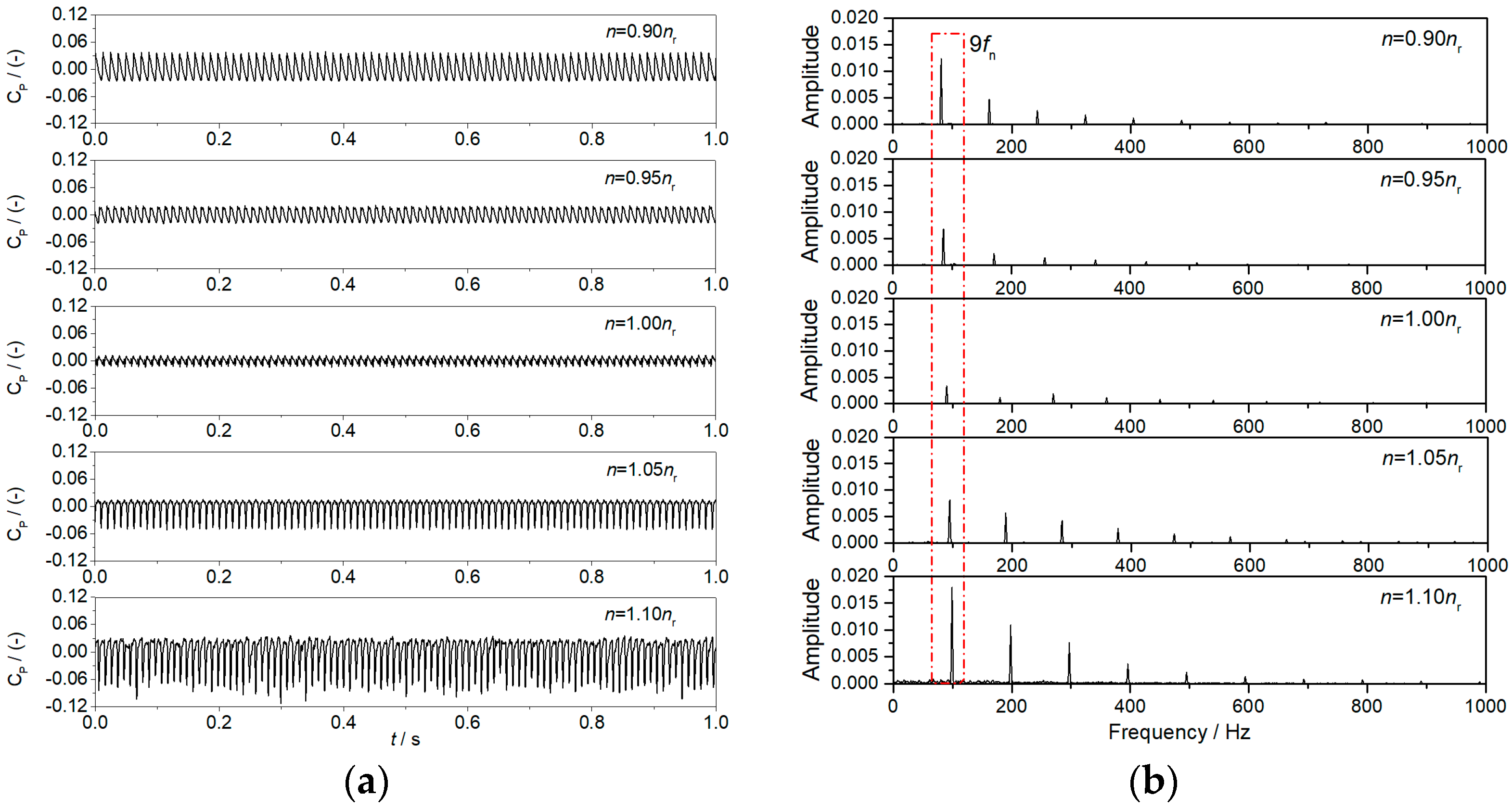
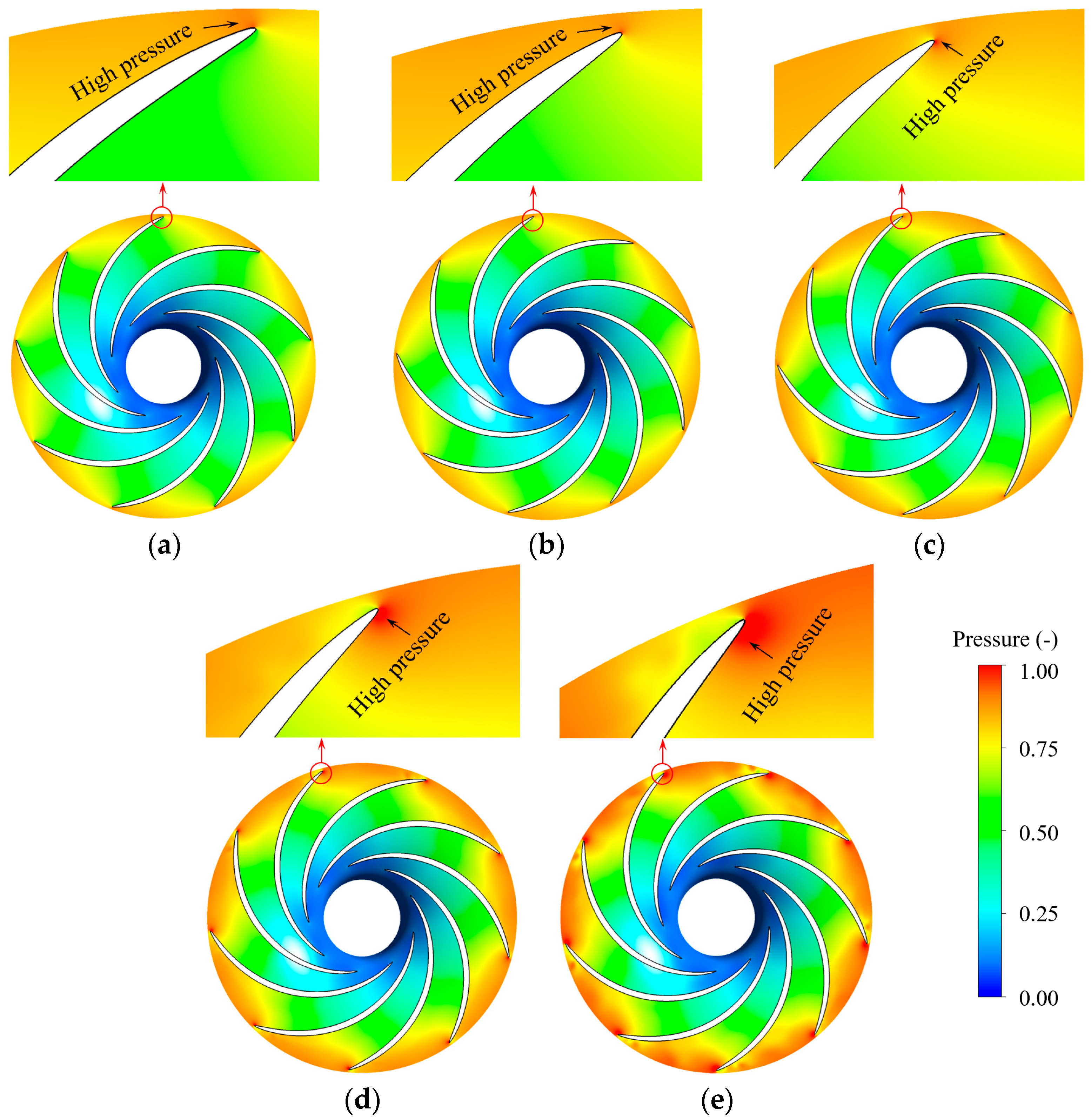
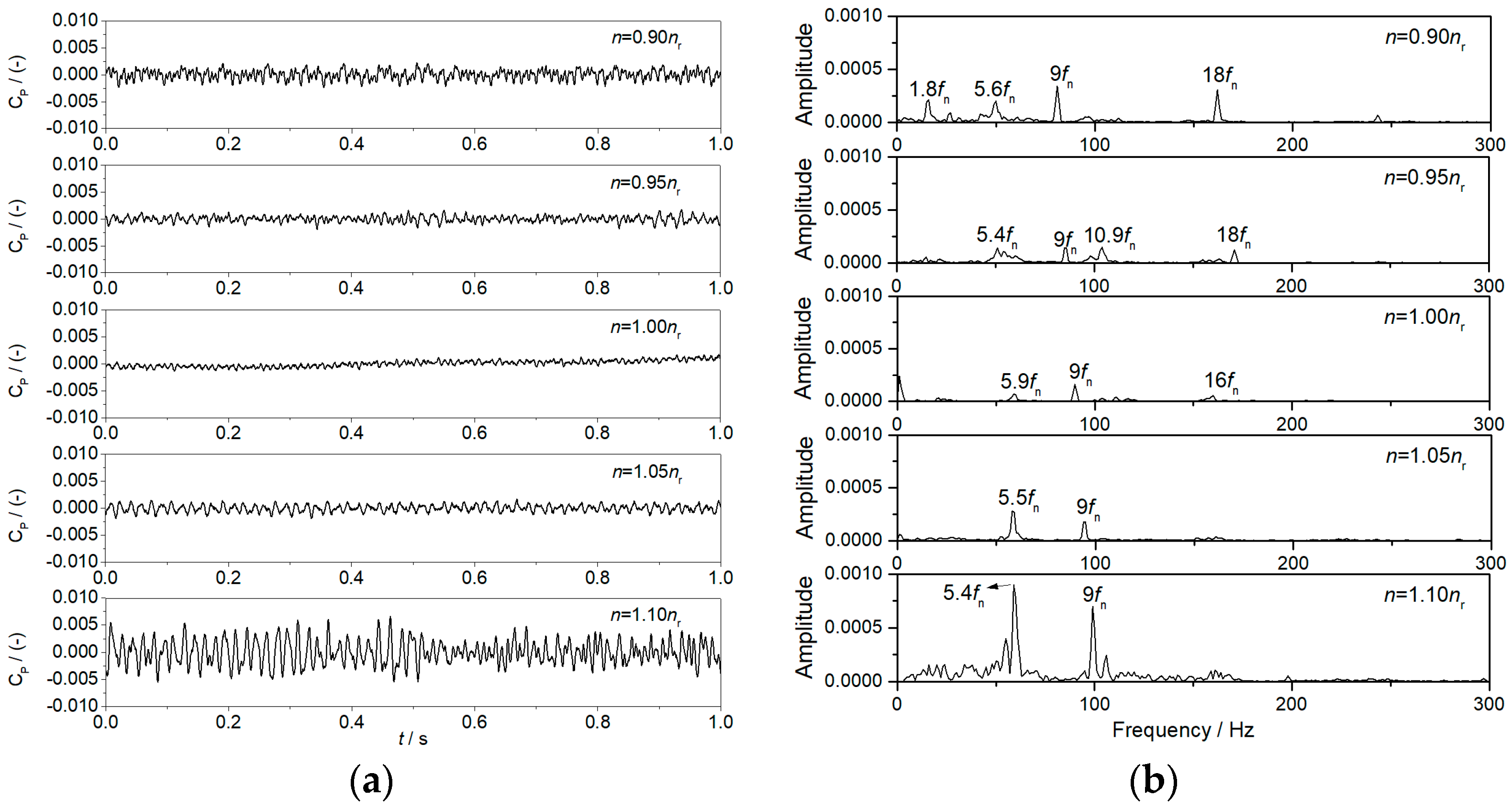
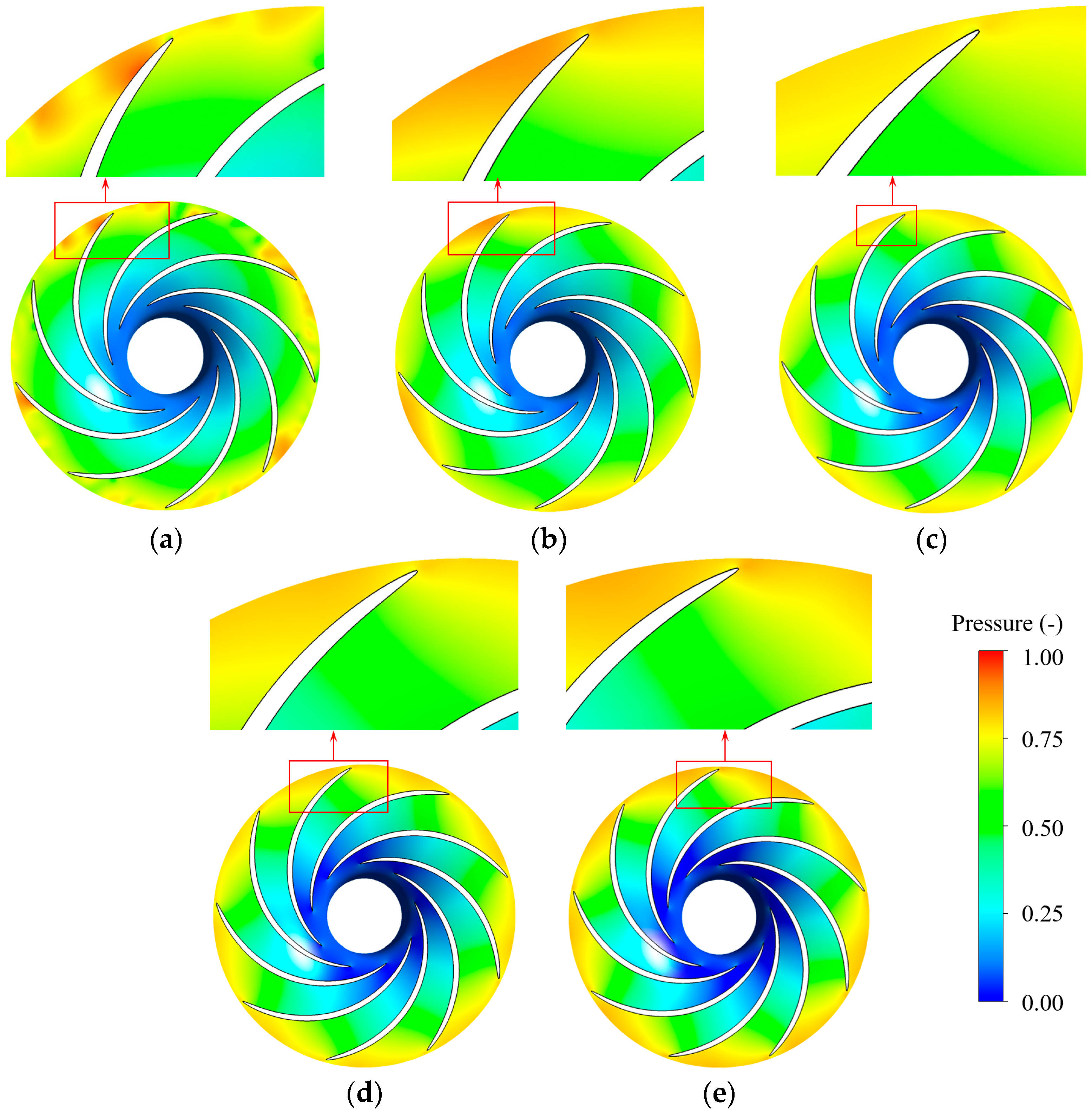
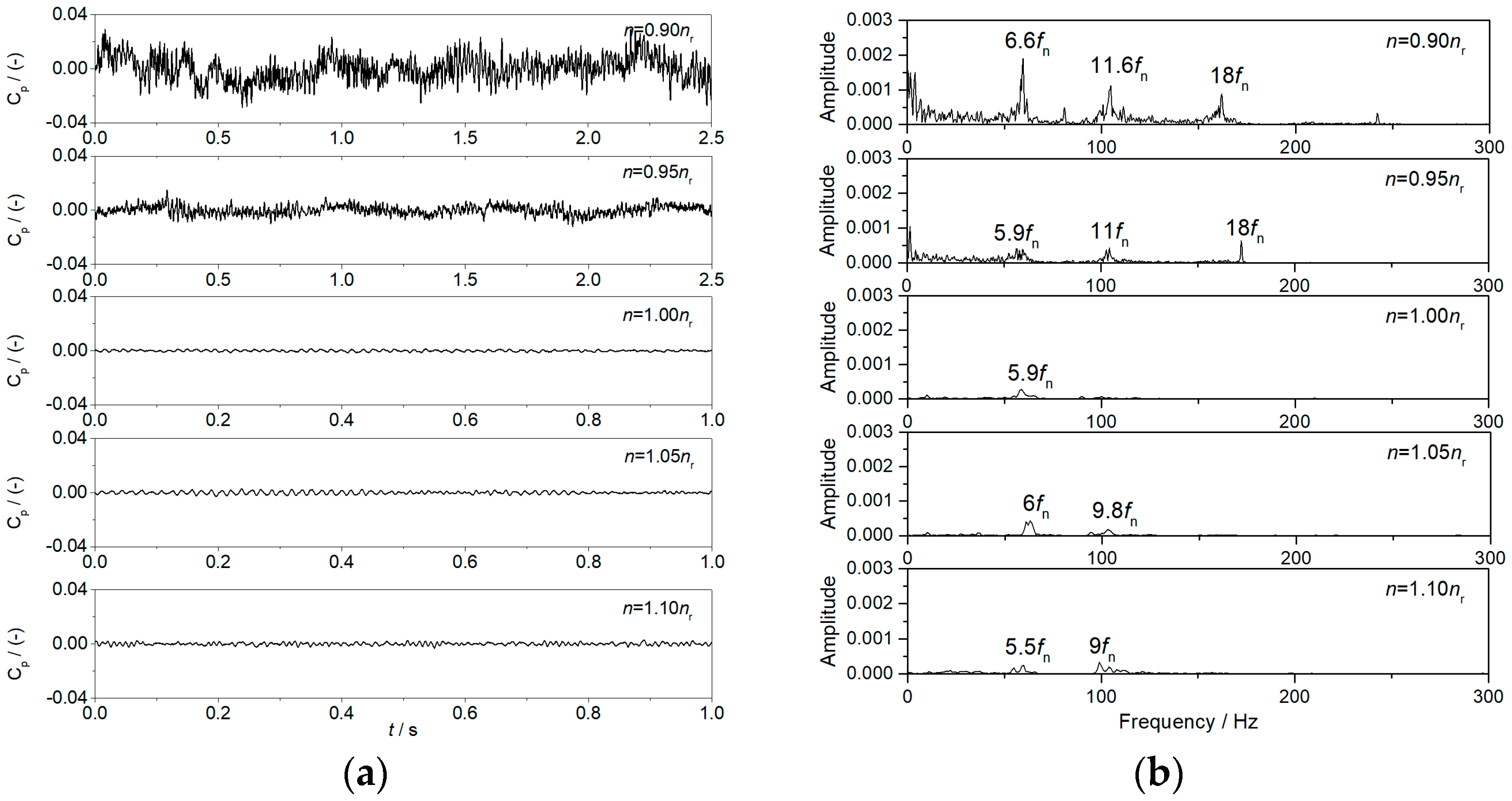
3.1.3. Pressure Pulsations and Detail Flow Patterns in the Turbine Mode
3.2. The Results in the Pump Mode
3.2.1. Variations of Macro-Parameters in the Pump Mode
3.2.2. Evolutions of Overall Flow Patterns in the Pump Mode
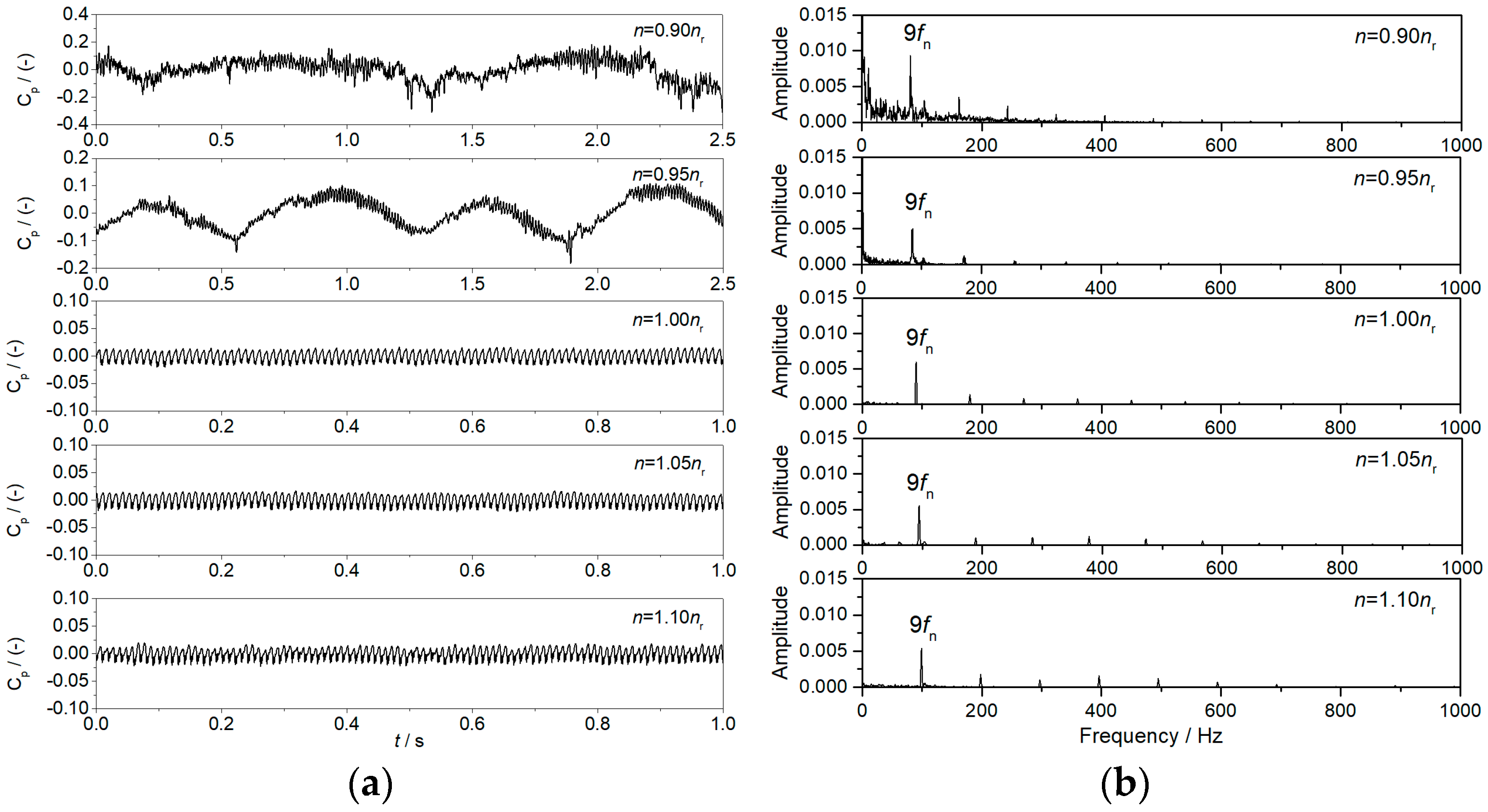
3.2.3. Pressure Pulsations and Detail Flow Patterns in the Pump Mode
4. Conclusions
- (1)
- The rotational speed changes in turbine mode have relatively small effects on output, discharge, and head, and these parameters decrease with the increase in the rotational speed, except that the head remains almost constant. The speed changes in pump mode have significant effects on input, discharge, and head, and these parameters increase with the increase in the rotational speed.
- (2)
- The rotational speed changes greatly affect the shape of the velocity triangle at the runner inlet and outlet, leading to different forms of vortex structures in the vane region, runner region, and draft tube, such as rotating stalls, low-velocity vortices, and backflows, accompanied by an amplitude increase in pressure pulsations.
- (3)
- This paper only analyzed the different rotational speed conditions near the optimal operating points; further investigations based on the combinations of different guide vane openings, head, output, or input can be conducted in future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xia, L. Mechanism of the S-Shaped Characteristics and the Flow-Induced Dynamic Instability of Pump-Turbines. Ph.D. Thesis, Wuhan University, Wuhan, China, 2017. (In Chinese). [Google Scholar]
- Wang, H.; Wang, J.; Gong, R.; Shang, C.; Li, D.; Wei, X. Investigations on Pressure Fluctuations in the S-Shaped Region of a Pump–Turbine. Energies 2021, 14, 6683. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, Z.; Han, S.; Zhu, B. Study on the Unsteady Flow Characteristics of a Pump Turbine in Pump Mode. Processes 2024, 12, 41. [Google Scholar] [CrossRef]
- Hu, D.; Cheng, Y.; Zhang, P.; Wang, X.; Ding, J.; Zhang, X. Distribution Features of Flow Patterns and Pressure Pulsations of Pump-Turbine in Five Operating Modes on the Four-Quadrant Plane. Front. Energy Res. 2022, 10, 880293. [Google Scholar] [CrossRef]
- Yang, X.; Lian, J.; Zhang, Z.; Zeng, Y. Theoretical Analysis of the Attenuation Characteristics of High-Frequency Pressure Vibration in Pumped Storage Power Station. J. Energy Storage 2023, 72, 108341. [Google Scholar] [CrossRef]
- Iliev, I.; Trivedi, C.; Dahlhaug, O.G. Variable-Speed Operation of Francis Turbines: A Review of the Perspectives and Challenges. Renew. Sustain. Energy Rev. 2019, 103, 109–121. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, J.; Dong, X.; Chen, M.; Peng, Y.; Yang, J. No-load Characteristics and Variable Speed Evolution of Doubly-fed Pumped Storage Unit Based on Dynamic Experiment Platform. Zhongguo Dianji Gong-Cheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2022, 42, 7439–7450. (In Chinese) [Google Scholar] [CrossRef]
- Kou, P.; Zhu, G. Simulation Study of Variable Speed Hydraulic Turbine Operation in Load Adjusting Conditions. Shuili Fadian Xuebao/J. Hydroelectr. Eng. 2022, 41, 87–97. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, T.; Wang, H.; Qin, D. Features of Pump Condition Selection for Variable Speed Pump-Turbine. Large Electr. Mach. Hydraul. Turbine 2020, 2, 65–69. (In Chinese) [Google Scholar]
- Rode, B.R.; Kumar, A. Unstable Pressure Fluctuations in the Vaneless Space of High-Head Reversible Pump-Turbines—A Systematic Review. J. Energy Storage 2023, 72, 108397. [Google Scholar] [CrossRef]
- Hasmatuchi, V.; Farhat, M.; Roth, S.; Botero, F.; Avellan, F. Experimental Evidence of Rotating Stall in a Pump-Turbine at off-Design Conditions in Generating Mode. J. Fluids Eng. Trans. ASME 2011, 133, 051104. [Google Scholar] [CrossRef]
- Liu, D.M.; Ma, L.B.; Li, N.; Zhao, Y.Z.; Cheng, H. Experimental Research on Flow Field of High Head Pump Turbine Based on PIV Test. IOP Conf. Ser. Earth Environ. Sci. 2021, 627, 012016. [Google Scholar] [CrossRef]
- Sun, H.; Xiao, R.; Wang, F.; Xiao, Y.; Liu, W. Analysis of the Pump-Turbine s Characteristics Using the Detached Eddy Simulation Method. Chin. J. Mech. Eng. 2015, 28, 115–122. [Google Scholar] [CrossRef]
- Xia, L.; Cheng, Y.; You, J.; Zhang, X.; Yang, J.; Qian, Z. Mechanism of the S-Shaped Characteristics and the Runaway Instability of Pump-Turbines. J. Fluids Eng. Trans. ASME 2017, 139, 031101. [Google Scholar] [CrossRef]
- Xiao, W.; Gui, Z.; Lu, Z.; Xiao, R.; Tao, R. Pressure Pulsation of Pump Turbine at Runaway Condition Based on Hilbert Huang Transform. Front. Energy Res. 2024, 12, 1344676. [Google Scholar] [CrossRef]
- Kirschner, O.; Ruprecht, A.; Göde, E.; Riedelbauch, S. Dynamic Runner Forces and Pressure Fluctuations on the Draft Tube Wall of a Model Pump-Turbine. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 082022. [Google Scholar] [CrossRef]
- Liu, D.M.; Zhao, Y.Z.; Zuo, Z.G. Experimental Research on Flow Field in the Draft Tube of Pump Turbines Based on LDV. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 072030. [Google Scholar] [CrossRef]
- Pang, S.; Zhu, B.; Shen, Y.; Chen, Z. Study on Cavitating Vortex Rope Characteristics of Reversible Pump-Turbine under Part Load Turbine Condition. Phys. Fluids 2023, 35, 085131. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Xiang, G.; Gong, R.; Wei, X.; Liu, Z. Unsteady Simulation and Analysis for Hump Characteristics of a Pump Turbine Model. Renew Energy 2015, 77, 32–42. [Google Scholar] [CrossRef]
- Xia, L.S.; Cheng, Y.G.; Zhang, X.X.; Yang, J.D. Numerical Analysis of Rotating Stall Instabilities of a Pump-Turbine in Pump Mode. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032020. [Google Scholar] [CrossRef]
- Lv, Y.; Li, S.; Wang, Z.; Zhou, L. Study on Pump Mode Cavitation Characteristic of Variable Speed Pump Turbine. Phys. Fluids 2023, 35, 065111. [Google Scholar] [CrossRef]
- Shang, L.; Cao, J.; Jia, X.; Yang, S.; Li, S.; Wang, L.; Wang, Z.; Liu, X. Effect of Rotational Speed on Pressure Pulsation Characteristics of Variable-Speed Pump Turbine Unit in Turbine Mode. Water 2023, 15, 609. [Google Scholar] [CrossRef]
- Rode, B.R.; Kumar, A.; Segoufin, C.; Laurant, Y. Numerical Study of Pressure Fluctuation in Vaneless Space of Variable Speed Reversible Pump-Turbine in Turbine Mode at Maximum Head. IOP Conf. Ser. Earth Environ. Sci. 2024, 1411, 012028. [Google Scholar] [CrossRef]
- Shang, L.; Cao, J.; Wang, Z.; Liu, X. Hydraulic Characterization of Variable-Speed Pump Turbine under Typical Pumping Modes. Processes 2023, 11, 2903. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Yu, S.; Li, S. Research on the Flow Characteristics in the Gap of a Variable-Speed Pump-Turbine in Pump Mode. Processes 2024, 12, 1424. [Google Scholar] [CrossRef]
- Shi, G.; Li, B.; Xiao, Y.; Tang, M.; Yang, X. Effect of Speed Linear Decrease on Internal Flow Characteristics and Pressure Pulsations of Variable-Speed Pump Turbine in Turbine Mode. J. Mar. Sci. Eng. 2024, 12, 2243. [Google Scholar] [CrossRef]
- Luo, X.; Chen, M.; Zhu, G.; Feng, J. Transient Characteristics Analysis in Variable-Speed Process of Pump-Turbine Based on Rothalpy Change and Vortex Method. Sustain. Energy Technol. Assess. 2025, 76, 104310. [Google Scholar] [CrossRef]
- Qin, Y.; Li, D.; Wang, H.; Liu, Z.; Wei, X.; Wang, X. Multi-Objective Optimization Design on High Pressure Side of a Pump-Turbine Runner with High Efficiency. Renew. Energy 2022, 190, 103–120. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, Y.; Xia, L.; Meng, W.; Liu, K.; Zhang, X. Evolutions of Flow Patterns and Pressure Fluctuations in a Prototype Pump-Turbine during the Runaway Transient Process after Pump-Trip. Renew. Energy 2020, 152, 1149–1159. [Google Scholar] [CrossRef]
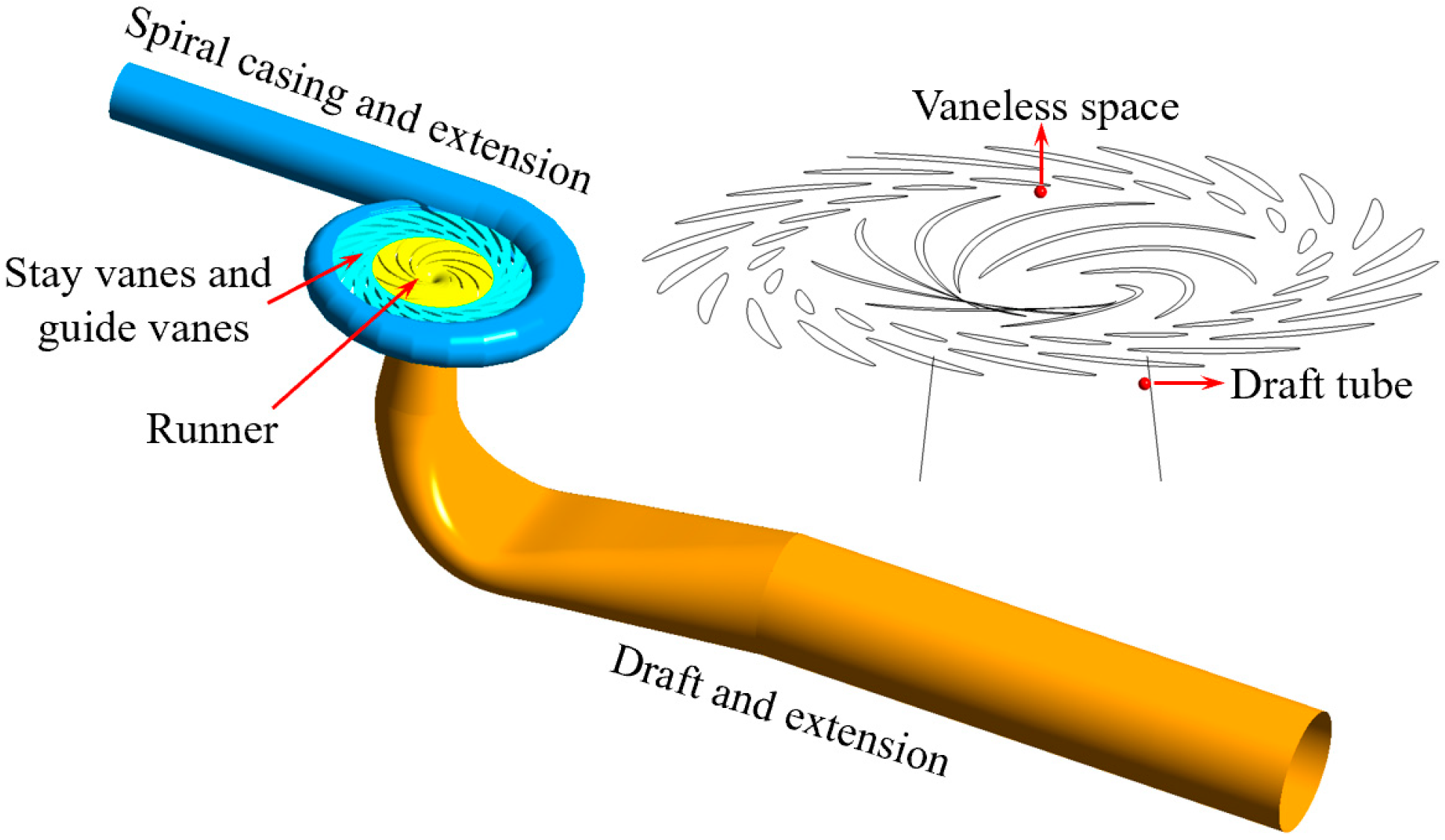
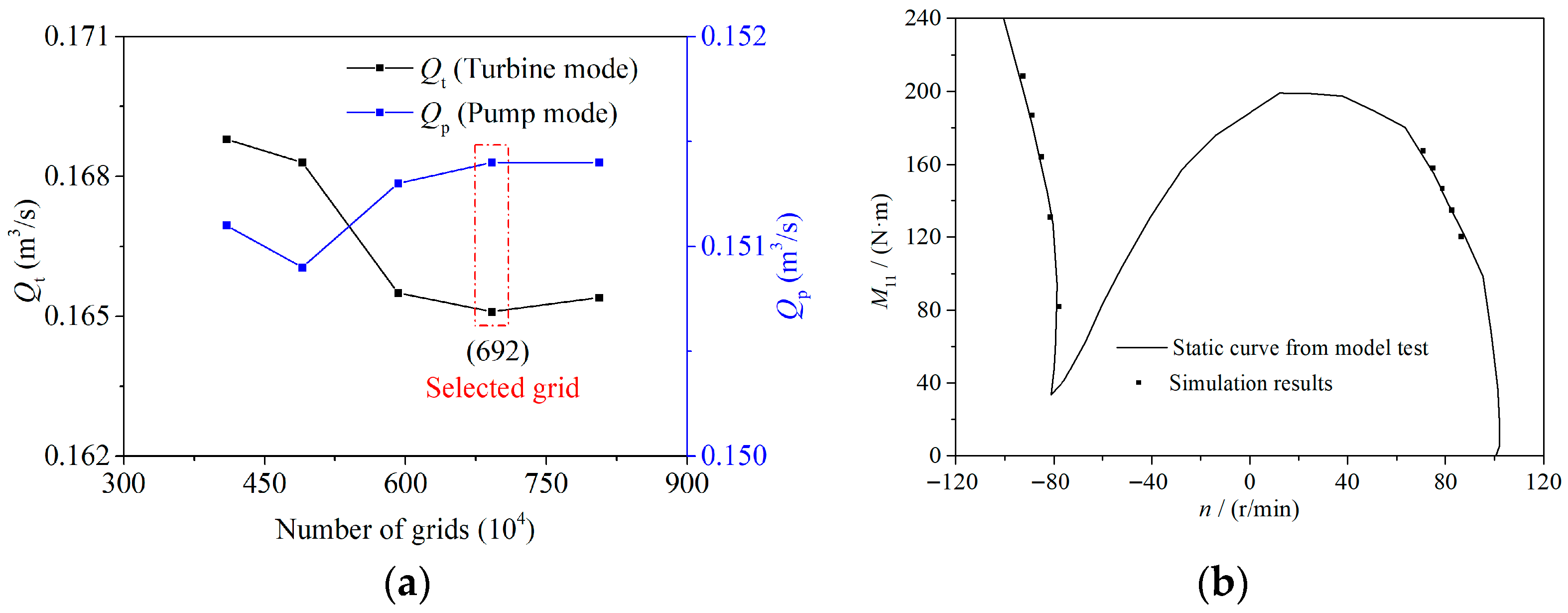




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| The runner inlet diameter D1 (m) | 0.54 | The number of runner blades zb | 9 |
| The runner outlet diameter D2 (m) | 0.25 | The number of guide vanes ngv | 22 |
| The rated speed ω0 (rpm) | 600 | The number of stay vanes nsv | 22 |
| Cases | ω (rad/s) | T (N·m) | N (N·m/s) | Q (m3/s) | H (m) | η (-) |
|---|---|---|---|---|---|---|
| Case-T-0.90 nr | 56.55 | 449 | 25,390 | 0.173 | 16.95 | 88.42% |
| Case-T-0.95 nr | 59.69 | 424 | 25,309 | 0.170 | 16.95 | 89.69% |
| Case-T-1.00 nr | 62.83 | 394 | 24,756 | 0.165 | 16.95 | 90.39% |
| Case-T-1.05 nr | 65.97 | 362 | 23,882 | 0.160 | 16.95 | 89.93% |
| Case-T-1.10 nr | 69.12 | 323 | 22,324 | 0.154 | 16.95 | 87.34% |
| Cases | n (rad/s) | T (N·m) | N (N·m/s) | Q (m3/s) | H (m) | η (-) |
|---|---|---|---|---|---|---|
| Case-P-0.90 nr | 56.55 | 184 | 10,405 | 0.044 | 14.12 | 58.47% |
| Case-P-0.95 nr | 59.69 | 297 | 17,728 | 0.110 | 14.32 | 87.01% |
| Case-P-1.00 nr | 62.83 | 377 | 23,688 | 0.151 | 14.52 | 90.64% |
| Case-P-1.05 nr | 65.97 | 434 | 28,632 | 0.177 | 14.68 | 89.86% |
| Case-P-1.10 nr | 69.12 | 489 | 33,797 | 0.201 | 14.84 | 86.42% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Cao, C.; Fang, J.; Zhang, B.; Li, C.; Hou, X. Mechanism of Pressure Fluctuations and Flow Patterns Under Steady Operating Conditions of a Variable Speed Pump-Turbine. Processes 2025, 13, 3511. https://doi.org/10.3390/pr13113511
Yang Z, Cao C, Fang J, Zhang B, Li C, Hou X. Mechanism of Pressure Fluctuations and Flow Patterns Under Steady Operating Conditions of a Variable Speed Pump-Turbine. Processes. 2025; 13(11):3511. https://doi.org/10.3390/pr13113511
Chicago/Turabian StyleYang, Zhiyan, Chunjian Cao, Jie Fang, Baoyong Zhang, Chengjun Li, and Xiaoxia Hou. 2025. "Mechanism of Pressure Fluctuations and Flow Patterns Under Steady Operating Conditions of a Variable Speed Pump-Turbine" Processes 13, no. 11: 3511. https://doi.org/10.3390/pr13113511
APA StyleYang, Z., Cao, C., Fang, J., Zhang, B., Li, C., & Hou, X. (2025). Mechanism of Pressure Fluctuations and Flow Patterns Under Steady Operating Conditions of a Variable Speed Pump-Turbine. Processes, 13(11), 3511. https://doi.org/10.3390/pr13113511





