Modeling Transient Vaporous Cavitating Flow in Pipelines by a Two-Phase Homogeneous Flow Model
Abstract
1. Introduction
2. Mathematical Model
2.1. Governing Equations
2.2. Boundary Conditions
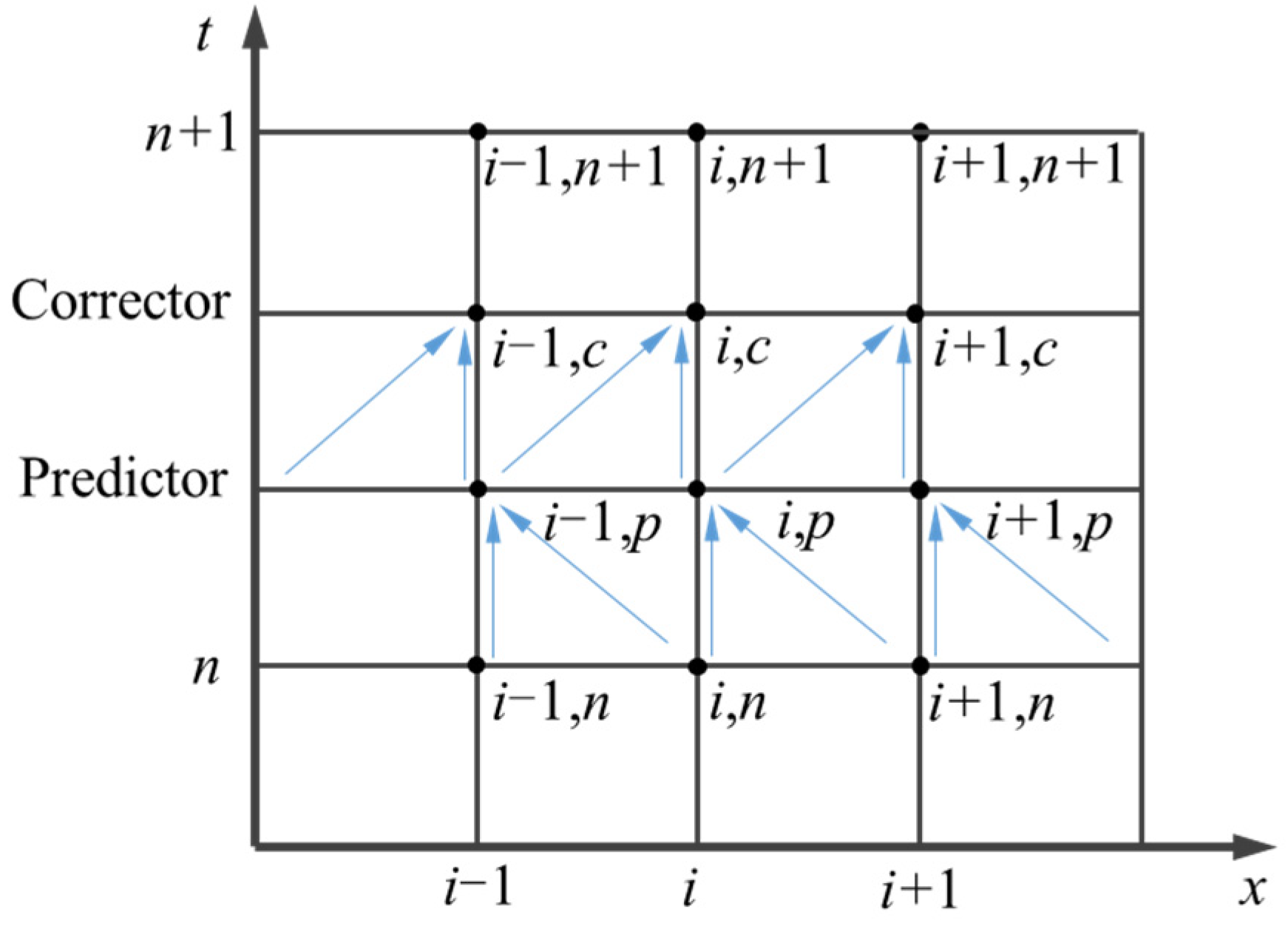
3. Numerical Scheme
4. Results and Discussion
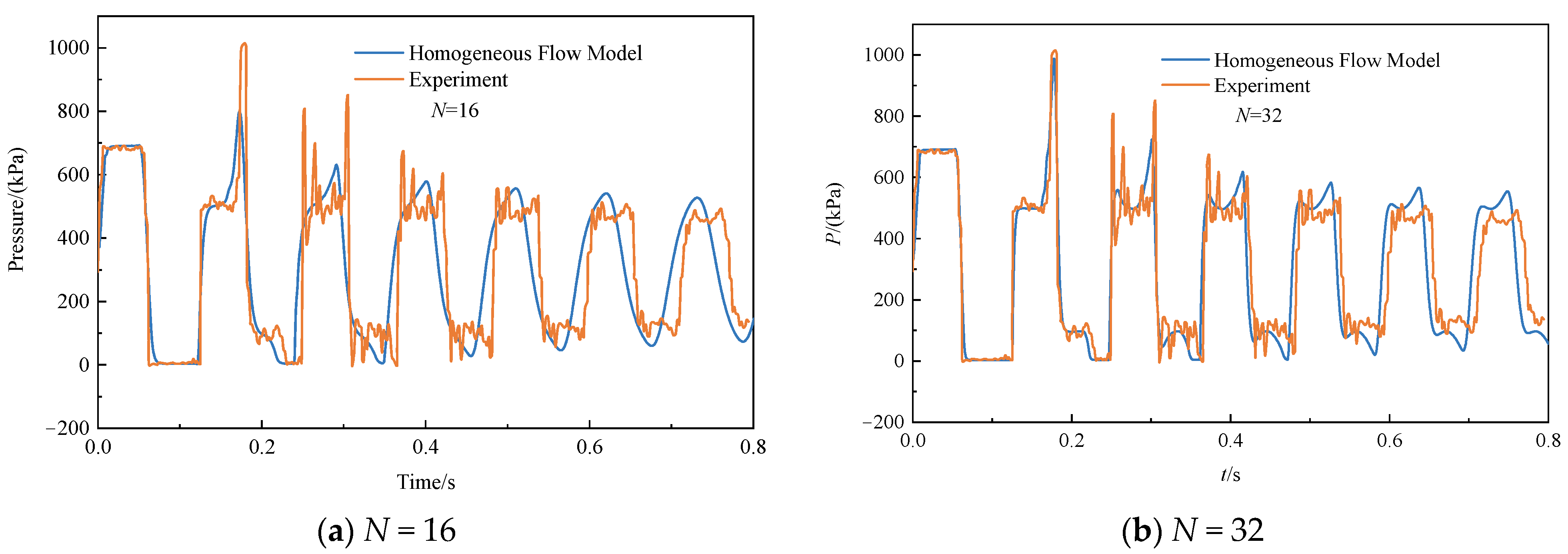
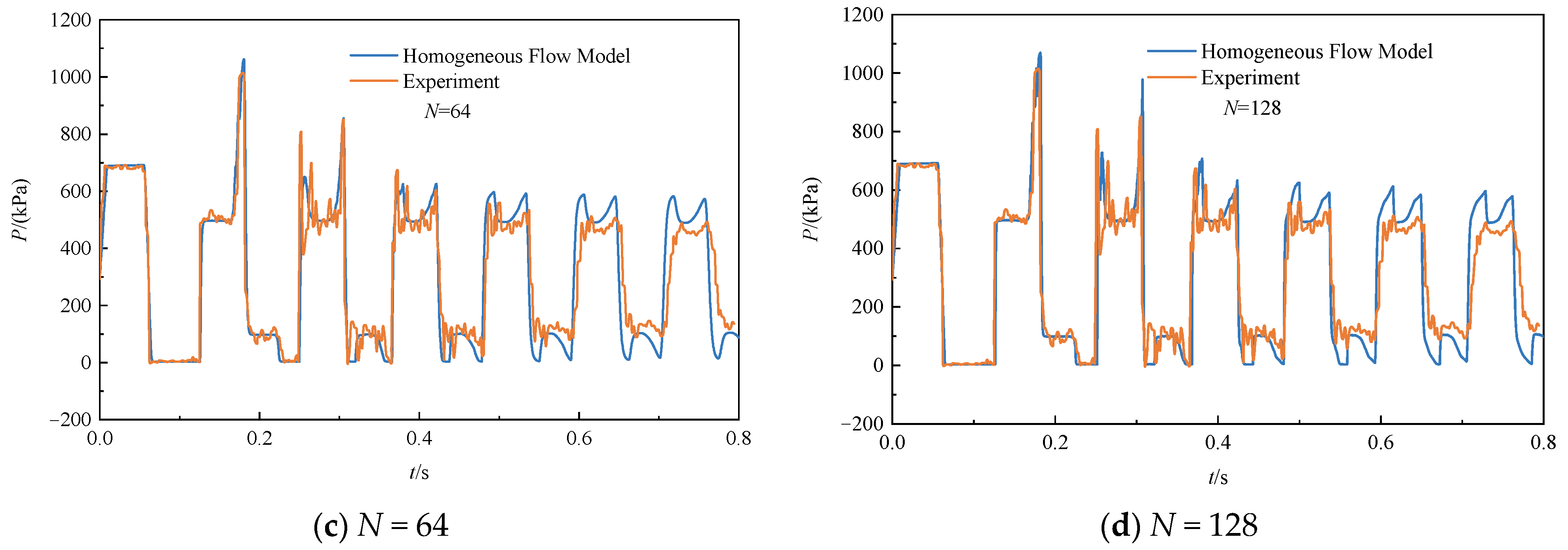
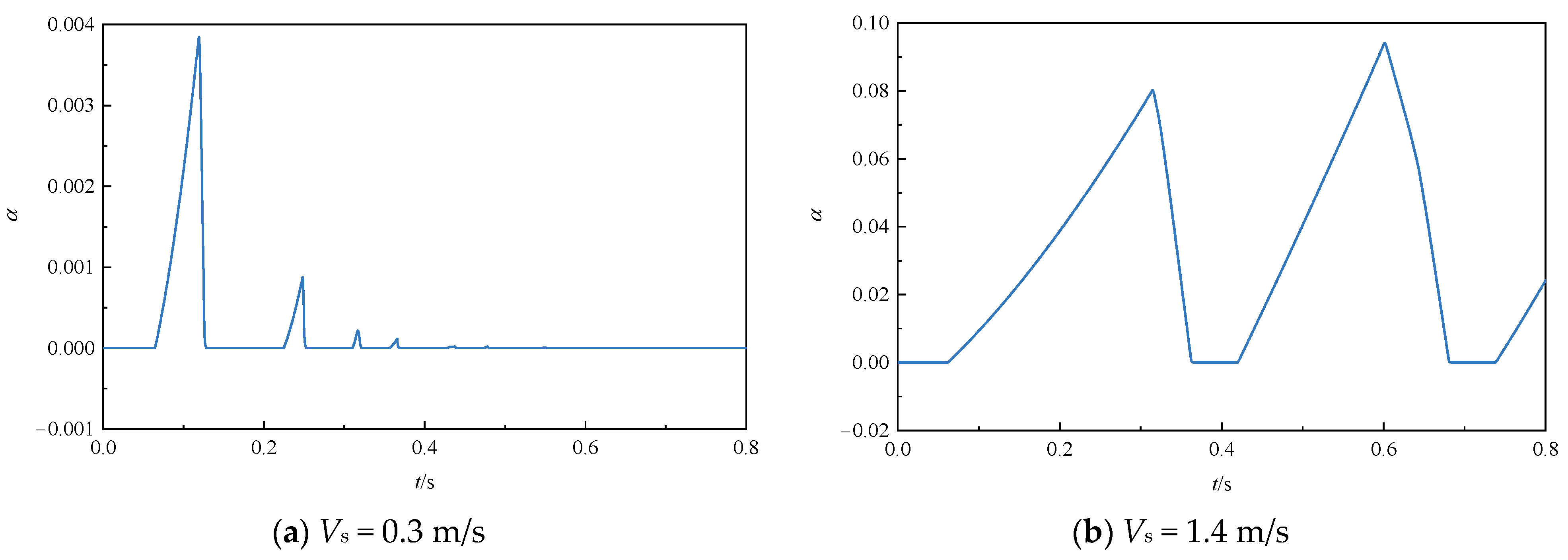
4.1. Comparison with Experimental Results from Bergant
4.2. Comparison with Experimental Results from Sanada
5. Conclusions
- The proposed model is a reliable approach for predicting transient cavitating flow in pipelines. For example, when the steady flow’s velocity is 1.4 m/s for Bergant’s experiment, the maximum pressure peaks predicted using the homogeneous flow model and measured experimentally are 1071 kPa and 1015 kPa, respectively.
- Compared to the classical model, the proposed model is capable of directly calculating the vapor volume fraction in the pipeline.
- The proposed model is sensitive to the initial vapor volume fraction, and this study suggests that the initial vapor volume fraction is 10−7 for Bergant’s and Sanada’s experiments.
- Comparisons of the calculated results with those of the DGCM show that the proposed model’s prediction capability is comparable to that of DGCM. For example, when the steady flow’s velocity is 0.3 m/s and 1.4 m/s for Bergant’s experiment, the maximum pressure peaks predicted by the homogeneous flow model and DGCM differ by 18 kPa and 100 kPa, respectively. The proposed model can be applied to the analysis of various operating conditions, such as valve closure and sudden pressure changes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Notation | |
| Pipe cross-sectional area; | |
| Maximum water hammer wave speed; | |
| ; | |
| Parameter related to the pipe support condition, 1; | |
| Inner diameter of the pipe; | |
| Pipe elasticity modulus; | |
| Pipe wall thickness; | |
| Darcy friction coefficient; | |
| Acceleration of gravity, 9.81 m/s2; | |
| Liquid elasticity modulus; | |
| Vapor elasticity modulus; | |
| Pressure; | |
| Saturated vapor pressure; | |
| Free gas partial pressure; | |
| Constant pressure generated by the tank; | |
| Pressure generated by the upstream tank at the steady flow; | |
| Constant value after the upstream tank pressure is reduced; | |
| Time; | |
| Valve closure time; | |
| Variation time of the upstream tank pressure; | |
| Fluid velocity; | |
| Length along the pipe axis; | |
| Vapor volume fraction; | |
| Constant vapor volume fraction; | |
| Pipe inclination angle; | |
| Liquid–vapor mixture density; | |
| Liquid density; | |
| Vapor density; | |
| Free gas volume; | |
| Volume of the pipeline segment; | |
| Time step; | |
| Space step. | |
| Subscripts | |
| l | Liquid; |
| v | Vapor; |
| s | Steady flow; |
| p | Prediction step; |
| c | Correction step; |
| 0 | Standard state. |
References
- Sadafi, M.; Riasi, A.; Nourbakhsh, S.A. Cavitating flow during water hammer using a generalized interface vaporous cavitation model. J. Fluids Struct. 2012, 34, 190–201. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993; Volume 1. [Google Scholar]
- Fu, Y.; Zhang, S. Comparison of multiple machine learning models for the regression of water hammer with column separation. Phys. Fluids 2025, 37, 023361. [Google Scholar] [CrossRef]
- Ivljanin, B.; Stevanovic, V.D.; Gajic, A. Water hammer with non-equilibrium gas release. Int. J. Press. Vessel. Pip. 2018, 165, 229–240. [Google Scholar] [CrossRef]
- Pezzinga, G. Gas release and solution as possible mechanism of oscillation damping in water hammer flow. Water 2023, 15, 1942. [Google Scholar] [CrossRef]
- Daude, F.; Tijsseling, A.; Galon, P. Numerical investigations of water-hammer with column-separation induced by vaporous cavitation using a one-dimensional finite-volume approach. J. Fluids Struct. 2018, 83, 91–118. [Google Scholar] [CrossRef]
- Wan, W.; Zhou, Y.; Geng, C.; He, B. Numerical modeling of cavity collapse water hammer in pipeline systems: Internal mechanisms and influential factors of transient flow and secondary pressure rise dynamics. Phys. Fluids 2024, 36, 087167. [Google Scholar] [CrossRef]
- Zhang, Q.; Tian, Z.; Lu, S.; Kang, H. Numerical simulation of water hammer in pipeline system using efficient wave tracking method. Water Resour. Manag. 2023, 37, 3053–3068. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R. Pipeline column separation flow regimes. J. Hydraul. Eng. 1999, 125, 835–848. [Google Scholar] [CrossRef]
- Saidani, A.; Fourar, A.; Massouh, F. Influence of temperature on transient flow with cavitation in copper pipe-rig. Model. Earth Syst. Environ. 2022, 8, 2449–2459. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H.; Bergant, A.; Tijsseling, A.S.; Liu, D.; Guo, S. Godunov-type solutions with discrete gas cavity model for transient cavitating pipe flow. J. Hydraul. Eng. 2018, 144, 04018017. [Google Scholar] [CrossRef]
- Sun, Q.; Hao, Y.; Cheng, P. Parametric analysis of discrete multiple-cavity models with the quasi-two-dimensional friction model for transient cavitating pipe flows. AQUA—Water Infrastruct. Ecosyst. Soc. 2022, 71, 355–372. [Google Scholar] [CrossRef]
- Pezzinga, G. MOC-Z Model of Transient Cavitating Flow in Viscoelastic Pipe. Water 2024, 16, 1610. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Bergant, A.; Kodura, A.; Kubrak, M.; Malesińska, A.; Bury, P.; Stosiak, M. Modeling transient pipe flow in plastic pipes with modified discrete bubble cavitation model. Energies 2021, 14, 6756. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M. Cavitation characteristics of shutoff valves in numerical modeling of transients in pipelines with column separation. J. Hydraul. Eng. 2015, 141, 04014077. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M. A new method for numerical prediction of liquid column separation accompanying hydraulic transients in pipelines. J. Fluids Eng. 2009, 131, 071302. [Google Scholar] [CrossRef]
- Soares, A.K.; Martins, N.M.; Covas, D.I. Transient vaporous cavitation in a horizontal copper pipe. J. Hydraul. Res. 2017, 55, 731–736. [Google Scholar] [CrossRef]
- Li, C.; He, J.; Jia, W.; Yang, F.; Ban, J.; Qiu, B. Modeling transient cavitating flow in large drop crude oil pipelines. J. Pet. Sci. Eng. 2023, 220, 111241. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R.; Tijsseling, A.S. Water hammer with column separation: A historical review. J. Fluids Struct. 2006, 22, 135–171. [Google Scholar] [CrossRef]
- Simpson, A.R.; Bergant, A. Numerical comparison of pipe-column-separation models. J. Hydraul. Eng. 1994, 120, 361–377. [Google Scholar] [CrossRef]
- Wylie, E.B. Simulation of vaporous and gaseous cavitation. J. Fluids Eng. 1984, 106, 307–311. [Google Scholar] [CrossRef]
- Bergant, A. Investigation of unsteady friction effects in transient two-phase pipe flow. J. Phys Conf. Ser. 2024, 2766, 012074. [Google Scholar] [CrossRef]
- Mousavifard, M.; Norooz, R. Numerical analysis of transient cavitating pipe flow by Quasi 2D and 1D models. J. Hydraul. Res. 2022, 60, 295–310. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, J.; Long, Z.; Peng, L.; Jiang, Y.; Cheng, W. Numerical Dissipation Compensation in Liquid Column Separation: An Improved DVCM Approach. Water 2025, 17, 805. [Google Scholar] [CrossRef]
- Qiu, B.; Wu, J.; He, J.; Chen, R.; Nie, Q.; Zhu, J.; Li, Y. Numerical simulation of water hammer in liquid hydrogen pipeline considering unsteady friction and cavitation. Int. J. Hydrogen Energy 2025, 180, 151771. [Google Scholar] [CrossRef]
- Shu, J.-J. Modelling vaporous cavitation on fluid transients. Int. J. Press. Vessels Pip. 2003, 80, 187–195. [Google Scholar] [CrossRef]
- Pezzinga, G. Second viscosity in transient cavitating pipe flows. J. Hydraul. Res. 2003, 41, 656–665. [Google Scholar] [CrossRef]
- Pezzinga, G.; Santoro, V. Unitary framework for hydraulic mathematical models of transient cavitation in pipes: Numerical analysis of 1D and 2D flow. J. Hydraul. Eng. 2017, 143, 04017053. [Google Scholar] [CrossRef]
- Hadj-Taieb, L.; Hadj-Taieb, E.; Thirriot, C. Numerical simulation of transient vaporous cavitating flow in horizontal pipelines. Int. J. Model. Simul. 2007, 27, 347–354. [Google Scholar] [CrossRef]
- Sumam, K.; Thampi, S.; Sajikumar, N. An alternate approach for modelling of transient vaporous cavitation. Int. J. Numer. Methods Eng. 2010, 63, 564–583. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Sanada, K.; Kitagawa, A.; Takenaka, T. A study on analytical methods by classification of column separations in a water pipeline. Trans. Japan Soc. Mech. Eng. 1990, 56, 585–593. [Google Scholar] [CrossRef]




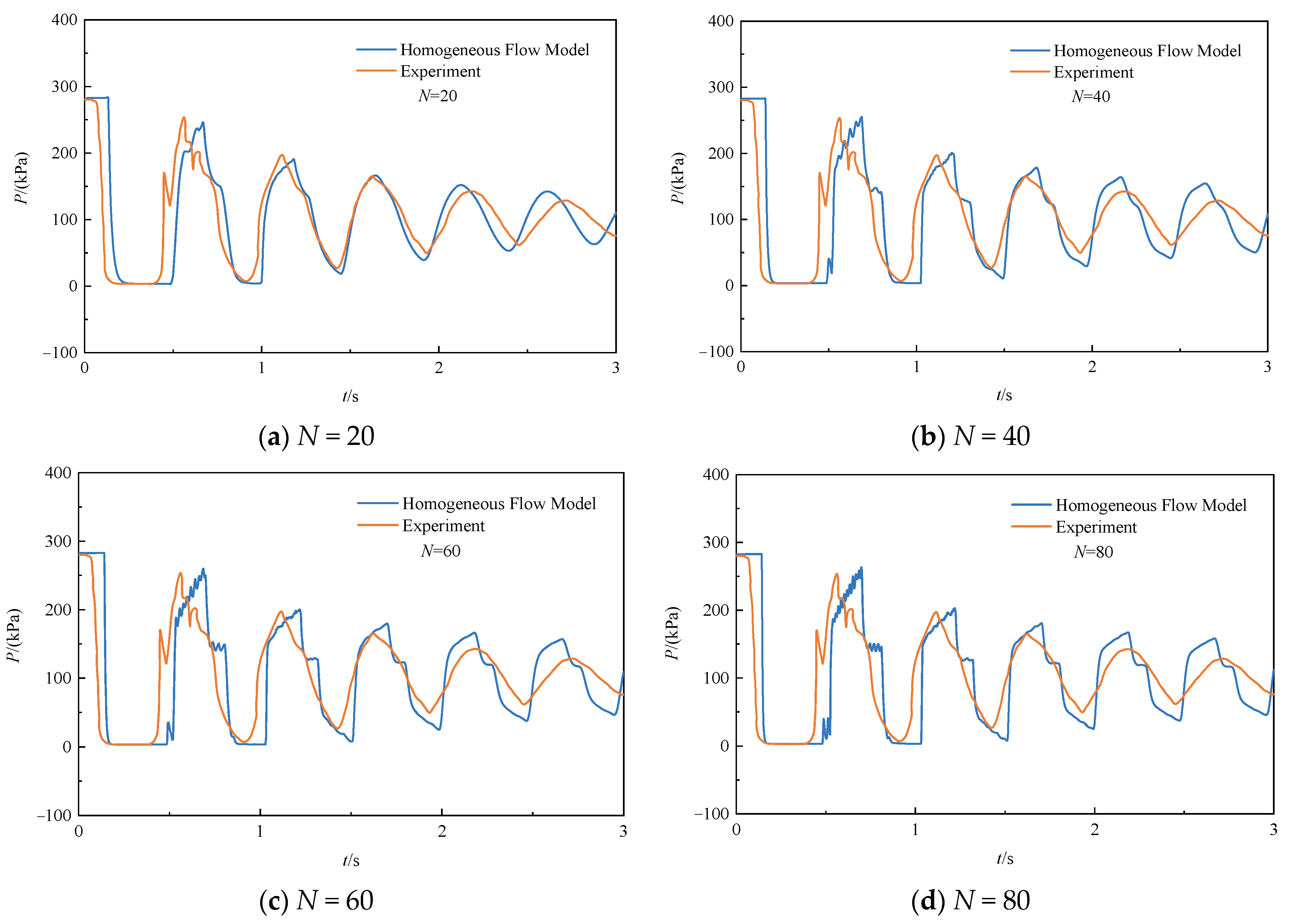
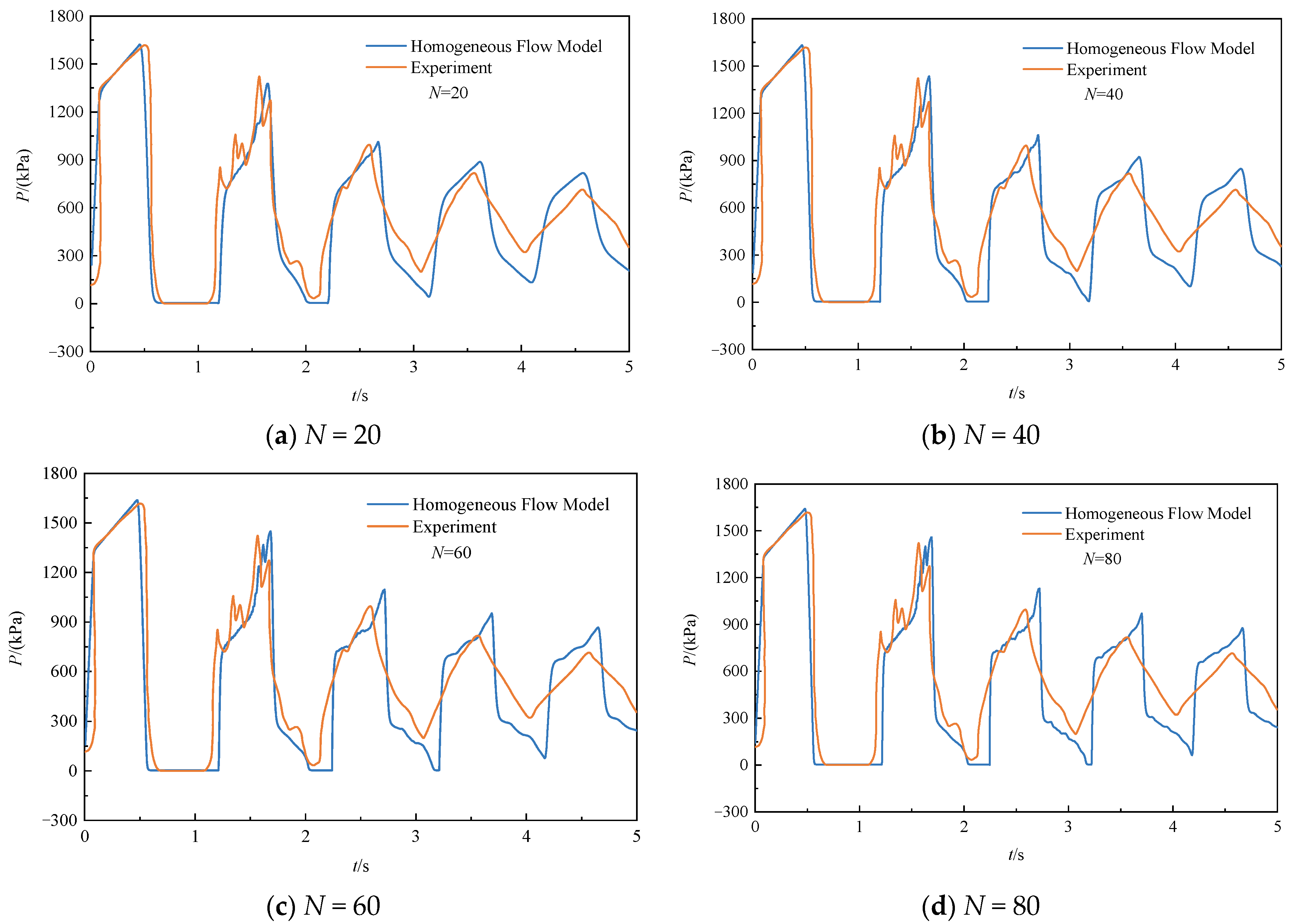
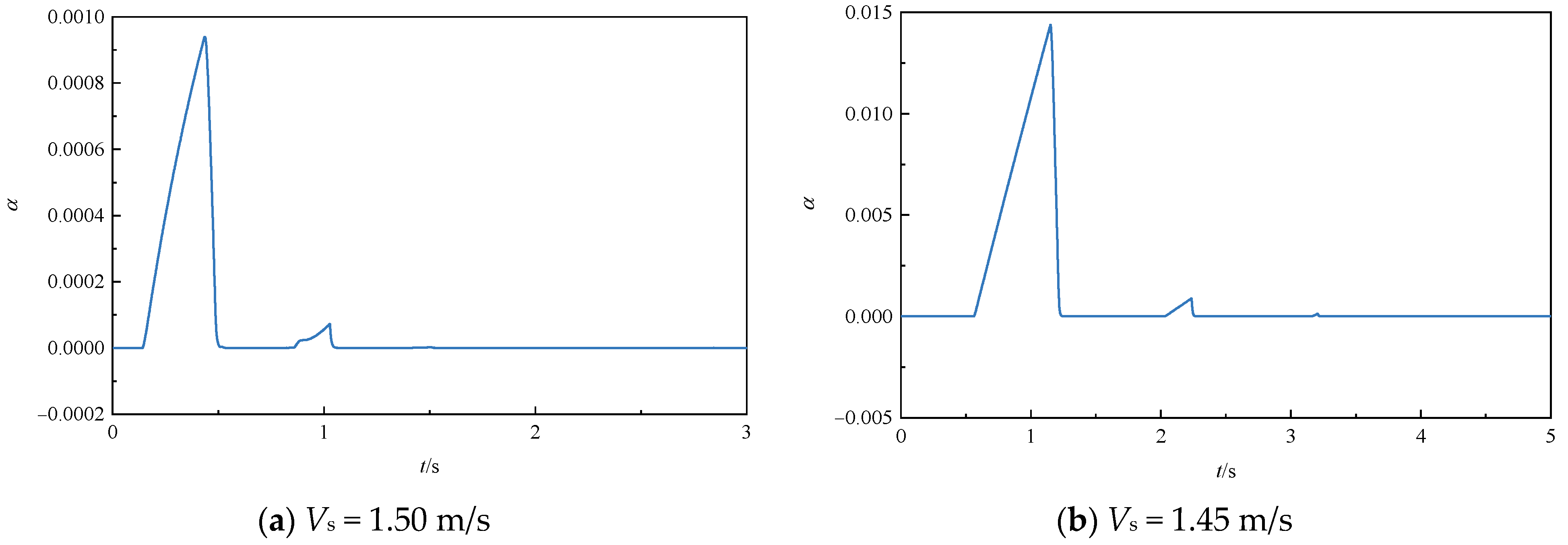
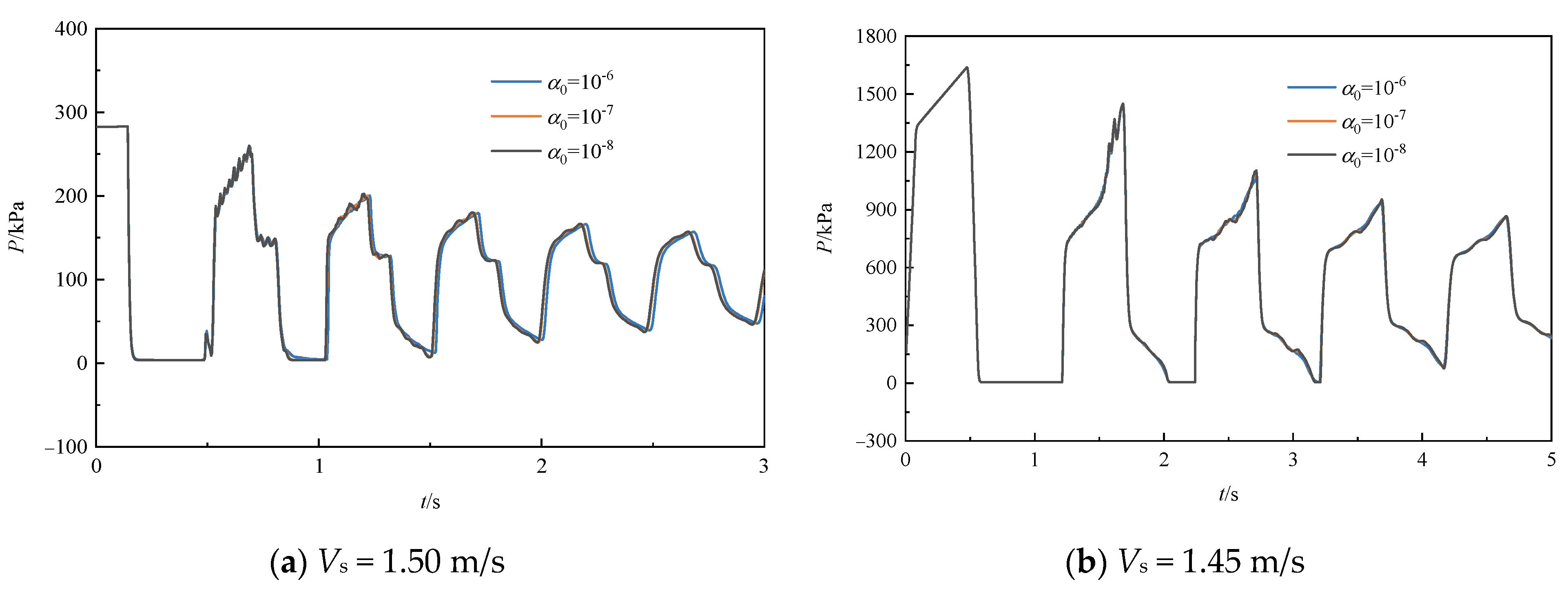

| Cavitation Type | Upstream Pressure (m) | Steady Velocity (m/s) |
|---|---|---|
| Moderate Cavitation | 22 | 0.3 |
| Severe Cavitation | 22 | 1.4 |
| Cavitation Type | Upstream Pressure (kPa) | Downstream Pressure (kPa) | Steady Velocity (m/s) |
|---|---|---|---|
| Midstream Cavitation | 558.971 | 98.065 | 1.50 |
| Downstream Cavitation | 490.325 | 98.065 | 1.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Li, C.; Guo, Y. Modeling Transient Vaporous Cavitating Flow in Pipelines by a Two-Phase Homogeneous Flow Model. Processes 2025, 13, 3510. https://doi.org/10.3390/pr13113510
He J, Li C, Guo Y. Modeling Transient Vaporous Cavitating Flow in Pipelines by a Two-Phase Homogeneous Flow Model. Processes. 2025; 13(11):3510. https://doi.org/10.3390/pr13113510
Chicago/Turabian StyleHe, Jie, Changjun Li, and Yuying Guo. 2025. "Modeling Transient Vaporous Cavitating Flow in Pipelines by a Two-Phase Homogeneous Flow Model" Processes 13, no. 11: 3510. https://doi.org/10.3390/pr13113510
APA StyleHe, J., Li, C., & Guo, Y. (2025). Modeling Transient Vaporous Cavitating Flow in Pipelines by a Two-Phase Homogeneous Flow Model. Processes, 13(11), 3510. https://doi.org/10.3390/pr13113510





