Multi-Objective Rolling Linear-Programming-Model-Based Predictive Control for V2G-Enabled Electric Vehicle Scheduling in Industrial Park Microgrids

Abstract

With the rapid growth of electricity demand in industrial parks and the increasing penetration of renewable energy, vehicle-to-grid (V2G) technology has become an important enabler for mitigating grid stress while improving charging economy. This paper proposes a multi-objective rolling linear-programming-model-based predictive control (LP-MPC) method for coordinated electric vehicle (EV) scheduling in industrial park microgrids. The model explicitly considers transformer capacity limits, EV state-of-charge (SOC) dynamics, bidirectional charging/discharging constraints, and photovoltaic (PV) generation uncertainty. By solving a linear programming problem in a receding horizon framework, the approach simultaneously achieves load peak shaving, valley filling, and EV revenue maximization with real-time feasibility. A simulation study involving 300 EVs, 100 kW PV, and a 1000 kW transformer over 24 h with 5-min intervals demonstrates that the proposed LP-MPC outperforms greedy and heuristic load-leveling strategies in peak load reduction, load variance minimization, and charging cost savings while meeting all SOC terminal requirements. These results validate the effectiveness, robustness, and economic benefits of the proposed method for V2G-enabled industrial park microgrids.

1. Introduction

With the ongoing global energy transition and the increasing penetration of renewable energy sources, the optimal scheduling of electric power systems has become an important research point in both academic research and engineering practice [1,2]. Industrial parks, as regions of concentrated high demand, exhibit large load fluctuations and high power densities, imposing more stringent requirements on the safe operation of transformers and distribution networks [3,4]. Meanwhile, the rapid proliferation of electric vehicles (EV) introduces both new challenges and opportunities for load management in industrial parks [5,6,7]. EV charging loads are highly controllable and dispatchable, and their inherent energy-storage capability enables participation in peak–valley regulation and the provision of ancillary services [8,9]. Consequently, EV participation in vehicle-to-grid (V2G) scheduling can simultaneously achieve peak shaving and valley filling, improve the return on EV investments, and reduce grid operating costs as well as equipment investment pressures, making it a key direction for smart-grid research in industrial parks [10,11,12].

To date, the research on EV scheduling has primarily focused on centralized optimization and heuristic control methods [13]. Representative heuristic strategies include greedy control based on load thresholds and simple time-segmented charging–discharging schemes [14]. These approaches preliminarily balance the grid load by prioritizing charging during low-load periods and curtailing or discharging during high-load periods [15]. Studies have shown that such strategies are computationally simple and easy to deploy; however, they exhibit limitations. Greedy strategies only consider instantaneous load or price information and cannot coordinate global scheduling, which may result in elevated valley loads or unmet state-of-charge (SOC) constraints. What is more, greedy strategies’ response to load surges and peak periods is insufficient, making it difficult to guarantee charging completion rates and equipment safety [16]. Nonetheless, threshold-based greedy control remains widely adopted as a benchmark for comparison, providing a reference for more sophisticated optimization strategies.

To overcome the limitations of centralized heuristic approaches, the academic community has recently proposed various scheduling methods grounded in optimization theory and game theory [17,18]. Linear programming (LP), mixed-integer linear programming (MILP), and model predictive control (MPC) have been extensively applied to V2G scheduling [19,20]. MPC, in particular, employs rolling optimization and forecasts of load and photovoltaic generation to enable dynamic decision making that coordinates charging and discharging while ensuring grid security [21]. Empirical studies demonstrate that linear programming model predictive control (LP-MPC) strategies can significantly reduce peak loads, increase renewable energy accommodation, and partially guarantee SOC constraint satisfaction [22]. Furthermore, multi-objective MPC integrates peak load, grid fluctuation, and EV revenue into a single optimization framework, achieving comprehensive performance optimization through weighted objective functions [23,24]. Compared with traditional heuristics, MPC benefits from its ability to anticipate load trends and balance local and global objectives, offering superior scheduling flexibility and real-time capability [25].

On the other hand, game-theoretic approaches have garnered widespread attention in distributed EV scheduling [26,27]. By constructing Stackelberg games or Nash equilibrium models, EV users autonomously determine charging and discharging strategies in response to dynamic electricity prices or incentive mechanisms, while aggregators guide user behavior via price or reward signals to achieve load balancing [28]. These methods exhibit strong distributed characteristics, making them suitable for large-scale multi-user scenarios; they optimize overall grid performance while preserving user autonomy [29]. Nevertheless, practical applications still confront challenges such as communication delays, forecast errors, and complex solution procedures, leaving real-time performance and scalability to be further improved [30]. In this study, due to the fixed electricity prices provided by the aggregator, the advantages of conventional game-theoretic strategies cannot be fully realized. Consequently, we set the benchmark algorithm to a more practical heuristic load-leveling strategy, retaining the greedy algorithm as the baseline to demonstrate the performance improvement offered by LP-MPC in the industrial park context.

In recent years, electric vehicles have achieved a series of significant results in participating in V2G scheduling. Domestic and international studies show that in industrial-park environments, LP-MPC or MPC schemes incorporating SOC constraints and power limits can achieve peak-load reductions of 10% and load-variance reductions of approximately 15% while ensuring charging-completion rates of 90% for the vast majority of EV [31]. With respect to renewable-energy accommodation, EV participation in V2G charging and discharging can increase photovoltaic utilization by roughly 5% to 10% with the most pronounced gains occurring during periods of pronounced peak–valley load variation [32]. Moreover, for industrial parks subject to abrupt load changes, the integration of multi-step predictive MPC, rolling optimization, and SOC-violation penalty terms renders the dispatch algorithm more robust and markedly improves SOC compliance and system reliability [33]. These findings provide both theoretical foundations and practical references for intelligent dispatch and energy management in industrial parks.

Industrial-park microgrids face distinctive operational challenges due to their concentrated load structure and high penetration of renewable and electric-vehicle demand [34]. During peak periods, massive synchronized charging can lead to transformer overloading, voltage deviation, and the frequent on–off cycling of distribution equipment. Meanwhile, the intermittent nature of photovoltaic (PV) generation causes unbalanced renewable utilization and increased difficulty in maintaining real-time load-generation equilibrium. Traditional static scheduling or heuristic methods are often unable to handle these dynamic and coupled constraints within short decision intervals [35].

In summary, previous studies have demonstrated the potential of MPC in microgrid optimization but often face challenges in balancing real-time solvability and multi-objective coordination. To address this gap, the present work develops a rolling LP-MPC framework that integrates linear-programming efficiency with predictive control flexibility for industrial-park EV scheduling.

This study addresses the high-penetration integration of EV in industrial parks and proposes a rolling LP-MPC dispatch method that simultaneously considers grid and user objectives. The contributions are as follows:

(1)

Unification of global optimality and real-time capability: By linearizing the EV-scheduling problem and leveraging an efficient linear solver, the method achieves second-level rolling optimization over a 24-h horizon with 288 steps, overcoming the traditional trade-off between real-time performance and global optimality inherent in nonlinear MPC or heuristic algorithms.

(2)

Integration of centralized optimization and grouped coordination: A new framework that combines centralized LP-MPC with grouped power allocation is introduced. Under large-scale EV integration, this framework significantly reduces computational and communication burdens while guaranteeing precise SOC attainment for each EV group.

(3)

Multi-dimensional, V2G-oriented multi-objective optimization: A comprehensive performance index is designed, encompassing three grid-operation metrics—peak load, peak–valley difference, and load fluctuation—and two user-benefit metrics—EV charging cost and SOC completion rate. Extensive validation demonstrates the proposed method’s superiority over greedy and heuristic strategies, offering a readily generalizable solution for V2G dispatch in industrial parks.

The paper is organized as follows. Section 2 presents the modeling of the EV-V2G system for the industrial park. Section 3 details the design of the LP-MPC algorithm. Section 4 provides experimental simulations and comparisons with heuristic load-leveling and greedy algorithms. Section 5 concludes the paper and outlines directions for future research.

2. System Modeling and Problem Formulation

2.1. Microgrid Power Balance and Point of Common Coupling Constraints

Within the industrial park, the base load, distributed PV generation, and EV charging/discharging powers are all coupled at the point of common coupling (PCC). The corresponding power-balance equation is outlined below:

$$P_{\mathrm{grid}}(t)=P_{\mathrm{load}}(t)-P_{\mathrm{PV}}(t)+P_{\mathrm{EVagg}}(t)$$

(1)

where $P_{\mathrm{grid}}(t)$ denotes the power exchanged with the upstream grid with a positive value indicating power import. $P_{\mathrm{load}}(t)$ denotes the base-load power; $P_{\mathrm{PV}}(t)$ denotes the PV output; $P_{\mathrm{EVagg}}(t)$ denotes the net power of the EV aggregator, which is positive for discharging and negative for charging.

To ensure safe operation, the following constraint must be satisfied:

$$|P_{\mathrm{grid}}(t)|\le P_{\mathrm{trans}}$$

(2)

where $P_{\mathrm{trans}}$ denotes power exchanged with the upstream grid. The condition of Equation (2) guarantees the power exchanged with the utility grid must not exceed the rated capacity of the distribution transformer.

2.2. Base-Load and PV Modeling

(1)

Base-load modeling

To preserve the regularity inherent in load calculations, we adopt a 24-h baseline profile at minute-scale resolution, onto which small-amplitude white noise and sharp peak events are superimposed.

$$P_{\mathrm{load}}(t)=P_0(t)+\Delta P_{\mathrm{pulse}}(t)+ϵ(t)$$

(3)

where $P_0(t)$ represents the smooth base load; $\Delta P_{\mathrm{pulse}}(t)$ represents the pulse load; and $ϵ(t)$ represents stochastic disturbance.

(2)

PV modeling

The industrial park hosts a PV installation sized for self-consumption first; any surplus is fed into the grid. The PV output is approximated by piecewise-linear segments:

• Night (00:00–05:00, 20:00–24:00): zero generation.
• 05:00–10:00: linear ramp to rated power $P_{\mathrm{PV}}(t)=0$.
• 10:00–16:00: constant plateau at $P_{\mathrm{PV},\max }$ ± 5 kW jitter.
• 16:00–20:00: linear descent to zero.

To capture the short-term stochasticity of solar irradiance, a ±5 kW random perturbation is superimposed on the piecewise-linear PV profile. This simplification reflects the short-term variability due to passing clouds or partial shading while keeping the optimization problem linear and computationally tractable.

This linearized representation facilitates LP-based optimization.

2.3. Electric Vehicle Aggregation Model

To reduce computational scale and communication volume, EV scheduling is performed via grouped aggregation. The industrial park accommodates N EVs, which are partitioned into G groups of M = N/G vehicles each. Each group is represented by an equivalent aggregated power, thereby reducing the dimensionality of the LP-MPC optimization.

2.3.1. Battery Energy Dynamics

The intra-group energy update is

$$E_g(t+1)=E_g(t)+P_g(t)\Delta t$$

(4)

where $E_g(t)$ is the state of energy (kWh) of group g at time step t; the initial value upon arrival at the park is uniformly distributed in [0.5, 0.8] of the full battery capacity to account for commuting usage $P_g(t)$; is the net charging power of group g, which is positive for charging and negative for discharging; and $\Delta t$ is the time-step duration.

The initial SOC and arrival times of individual EVs are assumed to follow uniform random distributions within practical bounds to represent the stochastic nature of user behavior. This probabilistic treatment allows the model to capture aggregate variability without increasing the dimensionality of the optimization problem. Extensions incorporating heterogeneous charger types such as 7 kW AC and 22 kW DC can be readily integrated into the same framework.

2.3.2. Safety and Journey Constraints

To ensure battery safety, the lithium-ion operating envelope is enforced via

$$0.2C_{\mathrm{batt}}\le E_g(t)\le C_{\mathrm{batt}}$$

(5)

where $C_{\mathrm{batt}}$ is the battery capacity.

Let $P_{\max }$ denote the maximum per-vehicle charging/discharging power. Consequently,

$$|P_g(t)|\le P_{\max }\times M$$

(6)

To guarantee users’ travel requirements, the terminal SOC at the end of the scheduling horizon must satisfy

$$E_g(t_{off})\ge 0.5C_{\mathrm{batt}}$$

(7)

where $t_{off}$ is the scheduled departure time.

2.3.3. Aggregated Power

In large-scale EV-scheduling contexts, optimizing the charge/discharge power of individual vehicles directly would yield an excessive number of decision variables, sharply increasing computational burden and demanding prohibitive communication bandwidth. To mitigate this, we introduce the aggregated power as an intermediate optimization variable: group or centralized decisions are first expressed in terms of a single aggregated group power, which is subsequently decomposed into individual vehicle setpoints via an internal allocation policy. Formally,

$$P_{\mathrm{EVagg}}(t)={\displaystyle \sum _{g=1}^G{P}_g}(t)$$

(8)

In this work, identical parameters were used for all EVs to provide a clear baseline for comparing scheduling strategies. However, the formulation in Equations (4)–(8) supports heterogeneous parameters $P_g(t)$, $E_g(t)$ and $C_{\mathrm{batt}}$, enabling straightforward extension to diverse EV types and charger configurations.

2.4. Optimization Problem Formulation

To achieve the coordinated optimization of EV charging/discharging with the grid and PV output in the industrial park, the scheduling problem is formulated as an LP-MPC problem. At each time step, the controller predicts the next 24 steps of load and PV generation with the decision variables being the charging/discharging power $P_g(t)$ for each EV group g. The optimization is subject to the following constraints:

(1)

PCC power limit: the total exchanged power must not exceed the transformer rated capacity.

(2)

SOC and power bounds: every group must operate within physical SOC and power limits.

(3)

Terminal SOC requirement: each group must reach at least 50% SOC by the end of the scheduling horizon.

The resulting bi-objective optimization is expressed in the single scalar form

$$\min [\alpha {\max }_t{P}_{\mathrm{grid}}(t) - (1-\alpha ){\displaystyle \sum _t(}{\pi }_d{P}_{\mathrm{dis}}(t)-{\pi }_c{P}_{\mathrm{ch}}(t))\Delta t]$$

(9)

where the first term minimizes the peak grid-exchange magnitude to prevent transformer overload and smooth the load profile; the second term maximizes EV economic benefit by rewarding discharge ${\pi }_d$ and penalizing charge cost ${\pi }_c$; the negative sign converts “higher profit” into a minimization objective; $\alpha$ is the weighting factor balancing peak-shaving performance against economic returns.

The optimization is subject to the physical and operational constraints defined in Section 2.1, Section 2.2 and Section 2.3, which are summarized as follows:

• Power-balance constraint: Equation (1) ensures that the grid exchange equals the sum of load, PV, and EV powers.
• PCC and transformer capacity limits: Equation (2) bounds the maximum allowable grid and transformer power.
• EV battery dynamics and SOC limits: Equations (4)–(7) describe the SOC evolution, charging/discharging power bounds, and terminal-SOC requirements.

All of the above constraints are linear equalities or inequalities; together with the scalarized objective (9), they define a convex linear-programming problem solvable by standard LP solvers including Gurobi or CPLEX.

3. Multi-Objective Rolling LP-MPC

3.1. Rolling LP-MPC Framework

At every control step k, the rolling LP-MPC initializes the EV SOC states to their current values, forecasts the grid-side load over the next S steps, and computes the optimal sequence of EV and storage powers. Only the first element of this sequence is applied; the horizon then shifts to step k + 1 and the process repeats. Decision variables are shared by EV groups, thereby drastically reducing the dimensionality of the optimization problem.

The optimization objective is

$${\min }_u{J}_k={\displaystyle \sum _{j=0}^{N-1}[}\alpha P_{\mathrm{peak},k}(j)-(1-\alpha )R_{\mathrm{EV},k}(j)]$$

(10)

where $J_k$ is the objective value at control step k; u is the decision-variable vector comprising EV and storage charge/discharge powers; N is the prediction-horizon length (number of steps); $P_{\mathrm{peak},k}(j)$ denotes the peak power at prediction step j within the horizon starting at step k; $R_{\mathrm{EV},k}(j)$ denotes the EV revenue at prediction step j within the horizon starting at step k; u represents the control-variable vector, that is charge/discharge powers; and $\alpha \in [0,1]$ is the weighting coefficient balancing peak-shaving and revenue objectives.

3.2. Peak Power Linearization

We introduce an auxiliary variable $z(j)$ representing the maximum grid-side power at step k + j:

$$\left\{\begin{array}{l}z(j)\ge P_{\mathrm{grid}}(k+j)\\ z(j)\ge -P_{\mathrm{grid}}(k+j)\end{array}\right.$$

(11)

then

$$Pea{k}_p(j)=z(j)$$

(12)

This transforms the nonlinear max function into linear inequalities that can be directly handled by the LP solver.

As both charging cost and discharging revenue are directly proportional to power, the EV benefit can be expressed as a linear function:

$${\mathrm{EV}}_{rev}(\mathrm{j})={\displaystyle \sum _{g=1}^G{\displaystyle \sum _{i=1}^M[{\pi }_d\cdot {\mathrm{P}}_{\mathrm{dis},\mathrm{g},\mathrm{i}}(\mathrm{k}+\mathrm{j})-}}{\pi }_c\cdot {\mathrm{P}}_{\mathrm{ch},\mathrm{g},\mathrm{i}}(\mathrm{k}+\mathrm{j})]\Delta \mathrm{t}$$

(13)

where ${\mathrm{P}}_{\mathrm{ch},\mathrm{g},\mathrm{i}}$, ${\mathrm{P}}_{\mathrm{dis},\mathrm{g},\mathrm{i}}$ denote the charging and discharging powers of the i-th EV in group g, respectively; ${\pi }_d$ and ${\pi }_c$ denote the constant discharging and charging electricity prices (CNY/kWh), respectively.

3.3. Linear Constraint Framework

To ensure system safety and meet the next schedule demands, the following linear constraints are imposed:

(1)

Power balance

The grid-side power equals the base load minus the photovoltaic output plus the net EV charging/discharging power:

$$P_{grid}\left(k+j\right) + P_{PV}\left(k+j\right) = P_{load}\left(k+j\right) + P_{EV}\left(k+j\right)$$

(14)

(2)

Transformer capacity

To prevent transformer overloading, the grid-side power must remain within the transformer’s rated capacity:

$$-P_{tra}^{\max }\le P_{grid}(k+j)\le P_{tra}^{max}$$

(15)

(3)

EV dynamics

The state of charge evolves according to charging/discharging power, remains within power limits, and satisfies the terminal constraint SOC ≥ 50%:

$$E_{g,i}(k+j+1)=E_{g,i}(k+j)+{\eta }_{ch}{P}_{ch,g,i}(k+j)\Delta t-{\displaystyle \frac{P_{dis,g,i}(k+j)}{{\eta }_{dis}}}\Delta t$$

(16)

Meanwhile, the battery SOC must at all times remain between its minimum and maximum allowable levels.

$$0.2C_{bat}\le E_{g,i}(k+j)\le C_{bat}$$

(17)

The charging and discharging powers are subject to the following limits:

$$\left\{\begin{array}{l}0\le P_{ch,g,i}(k+j)\le P_{max}\\ 0\le P_{dis,g,i}(k+j)\le P_{max}\end{array}\right.$$

(18)

To ensure that privately owned EVs can meet their commuting needs, the SOC before the end of the workday must satisfy the following requirement:

$$E_{g,i}(t_{of})\ge 0.5C_{bat}$$

(19)

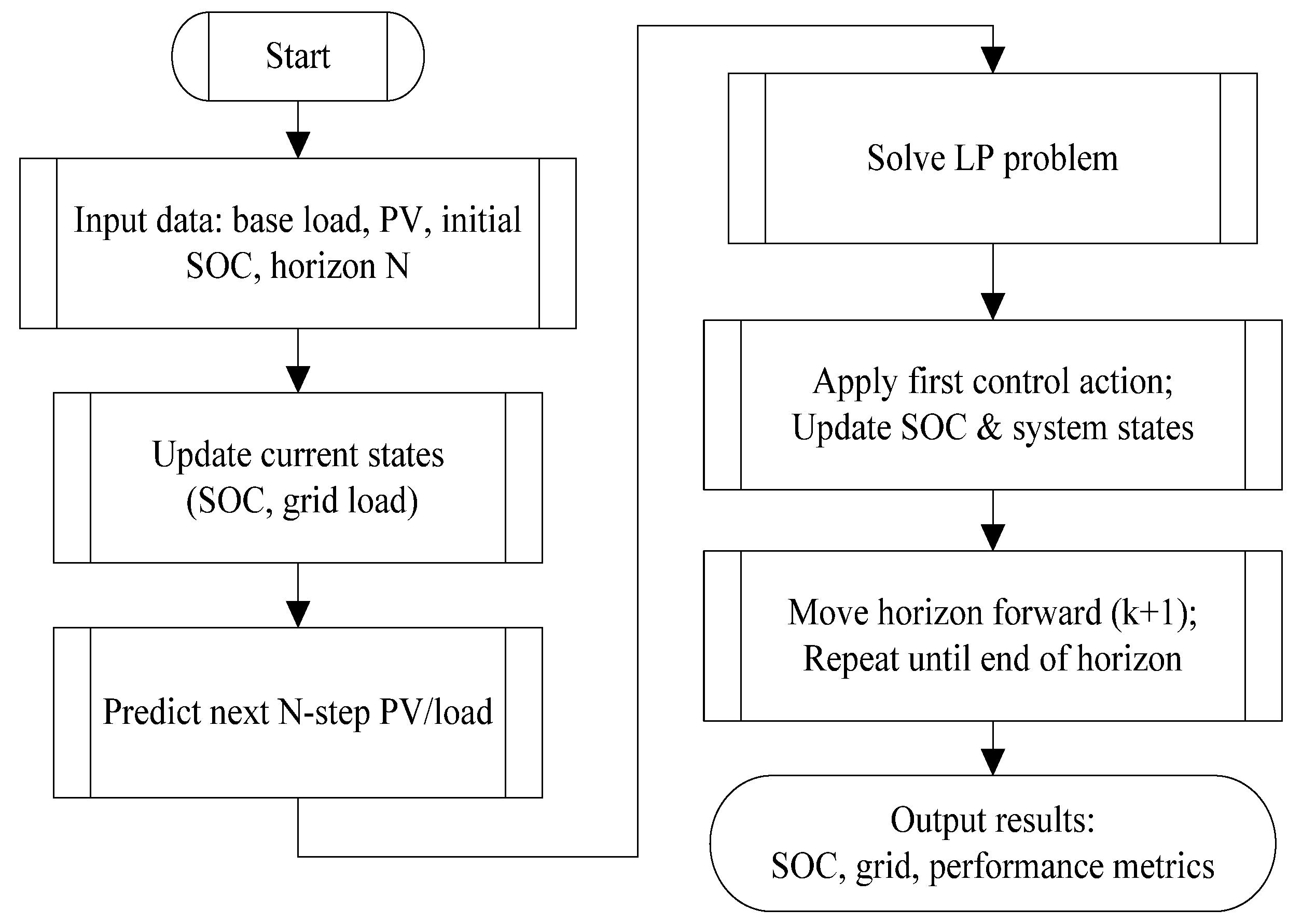
3.4. LP-MPC Algorithm Flow

The LP-MPC algorithm operates in three key stages: (1) predicting future load and PV generation over the rolling horizon, (2) solving the constrained linear optimization problem defined in Section 2.4, and (3) applying the first-step control action before advancing the prediction window.

Input: base load, PV output, EV initial SOC, prediction horizon length N;

Output: per-step EV power, grid-side power, EV SOC history.

Steps:

(1)

Initialize EV grouping and SOC.

(2)

For current_time = 0 → total_steps − 1

• Set prediction horizon H = min(current_time + N, total_steps).
• Compute future net load = base_load − PV_output.
• Define decision variables: EV_charge_power, EV_discharge_power.
• Formulate constraints: EV SOC dynamics, EV power limits, terminal SOC, transformer capacity, storage SOC and power limits.
• Construct objective function: J = α·peak_power − (1 − α)·EV_revenue.
• Call linear-programming solver.
• If solution is successful:
  • Apply first-step decision: EV_power = EV_charge_power − EV_discharge_power.
  • Update SOC and record.
  • Compute current grid-side power = future_net_load [0] + Σ EV_power.
• Else: set EV_power = 0.

(3)

End for

The overall computational process is summarized in Figure 1.

At each control step, the LP-MPC updates system states, predicts load and PV profiles, formulates a linear optimization problem, solves it, applies the first control command, and moves the prediction horizon forward. The loop repeats until the end of the scheduling period. The main pseudocode for scheduling is shown in Appendix A.

3.5. Benchmark Algorithms

To validate the effectiveness of the proposed LP-MPC strategy, two representative dispatch policies are adopted as benchmarks: the greedy algorithm and a heuristic load-leveling approach. All three algorithms guarantee that the EV SOC will not fall below 50% after 17:30.

(1)

Greedy Algorithm

At every dispatch interval, the greedy algorithm selects the time slots with the lowest current electricity price and charges at the maximum allowable power until the residual charging demand is satisfied. It disregards future load fluctuations and network constraints. The dispatch logic is expressed as follows:

$$P_i(k)=\left\{\begin{array}{ll}{P}_i^{\max },\hfill & \mathrm{if} c(k)=\min c(t), t\in {\mathcal{T}}_{\mathrm{avail}}\hfill \\ 0,\hfill & \mathrm{others}\hfill \end{array}\right.$$

(20)

where $c(k)$ denotes the current electricity price; and ${\mathcal{T}}_{\mathrm{avail}}$ denotes the set of available charging time windows for the vehicle.

(2)

Heuristic Load Leveling

The heuristic load-leveling policy is a rule-based dispatch method that relies on instantaneous load thresholds to achieve rapid EV charge/discharge response. Its core principles are outlined below:

• Valley filling: When the current net grid load is below a preset threshold, each EV group charges at its maximum allowable power.
• Peak shaving: When the net load exceeds the threshold, each group discharges at its maximum allowable power.
• SOC safeguard: At all times, the SOC must remain between the lower and upper bounds.

Formally,

$$P_{\mathrm{EV},i}(t)=\left\{\begin{array}{ll}{P}_{\mathrm{ch}}^{\max },\hfill & P_{\mathrm{net}}(t)<P_{\mathrm{th}}^{\mathrm{low}}{ \mathrm{and} \mathrm{SOC}}_i(t)<{\mathrm{SOC}}_{\max }\hfill \\ -P_{\mathrm{dis}}^{\max },\hfill & P_{\mathrm{net}}(t)>P_{\mathrm{th}}^{\mathrm{high}}{ \mathrm{and} \mathrm{SOC}}_i(t)>{\mathrm{SOC}}_{\min }\hfill \\ 0,\hfill & \mathrm{others}\hfill \end{array}\right.$$

(21)

where $P_{\mathrm{EV},i}(t)$ represents the charging or discharging power of EV group i at time t with positive values indicating charging and negative values indicating discharging; $P_{\mathrm{ch}}^{\max },P_{\mathrm{dis}}^{\max }$ are the maximum charging and discharging powers of group i; ${\mathrm{SOC}}_i(t)$ is the current SOC of group i.

The SOC is updated dynamically according to Equation (22) with $\Delta t$ in minutes.

$${\mathrm{SOC}}_i(t+1)={\mathrm{SOC}}_i(t)+{\displaystyle \frac{P_{\mathrm{EV},i}(t)\cdot \Delta t}{60}}$$

(22)

This method requires no future load forecasts; it responds solely to the present load threshold and SOC information, offering low complexity and straightforward deployment.

4. Experiments and Results

4.1. Simulation Parameter Settings

To validate the effectiveness of the proposed LP-MPC strategy for coordinated EV dispatch, a 24-h industrial-park scenario with 300 EVs is constructed. The simulation employs a 1000 kW transformer over 24 h with 5-min intervals resolution, yielding 288 steps, and incorporates a predicted PV generation profile, base-load fluctuations, and transformer capacity limits. To ensure fairness, all three dispatch algorithms—LP-MPC, greedy, and heuristic load-leveling—are subject to the common constraint that the SOC must not fall below 50% after 17:30, thereby guaranteeing users’ next-day mobility. During the periods of 10:00–11:00 and 14:00–15:00, two 400 kW pulses were injected into the PV to simulate spike events.

The electricity-price mechanism adopts a load-ratio tiered strategy: when the transformer loading ratio is below 98%, the price is 1 CNY/kWh; when the ratio exceeds 99%, the price rises to 2 CNY/kWh to suppress peak charging. The initial SOC of each EV is uniformly distributed between 30 kWh and 50 kWh, and the maximum per-vehicle charging power is 7 kW.

All computations were performed on the same machine: Windows 10, Intel i7-12700H @ 3.50 GHz (12 cores), 16 GB RAM, Python 3.13.3, NumPy 2.3.2, CVXPY 1.7.2. Random seeds were fixed to ensure reproducibility.

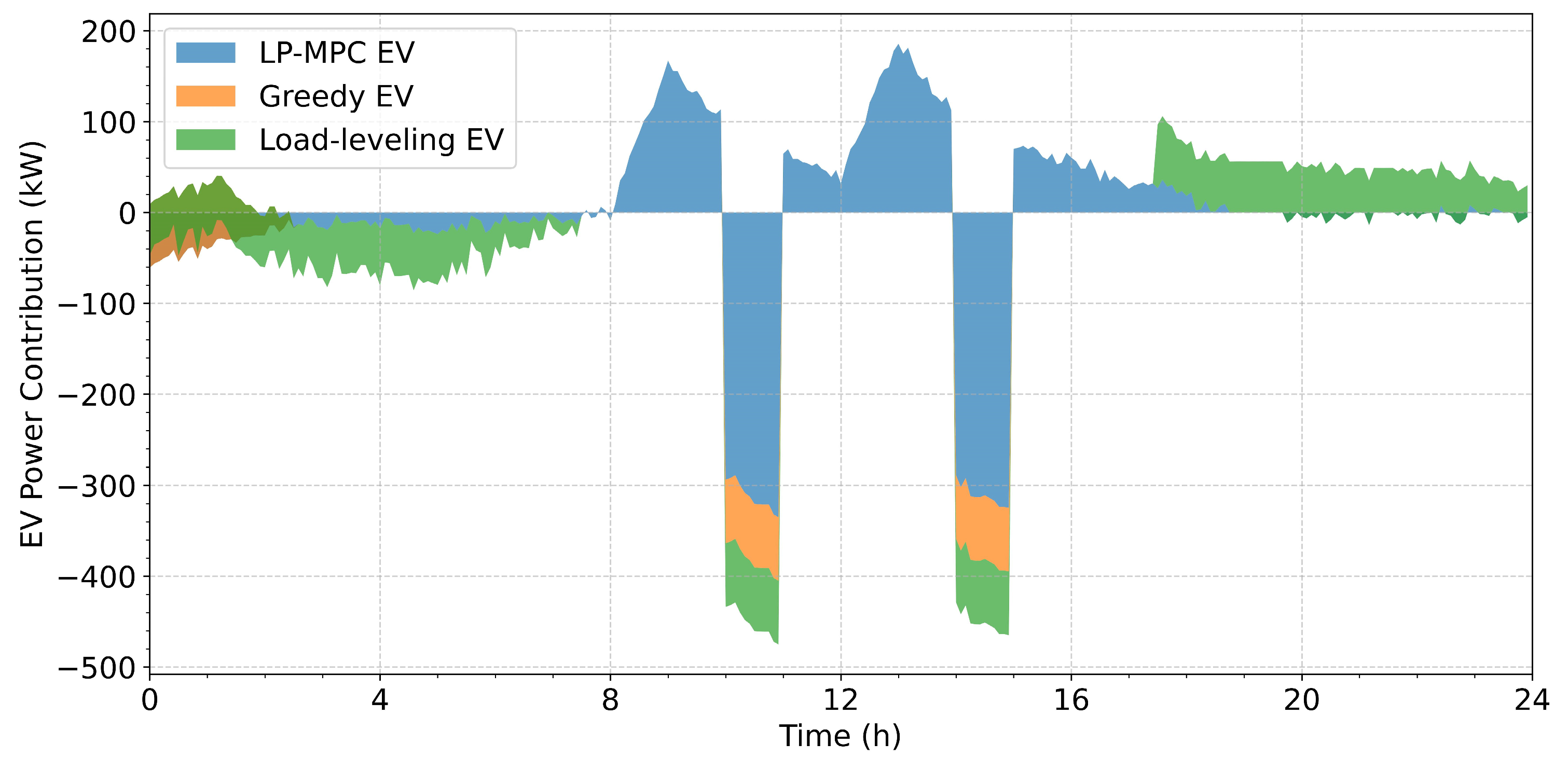
4.2. Performance Comparison of the Algorithms

The key performance indicators of the three dispatch strategies, including peak load, peak-to-valley difference, load standard deviation, EV revenue, SOC compliance rate, maximum overload power, charging completion rate, and execution time, is presented in

Table 1. Performance comparison of the three dispatch strategies.

Method	Peak Load (kW)	Peak-to-Valley Difference (kW)	Load Fluctuation Std (kW)	EV Revenue (CNY)	SOC Compliance Rate (%)	Maximum Overload (kW)	Execution Time (s)
LP-MPC	984.1	146.7	29.6	910	100.0	0.00	0.29
Greedy	1139.2	351.4	86.8	150	100.0	139.2	0.01
Load-Leveling	1139.2	351.4	90.7	630	50	139.2	0.01

. The following performance can be revealed in Table 1:

(1)

Peak-load suppression

LP-MPC effectively caps the peak load at approximately 984.1 kW—lower than the 1139.2 kW recorded under both greedy and load-leveling—thereby preventing transformer overload.

(2)

Load-smoothing performance

With a load standard deviation of only 29.6 kW, LP-MPC markedly outperforms greedy (86.8 kW) and load-leveling (90.7 kW), yielding a significantly flatter load profile.

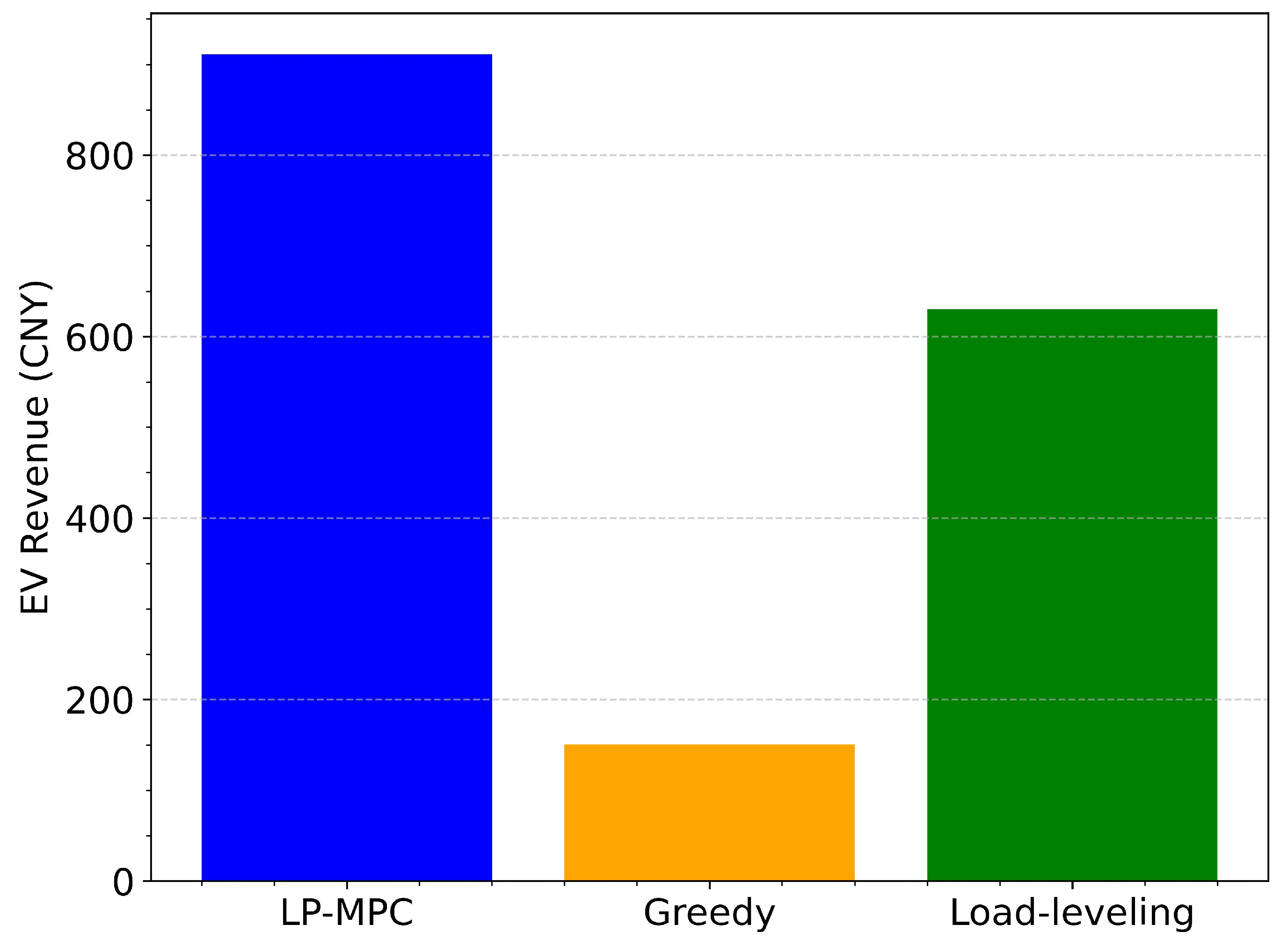
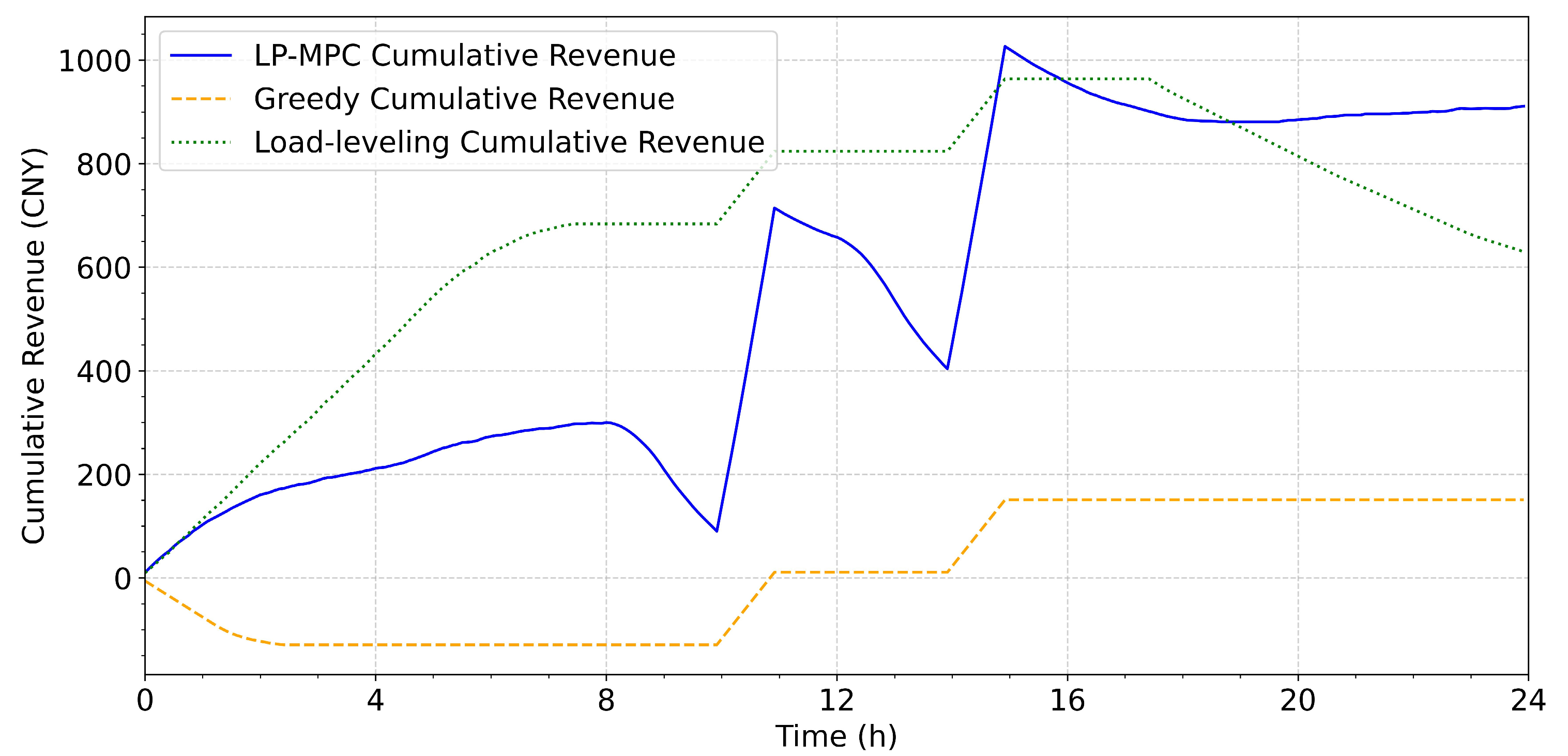
(3)

User-revenue assurance

The overall EV revenue under LP-MPC reaches about 910 CNY, whereas the benchmark strategies suffer economic degradation due to uncoordinated charging.

(4)

SOC compliance without overload

Although both LP-MPC and Greedy satisfy the SOC ≥ 50% requirement by the end of the workday, only LP-MPC operates without overload; greedy and load-leveling expose the transformer to a maximum overload risk of 139.2 kW.

(5)

Computational efficiency

Each rolling LP-MPC optimization finishes in approximately 0.29 s, summing to 85.3 s across the 288-step horizon, easily meeting the 5-min real-time dispatch requirement. greedy and load-leveling methods run somewhat faster yet deliver markedly worse performance.

4.3. Performance Analysis

The total load profiles under the three strategies are compared in Figure 2. The LP-MPC policy effectively suppresses load spikes, keeping the peak below 984.1 kW, whereas the greedy and heuristic load-leveling strategies both exceed 1139 kW, causing severe transformer overload. The LP-MPC curve is noticeably smoother and exhibits substantially smaller fluctuations, demonstrating that centralized optimization can globally balance PV output variability and EV charging demand. Moreover, LP-MPC prevents large-scale synchronous charging during peak hours, ensuring the transformer loading ratio remains within limits while simultaneously achieving peak-shaving and valley-filling objectives, thereby offering significant practical value.

The EV charging/discharging power profiles under the three strategies are shown in Figure 3. LP-MPC dynamically adjusts charge/discharge power in response to the transformer loading ratio, thereby avoiding the instantaneous load spikes caused by the greedy algorithm’s concentrated charging during low-price periods and suppressing the disorderly responses inherent in the load-leveling strategy. Notably, after 17:30, LP-MPC gradually raises the charging power to guarantee that all EVs reach an SOC of at least 50% on schedule instead of resorting to large, last-minute energy recovery. This approach markedly improves both dispatch smoothness and controllability.

The average SOC evolution of EVs under the three strategies is shown in Figure 4. With a full SOC of 50 kWh, LP-MPC maintains a smooth, steady SOC increase throughout the day and secures the ≥ 50% requirement well before 17:30, demonstrating superior scheduling flexibility and adequate margin. In contrast, although greedy satisfies the SOC constraint, it immediately starts charging an EV as soon as it is plugged in, lacking any foresight. Load-leveling, due to its conservatism, begins by discharging, causing the final SOC to fall short of the target.

The comparison of the three strategies in terms of peak load, peak-to-valley difference, and load standard deviation is shown in Figure 5. LP-MPC markedly outperforms both greedy and load-leveling on every metric: peak load is reduced to 984 kW, the peak-to-valley difference falls to 146.7 kW, and the load standard deviation is only 29.7 kW. These results demonstrate that LP-MPC not only curtails peak demand but also effectively suppresses load fluctuations, thereby enhancing grid stability and economic efficiency.

The aggregated EV revenue under the three strategies is shown in Figure 6. Under LP-MPC, the owner earns 910 CNY, while the greedy algorithm and load-leveling algorithm earn 150 CNY and 630 CNY respectively, with a significant difference. This result demonstrates that well-designed centralized scheduling can simultaneously perform peak shaving and valley filling while substantially improving owners’ economic returns, achieving a win–win outcome for the system and its users.

The composition of grid power under each strategy is illustrated by stacked curves in Figure 7. By rationally allocating charging power, LP-MPC coordinates changes in the PV output, base load, and EV charging demand, actively suppressing load surges during the peak period from 17:00 to 21:00 and yielding a smoother grid-power profile—further confirming its peak-shaving effectiveness.

It is also noted that the minimization of transformer peak power in the objective function implicitly reduces the total energy drawn from the grid. This outcome indicates an improvement in overall grid-side energy efficiency, as the LP-MPC naturally balances local PV utilization and EV charging demand.

The 24-h cumulative EV revenues under the three scheduling strategies are compared in Figure 8. LP-MPC starts slowly in the early-morning hours; its upward trend becomes more visible after sunrise, yet the slope is noticeably smoother than before. A brief acceleration appears around noon, but the former sharp jumps are absent. Revenues keep climbing steadily through mid-afternoon and taper slightly in the late evening; the draw-down is smaller than previously because the controller, constrained by the SOC bound, now trades more cautiously between morning and night. At the end of the day, LP-MPC still records the highest return.

The load-leveling approach is far more stable than the greedy algorithm: it gains gradually in the morning and afternoon, peaks around 16–17 h, then gives back a small portion as higher evening tariffs erode profit windows. The retreat is modest, leaving the curve in the upper-middle band and securing second place. Greedy performs worst throughout: revenue accumulates very slowly, barely moving in the morning, improving only slightly after noon and soon being dragged down by repeated charging during high-cost or non-profitable intervals. By midnight, greedy’s cumulative revenue is the lowest: well below those of LP-MPC and load-leveling. The results show that although LP-MPC has adjusted its charge–discharge rhythm to meet the revised SOC and price constraints, it still captures favorable discharge slots; load leveling suits mild scheduling but lacks aggressiveness; greedy, devoid of foresight and global planning, tends to charge at unfavorable times and thus depresses overall earnings.

Collectively, the above comparisons show that the proposed LP-MPC strategy outperforms both greedy and load leveling in peak shaving, user revenue enhancement, and grid security. While guaranteeing SOC ≥ 50% and a 100% charging completion rate, LP-MPC operates without overload risk and maintains second-level optimization speed, underscoring its practical engineering value.

4.4. Discussion

The numerical results demonstrate that the proposed LP-MPC framework achieves consistent improvements in peak-load reduction, load variance minimization, and charging-cost optimization.

Beyond quantitative performance, several theoretical implications can be observed.

(1)

The results validate that a linearized multi-objective predictive model can effectively approximate the nonlinear coupling between grid power balance, SOC dynamics, and PV uncertainty while preserving convexity and global optimality. This confirms the feasibility of reformulating the classical nonlinear MPC into a fully linear rolling program without loss of scheduling accuracy.

(2)

The study highlights the stability of the receding-horizon solution under prediction disturbances. The small deviation of the load-variance index under perturbed forecasts implies that the LP-MPC cost function forms a smooth convex landscape, ensuring the robustness of the optimal trajectory with respect to bounded uncertainties.

(3)

The results support the theoretical trade-off between model fidelity and real-time solvability. The LP formulation guarantees deterministic convergence and polynomial-time complexity, which explains the observed stability of optimization time across 288 rolling steps.

The modeling choices adopted in this study strike a balance between theoretical clarity and practical representativeness. By using controlled perturbations to emulate the stochastic effects of PV and user variability, the LP-MPC formulation remains generalizable and analytically tractable, providing a foundation for future stochastic and efficiency-oriented extensions to further enhance realism.

The current formulation assumes fixed electricity prices to focus on the control mechanism. In practice, dynamic or time-of-use tariffs can be incorporated by allowing the price coefficients in Equation (9) to vary with time, which preserves linearity but increases temporal coupling. The potential benefits and computational trade-offs of such dynamic-tariff extensions will be addressed in future work.

Furthermore, the LP-MPC structure remains applicable to heterogeneous EV populations, where different capacities and power limits may introduce additional scheduling flexibility and fairness considerations.

5. Conclusions

This paper proposes a rolling LP-MPC approach for the coordinated scheduling of electric vehicles with grid-side loads and photovoltaic generation in industrial-park microgrids. The method addresses load fluctuation and transformer peak-stress issues under high EV penetration by embedding multi-objective optimization into a real-time predictive framework.

The simulation results show that the proposed LP-MPC effectively reduces peak load, narrows the peak–valley gap, and suppresses load volatility, outperforming both greedy and heuristic load-leveling benchmarks. By incorporating charging and discharging revenues, the controller enhances user benefit while maintaining grid stability and meeting SOC constraints. The rolling optimization mechanism allows adaptive response to load and PV variations, ensuring stable operation and computational tractability.

Beyond numerical performance, this study demonstrates that a linearized predictive-control formulation can retain convexity and global optimality while coordinating multiple objectives within large-scale dynamic systems. The proposed framework thus provides not only an efficient dispatch strategy but also a general theoretical basis for scalable predictive coordination. Future work will extend the model to stochastic and distributed contexts, considering price signals and behavioral uncertainties to further enrich its analytical and practical depth. The LP-MPC framework could also be extended toward decentralized coordination paradigms inspired by recent game-theoretic developments in renewable energy systems.