Design and Gait Simulation Study of Wheel-Legged Conversion Device Used in Hexapod Bionic Robot
Abstract
1. Introduction
2. The Basic Idea of Design
3. Materials and Methods
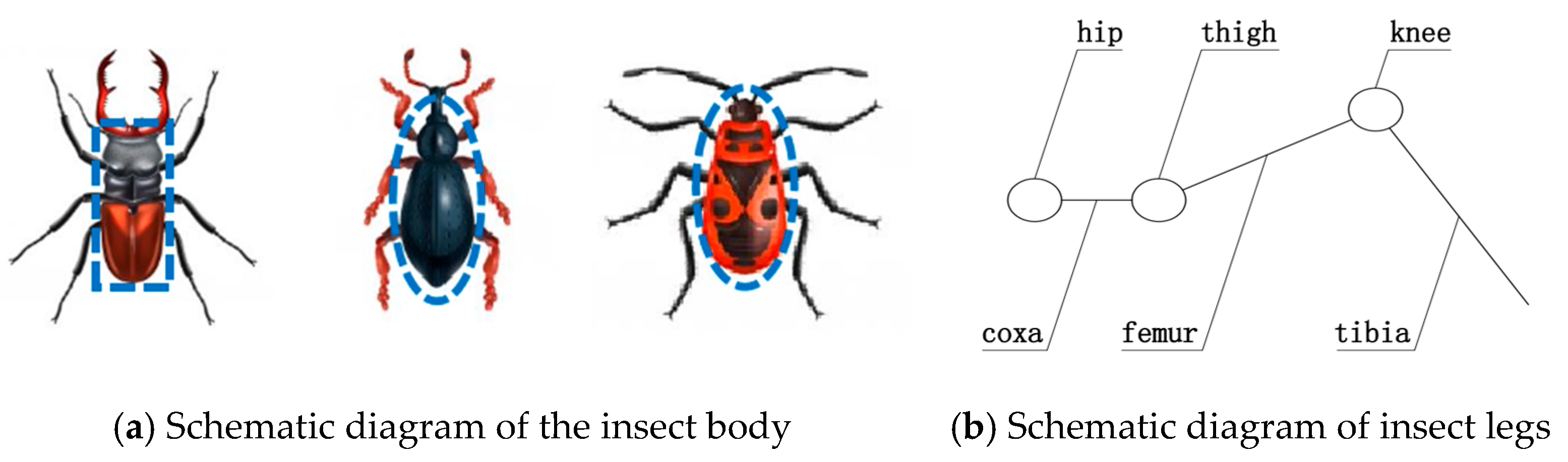
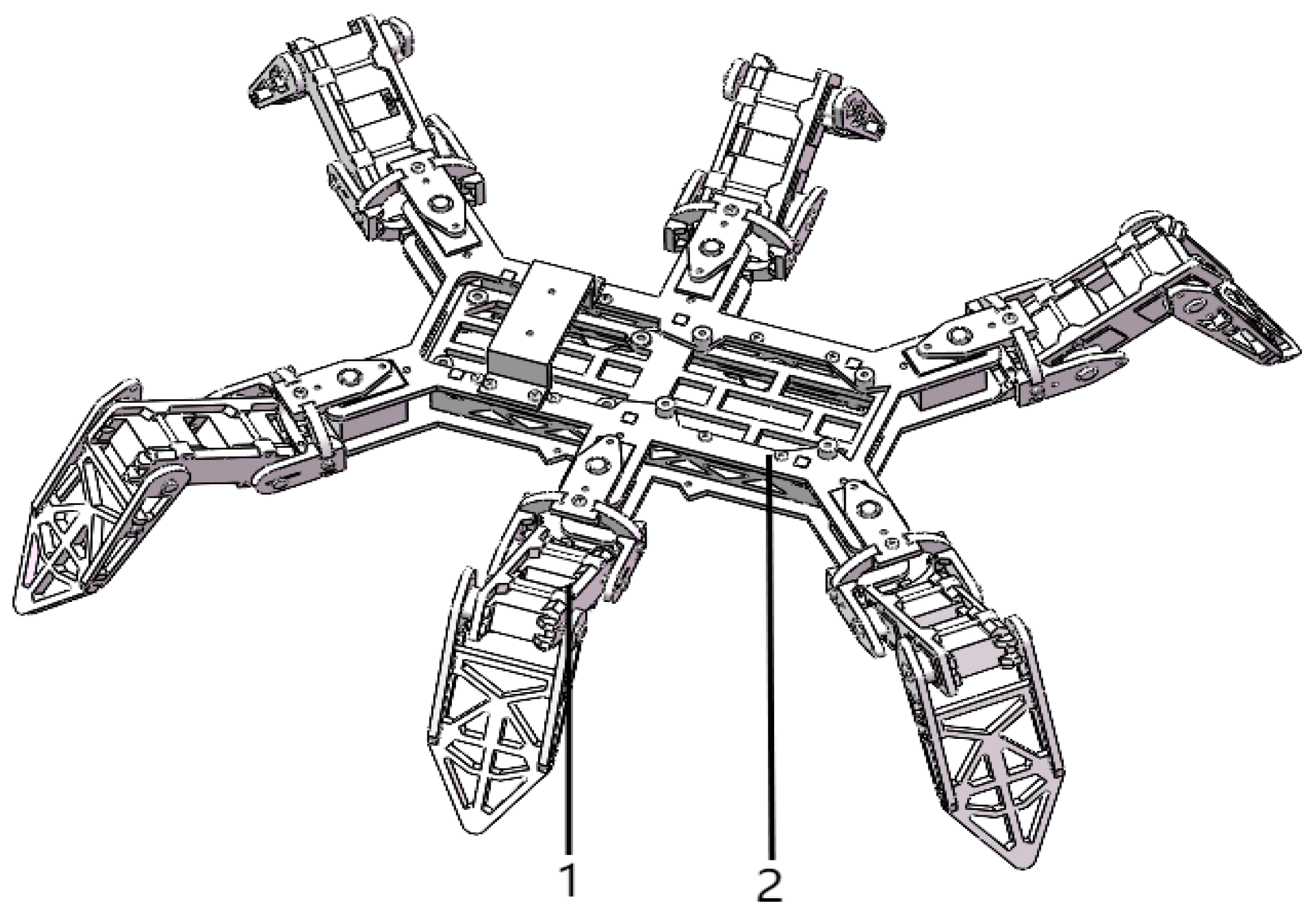
3.1. Design and Analysis of Bionic Hexapod Structure
3.2. Design of the Wheel-Legged Conversion Mechanism
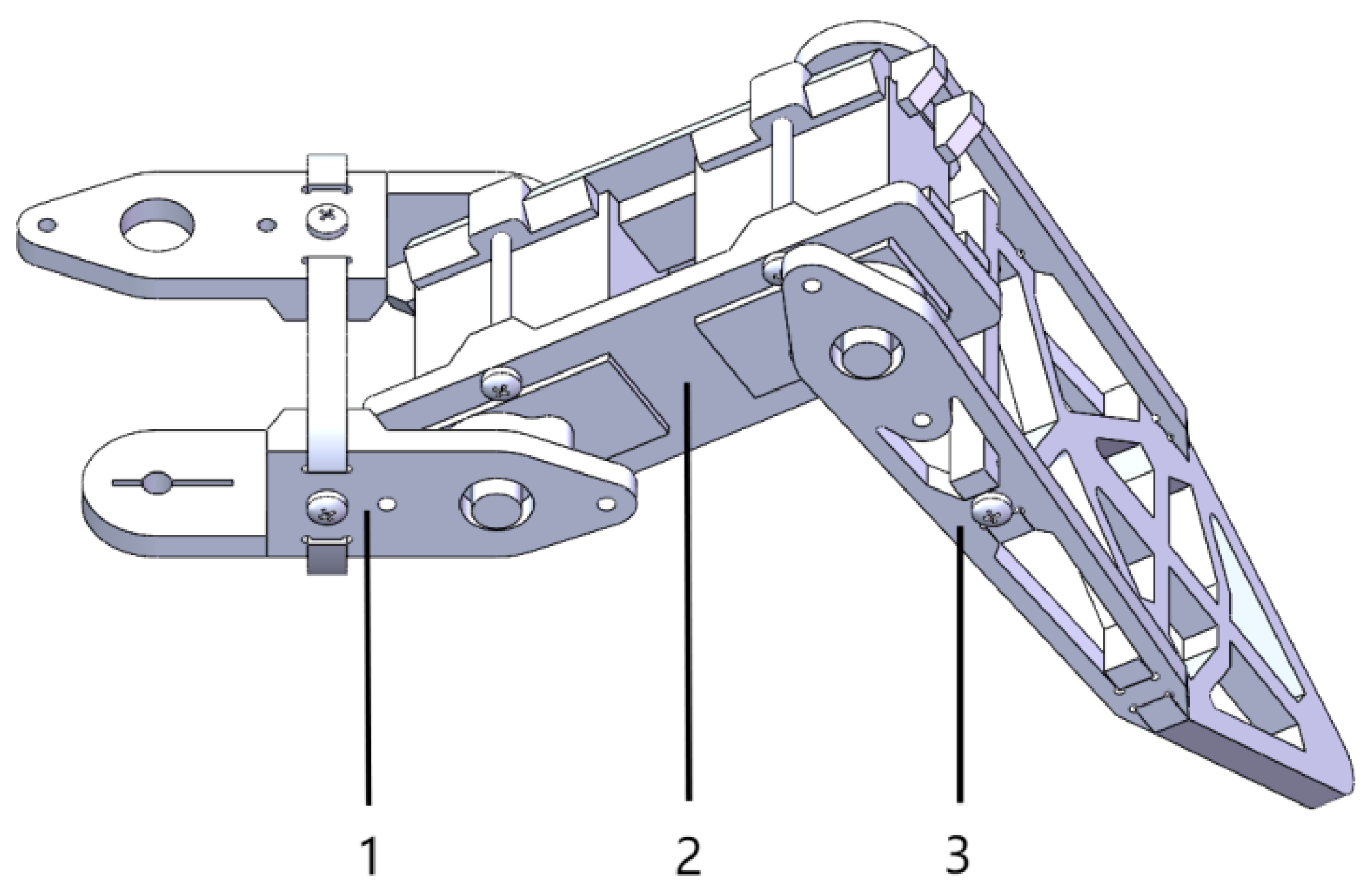
3.2.1. Three-Degree-of-Freedom Leg Structure
3.2.2. Establishment of Kinematic Model
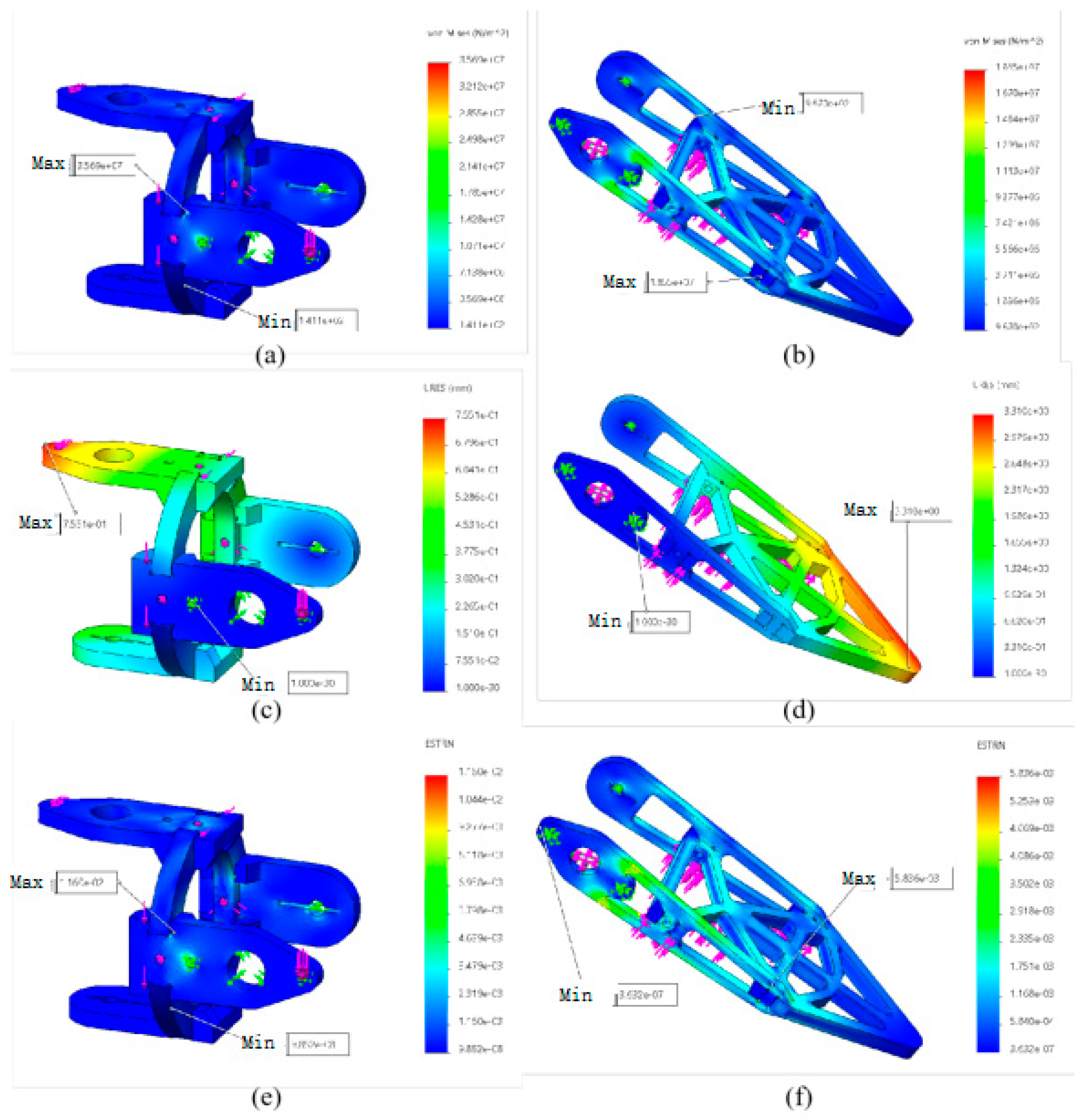
3.2.3. Finite Element Analysis of the Three-Degree-Freedom Leg
- (1)
- Solid Model Parameters of Leg’s Finite Element Analysis (version ANSYS 12.0)
- (2)
- Results of static analysis
3.3. Design and Analysis of Wheel
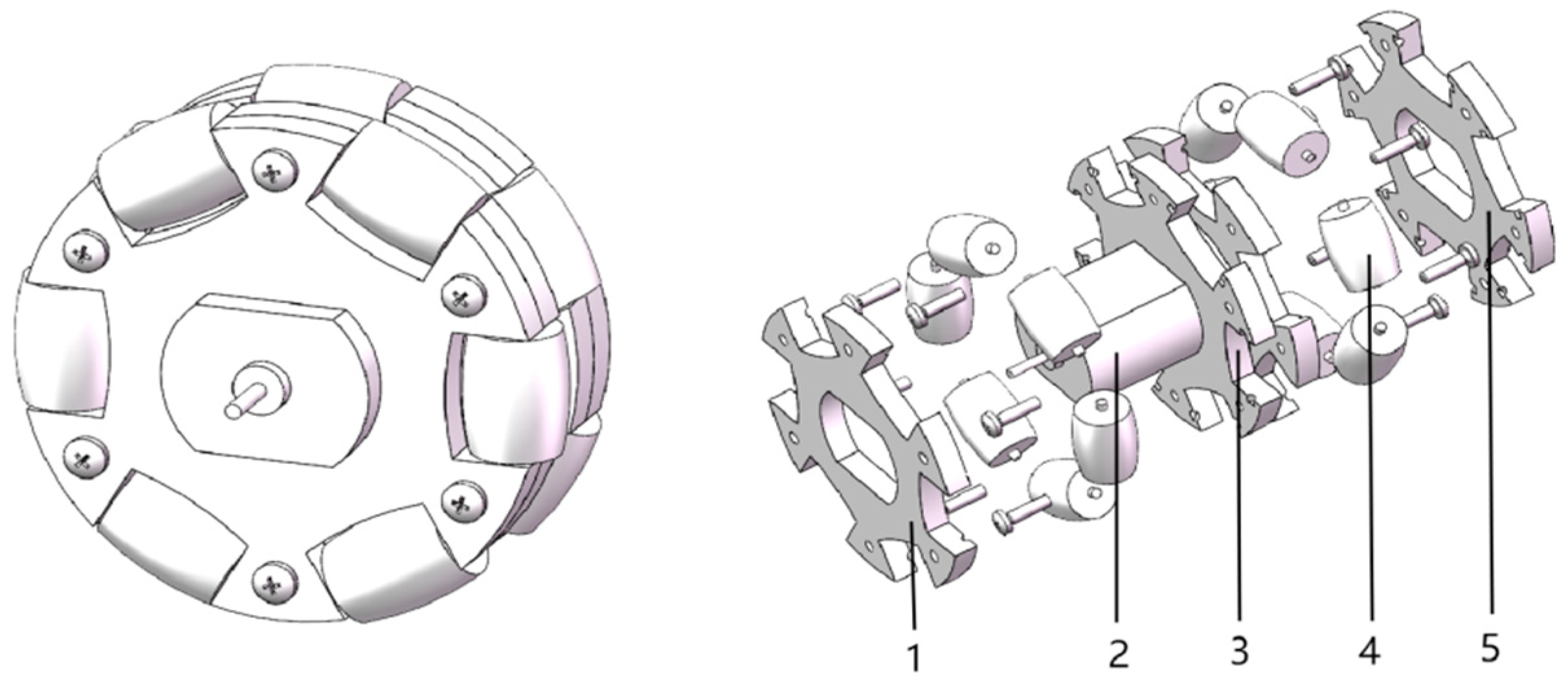
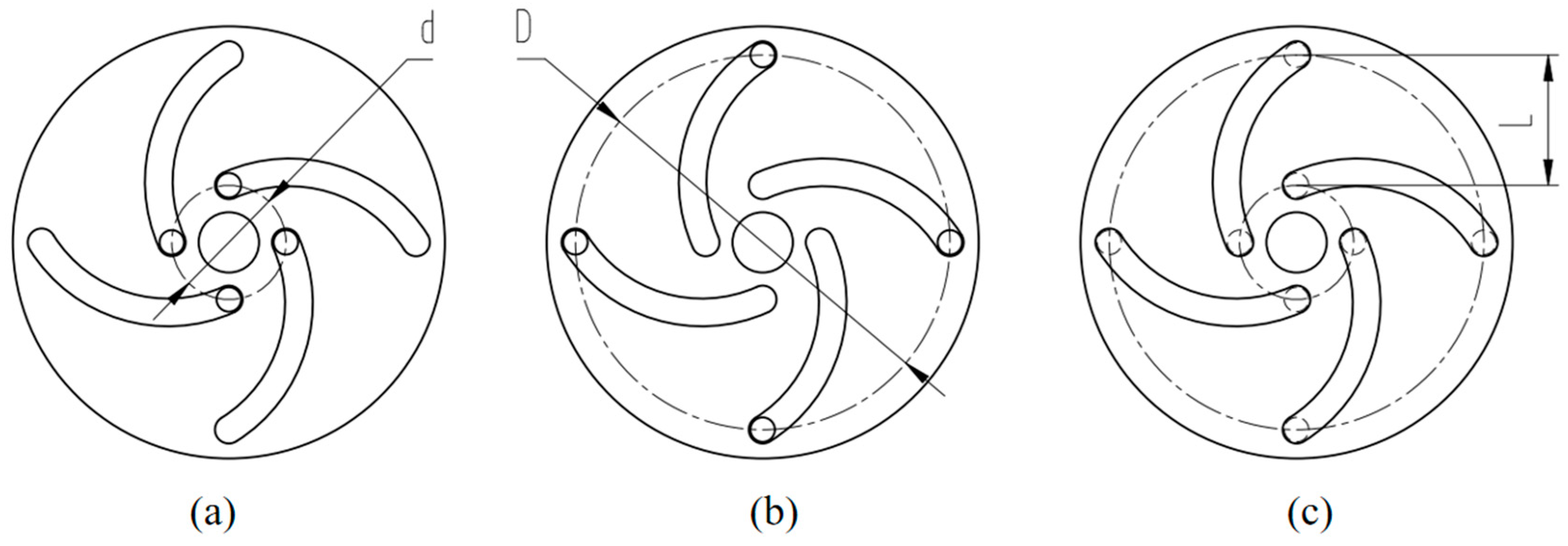
3.3.1. Scheme Design of Omni-Directional Wheel
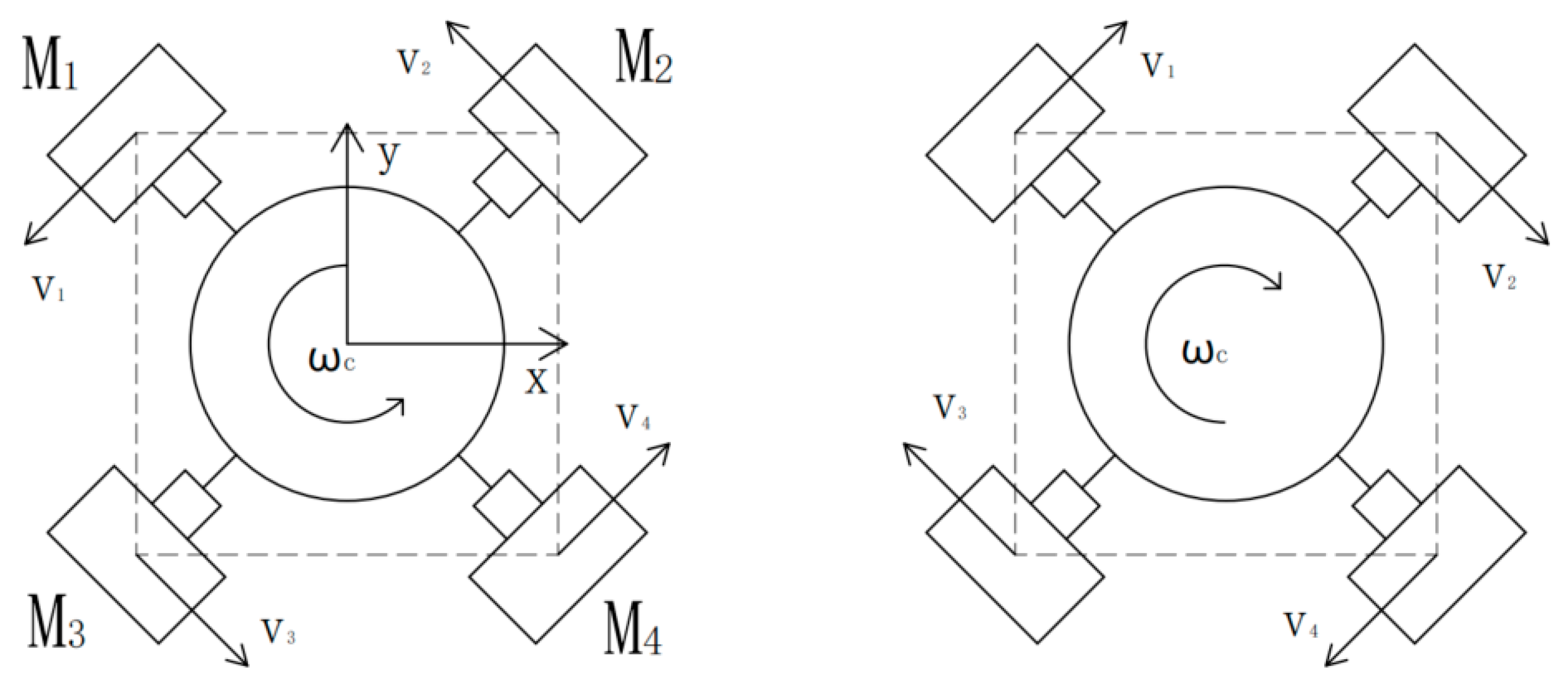
3.3.2. Analysis of the Motion Mode of Omni-Directional Wheels
3.4. Scheme Design and Working Principle of the Wheel-Legged Conversion Mechanism
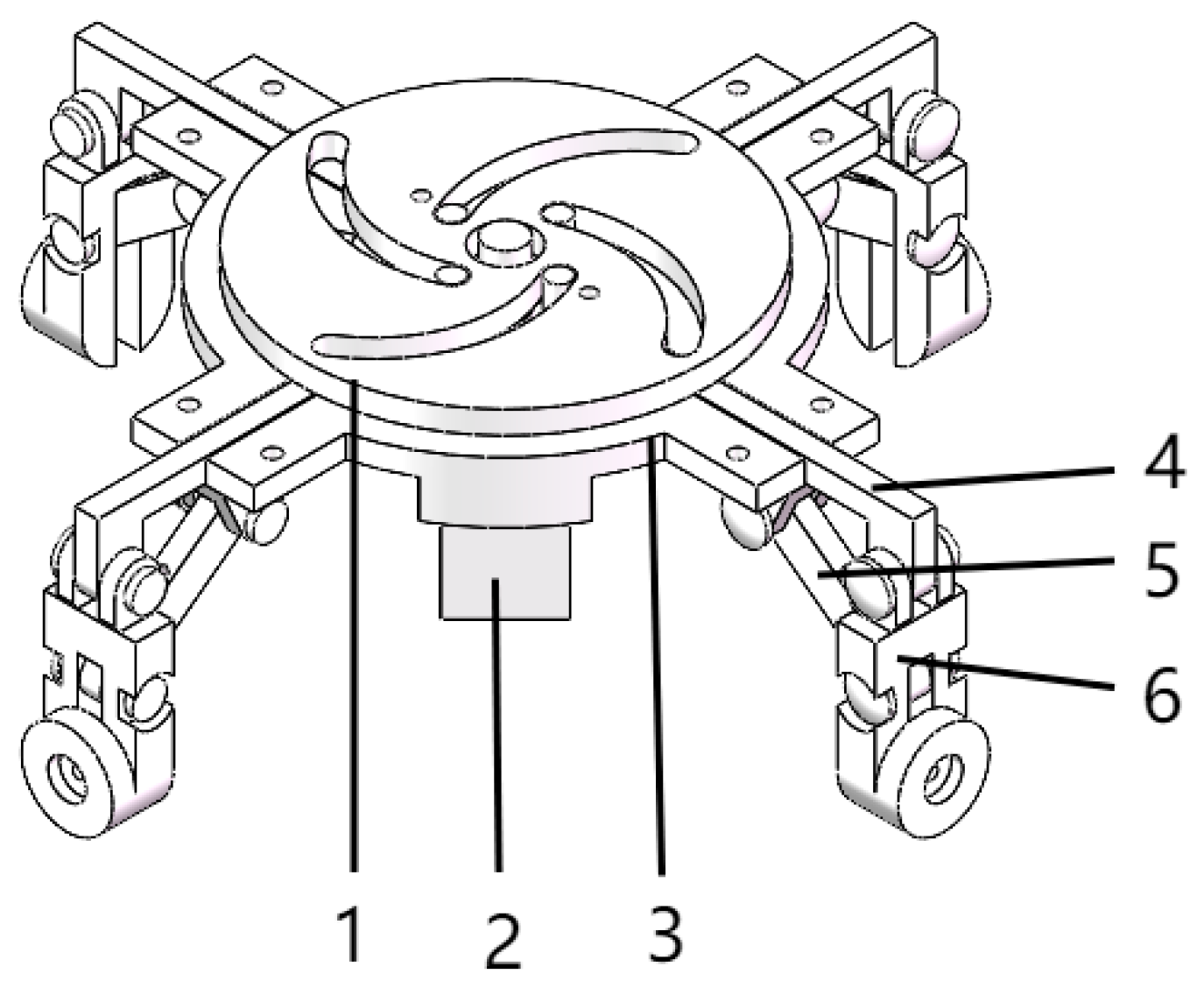
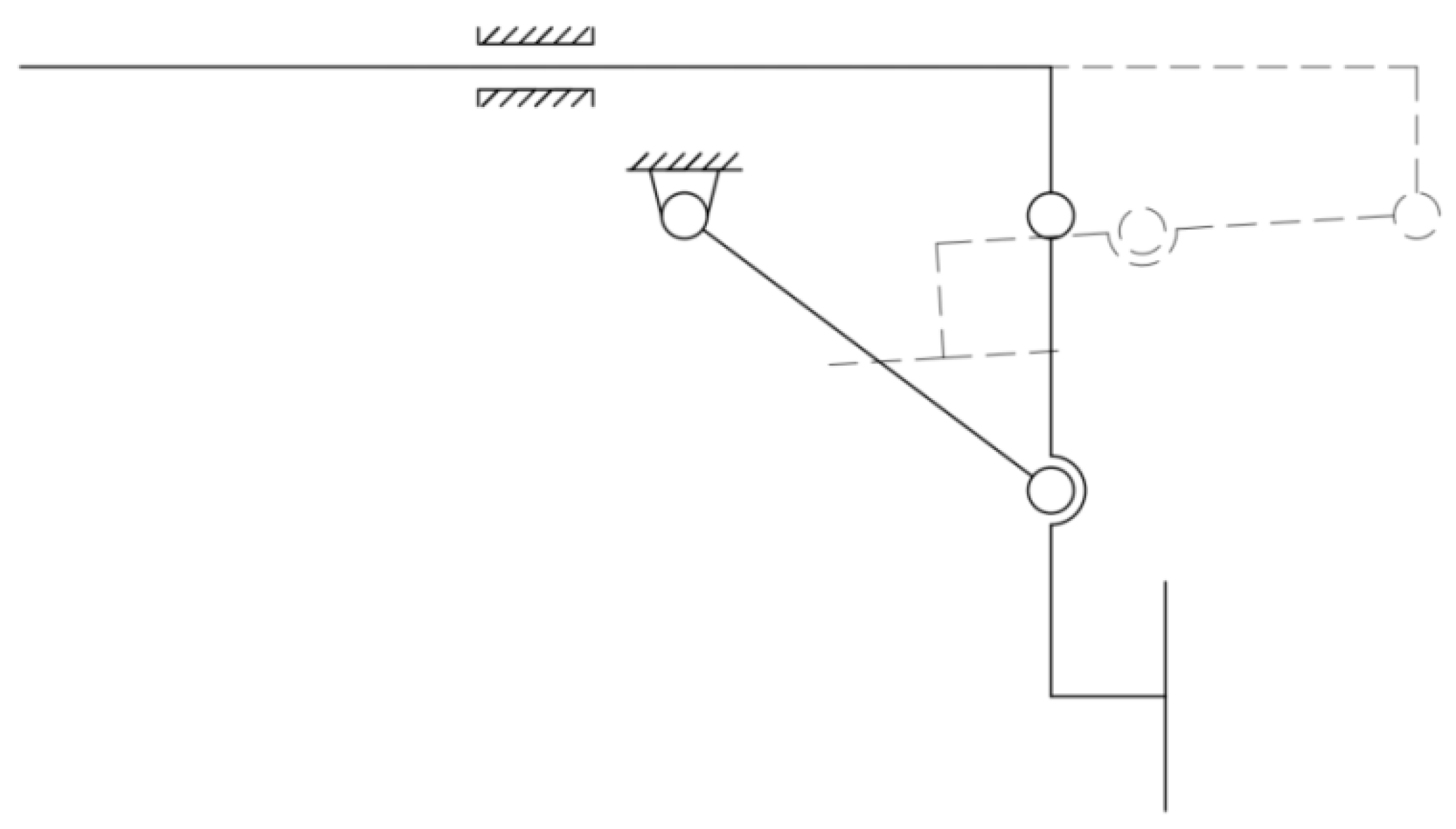
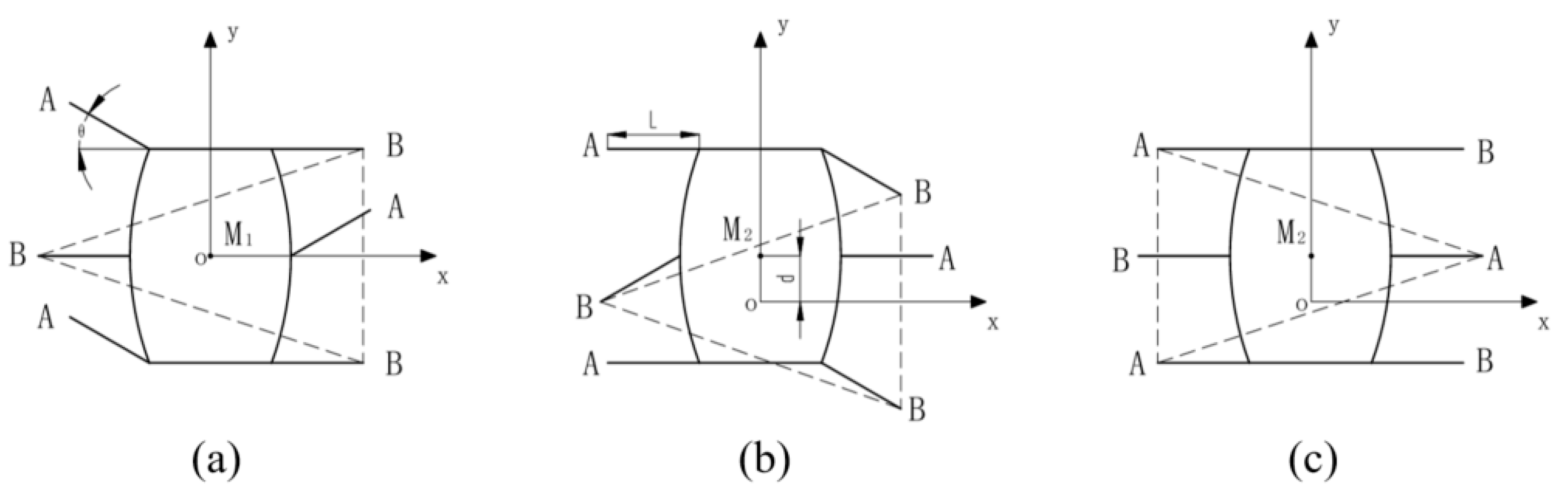
3.4.1. Scheme Design of Wheel-Legged Conversion Mechanism
3.4.2. Working Principle of Wheel-Legged Conversion Mechanism
4. Results
4.1. Construction of Simulation Environment
4.2. Design of the Abstract Hexapod Robot
4.3. Planning of Typical Gait of Bionic Hexapod Robot
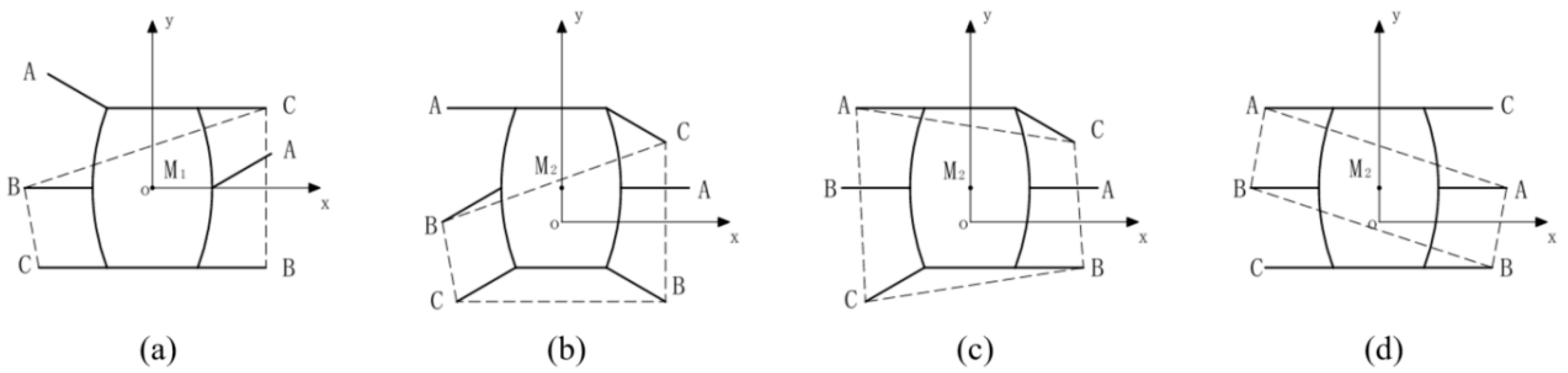
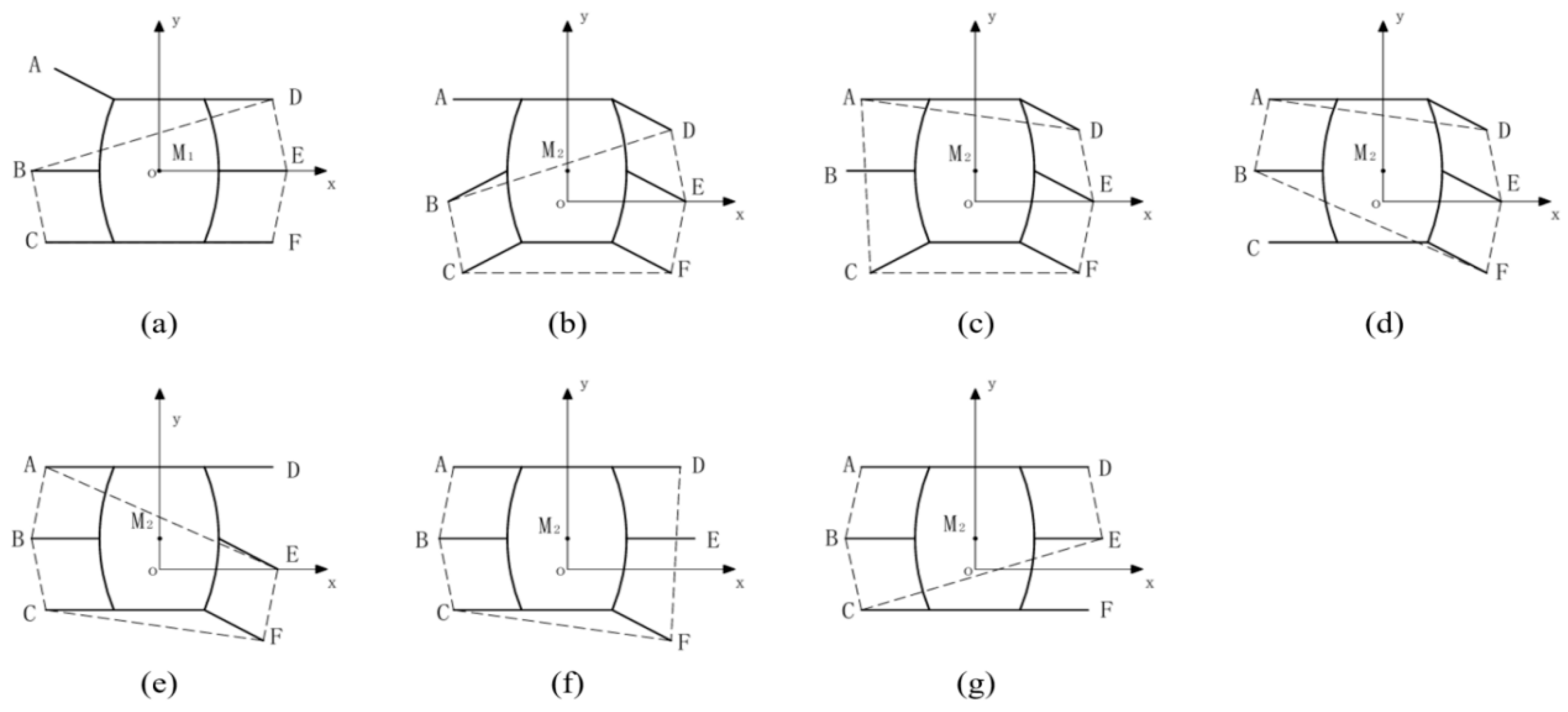
4.3.1. Triangular Gait
4.3.2. Ripple Gait
4.3.3. Wave Gait
4.4. Simulation Experiment and Result Analysis
4.4.1. Simulation of Triangular Gait
4.4.2. Simulation of Ripple Gait
4.4.3. Simulation of Wave Gait
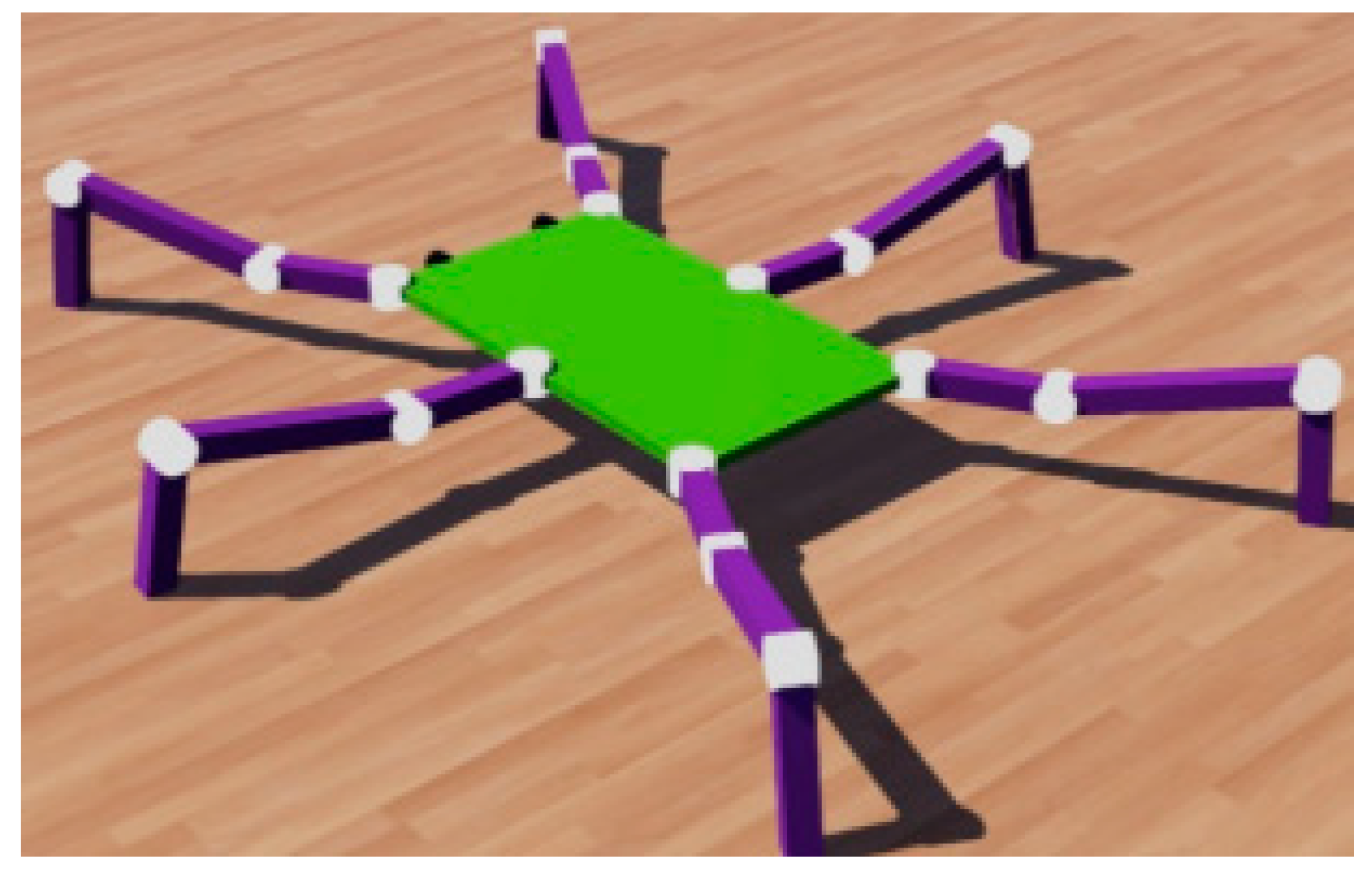
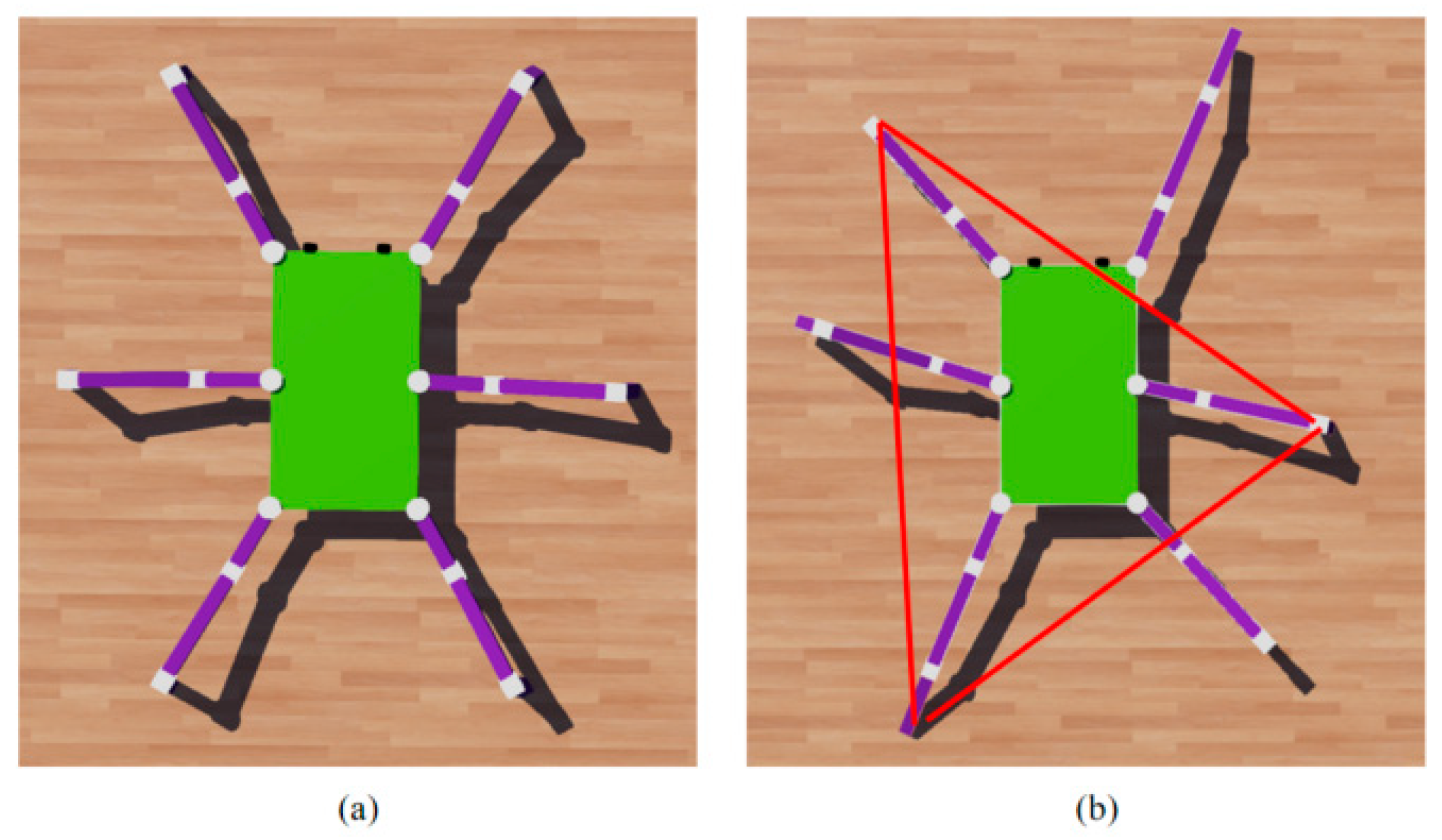
4.5. Model of the Wheel-Legged Bionic Hexapod Robot
4.6. Data Acquisition and Processing
4.7. Dynamic Analysis of Hexapod Bionic Robot with Wheel-Legged Transition Mechanism
4.7.1. Collection of Dynamic Data
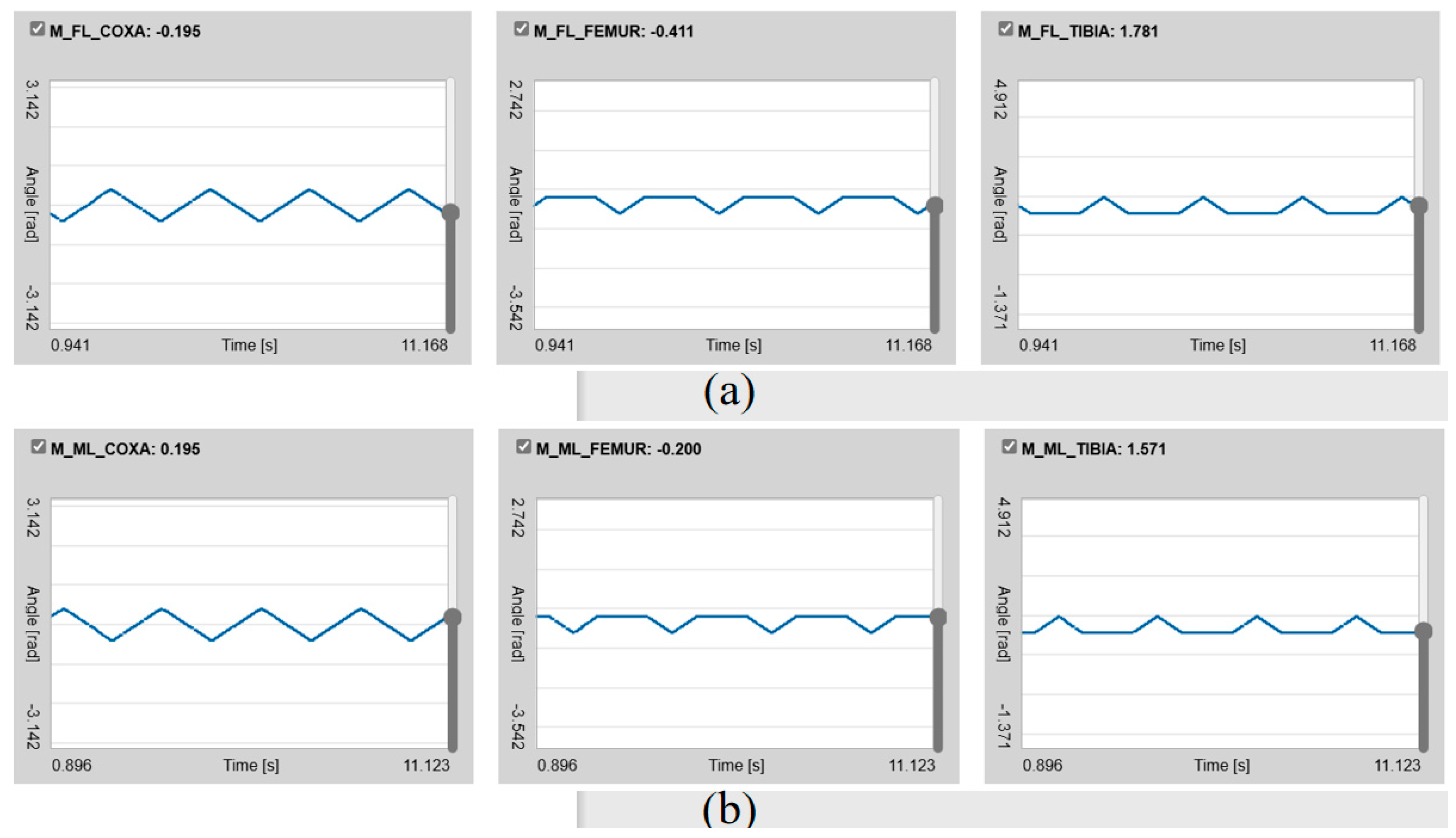
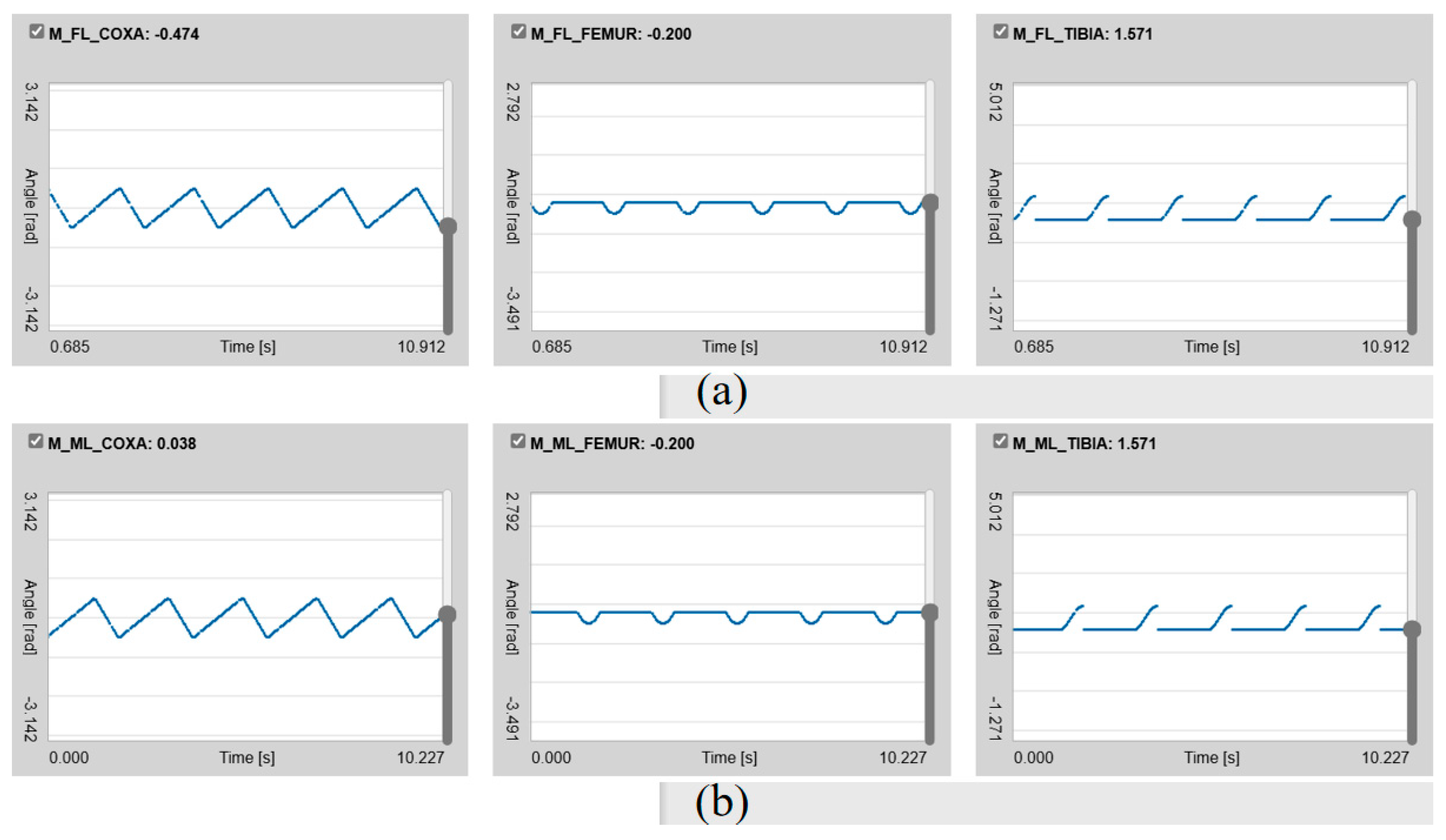
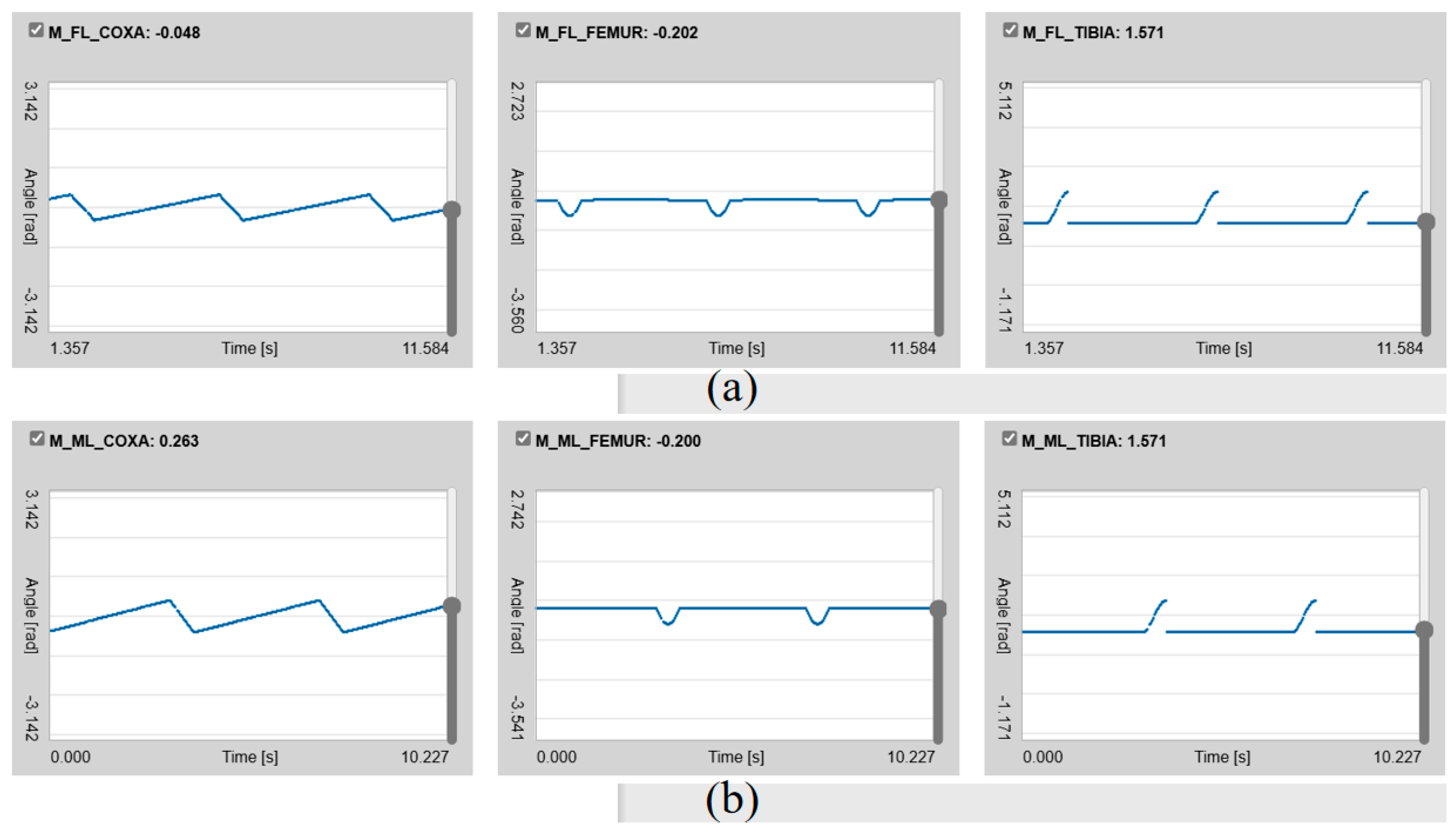
4.7.2. Change in Joint Angle
4.7.3. Phase Diagram of Joint
4.7.4. Analysis of Speed and Acceleration
4.7.5. Analysis of Power and Energy Consumption
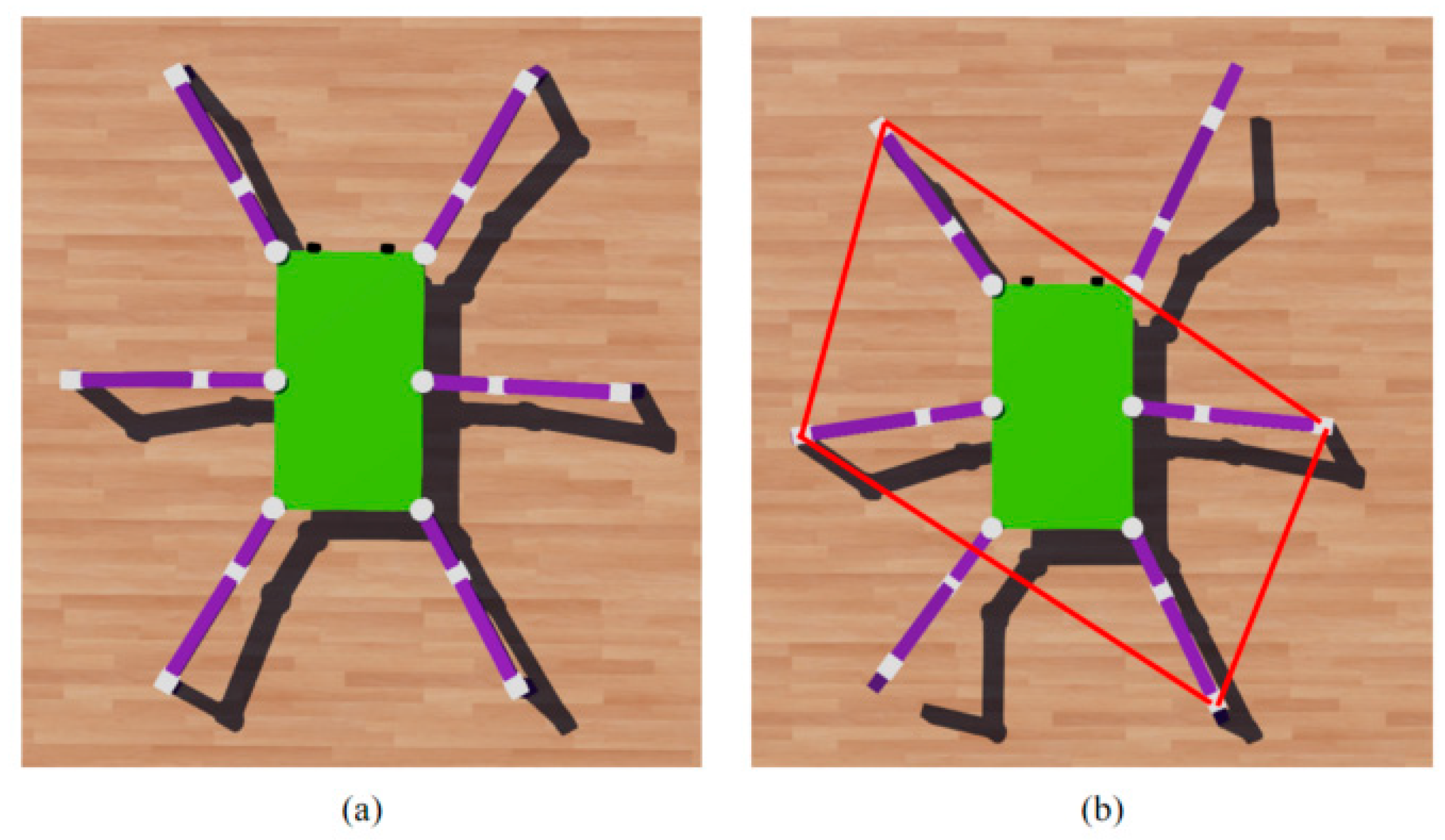
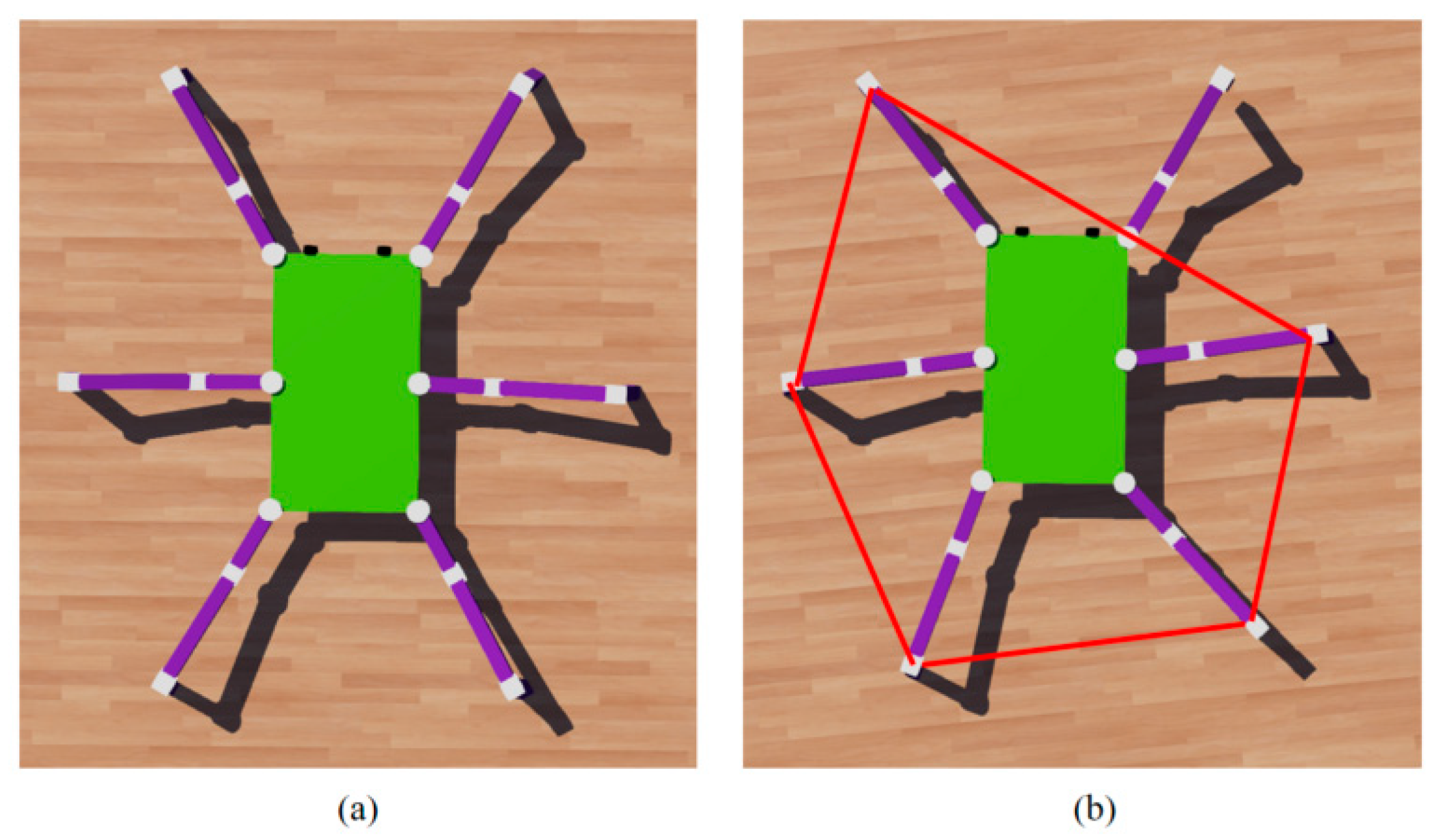
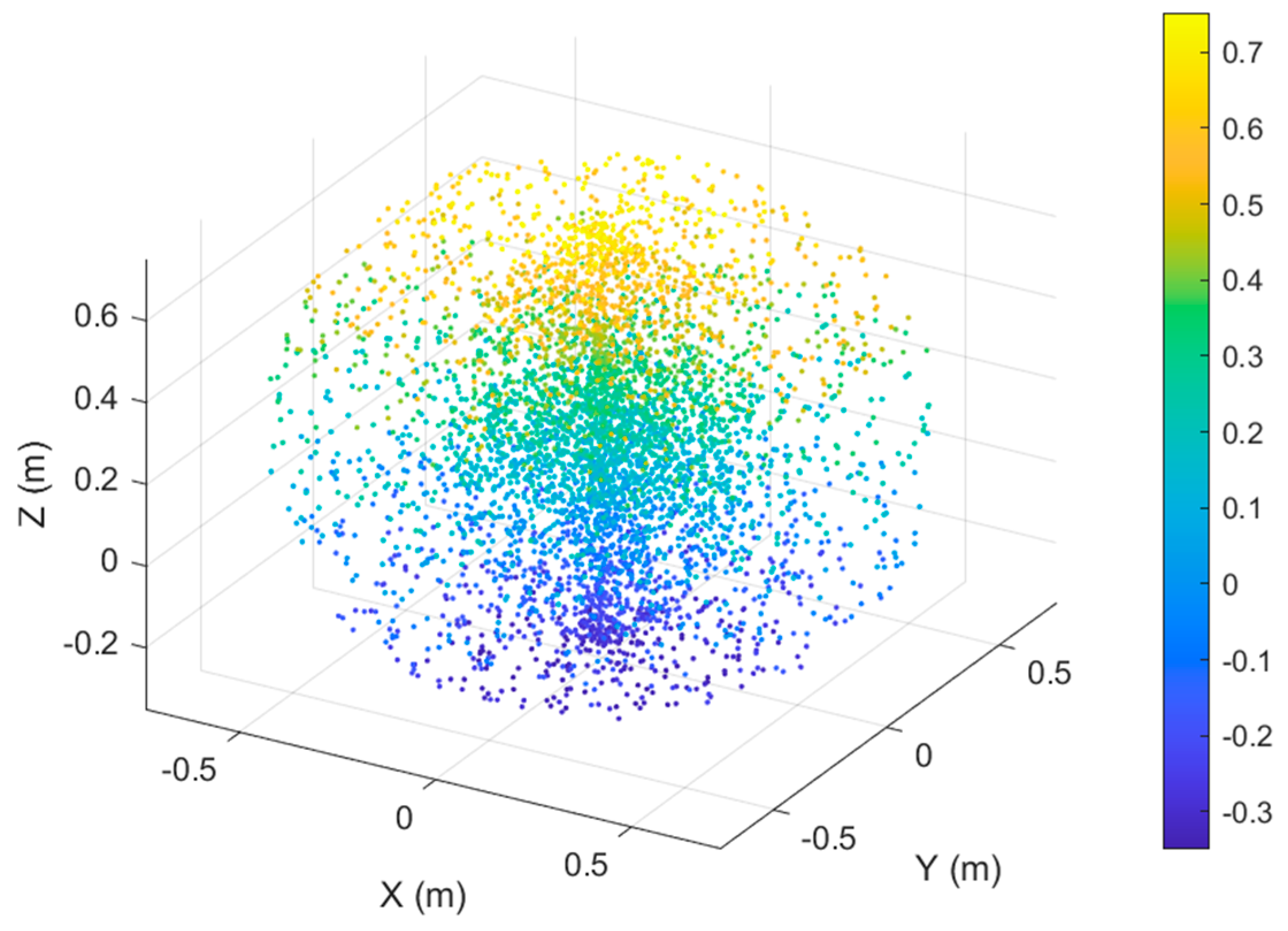
4.7.6. Workspace Analysis
5. Discussion
- (1)
- Transition Speed: the hollow-structured robot presented here achieves a wheel–leg transition time of 0.5 s, outperforming the four-bar linkage mechanism (0.8 s) by 37.5%. This signifies a substantial improvement in transformation agility.
- (2)
- Energy Efficiency: the iris-based transformation mechanism operates with minimal body fluctuation, leading to lower energy expenditure while ensuring motion stability and reliability. It completely avoids the dead-center issues inherent to four-bar linkages, which typically require counterweights to overcome, thereby further increasing energy demand. The robot in this study was fabricated as a 3D-printed model using ABS plastic, resulting in a significantly lighter structure compared to the referenced four-bar linkage robot. This weight reduction contributes directly to a substantial decrease in energy consumption. Experimental results confirm that our design achieves a reduction of over 50% in energy consumption while performing the same tasks as its counterpart.
- (3)
- Motion Stability: in its wheeled configuration, the robot maintains a low center of gravity, ensuring high stability during traversal. In its legged mode, the leg dimensions substantially exceed those of the central body, increasing the ground contact area and effectively enhancing terrain adaptability. This addresses the limitation of excessive structural rigidity that often constrains conventional robots in uneven environments. Furthermore, the hexapod bionic configuration inherently strengthens adaptability to varied terrains, providing fundamental guarantees for operational stability and reliability.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Viragh, Y.; Bjelonic, M.; Bellicoso, C.D.; Jenelten, F.; Hutter, M. Trajectory Optimization for Wheeled-Legged Quadrupedal Robots Using Linearized ZMP Constraints. IEEE Robot. Autom. Lett. 2019, 4, 1633–1640. [Google Scholar] [CrossRef]
- Nakajima, S. RT-Mover: A Rough Terrain Mobile Robot with a Simple Leg-Wheel Hybrid Mechanism. Int. J. Rob. Res. 2011, 30, 1609–1626. [Google Scholar] [CrossRef]
- Peng, P.; Zhang, X.J.; Yuan, G.M.; Liu, Z. Dynamic Analysis of the Wheel-Legged Mobile Robot. Appl. Mech. Mater. 2013, 344, 174–181. [Google Scholar] [CrossRef]
- Chen, W.-H.; Lin, H.-S.; Lin, Y.-M.; Lin, P.-C. TurboQuad: A Novel Leg–Wheel Transformable Robot with Smooth and Fast Behavioral Transitions. IEEE Trans. Robot. 2017, 33, 1025–1040. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, X.; Xu, H.; Zou, T.; Zhang, L. Transition Mechanism Design of a Hybrid Wheel-Track-Leg Based on Foldable Rims. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4788–4801. [Google Scholar] [CrossRef]
- Wei, C.; Yao, Y.; Wu, J.; Liu, R. Development and Analysis of a Closed-Chain Wheel-Leg Mobile Platform. Chin. J. Mech. Eng. 2020, 33, 80. [Google Scholar] [CrossRef]
- Wang, T.-H.; Lin, P.-C. A Reduced-Order-Model-Based Motion Selection Strategy in a Leg-Wheel Transformable Robot. IEEE/ASME Trans. Mechatron. 2022, 27, 3315–3321. [Google Scholar] [CrossRef]
- Bledt, G.; Powell, M.J.; Katz, B.; Di Carlo, J.; Wensing, P.M.; Kim, S. MIT Cheetah 3: Design and Control of a Robust, Dynamic Quadruped Robot. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2245–2252. [Google Scholar] [CrossRef]
- Zhang, M.; Su, Y. Research on Obstacle Performance and Tipping Stability of a Novel Wheel–Leg Deformation Mechanism. Mech. Sci. 2023, 14, 1–13. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Wang, T.-H.; Ho, K.-C.; Ko, C.-Y.; Lin, P.-C.; Lin, P.-C. Development of a Novel Leg-Wheel Module with Fast Transformation and Leaping Capability. Mech. Mach. Theory 2021, 163, 104348. [Google Scholar] [CrossRef]
- Li, H.; Xie, Z.; Cao, Y.; Zhang, R.; Qin, J. Design and Analysis of a Mobile Robot with Transformable Wheel-Legged Mechanism. J. Mech. Robot. 2025, 17, 061015. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, J.; Wang, T.; Meng, J.; Li, S.; Li, M. Mechanism Design and Dynamic Switching Modal Control of the Wheel-Legged Separation Quadruped Robot. Robotica 2023, 42, 660–683. [Google Scholar] [CrossRef]
- Zhang, R.; Pang, H.; Ji, Q.; Li, G.; Dong, W.; Wen, L.; Li, J. Structure Design and Traction Trafficability Analysis of Multi-Posture Wheel-Legs Bionic Walking Wheels for Sand Terrain. J. Terramechanics 2020, 91, 31–43. [Google Scholar] [CrossRef]
- Pan, K.; Zhang, Q.; Wang, Z.; Wang, S.; Zhou, A.; You, Y.; Wang, D. Method for the Posture Control of Bionic Mechanical Wheel-Legged Vehicles in Hilly and Mountainous Areas. Int. J. Agric. Biol. Eng. 2024, 17, 151–162. [Google Scholar] [CrossRef]
- Felton, S.M.; Tolley, M.T.; Onal, C.D.; Rus, D.; Wood, R.J. Robot Self-Assembly by Folding: A Printed Inchworm Robot. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2018; pp. 277–282. [Google Scholar] [CrossRef]
- Xu, K.; Wang, S.; Shi, L.; Li, J.; Yue, B. Horizon-Stability Control for Wheel-Legged Robot Driving over Unknow, Rough Terrain. Mech. Mach. Theory 2025, 205, 105887. [Google Scholar] [CrossRef]
- Mostyn, V.; Krys, V.; Kot, T.; Bobovsky, Z.; Novak, P. The Synthesis of a Segmented Stair-Climbing Wheel. Int. J. Adv. Robot. Syst. 2018, 15, 1–11. [Google Scholar] [CrossRef]
- Pan, Z.; Liu, S.; Zhou, S.; Li, B.; Niu, Z.; Wang, R. Collaborative Control of the Knee-Wheeled Wheel-Legged Robot: Considering Actuators Characteristics. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2024, 239, 272–289. [Google Scholar] [CrossRef]
- Wang, D.; Fang, B.; Zheng, J. Design and Research of Deformable Wheel-Legged Robot Based on Origami Mechanisms. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 8769–8784. [Google Scholar] [CrossRef]
- Li, Y.; Gao, J.; Chen, K.; Chen, W.; Yin, Z. Safe Trajectory Generation for Wheel-Leg Hybrid Mechanism Using Discrete Mechanics and Optimal Control. J. Mech. Robot. 2024, 16, 061014. [Google Scholar] [CrossRef]
- Raturi, P.; Chaudhary, S.; Mohan, S. Investigation of the Dynamic Behavior of a Slider Crank Mechanism-Based Wheel-Legged Mobile Robot. Robotica 2025, 43, 2803–2832. [Google Scholar] [CrossRef]
- Park, I.; Yoon, H.; Kim, S.; Kim, H.S.; Seo, T. Review on Transformable Wheel: Mechanism Classification and Analysis According to Mechanical Complexity. Int. J. Precis. Eng. Manuf. 2025, 26, 737–755. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, J.; Yang, P.; Cui, T.; Wu, D.; Zhang, L. Modeling and Stability Control of Steering and Reconfiguration Motion for Wheel-Legged Metamorphic Robot. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2025, 239, 4256–4272. [Google Scholar] [CrossRef]
- Du, Y.; Ruan, Q.; Yao, Y. Integrated Wheel–Foot–Arm Design of a Mobile Platform with Linkage Mechanisms. J. Mech. Robot. 2024, 16, 081017. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, H.S.; Seo, T. Type Synthesis and Kinematic Analysis of a 2-DOF Shape-Morphing Wheel Mechanism for Step-Overcoming. IEEE Access 2021, 9, 86500–86513. [Google Scholar] [CrossRef]
- Comin, F.J.; Saaj, C.M. Models for Slip Estimation and Soft Terrain Characterization with Multilegged Wheel–Legs. IEEE Trans. Robot. 2017, 33, 1438–1452. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Yu, Z.; Guan, Y.; Zhao, Y.; Zhuang, Z.; Sun, T. Design, Analysis, and Experiment of a Wheel-Legged Mobile Robot. Appl. Sci. 2023, 13, 9936. [Google Scholar] [CrossRef]
- Qiao, G.; Song, G.; Zhang, Y.; Zhang, J.; Li, Z. A Wheel-Legged Robot with Active Waist Joint: Design, Analysis, and Experimental Results. J. Intell. Robot Syst. 2016, 83, 485–502. [Google Scholar] [CrossRef]
- Won, J.; Ryu, S.; Kim, S.; Yoo, K.Y.; Kim, H.S.; Seo, T. Design Optimization of a Linkage-Based 2-DOF Wheel Mechanism for Stable Step Climbing. Sci. Rep. 2022, 12, 16912. [Google Scholar] [CrossRef]
- Shin, J.; Son, D.; Kim, Y.; Seo, T. Design Exploration and Comparative Analysis of Tail Shape of Tri-Wheel-Based Stair-Climbing Robotic Platform. Sci. Rep. 2022, 12, 19488. [Google Scholar] [CrossRef]
- Zhai, Z.; Wang, S.; Yang, G.; Guo, A.; Qu, P.; Song, Y.; Shao, S.; Zang, J. Novel Sandwich Structures with Double-Row and Crossed Pyramidal Lattice Cores: Design, Fabrication and Bending Behavior. Eng. Fail. Anal. 2025, 170, 109267. [Google Scholar] [CrossRef]
- Su, X.; Wang, S.; Guo, A.; Qu, P.; Guo, S.; Yang, G.; Yin, L.; Guo, M. Coupled Structure of Double-Layer Conical Shells and Annular Plates: Design, Fabrication and Compressive Property. Mater. Today Commun. 2025, 47, 113128. [Google Scholar] [CrossRef]
- Cornejo, J.; Weitzenfeld, A.; Baca, J.; Gecilia, E. Aerospace Bionic Robotics: BEAM-D Technical Standard of Biomimetic Engineering Design Methodology Applied to Mechatronics Systems. Biomimetics 2025, 10, 668. [Google Scholar] [CrossRef]
- Wang, S.; Yang, G.; Song, Y.; Shao, S.; Huang, S.; Zhang, J. Vibration characteristics of composite spherical shell with different numbers of damping cores. Alex. Eng. J. 2025, 120, 598–613. [Google Scholar] [CrossRef]
- Zhai, Z.; Wang, S.; Li, S.; Guo, A.; Qu, P.; Song, Y.; Yang, G.; Shao, S.; Tang, R. An experimental and numerical investigation into compressive failure of pyramidal lattice sandwich structures fabricated using stereolithography technology. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 2823–2840. [Google Scholar] [CrossRef]
- Wang, S.; Song, Y.; Qiao, Y.; Shao, S.; Wang, W. Dynamic performance of functionally graded composite structures with viscoelastic polymers. Sci. Rep. 2024, 14, 7613. [Google Scholar] [CrossRef] [PubMed]
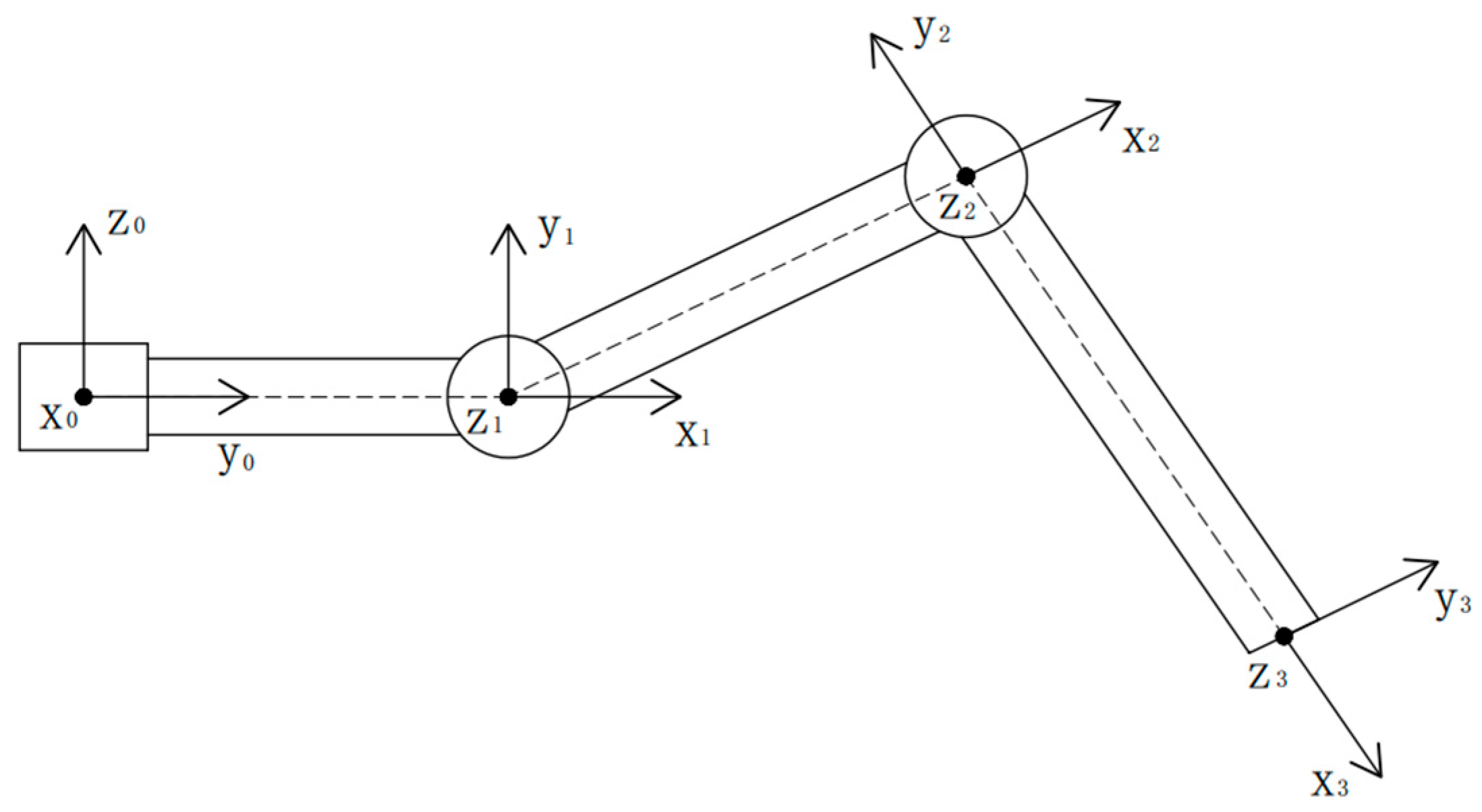




| i | θi/rad | di/mm | ai/mm | αi/rad |
|---|---|---|---|---|
| 1 | π/2 | 0 | 20 | π/2 |
| 2 | π/6 | 0 | 25 | 0 |
| 3 | −π/2 | 0 | 35 | 0 |
| Item | Coxa Parameters | Tibia Parameters |
|---|---|---|
| Type of grid | solid | solid |
| The used grid | standard | standard |
| Jacobian points with high quality grid | 16 points | 16 points |
| Size of cell | 0.981292 mm | 0.965056 mm |
| Tolerance | 0.0490646 mm | 0.0482528 mm |
| Quality of grid | excellent | excellent |
| Number of nodes | 105,665 | 104,227 |
| Number of cells | 65,243 | 62,863 |
| Maximum aspect ratio | 7.9613 | 7.0838 |
| Direction | M1 | M2 | M3 | M4 |
|---|---|---|---|---|
| left front | 0 | − | + | 0 |
| left rear | − | 0 | 0 | + |
| right front | + | 0 | 0 | − |
| right rear | 0 | + | − | 0 |
| Item | Value | Function |
|---|---|---|
| Gravitational acceleration | 9.81 m/s2 | Simulation of a real gravity environment |
| Coefficient of ground elasticity | 0.2 | Preventing reboundence from the end of the foot |
| Air density | 1.29 kg/m3 | Affecting wind resistance during high-speed motion |
| Step size | 30 mm | Maximum distance of a single leg in a single movement |
| Speed | 900 mm/min | Movement speed of hexapod robot |
| Time Step | Hip Joint | Thigh Joint | Knee Joint |
|---|---|---|---|
| 0 | 0 | pi/6 | −pi/2 |
| 1 | 0 | pi/4 | −pi/2 |
| 2 | 0 | pi/4 | −pi/3 |
| 3 | pi/6 | pi/4 | −pi/3 |
| 4 | pi/6 | pi/4 | −pi/2 |
| 5 | pi/6 | pi/6 | −pi/2 |
| 6 | −pi/6 | pi/6 | −pi/2 |
| 7 | −pi/6 | pi/4 | −pi/2 |
| 8 | −pi/6 | pi/4 | −pi/3 |
| 9 | pi/6 | pi/4 | −pi/3 |
| 10 | pi/6 | pi/4 | −pi/2 |
| 11 | pi/6 | pi/6 | −pi/2 |
| 12 | 0 | pi/6 | −pi/2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, Y.; Wang, S.; Guo, A.; Qu, P.; Han, W.; Yan, Q.; Liu, H.; Liu, C. Design and Gait Simulation Study of Wheel-Legged Conversion Device Used in Hexapod Bionic Robot. Processes 2025, 13, 3364. https://doi.org/10.3390/pr13103364
Mu Y, Wang S, Guo A, Qu P, Han W, Yan Q, Liu H, Liu C. Design and Gait Simulation Study of Wheel-Legged Conversion Device Used in Hexapod Bionic Robot. Processes. 2025; 13(10):3364. https://doi.org/10.3390/pr13103364
Chicago/Turabian StyleMu, Yidong, Shaoqing Wang, Anfu Guo, Peng Qu, Wenchao Han, Qing Yan, Haibin Liu, and Chunxia Liu. 2025. "Design and Gait Simulation Study of Wheel-Legged Conversion Device Used in Hexapod Bionic Robot" Processes 13, no. 10: 3364. https://doi.org/10.3390/pr13103364
APA StyleMu, Y., Wang, S., Guo, A., Qu, P., Han, W., Yan, Q., Liu, H., & Liu, C. (2025). Design and Gait Simulation Study of Wheel-Legged Conversion Device Used in Hexapod Bionic Robot. Processes, 13(10), 3364. https://doi.org/10.3390/pr13103364






