Smart Risk Assessment and Adaptive Control Strategy Selection for Human–Robot Collaboration in Industry 5.0: An Intelligent Multi-Criteria Decision-Making Approach

Abstract

The emergence of Industry 5.0 brings a paradigm shift towards collaborative environments where humans and intelligent robots work side-by-side, enabling personalized, flexible, and resilient manufacturing. However, integrating humans and robots introduces new operational and safety risks that require proactive and adaptive control strategies. This study proposes an intelligent multi-criteria decision-making framework for smart risk assessment and the selection of optimal adaptive control strategies in human–robot collaborative manufacturing settings. The proposed framework integrates advanced risk analytics, real-time data processing, and expert knowledge to evaluate alternative control strategies, such as real-time wearable sensor integration, vision-based dynamic safety zones, AI-driven behavior prediction models, haptic feedback, and self-learning adaptive robot algorithms. A cross-disciplinary panel of ten experts structures six main and eighteen sub-criteria spanning safety, adaptability, ergonomics, reliability, performance, and cost, with response time and implementation/maintenance costs modeled as cost types. Safety receives the most significant weight; the most influential sub-criteria are collision avoidance efficiency, return on investment (ROI), and emergency response capability. The framework preserves linguistic semantics from elicitation to aggregation and provides a transparent, uncertainty-aware tool for selecting and phasing adaptive control strategies in Industry 5.0 collaborative cells.

1. Introduction

The transition from Industry 4.0 to Industry 5.0 positions human–robot interaction (HRI) as a cornerstone of human-centric, sustainable, and resilient manufacturing. In collaborative work cells, the robot is no longer caged but shares physical space, tasks, and decision-making authority with operators, intertwining occupational safety, ergonomics, psychological trust, and ethical compliance. Safety 5.0 concepts, therefore, call for continuous risk monitoring via digital twins or adaptive safety envelopes embedded in the workflow of collaborative robots [1,2]. Yet accident statistics and field studies still report musculoskeletal strain, unintended collisions and data privacy breaches, hindering large-scale collaborative robotics (cobots) adoption [3,4,5].

Concurrently, Safety 5.0 research advocates real-time “human–digital twin” supervision in which worker and cobots twins exchange data to predict and neutralize hazards before contact occurs. Pasman [1] frame Safety 5.0 as the safety analog of Industry 5.0, positing a closed feedback loop that mediates adaptive speed and separation monitoring. Recent demonstrators merge ROS messages with neuro ergonomic streams to create “collaboration twins” that update collision envelopes in under 10 ms, tightening risk response latency without throttling productivity [2]. Early contributions, such as Krüger [6], shed light on technical and organizational challenges for human and robot coexistence in shared workspaces and described key enablers such as real-time communication, dynamic task assignment, and workplace ergonomic design.

Subsequently, those able to inform working staff in human–robot collaboration (HRC) embraced these concepts. Cherubini [7] took these bases, structuring physical HRI to promote intuitive control and user interface design in collaborative manufacturing. Their work highlights the necessity of co-adaptation, where both robot and human dynamically adjust behavior based on real-time feedback, an idea that remains central in adaptive robotics. In contrast, Mourtsiz [8] studied digital transformation in HRC, showing that digital twins and predictive maintenance can increase both the reliability of robotic cells and the system’s responsiveness. Their work quantitatively showed operational efficiency and reliability improvements when HRC systems were augmented with virtual replicas and analytics-driven feedback loops. Regarding operator trust and acceptance, Charalambous [9] created a validated measure for industrial HRC to determine trust in industrial HRC with key psychological and behavioral constructs affecting trust development.

HRC is steadily moving toward production cells that feel practical on the shop floor: safer by design, easier to integrate, and clearer to operate. Studies now pair augmented-reality task cues with multimodal perception to smooth handovers and reduce avoidable pauses during assembly—essentially providing people with timely, context-aware hints that keep work flowing [10]. Mapping the construction sector in terms of “Construction 5.0” highlights a similar momentum: safety, planning, and perception dominate, yet a further need arises for standardization and data privacy [11]. On the control front, hybrid Speed and Separation Monitoring represent something valuable in practice: series protection distance enforcement, speed adjustment in real time, and reduction in collision risk; ROS2 implementations show that these views could well be applied in real life [12]. Optimization joins with this by framing human operator lines as formal balancing problems: mixed-integer formulations, together with clever neighborhood heuristics, give competitive cycle times and scale much better than exact solvers on hard instances [13]. If safety is considered as part of the objective from the start, that is, through the protective distance and speed limits, then the “optimal” plan gets meaningfully changed and trades a little throughput for a big gain in reliability [14]. Taken together, these threads outline a clear direction: AR-assisted guidance, ISO-grounded safety logic, and operations research tooling evolving side by side to make collaborative assembly both productive and genuinely safe.

Their study was followed by recent research such as Yu et al. [15], which explored AI-based situational awareness to actively guarantee safety in complex scenarios, showing that greater transparency and explainability play a significant role in maintaining user confidence. The economic effects of service robotics have also been a topic of interest among academicians. Shanksharalambous [16] demonstrated a comprehensive cost–benefit analysis of robotic and cobotic systems, specifically in service industries like healthcare and hospitality. They illustrated that customers’ willingness to pay is enhanced under certain conditions; for example, if cobots serve non-leadership roles and customers are allowed to choose service delivery modes. Regarding performance engineering, Boschetti [12] developed a mathematical performance evaluation model for collaborative assembly systems with multiple robots and operators. Their simulations and experiment validations determined that the most critical factors, such as resource setup, quantity of feeding devices, and overlap between tasks, significantly influence cycle time and throughput.

Researchers increasingly model HRI safety as a multi-criteria decision-making (MCDM) problem to structure this multi-faceted risk landscape. Early work balanced ergonomic and economic objectives in robot cell design [17], while real-time sensor streams were coupled with fuzzy comprehensive evaluation to update risk estimates dynamically [18]. Factor prioritization studies followed: decision-making trial and evaluation laboratory (DEMATEL) analysis revealed that robot reliability and automation level dominate medical device assembly hazards [19], and a Z-number enhanced Delphi–DEMATEL–VIKOR chain captured expert hesitancy in automotive welding [20,21]. Fuzzy TOPSIS integration has since shown that physical safety concerns outweigh psychological or legal issues in a 28-factor hierarchy [22], while related studies employ Z-numbers in warehousing or neutrosophic sets in healthcare robotics to manage epistemic uncertainty [20,21,23]. Comparative analyses of fuzzy AHP/VIKOR pipelines in autonomous vehicle risk assessment further broaden the toolbox [24].

Beyond classical fuzzy sets, higher order representations encode the confidence experts attach to their judgements. Abdel-Basset et al. [19] show that Z-number Delphi weighting tempers outlier influence in automotive welding, while Bozkus et al. [16] report that single-valued neutrosophic TOPSIS improves near-miss discrimination by 9% in smart warehouse data. Such evidence reinforces calls to preserve linguistic semantics end-to-end and aligns with survey warnings on semantic drift in Analytic Hierarchy Process (AHP)–TOPSIS pipelines [25] and safety assurance reviews [5].

Despite notable advancements, the literature on collaborative robotics still reveals several structural and conceptual shortcomings that hinder broader applicability and system robustness. Firstly, while the field has evolved from safety-centric design toward economically viable, socially aware, and digitally integrated frameworks, real-time uncertainty in dynamic human–robot interactions remains insufficiently addressed, limiting responsiveness in unstructured environments. Second, cobot service-pricing models have not been well studied, though robotic and human services price imbalances may enhance social inequalities. Furthermore, scalability issues persist in multi-agent HRC systems due to computational and spatial coordination difficulties, especially in high-variability tasks. In addition to these gaps, three structural limitations further constrain the generalizability of current approaches:

(i)

Criteria hierarchies are often narrowly sector-specific methods designed for automotive or medical domains, and frequently fail to transfer to logistics or service robotics.

(ii)

Weighting tools are often paired with ranking engines like TOPSIS or VIKOR without verifying that their linguistic scales remain compatible end-to-end, producing semantic drift [5,25].

(iii)

Expert panels rarely fuse engineering, ergonomic, and cognitive science perspectives, although high-reliability settings require such triangulation [26].

Addressing these challenges will require sustained, interdisciplinary research efforts that blend technical, human-centered, and ethical dimensions to fully realize the transformative promise of collaborative robotics in the Industry 5.0 era. The pressing need for a generalizable and uncertainty-aware framework is reinforced by projections estimating the collaborative robot market to reach approximately USD 2 billion by 2030 [4] and by meta-analytic findings indicating a significant decline in operator trust when safety-related explanations lack transparency [3].

To close these gaps, we introduce an end-to-end spherical fuzzy MCDM framework for selecting adaptive control strategies in human–robot collaboration. A cross-disciplinary panel of ten experts structures six main and 18 sub-criteria spanning safety, adaptability, ergonomics, reliability, performance, and cost. We elicit criterion weights with Spherical Fuzzy–Stepwise Weight Assessment Ratio Analysis (SF SWARA) and rank five candidate strategies with SF VIKOR. We explicitly treat response time and implementation/maintenance costs as cost-type criteria and apply VIKOR acceptance and sensitivity tests. This design preserves linguistic semantics across elicitation and aggregation and yields a transparent, uncertainty-aware decision tool for Industry 5.0 deployments.

In HRC, uncertainty stems simultaneously from expert judgment ambiguity and real-time sensing noise (occlusion, latency, workload effects). Spherical fuzzy sets (SFSs) are well suited to this context because membership, non-membership, and hesitancy are modeled independently under a spherical constraint, preserving linguistic semantics from elicitation to aggregation and stabilizing downstream weighting/ranking compared with classical. Intuitionistic Fuzzy Sets (IFSs), Z-numbers, or single-valued neutrosophic formulations [27]. Spherical fuzzy logic aligns with HRC safety evidence and practice where risk drivers span safety assurance, vision-based protective zones, and ergonomics/trust, by enabling robust aggregation of multidisciplinary expert inputs while remaining methodologically compatible with our SF-SWARA–SF-VIKOR pipeline [4]. Accordingly, SFSs are adopted to encode expert assessments and propagate them consistently through weighting and compromise ranking in the proposed Industry 5.0 decision framework.

2. The Proposed Methodology

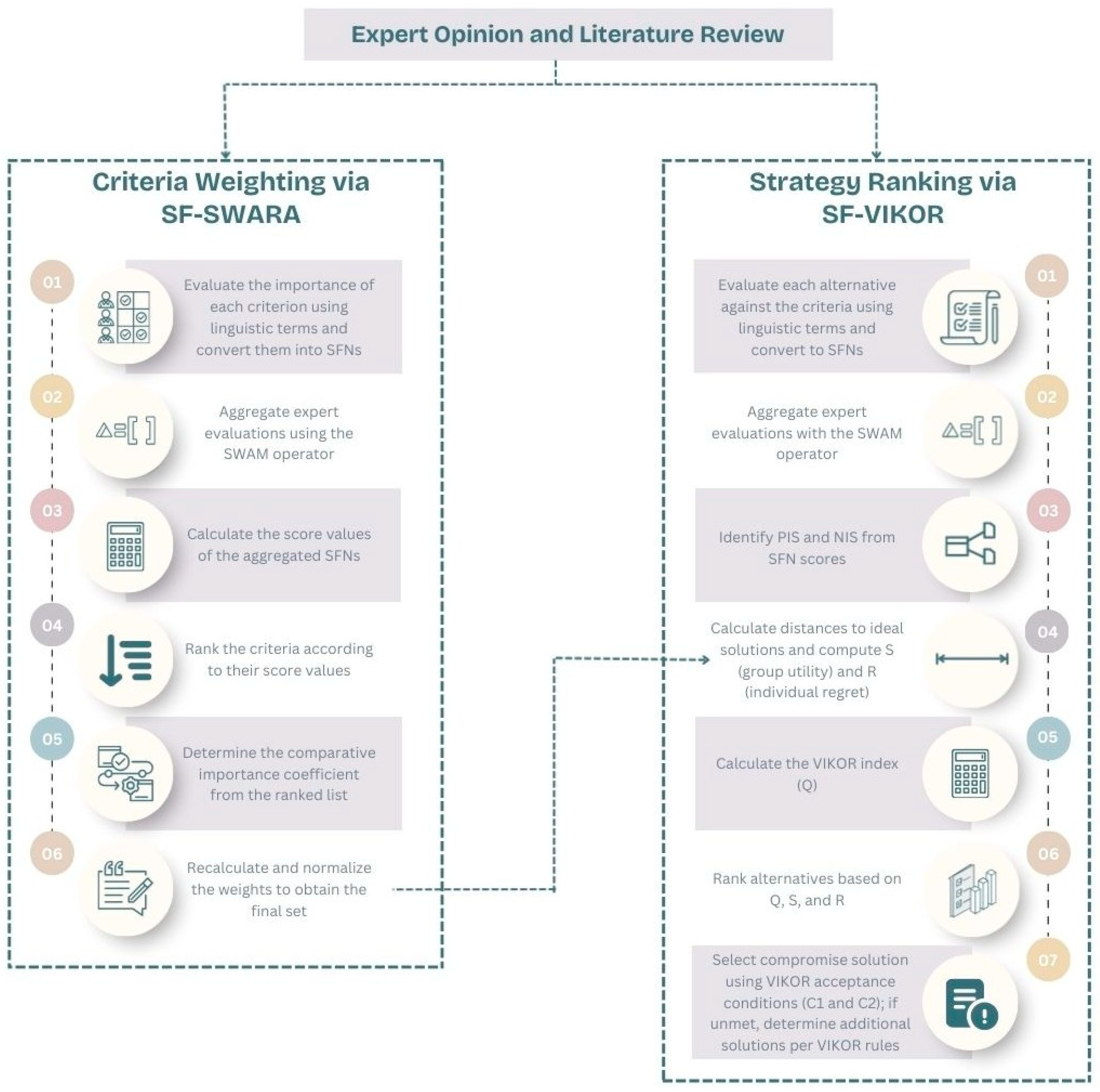
This study proposes an integrated MCDM framework that combines SF-SWARA and SF-VIKOR to determine the most appropriate adaptive control strategy for human–robot collaboration in Industry 5.0 environments. The methodological flow is illustrated in Figure 1, which presents the sequential process from criteria definition to final strategy ranking. The proposed framework enables decision-makers to incorporate uncertainty, hesitation, and subjectivity in expert evaluations while ensuring a structured and mathematically consistent prioritization process. This methodological framework ensures that (i) expert opinions are aggregated in a way that preserves linguistic meaning, (ii) uncertainty is explicitly represented throughout the decision-making process, and (iii) the selected strategy reflects a balanced trade-off among multiple, potentially conflicting objectives.

In the first phase, SF-SWARA is applied to determine the importance of the weights of the evaluation criteria. Unlike traditional SWARA, which operates on crisp or classical fuzzy values, the spherical fuzzy environment allows experts to express their assessments through three independent degrees: membership, non-membership, and hesitancy. This extension ensures that the inherent uncertainty of expert judgments is more comprehensively captured. In the second phase, SF-VIKOR is employed to rank the alternative adaptive control strategies. The VIKOR method is particularly suitable when decision problems involve conflicting criteria, as it identifies a compromise solution that balances group utility and individual regret. Integrating VIKOR with spherical fuzzy sets further strengthens its capability to handle vague and imprecise evaluations.

Figure 1 illustrates the stepwise integration of SF-SWARA and SF-VIKOR. Expert judgments on the main and sub-criteria are first elicited in linguistic form and encoded as spherical fuzzy numbers using Table 1, then aggregated with the Spherical Weighted Arithmetic Mean (SWAM) operator to preserve the semantics of uncertainty and hesitation. SF-SWARA converts these aggregated assessments into normalized criterion weights by ranking criteria via score values and applying comparative coefficients. The alternative strategies are then evaluated under each criterion with the same linguistic scale in Table 2, aggregated across experts, and mapped to positive ideal number (PIS) and negative ideal number (NIS) while treating Response time (C53), Implementation cost (C61), and Maintenance cost (C62) as cost-type criteria. SF-VIKOR computes group utility (S), individual regret (R) from distances to these ideals and obtains Q with λ set to 0.5 to balance group utility and individual regret alternatives are ranked by compromise index (Q), and the solution is validated by the acceptable advantage and acceptable stability conditions. For illustration, if Safety is mostly judged “Very High,” its encoded SFNs are aggregated and scored to yield a high SF-SWARA weight, and the same encoded structure is used when calculating each strategy’s S, R, and Q under the Safety criterion. A strategy that is highly efficient but less safe will be compared with others in terms of trade-offs, allowing the method to reveal a balanced compromise solution.

2.1. Preliminaries of Spherical Fuzzy Sets

Fuzzy set theory traditionally represents uncertainty using a membership degree (μ) in the range [0, 1], with the non-membership degree defined as (1 − μ). However, this formulation is insufficient when the decision context involves hesitation and incomplete information. IFSs, introduced by Atanassov [28], extended the classical approach by incorporating both membership (μ) and non-membership (ν) degrees, along with a hesitation degree (π), where μ + ν + π ≤ 1.

Building on this concept, Spherical Fuzzy Sets (SFSs), proposed by Gündoğdu and Kahraman [27], further generalized uncertainty representation by allowing μ, ν, and π to be defined independently in [0, 1], subject to the constraint μ² + ν² + π² ≤ 1. This geometric representation on a spherical surface offers enhanced flexibility for modeling complex decision environments [29,30]. Figure 2 presents the schematic view of SFSs. As illustrated, the admissible domain of spherical fuzzy membership grades strictly encompasses those of Pythagorean and intuitionistic fuzzy sets, reflecting their respective constraint conditions.

Mathematically, a SFN is expressed as [31]:

$$\tilde{S}\cong \left\{x, {\tilde{S}(\mu }_{\tilde{s}}\left(x\right), v_{\tilde{s}}\left(x\right), {\pi }_{\tilde{s}}\left(x\right));x\in X\right\}$$

(1)

where ${\mu }_{\tilde{s}}\left(x\right)$, $v_{\tilde{s}}\left(x\right)$ and ${\pi }_{\tilde{s}}\left(x\right)$ are the membership, non-membership, and hesitancy degrees, respectively. Operations such as addition, multiplication, scalar multiplication, exponentiation, score computation, and Euclidean distance are defined to enable SFS-based decision modeling [31,32,33].

Let SFNs $\tilde{\alpha }=S\left({\mu }_{\tilde{\alpha }},v_{\tilde{\alpha }},{\pi }_{\tilde{\alpha }}\right)$ and $\tilde{\beta }=S\left({\mu }_{\tilde{\beta }},v_{\tilde{\beta }},{\pi }_{\tilde{\beta }}\right)$ be two SFNs and $\lambda$ be a positive scalar

Summation:

$$\tilde{\alpha }\oplus \tilde{\beta }=\tilde{S}\left(\sqrt{{{\mu }_{\tilde{\alpha }}^2+{\mu }_{\tilde{\beta }}^2-\mu }_{\tilde{\alpha }}^2{\mu }_{\tilde{\beta }}^2}, { v}_{\tilde{\alpha }}{v}_{\tilde{\beta },} \sqrt{\left(1-{\mu }_{\tilde{\alpha }}^2\right){\pi }_{\tilde{\beta }}^2+\left(1-{\mu }_{\tilde{\beta }}^2\right){\pi }_{\tilde{\alpha }}^2-{\pi }_{\tilde{\alpha }}^2{\pi }_{\tilde{\beta }}^2}\right)$$

(2)

Multiplication:

$$\tilde{\alpha }\otimes \tilde{\beta }=\tilde{S}\left({\mu }_{\tilde{\alpha }}{\mu }_{\tilde{\beta },} \sqrt{{v_{\tilde{\alpha }}^2+v_{\tilde{\beta }}^2-v}_{\tilde{\alpha }}^2{v}_{\tilde{\beta }}^2} ,\sqrt{\left(1-v_{\tilde{\alpha }}^2\right){\pi }_{\tilde{\beta }}^2+\left(1-v_{\tilde{\beta }}^2\right){\pi }_{\tilde{\alpha }}^2-{\pi }_{\tilde{\alpha }}^2{\pi }_{\tilde{\beta }}^2} \right)$$

(3)

Scalar multiplication:

$$\lambda \tilde{\alpha }=\tilde{S}\left(\sqrt{1-{(1-{\mu }_{\tilde{\alpha }}^2)}^{\lambda }},v_{\tilde{\alpha }}^{\lambda }, \sqrt{{(1-{\mu }_{\tilde{\alpha }}^2)}^{\lambda }-{(1-{\mu }_{\tilde{\alpha }}^2-{\pi }_{\tilde{\alpha }}^2)}^{\lambda }} \right)$$

(4)

Exponentiation:

$${\tilde{\alpha }}^{\lambda }=\tilde{S}\left({\mu }_{\tilde{\alpha }}^{\lambda }, \sqrt{1-{(1-v_{\tilde{\alpha }}^2)}^{\lambda }}, \sqrt{{(1-v_{\tilde{\alpha }}^2)}^{\lambda }-{(1-v_{\tilde{\alpha }}^2-{\pi }_{\tilde{\alpha }}^2)}^{\lambda }}\right)$$

(5)

Score function:

$$S\left(\tilde{\alpha }\right)={\displaystyle \frac{1}{3}}\left(2+{\mu }_{\tilde{\alpha }}^2-v_{\tilde{\alpha }}^2-{\pi }_{\tilde{\alpha }}^2\right)$$

(6)

Euclidean distance:

$$D(\tilde{\alpha },\tilde{\beta })=\sqrt{\left({\left({\mu }_{\tilde{\alpha }}-{\mu }_{\tilde{\beta }}\right)}^2+{\left(v_{\tilde{\alpha }}-v_{\tilde{\beta }}\right)}^2+{\left({\pi }_{\tilde{\alpha }}-{\pi }_{\tilde{\beta }}\right)}^2\right)}$$

(7)

Spherical Weighted Arithmetic Mean (SWAM) operator:

$$\begin{gathered} {\mathrm{S}\mathrm{W}\mathrm{A}\mathrm{M}}_w\left({\tilde{A}}_{s_1},{\tilde{A}}_{s_2},\dots ,{\tilde{A}}_{s_n}\right)=\left\{{\left[1-{\prod }_{i=1}^n {\left(1-{\mu }_{{\tilde{A}}_S}^2\right)}^{w_i}\right]}^{1/2},\right.{\prod }_{i=1}^n v_{{\tilde{A}}_s}^{w_i}, \\ \left[{\prod }_{i=1}^n {\left(1-{\mu }_{{\tilde{A}}_S}^2\right)}^{w_i}\left.{\left.-{\prod }_{i=1}^n {\left(1-{\mu }_{{\tilde{A}}_s}^2-{\pi }_{{\tilde{A}}_s}^2\right)}^{w_i}\right]}^{1/2}\right\}\right. \end{gathered}$$

(8)

where $w=\left(w_1,w_2,\dots ,w_n\right);w_i\in [0, 1];\sum _{i=1}^n w_i=1$.

2.2. Steps of Proposed Decision Framework

The SWARA method, first introduced by Keršulienė et al. [34], is a systematic approach for determining the relative importance of evaluation criteria based on expert judgment. By allowing decision-makers to provide pairwise comparative importance assessments, SWARA ensures that each criterion’s weight reflects current operational priorities and expert insights [35]. In this study, the method is implemented within a spherical fuzzy environment, resulting in SF-SWARA, to more accurately capture uncertainty, hesitation, and vagueness in expert evaluations. This enhancement provides a richer and more reliable weighting process for both main and sub-criteria at different hierarchical levels. SF-SWARA was used due to its simplicity and transparency in capturing expert judgments, imposing a lower cognitive burden compared to SF-AHP, while simultaneously incorporating uncertainty into the process through SFSs [36]. On the other hand, SF-VIKOR stands out as a critical method in Industry 5.0 contexts with conflicting objectives, owing to its compromise-based logic that balances group utility and individual regret [37,38]. Compared to methods such as SF-TOPSIS, which primarily focus on closeness or outranking relations, SF-VIKOR more effectively reflects the trade-offs required in adaptive control and risk assessment [36]. When these two methods are integrated, they provide a practical and uncertainty-sensitive decision-making framework for addressing complex problems in modern industrial and technological domains.

Once the criteria weights are obtained, the VIKOR method is applied to rank alternative adaptive control strategies. Recognized for its robustness in handling decision problems with conflicting objectives, VIKOR seeks compromise solutions that best balance group utility and individual regret [38,39]. This capability is particularly valuable in Industry 5.0 contexts, where safety, efficiency, and adaptability may present competing demands. However, classical VIKOR can be limited when processing vague or imprecise data, a challenge frequently encountered in real-world decision-making. The method can effectively address these shortcomings by embedding VIKOR within the spherical fuzzy environment, ensuring that the rankings fully reflect the uncertainty present in expert assessments.

Through the integration of SF-SWARA for weighting and SF-VIKOR for ranking, the proposed methodology delivers a transparent, mathematically rigorous, and uncertainty-aware decision-support mechanism. The detailed procedural steps of the framework are outlined below.

Stage 1—Criteria Weighting via SF-SWARA

Step 1.1—Evaluation of Criteria: Experts assess the relative importance of each criterion using predefined linguistic terms (Table 1), which are then converted into SFNs.

Table 1. The description and fuzzy scales of linguistic parameters [31,40].

Linguistic Terms	$\mathbf{SFN} \left(\mathit{\mu },\mathit{v},\mathit{\pi }\right)$
ALI—Absolutely Low Importance	(0.1, 0.9, 0.0)
VLI—Very Low Importance	(0.2, 0.8, 0.1)
LI—Low Importance	(0.3, 0.7, 0.2)
MLI—Medium Low Importance	(0.4, 0.6, 0.3)
EEI—Equal Importance	(0.5, 0.5, 0.4)
MHI—Medium High Importance	(0.6, 0.4, 0.3)
HI—High Importance	(0.7,0.3, 0.2)
VHI—Very High Importance	(0.8, 0.2, 0.1)
AHI—Absolutely High Importance	(0.9, 0.1, 0.0)

Table 1. The description and fuzzy scales of linguistic parameters [31,40].

Linguistic Terms	$\mathbf{SFN} \left(\mathit{\mu },\mathit{v},\mathit{\pi }\right)$
ALI—Absolutely Low Importance	(0.1, 0.9, 0.0)
VLI—Very Low Importance	(0.2, 0.8, 0.1)
LI—Low Importance	(0.3, 0.7, 0.2)
MLI—Medium Low Importance	(0.4, 0.6, 0.3)
EEI—Equal Importance	(0.5, 0.5, 0.4)
MHI—Medium High Importance	(0.6, 0.4, 0.3)
HI—High Importance	(0.7,0.3, 0.2)
VHI—Very High Importance	(0.8, 0.2, 0.1)
AHI—Absolutely High Importance	(0.9, 0.1, 0.0)

Step 1.2—Aggregation of Evaluations: Individual expert opinions are aggregated using the SWAM operator.

Step 1.3—Score Computation: Score values of the aggregated SFNs are calculated.

Step 1.4—Criteria Ranking: Criteria are ordered according to their score values.

Step 1.5—Comparative Importance Determination: The relative importance of each criterion is determined from the ranked list, and the comparative coefficient $k_j$ is computed. Here, $c_j$ denotes the comparative importance of criterion $j$ relative to the previous one, while $k_j$ indicates the comparative importance coefficient derived from these values.

$$k_j=\left\{\begin{array}{l}1, j=1\hfill \\ c_j+1, j>1\end{array}\right.$$

(9)

Step 1.6—Weight Recalculation and Normalization: Criteria weights are recalculated and normalized to obtain the final set of weights. Here, $q_j$ denotes the recalculated relative importance value of criterion $j$, which is obtained iteratively based on the comparative importance coefficients $\left(k_j\right)$.

$$q_j=\left\{\begin{array}{l}1, j=1\\ {\displaystyle \frac{q_{(j-1)}}{k_j}}, j>1\end{array}\right.$$

(10)

$$w_j={\displaystyle \frac{q_j}{\sum _{j=1}^n q_j}}$$

(11)

Stage 2—Strategy Ranking via SF-VIKOR

Step 2.1—Evaluation of Alternatives: Experts evaluate each alternative strategy against the criteria using linguistic terms (Table 2), then convert them to SFNs.

Table 2. Linguistic terms [31,40].

Linguistic Term	$\mathbf{SFN} \left(\mathit{\mu },\mathit{v},\mathit{\pi }\right)$
Absolutely Low (AL)	0.1, 0.9, 0.1
Very Low (VL)	0.2, 0.8, 0.2
Low(L)	0.3, 0.7, 0.3
Medium Low (ML)	0.4, 0.6, 0.4
Fair (F)	0.5, 0.5, 0.5
Medium High (MH)	0.6, 0.4, 0.4
High (H)	0.7, 0.3, 0.3
Very High (VH)	0.8, 0.2, 0.2
Absolutely high (AH)	0.9, 0.1, 0.1

Table 2. Linguistic terms [31,40].

Linguistic Term	$\mathbf{SFN} \left(\mathit{\mu },\mathit{v},\mathit{\pi }\right)$
Absolutely Low (AL)	0.1, 0.9, 0.1
Very Low (VL)	0.2, 0.8, 0.2
Low(L)	0.3, 0.7, 0.3
Medium Low (ML)	0.4, 0.6, 0.4
Fair (F)	0.5, 0.5, 0.5
Medium High (MH)	0.6, 0.4, 0.4
High (H)	0.7, 0.3, 0.3
Very High (VH)	0.8, 0.2, 0.2
Absolutely high (AH)	0.9, 0.1, 0.1

Step 2.2—Aggregation of Alternative Evaluation: The SWAM operator is applied to consolidate expert assessments for each alternative–criterion pair.

Step 2.3—Ideal Solutions Identification: Positive (${\tilde{X}}^{*}$) and negative (${\tilde{X}}^{-}$) ideal solutions are determined based on the highest and lowest SFN score values.

Step 2.4—Distance Calculation: The distances of each alternative from the ideal solutions are computed, and group utility (S) and individual regret (R) are calculated.

$$S_i=\sum _{j=1}^n w_j{\displaystyle \frac{\mathcal{D}\left({\tilde{X}}_{ij},{\tilde{X}}_j^{*}\right)}{\mathcal{D}\left({\tilde{X}}_j^{-},{\tilde{X}}_j^{*}\right)}}$$

(12)

$$R_i=\underset{j}{max} \left(w_j{\displaystyle \frac{\mathcal{D}\left({\tilde{X}}_{ij},{\tilde{X}}_j^{*}\right)}{\mathcal{D}\left({\tilde{X}}_j^{-},{\tilde{X}}_j^{*}\right)}}\right)$$

(13)

Step 2.5—VIKOR Index Calculation: The VIKOR index (Q) is calculated.

$$Q_i=v{\displaystyle \frac{\left(S_i-S^{+}\right)}{{(S}^{-}-S^{+})}}+\left(1-v\right){\displaystyle \frac{\left(R_i-R^{+}\right)}{{(R}^{-}-R^{+})}}$$

(14)

where

$$S^{+}=\underset{i}{\min }{S}_i;S^{-}=\underset{i}{\max }{S}_i$$

(15)

$$R^{+}=\underset{i}{\min }{R}_i;R^{-}=\underset{i}{\max }{R}_i$$

(16)

$v$ represents the weight of the strategy of maximum group utility.

Step 2.6—Alternative Ranking: Alternatives are ranked according to Q, S, and R values.

Step 2.7—Compromise Solution Selection: The final strategy is determined based on the VIKOR acceptance conditions [41,42]:

C1: “Acceptable advantage”:

$$Q\left(a^{″}\right)-Q\left(a^{\prime }\right)\ge 1/(m-1)$$

(17)

where $\left(a^{″}\right)$ is the second alternative for $Q_i$ ranking and $m$ indicates the total number of alternatives.

C2: “Acceptable Stability”:

The best alternative $\left(a^{\prime }\right)$ also ranks first by either S or R.

If not, additional compromise solutions are determined according to VIKOR rules.

3. Application

This study’s evaluation framework is built upon a comprehensive set of criteria specifically tailored to adaptive control strategy selection for human–robot collaboration in Industry 5.0 environments. The six main criteria (Safety, Adaptability, Human Comfort and Ergonomics, System Reliability, Performance Efficiency, and Cost Effectiveness) and their 18 sub-criteria are framed through a dual lens combining Environmental–Social–Governance (ESG) and Reliability–Availability–Maintainability–Safety (RAMS), two widely adopted perspectives in industrial systems. Safety aligns with ESG–Governance (regulatory conformity, organizational risk controls, e.g., ISO/TS 15066) and with RAMS–Safety as a core dependability attribute [41,42,43,44,45,46,47]. Safety denotes the attainment of an acceptable risk level for HRC in accordance with recognized collaborative-robot safety principles (e.g., limits for power/force, speed-and-separation monitoring, and emergency stop behavior) and site procedures. Human Comfort and Ergonomics maps to ESG–Social, emphasizing acceptance and worker well-being in collaborative task. Cost Effectiveness is treated in line with ESG’s resource/impact considerations and standard life cycle cost thinking in dependability engineering. RAMS cover the engineering side: System Reliability (R) addresses failure behavior and assurance; Adaptability is linked to Maintainability/Availability through flexibility, changeover, and recoverability; Performance Efficiency relates to Availability-driven throughput and responsiveness in operation. This dual lens clarifies organizational/worker expectations versus engineering dependability, reduces perceived overlaps (criteria vs. alternatives), and is consistent with HRC safety and dependability guidance.

These criteria were identified through an extensive literature review and refined with domain experts’ insights. The final structure comprises six main criteria (Safety, Adaptability, Human Comfort and Ergonomics, System Reliability, Performance Efficiency, and Cost Effectiveness), each decomposed into relevant sub-criteria, as presented in

Table 3. Definitions of criteria.

Main Criterion	Sub-Criterion	Definition
Safety [1,2,3]	C11. Collision avoidance efficiency	Ability to prevent human–robot collisions, human safety assurance
	C12. ISO/TS 15066 compliance	Alignment with collaborative robot safety standards
	C13. Emergency response capability	Speed and adequacy of emergency interventions
Adaptability [4,5]	C21. Real-time adjustment capability	Ability to adapt parameters instantly
	C22. Task flexibility	Capability to handle changing or new tasks
	C23. ML integration	Evaluates the maturity of ML integration pipelines, not the presence of self-learning or on-line adaptation
Human Comfort & Ergonomics [6,7,8]	C31. Ergonomic stress reduction	Reduction in physical strain on human workers
	C32. Psychological acceptance	Level of worker acceptance and comfort
	C33. Haptic feedback quality	Effectiveness of tactile communication
System Reliability [9,10]	C41. Mean time between failure (MTBF)	Average operational time between failures
	C42. Predictive maintenance	Ability to anticipate and prevent system failures
	C43. Fault tolerance	The system’s ability to function despite faults
Performance Efficiency [11,12]	C51. Task completion rate	Proportion of successfully finished tasks
	C52. Throughput optimization	Maximizing production output
	C53. Response time	Time required to react to events
Cost Effectiveness [13]	C61. Implementation cost	Initial investment needed
	C62. Maintenance cost	Ongoing operational expenses
	C63. ROI	Financial benefits over costs

.

3.1. Expert Group

A panel of ten experts, each possessing extensive knowledge and practical experience in human–robot collaboration, industrial safety, and adaptive control systems, was convened to guide the decision-making process. Individual briefing sessions were conducted with each expert to ensure a consistent understanding of the evaluation methodology and assessment procedures. This study addresses a clearly defined decision problem: prioritizing adaptive control strategies for HRC in Industry 5.0 by balancing Safety, Adaptability, Human Comfort and Ergonomics, System Reliability, Performance Efficiency, and Cost Effectiveness to identify a robust compromise solution. The experts contributed to three critical phases of the study: (i) identifying the essential evaluation criteria, (ii) determining the relative importance of these criteria using the SF-SWARA approach, and (iii) assessing the performance of alternative adaptive control strategies through the SF-VIKOR method. Evaluation forms, designed in alignment with the proposed methodology, were completed independently by each expert to maintain the objectivity and reliability of the collected judgments. Ten experts that cover industrial safety/standards, robotics and control, reliability/RAMS, human factors/ergonomics, and production systems independently evaluated (i) the relevance of the six main criteria and 18 secondary criteria, (ii) the relative importance of these criteria using SF-SWARA, and (iii) the performance of five strategies under each criterion using SF-VIKOR. Judgments were elicited with common linguistic scales mapped to spherical fuzzy numbers and aggregated via SWAM to preserve uncertainty and hesitancy; benefit/cost orientations were specified a priori, and SF-VIKOR was run. In order to enhance transparency and minimize subjectivity, standardized instructions and evaluation forms were employed, individual judgments were made by experts with no cross-influence, and sensitivity analyses were performed (expert-weight variation and sub-criterion weight redistribution), both of which confirmed the robustness of the top ranking. Detailed background information on the expert panel is provided in

Table 4. Information about the expert group.

	Experience (Years)	Industry Sector	HRC Practical Exp. (yrs/deploy)	Education Degree	Job Title	Research Area
E-1	15	Manufacturing (electronics)	6/3	PhD in Industrial Engineering	Associate Professor	Human–robot collaboration, multi-criteria decision-making
E-2	12	Automotive	8/6	PhD in Mechanical Engineering	Senior Robotics Engineer	Collaborative robot design, safety compliance
E-3	10	Healthcare/ Med-devices	5/2	PhD in Ergonomics	Associate Professor	Human factors, workplace ergonomics in robotics
E-4	8	Logistics/warehousing	4/2	MSc in Computer Science	AI Systems Specialist	Machine learning integration in adaptive robotics
E-5	20+	FMCG/Process industry	12/9	PhD in Automation Engineering	Senior Automation Consultant	Industrial automation, adaptive control systems
E-6	7	Industry	5/3	MSc in Occupational Health and Safety	Safety Specialist	Risk assessment, ISO/TS 15066 compliance
E-7	14	Energy/utilities	3/2	PhD in Systems Engineering	Professor	System reliability, predictive maintenance
E-8	9	Consumer robotics	4/2	MSc in Human–Computer Interaction	Research Scientist	Haptic feedback, interaction design
E-9	11	Discrete manufacturing	7/5	PhD in Manufacturing Engineering	Senior Process Engineer	Performance optimization, throughput improvement
E-10	6	SMEs/Assembly	3/2	MSc in Industrial Engineering	Research Associate	Cost analysis and ROI assessment in automation projects

.

3.2. Calculation of Criteria Weights with SF-SWARA

After establishing the criteria hierarchy, all ten experts involved in the human–robot collaboration study were assigned equal weighting in the analysis. The analysis was performed using Microsoft Excel. Each expert independently evaluated the criteria using the linguistic variables defined in Table 1, providing assessments based on their expertise and professional experience. These evaluations were then aggregated to construct the final decision matrices used in the subsequent analysis. Assigning equal weight to all expert judgments ensured a fair and unbiased integration of perspectives within the MCDM framework. The aggregated evaluations of the main criteria, as provided by the experts, are presented in

Table 5. Evaluations for main criteria.

	E-1	E-2	E-3	E-4	E-5	E-6	E-7	E-8	E-9	E-10
C1. Safety	AHI	AHI	AHI	AHI	AHI	VHI	AHI	AHI	HI	AHI
C2. Adaptability	EEI	VHI	MHI	VHI	MHI	HI	VHI	HI	MHI	VHI
C3. Human Comfort and Ergonomics	EEI	HI	MHI	VHI	EEI	MHI	VHI	VHI	MHI	MHI
C4. System Reliability	HI	AHI	VHI	AHI	AHI	MHI	HI	MHI	VHI	MLI
C5. Performance Efficiency	EEI	VHI	MHI	HI	MHI	MHI	MHI	HI	VHI	HI
C6. Cost Effectiveness	AHI	HI	AHI	VHI	AHI	MLI	HI	HI	AHI	HI

, serving as the foundation for the criteria assessment matrix.

The linguistic evaluations provided by the experts were converted into SFNs according to the scale presented in Table 1. These individual assessments were then aggregated using Equation (10), and the aggregated scores for the main criteria were calculated using Equation (9). Based on these scores, the main criteria were ranked in descending order of importance. Subsequently, Steps 5–9 of the SF-SWARA method were implemented to finalize the weight of each main criterion, as illustrated in Figure 3.

The results reveal that, in Expert Group opinion, Safety received the highest weight (0.188), underscoring its paramount role in selecting adaptive control strategies for human–robot collaboration in Industry 5.0. This finding highlights that minimizing risks and ensuring secure interaction between humans and robots is the foremost priority for decision-makers. In contrast, Human Comfort and Ergonomics (0.154) and Performance Efficiency (0.154) received the lowest weights, indicating that, while still important, they are considered relatively less critical compared to other main criteria in the prioritization process.

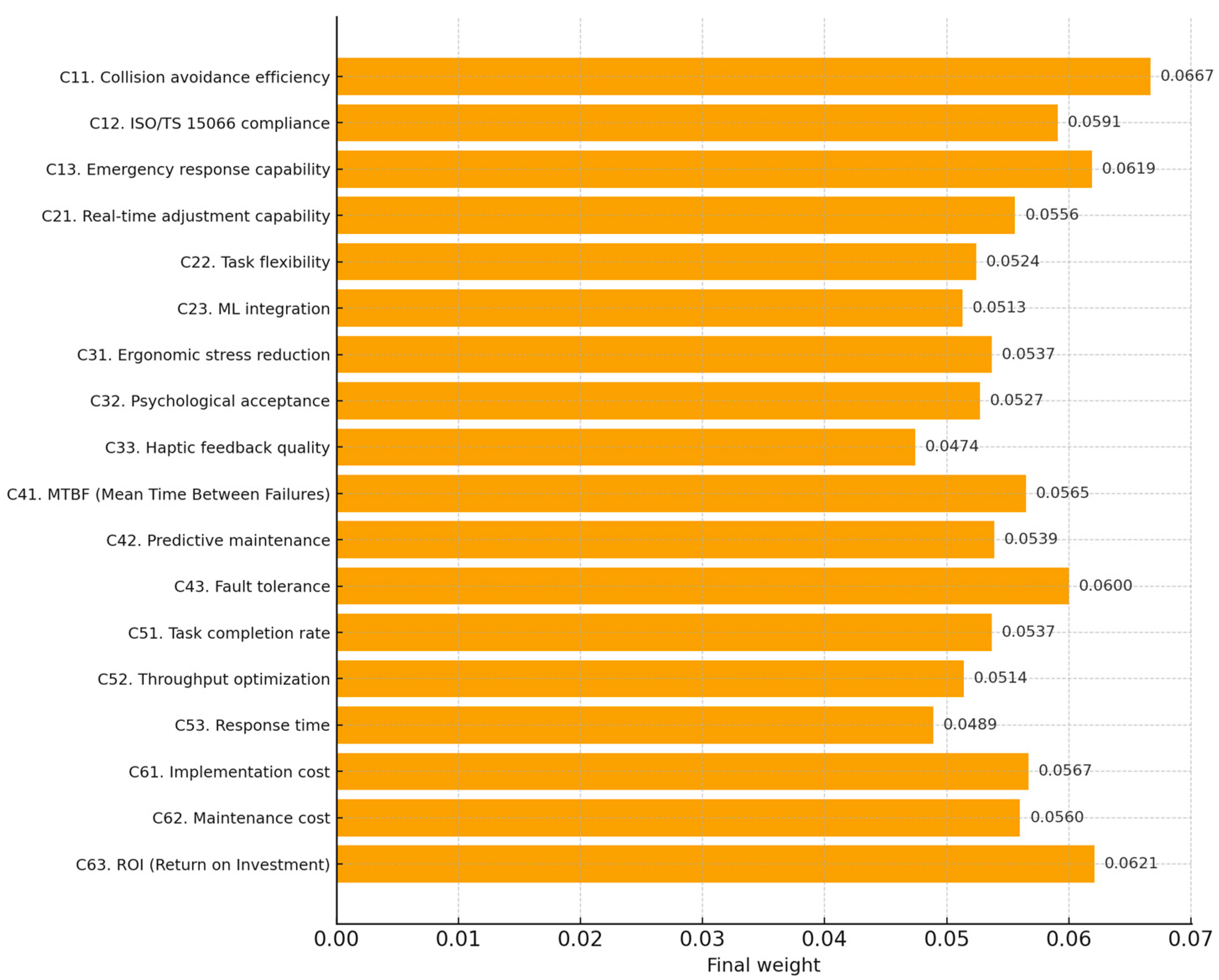
The same panel of experts was subsequently consulted to evaluate the sub-criteria under each main criterion. These assessments were processed using the SF-SWARA methodology, following the same steps for the main criteria. Each sub-criterion’s local weight was multiplied by the weight of its corresponding main criterion to obtain the global weights of sub-criteria. Local and global weights of the sub-criteria are presented in

Table 6. Expert evaluations and the criteria weights for sub-criteria.

	E-1	E-2	E-3	E-4	E-5	E-6	E-7	E-8	E-9	E-10	Local Weights	Final Weights	Rank
C11	AHI	VHI	AHI	AHI	AHI	AHI	AHI	HI	VHI	MHI	0.3555	0.0667	1
C12	HI	HI	EEI	AHI	HI	VHI	HI	MHI	MHI	VHI	0.3146	0.0591	5
C13	VHI	AHI	EEI	AHI	MHI	HI	AHI	VHI	HI	MLI	0.3299	0.0619	3
C21	MHI	HI	MHI	AHI	MHI	VHI	AHI	HI	HI	VHI	0.3489	0.0556	9
C22	MHI	HI	LI	AHI	LI	HI	VHI	MHI	VHI	HI	0.3290	0.0524	14
C23	EEI	MHI	EEI	AHI	EEI	MHI	HI	VHI	HI	MHI	0.3221	0.0513	16
C31	HI	HI	MHI	VHI	MHI	HI	VHI	VHI	MHI	MHI	0.3490	0.0537	12
C32	AHI	MHI	MHI	VHI	HI	MHI	HI	MHI	EEI	EEI	0.3429	0.0527	13
C33	HI	EEI	VLI	AHI	VLI	LI	MHI	EEI	EEI	MLI	0.3080	0.0474	18
C41	HI	MHI	AHI	AHI	AHI	MHI	HI	HI	HI	MLI	0.3317	0.0565	7
C42	VHI	VHI	EEI	AHI	LI	MHI	MHI	VHI	HI	MHI	0.3160	0.0539	10
C43	VHI	VHI	AHI	AHI	AHI	HI	VHI	VHI	VHI	HI	0.3523	0.0600	4
C51	HI	HI	AHI	AHI	HI	MHI	VHI	VHI	AHI	VHI	0.3486	0.0537	11
C52	HI	VHI	AHI	HI	VHI	EEI	HI	VHI	VHI	HI	0.3341	0.0514	15
C53	VHI	HI	HI	VHI	HI	EEI	VHI	MHI	VHI	MLI	0.3173	0.0489	17
C61	AHI	HI	VLI	AHI	ALI	MLI	MHI	HI	VHI	VHI	0.3246	0.0567	6
C62	AHI	HI	HI	MHI	HI	MLI	HI	HI	HI	HI	0.3204	0.0560	8
C63	AHI	VHI	VHI	AHI	VHI	MHI	VHI	VHI	AHI	MHI	0.3551	0.0621	2

and Figure 4.

The results indicate that among the sub-criteria, Collision avoidance efficiency (C11) obtained the highest final weight (0.0667), demonstrating the experts’ strong emphasis on minimizing the risk of human–robot collisions in collaborative environments. Return on Investment (C63) and Emergency response capability (C13) followed closely, highlighting that economic justification and the ability to respond effectively to emergencies are essential in selecting optimal human–robot collaboration strategies. Fault tolerance (C43) and ISO/TS 15066 compliance (C12) also ranked highly, reflecting the importance of robust system performance and adherence to international safety standards. On the other hand, Haptic feedback quality (C33), Response time (C53), and ML integration (C23) received comparatively lower weights, suggesting that while these technical and interaction-related aspects are essential, they are considered less critical compared to direct safety measures, financial viability, and regulatory compliance in the decision-making process.

3.3. Ranking the Alternative Strategies with SF-VIKOR

The proposed strategies for enhancing safety and efficiency in human–robot collaboration were developed based on a review of relevant literature, industry practices, and international safety standards, particularly ISO/TS 15066. The focus was on solutions that balance technological capability with practical applicability in industrial environments.

S1. Real-time Wearable Sensor Integration: Continuous monitoring of workers’ conditions and surroundings through wearable devices, enabling adaptive safety control and timely risk prevention [48,49].

S2. Vision-Based Dynamic Safety Zones: Use of cameras and AI to dynamically adjust safety zones based on real-time human and robot positions, ensuring safe distances without disrupting workflow [6,50].

S3. AI-driven Behavior Prediction Models: Artificial intelligence algorithms predict human actions and proactively adjust robot behavior, reducing collision risks and improving coordination [51].

S4. Haptic Feedback Implementation: Provision of tactile signals to workers for instant and intuitive communication during collaboration, enhancing awareness and response time [7].

S5. Self-Learning Adaptive Robot Algorithms: Robots autonomously learn from their environment, improving adaptability and performance over time in dynamic work settings [15].

S1 provides proximity and situation awareness in the operator–robot cell using physiological/kinematic cues and logs events; it is deployed via a secure cell-level gateway with authenticated streaming, is widely piloted in HRC, and requires minimal structural change, with key risks around device hygiene/charging, data minimization, and privacy governance. S2 utilizes workspace zoning, speed-and-separation envelopes, and layout retuning, implemented with re-marking, light curtains, and fencing, offering codified safety at the cost of potential throughput loss, revalidation time, and floor constraints. S3 learns task patterns to issue early warnings with edge inference; its benefits scale with data breadth/quality and hinge on representativeness, drift monitoring, and bias/privacy controls. S4 maps risk states and confirmations to standardized tactile/audio alerts via wearable or handheld actuators, strengthening human factors but requiring consistent mapping and onboarding. Therefore, in the presence of noise and alarm fatigue, difficulties arise. The S5 policy adapts in the presence of explicit safety constraints to tackle the variability of tasks and changeovers using offline learning combined with supervised commissioning and guarded, gradual activation. It has the highest chance of success under variability, but also demands more readiness from governance, more effort in validation, and well-designed rollback plans. Here, S1 shines as a low-overhead “baseline layer,” addressing safety levers that are deemed the most important. At the same time, S2 ensures regulatory alignment, S3 adds data-dependent incremental gains, S4 enhances operator effectiveness, and S5 provides powerful but governance-intensive flexibility for highly variable tasks.

In the final stage of the analysis, the proposed HRC safety enhancement strategies were ranked using the SF-VIKOR method. All ten experts evaluated each alternative under the determined criteria by applying the same linguistic variables in Table 2, ensuring consistency and comparability in their assessments. The individual expert evaluations were aggregated to form the final decision matrices, which were then processed using the SF-VIKOR procedure. The complete set of aggregated assessments and the resulting ranking scores are presented in

Table A1. Expert evaluations for alternatives.

A1

A2

A3

A4

A5

A1

A2

A3

A4

A5

A1

A2

A3

A4

A5

A1

A2

A3

A4

A5

A1

A2

A3

A4

A5

C11

VH

AH

AH

H

H

VH

AH

MH

MH

H

L

AH

VH

L

AH

H

AH

H

AH

H

AH

L

VH

VH

L

C12

H

H

VH

H

VH

H

H

F

F

MH

MH

H

VH

VL

H

AH

MH

MH

AH

VH

H

MH

VH

VH

VL

C13

AH

AH

H

H

H

VH

AH

VH

MH

MH

ML

AH

AH

VL

MH

AH

AH

VH

H

VH

AH

ML

AH

AH

VL

C21

H

H

MH

H

MH

VH

VH

MH

H

MH

MH

F

F

MH

ML

AH

AH

AH

AH

AH

MH

F

F

F

MH

C22

H

H

VH

H

H

H

H

MH

H

MH

L

VL

ML

ML

F

AH

H

H

H

AH

L

VL

ML

ML

ML

C23

AH

AH

AH

AH

AH

H

VH

VH

H

AH

L

L

ML

L

VL

AH

AH

AH

AH

AH

L

L

ML

ML

L

C31

MH

ML

ML

F

ML

VH

H

H

H

MH

L

ML

VL

L

L

AH

AH

AH

AH

AH

L

ML

VL

VL

L

C32

MH

ML

ML

ML

ML

H

VH

H

MH

F

ML

VL

L

L

L

MH

MH

MH

MH

VH

ML

VL

L

L

L

C33

F

L

L

AH

F

H

ML

ML

AH

F

VL

VL

L

L

VL

AH

H

VH

AH

AH

VL

VL

L

L

L

C41

MH

MH

H

VH

H

F

ML

F

ML

F

AH

VH

VH

VH

AH

H

H

VH

H

VH

AH

VL

VH

VH

VH

C42

H

H

VH

H

VH

MH

MH

MH

MH

MH

VL

L

VL

L

L

VH

VH

VH

VH

AH

VL

VH

VL

VL

L

C43

VH

VH

AH

VH

AH

F

F

F

MH

ML

AH

AH

VH

VH

AH

AL

AL

AL

AL

AL

AH

VH

VH

VH

VH

C51

F

F

MH

F

MH

H

H

F

F

H

AH

AH

VH

F

AH

AH

VH

AH

AH

AH

AH

AH

VH

VH

F

C52

H

H

VH

H

VH

MH

H

MH

F

H

AH

AH

AH

F

AH

AH

AH

AH

AH

AH

AH

H

AH

AH

F

C53

H

H

ML

H

ML

ML

L

F

ML

L

H

VH

H

L

AH

AL

AL

AL

AL

AL

H

MH

H

H

L

C61

AH

AH

AH

AH

AH

H

H

H

MH

H

VH

ML

MH

VH

VL

AH

AH

VH

VH

AH

VH

H

MH

MH

VH

C62

VH

VH

AH

VH

AH

H

H

H

H

VH

VL

VL

H

F

VL

AL

AL

AL

AL

AL

VL

VL

H

H

F

C63

AH

AH

AH

AH

AH

VH

H

H

H

VH

AH

VL

VL

AH

VH

AH

AH

AH

AH

AH

AH

AH

VL

VL

AH

A1

A2

A3

A4

A5

A1

A2

A3

A4

A5

A1

A2

A3

A4

A5

A1

A2

A3

A4

A5

A1

A2

A3

A4

A5

C11

MH

VH

H

L

MH

AH

VH

H

F

MH

ML

ML

MH

AH

MH

VH

H

VH

VH

VH

H

VH

ML

L

H

C12

MH

H

ML

VL

VL

VH

H

MH

L

ML

MH

MH

MH

H

H

H

VH

VH

H

H

H

ML

L

H

H

C13

H

VH

H

ML

MH

VH

H

MH

H

ML

ML

AH

MH

VH

VH

H

AH

H

H

H

ML

VH

H

ML

VH

C21

MH

VH

VH

L

VH

MH

F

VH

L

H

AH

VH

VH

VH

VH

VH

VH

VH

VH

H

AH

VH

MH

ML

H

C22

ML

L

MH

ML

H

F

MH

VH

L

AH

F

ML

H

ML

MH

VH

H

VH

H

VH

H

MH

ML

L

AH

C23

MH

H

VH

VL

VH

ML

MH

AH

L

AH

L

AH

AH

VH

AH

VH

H

VH

H

AH

H

VH

H

MH

AH

C31

VH

L

ML

H

MH

VH

MH

H

AH

MH

VH

VH

H

VH

H

H

VH

H

VH

VH

MH

F

ML

ML

H

C32

ML

ML

ML

H

L

H

MH

ML

MH

H

H

AH

F

F

F

H

VH

VH

VH

H

H

ML

VH

H

MH

C33

VL

AL

AL

VH

AL

L

L

ML

AH

MH

ML

VL

ML

AH

ML

H

VH

AH

H

H

H

MH

ML

AH

F

C41

MH

ML

ML

MH

ML

MH

H

F

H

MH

VH

VH

VH

H

F

VH

H

H

VH

VH

L

L

MH

H

VH

C42

H

L

MH

L

H

VH

H

MH

L

H

H

MH

H

MH

ML

VH

H

VH

VH

VH

L

L

ML

F

ML

C43

ML

ML

MH

L

H

MH

F

ML

H

VH

H

ML

ML

ML

ML

H

VH

AH

VH

H

MH

F

L

VL

AL

C51

MH

MH

H

ML

H

MH

H

H

ML

VH

MH

VH

VH

VH

H

VH

H

VH

VH

VH

F

MH

H

MH

VH

C52

ML

ML

H

ML

H

ML

MH

H

L

H

H

H

H

MH

MH

VH

VH

H

H

VH

F

MH

H

MH

VH

C53

MH

H

H

L

MH

VH

H

MH

H

MH

VH

H

L

AH

F

VH

AH

H

H

VH

H

VH

H

AH

VH

C61

MH

ML

L

MH

L

MH

H

VH

ML

VH

VH

ML

H

VH

H

H

H

H

H

VH

MH

H

MH

H

H

C62

ML

ML

L

MH

L

H

MH

H

ML

H

MH

MH

ML

H

VH

VH

H

VH

VH

H

F

MH

H

H

MH

C63

H

H

MH

MH

H

H

MH

H

MH

VH

VH

MH

H

VH

VH

AH

H

AH

AH

H

L

ML

MH

F

H

(see Appendix A).

Subsequently, the decision matrix was constructed by converting the linguistic evaluations into spherical fuzzy numbers. For each criterion, the positive ideal value ${\tilde{X}}^{*}$ and the negative ideal value ${\tilde{X}}^{-}$ were determined according to its type. In this study, all criteria were treated as benefit-type, except C53 (Response time), C61 (Implementation cost), and C62 (Maintenance cost), which were considered cost-type criteria. Using the aggregated expert evaluations and the final criteria weights obtained from the SF-SWARA stage, the $S_i$, $R_i$ and $Q_i$ values were calculated for each alternative strategy following the SF-VIKOR procedure. The parameter was set to 0.5 to ensure equal consideration of group utility and individual regret. The resulting $S_i$, $R_i$ and $Q_i$ values for all alternatives are provided in

Table 7. $S_i$, $R_i$ and $Q_i$ values.

	${\mathit{S}}_{\mathit{i}}$	${\mathit{R}}_{\mathit{i}}$	${\mathit{Q}}_{\mathit{i}}$	Ranking
S1. Real-time Wearable Sensor Integration	0.384	0.057	0.000	1
S2. Vision-Based Dynamic Safety Zones	0.517	0.066	0.693	5
S3. AI-driven Behavior Prediction Models	0.524	0.062	0.485	2
S4. Haptic Feedback Implementation	0.728	0.060	0.675	4
S5. Self-Learning Adaptive Robot Algorithms	0.499	0.066	0.653	3

, while the overall ranking based on the lowest $Q_i$ values is also presented in the same table.

The SF-VIKOR results indicate that, in Expert Group opinion, S1 emerges as the most favorable strategy, achieving the lowest $Q_i$ value and thus ranking first. This suggests that S1 offers the best compromise solution among the evaluated alternatives, balancing overall performance ($S_i$) and individual worst-case performance ($R_i$). S3 follows in second place with a relatively low $Q_i$ (0.485), reflecting strong overall potential but slightly lower best-worst balance than S1. S5 and S4 take the third and fourth positions, respectively, showing competitive but not leading performance profiles. In contrast, S2 ranks last, with the highest $Q_i$ (0.693), implying that despite potential strengths in certain criteria, it falls short in maintaining balanced performance across all decision factors. This ranking suggests that prioritizing S1 and S3 could yield the most effective implementation outcomes under the current decision framework, while S2 may require targeted improvements to address its weakest performance areas.

3.4. Sensitivity Analysis

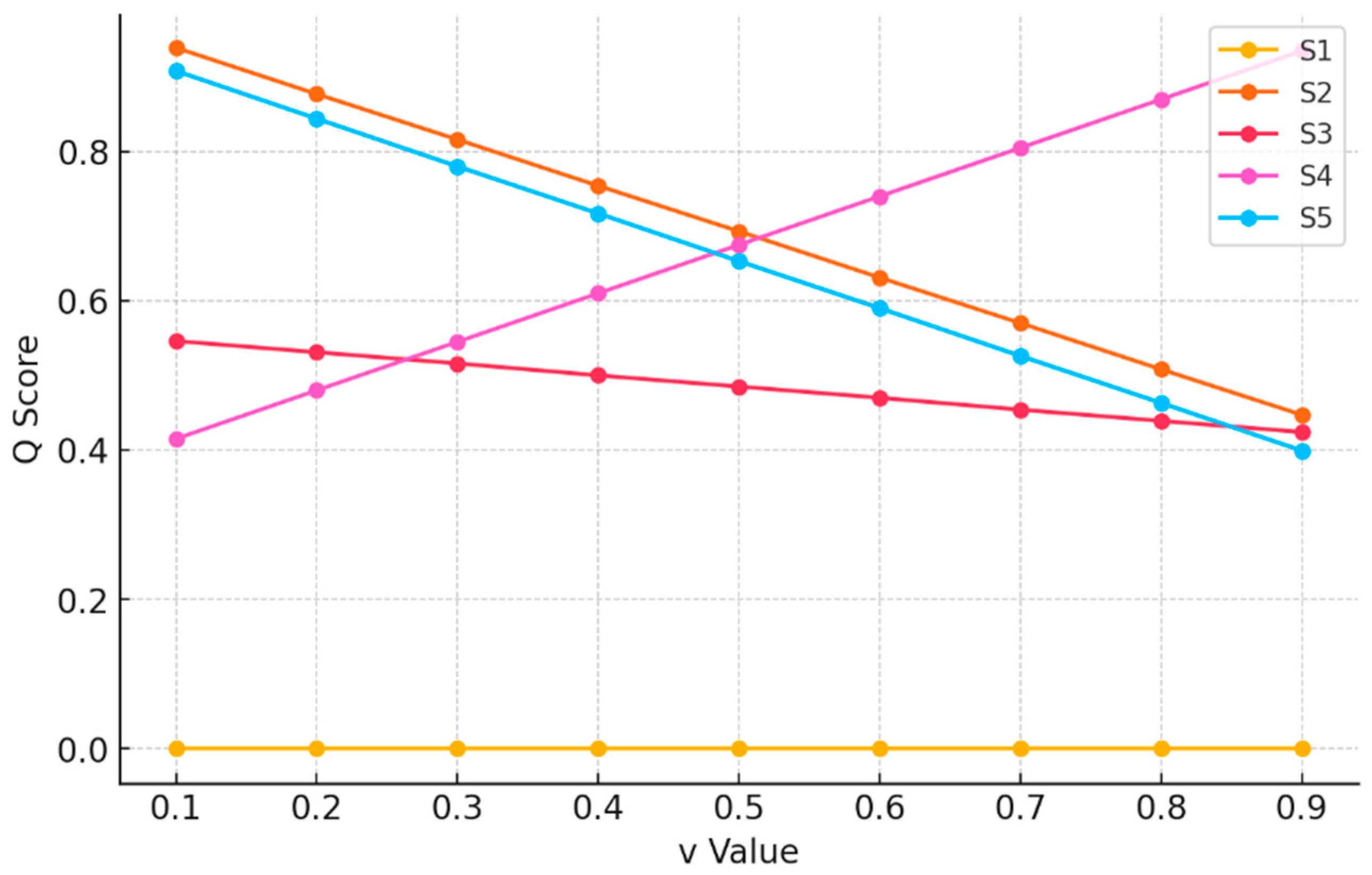
To assess the robustness of the ranking results obtained by the SF-VIKOR method, a sensitivity analysis was conducted by varying the parameter $v$ from 0.1 to 0.9 in increments of 0.1. This parameter controls the balance between the maximum group utility ($S_i$) and the minimum individual regret ($R_i$) in the VIKOR framework. The corresponding $Q_i$ scores and rankings for each alternative under different $v$ values are presented in

Table 8. The sensitivity analysis for different threshold parameter values.

v	S1	S2	S3	S4	S5
0.1	1	5	3	2	4
0.2	1	5	3	2	4
0.3	1	5	2	3	4
0.4	1	5	2	3	4
0.5	1	5	2	4	3
0.6	1	4	2	5	3
0.7	1	4	2	5	3
0.8	1	4	2	5	3
0.9	1	4	3	5	2

. The trends in Q scores across scenarios are depicted in Figure 5.

The sensitivity analysis results show that the top-ranked strategy, S1, remains consistently in first place across all $v$ values from 0.1 to 0.9. This stability demonstrates that S1 is highly robust to changes in the decision-maker’s preference between group utility and individual regret, making it a reliable choice regardless of whether the emphasis is placed on collective performance or minimizing the worst-case scenario. On the other hand, S2 consistently ranks last until $v=0.5$, after which its performance improves slightly, reaching fourth place for $v\ge 0.6$. This shift indicates that S2 benefits from scenarios where decision-makers prioritize minimizing individual regret over maximizing group utility. The intermediate alternatives exhibit ranking fluctuations, suggesting a moderate sensitivity to changes in $v$. S3 generally holds the second position but occasionally drops to third at the extremes, showing that decision-making preferences somewhat influence its standing. S4 and S5 display notable ranking swaps, particularly between $v=0.5$and $v=0.9,$ reflecting their close performance and competitive nature. Overall, while S1’s dominance confirms its robustness, the shifting rankings of other strategies highlight the importance of considering preference-based parameter variation in the VIKOR method to ensure decision-making resilience across different priority scenarios.

In the second step, a sensitivity analysis was conducted by modifying the distribution of expert weights (Sc1.1–Sc1.10). In each scenario, one expert was assigned a dominant weight of 0.5, while the remaining nine experts equally shared the residual 0.5 (approximately 0.0556 each). This procedure systematically highlights the influence of each expert in turn, thereby allowing an assessment of how biased weighting toward a single decision-maker might affect the ranking of the alternatives. The baseline scenario (S0) represents the final ranking results obtained in the main analysis, serving as the reference point for comparison.

Figure 6 illustrates the ranking patterns of the five alternatives under both the baseline case and the ten sensitivity scenarios. Although the assignment of dominant weight to different experts produces some variations in rank positions, the general hierarchy of alternatives shows strong stability compared with the baseline outcome. In particular, S1 remains the leading option across nearly all scenarios, with S3 and S5 frequently following in higher ranks, whereas S4 and S2 tend to remain in the lower part of the ranking spectrum. The close correspondence between S0 and the sensitivity scenarios demonstrates that even considerable shifts in expert weight distribution do not alter the overall preference structure. This outcome reinforces the robustness of the evaluation framework and enhances confidence in the reliability of the final decision.

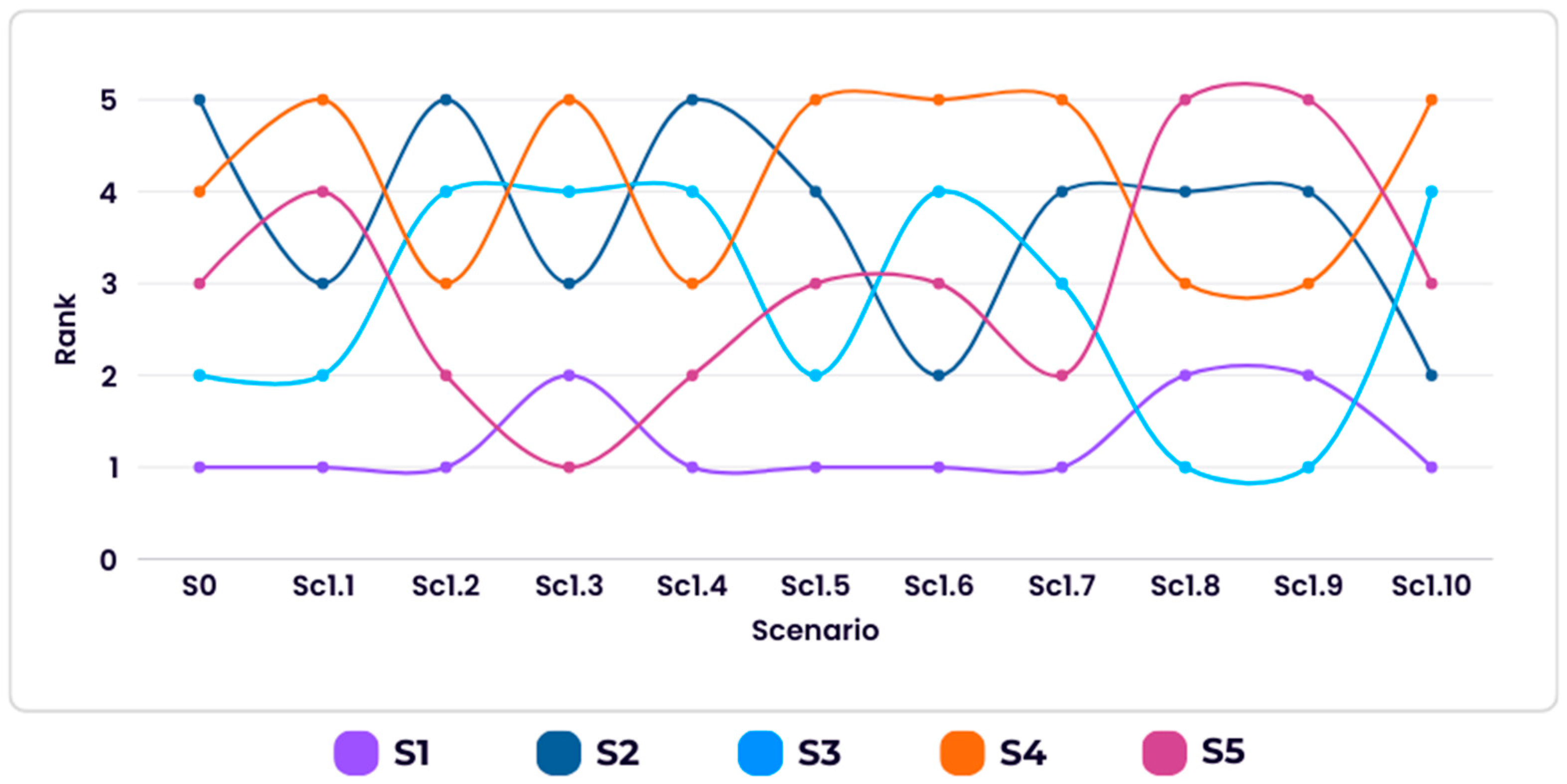
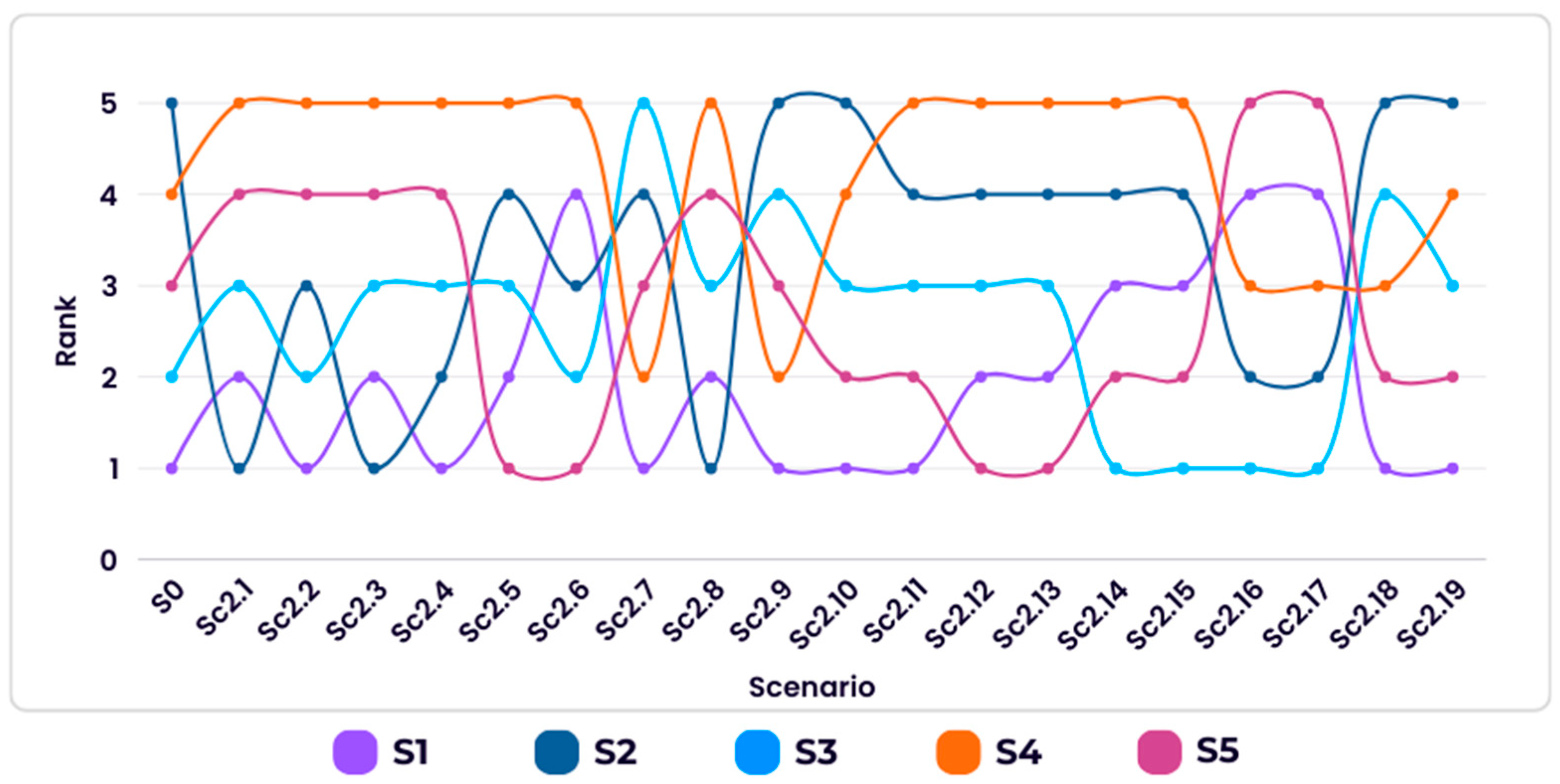
In the last step, a sensitivity analysis was conducted by varying the distribution of sub-criterion weights across eighteen scenarios (S2.1–S2.18). In each scenario, one sub-criterion was assigned a dominant weight of 0.25, while the remaining seventeen sub-criteria equally shared the residual 0.75 (approximately 0.0441 each). This procedure was designed to isolate the influence of each individual sub-criterion and examine how disproportionate emphasis on a single factor could alter the ranking of the alternatives. Additionally, scenario S2.19 represents the case in which all sub-criteria were assigned equal weights (1/18), providing a balanced benchmark for comparison. The baseline scenario (S0) corresponds to the final ranking results obtained in the main analysis.

Figure 7 presents the rank trajectories of the five alternatives across the 19 scenarios. Although the rankings fluctuate under different weighting structures, the overall ordering remains highly consistent with the baseline results. Specifically, S1 frequently emerges as the top-ranked alternative, followed by S2 and S3, while S4 and S5 predominantly occupy the lower positions. The consistency between S0 and the majority of sensitivity scenarios indicates that even under substantial variations in sub-criterion weight allocations, the preference order remains largely stable. This finding provides further evidence of the model’s resilience and confirms the credibility of the final decision-making results.

4. Discussion

This study proposes an end-to-end spherical-fuzzy MCDM pipeline, SF-SWARA for weighting and SF-VIKOR for ranking to select adaptive control strategies for HRC. Response time (C53) and implementation/maintenance costs (C61/C62) are modeled as cost-type criteria, and the overall design is aligned with ISO/TS 15066 (see Figure 1, Table 2, Table 3 and Table 4). This is an alignment that retains the linguistic semantics used during expert elicitation and aggregation, thus serving as an auditable, standards-conformant basis upon which deployment decisions shall be carried out for Industry 5.0 cells.

At the main-criteria level, Safety receives the highest weight (0.188), while Human Comfort and Ergonomics and Performance Efficiency receive the lowest (0.154 each), indicating a safety-first stance. Among the sub-criteria, Collision-Avoidance Efficiency (C11) is the most influential (0.0667), followed by Return on Investment (C63; 0.0621) and Emergency-Response Capability (C13; 0.0619). Fault Tolerance (C43) and ISO/TS 15066 Compliance (C12) also rank highly (Table 7). Collectively, these Expert Group opinion results highlight an emphasis on direct risk-mitigation levers and economic defensibility, relative to interaction-quality refinements.

In the SF-VIKOR solution, S1 is the only compromise solution. S1 dominates S3 and S5, and S2 has the lowest rank. The outcome passes both VIKOR acceptance tests with clear superiority over the second best (ΔQ = 0.485 ≥ 0.25) as well as stability under various parameter choices. Therefore, S1’s best ranking is true and credible. Sensitivity analysis varying $v$ from 0.1 to 0.9 leaves the top rank invariant; S1 remains first in all scenarios. Mid-tier swaps are limited; S2 improves only under strong regret aversion, yet never surpasses S1/S3. These results indicate that organizations can adopt S1 confidently across a wide preference spectrum, while S3 becomes an attractive augment as data maturity grows. S1’s lead follows directly from the weight structure. With Safety as its highest priority (0.188), S1 targets the top safety levers: collision-avoidance efficiency (C11 = 0.0667) via continuous proximity/situation awareness, and Emergency response capability (C13 = 0.0619) through immediate alarms/acknowledgments, while also adding redundancy for Fault tolerance (C43). On the business side, S1 yields early ROI (C63 = 0.0621) because it requires minimal structural change, rapidly reduces incident exposure, and produces auditable logs that accelerate payback verification. In contrast, S3 aligns with the same levers, but its gains depend on data maturity. S5 can outperform under high task variability but carries heavier validation/governance burdens that weaken near-term ROI; and S2 improves worst-case envelopes at a throughput cost. This feature-to-criterion alignment accounts for S1’s robustness across preference shifts (Table 7).

Furthermore, a pragmatic roadmap follows: implement S1 as the baseline safety layer to secure immediate gains on C11/C13 and the business case via C63; augment with S3 for predictive coordination; consider S5 where learning yields compounding benefits. S2 can complement highly worst-case-averse cells but has limited stand-alone value under current weights.

In this study, SF-VIKOR is employed to achieve a balanced compromise among competing criteria. The consistency of our results, along with our reported sensitivity checks, indicates that this choice is appropriate for the present context. As with any compromise scheme, the compensatory nature of aggregation can allow weaker performance on one dimension to be partially offset elsewhere; this is a design property rather than a flaw, and in domains with non-negotiable safety minima, it is best paired with explicit rule sets applied before or after aggregation. In our pipeline, options that violate mandated safety minima are excluded before aggregation, and compromise ranking only discriminates among the survivors. The expert judgments and criterion scores provide a sufficient yet extensible basis, while variability in operating conditions (equipment, environment, shift patterns) is already addressed through embedded sensitivity scenarios. Building on this, and where institutions seek additional assurance, sensitivity scenarios can be extended to explicitly model temperature- and electromagnetic-interference-related debating so that any potential signal-quality loss is transparently reflected in decision inputs and rankings. To accommodate heterogeneous organizational preferences and governance requirements, future studies may, as context permits, augment the current pipeline with clear exclusion rules for safety-critical violations, robustness checks that do not rely on compensation alone, and acceptability summaries under preference uncertainty; these are context-sensitive extensions intended to enhance transparency and transferability, not requirements nor replacements for the present approach.

Managerial Implications: Technology–Economy–Organization (T–E–O) Deployment Perspective

We prioritize S1 as the baseline safety layer because it wins on three reinforcing fronts—Technology, Economy, and Organization.

In technology perspective, S1 can be deployed with minimal disruption and integrates cleanly with typical production stacks. It collects cell-level signals via industrial wearables, aligns them locally in time, and exchanges events with existing manufacturing execution and enterprise resource planning systems using stable, widely adopted interfaces. Within this architecture, S3 serves as a contextual enhancement, learning recurring task patterns and providing local inference, while the model remains under central governance for updates. At the same time, S5 is released into the environment only after commissioning under supervision and explicit safety policies so that it can adapt without disrupting throughput. Empirically, S1 ranks first in the baseline SF-VIKOR, stays first across wide v-parameter and expert-weight sweeps, and aligns with our weight structure where ROI (C63) is among the most influential sub-criteria.

In economy perspective, adoption is evaluated through a scale-aware ROI/payback lens that balances upfront investment costs with ongoing operating costs, against quantified benefits. This mirrors the weight structure (ROI C63 is highly influential) and the robustness checks (S1 remains top-ranked across sensitivity analysis Table 7). In practice, S1 is the rational first move for small cells, multi-cell clusters, and line-level rollouts, as it delivers early, defensible risk reduction at a modest cost. S3 and S5 are then added, where incremental gains justify further investment under the same economic logic.

In organization perspective, Focused operator preparation and clear governance sustain impact. Brief, task-specific training, run by the Environmental, Health, and Safety function, along with drills, builds trust in safety overrides and updates procedures, a gated rollout anchors accountability through defined roles, feedback loops, and approval trails. The criteria system explicitly includes worker acceptance (C32); the SF-VIKOR baseline ranks S1 first; and robustness analyses (over v, expert-weights, and sub-criterion weights) keep S1 at or near the top (Table 7 and Table 8), showing that staged rollout and governance preserve the decision under broad preference shifts. Start with S1 to secure quick, traceable safety gains and positive ROI; layer in S3 and S5 where context and returns warrant it.

From a managerial standpoint, the staged deployment (S1, S3, and S5) mirrors ISO 45001’s continual improvement cycle: plan–do–check–act. S1 establishes baseline controls and monitoring (“plan/do”) with minimal disruption and high traceability; S3 adds local intelligence and pattern learning to “check,” enabling data-driven verification of risk controls in real workflows; S5 extends adaptive capabilities under explicit safety policies to “act,” closing the loop with governed updates and corrective actions. This coupling anchors human safety as an organizational property—validated iteratively via RAMS (C41–C43) and safeguarded by C11–C13, while preserving the human-centered principles reflected in C31–C33.

5. Conclusions

This paper presents an end-to-end spherical fuzzy MCDM framework to select adaptive control strategies for human–robot collaboration in Industry 5.0. These results reflect the consolidated judgments of a ten-member expert panel, aggregated within the proposed spherical-fuzzy MCDM framework. Using a cross-disciplinary panel of experts, we structured six main and eighteen sub-criteria spanning safety, adaptability, ergonomics, reliability, performance, and cost, and explicitly modeled response time (C53) and implementation/maintenance costs (C61/C62) as cost types. The analysis shows that Safety dominates the weight vector (0.188), with Collision avoidance efficiency (C11), ROI (C63), and Emergency response capability (C13) as the most influential sub-criteria. S1—real-time Wearable Sensor Integration—emerges as the unique compromise solution (Q = 0.000), satisfying VIKOR’s acceptable advantage and stability conditions and remaining top-ranked across extensive sensitivity tests (v = 0.1–0.9). These results support a pragmatic deployment path in which S1 forms the safety baseline, complemented by S3 (AI-driven behavior prediction) as data maturity increases and S5 (self-learning algorithms) where task variability favors continual adaptation. While findings reflect a single expert panel and a pilot context, and VIKOR’s compensatory logic may warrant hybrid (compensatory + veto) extensions in veto-critical cells, the proposed framework offers a transparent, uncertainty-aware template aligned with collaborative-robot safety guidance for high-stakes decision-making in next-generation manufacturing. For industrial deployment, we recommend a staged pathway: adopt S1 as the baseline safety layer to capture near-term risk reduction and business benefits; add S3 as data maturity increases to anticipate human–robot interactions; and consider S5 where task variability and governance readiness justify continual adaptation. In parallel, align data governance with corporate privacy and security policy, provide brief operator training and EHS-led drills, and conduct site-level ROI/payback checks before line-wide scale-up. This sequencing enables quick wins while preserving interoperability with existing MES/ERP systems and maintaining a clear audit trail for safety governance.

This study has several limitations that suggest directions for future inquiry. This study does not explicitly operationalize data privacy and security risks within Industry 5.0 human–robot collaboration (e.g., leakage from wearable sensors, algorithmic bias and model governance). We acknowledge this as a limitation and will, in subsequent work, incorporate a dedicated privacy/security criterion together with a causal analysis of its interactions with safety, reliability, and adaptability. The expert panel lacks frontline stakeholders such as operators and production managers; subsequent research should broaden participation and report subgroup analyses. Although equal expert weights were used, extensive sensitivity analyses on expert-weight schemes, criterion-weight perturbations, and the VIKOR preference parameter v indicate that the top ranking is robust; nevertheless, criterion-dependent or data-driven weighting could be further examined. Criterion weights may also be affected by the choice of linguistic scales and aggregation operators; alternative designs merit evaluation. Finally, the results rely primarily on expert elicitation; multi-site validation with real-time logs and incident histories would strengthen external validity.

Our findings position the proposed intelligent MCDM pipeline as consonant with Industry 5.0 priorities—human-centricity, resilience, and sustainability. In future studies, the Industry 5.0 linkage can be strengthened by validating the proposed intelligent MCDM pipeline across multiple sectors with broader, culturally diverse expert panels, systematically quantifying pilot-stage challenges through comparative case studies, and replicating lessons learned in multi-site deployments to derive generalizable implementation recommendations.