Kolmogorov–Arnold Network for Predicting CO2 Corrosion and Performance Comparison with Traditional Data-Driven Approaches
Abstract
1. Introduction
2. Methods
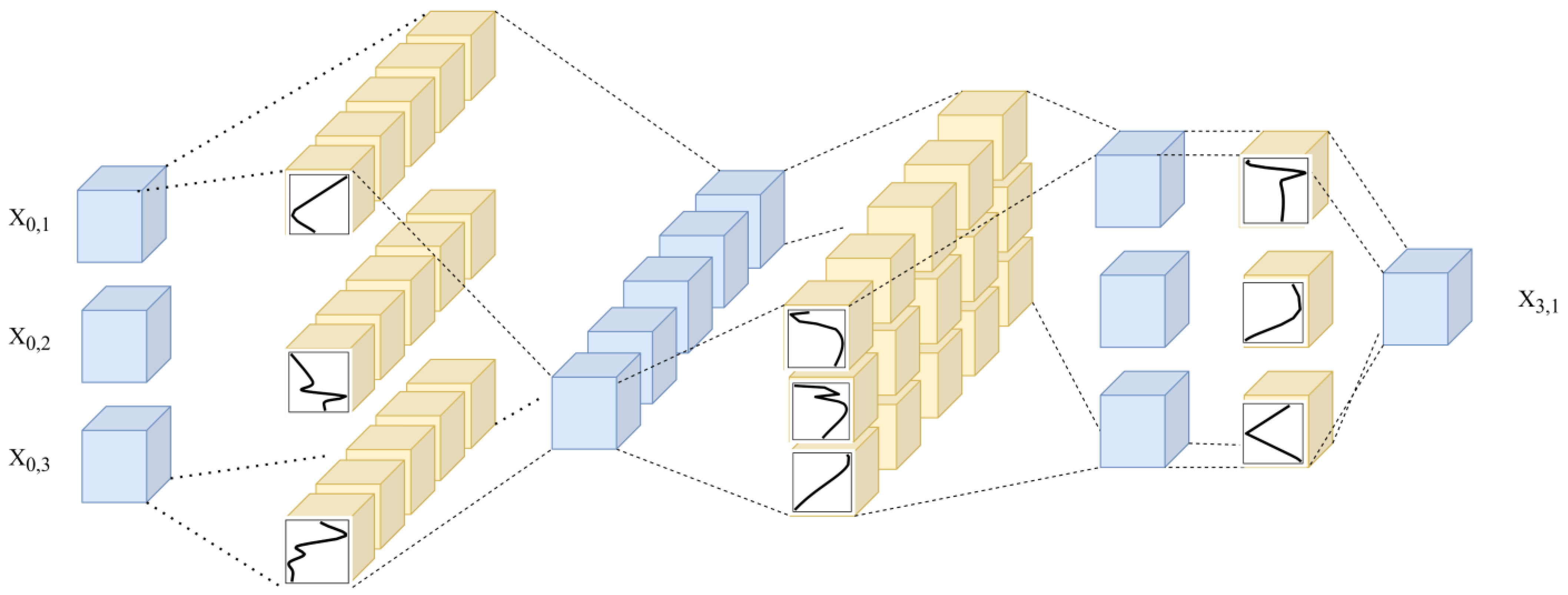
2.1. Introduction of the Kolmogorov–Arnold Network (KAN)
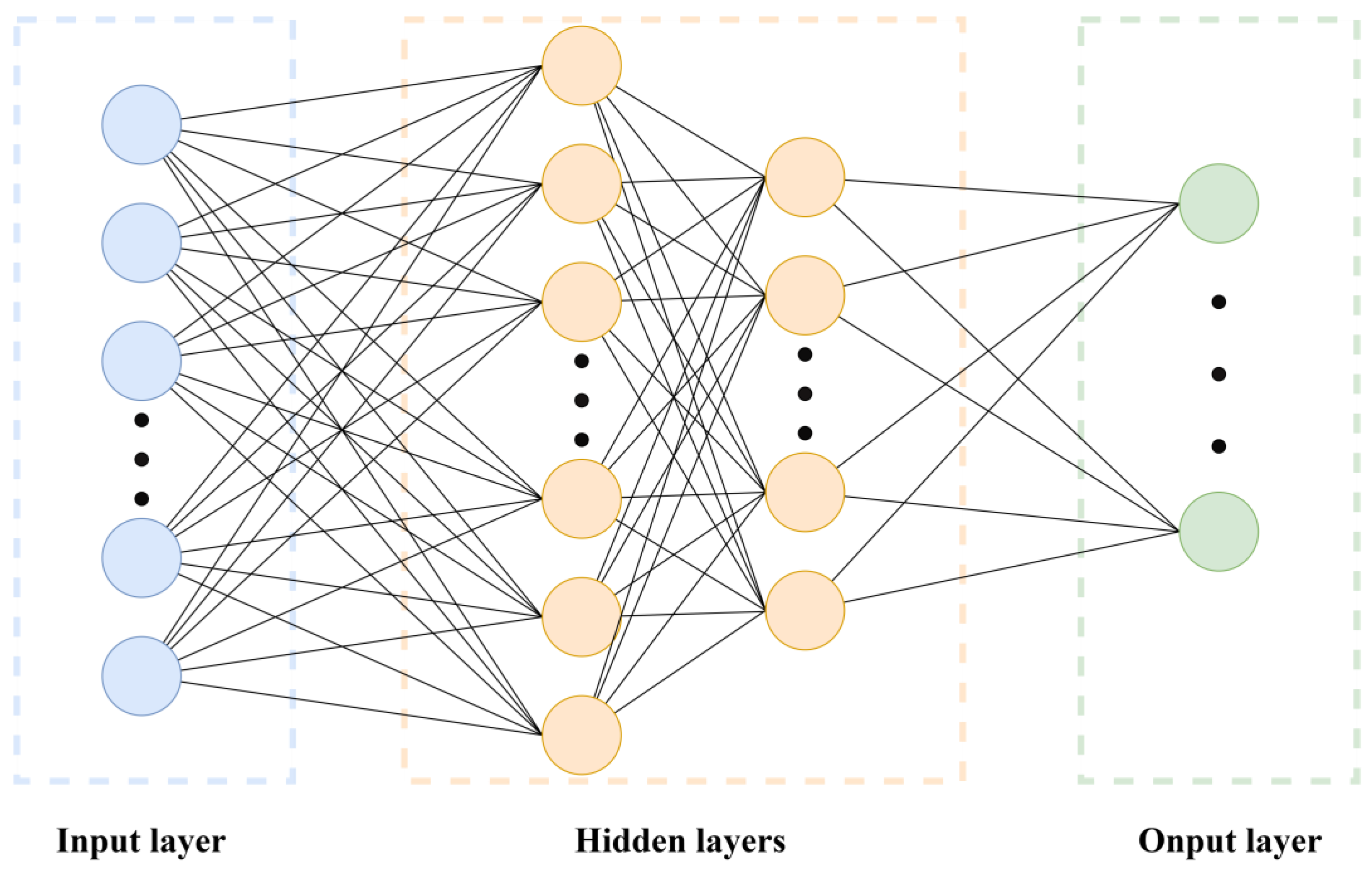
2.2. MLP (Multilayer Perceptron)
2.3. Parameter Sensitivity Analysis and Experimental Design
- ➀
- Number of Hidden Layers: The depth of the network was varied across {1, 2, 3, 4} layers. The number of neurons per hidden layer was held constant for a given experimental series.
- ➁
- Grid Size (grid_size): The number of grid points used to define the spline functions was tested across a range of {1, 2, 3, 4, 5}. This parameter directly controls the expressivity and complexity of the spline approximations.
- ➂
- Number of steps (steps): The number of gradient descent updates per training session was evaluated for values of {5, 10, 15, 20}. This parameter influences both the convergence behavior and the computational cost.
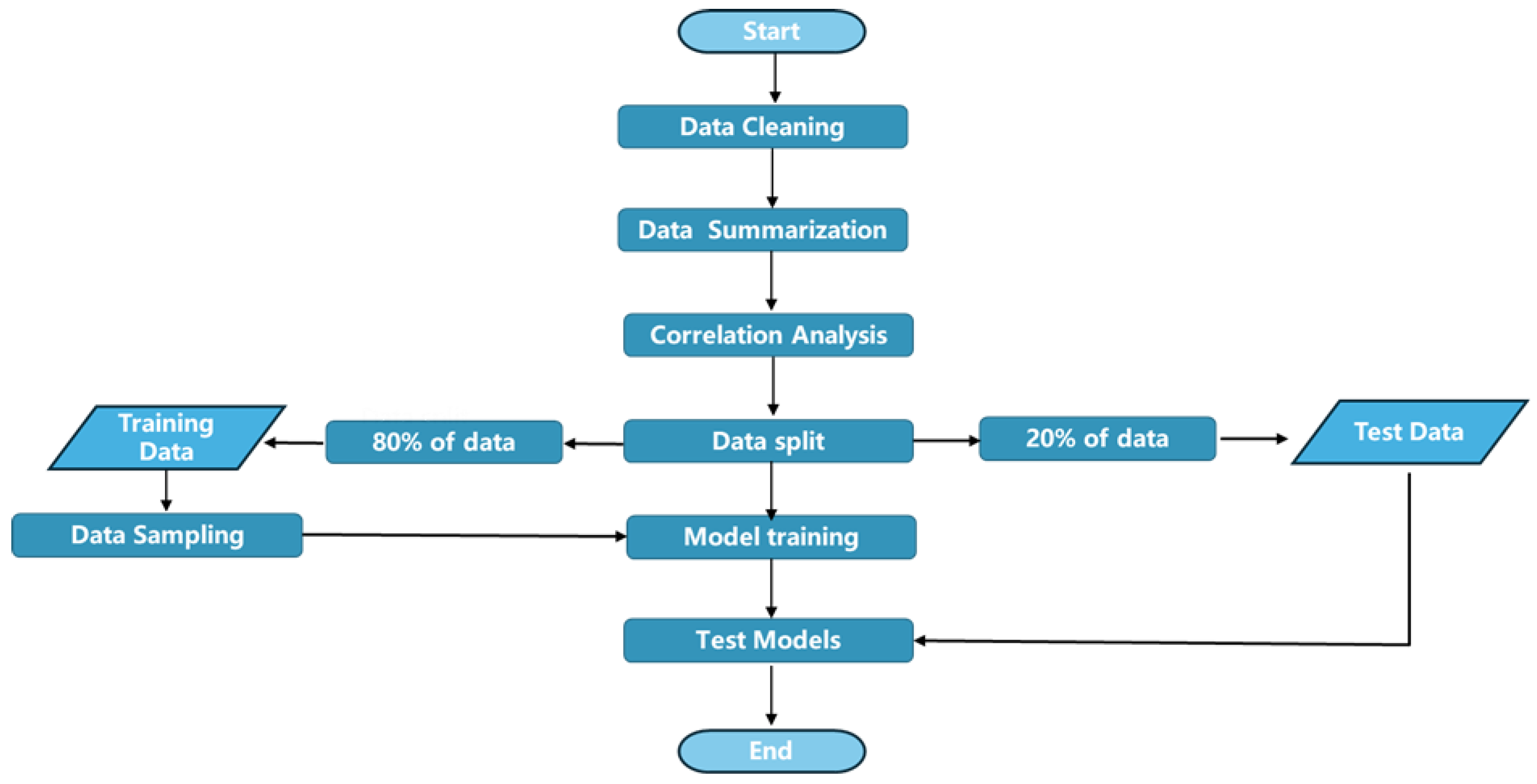
3. Data Description and Analysis
3.1. Data Summary
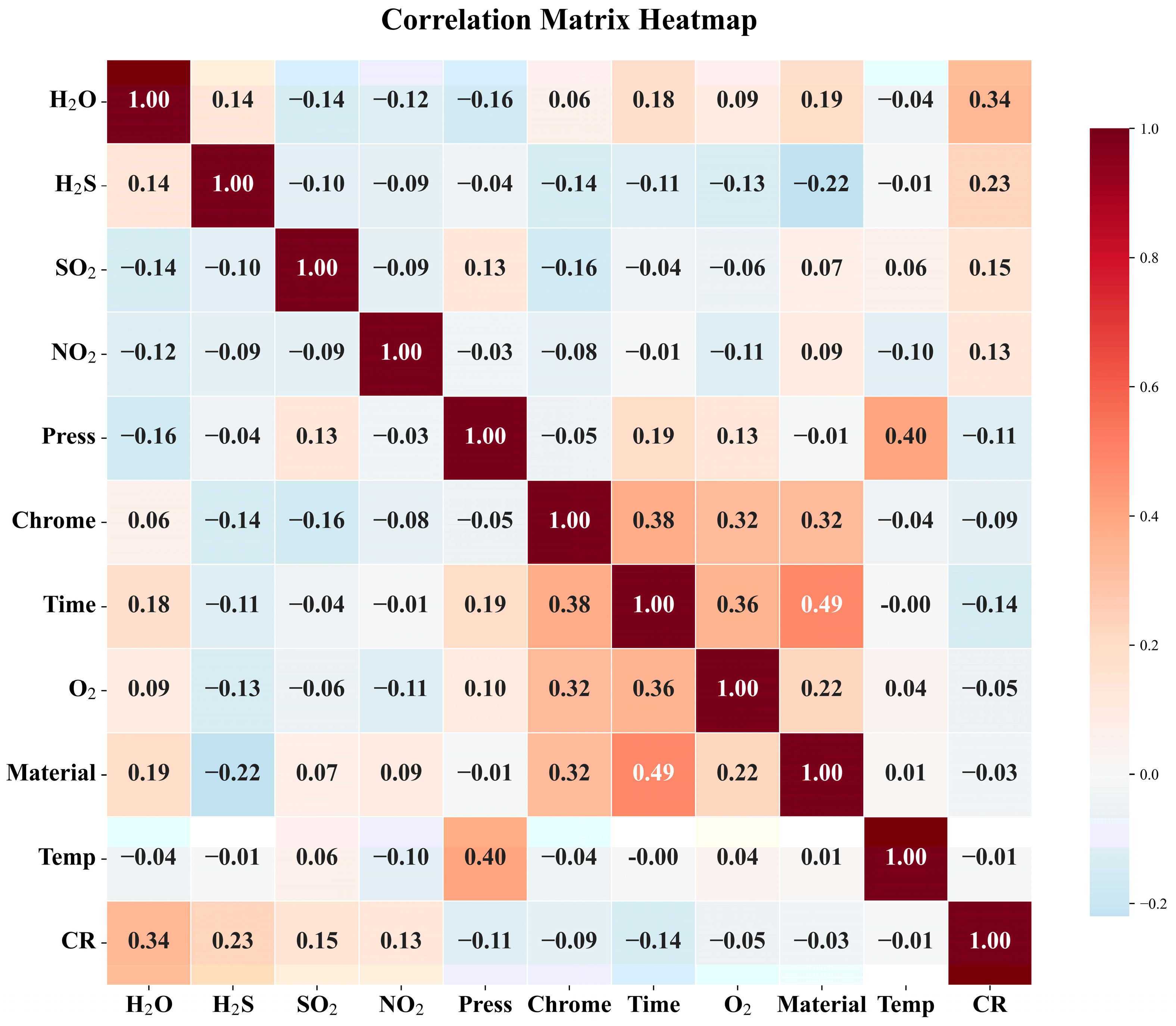
3.2. Correlation Analysis
4. Results and Discussion
4.1. Hyperparameter Optimization Analysis
4.1.1. The Impact of the Number of Hidden Layers on Model Performance
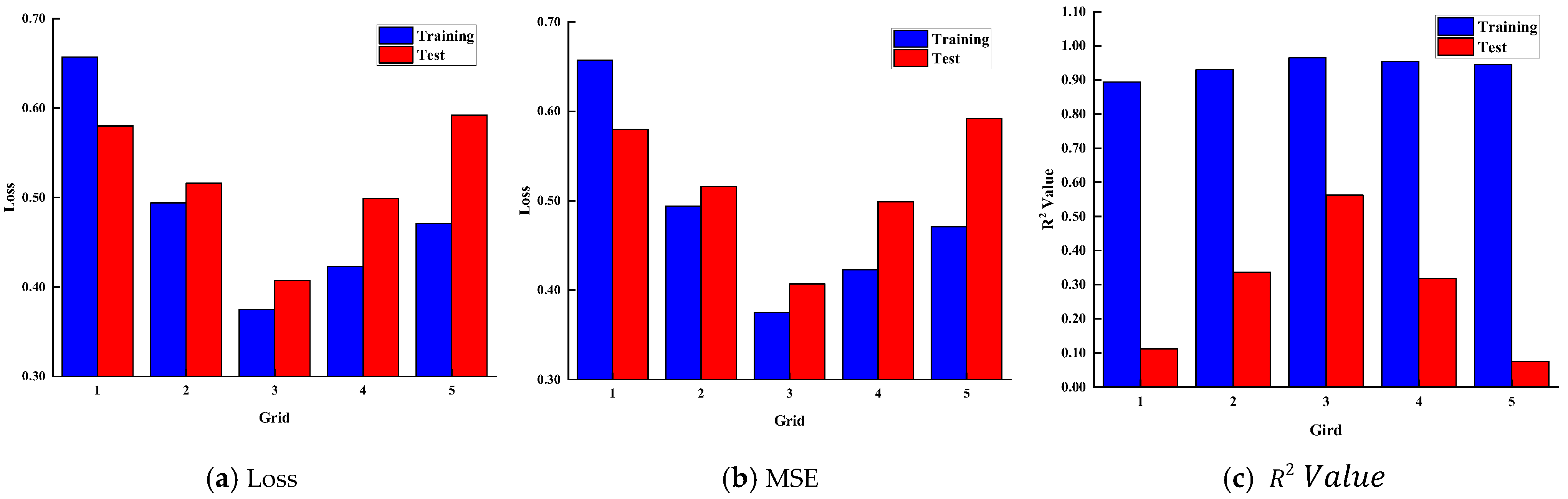
4.1.2. The Impact of Grid on Model Performance
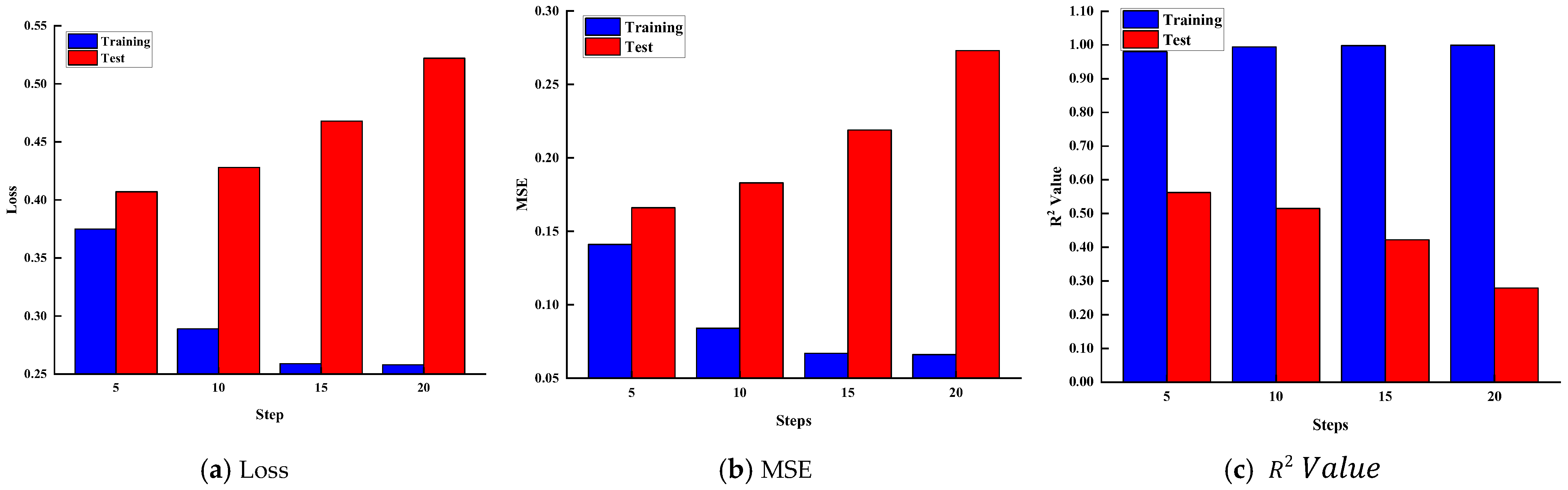
4.1.3. The Impact of Steps on Model Performance
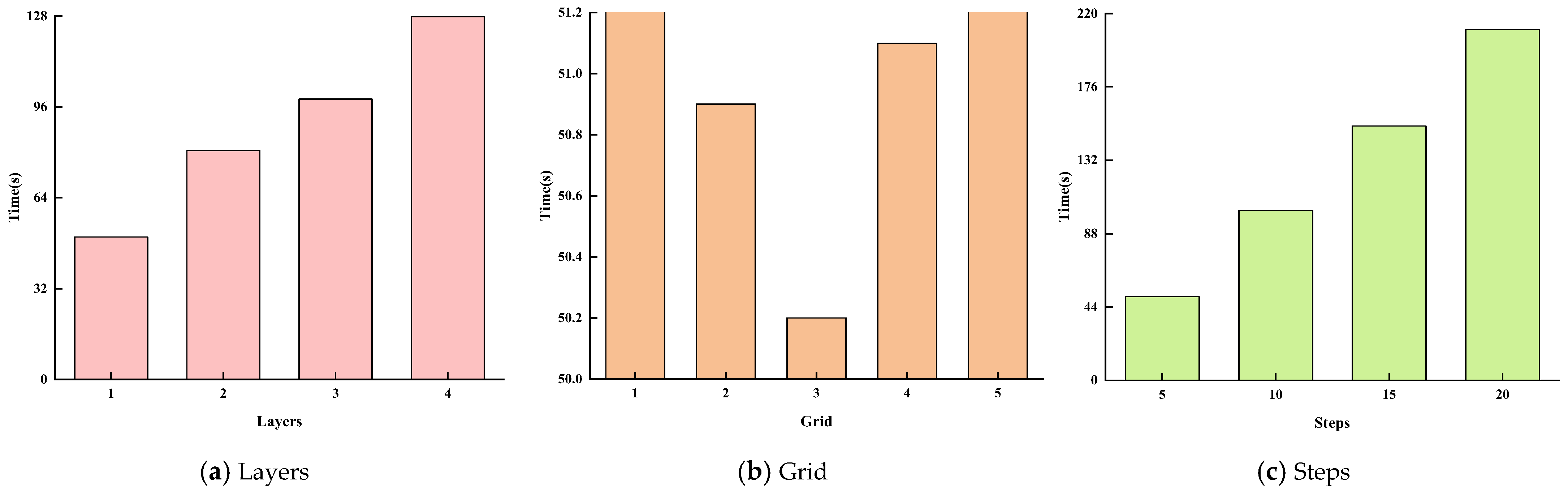
4.1.4. Impact of Hyperparameters on Computation Time
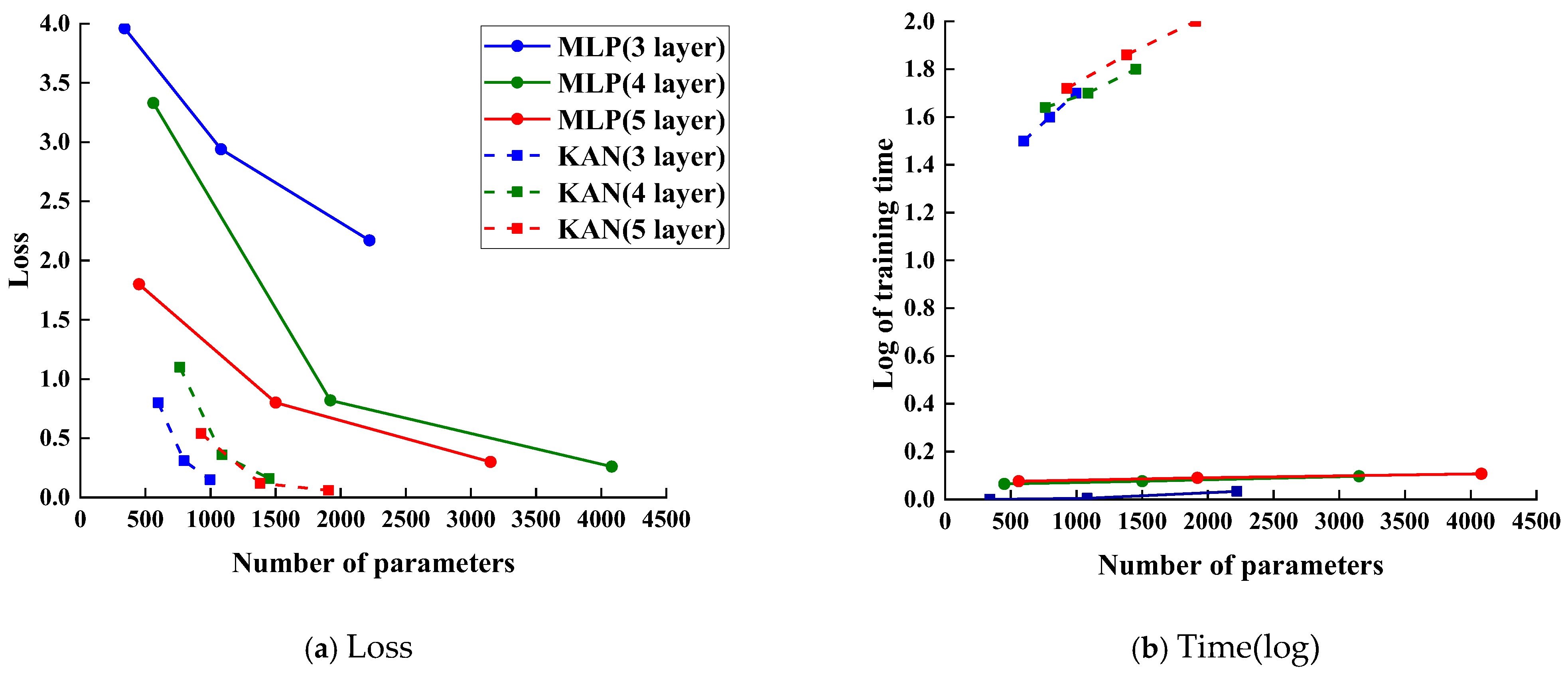
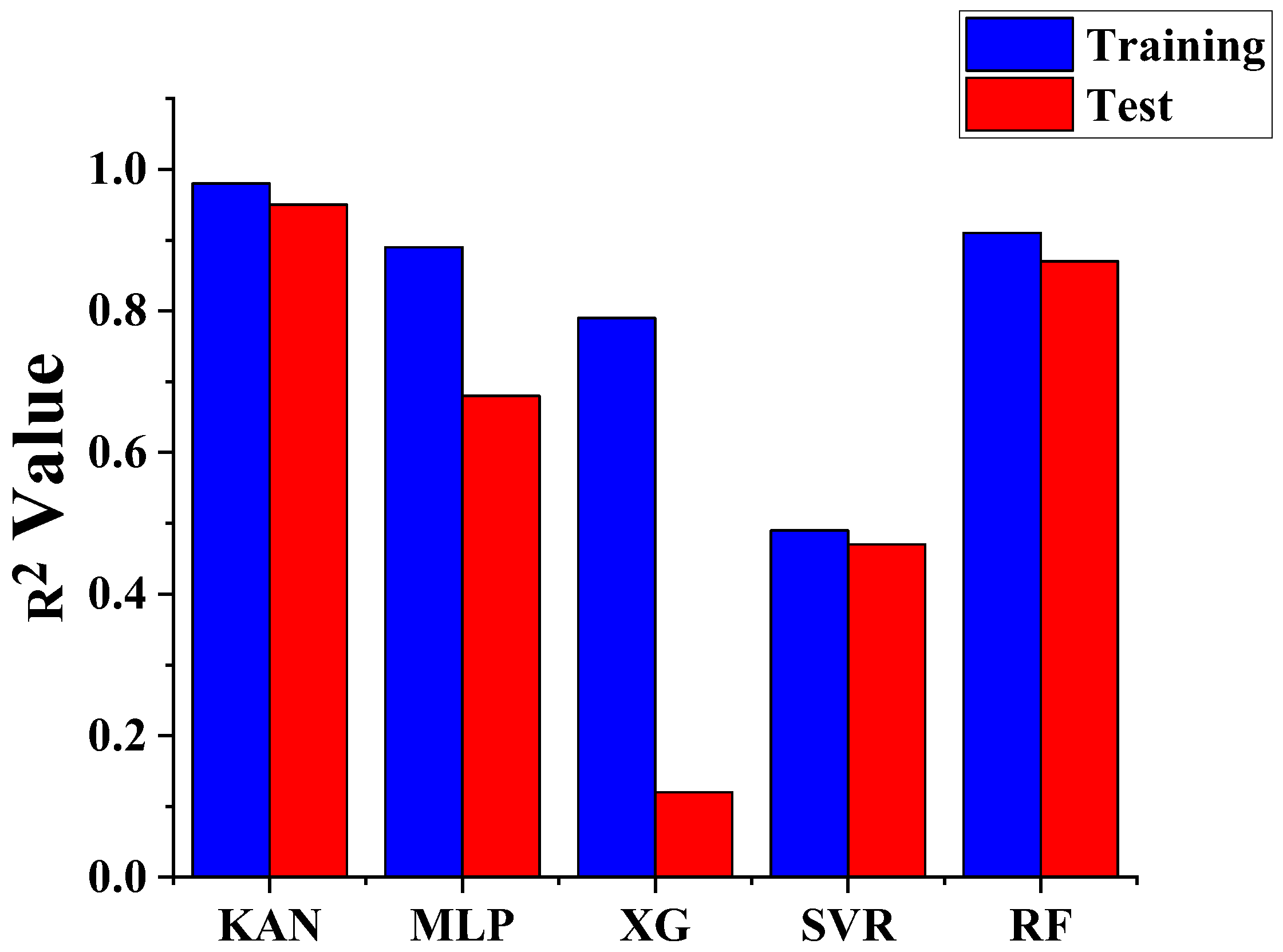
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| KAN | Kolmogorov–Arnold Network |
| MLP | Multilayer Perceptron |
| RF | Random Forest |
| XGBoost | Extreme Gradient Boosting |
| GBDT | Gradient Boosting Decision Tree |
| SVR | Support Vector Machine |
| R2 | Coefficient of Determination |
| MSE | Mean Squared Error |
| MAE | Mean Absolute error |
| RMSE | Root Mean Squared Error |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| LS | Least Squares |
| CV | Cross-Validation |
References
- Zhao, Z.; Xu, K.; Xu, P.; Wang, B. CO2 corrosion behavior of simulated heat-affected zones for X80 pipeline steel. Mater. Charact. 2021, 171, 110772. [Google Scholar] [CrossRef]
- Dou, X.; He, Z.; Zhang, X.; Liu, Y.; Liu, R.; Tan, Z.; Zhang, D.; Li, Y. Corrosion behavior and mechanism of X80 pipeline steel welded joints under high shear flow fields. Colloids Surf. A Physicochem. Eng. Asp. 2023, 665, 131225. [Google Scholar] [CrossRef]
- Yevtushenko, O.; Bettge, D.; Bohraus, S.; Bäßler, R.; Pfennig, A.; Kranzmann, A. Corrosion behavior of steels for CO2 injection. Process Saf. Environ. Prot. 2014, 92, 108–118. [Google Scholar] [CrossRef]
- Pessu, F.; Barker, R.; Neville, A. Pitting and uniform corrosion of X65 carbon steel in sour environment: The influence of CO2, H2S, and temperature. Corrosion 2017, 73, 1168–1183. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, Z.; Xu, M.; Li, Z.; Ni, W. A mechanistic model for pipeline steel corrosion in supercritical CO2-SO2-O2-H2O environments. J. Supercrit. Fluids 2013, 82, 1–12. [Google Scholar] [CrossRef]
- Choi, Y.S.; Nesic, S.; Young, D. Effect of impurities on the corrosion behavior of CO2 transmission pipeline steel in supercritical CO2-water environments. Environ. Sci. Technol. 2010, 44, 9233–9238. [Google Scholar] [CrossRef] [PubMed]
- Hua, Y.; Barker, R.; Neville, A. Understanding the influence of SO2 and O2 on the corrosion of carbon steel in water-saturated supercritical CO2. Corrosion 2015, 71, 667–683. [Google Scholar] [CrossRef]
- Newman, R. Pitting corrosion of metals. Electrochem. Soc. Interface 2010, 19, 33–38. [Google Scholar] [CrossRef]
- Sim, S.; Cole, I.; Choi, Y.-S.; Birbilis, N. A review of the protection strategies against internal corrosion for the safe transport of supercritical CO2 via steel pipeline for CCS purposes. Int. J. Greenhouse Gas Control 2014, 29, 185–199. [Google Scholar] [CrossRef]
- Gao, K.; Yu, F.; Pang, X.; Zhang, G.; Qiao, L.; Chu, W.; Lu, M. Mechanical properties of CO2 corrosion products scales and their relationship to corrosion rates. Corros. Sci. 2008, 50, 2796–2803. [Google Scholar] [CrossRef]
- Obeyesekere, N.U. Pitting corrosion. In Trends in Oil and Gas Corrosion Research and Technologies; El-Sherik, A.M., Ed.; Woodhead Publishing: Boston, MA, USA, 2017; pp. 215–248. [Google Scholar] [CrossRef]
- Doğan, B.; Altınten, A. Mathematical modeling of CO2 corrosion with NORSOK M 506. Bitlis Eren Univ. J. Sci. Technol. 2023, 12, 84–92. [Google Scholar] [CrossRef]
- Jepson, W.P.; Stitzel, S.; Kang, C.; Gopal, M. Model for sweet corrosion in horizontal multiphase slug flow. In Proceedings of the Corrosion 1997, New Orleans, LA, USA, 9–14 March 1997; OnePetro: Richardson, TX, USA, 1997. [Google Scholar] [CrossRef]
- De Waard, C.; Milliams, D.E. Carbon acid corrosion of steel. Corrosion 1975, 31, 177–181. [Google Scholar] [CrossRef]
- De Waard, C.; Lotz, U. Prediction of CO2 corrosion for carbon steel. In Proceedings of the Corrosion 1993, New Orleans, LA, USA, 7–12 March 1993; NACE: Houston, TX, USA, 1993; Volume 93, p. 69. [Google Scholar] [CrossRef]
- Wu, L.; Liao, K.; He, G.; Qin, M.; Tian, Z.; Ye, N.; Wang, M.; Leng, J. Wet gas pipeline internal general corrosion prediction based on improved De Waard 95 model. J. Pipeline Syst. Eng. Pract. 2023, 14, 04023041. [Google Scholar] [CrossRef]
- Pérez-Miguel, C.; Mendiburu, A.; Miguel-Alonso, J. Modeling the availability of Cassandra. J. Parallel Distrib. Comput. 2015, 86, 29–44. [Google Scholar] [CrossRef]
- Ricciardi, V.; Travagliati, A.; Schreiber, V.; Klomp, M.; Ivanov, V.; Augsburg, K.; Faria, C. A novel semi-empirical dynamic brake model for automotive applications. Tribol. Int. 2020, 146, 106223. [Google Scholar] [CrossRef]
- Ghorbani, Z.; Webster, R.; Lázaro, M.; Trouvé, A. Limitations in the predictive capability of pyrolysis models based on a calibrated semi-empirical approach. Fire Saf. J. 2013, 61, 274–288. [Google Scholar] [CrossRef]
- Nesic, S.; Postlethwaite, J.; Olsen, S. An electrochemical model for prediction of corrosion of mild steel in aqueous carbon dioxide solutions. Corrosion 1996, 52, 280–294. [Google Scholar] [CrossRef]
- Fellet, M.; Nyborg, R. Understanding corrosion of flexible pipes at subsea oil and gas wells. MRS Bull. 2018, 43, 654–655. [Google Scholar] [CrossRef]
- Wang, P.; Quan, Q. Prediction of corrosion rate in submarine multiphase flow pipeline based on PSO-SVR model. IOP Conf. Ser. Mater. Sci. Eng. 2019, 688, 044015. [Google Scholar] [CrossRef]
- Fang, J.; Cheng, X.; Gai, H.; Lin, S.; Lou, H. Development of machine learning algorithms for predicting internal corrosion of crude oil and natural gas pipelines. Comput. Chem. Eng. 2023, 177, 108358. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Q.; Zhang, X.; Dong, L.; Bai, S.; Zeng, D.; Zhang, Z.; Zhang, H.; Xi, Y. Interpretable machine learning for maximum corrosion depth and influence factor analysis. Npj Mater. Degrad. 2023, 7, 9. [Google Scholar] [CrossRef]
- Peng, S.; Zhang, Z.; Liu, E.; Liu, W.; Qiao, W. A new hybrid algorithm model for prediction of internal corrosion rate of multiphase pipeline. J. Nat. Gas Sci. Eng. 2021, 85, 103716. [Google Scholar] [CrossRef]
- Ben Seghier, M.E.A.; Höche, D.; Zheludkevich, M. Prediction of the internal corrosion rate for oil and gas pipeline: Implementation of ensemble learning techniques. J. Nat. Gas Sci. Eng. 2022, 99, 104425. [Google Scholar] [CrossRef]
- Wang, G.; Wang, C.; Shi, L. CO2 corrosion rate prediction for submarine multiphase flow pipelines based on multi-layer perceptron. Atmosphere 2022, 13, 1833. [Google Scholar] [CrossRef]
- Wuest, T.; Weimer, D.; Irgens, C.; Thoben, K.-D. Machine learning in manufacturing: Advantages, challenges, and applications. Prod. Manuf. Res. 2016, 4, 23–45. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar] [CrossRef]
- Mia, M.M.A.; Biswas, S.K.; Urmi, M.C.; Siddique, A. An algorithm for training multilayer perceptron (MLP) for image reconstruction using neural network without overfitting. Int. J. Sci. Technol. Res. 2015, 4, 271–275. [Google Scholar]
- Mai-Cao, L.; Truong-khac, H. A comparative study on different machine learning algorithms for petroleum production forecasting. Improv. Oil Gas Recovery 2022, 6. [Google Scholar] [CrossRef]
- Doan, T.; Vo, M.V. Using machine learning techniques for enhancing production forecast in North Malay Basin. Improv. Oil Gas Recovery 2021, 5, 2–5. [Google Scholar] [CrossRef]
- Brown, J.; Graver, B.; Gulbrandsen, E.; Dugstad, A.; Morland, B. Update of DNV recommended practice RP-J202 with focus on CO2 corrosion with impurities. Energy Procedia 2014, 63, 2432–2441. [Google Scholar] [CrossRef]
- Hua, Y.; Jonnalagadda, R.; Zhang, L.; Neville, A.; Barker, R. Assessment of general and localized corrosion behavior of X65 and 13Cr steels in water-saturated supercritical CO2 environments with SO2/O2. Int. J. Greenh. Gas Control 2017, 64, 126–136. [Google Scholar] [CrossRef]
- Sui, P.; Sun, J.; Hua, Y.; Liu, H.; Zhou, M.; Zhang, Y.; Liu, J.; Wang, Y. Effect of temperature and pressure on corrosion behavior of X65 carbon steel in water-saturated CO2 transport environments mixed with H2S. Int. J. Greenh. Gas Control 2018, 73, 60–69. [Google Scholar] [CrossRef]
- Yan, S.; Li, W.; Zhang, M.; Wang, Z.; Liu, Z.; Lin, K.; Yi, H. An innovative method for hydraulic fracture parameters optimization to enhance production in tight oil reservoirs. Improv. Oil Gas Recovery 2023, 8, 12–13. [Google Scholar] [CrossRef]
- De Winter, J.C.F.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol. Methods 2016, 21, 273–290. [Google Scholar] [CrossRef] [PubMed]


| Factor | Chrome Wt-% | Temp °C | ppmv | ppmv | ppmv | ppmv | Time hours | CR mm/year | Severity | |
|---|---|---|---|---|---|---|---|---|---|---|
| Statistics | ||||||||||
| mean | 0.09 | 48.27 | 29.50 | 5208.75 | 2034.76 | 34.30 | 191.01 | 0.50 | 1.14 | |
| std | 0.13 | 20.37 | 62.88 | 11,634.29 | 5961.86 | 127.01 | 254.14 | 1.81 | 1.17 | |
| min | 0.00 | 25.00 | 0.08 | 0.00 | 0.00 | 0.00 | 1.50 | 0.00 | 0.00 | |
| 25% | 0.01 | 40.00 | 0.96 | 0.00 | 0.02 | 0.00 | 48.00 | 0.03 | 0.00 | |
| 50% | 0.04 | 50.00 | 2.73 | 20.00 | 0.08 | 0.00 | 120.00 | 0.08 | 1.00 | |
| 75% | 0.11 | 50.00 | 34.00 | 1000.00 | 0.33 | 0.00 | 168.00 | 0.30 | 2.00 | |
| max | 0.54 | 200.00 | 400.00 | 47,000.00 | 26.00 | 1000.00 | 1512.00 | 26.00 | 3.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Zou, L.; Xu, Y.; Guo, C.; Wen, F.; Wang, W.; Qi, J.; Zhang, M.; Dong, G.; Li, W. Kolmogorov–Arnold Network for Predicting CO2 Corrosion and Performance Comparison with Traditional Data-Driven Approaches. Processes 2025, 13, 3174. https://doi.org/10.3390/pr13103174
Dong Z, Zou L, Xu Y, Guo C, Wen F, Wang W, Qi J, Zhang M, Dong G, Li W. Kolmogorov–Arnold Network for Predicting CO2 Corrosion and Performance Comparison with Traditional Data-Driven Approaches. Processes. 2025; 13(10):3174. https://doi.org/10.3390/pr13103174
Chicago/Turabian StyleDong, Zhenzhen, Lu Zou, Yiming Xu, Chenhong Guo, Fenggang Wen, Wei Wang, Ji Qi, Min Zhang, Guoqing Dong, and Weirong Li. 2025. "Kolmogorov–Arnold Network for Predicting CO2 Corrosion and Performance Comparison with Traditional Data-Driven Approaches" Processes 13, no. 10: 3174. https://doi.org/10.3390/pr13103174
APA StyleDong, Z., Zou, L., Xu, Y., Guo, C., Wen, F., Wang, W., Qi, J., Zhang, M., Dong, G., & Li, W. (2025). Kolmogorov–Arnold Network for Predicting CO2 Corrosion and Performance Comparison with Traditional Data-Driven Approaches. Processes, 13(10), 3174. https://doi.org/10.3390/pr13103174





