Numerical Study on Hydraulic Fracture Propagation in Sand–Coal Interbed Formations
Abstract
1. Introduction
2. Mathematical Model
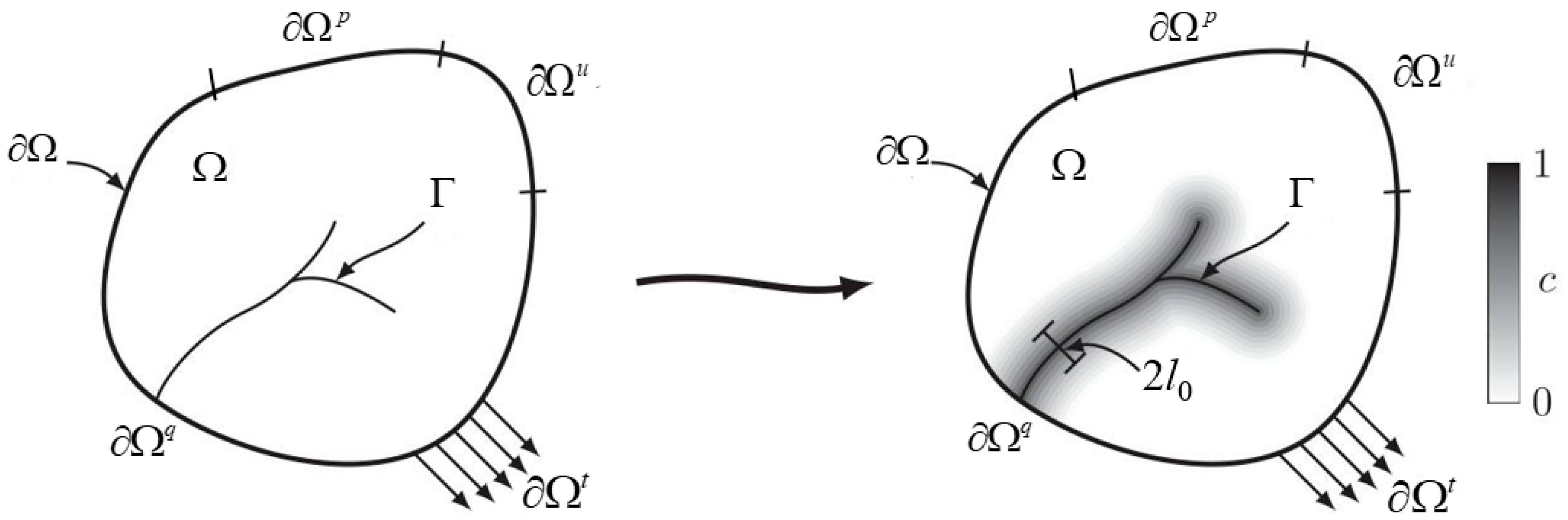
2.1. Description of Fractures by Phase-Field Approximation Method
2.1.1. Brief Introduction to Phase-Field Method
2.1.2. Constitutive Energy Function
2.1.3. Phase-Field Evolution
2.2. Stress Balance Equation
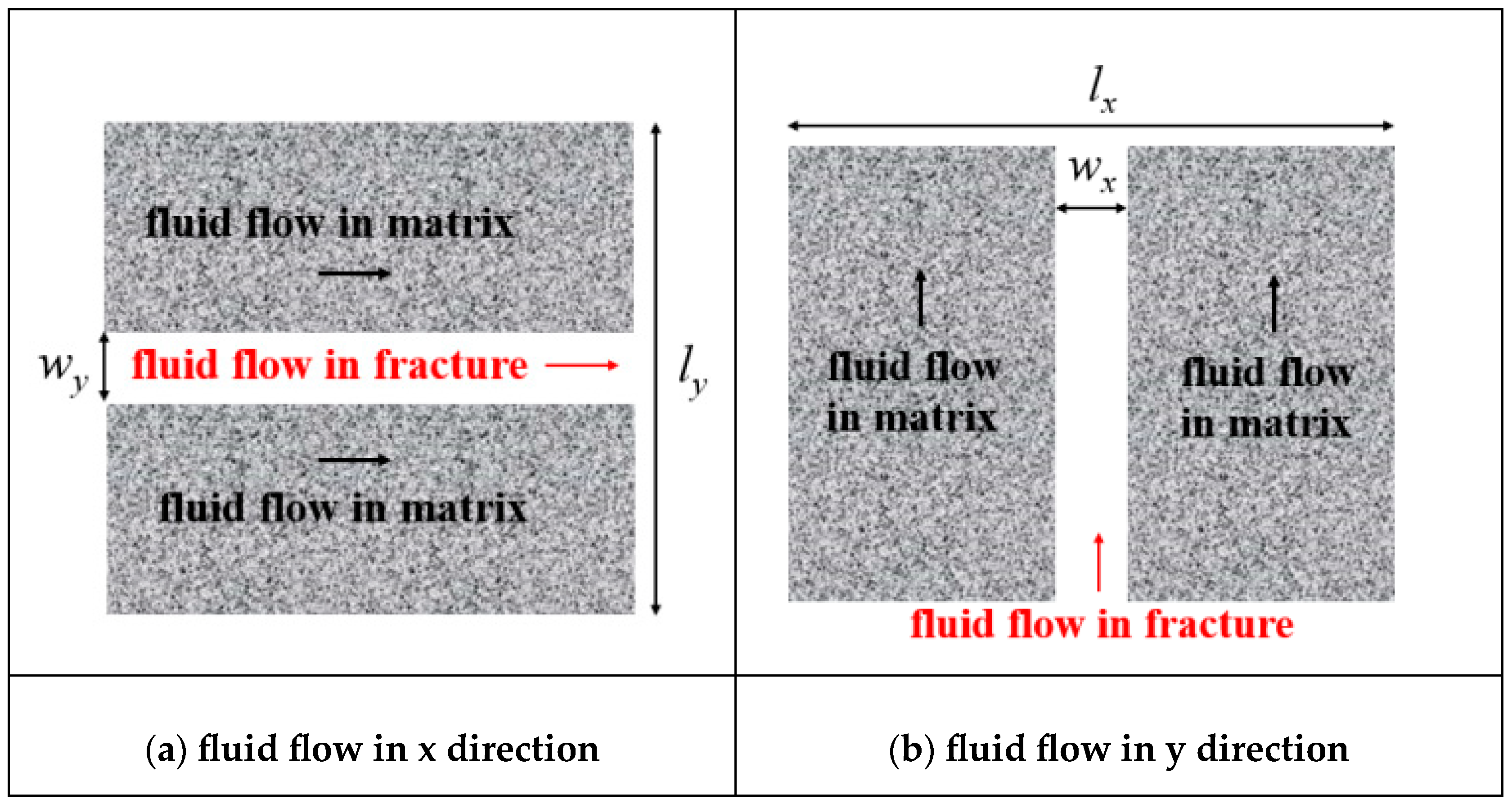
2.3. Control Equations for Fluid Flow
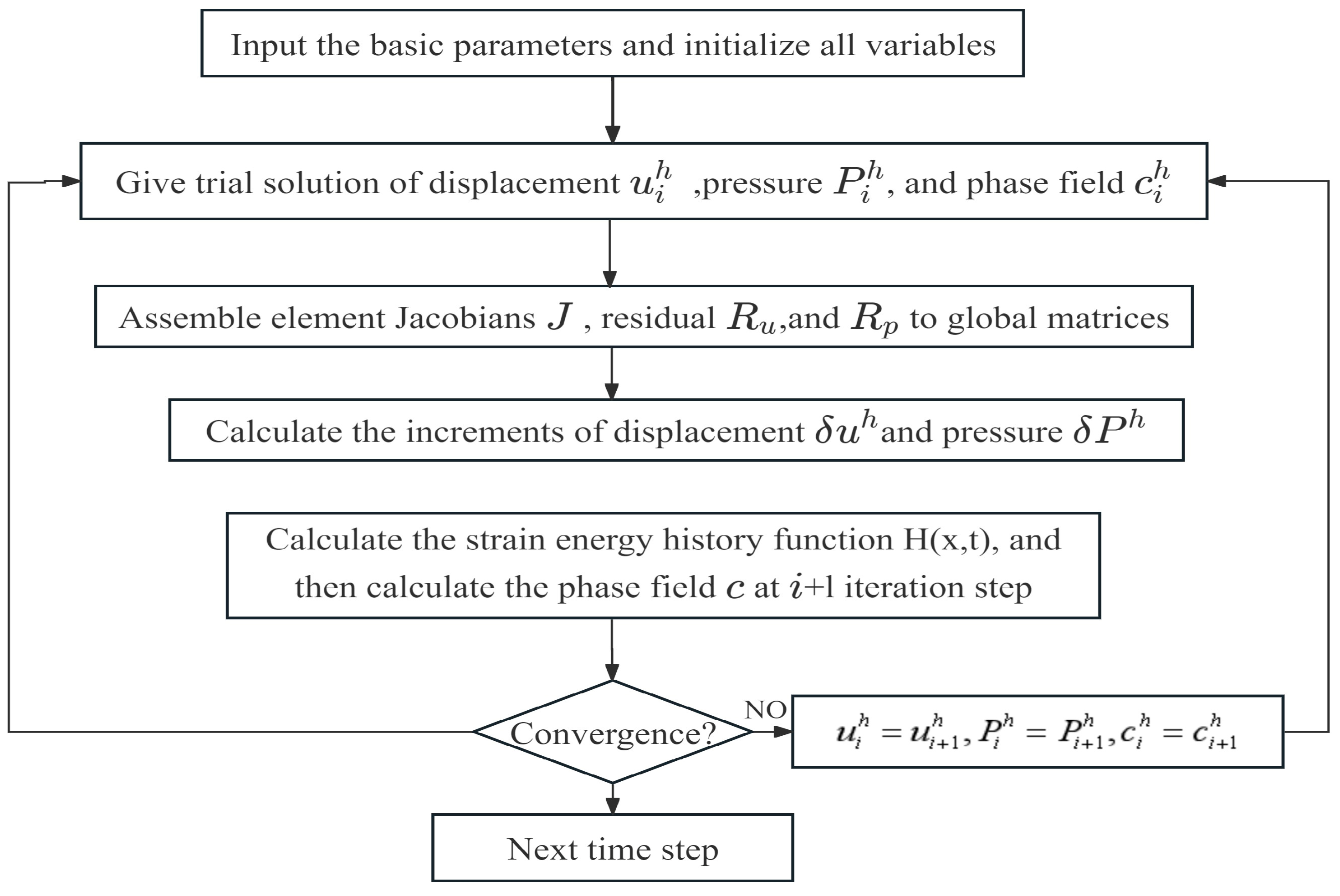
2.4. Numerical Implementation
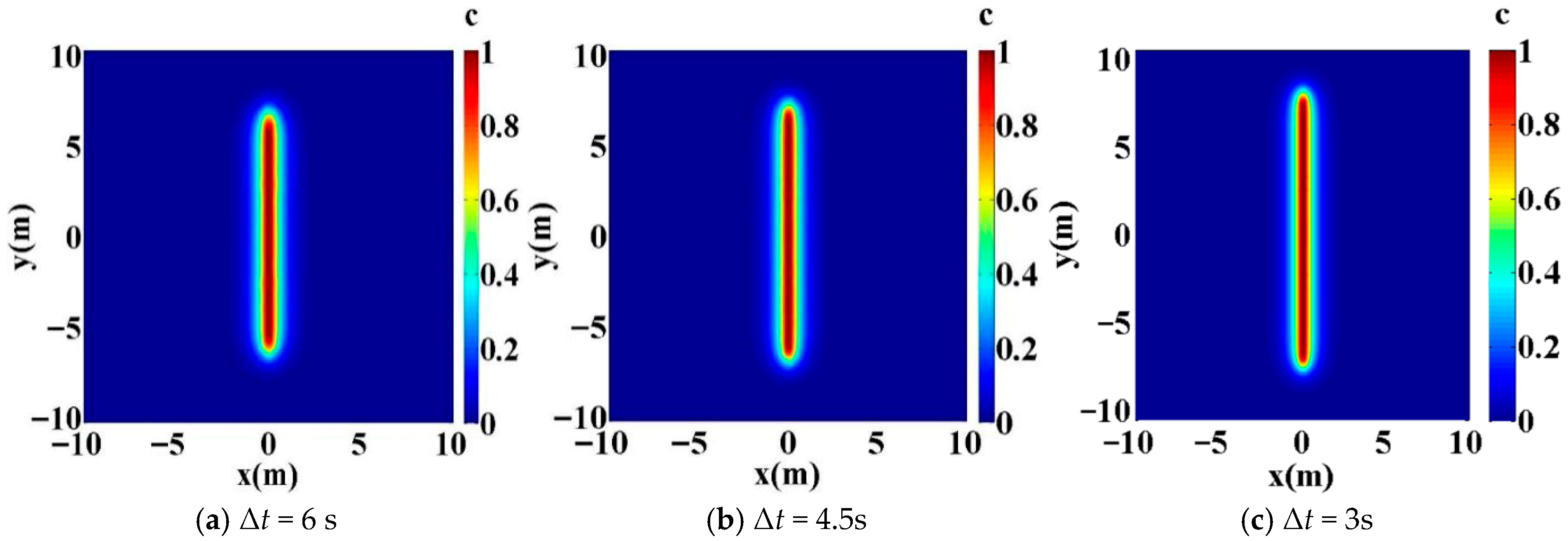
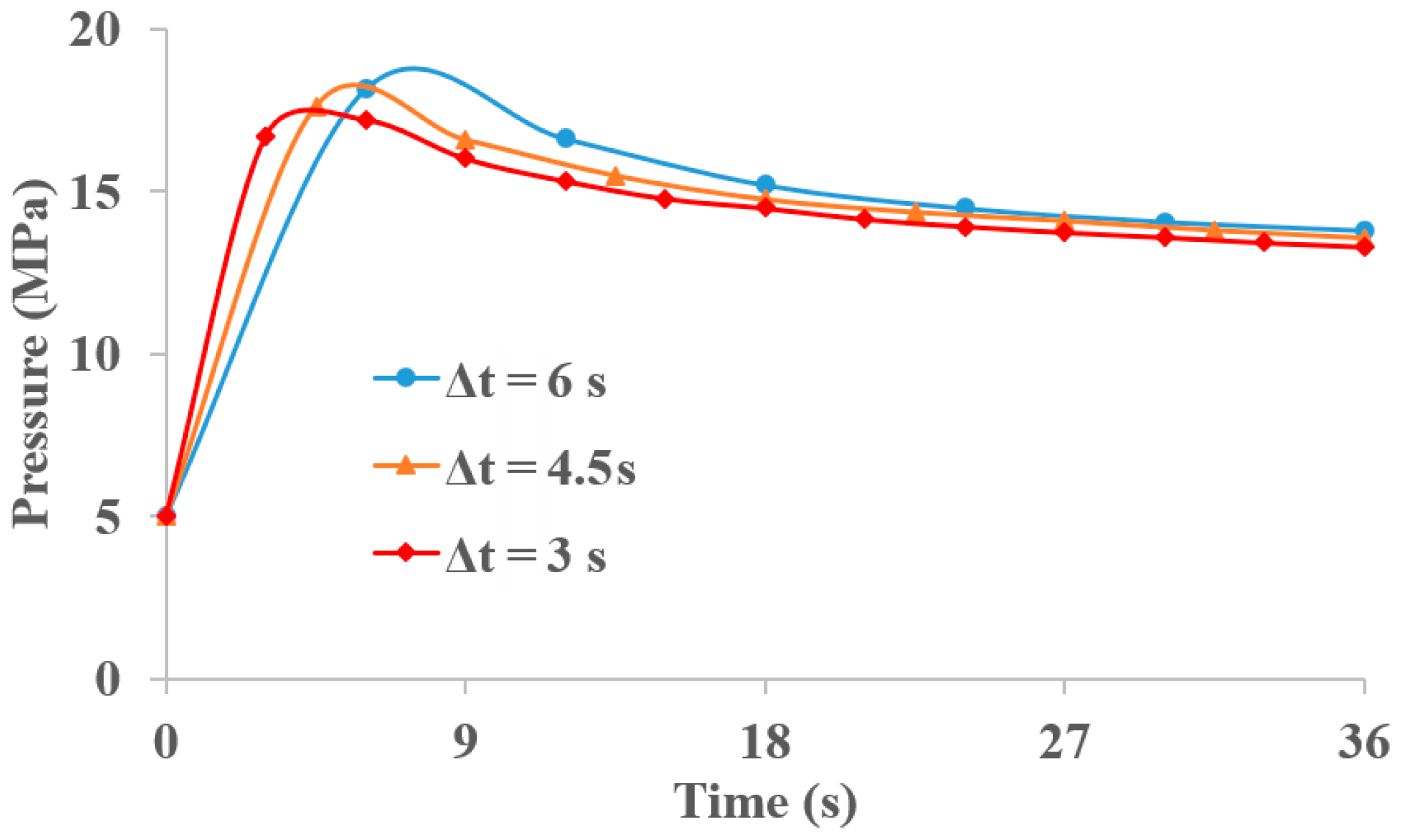
3. Study on Model Convergence and Stability
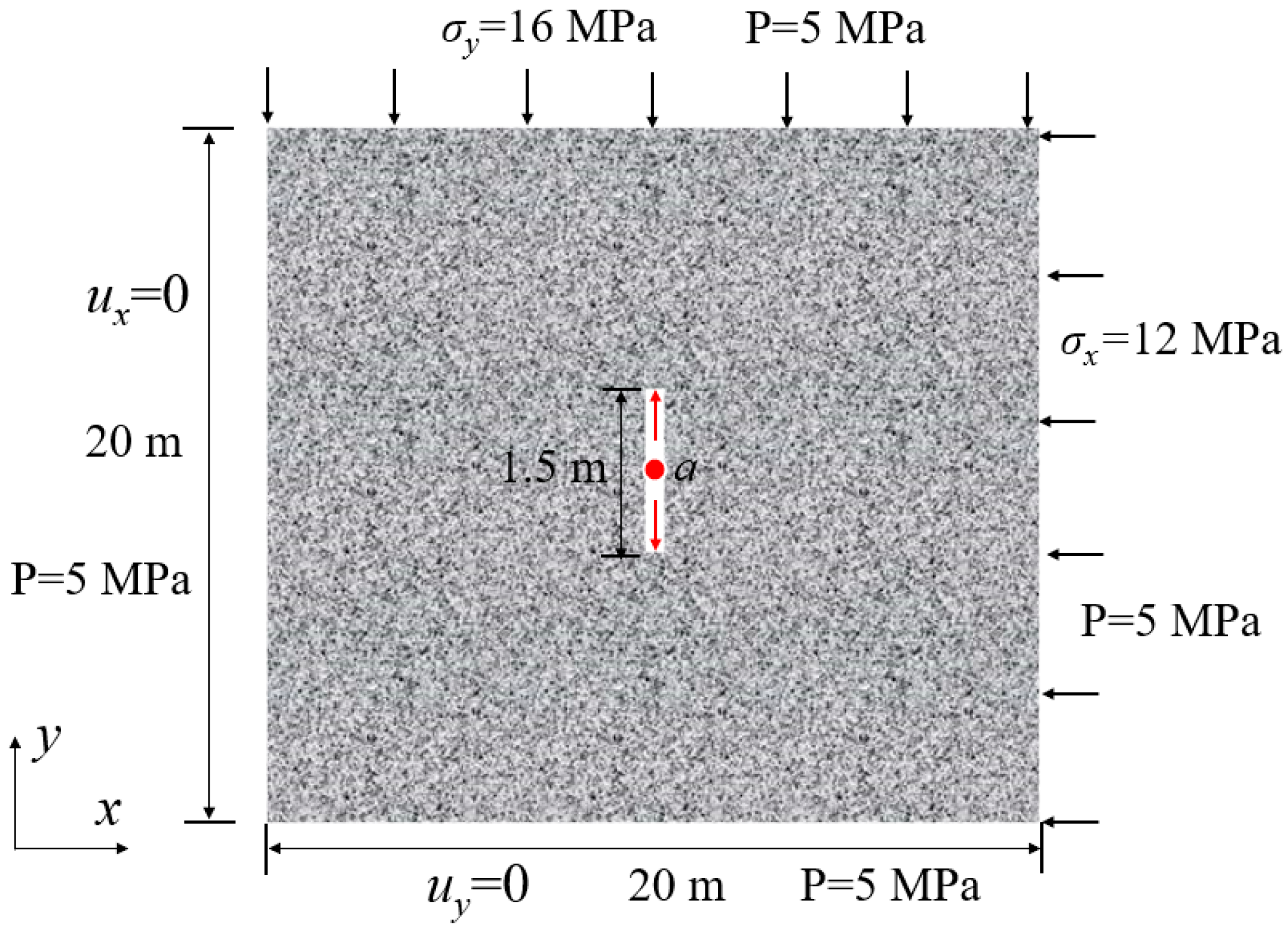
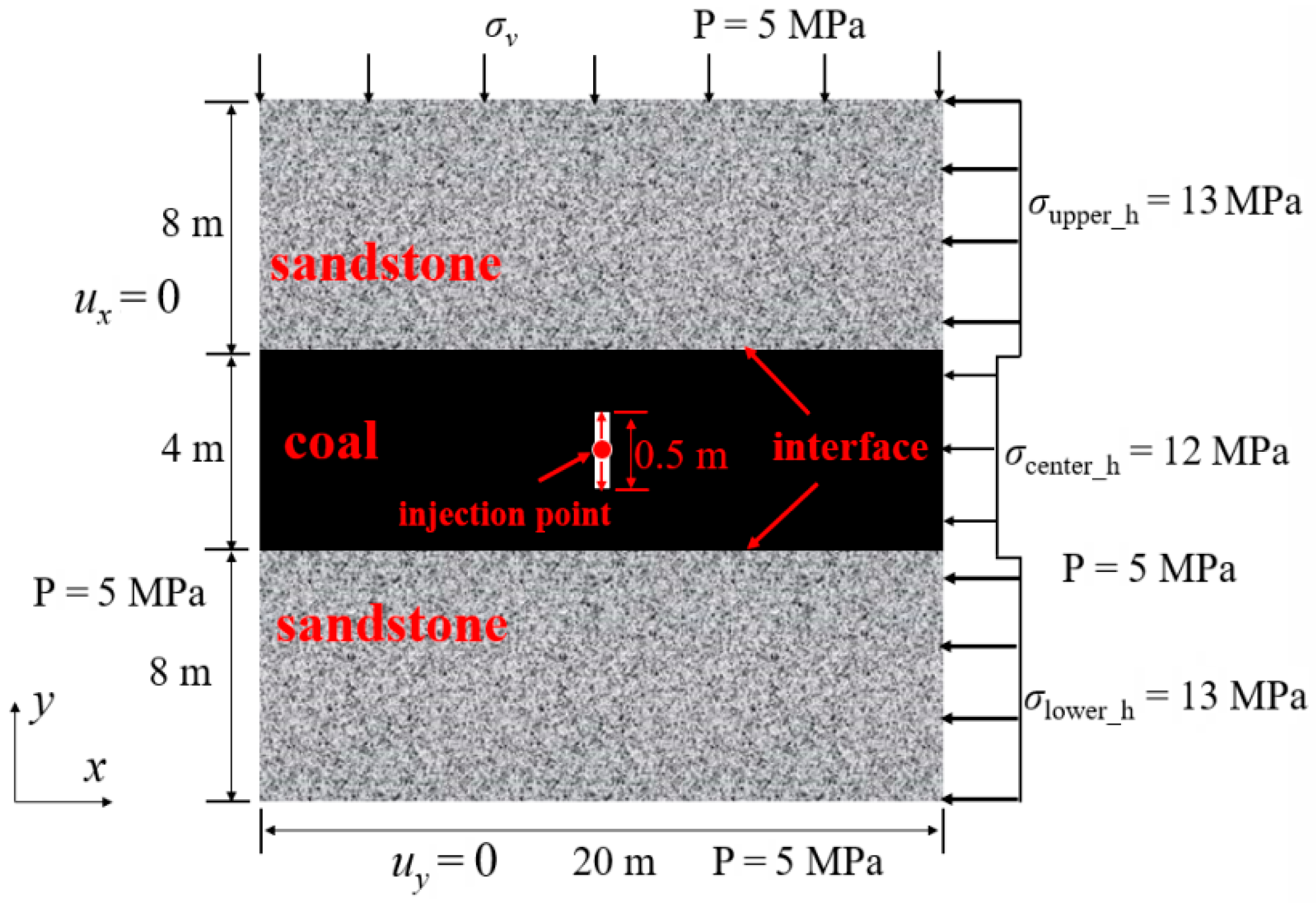
4. Numerical Simulation
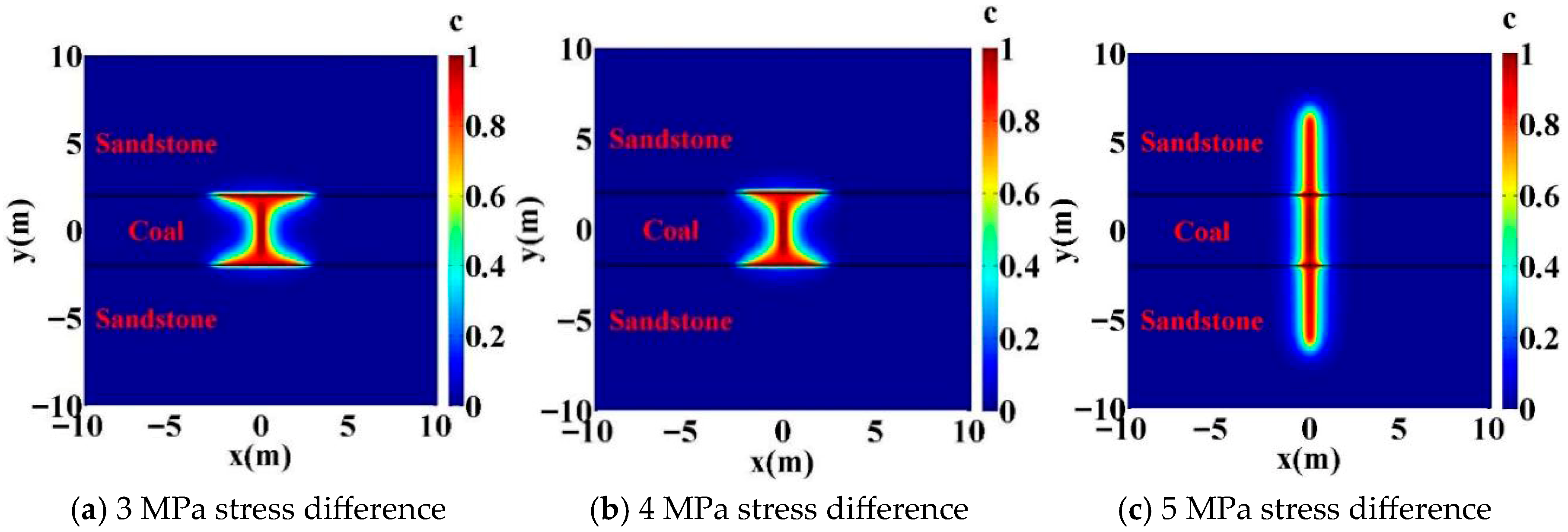
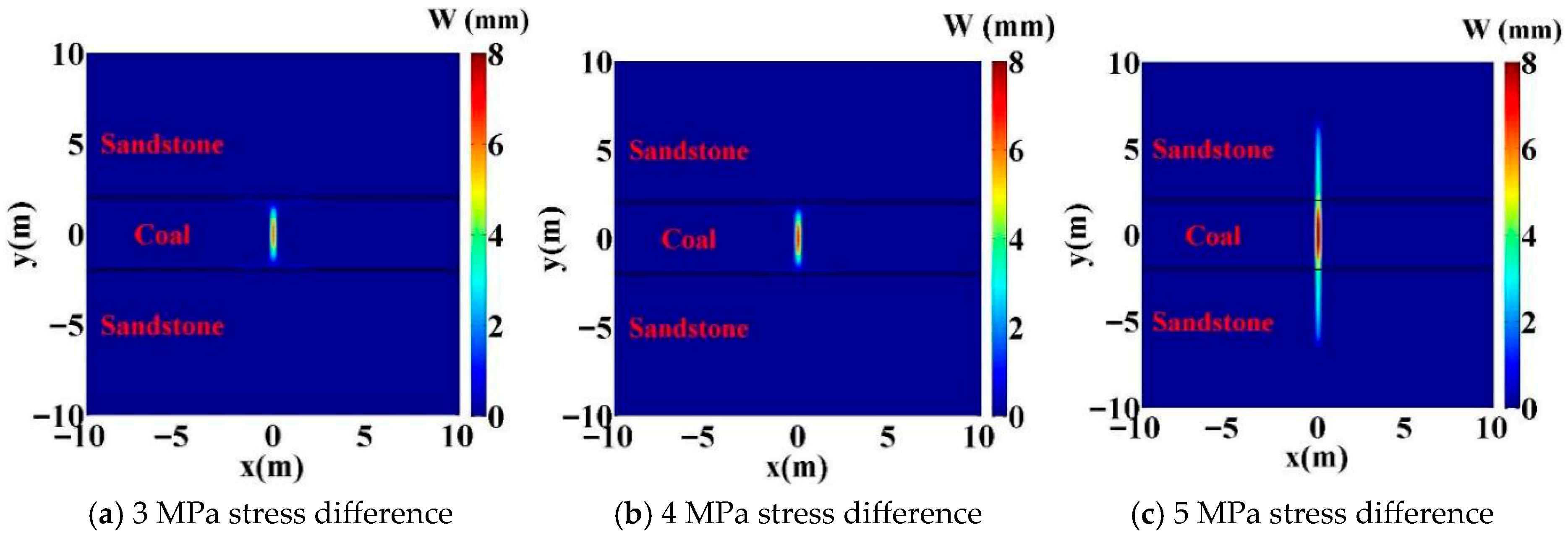
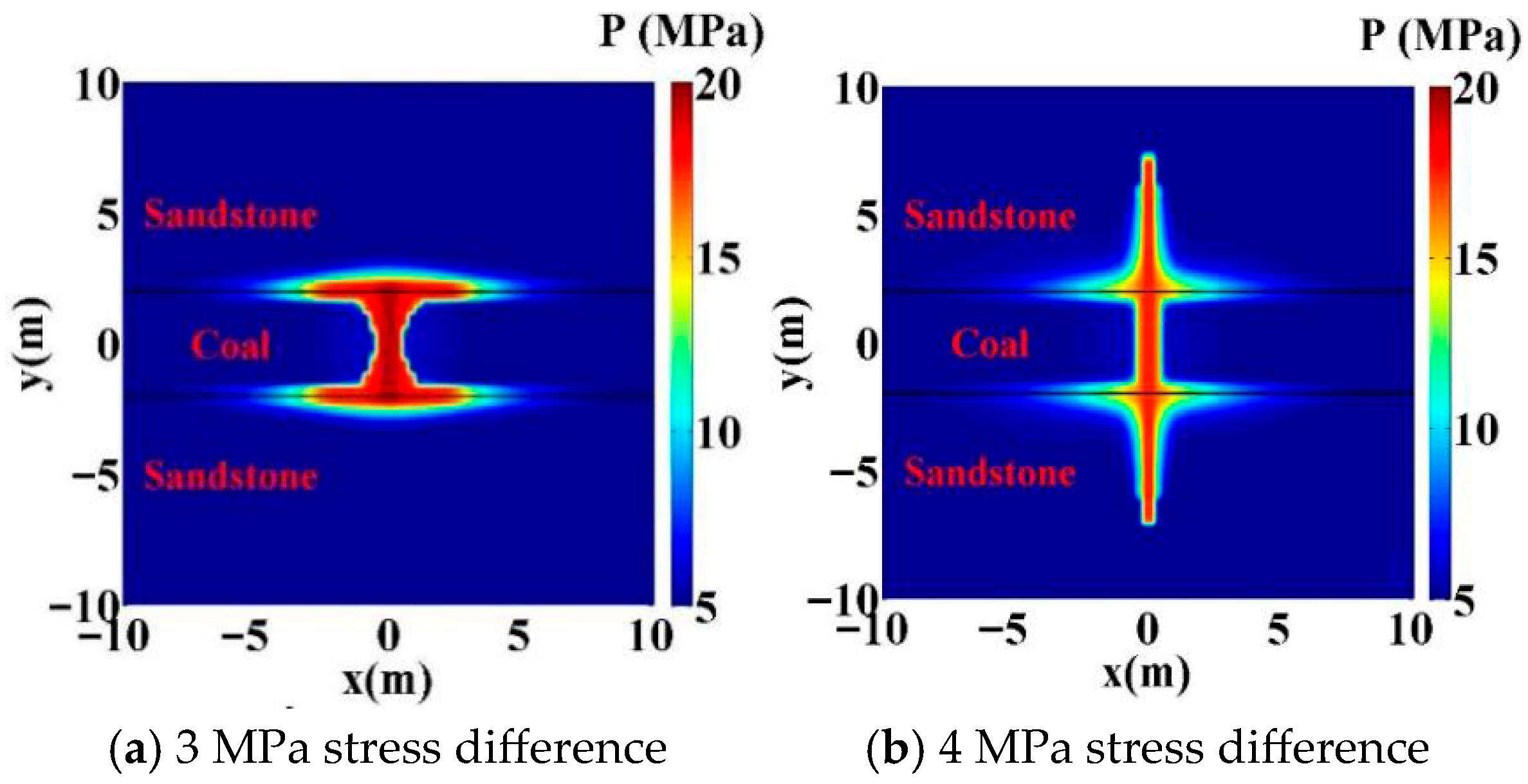
4.1. Effects of Ground Stress Differences
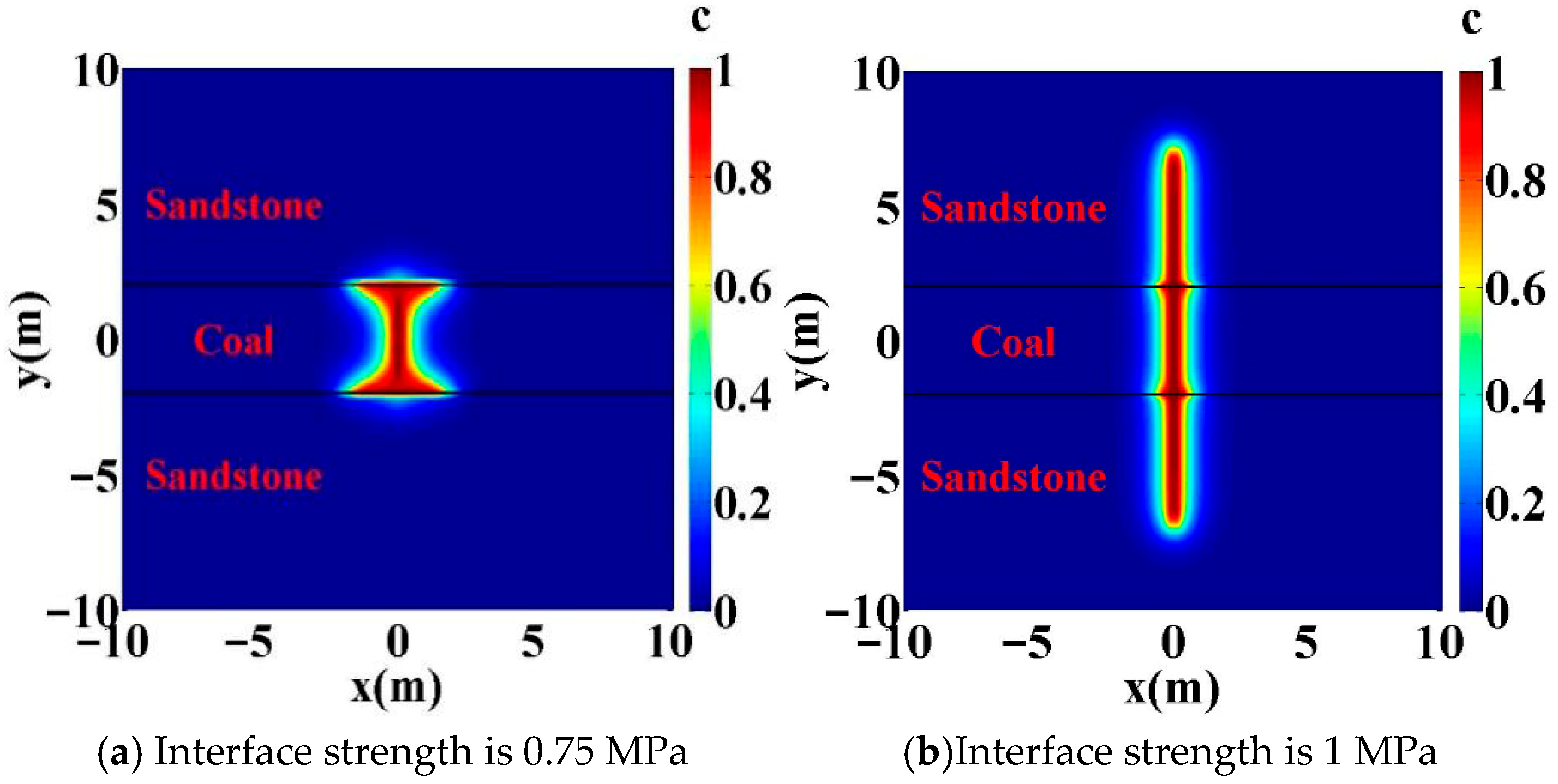
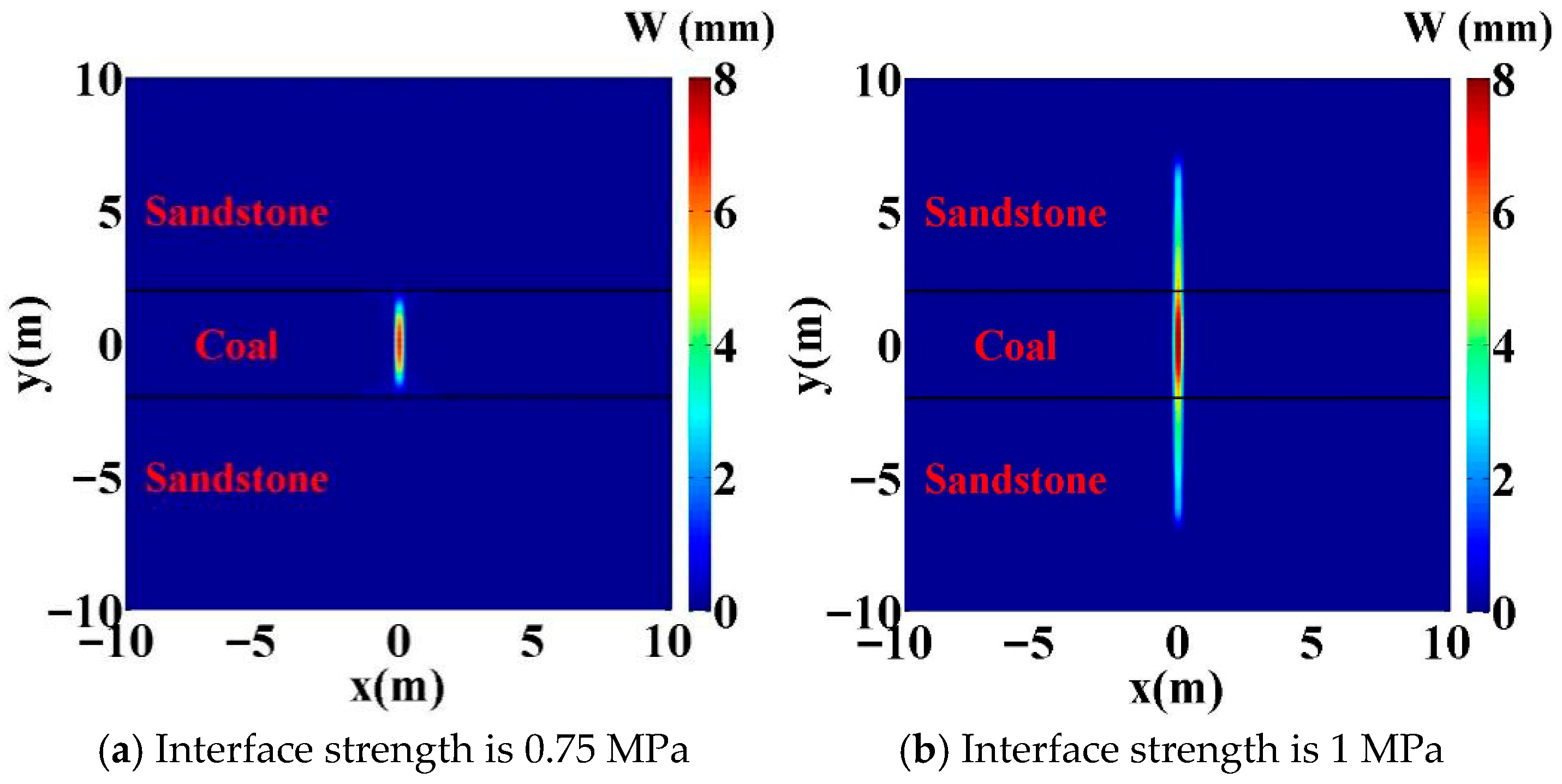
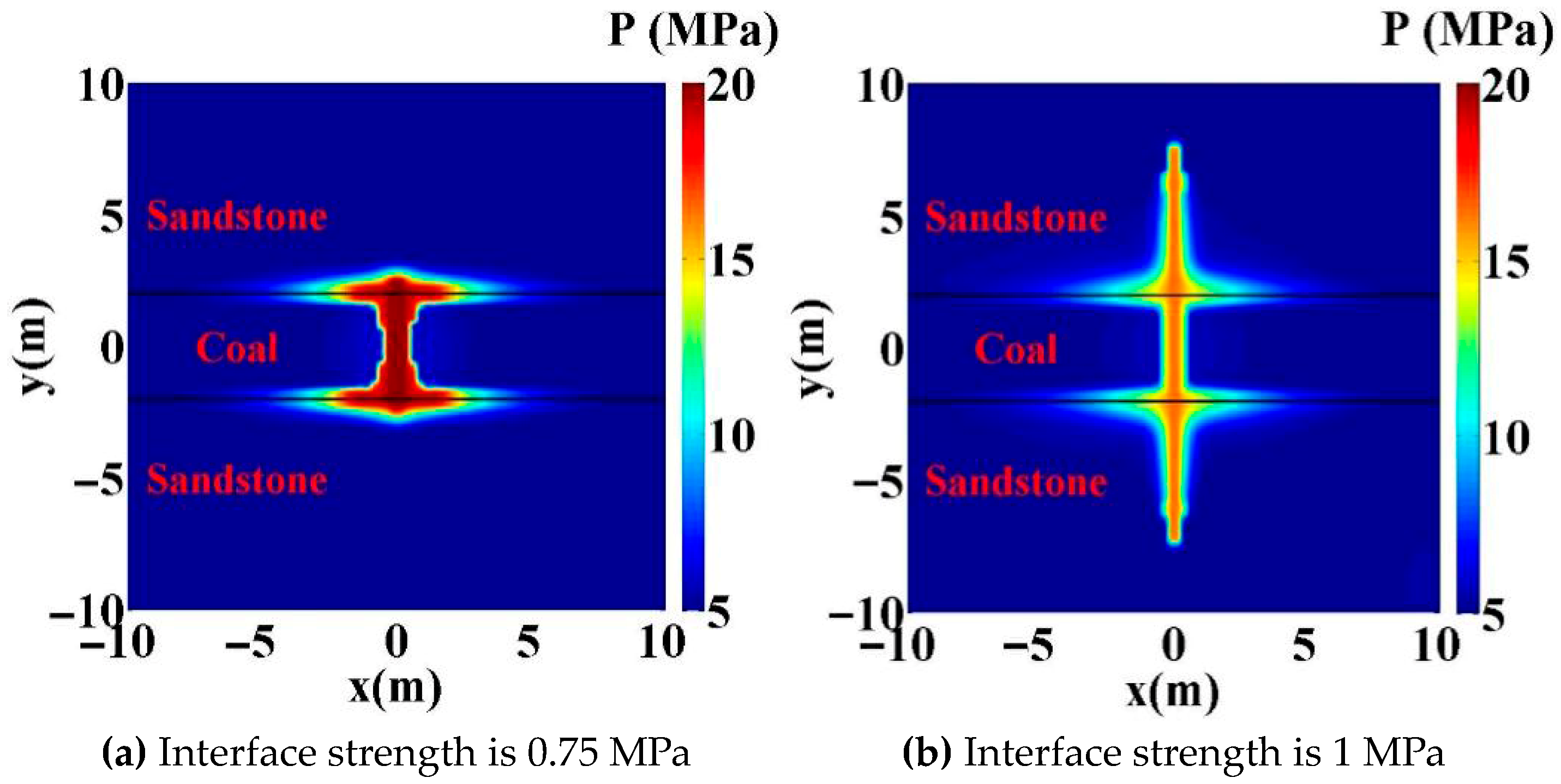
4.2. Influence of Interface Strength
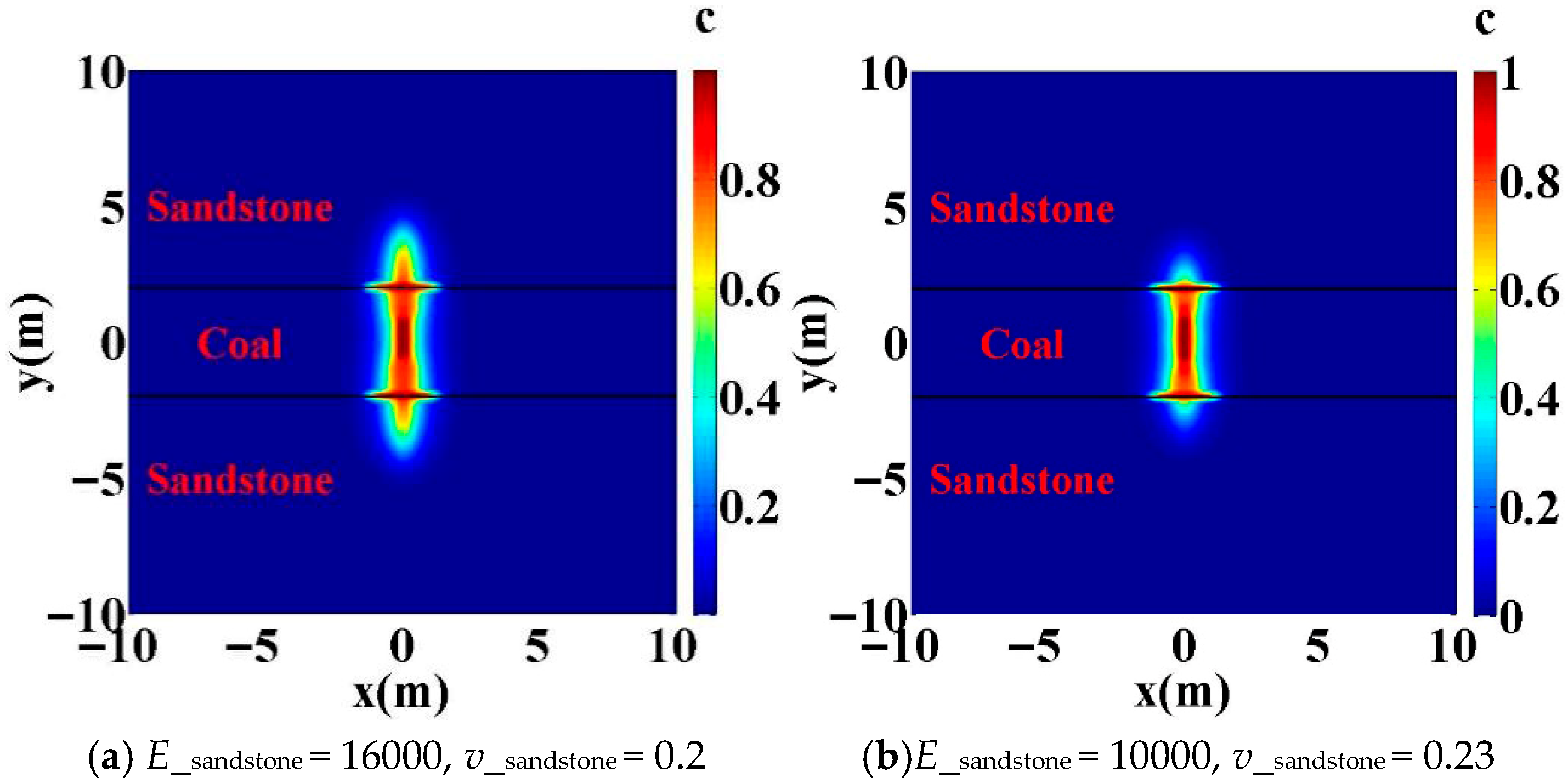
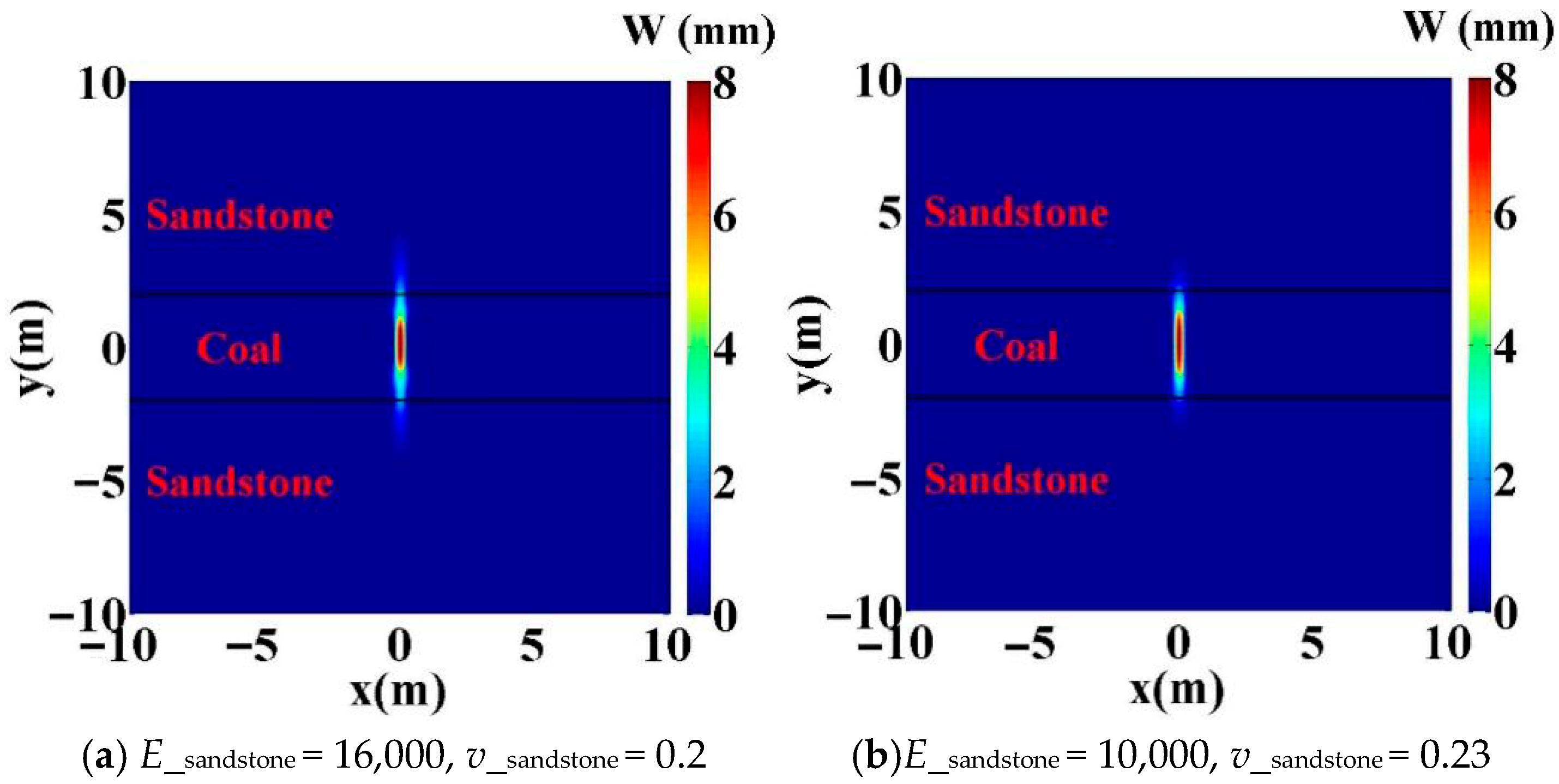
4.3. Influence of Young’s Modulus and Poisson’s Ratio
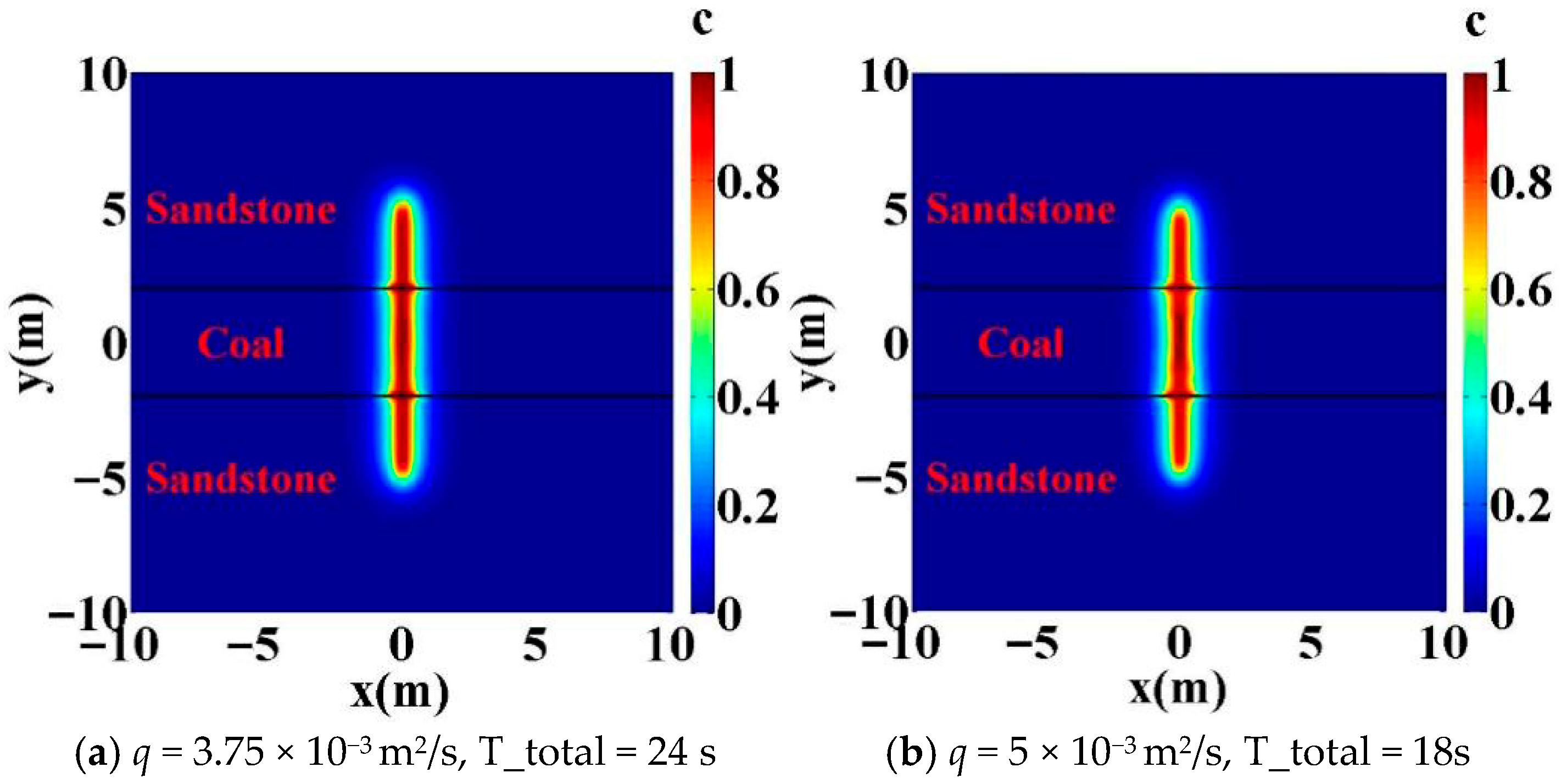
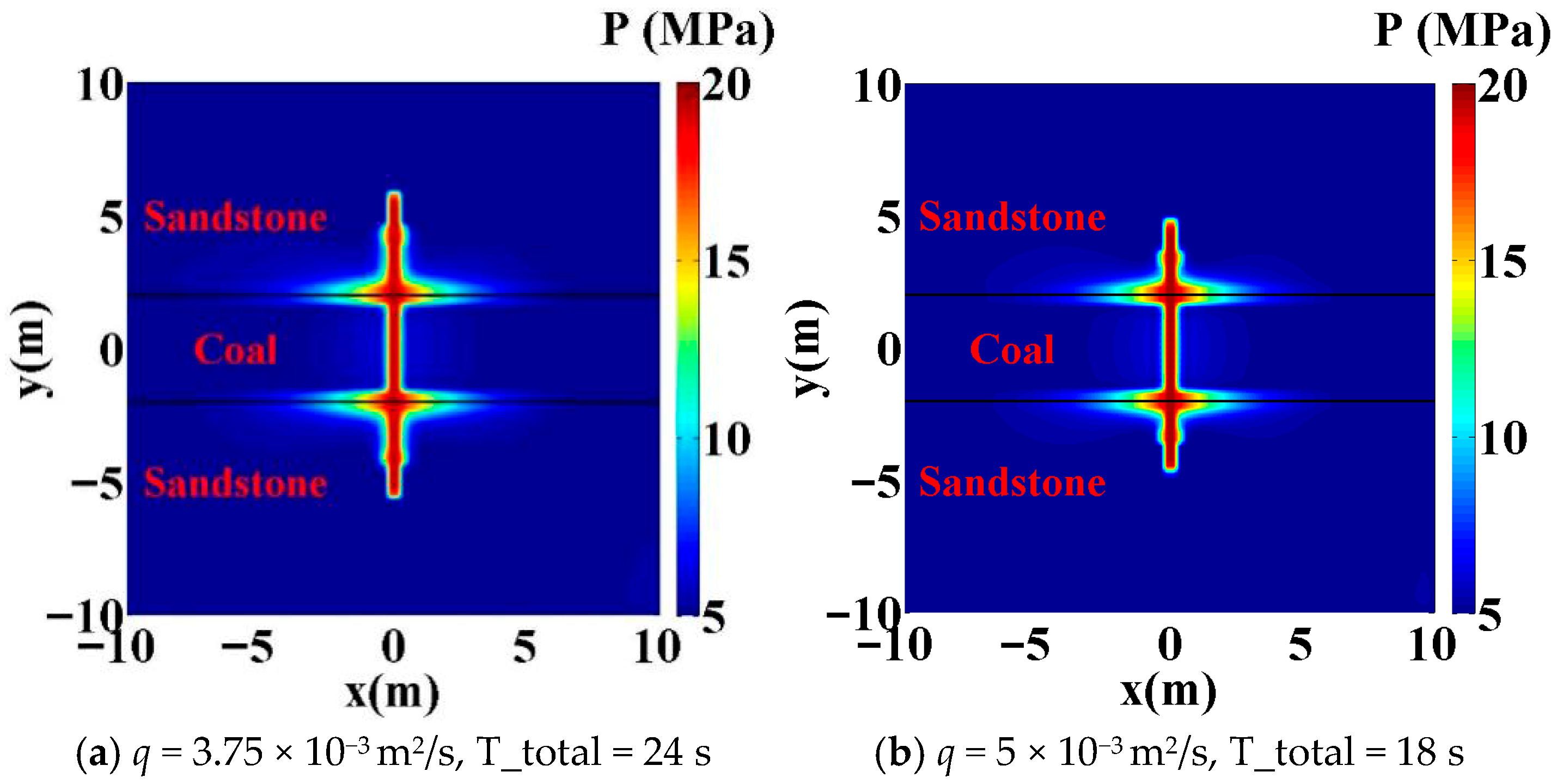
4.4. Effect of Injection Speed
5. Conclusions
- (1)
- Higher in situ stress differences, interface strengths, Young’s moduli, and injection rates facilitate hydraulic fracturing propagation through the interface and into the barrier layer. Quantitatively, for wells with geological characteristics similar to those examined here, crossing occurred at either an in situ stress difference of 5 MPa with an injection rate ≥ 2.5 × 10−3 m2/s or 4 MPa with an injection rate ≥ 3.5 × 10−3, provided that the barrier-layer Young’s modulus was >10,000 MPa (10 GPa) and the interface strength was >1.0 MPa.
- (2)
- Although hydraulic fracturing may open the interface in some cases, the fracture width in the interface region is significantly smaller.
- (3)
- The pressure during hydraulic fracturing propagation along the interface is higher than that during direct propagation through the interface.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, H.F.; Wang, X.H.; Liu, Z.Y.; Yan, Y.J.; Yang, H.X. Investigation on the hydraulic fracture propagation of multi-layers-commingled fracturing in coal measures. J. Petrol. Sci. Eng. 2018, 167, 774–784. [Google Scholar] [CrossRef]
- He, J.; Zhang, X.; Ma, L.; Wu, H.; Ashraf, M. Geological Characteristics of Unconventional Gas in Coal Measure of Upper Paleozoic Coal Measures in Ordos Basin, China. Earth Sci. Res. J. 2016, 20, 1–5. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, Y.; Bai, J.; Fu, X.; Liu, D. Evaluation of favorable regions for multi-seam coalbed methane joint exploitation based on a fuzzy model: A case study in southern Qinshui Basin, China. Energy Explor. Exploit. 2016, 34, 400–417. [Google Scholar] [CrossRef]
- Hou, X.W.; Zhu, Y.M.; Fu, C.Q.; Liu, J. Fractures distribution of Qinshui basin and its indicative significance to unconventional gas co-exploration in coal measures. J. China Uni. Min. Technol. 2016, 45, 729–738. [Google Scholar]
- Warpinski, N.R.; Schmidt, R.A.; Northrop, D.A. In-Situ Stresses: The Predominant Influence on Hydraulic Fracture Containment. J. Pet. Technol. 1982, 34, 653–664. [Google Scholar] [CrossRef]
- Teufel, L.W.; Warpinski, N.R. In-situ stress variations and hydraulic fracture propagation in layered rock-observations from a mineback experiment. In Proceedings of the 5th ISRM Congress, Melbourne, Australia, 10–15 April 1983. [Google Scholar]
- Teufel, L.W.; Clark, J.A. Hydraulic Fracture Propagation in Layered Rock: Experimental Studies of Fracture Containment. Soc. Pet. Eng. J. 1984, 24, 19–32. [Google Scholar] [CrossRef]
- Meng, S.Z.; Hou, B.; Zhang, J.; Peng, T. Experimental research on hydraulic fracture propagation through mixed layers of shale, tight sand and coal seam. J. China Coal Soc. 2016, 41, 221–227. (In Chinese) [Google Scholar]
- Yang, J.S.; Wang, Y.B.; Li, A.Q.; Chen, Z.H. Experimental study on propagation mechanism of complex hydraulic fracture in coal-bed. J. China Coal Soc. 2012, 37, 73–77. (In Chinese) [Google Scholar]
- Li, D.Q.; Zhang, S.C.; Zhang, S.A. Experimental and numerical simulation study on fracturing through interlayer to coal seam. J. Nat. Gas Sci. Eng. 2014, 21, 386–396. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Han, K.; Zheng, X.; Hou, B.; Gao, J.; Chen, M.; Zhang, Y. Vertical propagation behavior of hydraulic fractures in coal measure strata based on true triaxial experiment. J. Pet. Sci. Eng. 2017, 158, 398–407. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, M. Extending behavior of hydraulic fracture when reaching formation interface. J. Pet. Sci. Eng. 2010, 74, 26–30. [Google Scholar] [CrossRef]
- Zhang, X.; Jeffrey, R.G.; Thiercelin, M. Deflection and propagation of fluid-driven fractures at frictional bedding interfaces: A numerical investigation. J. Struct. Geol. 2007, 29, 396–410. [Google Scholar] [CrossRef]
- Tang, J.; Wu, K.; Li, Y.; Hu, X.; Liu, Q.; Ehlig-Economides, C. Numerical investigation of the interactions between hydraulic fracture and bedding planes with non-orthogonal approach angle. Eng. Fract. Mech. 2018, 200, 1–16. [Google Scholar] [CrossRef]
- Guo, J.; Luo, B.; Lu, C.; Lai, J.; Ren, J. Numerical investigation of hydraulic fracture propagation in a layered reservoir using the cohesive zone method. Eng. Fract. Mech. 2017, 186, 195–207. [Google Scholar] [CrossRef]
- Wang, H.; Liu, H.; Wu, H.A.; Wang, X.X. A 3D numerical model for studying the effect of interface shear failure on hydraulic fracture height containment. J. Pet. Sci. Eng. 2015, 133, 280–284. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Xiong, Z.; Mian, C.; Hou, B. Effect of interface property on hydraulic fracture vertical propagation behavior in layered formation based on discrete element modeling. J. Geophys. Eng. 2018, 15, 1542–1550. [Google Scholar] [CrossRef]
- Abbas, S.E.; Gordeliy, E.; Peirce, A.; Lecampion, B.; Chuprakov, D.; Prioul, R. Limited height growth and reduced opening of hydraulic fractures due to fracture offsets: An XFEM application. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014. [Google Scholar]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. The variational approach to fracture. J. Elasticity 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Guo, J.; Lu, Q.; Chen, H.; Wang, Z.; Tang, X.; Chen, L. Quantitative phase field modeling of hydraulic fracture branching in heterogeneous formation under anisotropic in-situ stress. J. Nat. Gas Sci. Eng. 2018, 56, 455–471. [Google Scholar] [CrossRef]
- Nguyen, T.; Yvonnet, J.; Zhu, Q.-Z.; Bornert, M.; Chateau, C. A phase field method to simulate crack nucleation and propagation in strongly heterogeneous materials from direct imaging of their microstructure. Eng. Fract. Mech. 2015, 139, 18–39. [Google Scholar] [CrossRef]
- Nguyen, T.; Yvonnet, J.; Zhu, Q.-Z.; Bornert, M.; Chateau, C. A phase-field method for computational modeling of interfacial damage interacting with crack propagation in realistic microstructures obtained by microtomography. Comput. Methods Appl. Mech. Eng. 2016, 312, 567–595. [Google Scholar] [CrossRef]
- Miehe, C.; Schänzel, L.-M.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Schänzel, L.-M.; Aldakheel, F. Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic–plastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 486–522. [Google Scholar] [CrossRef]
- Miehe, C.; Mauthe, S. Phase field modeling of fracture in multi-physics problems. Part III. Crack driving forces in hydro-poro-elasticity and hydraulic fracturing of fluid-saturated porous media. Comput. Methods Appl. Mech. Eng. 2016, 304, 619–655. [Google Scholar] [CrossRef]
- Mauthe, S.; Miehe, C. Hydraulic fracture in poro-hydro-elastic media. Mech. Res. Commun. 2017, 80, 69–83. [Google Scholar] [CrossRef]
- Xia, L.; Yvonnet, J.; Ghabezloo, S. Phase field modeling of hydraulic fracturing with interfacial damage in highly heterogeneous fluid-saturated porous media. Eng. Fract. Mech. 2017, 186, 158–180. [Google Scholar] [CrossRef]
- Mikelić, A.; Wheeler, M.F.; Wick, T. A Phase-Field Method for Propagating Fluid-Filled Fractures in a Poroelastic Medium. Multiscale Model. Simul. 2015, 13, 367–398. [Google Scholar] [CrossRef]
- Lee, S.; Wheeler, M.F.; Wick, T. Pressure and Fluid-Driven Fracture Propagation in Porous Media Using an Adaptive Finite Element Phase Field Model. Comput. Methods Appl. Mech. Eng. 2016, 305, 111–132. [Google Scholar] [CrossRef]
- Chukwudozie, C.; Bourdin, B.; Yoshioka, K. A Variational Phase-Field Model for Hydraulic Fracturing in Porous Media. Comput. Methods Appl. Mech. Eng. 2019, 347, 957–982. [Google Scholar] [CrossRef]
- Yoshioka, K.; Naumov, D.; Kolditz, O. On Crack Opening Computation in Variational Phase-Field Models for Fracture. Comput. Methods Appl. Mech. Eng. 2020, 369, 113210. [Google Scholar] [CrossRef]
- Yoshioka, K.; Mollaali, M.; Kolditz, O. Variational Phase-Field Fracture Modeling with Interfaces. Comput. Methods Appl. Mech. Eng. 2021, 384, 113951. [Google Scholar] [CrossRef]
- Arriaga, M.; Waisman, H. Stability analysis of the phase-field method for fracture with a general degradation function and plasticity induced crack generation. Mech. Mater. 2018, 116, 33–48. [Google Scholar] [CrossRef]
- Shen, R.; Waisman, H.; Guo, L. Fracture of viscoelastic solids modeled with a modified phase field method. Comput. Methods Appl. Mech. Eng. 2019, 346, 862–890. [Google Scholar] [CrossRef]
- Adim, A.; Riahi, M.; Bagheri, M. Estimation of Pore Pressure by Eaton and Bowers Methods Using Seismic and Well Survey Data. J. Appl. Geophys. Res. 2018, 4, 267–275. [Google Scholar]
- She, C.; Peng, H.; Yang, J.; Peng, J.; Han, H.; Yang, X.; Peng, Y. Experimental study on the true triaxial fracturing of tight sandstone with supercritical CO2 and slickwater. Geoenergy Sci. Eng. 2023, 228, 211977. [Google Scholar] [CrossRef]
- Wu, X.; Guo, Y.; Chang, X.; Bi, Z.; Zhao, G.; Yang, H.; Guo, W. Experimental Study on Cyclic Hydraulic Fracturing of Tight Sandstone under High-Stress Conditions. Processes 2023, 11, 875. [Google Scholar] [CrossRef]
- Su, H.; Li, R.; Deng, H.; Qin, Y.; Fu, M.; He, J.; Zeng, Q.; Song, L.; Zhang, J. Comprehensive Evaluation of Geological and Engineering Factors Affecting Fracturing Effectiveness in Tight Sandstone Reservoirs. Pet. Geol. Exp. 2024, 46, 1349–1361. [Google Scholar] [CrossRef]




| Representative | Fracture Normal and Criterion | Flow in Fracture | Permeability Mapping |
|---|---|---|---|
| Andro Mikelić [31] | Normal from phase-field gradient; variational energy framework | Lubrication/Poiseuille | Often treats fracture flow as a separate channel; not a direct k(d) mapping |
| Sanghyun Lee [32] | Phase field normal; embedded in porous matrix | Lubrication or equivalent Darcy along the fracture | Frequently derives transmissivity from aperture; some variants use damage-based k(d) |
| Chukwudozie [33] | Variational phase field; path from energy minimization | Lubrication coupled consistently to the fracture set | Emphasizes energy-consistent fracture description rather than isotropic k(d) |
| Yoshioka et al. (≈2019–2021) [34] | Phase-field framework; extracts aperture from displacement/phase field | Lubrication requires stable, explicitly computed aperture | Warns that direct damage-to-permeability mapping can be distortive; favors width-based coupling |
| Parameter Name | Parameters | Numerical Value |
|---|---|---|
| Critical stress | σc | 1 MPa |
| Young’s modulus | E | 6000 MPa |
| Undrained Poisson’s ratio | vu | 0.3 |
| Poisson’s ratio | v | 0.25 |
| Matrix permeability | kmatrix | 0.1 mD |
| Viscosity of fluids | μ | 1 × 10−3 Pa·s |
| Parameter Name | Parameter | Numerical Value |
|---|---|---|
| Critical stress of sand particles | σc_sandstone | 3 MPa |
| Critical stress of coal | σc_coal | 1 MPa |
| Interfacial critical stress | σc_interface | 0.5 MPa |
| Young’s modulus of sandstone | E_sandstone | 22,000 MPa |
| Young’s modulus of coal | E_coal | 6000 MPa |
| Poisson’s ratio of sandstone | v_sandstone | 0.17 |
| Poisson’s ratio of coal | v_coal | 0.25 |
| Permeability of sandstone | k0_sandstone | 1 mD |
| Permeability of coal | k0_coal | 0.1 mD |
| Interface permeability | k0_interface | 50 mD |
| Initial pore fluid pressure | pinitial | 5 MPa |
| Fluid viscosity | μ | 1 × 10−3 Pa·s |
| Time step | Δt | 3 s |
| Total injection time | T_total | 36 s |
| Injection rate | q | 2.5 × 10−3 m2/s |
| Mesh size | he | 0.25 m |
| Process area parameters | l0 | 0.5 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Xu, L.; Guo, X.; Zhu, M.; Bai, Y. Numerical Study on Hydraulic Fracture Propagation in Sand–Coal Interbed Formations. Processes 2025, 13, 3128. https://doi.org/10.3390/pr13103128
Liu X, Xu L, Guo X, Zhu M, Bai Y. Numerical Study on Hydraulic Fracture Propagation in Sand–Coal Interbed Formations. Processes. 2025; 13(10):3128. https://doi.org/10.3390/pr13103128
Chicago/Turabian StyleLiu, Xuanyu, Liangwei Xu, Xianglei Guo, Meijia Zhu, and Yujie Bai. 2025. "Numerical Study on Hydraulic Fracture Propagation in Sand–Coal Interbed Formations" Processes 13, no. 10: 3128. https://doi.org/10.3390/pr13103128
APA StyleLiu, X., Xu, L., Guo, X., Zhu, M., & Bai, Y. (2025). Numerical Study on Hydraulic Fracture Propagation in Sand–Coal Interbed Formations. Processes, 13(10), 3128. https://doi.org/10.3390/pr13103128