Bayesian Optimization of LSTM-Driven Cold Chain Warehouse Demand Forecasting Application and Optimization

Abstract

With the gradual adoption of smart hardware such as the Internet of Things (IoT) in warehousing and logistics, the efficiency bottlenecks and resource wastage inherent in traditional storage management models are now poised for breakthrough through digital and intelligent transformation. This study focuses on the cross-border cold chain storage scenario for Malaysia’s Musang King durians. Influenced by the fruit’s extremely short 3–5-day shelf life and the concentrated harvesting period in primary production areas, the issue of delayed dynamic demand response is particularly acute. Utilizing actual sales order data for Mao Shan Wang durians from Beigang Logistics in Guangxi, this study constructs a demand forecasting model integrating Bayesian optimization with bidirectional long short-term memory networks (BO-BiLSTM). This aims to achieve precise forecasting and optimization of cold chain storage inventory. Experimental results demonstrate that the BO-BiLSTM model achieved an R² of 0.6937 on the test set, with the RMSE reduced to 19.1841. This represents significant improvement over the baseline LSTM model (R² = 0.5630, RMSE = 22.9127). The bidirectional Bayesian optimization mechanism effectively enhances model stability. This study provides a solution for forecasting inventory demand of fresh durians in cold chain storage, offering technical support for optimizing the operation of backbone hub cold storage facilities along the New Western Land–Sea Trade Corridor.

1. Introduction

Durian, known as the ‘King of Fruits’ [1], is a tropical fruit with a distinctive flavor originating from Southeast Asian nations. Its primary center of origin lies on the island of Kalimantan (also known as Borneo), situated at the tripoint of Indonesia, Malaysia, and Brunei. It is highly favored by consumers across Southeast Asia and within China [2]. According to export volume data compiled by the Food and Agriculture Organization of the United Nations (FAO) from 2003 to 2022, exports of fresh durian (HS code: 08106000) surged from under 100,000 tons in 2003 to nearly 900,000 tons in 2022. This represents an almost eightfold increase over two decades, with a compound annual growth rate exceeding 10%. In 2021 and 2022, the average import price per unit of fresh durian was approximately double that of major tropical fruits, highlighting its high-value nature. From 2020 to 2022, China’s annual average durian imports accounted for 95% of global durian exports [3,4]. However, durian storage conditions are exceptionally demanding, with environmental factors such as temperature and relative humidity significantly influencing requirements across different varieties. Fresh Musang King durians from Malaysia possess an exceptionally short shelf life of merely 3–5 days, resulting in persistently high export difficulties and costs. Furthermore, optimal cooling for durian storage is achieved at 1 °C, which significantly extends the product’s shelf life [5]. Currently, durian sales in the market primarily follow two models: fresh fruit sold online or offline, and durian products made from fruit that fails to meet fresh fruit sales standards. Selling durian as processed products not only increases costs but also reduces product turnover rates.

Forecasting durian sales orders forms the foundation for effectively reducing wastage rates and improving turnover, playing a crucial role in optimizing storage costs and enhancing efficiency. Traditionally, primary order forecasting methods encompassed both standalone and combined predictive models such as artificial neural networks, linear regression, genetic algorithms, and the GM(1,1) model. K. Nemati Amirkolaii et al. [6] employed ABC classification to select the most effective AI methodology and performance metrics, comparing four forecasting approaches—neural networks, mean squared error, moving averages, and single exponential smoothing—to enhance demand forecasting accuracy within commercial aircraft spare parts supply chains under irregular demand patterns. Mikrant M et al. [7] combined exponential smoothing with ARIMA models to forecast demand for Unit Load Devices (ULDs) in air cargo, achieving optimized cost management. Qin C et al. [8] proposed a hybrid forecasting model integrating grey prediction with exponential smoothing, employing simulated annealing to optimize weights and enhance demand forecasting accuracy for logistics parks. Rashidi Gooya H et al. [9] successfully forecasted groundwater fluctuations in unconfined aquifers using fuzzy logic and the Analytic Hierarchy Process (AHP). Lu SX et al. [10] employed grey relational analysis combined with Gaussian process regression to improve the prediction accuracy of dissolved gas concentrations in oil-immersed transformers, effectively accounting for gas interrelationships and sampling errors. Compared to these methods, neural networks represented by Long Short-Term Memory (LSTM) have emerged as a new focal point in the forecasting domain. LSTMs possess the advantage of efficiently learning and retaining long-term, complex nonlinear dependencies within time series data without requiring intricate feature engineering or stringent model assumptions [11]. Presently, LSTMs have delivered precise predictions and optimizations across multiple sectors, including rainfall forecasting, agricultural commodity pricing, and stock market analysis. Bhimavarapu U [12] evaluated the performance of an improved regularized function long short-term memory (IRF-LSTM) for rainfall prediction. Baek Y et al. [13] proposed a framework incorporating an overfitting prevention LSTM module and a predictive LSTM module for stock market index forecasting. Wang Y et al. [14] developed a short-term energy consumption prediction model for cold storage refrigeration systems based on LSTM neural networks, achieving innovative breakthroughs in prediction accuracy for high-energy-consumption cold storage. Liu Q et al. [15] successfully predicted erosion wear in butterfly valves using LSTM networks, revealing that wear primarily affects the disc and seat regions, significantly impacting valve performance and lifespan. Sheng Z [16] proposed a short-term load forecasting model based on an enhanced deep residual network and a long short-term memory neural network, effectively improving load prediction accuracy.

However, whilst LSTMs are powerful recurrent neural networks, their performance is highly dependent on a set of hyperparameters. A single LSTM model requires manual adjustment of these parameters, which is not only extremely time-consuming but also inefficient, making it difficult to find the optimal solution [17]. Bayesian optimization, as an advanced global optimization technique, can effectively utilize statistical surrogate models to enhance the efficiency of objective function optimization [18,19]. Applying Bayesian optimization to LSTM hyperparameter tuning enables the LSTM model to achieve higher accuracy and lower error rates. Li B et al. [20] proposed a Bayesian Optimization-based Long Short-Term Memory (BO-LSTM) method for short-term thermal load forecasting, enabling accurate prediction of heating system thermal loads. Liu G et al. [21] introduced a Bayesian Optimization-based Bidirectional Long Short-Term Memory (BO-BiLSTM) neural network for accurately predicting the service life of residual current circuit breakers. Yao M et al. [22] employed ultrasonic monitoring to detect debonding defects in CFST arch bridges, developing a Bayesian-optimized LSTM network to enhance defect classification accuracy and reliability. Zuo Q et al. [23] established a Bayesian-optimized LSTM model for rapid diagnosis of sensor failures in organic Rankine cycle systems. Peng K et al. [24] proposed a rapid prediction method based on a self-optimizing Bayesian BiLSTM hybrid network for seismic response forecasting in high-speed rail track-bridge systems.

Although Bayesian optimization-based LSTM models offer substantial advantages, few studies have focused on cold chain warehousing, let alone order forecasting for fresh agricultural produce within cold chains. Indeed, due to durian’s irregular storage periods and pronounced data noise fluctuations, accurately predicting durian order volumes proves challenging. Concurrently, the fruit’s distinctive storage characteristics and expanding market demand urgently necessitate a dedicated forecasting model for durian storage requirements.

Given these considerations, this paper employs the Savitzky–Golay smoothing filter to eliminate data noise. It constructs a ‘Bayesian hyperparameter-optimized LSTM demand forecasting’ algorithmic model to enhance order prediction accuracy. This provides precise forecast order information for operational scheduling, offering data-driven decision support. In summary, the main contributions of this paper are as follows:

(1)

This paper proposes and validates the effectiveness of the BO-BiLSTM model. During hyperparameter tuning, the efficient search strategy of Bayesian optimization effectively enhances the model’s predictive performance.

(2)

This paper delves into the characteristics of order data driving durian inventory demand forecasting. By applying Savitzky–Golay smoothing to eliminate noise from time series, it effectively preserves detailed features and boundary inflection points, making it suitable for analyzing demand fluctuations sensitive to changes within the cold chain.

(3)

This paper introduces a novel demand forecasting model for fresh agricultural products that integrates Bayesian optimization with bidirectional Long Short-Term Memory (LSTM) networks. This model can empower over 30 key hub cold storage facilities along the new maritime and land trade routes, reducing the comprehensive logistics costs for fresh agricultural products like durians entering the Chinese market.

The remainder of this paper is organized as follows. First, relevant methodologies and data preprocessing techniques are introduced, alongside the proposed Bayesian-optimized neural network model. Subsequently, the model is tested using order data from the durian cold storage facility at Beigang Logistics in Guangxi as an analytical sample. The prediction results are then analyzed, concluding with findings and future directions.

2. Methods

2.1. Data Pre-Processing

Given the specific characteristics of cold chain scenarios, order data frequently exhibits quality issues, including missing values, outliers, inconsistent formats, and redundant information. These problems primarily stem from multiple factors, such as instability and irregularities in data collection processes, difficulties in integrating disparate data sources, potential oversights or errors during manual entry, and data inconsistencies arising from untimely system updates or maintenance. Such data quality issues not only compromise data integrity and accuracy but may also undermine the effectiveness of subsequent analyses and model predictions. Consequently, it is imperative to undertake data cleansing and preprocessing to address these problematic datasets.

During the cleaning phase of data preprocessing, duplicate values, missing values, and invalid data were identified and removed. Common methods employed include interpolation or mean imputation for handling missing values, alongside rule-based filtering or manual verification to eliminate invalid data and duplicate records, thereby enhancing the overall quality and reliability of the dataset. To further standardize the range of feature values, data undergoes normalization processing. Common techniques include Min-Max normalization, which enhances the model’s sensitivity and balance across different features. This approach is particularly well-suited for neural network models operating on sensitive scales.

To mitigate random noise fluctuations within time series and render the cold chain logistics order time series data smoother for analysis, smoothing techniques must balance statistical properties with the specific requirements of cold chain scenarios. This approach aims to scientifically and effectively reduce noise while revealing underlying trends and cyclical variations. Common smoothing methods include: Simple Moving Average (SMA), Exponential Smoothing, Locally Weighted Scatterplot Smoothing (LOWESS), and the Savitzky–Golay Filter. This case employs the Savitzky–Golay Filter method for smoothing the time series data.

Savitzky–Golay Filter [25,26]: Proposed by Savitzky and Golay in 1964, this is a local polynomial fitting method based on the least squares approach and a sliding window. In this approach, discrete data within the window undergoes least-squares fitting to mitigate the impact of extraneous noise signals on the data. Consequently, this filter finds extensive application in smoothing and denoising data streams, effectively preserving detailed features and boundary inflection points. It is well-suited for analyzing demand fluctuations sensitive to variations within cold chain operations.

When applied in practical cold chain scenarios, appropriate models may be selected based on the actual characteristics of the data, balancing smoothing effects with information retention to ensure data continuity and accuracy. This provides a reliable foundation for subsequent analysis and forecasting.

2.2. Feature Engineering

To enhance the model’s capability for modelling complex dynamic sequences, this paper designs a series of feature engineering strategies based on the original data. These include time-lag features, temporal features, periodic features, and other characteristics, thereby capturing the temporal dependencies and exogenous disturbances affecting the target variable.

Lag Features: By incorporating historical data points as features, these assist the model in capturing temporal dependencies and dynamic patterns within time series data.

Temporal features: By extracting time-related attributes, these enhance the model’s understanding of periodic, trend-based, and seasonal patterns within the data. Commonly used temporal features include fundamental time information such as year, month, day, week, hour, and minute.

Holiday characteristics: By flagging significant holidays, the duration of breaks, and special events, this assists the model in capturing periodic fluctuations and abrupt changes stemming from variations in human activity.

2.3. LSTM Neural Network

Long Short-Term Memory (LSTM) is a recurrent neural network with a specialized architecture, first proposed by Hochreiter and Schmidhuber in 1997 [27]. It was designed to address the vanishing and exploding gradient issues encountered by traditional RNNs during sequence modelling. Compared to conventional RNNs, LSTM effectively captures and preserves long-term dependencies through its memory cells and gating mechanisms, thereby significantly enhancing the model’s performance in complex sequence tasks.

The core structure of an LSTM comprises three components: the input gate, the forget gate, and the output gate. These gating mechanisms dynamically adjust the memory state based on historical information, effectively preventing information loss or excessive accumulation within long sequences. An LSTM not only captures short-term transient variations but also efficiently uncovers long-term dependencies within sequences. This characteristic enables LSTMs to deliver outstanding performance in fields such as natural language processing and time series forecasting, making them well-suited for handling time-series data with pronounced seasonality and sudden spikes, such as cold chain orders.

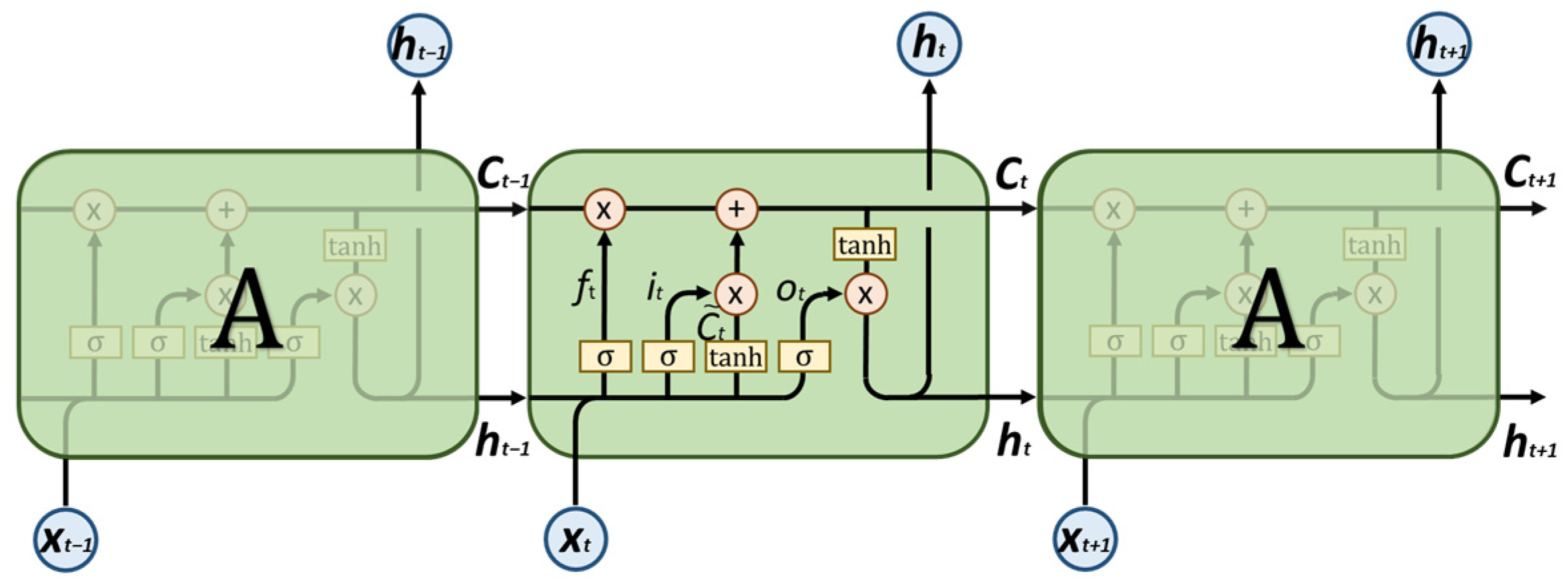
2.3.1. Basic Structure of LSTM

As shown in Figure 1, this depicts the fundamental structural unit of a classical LSTM. Each LSTM primarily comprises three gate structures and a cell state, namely:

Forget Gate: Determines whether the previous state information is discarded at the current time step;

$$f_t=\sigma \left(W_f·\left[h_{t-1},x_t\right]+b_f\right)$$

(1)

Input Gate: Determines which portions of the current input information are incorporated into the unit state;

$$i_t=\sigma \left(W_i·\left[h_{t-1},x_t\right]+b_i\right)$$

(2)

Subsequently, candidate cell states are generated, representing new information that can be incorporated into the cell state;

$${\tilde{C}}_t=\tanh \left(W_C·\left[h_{t-1},x_t\right]+b_C\right)$$

(3)

Update cell state: Combining the forget gate and input gate to update the cell state;

$$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$$

(4)

Output Gate: Serves as the information “conveyor belt”, running throughout the entire sequence to perform a long-term memory function, controlling how the current state influences the final output.

$$o_t=\sigma \left(W_o·\left[h_{t-1},x_t\right]+b_o\right)$$

(5)

$$h_t=o_t\ast \tanh \left(C_t\right)$$

(6)

Among these, $x_t$ denotes the input at the current time step, $h_t$ represents the hidden state at the current time step, $h_{t-1}$ signifies the hidden state at the previous time step, $C_t$ indicates the unit state at the current time step, $C_{t-1}$ denotes the unit state at the previous time step, $\tilde{C}$ signifies the candidate unit state at the current time step, $i_t$ represents the activation value of the input gate, $f_t$ denotes the activation value of the forget gate, $o_t$ signifies the activation value of the output gate, $\sigma$ denotes the sigmoid activation function, while $W_f$, $W_i$, $W_C$, $W_o$ are the weight matrices, $b_f$, $b_i$, $b_C$, $b_o$ are the bias vectors, and the asterisk (*) denotes element-wise multiplication.

2.3.2. BiLSTM Neural Network

Unidirectional LSTM networks can only predict information sequentially from start to finish. Building upon this unidirectional architecture, Schuster [28] proposed a BiLSTM network that simultaneously considers both early and late information. The structural diagram of the BiLSTM network is shown in Figure 2.

The BiLSTM network concurrently performs forward and backward computations. The horizontal axis represents bidirectional information flow along the time series, while the vertical axis denotes unidirectional information flow from the input layer to the hidden layer, and subsequently to the output layer. The hidden layer comprises two LSTM models: the forward propagation layer and the backward propagation layer. Upon receiving input data, the model generates new latent vectors $\overrightarrow{h}$ and ${\overleftarrow{h}}_t$.

$${\overrightarrow{h}}_t=LSTM\left(x_t,{\overrightarrow{h}}_{t-1}\right)$$

(7)

$${\overleftarrow{h}}_t=LSTM\left(x_t,{\overleftarrow{h}}_{t-1}\right)$$

(8)

$$y_t=\overrightarrow{W}\overrightarrow{h}+\overleftarrow{W}\overleftarrow{h}+b_y$$

(9)

Among these, $W$ is the weight coefficient, and $b_y$ is the bias vector.

In the network’s structural diagram, the horizontal axis represents bidirectional information flow along the time series, illustrating both forward and backward transmission paths; the vertical axis depicts unidirectional information flow from the input layer through the hidden layer to the output layer. Through this bidirectional processing approach, BiLSTM enhances the model’s ability to capture bidirectional dependencies within sequential data, thereby demonstrating superior performance in tasks such as time series forecasting and natural language processing.

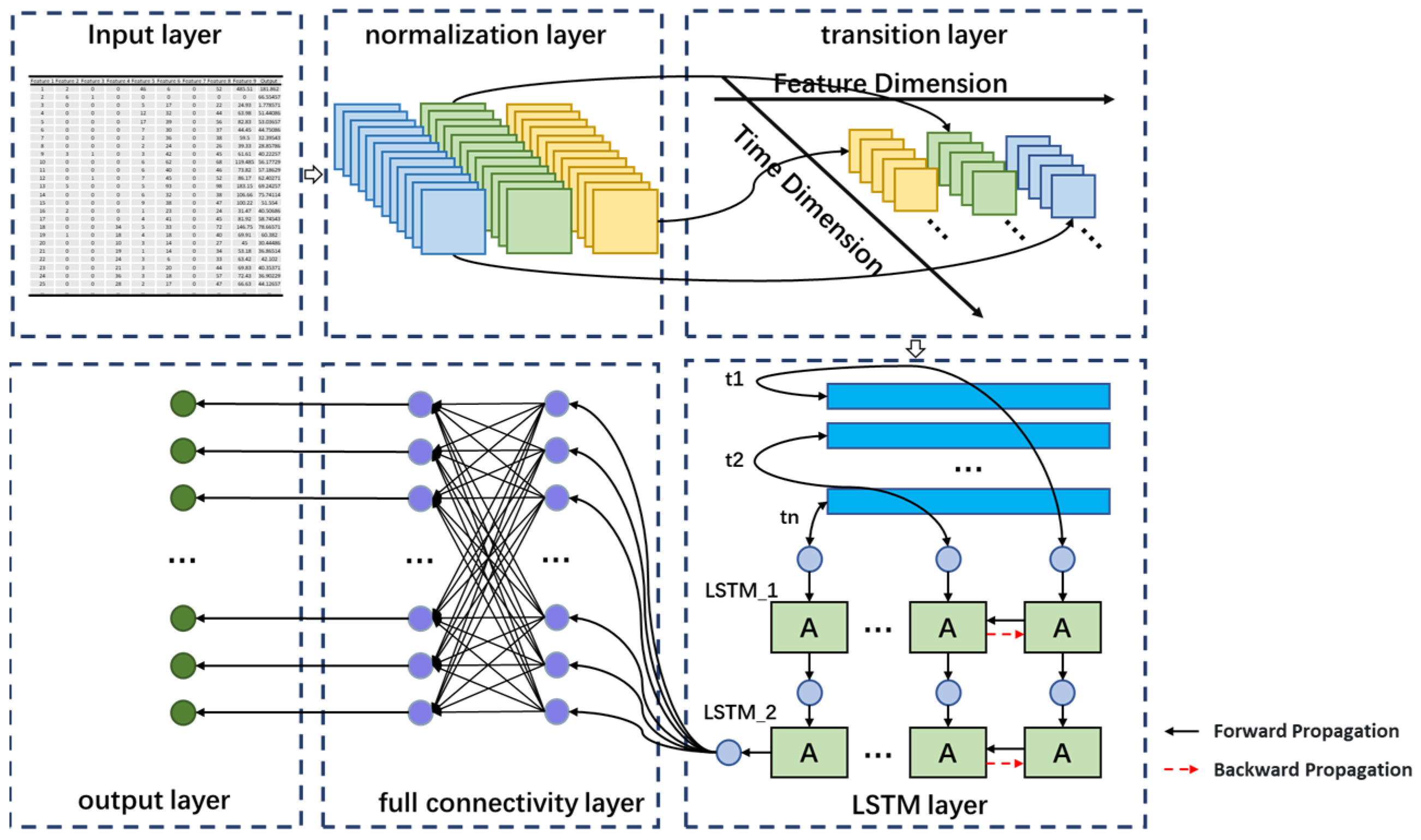
As illustrated in Figure 3, the input order data is first normalized, followed by the extraction of relevant feature variables to construct a multivariate time series as the training set. This training set is then fed into an LSTM (or BiLSTM) layer for model training, with the final prediction results generated via a fully connected layer.

2.4. Bayesian Optimization Algorithm

The selection of hyperparameters exerts a decisive influence on the learning and generalization capabilities of speed prediction models. Manual parameter tuning proves time-consuming and offers little assurance of identifying optimal parameter combinations. To enhance both model generalization and training efficiency, this paper introduces Bayesian optimization algorithms into the LSTM model design. This approach aims to reduce the time expenditure required for parameter tuning whilst improving the model’s performance in predicting speed.

Bayesian optimization algorithms constitute a global optimization method [29] capable of obtaining optimal solutions with fewer iterations and known data, and may be employed to adjust hyperparameters in machine learning algorithms. The core of Bayesian optimization comprises two components: firstly, establishing a mathematical model for the objective function via Gaussian process regression to approximate the current black-box objective function, and calculating the mean and variance of the function value at each point. Secondly, constructing a sampling function based on the posterior probability distribution to estimate the most probable location of the optimum point under the current known data conditions. To avoid getting stuck in local minima, Bayesian optimization algorithms typically incorporate a degree of randomness, balancing between random exploration and sampling from the posterior distribution. As per Bayes’ theorem:

$$P\left(A|B\right)={\displaystyle \frac{P\left(B|A\right)·P\left(A\right)}{P\left(B\right)}}$$

(10)

Here, $P\left(A\right)$ and $P\left(B\right)$ denote the prior distributions of data $A$ and $B$ respectively, i.e., the proxy models, implemented as Gaussian processes; $P\left(B\right|A)$ represents the distribution of observed data using the proxy model; $P\left(A\right|B)$ constitutes the posterior distribution, i.e., the updated distribution of proxy model $A$ derived from observing data $B$.

2.4.1. Objective Function

The mapping from the hyperparameter vector x to the model’s generalization performance serves as the objective function $f\left(x\right)$. Typically, error metrics on the training set—such as mean squared error (MSE) or root mean squared error (RMSE)—are set as the objective function to be optimized, where $x$ denotes the hyperparameter vector comprising parameters like learning rate, number of hidden layer units, and regularisation parameters. The objective of hyperparameter optimization is to identify the hyperparameters $x^{*}$ within the hyperparameter space that yields optimal model generalization performance. Taking minimization of the error metric as an example, the objective function minimizes the error of the LSTM model on the validation set, expressed as in Equation (11):

$$x^{*}=arg minf\left(x\right)$$

(11)

As function $f$ quantifies model generalization metrics such as generalization accuracy in relation to model hyperparameters and given that training and evaluating a model using a single set of hyperparameters currently demands substantial computational resources and considerable time, $f$ constitutes a black-box objective function with a high evaluation cost.

2.4.2. Gaussian Process

The Bayesian optimization algorithm employs a Gaussian process (GP) as a surrogate model. A defining characteristic of Gaussian processes is that their “prior distribution” can be updated using observed data, thereby enabling the updated prior to capture the distribution of the new function and facilitate the optimization fitting process. A Gaussian process comprises a mean function and a covariance function, as illustrated in Equation (12).

$$f\left(x\right)~GP\left(m\left(x\right),k\left(x, x^{\prime }\right)\right)$$

(12)

$$f\left(x\right)\mid Q\sim N\left({\mu }_Q\left(x\right),{\mathit{\sigma }}_Q^2\left(x\right)\right)$$

(13)

Here, $m\left(x\right)$ denotes the mean function, while $k\left(x, x^{\prime }\right)$ represents the kernel function or covariance function, such as the Squared Exponential Kernel or Exponential Kernel, and assume $f\left(x\right)$ follows a normal distribution.

In the Gaussian process employed within this research case study, the Squared Exponential Kernel was utilized. This constitutes a kernel function frequently employed within machine learning and statistical modelling, with its specific formulation as per Equation (14):

$$k\left(x_i,x_j\right)={\mathit{\sigma }}_f^{2}exp\left[-{\displaystyle \frac{{\left(x_i-x_j\right)}^T\left(x_i-x_j\right)}{2{\mathit{\sigma }}_l^2}}\right]$$

(14)

Here, ${\mathit{\sigma }}_l$ denotes the feature length scale, and ${\mathit{\sigma }}_f$ denotes the signal standard deviation.

Gaussian process models possess strong expressive capabilities and high computational efficiency, enabling them to effectively accommodate complex objective function structures. Although computational costs may be elevated for large-scale datasets, techniques such as sparse approximation and kernel function selection maintain substantial computational efficiency. This enables Gaussian process models to demonstrate superior adaptability when handling intricate, variable objective functions, providing robust surrogate modelling support for Bayesian optimization. Consequently, efficient and precise global optimization is achieved.

2.4.3. Collection Function

The sampling function plays a pivotal role in Bayesian optimization. As Gaussian processes can only provide estimates of the mean and variance of the objective function, the sampling function must be employed during the actual optimization process to strike a judicious balance between exploration and exploitation. In practical Bayesian optimization applications, excessive exploration may prevent the model from fully utilizing acquired prior information, thereby limiting optimization effectiveness under constrained evaluation resources. Conversely, excessive exploitation risks premature convergence to local optima, compromising the model’s capacity for thorough search space exploration. Consequently, designing a judicious sampling strategy that balances exploring new regions with exploiting known optimal areas based on the mean and variance outputs of the Gaussian process is pivotal to achieving efficient global optimization.

In each iteration of Bayesian optimization, a sampling function $\alpha \left(x\right)$ is typically employed to obtain the next sample point for evaluation. This sampling function is constituted by the posterior distribution of the observed data, which is maximized to select the next point requiring assessment, as demonstrated in Equation (15).

$$x_{opt}=arg minf\left(x\right),\left(x\in X\right)$$

(15)

Among these, $x_{opt}$ denotes the optimal hyperparameter combination, $f\left(x\right)$ represents the objective function for hyperparameters, and $X$ signifies the hyperparameter set.

Common acquisition functions include the Probability Improvement (PI) function, Expected Improvement (EI) function, and Upper Confidence Bound (UCB) function. A well-designed acquisition function can guide the optimization process to concentrate on search regions with higher improvement potential, thereby finding solutions closer to the global optimum within a finite number of evaluations. This significantly enhances the efficiency and effectiveness of the optimization. This study employs the Expected Improvement function (EI) [30] as the acquisition function, introducing both per-second and plus strategies. The plus strategy is a technique within Bayesian optimization designed to select the most promising hyperparameter combinations for evaluation during the optimization process.

Expected Improvement: Measures the anticipated enhancement delivered by a given set of hyperparameters relative to the current optimal value. A higher value indicates a greater likelihood of yielding superior outcomes, as per Formula (16).

$${EI}_{\left(x,Q\right)}=E_Q\left[max\left(0,{\mu }_Q\left(x_{best}\right)-f\left(x\right)\right)\right]={\int }_{-\infty }^{\infty }max(0,{\mu }_Q\left(x_{best}\right)-f)N\left(f\right|\mu ,{\mathit{\sigma }}^2)df$$

(16)

where $x_{best}$ denotes the position with the lowest posterior mean, and ${\mu }_Q\left(x_{best}\right)$ represents the minimum value of the posterior mean.

When ${\mu }_Q\left(x_{best}\right)-f\ge 0$, we can obtain Formula (17):

$${EI}_{\left(x,Q\right)}={\int }_{-\infty }^{\infty }({\mu }_Q\left(x_{best}\right)-f)N\left(f\right|\mu ,{\mathit{\sigma }}^2)df$$

(17)

Then, using the properties of the standard normal distribution, we can obtain:

$${EI}_{\left(x,Q\right)}=\left({\mu }_Q\left(x_{best}\right)-{\mu }_Q\left(x\right)\right)\Phi \left({\displaystyle \frac{{\mu }_Q\left(x_{best}\right)-{\mu }_Q\left(x\right)}{\mathit{\sigma }}}\right)+\mathit{\sigma }\phi \left({\displaystyle \frac{{\mu }_Q\left(x_{best}\right)-{\mu }_Q\left(x\right)}{\mathit{\sigma }}}\right)$$

(18)

Evaluation Speed (per Second): The time required to evaluate the objective function may occasionally depend on the region. Considering the time expended per evaluation, this approach combines improvement outcomes with evaluation duration, prioritizing parameter combinations that yield the greatest improvement within a given unit of time.

$${EI}_{pS}\left(x\right)={\displaystyle \frac{{EI}_Q\left(x\right)}{{\mu }_S\left(x\right)}}$$

(19)

Among these, ${\mu }_S\left(x\right)$ denotes the posterior mean of the Gaussian process model.

This modification enables Bayesian optimization to favour candidates with greater potential for improving the expected value and lower computational cost when selecting the next experimental point, thereby achieving superior results within the same total optimization time budget.

Plus: Denotes the incorporation of additional adjustment mechanisms on top of the original framework, aimed at avoiding local optima and escaping the minimum of the local objective function, thereby further balancing the relationship between exploration and exploitation.

$${EI}_{\mathrm{p}\mathrm{l}\mathrm{u}\mathrm{s}}=E_Q\left[max\left(0,{\mu }_Q\left(x_{best}\right)-f\left(x\right)+\xi \right)\right]$$

(20)

$${EI}_{plus}=\left({\mu }_Q\left(x_{best}\right)+\mathit{\xi }-{\mu }_Q\left(x\right)\right)\Phi \left({\displaystyle \frac{{\mu }_Q\left(x_{best}\right)+\mathit{\xi }-{\mu }_Q\left(x\right)}{\mathit{\sigma }}}\right)+\mathit{\sigma }\mathit{\phi }\left({\displaystyle \frac{{\mu }_Q\left(x_{best}\right)+\mathit{\xi }-{\mu }_Q\left(x\right)}{\mathit{\sigma }}}\right)$$

(21)

Here, $\mathit{\xi }>0$ is a small positive number, commonly referred to as the improved offset.

This strategy prevents EI from converging prematurely near the optimum value, compelling the algorithm to escape local optima and further explore uncharted regions, thereby enhancing the algorithm’s utility.

2.5. Model Evaluation Metric

To evaluate the demand forecasting BO-LSTM model proposed in this paper for cold chain logistics warehouse optimization, the model performance is primarily assessed through five metrics: Mean Squared Error ($MSE$), Root Mean Squared Error ($RMSE$), Mean Absolute Error ($MAE$), Coefficient of Determination ($R^2$), and Residual Prediction Deviation ($RPD$). Minimising the Root Mean Squared Error ($RMSE$) is set as the optimization objective. Their definitions are as follows:

$$MSE={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2$$

(22)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$$

(23)

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{\left|y_i-\widehat{y_i}\right|}{n}}$$

(24)

$$RPD={\displaystyle \frac{std\left(y_i\right)}{std\left(y_i-\widehat{y_i}\right)}}$$

(25)

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

(26)

where $y_i$ denotes the actual value of the $i$-th sample, $\widehat{y_i}$ represents the predicted value of the $i$-th sample, $\overline{y}$ signifies the mean of the actual samples, and $std(·)$ denotes the standard deviation.

3. Demand Forecasting Case Study

To validate the effectiveness of the LSTM model based on Bayesian optimization proposed in this study, order data from the Beigang Logistics Cold Storage Warehouse in Guangxi, China was selected as the analysis sample. The data spans from 5 February 2024 to 1 June 2025. Using fresh Musang King durian fruit orders as an example, a time series was constructed. Key variables such as promotional methods, weekly order volumes, and holiday patterns were employed to establish an order-inventory forecasting mapping relationship. Bayesian optimization was applied to fine-tune the model parameters, yielding the optimal configuration. Finally, this paper compares the performance differences between LSTM and BiLSTM models, evaluating their accuracy and stability in demand forecasting to achieve the objectives and results analysis of demand prediction.

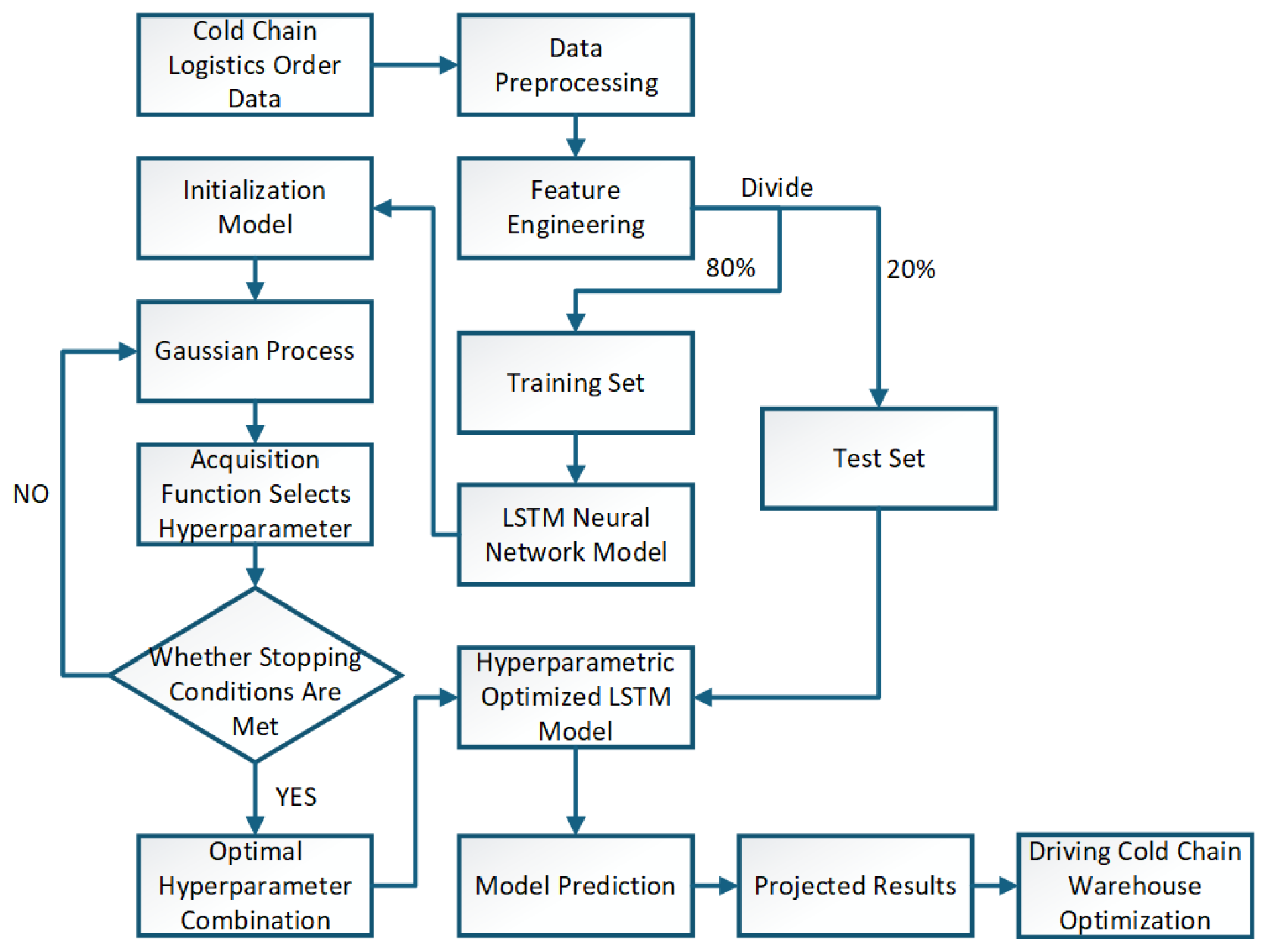
As illustrated in Figure 4, the cold chain order data undergoes preprocessing, followed by feature engineering to extract key characteristics. The dataset is then partitioned into training and test sets at a 2:8 ratio, with the training set fed into a Long Short-Term Memory (LSTM) network for modelling and training. To enhance model performance, Bayesian optimization was introduced with RMSE minimization as the objective. The objective function was approximated using a Gaussian process, with an acquisition function enabling adaptive selection of hyperparameter combinations. During iteration, Gaussian process optimization continued if the termination criteria were unmet. Upon fulfillment of these criteria, the optimal hyperparameter combination was determined, forming the basis for constructing an optimized LSTM prediction model. Ultimately, this optimized model yielded predictive outcomes, thereby providing data-driven support for scientific decision-making and efficiency enhancement in cold chain storage management.

3.1. Data Explanation

The raw data utilized for this analysis of logistics warehousing order information comprises 25 key fields, as detailed in

Table 1. Original order data fields.

No.	Field	No.	Field	No.	Field	No.	Field	No.	Field
1	Product code	6	Quantity of sales	11	Discount type	16	Type of offer	21	Position code
2	Product barcode	7	sales unit price	12	Sales time	17	channel	22	Payment methods
3	Product name	8	Sales amount	13	categorization	18	Membership number	23	Number of sales
4	norm	9	Cost amount	14	brands	19	cashier	24	Methods
5	unit	10	gross profit	15	Order flow	20	Gross margin %	25	note

. These fields encompass relevant information concerning merchandise, sales, storage locations, and temporal aspects, thereby providing foundational data support for subsequent demand forecasting.

Based on raw sales order data, core fields such as product name, unit of measure, sales quantity, discount type, sales time, product category, and position code are filtered and retained. Feature engineering and feature identification are then performed on these fields to provide reliable data support for warehouse demand forecasting.

3.2. Data Processing

Prior to model training, this paper first conducted systematic preprocessing of the raw data, encompassing steps such as data cleansing and format conversion to ensure accuracy, standardization, and consistency. Based on the order placement times from the Musang King data, the information was aggregated on a weekly basis to form a continuous time series. Concurrently, this time series underwent smoothing processing using a second-order Savitzky–Golay filter with a window size of five. This approach reduced fluctuations and anomalies within the data while preserving its detailed characteristics and boundary inflection points, thereby enhancing the model’s stability and the accuracy of its predictions.

As illustrated in Figure 5, when comparing different time series smoothing methods, the Savitzky–Golay filter demonstrates the most favourable performance in terms of smoothing quality and peak retention. This filter effectively removes noise whilst maximising the retention of data details and peaks by fitting a polynomial within a sliding window. Compared to traditional moving average methods, the Savitzky–Golay filter not only handles data at window boundaries more effectively but also preserves the overall signal morphology during smoothing, rendering data characteristics more complete and authentic.

3.3. Feature Engineering

Feature engineering was conducted on the processed data to transform raw inputs and extract key indicators that effectively capture time-series characteristics. This enhances the model’s ability to comprehend data structures, thereby improving accuracy and generalization capabilities. Extracted features include date, compensatory leave, public holidays, promotional methods, and lag.

Given that order data is significantly influenced by holidays, holiday information has been specifically incorporated as a key feature variable to enhance the model’s sensitivity to seasonal patterns and special events.

As shown in

Table 2. List of Public Holidays and Compensatory Leave.

Year	Festival	Holiday Dates	Number of Days	Compensatory Leave Arrangement
2024	New Year’s Day	1 January	1	Long Weekend
	Spring Festival	10–17 February	8	4 & 18 February: Workdays
	Tomb-Sweeping Day	4–6 April	3	7 April: Workday
	Labour Day	4–6 April	5	28 April & 11 May: Workdays
	Valentine’s Day	20–21 May	0	None
	Dragon Boat Festival	10 June	1	Long Weekend
	Mid-Autumn Festival	15–17 September	3	14 September: Workday
	National Day	7–11 October	7	29 September & 12 October: Workdays
2025	New Year’s Day	1 January	1	No Comp Time
	Spring Festival	28 January–4 February	8	26 January & 8 February: Workdays
	Tomb-Sweeping Day	4–6 April	3	None
	Labour Day	1–5 May	5	None
	Valentine’s Day	20–21 May	0	None
	Dragon Boat Festival	31 May–2 June	3	None

, the list includes public holidays such as New Year’s Day, Spring Festival, Tomb-Sweeping Day, Labour Day, Valentine’s Day, Dragon Boat Festival, Mid-Autumn Festival, and National Day, along with their corresponding compensatory rest days. Utilizing this information helps enhance the model’s predictive capability regarding order fluctuations during holiday periods, thereby improving forecast accuracy and timeliness.

Time characteristics: As shown in the

Table 3. Example of Date Feature Extraction.

Date	Weeks
5 February 2024–11 February 2024	1
12 February 2024–18 February 2024	2
19 February 2024–25 February 2024	3
26 February 2024–3 March 2024	4
4 March 2024–10 March 2024	5
11 March 2024–17 March 2024	6
18 March 2024–24 March 2024	7
25 March 2024–31 March 2024	8
1 April 2024–7 April 2024	9
……	……

, Calendar weeks, with week one commencing on 5 February 2024. Thus, the period from 5 February 2024 to 11 February 2024 constitutes week one, 12 February 2024 to 18 February 2024 constitutes week two, and so forth.

Holiday Characteristics: As shown in the Table 2, Festivals and public holidays, primarily including New Year’s Day, Spring Festival, Tomb-Sweeping Day, Labour Day, Valentine’s Day, Dragon Boat Festival, Mid-Autumn Festival, and National Day. These are aggregated from daily holiday classification data into weekly totals, representing the number of holiday days within a week.

Compensatory Leave Feature: Adjusted leave days based on nationally mandated public holidays. According to

Table 4. Classified Data Characteristic Coding Table.

Data Type	Field Name	Encoding	Meaning
Classification data	Whether to take time off	0	No
		1	Yes
	Whether it is a public holiday	0	No
		1	Yes
	Whether it is a promotional price	0	No
		1	Yes
	Whether it is a discounted price	0	No
		1	Yes
	Whether it is a normal price	0	No
		1	Yes

, Aggregated from daily adjusted leave classification data into weekly totals, representing the number of adjusted leave days within a week.

Discount characteristics: According to Table 4, Includes promotional prices, discounted prices, and standard prices, representing the number of promotional, discounted, and standard pricing instances within a week, respectively.

Lag characteristics: To capture data dependencies and cyclical patterns, lag fields are added with a time step of 1, using the previous week’s demand volume as one of the input features for the current week.

3.4. Model Training and Bayesian Optimization Configuration

This paper establishes the corresponding model architecture within the MATLAB 2023b development environment. The system operates on a Windows 11 operating system, with hardware comprising an AMD Ryzen 7 6800H processor (base frequency 3.20 GHz), NVIDIA GeForce RTX 3060 Laptop GPU, and 16 GB of memory. During model training, GPU-accelerated training was employed alongside the Adam optimizer. Its superior adaptive learning rate adjustment capabilities effectively enhanced training efficiency and accelerated model convergence. By rationally configuring Bayesian optimization parameters, the model’s hyperparameters were further optimized to achieve optimal predictive performance and generalization capability. The search space configuration is detailed in

Table 5. Search Space Configuration Table.

Hyperparameter Name	Description	Value Range
Num Of Units	Number of LSTM hidden layer neurons	(10, 800)
Initial Learn Rate	Step Size for Updating Control Parameters	[1 × 10−3, 1]
L2Regularization	Preventing Model Overfitting	[1 × 10−10, 1 × 10−2]

.

In this study, Bayesian optimization is used to tune the hyperparameters of the LSTM model to improve its performance and robustness in time series prediction tasks. The hyperparameters to be tuned include: the number of neurons in the LSTM hidden layer, the learning rate of the optimizer, and the L2 regularization coefficient. The Root Mean Squared Error (RMSE) is used as the objective function to evaluate the predictive performance of different hyperparameter configurations on the validation set.

Bayesian optimization conducts efficient searches of hyperparameter spaces by constructing Gaussian Process (GP) surrogate models of objective functions. This study employs the Squared Exponential Kernel as the GP kernel function, which possesses a strong functional smoothness assumption and is well-suited for modelling continuous performance response surfaces.

In selecting the sampling function, the Expected Improvement per Second Plus criterion was adopted to further enhance optimization efficiency. This sampling function evaluates potential hyperparameters by considering both the magnitude of potential improvement and the time expended per evaluation, enabling the tuning process to identify superior hyperparameter configurations more rapidly and effectively within finite time constraints.

The maximum iteration count for Bayesian optimization was set to 20, meaning the optimization process ceased after exploring 20 sets of hyperparameter configurations. Training was conducted separately for the LSTM and BiLSTM models, with training terminated after reaching 800 iterations to ensure adequate model fitting and comparability of optimization results.

4. Analysis of Prediction Results

4.1. Hyperparameter Optimization Results and Prediction Outcomes

This paper employs LSTM and BiLSTM models as benchmarks, incorporating Bayesian optimization algorithms during model parameter refinement to establish a Bayesian-optimized long short-term memory network prediction framework. This yields an optimal cold chain storage demand forecasting model. Through Bayesian estimation, the optimal feasible parameter combinations for the model were obtained, as presented in

Table 6. Table of Hyperparameter Values Following Bayesian Optimization.

Model	Hyperparameter	Description	Value Range
BO-LSTM	Num Of Units	Number of LSTM hidden layer neurons	670
	Initial Learn Rate	Step Size for Updating Control Parameters	2.44435 × 10−3
	L2 Regularization	Preventing Model Overfitting	1.04438 × 10−8
BO-BiLSTM	Num Of Units	Number of LSTM hidden layer neurons	764
	Initial Learn Rate	Step Size for Updating Control Parameters	1.5347 × 10−3
	L2 Regularization	Preventing Model Overfitting	1.0827 × 10−10

.

Upon obtaining the optimal feasible parameter combinations, the performance of the two optimized models was validated by comparing their training and test sets, as illustrated in Figure 6.

The performance of the two optimized models was assessed on both training and test sets following the acquisition of the ideal parameter combination, as shown in Table 6. All measures were greater for BO-BiLSTM on the training set than for BO-LSTM: $R^2$ was higher (0.99147 vs. 0.99055), RMSE was lower (4.1926 vs. 4.4129), MSE was lower (17.5777 vs. 19.4734), and RPD was higher (10.826 vs. 10.5213). With a higher $R^2$ (0.69367 vs. 0.56856), lower RMSE (19.1841 vs. 22.7672), lower MSE (368.031 vs. 518.3456), and higher RPD (1.8119 vs. 1.5449), BO-BiLSTM also performed better on the test set. Together, these findings show that BO-BiLSTM outperforms BO-LSTM in terms of generalization and fitting ability across both sets.

The BO-BiLSTM model outperformed the BO-LSTM in the example study of cold-chain fresh durian inventory demand forecasting, better capturing temporal fluctuations and intricate nonlinear linkages in demand. Bayesian optimization of the BiLSTM model’s hyperparameters successfully improved the model’s capacity for generalization and prediction accuracy.

4.2. Performance Evaluation and Visualisation

Following the completion of model training, this paper conducted evaluations using multiple assessment metrics, including $R^2$, $RMSE$, $MSE$, and $RPD$. Furthermore, it presents various evaluation metrics alongside comparative visualisations of actual versus predicted values, linear fitting plots, and other data to demonstrate the model’s performance, thereby facilitating in-depth analysis and research.

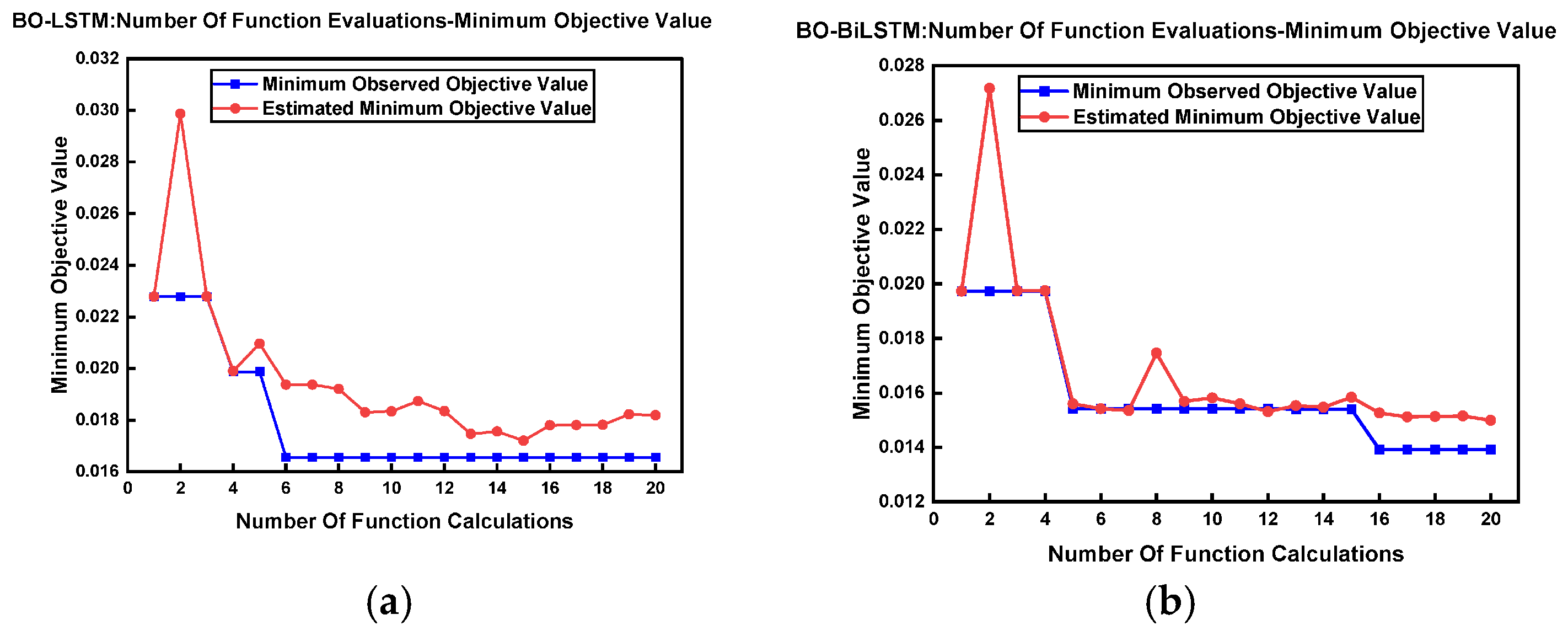
As illustrated in Figure 7, during the iterative process of the BO-LSTM model, the model converged rapidly, stabilising after six iterations and demonstrating favourable optimization efficiency. During this process, the target value’s RMSE reaches its minimum, with the lowest value exceeding 0.016. As illustrated in Figure 7, during the iteration process of the BO-BiLSTM model, the target value exhibits a brief period of stability in the early stages before continuing to decrease and gradually converging. After 16 iterations, the target value remains largely stable, with its lowest value falling below 0.014.

The results validated the effectiveness of the Bayesian optimization algorithm employed for model parameter tuning. Not only did it locate optimal solutions within a reduced number of iterations, but it also significantly enhanced the model’s predictive performance, thereby providing robust technical support for subsequent practical applications. Furthermore, this optimization strategy demonstrated commendable stability and generalization capabilities, rendering it equally applicable to parameter adjustment in other deep learning models.

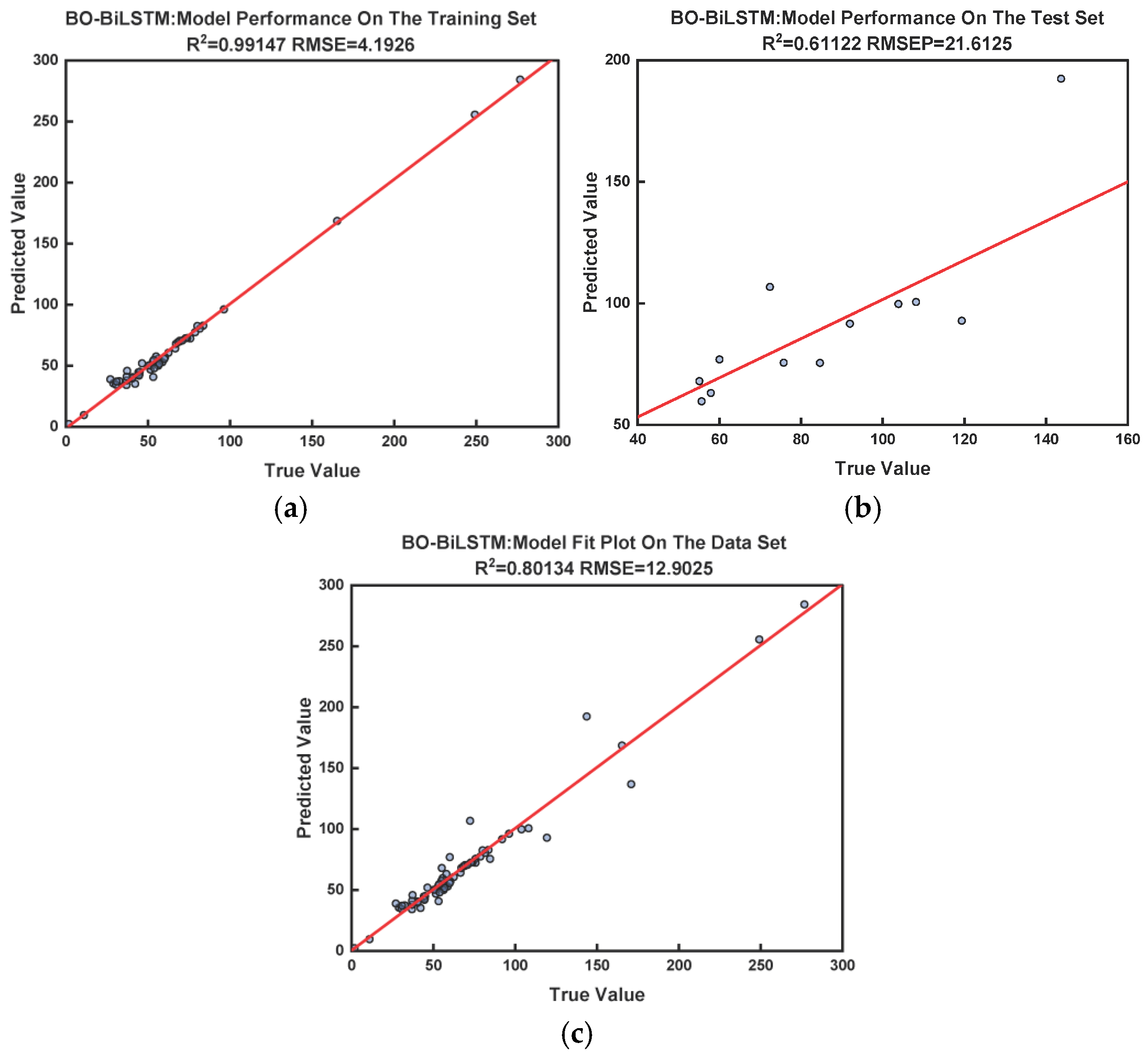
As demonstrated by Figure 8, the BO-LSTM model, having undergone Bayesian optimization for hyperparameter tuning, exhibits merely adequate predictive performance in the cold-chain fresh durian case study. On the training set, the model achieved an adjusted $R^2$ of 0.99055 and $RMSE$ of 4.4129. However, on the test set, the model exhibited an $RMSE$ of 22.7672 and an $R^2$ of 0.56856 < 0.6, indicating poor model fit and weak generalization capability.

As demonstrated in Figure 9, the BO-BiLSTM model, following Bayesian optimization hyperparameter tuning, has achieved substantial accuracy in forecasting Musang King durian order data. On the training set, the model attained an $R^2$ of 0.99147 with an $RMSE$ of 4.1926; on the test set, the model achieved an $R^2$ of 0.61122 (exceeding 0.6) and an $RMSE$ of 21.6125, indicating robust generalization capability. Overall, across all datasets, the model recorded an $R^2$ of 0.80134 and an $RMSE$ of 12.9025, demonstrating stable predictive performance and strong practical applicability throughout the entire dataset.

A comparison of the results from both models validated the effectiveness of the Bayesian optimization method in tuning the hyperparameters of the BiLSTM model. This approach not only enhanced the model’s fitting capability but also strengthened its potential for practical application in order forecasting, thereby providing robust technical support for optimizing cold chain supply chain management.

To evaluate the improvement in model performance achieved through Bayesian optimization, this paper employs LSTM and BiLSTM models without Bayesian optimization as baseline models. These baseline models uniformly set the number of hidden layer neurons to 300, the initial learning rate to 1 × 10⁻², and L2 regularisation to 1 × 10⁻⁵. All other parameters and training environments remain identical. Their performance in cold chain demand forecasting is compared, with results presented in

Table 7. Performance Comparison of Different Combination Methods for Bayesian Optimization and LSTM Models.

Method	Training Set				Test Set				Running Time/s
	${\mathit{R}}^2$	$\mathit{R}\mathit{M}\mathit{S}\mathit{E}$	$\mathit{M}\mathit{S}\mathit{E}$	$\mathit{R}\mathit{P}\mathit{D}$	${\mathit{R}}^2$	$\mathit{R}\mathit{M}\mathit{S}\mathit{E}$	$\mathit{M}\mathit{S}\mathit{E}$	$\mathit{R}\mathit{P}\mathit{D}$
LSTM	0.9730	7.4566	55.6012	6.2551	0.5630	22.9127	524.9898	1.5151	20.9682
BiLSTM	0.9706	7.7838	60.5870	6.2087	0.6606	20.1921	407.7197	1.7328	23.2236
BO-LSTM	0.9906	4.4129	19.4734	10.5213	0.5686	22.7672	518.3456	1.5449	215.9888
BO-BiLSTM	0.9915	4.1926	17.5777	10.8260	0.6937	19.1841	368.031	1.8119	240.8367

.

Comparing the performance of LSTM and BiLSTM models reveals that BiLSTM demonstrates superior fitting capability and lower prediction error on both training and test datasets, though LSTM retains certain advantages in computational efficiency. Following the introduction of Bayesian optimization, both the BO-LSTM and BO-BiLSTM models outperformed the unoptimized baseline models across all performance metrics. This demonstrates the effectiveness of Bayesian optimization in hyperparameter tuning, particularly as the BO-BiLSTM model maintained relatively strong generalization capabilities on the test set. It is worth noting that incorporating Bayesian optimization significantly increases model training time. The results indicate that, where training resources permit, combining BiLSTM with Bayesian optimization effectively enhances prediction accuracy and model stability. This provides a more reliable and scalable solution for inventory forecasting of Musang King durians and, by extension, the entire cold-chain fresh produce sector.

5. Conclusions

This study addresses key challenges in forecasting demand for fresh durian inventory within cold chain logistics. Stringent storage and transportation requirements necessitate precise and reliable demand forecasting to optimize operations and reduce costs. Based on real order data from Beigang Logistics as raw data, this paper designs a series of feature engineering strategies—including time lag, holidays, compensatory leave, and periodicity features—to capture time dependency and external disturbance factors. Subsequently, SMA, Exponential Smoothing, LOWESS, and Savitzky–Golay smoothing were compared, confirming Savitzky–Golay smoothing as the optimal method for noise reduction. This approach preserves critical demand fluctuation patterns while ensuring high-quality modeling data. A machine learning model incorporating Bayesian optimization was then proposed to enhance the accuracy and reliability of demand forecasting. Experimental results confirm that under sufficient training resources, Bayesian optimization significantly improves hyperparameter tuning. The BO-BiLSTM model demonstrates superior performance compared to LSTM, BiLSTM, and BO-LSTM baseline models, particularly excelling in handling complex noise-type demand sequence data characteristic of cold chain logistics.

Beyond this, the study delivers practical contributions to the cold chain industry and has been implemented in production at Beigang Logistics’ durian cold chain warehouse. The proposed method provides a replicable data-driven forecasting tool. The research outcomes can empower over 30 backbone hub cold storage facilities along the New Western Land–Sea Trade Corridor and cold storage facilities owned by members of the Guangxi Cold Chain Association. When integrated with warehouse digital twin systems, its core algorithms can reduce the comprehensive logistics costs for ASEAN durians and other fresh agricultural products entering the Chinese market. This supports the sustained growth of ASEAN agricultural trade while offering insights for building supply chain resilience for specialty agricultural products within the context of rural revitalization.

Although the deep learning method based on Bayesian optimization proposed in this paper demonstrates broad application prospects and theoretical value in the field of cold chain logistics warehouse optimization, it still has several shortcomings and areas for future improvement, such as the following:

The current Bayesian optimization algorithm significantly increases computational burden during the parameter search phase, leading to substantially extended computation time. Future efforts could explore using other advanced optimization algorithms to enhance search efficiency while avoiding getting stuck in local optima.

Although BO-BiLSTM effectively captures time-series features, its modeling capabilities may struggle with nonlinear, sudden demand spikes, and multi-source heterogeneous data inherent in cold chain orders. Future work could incorporate additional influencing factors, introduce attention mechanisms, or adopt Transformer architectures to enhance the model’s ability to capture temporal characteristics.

The current cold chain warehousing industry is constrained by insufficient available data samples, which limits the model’s generalization ability to some extent. In the future, obtaining richer and more accurate data can further improve the model’s predictive performance.