Sensitivity Analysis in Simple Cycles for Hydrogen Liquefaction

Abstract

Due to the increase in global energy demand, as well as environmental concerns, hydrogen presents itself as a promising energy source. Liquid hydrogen is more suited for long-distance transportation, but hydrogen liquefaction is an energy-intensive process, and many studies have been published proposing more efficient liquefaction cycles. In this study, simple hydrogen liquefaction cycles like Claude, pre-cooled Linde–Hampson (PLH), single mixed refrigerant (SMR), and dual mixed refrigerant (DMR) were assessed regarding the influence of the cycle’s high pressure on energy efficiency, exergy destruction, and its distribution along the equipment. Among the main results, Claude presented the best specific energy consumption (SEC) of 16.47 kWh/kg_LH, followed by DMR with an SEC of 17.30 kWh/kg_LH, SMR with 17.58 kWh/kg_LH, and finally PLH, with an SEC of 45.07 kWh/kg_LH. The exergy efficiency followed the same pattern as the SEC, with Claude having the lowest exergy destruction, followed by DMR and SMR with close exergy destruction, and finally PLH. Nonetheless, although cycles were not optimized in evaluating the effect of increasing the high pressure, which constrains the direct applicability of the result found, especially in the pre-cooled cycles, the analysis provides valuable insights into the sensitivity of cycle performance. The method and its findings provide the basis for further studies, including optimization steps.

1. Introduction

Relentless population growth, combined with improvements in life expectancy, promotes an increasingly greater energy demand worldwide. As it is currently, the energy system is fossil fuel based, with about 80% of the world’s primary energy supply covered by this source [1]. However, fossil fuels are not a renewable source, and geologists and petroleum engineers estimate that over 40% of the available petroleum reserves have already been used [2]. In this scenario, finding new ways to produce energy is a critical issue. Moreover, the increase in energy demand is not the only challenge. As the evidence of the effects of global warming and climate change is overwhelming, the quality of energy as a clean, sustainable, and renewable source will be a priority as well.

Hydrogen stands out amidst the diverse alternatives that arise for new forms of clean energy since it has significant advantages over other fuels. Some of the advantages can be listed: (a) it is simpler chemically than other fuels; (b) hydrogen combustion in engines or its uses in fuel cells does not release CO₂ as a product, only water; (c) feedstock for hydrogen production is plentiful; (d) it can be produced with zero greenhouse gas (GHG) emissions with water electrolysis; (e) in the liquid form, it has a high lower heating value (LHV) of 120 MJ/kg, about 2.5 greater than gasoline; and (f) it can be used as chemical storage of electrical energy [1,3].

Due to the investments in technological advances, renewable and clean power plants like hydroelectric, wind power, and solar power plants are increasingly economically competitive [4]. Nonetheless, some obstacles remain in the renewable electrical energy application. Firstly, some of the natural sources, like wind or sunlight, are not available continuously; thus, when lacking the means for clean energy production, the energy still has to be obtained from nonrenewable resources [4]. Producing and storing energy as much as possible during a certain period and using the storage when in need would be a solution, but it faces the impossibility of energy storage in electrical form. Despite physical and chemical methods of energy storage being available, electrical generating plants usually do not have a storage system and are subject to matching the energy demand via generation [5].

In this scenario, hydrogen as an energy carrier, produced by the electrolysis of water, has great prospects. Despite the initial gaseous form of the hydrogen produced, utilizing hydrogen liquefaction after the electrolysis cycle would guarantee a low volume-consuming way to store energy in a high-energy content and low-weight form, considering the aforementioned liquid hydrogen LHV [6]. The liquefaction of hydrogen also ensures a more cost-effective way to transport hydrogen, since pipelines are not efficient in long-distance transportation [7].

Nevertheless, liquid hydrogen has some economic drawbacks regarding the boil-off in storage and transportation as well as the liquefaction energy cost [8]. The transportation and storage of hydrogen in liquid form suffer from the constant heat absorption from the environment, causing the hydrogen to evaporate, a phenomenon called “boil off”. Compared with liquefied natural gas (LNG), hydrogen has an 18 times lower heat of vaporization [9], thus requiring special design vessels to prevent boil-off, which can consume up to 40% of the hydrogen combustion energy [10]. Recent and active studies have approached methods to mitigate hydrogen boil-off losses, and a revision of the three main methods employed—hydrogen compression, zero boil-off, and hydrogen reliquefaction—is made by Morales-Ospino, Celzard, and Fierro (2023) [9]. Hydrogen liquefaction is also a highly cost-intensive process, given that hydrogen is the second hardest gas to liquefy, with a liquefaction temperature of about 20 K at ambient pressure, only having a greater liquefaction temperature than helium, whose boiling point is 4 K.

Furthermore, hydrogen liquefaction has another specificity regarding the hydrogen molecular property, which is the occurrence of two isomeric forms: ortho-hydrogen and para-hydrogen [8]. The isomers differ by the nuclear spin: while ortho-hydrogen presents both protons with the same direction spins, implying a higher energy state, in the para form, hydrogen has protons with opposite spins and has a lower energy state [11]. At ambient temperature, hydrogen is a mixture composed of about 75% ortho-hydrogen and 25% para-hydrogen (also known as normal hydrogen), but with a temperature decrease, the equilibrium shifts toward an increase in the para-hydrogen content. Since the ortho–para reaction heat is about 0.388 kcal/mol, overcoming the hydrogen evaporation heat of approximately 0.213 kcal/mol, the ortho–para conversion must be carried out in the cooling/liquefaction process; otherwise, the reaction heat of the posterior conversion would be enough to evaporate all the liquefied gas [12]. Therefore, the liquefiers have ortho–para conversion systems with appropriate catalysts, usually packaged inside the heat exchangers [8], to favor the increase in para-hydrogen content and reduce storage losses [13]. Hydrous ferric oxide is mostly used as a catalyst, but other materials, such as CrO₂ on Al₂O₃ and CrO or Ni on silica, can also be used [14].

Historically, hydrogen liquefaction is a relatively new process, since it was first achieved only in 1898 by J. Dewar, overruling the previous “permanent gas” status of hydrogen [15,16]. Once it was proved that hydrogen liquefaction was a possibility, the race for creating liquefaction cycles started. The Linde–Hampson cycle (with a pre-cooling section), developed in 1895, and the Claude (or Simple Claude) cycle, developed in 1902, were the first systems able to liquefy hydrogen [17], and since then, other cycles or variations, like Kapitza, Joule–Bryton, dual pressure Claude, pre-cooled Claude, pre-cooled mixed refrigerant cycles, among others, were designed to achieve a more efficient process. Despite those efforts, all existing and operating liquefaction plants still use versions of the pre-cooled Claude cycle and have not presented major improvements in the last 50 years [7,8].

Usually, the specific energy consumption (SEC) is the main parameter to compare cycle efficiency. While more classical cycles, such as Claude and pre-cooled Linde–Hampson, present an SEC of 27.8 kWh/kg_LH and 72.2 kWh/kg_LH [18], respectively, actual operating plants, like Paxair’s in the United States and Linde’s in Germany, already achieved SEC in the range of 12 to 15 kWh/kg_LH [12,17] using a modification of the pre-cooled Claude cycle. Additionally, plenty of research has been published with new conceptual plants with more promising SEC. The WE-NET, a Japanese project that was proposed in 1993 to develop and establish the technology for a global hydrogen-based energy network [19], indicates three conceptual liquefaction cycles, based on Claude, Helium Brayton, and Neon Brayton cycles, that would be capable of reaching an SEC of 8.5 kWh/kg_LH [20].

Furthermore, Valenti and Macchi (2008) [21] proposed a liquefaction system with a Helium recuperative Joule–Brayton cycle and achieved an SEC of 5.04 kWh/kg_LH and found out that the majority of the exergy losses occur in the helium compression system, followed by the heat exchangers. The lower SEC for hydrogen liquefaction, 4.41 kWh/kg_LH, is reported by Sadaghiani and Mehrpooya (2017) [22], who developed a system combining two refrigeration systems. The first refrigeration cycle with a mixed refrigerant, composed of methane, ethane, n-butane, hydrogen, nitrogen, propane, n-pentane, R-14, and ethylene, reduces the hydrogen temperature to −193 °C. The second refrigeration, with hydrogen, neon, and helium, achieved a hydrogen refrigeration to −253 °C [22]. By using mixed refrigerants, it is possible to achieve more efficient cooling by better-suited composite curves in the heat exchangers and ease compression with better compressibility properties [22]. When multiple refrigeration cycles are used, the composition of the external ones (warmer) consists mostly of hydrocarbons (methane, ethane, propane, and butane), while the internal cycles (colder) employ substances with a lower boiling point, like nitrogen, helium, hydrogen, and neon. This way, the cooling is divided into two steps with different heat transfer properties, which allows a better adjustment of the composite curves and enhances the cooling of hydrogen.

It is visible from the aforementioned studies that, compared with the thermodynamical ideal SEC for the hydrogen liquefaction of 3.92 kWh/kg_LH [23,24], the conceptual plants already present a performance close to the ideal limit, and, therefore, there is not much more expectation for the development of concepts on new cycles [12]. However, advances in technology for achieving the practical application of the new concepts are still needed. More about hydrogen liquefaction can be found in the review articles by Aasadnia and Mehrpooya (2018) and Krasae-in et al. (2010) [12,17].

Despite the rapid improvement in the conceptual plants, a significant amount of the studies focused on the development of new and conceptual designs and the determination of optimal conditions for achieving better efficiency, to the detriment of a more complete analysis of real cycles’ performance in a wide range of operations conditions, which could provide a better understanding of these systems at a fundamental level. Some examples of analysis beyond the SEC value would be exergy destruction, exergy destruction distribution, the temperature profile in the heat exchangers, the influence of ortho–para conversion, and their behavior under different operating conditions. Yang et al. (2023) [25], for example, compared Claude and Brayton cycles, which are the basis for most of the operating hydrogen liquefaction plants, using sensitivity analysis to optimize operating conditions and assessed both cycles regarding their SEC, refrigerant use, and exergy efficiency. The authors reported an SEC of 5.62 kWh/kg_LH and 5.87 kWh/kg_LH for the Claude and Brayton cycles, respectively. With regard to exergy efficiency, in the study, Claude was also more effective, with a 6.6% lower exergy destruction.

Additionally, most of the new conceptual designs grow in complexity and number of devices, and little investigation is performed regarding operating conditions like the cycle’s high pressure. While the majority of the aforementioned studies considered the liquefaction of hydrogen at 21 bar, Quack (2002) [26] approached the effect of the hydrogen initial pressurization in the cycle exergy requirements, and reported that, especially from 80 to 30 K, cooling can be eased by a pressure increase in the range of 2 to 10 MPa. The author emphasized that the increase in pressure is limited by the existence of equipment (cryogenic heat exchangers and expanders) that can tolerate these higher pressures. In this context, the development of the new and different designs could also benefit from the evaluation of the hydrogen pressure effect in the liquefaction process. Even for simpler and well-known cycles, as is the case for Claude, Linde–Hampson, single mixed, and dual mixed refrigerants, the effect of increasing the hydrogen pressure for liquefaction is not assessed in the existing literature.

To address this gap, the present study aims to address and compare the effect of high pressure in the liquefaction process for four liquefaction cycles: Claude, Linde–Hampson, single mixed, and dual mixed refrigerants.

2. Materials and Methods

To compare the cycles’ efficiency and their behavior under different operating conditions, all four cycles were modeled in Aspen Hysys® V14, from Aspen Technology, as described in Section 2.1. The method for comparing the efficiency and analyzing the cycles from an energy and exergy point of view is based on the method previously proposed by Yang et al. (2023) [25] and reported in Section 2.2.

2.1. Cycles Description and Specification

Aiming to verify the influence of pressure on the hydrogen liquefaction cycle, four cycles were analyzed in the study: Claude cycle, pre-cooled Linde–Hampson (PLH) system, single mixed refrigerant (SMR) pre-cooling system, and dual mixed refrigerant (DMR) pre-cooling system. The construction of the simulation for each liquefaction cycle is presented in Figure 1.

In the Claude cycle, as can be seen in Figure 1A, the hydrogen feed goes through the compressor train, where the pressure is elevated, and then is cooled in a series of three heat exchangers. After the first cooling stage (HEX-A1), a fraction of the hydrogen, usually between 60% and 80% [27], is sent to an expander, where the pressure reduction also reduces the gas temperature. The remaining fraction of hydrogen that was not diverted passes through HEX-A2 and HEX-A3, reaching a temperature at which the isenthalpic expansion of the gas in a Joule–Thompson valve causes a partial liquefaction. All liquefied hydrogen is removed, while the saturated gas is recycled and used as the refrigerant in the heat exchangers, from HEX-A3 to HEX-A1. Moreover, after HEX-A3, the diverted expanded hydrogen is mixed with the cold recycled hydrogen. After the recuperative cooling, the recycled hydrogen is mixed with a make-up stream and returns to the compression train.

The Linde–Hampson liquefaction is one of the simplest gas liquefaction systems, but it cannot be used to liquefy hydrogen since its maximum inversion temperature is lower than ambient temperature, i.e., if not pre-cooled, hydrogen will not be cooled on throttling [12]. The Claude cycle, which uses only hydrogen as the working fluid, makes use of the expander to produce low temperatures and achieve a cooling effect in the isenthalpic expansion. However, other cycles applied to hydrogen liquefaction need a pre-cooling section in the absence of expansion in an expander stage. The pre-cooled Linde–Hampson, shown in Figure 1B, for example, uses liquid nitrogen as a refrigerant in the first heat exchanger (HEX-B1), and the liquid nitrogen, in turn, is produced in a simple Linde–Hampson system. The pre-cooled hydrogen, at a temperature near the nitrogen saturation temperature, passes through a last heat exchanger (HEX-B2), where it is cooled by the non-liquefied fraction of hydrogen, in the same way as the Claude cycle.

The application of nitrogen in the PLH system, however, presents a clear exergy disadvantage, since a pure component always maintains a constant temperature in its evaporation, which causes the distancing of the refrigerant and hydrogen temperature profiles in the heat exchanger, leading to exergy losses. Using mixed refrigerants, on the other hand, allows the refrigerant to undergo a temperature rise (temperature glide) between bubble and dew point, thus allowing a better fitting of the hot and cold composite curves, and a more reversible process, with less exergy losses. In that sense, in the SMR and DMR pre-cooled cycles, mixed refrigerants are used instead of pure nitrogen.

In the SMR cycle (Figure 1C), only one mixed refrigerant is used. The refrigerant is cooled in a first heat exchanger (HEX-C1) and then expanded through a JT valve, where its temperature is reduced, and it then returns to the same heat exchanger, now acting like the cold end (along with the recycled hydrogen) to reduce the hydrogen temperature. The DMR process (Figure 1D) is analogous to the SMR but with two refrigerants. The internal refrigerant cycle, also called warm mixed refrigerant (WMR), is used to reduce both hydrogen and the external refrigerant to an intermediate temperature in a first heat exchanger (HEX-D1), and in the external refrigeration cycle, the cold mixed refrigerant (CMR) is used to cool hydrogen to the final pre-cooling temperature in a second heat exchanger (HEX-D2). Finally, as in the Claude cycle, hydrogen is then cooled to the isenthalpic expansion temperature with the non-liquefied fraction of the gas. In Figure 2, an illustration of the temperature-entropy (T-S) diagram is shown for Claude (Figure 2a), PLH and SMR (analogous) (Figure 2b), and DMR cycles (Figure 2c).

For the analysis of those cycles described, the Aspen HYSYS® V14 interface was used to perform the simulations. Hydrogen is defined as normal hydrogen in the software, and two thermodynamic packages were used. The “Hydrogen” thermodynamic package was chosen for hydrogen. In this package, ortho- and para-hydrogen properties are accounted for, even if only normal hydrogen is selected in the component list. For the refrigerants, Peng–Robinson was selected.

While using the “Hydrogen” package, the hydrogen composition is always supposed to reach equilibrium accordingly to the stream temperature, i.e., the simulation considers the ortho–para conversion (OPC) reaction heat for each piece of equipment where hydrogen suffers a change in its temperature. The hot hydrogen (i.e., hydrogen stream which flows towards the valve while being cooled, for liquefaction), which passes through the series of heat exchangers (where a catalyst is used to enhance the conversion), not only has sensible heat being removed, but also the reaction heat from ortho to para conversion. Using this package, however, the OPC is indistinguishably accounted for in every piece of equipment. Because of this, the consideration of the catalyst being used in the cold hydrogen (i.e., hydrogen stream which flows towards the compression train while cooling the hot hydrogen stream) side of the multi-stream heat exchangers must be inherently made, as the endothermic reaction of para- to ortho-hydrogen is also being considered as hydrogen temperature increases, and the conversion reaction is slow in the absence of a catalyst other than ortho-hydrogen itself [28]. Furthermore, as the valve inlet only reaches temperatures from 30 to 40 K, when the equilibrium fraction of ortho-hydrogen still corresponds to 10–20%, one last conversion stage is usually employed in liquefaction plants, where the p-hydrogen fraction reaches 99.8% at the saturation temperature at 1 bar. However, due to the “Hydrogen” package, in the JT valve, OPC is already accounted for, making the modeling of one last OPC stage unnecessary. Notwithstanding the OPC being considered in the compression train, the change in the equilibrium in high temperatures is not significant, and the reaction, which would not occur in real plants due to the lack of catalyst material [18], should present a minor influence on the results.

To perform the simulations, some assumptions were made to reduce the degree of freedom of the system until the pressure is the only unknown parameter in the cycle. It is important to highlight that the considerations made and the value of the parameters were arbitrarily chosen and can be further optimized if finding the optimal efficiency of the cycle is the objective. Hydrogen feed conditions and design specifications for all cycles are shown in

Table 1. Feed and equipment design specification.

Parameter	Value	Ref.
Hydrogen feed to the compressor train [kg/h]	100	-
Hydrogen feed pressure [bar]	1.0	-
Liquid hydrogen pressure [bar]	1.0	-
Intercooler temperature [K]	298	-
Hydrogen feed temperature [K]	298	-
Compressor and expander isentropic efficiency [%]	85	[12]
Pressure drops (overall)	0	[12]
Multi-stream heat exchanger minimum approach temperature [K]	2.0	[12]
Number of stages in the hydrogen compression train	4	(a)

(a) The number of compressors in every compression train was defined to maintain the pressure ratio in every compressor within the optimal range of 2 and 5 [29] for all of the high-pressure range of the sensitivity analysis (20 to 150 bar).

. The hydrogen inlet and outlet pressures were considered to be 1 bar in the simulations. The hydrogen inlet as well as intercooler temperature is considered to be ambient temperature so that water can be used as the cold fluid.

Moreover, additional specifications are required in the cycles according to their design. The high and low pressures for the refrigerant, the refrigerant composition, and the number of compression stages for the refrigerant in each cycle are summarized in

Table 2. Assumed refrigerant cycle specifications.

Parameter	PLH	SMR	DMR
			WMR	CMR
High pressure [bar]	200	30.0	10.0	20.0
Low pressure [bar]	0.1	0.1	1.0	0.1
Number of compression stages	5	3	3	3
Composition [%]
nitrogen	100.00	54.55	0.00	45.46
methane	0.00	9.09	20.00	18.18
ethane	0.00	9.09	20.00	18.18
propane	0.00	9.09	20.00	18.18
i-butane	0.00	9.09	20.00	0.00
n-butane	0.00	9.09	20.00	0.00

.

In pursuing the goal of reducing the system’s degrees of freedom, additional considerations were taken. To achieve these conditions, “adjust” and “set” blocks were used. These blocks use iterative methods to converge the simulation, respecting the aforementioned conditions. These other specifications, and the respective tolerances adopted, are as follows:

• In the Claude cycle, a split fraction of 65% are present for the expansion in the expander.
• In the pre-cooled Linde–Hampson cycle, the fraction of liquefied hydrogen after the isenthalpic expansion is adjusted so the minimum temperature approach (MITA) in HEX-B1 is 2.0 K (±0.1 K).
• In the pre-cooled SMR cycle, the fraction of liquefied hydrogen after the isenthalpic expansion is adjusted so the MITA in HEX-C2 is 2.0 K (±0.1 K). The refrigerant mass flow rate is adjusted so in HEX-C1, the cold hydrogen outlet approaches 293.0 K, and the cold MR outlet approaches 296.0 K (tolerance of the summed error of both streams ±2.0 K).
• In the pre-cooled DMR cycle, equal WMR and CMR mass flow rates are present. The CMR flow rate is adjusted so HEX-D1 and HEX-D2 approach an MITA of 2 K (tolerance of the summed error of both MITA ±0.2 K). The HEX-D1 CMR outlet temperature is 2 K above (set) the WMR cold inlet in the same HEX. The fraction of liquefied hydrogen after isenthalpic expansion is adjusted so the hot hydrogen outlet temperature in HEX-C2 approaches 65.0 K (±0.1 K).

It is worth highlighting that neither the composition of the mixed refrigerants for the pre-cooled cycles, shown in Table 2, nor the specifications adopted were optimized, but they were arbitrarily chosen. While many studies report the optimal composition and operating conditions for their pre-cooling cycles, these results are valid only for a single high pressure of the main cycle. As a sensitivity analysis was performed from 20 to 150 bar for the high pressure, applying values from other studies would not guarantee optimal conditions for the pressure range, and could even hinder convergence. Thus, values for the specifications and refrigerant compositions were set to guarantee a convergence for the entire pressure range.

2.2. Energy and Exergy Analysis

Aiming to compare the cycles’ energetic performance, three indicators were evaluated: the specific energy consumption (SEC), the figure of merit (FOM), and the coefficient of performance (COP).

The specific energy consumption is defined, as shown in Equation (1), as being the net power consumption ($\dot{W}$) in the cycle per mass flow rate of liquefied hydrogen (${\dot{m}}_{LH}$). The net power consumption can be defined as presented in Equation (2), in which ${\dot{W}}_{comp}$ stands for the power consumed in the compressors and ${\dot{W}}_{exp}$ the power produced in the expanders.

$$SEC={\displaystyle \frac{\dot{W}}{{\dot{m}}_{LH}}}$$

(1)

$$\dot{W}=\sum {\dot{W}}_{comp}-\sum {\dot{W}}_{exp}$$

(2)

Apart from the SEC, another form of analyzing the liquefaction energy consumption is in terms of a fraction of the fuel heat (FFH). For the liquid hydrogen, the FFH can be defined as shown in Equation (3).

$$FFH={\displaystyle \frac{SEC}{LHV}}={\displaystyle \frac{SEC}{120MJ/{\mathrm{k}\mathrm{g}}_{\mathrm{L}\mathrm{H}}}}$$

(3)

The FOM parameter assesses the approximation of the process of an ideal system and can be defined as the ratio of the ideal work theoretically required (${\dot{W}}_i$) by the actual work, as shown in Equation (4).

$$FOM={\displaystyle \frac{{\dot{W}}_i}{\dot{W}}}$$

(4)

In an ideal, reversible system, the amount of work for the liquefaction can be defined as presented by Equation (5).

$${\dot{W}}_i={\dot{m}}_{HL}\left[\left(h_{HF}-h_{LH}\right)-T_0\left(s_{HF}-s_{LH}\right)\right]$$

(5)

In Equation (5), $T_0$ is the dead state temperature (298.15 K), and $h_{LH}$, $h_{HF}$, $s_{LH}$ and $s_{HF}$ are the specific enthalpy and entropy of the liquefied hydrogen outlet and the hydrogen feed in the cycle, respectively.

Lastly, the COP measures the ratio between the cooling needed for liquefaction and the net amount of work, as defined in Equation (6).

$$COP={\displaystyle \frac{{\dot{m}}_{LH}\left(h_{HF}-h_{LH}\right)}{\dot{W}}}$$

(6)

Moreover, for the exergy analysis, aiming to verify the exergy destruction distribution along each piece of equipment, i.e., the equipment contribution to the irreversibility,

Table 3. Exergy balance equation for each piece of equipment [7,25].

Piece of Equipment	Exergy Balance
Heat exchangers, coolers, mixers, splitters, valves, separators, and OPC	$\dot{I}={\displaystyle \sum _{i=1}^n}{\dot{E}}_i-{\displaystyle \sum _{j=1}^m}{\dot{E}}_j$	(7)
Expanders	$\dot{I}={\dot{E}}_{in}-{\dot{E}}_{out}-\sum {\dot{W}}_{exp}$	(8)
Compressors	$\dot{I}={\dot{E}}_{in}-{\dot{E}}_{out}+\sum {\dot{W}}_{comp}$	(9)
Total	$\dot{I}={\dot{E}}_{in}-{\dot{E}}_{out}+\dot{W}$	(10)

presents the exergy balance equation for each piece of equipment in the simulated systems. The exergy from each stream can be obtained directly from the simulation. In Table 3, $\dot{I}$ stands for the irreversibility rate or exergy destruction rate, ${\dot{E}}_i$ and ${\dot{E}}_j$ stand for the i-th inlet and j-th outlet exergy rate, while n and m represent the number of inlets and outlets in the device, respectively. Moreover, ${\dot{E}}_{in}$ is the inlet exergy rate and ${\dot{E}}_{out}$ the outlet exergy rate for the devices with only one inlet and outlet.

For comparing and evaluating the cycles, a sensitivity analysis was made regarding the effect of the cycle’s high pressure on the energy and exergy efficiency parameters (SEC, FOM, and COP): the hydrogen liquefied fraction; the FFH; and exergy destruction, and its distribution by device. For the analysis, the high pressure spanned the interval from 20 to 150 bar. Nonetheless, a comparison of the heat exchangers of PLH and SMR cycles was made to assess the implications of using a mixed refrigerant.

3. Results and Discussion

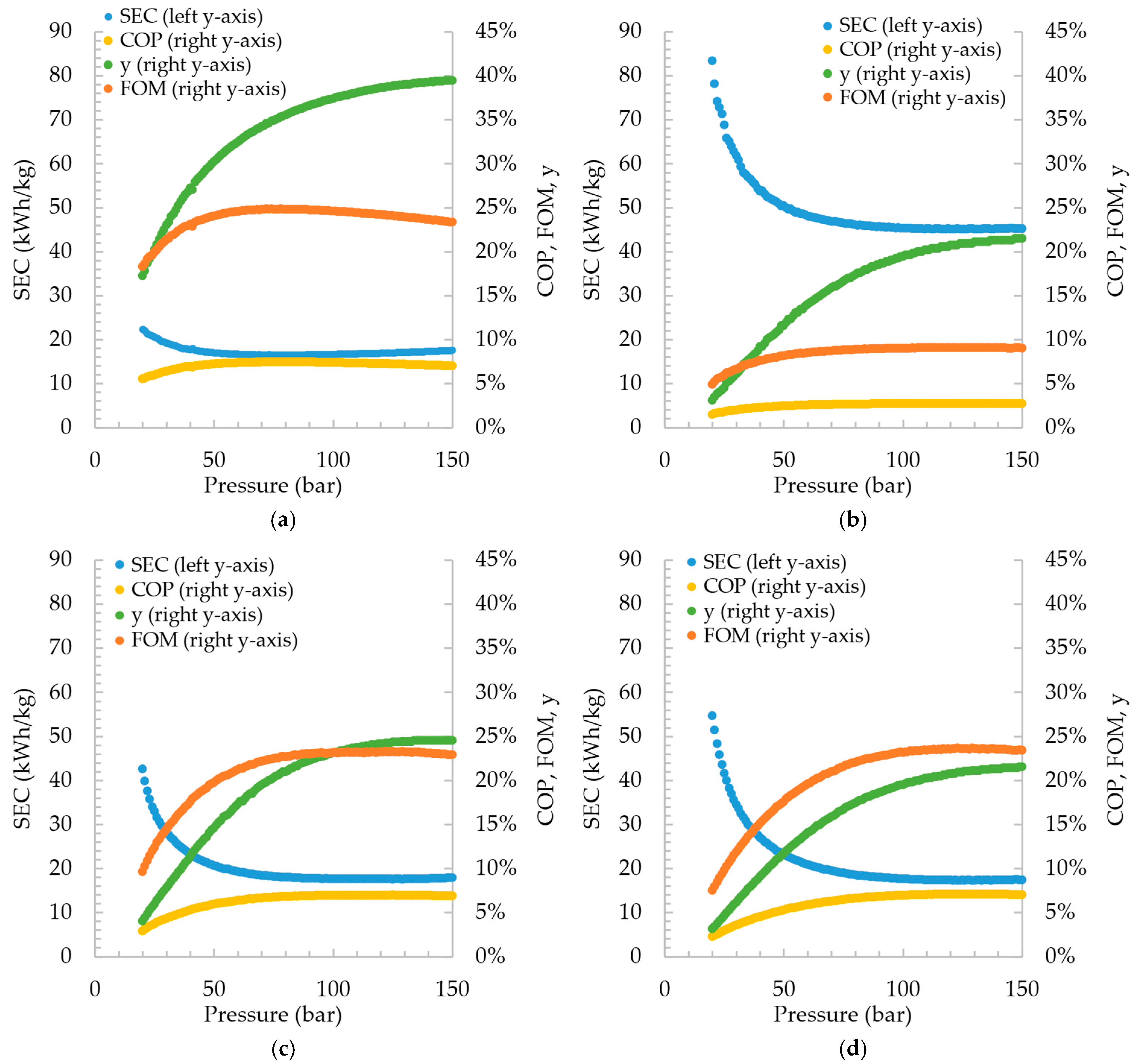
From the simulations carried out, the process efficiency indicators, SEC, COP, and FOM, as well as the fraction of liquefied hydrogen after expansion in the valve, are shown in Figure 3. The pressure range for which the results were plotted is from 20 to 150 bar, with a 1 bar interval. Among the cycles, the Claude cycle presented the best energy efficiency, with a minimum SEC of 16.47 kWh/kg_LH and a maximum FOM of 24.85% when the high pressure of the cycle is 78 bar. Among the pre-cooled cycles, the DMR showed better results, with an SEC of 17.30 kWh/kg_LH at 123 bar, followed by the SMR cycle, with an SEC of 17.58 kWh/kg_LH at 125 bar, and finally, the PLH with an SEC of 45.07 kWh/kg_LH operating at 124 bar.

While it is difficult to compare the results for the pre-cooled cycles, as the operating conditions and refrigerant composition were arbitrarily chosen, the Claude cycle can be considered for model validation. Assuming the cycle’s high pressure at 21 bar, the SEC found for Claude is 22.01 kWh/kg_LH, which is close to the reported 22.1 obtained by Aasadnia and Mehrpooya (2018) [12] for the same cycle.

Despite the different efficiencies due to the different heat exchangers and refrigeration cycle design, the same behavior regarding the increase in the high pressure is noted in all four cycles. Increasing the pressure improved efficiency parameters (SEC, FOM, and COP) up to a limit beyond which the increase in irreversibility implies greater exergy losses than facilitates liquefaction. These results are corroborated by Quack’s (2002) [26] statement that there is a tradeoff between increased power for compression and gain in cooling efficiency.

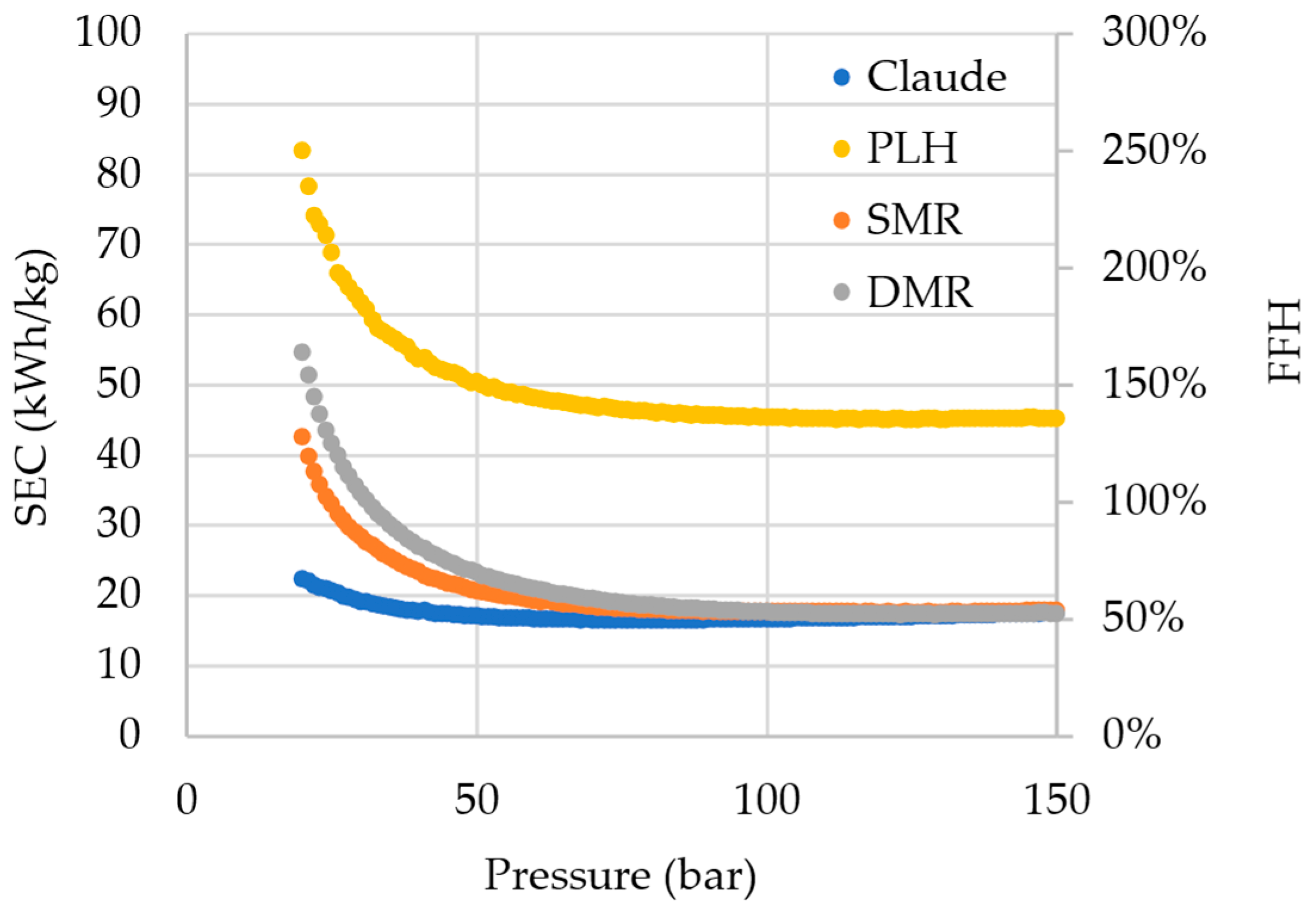
For a comparison effect, Figure 4 shows the SEC and the FFH of all simulated cycles, and only Claude, SMR (operating above 25 bar), and DMR (operating above 32 bar) cycles were found to exhibit an FFH lower than 100%, i.e., presenting a lower energy cost for hydrogen liquefaction than what hydrogen itself contains. Nonetheless, it is important to highlight that the FFH alone cannot provide enough information for evaluating the worthiness of the liquefaction cycle, being only a cycle efficiency indicator, as the SEC. Since liquefaction is an alternative for storing and transporting hydrogen, especially over long distances, its cost should be compared to gas hydrogen transportation through pipelines, for example. The tendency of the points in the graphs is not perfect. This is caused by the recycle and adjust blocks, and even multi-current heat exchangers, which have a tolerance for the simulation’s convergence.

It can be noticed that the Claude cycle has a significant superiority over the other cycles. This is essentially due to the presence of an expander, which always guarantees more effective cooling than the isenthalpic expansion in the valves. The expander makes the addition of a pre-cooling cycle unnecessary and concomitantly produces work that can be integrated and used in the process compression or other operations and also reduces the net power consumption by the system. The SEC found (16.47 kWh/kg_LH) even approaches the current SEC of operating hydrogen liquefaction plants (12–15 kWh/kg_LH).

The SEC of the Claude cycle operating at a high pressure of 21 bar was 22.01 kW/kg_LH, which is significantly higher than the value reported by Yang et al. (2023) [25] of 5.62 kW/kg_LH. The contrast in values is due to differences in the construction of the liquefaction cycle model. While those authors considered pre-cooling external to the hydrogen liquefaction line (using nitrogen), in the present work, the Claude cycle did not consider the use of a refrigerant. Furthermore, the designs differ regarding the number of compressors and expanders applied in series, as well as the number of splits of the hydrogen stream for temperature reduction in expanders. In addition, those authors assumed that the hydrogen supplied to the cycle would be at a pressure of 21 bar, compared to the ambient pressure (1 bar) considered in this work. Considering a hydrogen feed pressure of 21 bar of the cycle, the SEC value would be 20.40 kW/kg_LH, and the reduction would progress with the increase in the high pressure of the cycle, since a greater fraction of the hydrogen would be liquefied, and therefore a greater quantity of high-pressure hydrogen would be fed to the cycle and not pressurized internally.

The lower SEC obtained in the mixed refrigerant cycles in comparison with PLH is associated with the use of a non-pure refrigerant. The use of mixed refrigerants allows a better adjustment of the composite curve by taking advantage of the temperature glide, i.e., the range over which a mixed refrigerant evaporates or condenses, which is inherent to the mixture. Moreover, when two refrigeration cycles are used (as is the case with DMR), the adjustment of the composite curves can be divided between the cycles, and each one can be adjusted separately, further enhancing the heat transfer efficiency, which could explain the lower SEC obtained considering the DMR over the SMR pre-cooled cycle. The efficiency of compression is also improved with the increase in the number of cycles and mixed refrigerants, as each compressor train only has to operate with a fraction of the total refrigerant flow regarding a specific pre-cooling cycle, and the refrigerant mixture can be chosen to provide better compressibility.

The refrigerant demands for each pre-cooled cycle are presented in Figure 5. In this figure, only three cycles—PLH, SMR, and DMR—are analyzed, as the Claude cycle does not require a refrigerant. An increase in the demand can be verified as the pressure increases, proportional to the liquefied hydrogen fraction. With the reduction in the non-liquefied hydrogen, the amount of heat that can be removed by the recycled hydrogen also decreases, and the cooling, previously provided by the cold hydrogen, has to be supplied by the additional refrigerant. For the DMR cycle, since WMR and CMR were set to have the same mass flow rate, only one data set is shown. Considering both WMR and CMR, the total refrigerant demand in SMR and DMR is almost identical, while in PLH, the nitrogen needed for pre-cooling is close to two times the amount needed in the other two pre-cooled cycles.

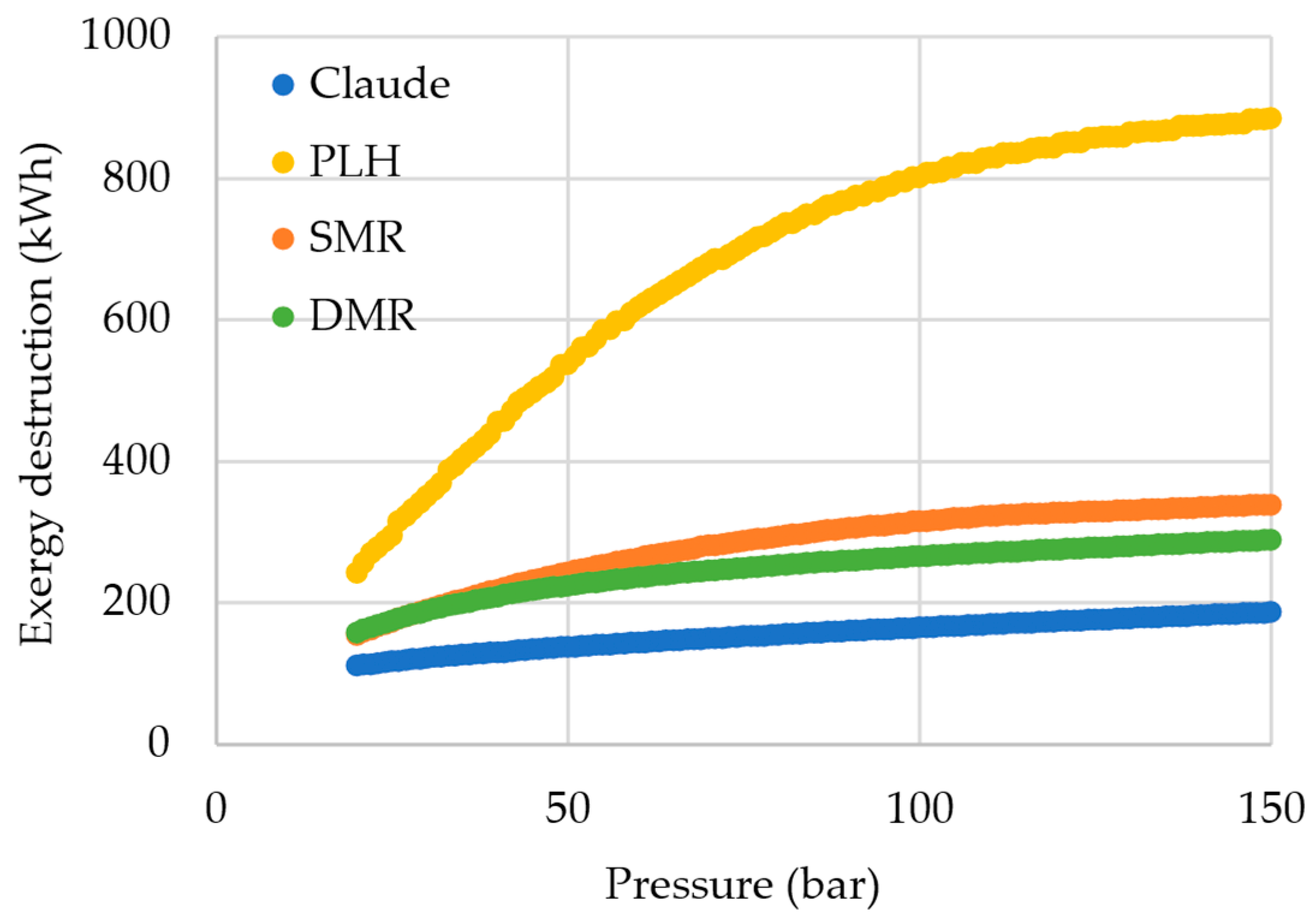
Furthermore, in terms of exergy, the SMR system has a significant advantage over the PLH. Figure 6 presents a comparison of the total exergy destruction among the cycles, while Figure 7 presents the distribution profiles of exergy destruction among the pieces of equipment. In the exergy destruction distribution, the fractions of exergy destruction in mixers, splitters, and flash vessels are negligible.

It is noted that in the PLH cycle, exergy destruction is more intense in the valves, while for the SMR, exergy destruction occurs more significantly in the heat exchangers. Even though heat exchangers are the device that has the greatest relative contribution to exergy destruction in the SMR, when absolute values are analyzed, the exergy destruction is slightly inferior in the mixed refrigerant cycle. With a multi-component refrigerant, the temperature glide allows the adjustment of the hot and cold composite curves more properly, considering that the refrigerant varies its temperature throughout its boiling.

Comparing SMR and DMR exergy distribution profiles (Figure 7), there is an inversion in the device with the major contribution to the exergy destruction, changing from the heater exchangers in the SMR to the valves in the DMR. In the DMR, with the addition of a new refrigeration cycle, another valve was added, thus increasing the exergy destruction in this piece of equipment. The increase is not verified in the same intensity on the heat exchanger due to the fact that hydrogen is cooled equally in both cases, i.e., essentially there is no increase in the heat exchanger duty, with the main factor in changes in the exergy destruction in this device being the suiting of the composition curve. Nonetheless, it is noticeable that DMR presented a lower or near-total exergy destruction than SMR. This result is expected, because as the number of pre-cooling cycles increases, thus performing the hydrogen liquefaction through a greater number of stages, the process becomes closer to a reversible process with less exergy destruction. Despite the close SEC found for the DMR and SMR, the lower exergy destruction in the DMR is a clear indication that the cycle could be more efficient than the SMR, as more suitable operating conditions were considered. These more appropriate conditions could be obtained by the optimization of the cycle specifications and mixed refrigerant compositions.

When comparing the exergy destruction results with those reported by Yang et al. (2023) [25], it is visible that the participation of the valves in the exergy destruction was much more relevant in the present study. However, it is important to highlight that those authors conducted an optimization study to reduce SEC, which jointly reduces irreversibility. Thus, the optimal conditions shift the cooling need to be mainly provided in heat exchangers at the detriment of valves, since isenthalpic expansion inherently has a significant irreversibility. In heat exchangers, irreversibility and exergy destruction can be more easily avoided by well-suited composite curves.

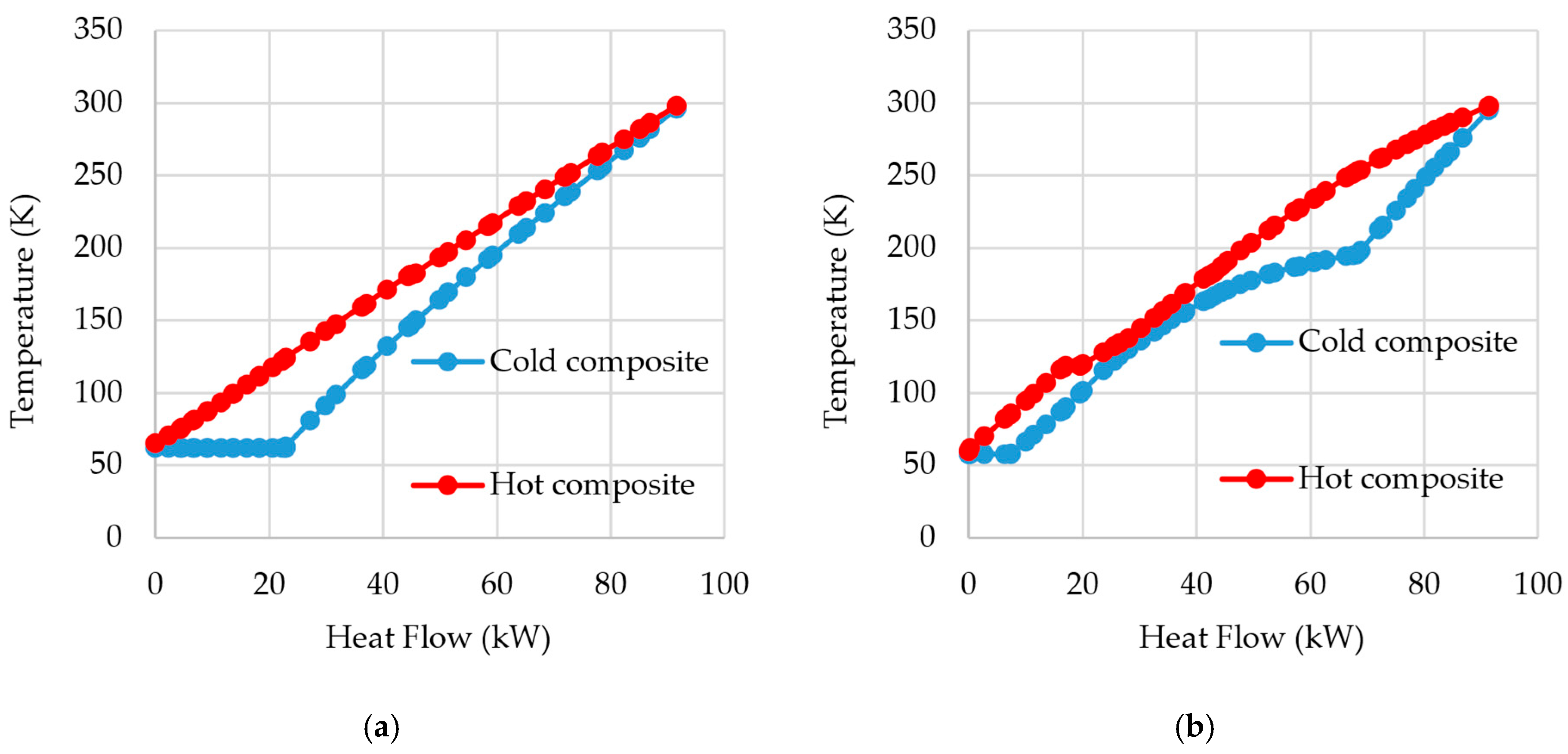
In Figure 8, the composite curves for HEX-B1 and HEX-C1 are shown when both cycles, PLH and SMR, operate with a high pressure of 94 bar. It is notable that in lower temperatures, the composite curves are closer to each other in SMR than in PLH. That is because a multi-component refrigerant allows not only the temperature glide but also the adjustment of the specific heat capacity of that refrigerant. By optimizing the refrigerant composition, its specific heat capacity can be varied, and thus it would be possible to further decrease the distance between the hot and cold composite curves. The difference in both graphs is diminished as nitrogen cooling prior to the isenthalpic expansion is performed in HEX-B3. On the other hand, the mixed refrigerant pre-cooling is performed in HEX-C1, which is the same heat exchanger that promotes the hydrogen pre-cooling. If both cycles were constructed analogously, i.e., with nitrogen pre-cooling, which is performed separately at HEX-B3, being performed at HEX-B1, as it is for the SMR cycle, a greater difference would be perceived regarding SMR’s greater effectiveness.

Still, in Figure 8, it can be noticed that at higher temperatures, over 200 K, the mixed refrigerant in the SMR does not promote a well-suited cold composite curve, as the lightweight components of the refrigerant, despite their capacity to provide low temperatures for the cooling process, do not match the heat load needed in higher temperatures. Hence, using an external refrigeration cycle, with a refrigerant with heavier components, as in the DMR processes, would not only guarantee a well-suited curve in both temperature intervals but also a lower compression power [7].

Despite those advantages, the DMR process presented SEC and exergy destruction values higher than expected, since with the increase in the degrees of freedom, the adjustment of the variables along the cycle without an optimization method is a more difficult procedure compared to the other simpler cycles. In addition, in neither the SMR nor DMR cycles was the refrigerant composition effect in the SEC analyzed. Thus, for future research, evaluating the effect of the refrigerant’s composition and its physical properties on the cycle performance, and even optimizing the refrigerants’ composition and cycle parameters, such as intermediate temperatures and/or refrigerant mass flow ratios for a proper comparison of the mixed refrigerant cycles, could be a possibility. Additionally, it is evident that the increase in the cycle complexity, i.e., increasing compression stages and the number of refrigerants and the number of refrigerant components, can improve its performance and reduce the SEC. Thus, to fully understand the applicability of the proposed cycles, an economic analysis must be made in future studies. Moreover, optimization could also be performed from the economic point of view.

4. Conclusions

Despite the increasing research in hydrogen liquefaction, with the proposal of theoretical cycles that may even approach the ideal efficiency, few studies fully investigate the behavior of hydrogen liquefaction cycles under varied conditions, only focusing on optimal points. In this study, therefore, four simple hydrogen liquefaction cycles, Claude, PLH, SMR, and DMR, were assessed regarding the influence of the cycle’s high operating pressure from 20 to 150 bar, on energy efficiency parameters, exergy destruction, and its distribution along the pieces of equipment, considering the influence of the hydrogen ortho–para conversion.

The Claude cycle presented the best (lowest) SEC among the cycles, reaching 16.47 kWh/kg_LH at 78 bar, followed by DMR, with 17.30 kWh/kg_LH at 123 bar, then SMR, with 17.58 kWh/kg_LH at 125 bar, and PLH, with 45.07 kWh/kg_LH, operating at 124 bar. Regarding the exergy destruction, the pattern was the same, with Claude presenting the better exergy efficiency, while PLH presented the greater exergy destruction. Amidst the pre-cooled based cycles, the DMR presented the best efficiency, as, in contrast to PLH, it uses a non-pure refrigerant and makes use of the temperature glide to promote a hydrogen pre-cooling to lower temperatures as well as a better suit of the composite curves.

In general, all the cycles benefit from the increase of hydrogen high pressure at ambient temperature, as cooling is facilitated.

Limitations and Future Scope

Regarding the limitations, it is necessary to emphasize that the applicability of the results found is restricted to non-optimal conditions. Optimization methods could be employed within the analysis to ensure a fairer comparison of the cycle’s gain of performance with changes in the high pressure of the main cycle. This development is mainly needed for pre-cooled cycles, in which the variable composition of the refrigerant and the greater number of devices increase the degree of freedom. Furthermore, further work could focus on the assessment of more complex cycles.