A Fuzzy Inertia-Based Virtual Synchronous Generator Model for Managing Grid Frequency Under Large-Scale Electric Vehicle Integration

Abstract

The rapid proliferation of EVs has ushered in a transformative era for the power industry, characterized by increased demand volatility and grid frequency instability. In response to these challenges, this paper introduces a novel approach that combines fuzzy logic with adaptive inertia control to improve the frequency stability of grids amidst large-scale electric vehicle (EV) integration. The proposed methodology not only adapts to varying charging scenarios but also strikes a balance between steady-state and dynamic performance considerations. This research establishes a solid theoretical foundation for the inertia-adaptive virtual synchronous generator (VSG) concept and introduces a pioneering fuzzy inertia-based VSG methodology. Additionally, it incorporates adaptive output scaling factors to enhance the robustness and adaptability of the control strategy. These contributions offer valuable insights into the evolving landscape of adaptive VSG strategies and provide a pragmatic solution to the pressing challenges arising from the integration of large-scale EVs, ultimately fostering the resilience and sustainability of contemporary power systems. Finally, simulation results illustrate that the new proposed fuzzy adaptive inertia-based VSG method is effective and has superior advantages over the traditional VSG and droop control strategies. Specifically, the proposed method reduces the maximum frequency change by 25% during load transitions, with a peak variation of 0.15 Hz compared to 0.2 Hz for the traditional VSG.

1. Introduction

Electric vehicles (EVs) have garnered significant attention and adoption, primarily owing to their eco-friendly attributes and the consequential reduction in greenhouse gas (GHG) emissions [1,2,3]. The exponential growth in EV adoption underscores their pivotal role in the grid, contributing to the emergence of a substantial era of large-scale EV penetration. This is substantiated by findings in the literature [4], which indicate that EVs could potentially satisfy short-term grid storage demands as early as 2030. While this development holds promise for enhancing grid integration and energy storage capabilities [5], it simultaneously raises crucial concerns pertaining to grid stability. For instance, in China, strict regulations dictate that grid frequency deviations should be controlled within a narrow range of ±0.2 to ±0.5 Hz [6]. However, the swift and widespread adoption of fast-charging methods for EVs can introduce substantial fluctuations in grid frequency, consequently degrading the overall stability of the power grid [7]. These challenges underscore the imperative need for innovative solutions to effectively address the intricate interactions between EV integration and grid frequency management.

Ensuring the power grid stability, which is integrated with a large number of EVs is a crucial challenge that demands precise control mechanisms. Figure 1 illustrates that power grids heavily employ power electronic devices for rectification and inversion to achieve the required voltage and frequency levels [8]. However, this results in low inertia and damping, leading to rapid response time [9,10,11]. When a significant number of EVs begin charging simultaneously, the grid’s rapid frequency response can cause a substantial drop, resulting in power grid instability [12]. To address this issue, control algorithms must compensate for the system’s inertia and damping, enhancing the grid’s resilience against disturbances caused by EV loads.

Traditional control strategies used for regulating power grid voltage and frequency include P-Q control, V-f control, and droop control [13,14,15]. P-Q control, often referred to as constant power control, focuses solely on managing the active and reactive power injected into the grid, disregarding frequency and voltage. V-f control, on the other hand, aims to stabilize the output voltage and frequency at rated values, even in the presence of power fluctuations. Droop control is further classified into P-f/Q-V control and f-P/V-Q control, distinguished by their control topologies. P-f/Q-V control employs outer loops for power regulation and inner loops for frequency and voltage stabilization, whereas f-P/V-Q control adopts an alternative configuration. However, it is critical to highlight that these traditional methods fail to provide the power grid with sufficient inertia and damping, akin to real synchronous generators (RSGs). This deficiency leaves the grid vulnerable to sharp voltage and frequency fluctuations, particularly during high-demand events such as large-scale EV charging.

A potential solution to enhance grid resilience against disturbances caused by EV loads is the virtual synchronous generator (VSG), designed to mimic the behavior of RSGs. The VSG concept was first introduced by Beck in 2007 [16], incorporating the swing equation of RSGs into its control framework. This innovation imbues the grid with virtual inertia and damping properties. Zhong further refined the VSG model by integrating electromagnetic characteristics, thereby achieving a more comprehensive representation of RSG behavior [17]. These advancements have laid a solid foundation for improving power quality and grid stability through VSG technology. Nevertheless, traditional VSG systems with fixed virtual inertia and damping parameters struggle to fully address frequency oscillations, especially under high EV penetration [18]. The challenge lies in balancing design trade-offs: low inertia and damping values ensure rapid system response, but increasing these values compromises transient control performance.

To overcome the limitations of static inertia and damping in traditional VSG strategies, researchers have developed adaptive methodologies [19,20,21,22,23,24,25,26,27]. A notable approach is the self-adaptive inertia and damping combination control method proposed in [19], which employs an interleaving control technique to improve frequency stability. Similarly, Ref. [20] presents an adaptive inertia and damping coordination control strategy for grid-forming VSGs, enhancing transient stability by enabling real-time adjustments to virtual inertia and damping coefficients based on operational frequency deviations and their rates of change. Another innovative method described in [21] uses a fuzzy adaptive damping-based VSG control framework, which simultaneously mitigates microgrid frequency fluctuations and ensures dynamic system stability by accounting for dynamic characteristics and maximum allowable frequency deviations. Additionally, Ref. [22] proposes an optimal coordination control strategy for microgrid inverters and energy storage, leveraging variable virtual inertia and damping through linear quadratic optimal control to enhance system performance based on real-time conditions and dynamic metrics. An alternative strategy in [23] introduced an improved adaptive inertia approach that bypasses the need for angular velocity derivatives. Meanwhile, the technique in [24] explores VSG power–angle characteristics during stable operation and output current saturation. Using the equal area criterion from synchronous generator stability analysis, it calculates the fault critical clearing angle and devises an adaptive control strategy for inertia and damping coefficients. Efforts to optimize VSG performance are further exemplified in [25], where a strategy ensures an optimal damping ratio throughout operations to suppress power and frequency oscillations, refining response times and minimizing overshoots. Moreover, Ref. [26] integrates a fuzzy controller into the VSG topology to enhance transient dynamics by augmenting inertia, though its emphasis on steady-state performance is limited. Building on this, Ref. [27] introduces an optimized fuzzy VSG inertia adaptive algorithm that considers both steady-state and dynamic performance. This approach establishes fuzzy control rules by analyzing the relationship between inertia and frequency changes, although certain aspects of these rules remain unclear.

Based on the previous analysis, several key issues necessitate further exploration. First, despite the proliferation of adaptive VSG strategies, their applicability to address challenges posed by large-scale EV integration remains limited. Second, the adoption of diverse optimization methodologies for damping and inertia, with fuzzy control being prominent, requires further refinement and standardization. Third, the predominant focus on dynamic characteristics in adaptive VSG methods often neglects steady-state performance considerations. Lastly, while fuzzy adaptive inertia methods have surfaced to enhance frequency response, the underlying relationship between inertia and frequency remains elusive, posing challenges in the design of precise fuzzy control rules.

This paper presents a fuzzy adaptive inertia control strategy to adjust the real-time parameter of the VSG for power grids with large-scale EVs integrated. The primary objective of this strategy is to ensure the stability of grid frequency, particularly when confronted with the imminent scenario of simultaneous charging by a multitude of EVs. The main contributions and novelties in comparison with existing studies can be summarized as follows:

• Theoretical groundwork: This paper comprehensively presents the theoretical rationale of an inertia-adaptive VSG and its pivotal role in enhancing power grid frequency stability. These theoretical foundations provide a solid basis for future investigations in this domain;
• Fuzzy inertia-based VSG: A novel fuzzy inertia-based VSG methodology is introduced to improve the frequency stability of power grids grappling with the integration of large-scale EVs. This innovative approach is attuned to the fact that large-scale EV charging does not always occur concurrently. Consequently, the proposed fuzzy method takes into account both steady-state and dynamic scenarios, which can ensure that the power grid maintains frequency stability during large-scale EV charging events without compromising response time when the power grid works stably;
• Adaptive output scaling: By incorporating alternative output coefficients, the new fuzzy inertia controller can dynamically modulate the entire VSG control system in response to the magnitude of frequency and frequency deviations.

The remaining sections of this paper are structured as follows. Section 2 expounds upon the basic VSG method’s applicability to power grids incorporating large-scale EV integration. Section 3 lays a theoretical foundation by analyzing the relationship between inertia and frequency change, serving as a crucial underpinning for the subsequent development of an effective fuzzy adaptive VSG controller. In Section 4, we introduce and elaborate on the novel fuzzy inertia-based VSG technique, highlighting its multifaceted capabilities. Section 5 presents empirical evidence through comparative simulation results, substantiating the effectiveness and practicality of our proposed method. Finally, Section 6 provides a concise conclusion, summarizing the key findings and implications of this study.

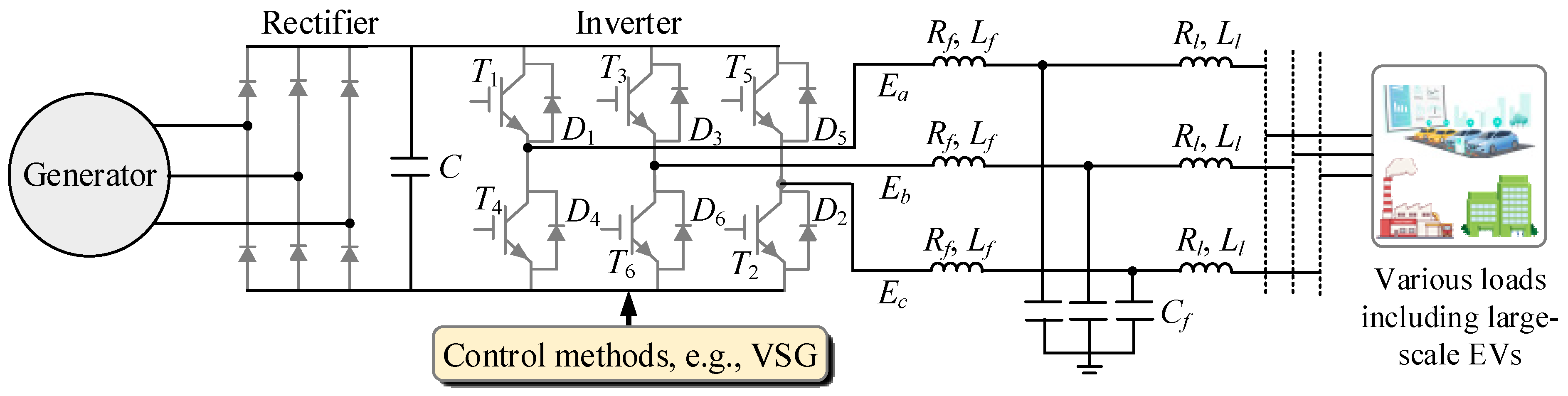
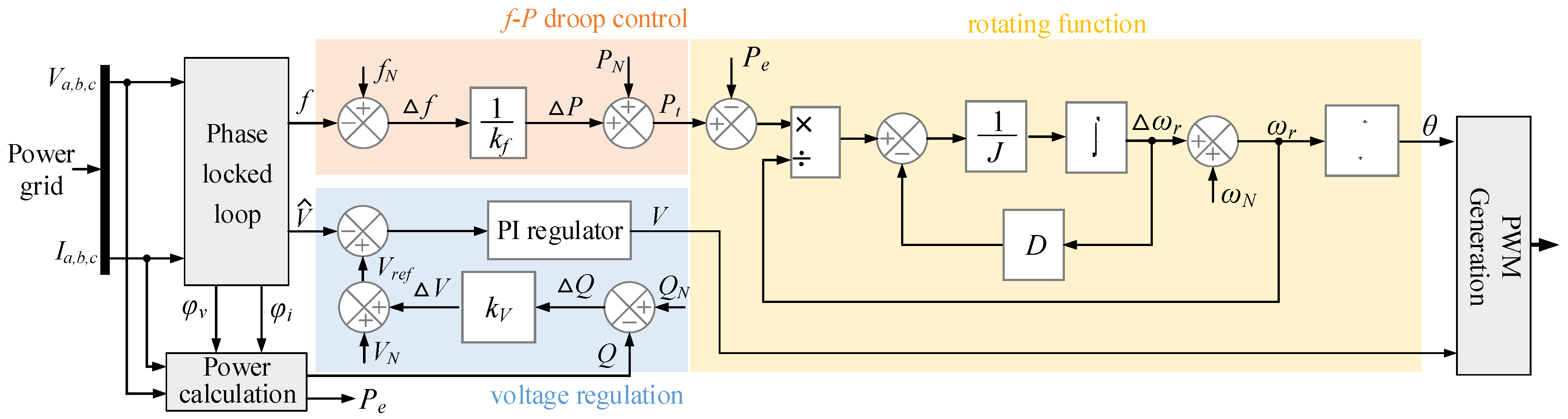
2. Basic VSG Strategy Used for Power Grids with Large-Scale EV Integration

The basic VSG control method used for power grids with large-scale EV integration is depicted in Figure 2. It can be seen that there are five important parts within the VSG control strategy: phase-locked loop, power calculation, voltage regulation, f-P droop control, and the rotating function. In terms of VSG techniques, these parts are necessary, especially the rotating function [21,28,29,30,31]. This section will introduce the implementations of these parts in detail.

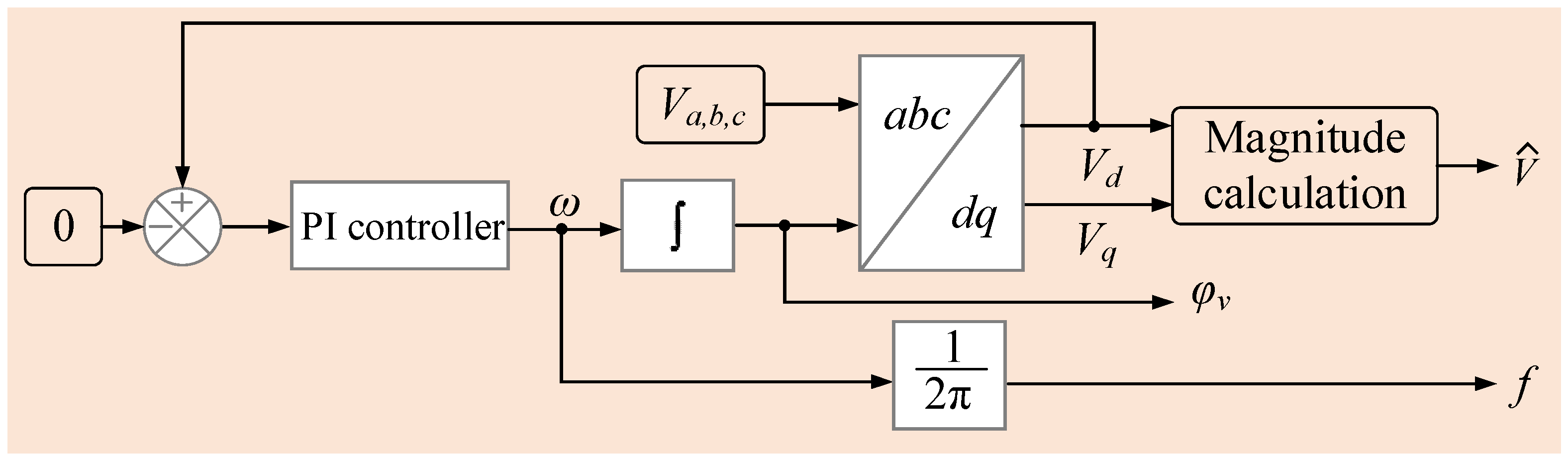
2.1. Phase-Locked Loop

The phase-locked loop is used to extract the frequency and voltage magnitude of the measured voltages of the power grid. With reference to [21], the structure of the phase-locked loop is presented in Figure 3. The phase-locked loop operation involves several key steps. Firstly, the measured phase voltages undergo a transformation into the rotating reference frame, represented as the d- and q-axis voltages, denoted as V_d and V_q, respectively:

$$\left[\begin{array}{l}{V}_d\\ V_q\end{array}\right]={\displaystyle \frac{2}{3}}\left[\begin{array}{l}\cos {\phi }_V {\displaystyle \frac{\sqrt{3}\sin {\phi }_V-\cos {\phi }_V}{2}} {\displaystyle \frac{-\sqrt{3}\sin {\phi }_V-\cos {\phi }_V}{2}}\\ -\sin {\phi }_V {\displaystyle \frac{\sin {\phi }_V+\sqrt{3}\cos {\phi }_V}{2}} {\displaystyle \frac{\sin {\phi }_V-\sqrt{3}\cos {\phi }_V}{2}}\end{array}\right]·\left[\begin{array}{l}{V}_a\\ V_b\\ V_c\end{array}\right]$$

(1)

where V_a, V_b, and V_c are measured voltages of the power grid, and φ_v is the phase angle of the voltages.

Subsequently, a proportional-integral (PI) regulator is employed to minimize the discrepancies between the reference value and V_d, which is typically set to zero. The output value of this PI regulator corresponds to the working frequency denoted as ω, serving as the operational velocity of the VSG. Upon applying the integral operation to ω, the result can be aligned with the instantaneous phase angle of the voltage. This process ultimately produces real-time voltage frequency and amplitude:

$$\left\{\begin{array}{l}f={\displaystyle \frac{\omega }{2\pi }}\\ \widehat{V}=\sqrt{{V_d}^2+{V_q}^2}\end{array}\right.$$

(2)

where f is the voltage frequency, ω is the angular frequency of the voltage, and $\widehat{V}$ is the magnitude of the voltage.

2.2. Power Calculation

This component is utilized to determine the active and reactive power of the grid, which are subsequently applied for voltage and frequency regulation. Using the measured voltages and currents, the active power is calculated as follows:

$$P_e=(V_a·I_a+V_b·I_b+V_c·I_c)·\cos ({\phi }_V-{\phi }_I)$$

(3)

where P_e is the active power, φ_v is the phase angle of the current which can be calculated by a phase-locked loop shown in Figure 3. In addition, Q (reactive power) can be calculated:

$$Q=(V_c·I_c+V_b·I_b+V_a·I_a)·\sin ({\phi }_V-{\phi }_I)$$

(4)

where Q is the reactive power.

2.3. Voltage Regulation

In Section 2.1 and Section 2.2, the real-time voltage magnitude and reactive power are calculated, which should be subsequently employed in voltage regulation to determine the output voltage value for generating control signals. As shown in Figure 2, Q-V droop control is used to generate the reference voltage first. Specifically, the error between the rated reactive power and real-time reactive power will be regulated by the voltage droop factor, and the output will be added to the rated voltage to obtain the reference voltage:

$$V_{ref}=V_N+k_V(Q_N-Q)$$

(5)

where V_ref is the initial reference voltage, V_N is the rated voltage of the power grid, k_V is the voltage droop factor, and Q_N is the rated reactive power.

Furthermore, to maintain the inverter’s output voltage at the desired value, a closed-loop control system employing a PI controller capable of achieving zero-error output adjustment should be employed. Specifically, the error between the initial reference voltage V_ref and the real-time voltage magnitude $\widehat{V}$ are regulated by a PI controller, which can be represented by:

$$V={\displaystyle \frac{k_{pv}s+k_{iv}}{s}}·(V_{ref}-\widehat{V})$$

(6)

where V is the output voltage value, and k_pv and k_iv are the gain and integral coefficients of the PI controller. Based on the system’s stability requirements and performance criteria, k_pv is tuned to control the response speed and overshoot, while k_iv is adjusted to eliminate steady-state error, achieving optimal PI controller performance.

2.4. f-P Droop Control

Figure 2 illustrates that the f-P droop control mechanism is a critical component of the frequency regulation system. It plays a central role in managing primary frequency control and determining the virtual synchronous generator’s mechanical power output. This control mechanism mimics the droop behavior characteristic of a rotating synchronous generator. In the power grid, the generator’s electromagnetic power corresponds to the active power. Any deviation from the generator’s nominal load affects this electromagnetic power. However, due to the slower response of the generator’s mechanical power, a mismatch arises between the two. This imbalance induces synchronous variations in the generator’s rotational speed. To stabilize the output power and accommodate load fluctuations, the controller adjusts the mechanical power to achieve equilibrium. Despite restoring the power balance, the generator’s speed does not return to its original state. Consequently, changes in output power cause deviations in grid frequency, reflecting the frequency droop characteristics. Using these characteristics, the correlation between power variation and frequency shifts can be expressed as [32]:

$$P_t-P_N={\displaystyle \frac{1}{k_f}}(f_N-f)\to P_t=P_N+{\displaystyle \frac{1}{k_f}}(f_N-f)$$

(7)

where P_t is the mechanical power, P_N is the rated power, k_f is the frequency droop factor, and f_N is the rated frequency.

2.5. Rotating Function

The mechanical equation of a synchronous generator is used for secondary frequency regulation, with its inputs being the mechanical power and electrometric power and the output being the generator angular frequency ω. As a core component of VSG technology, the mechanical equation of the synchronous generator imparts inertia and damping characteristics to the grid control system. The mechanical equation of the synchronous generator is as follows:

$${\displaystyle \frac{\mathrm{d}{\omega }_r}{\mathrm{d}t}}={\displaystyle \frac{P_t-P_e}{J{\omega }_N}}-{\displaystyle \frac{D}{J}}({\omega }_r-{\omega }_N)$$

(8)

$${\displaystyle \frac{\mathrm{d}\theta }{\mathrm{d}t}}={\omega }_r$$

(9)

where D is the virtual damping, θ is the angle used for pulse width modularization (PWM) signal generation, ω_r is the virtual speed of the generator, J is the virtual inertia, and ω_N is the rated speed and it equals 2πf_N.

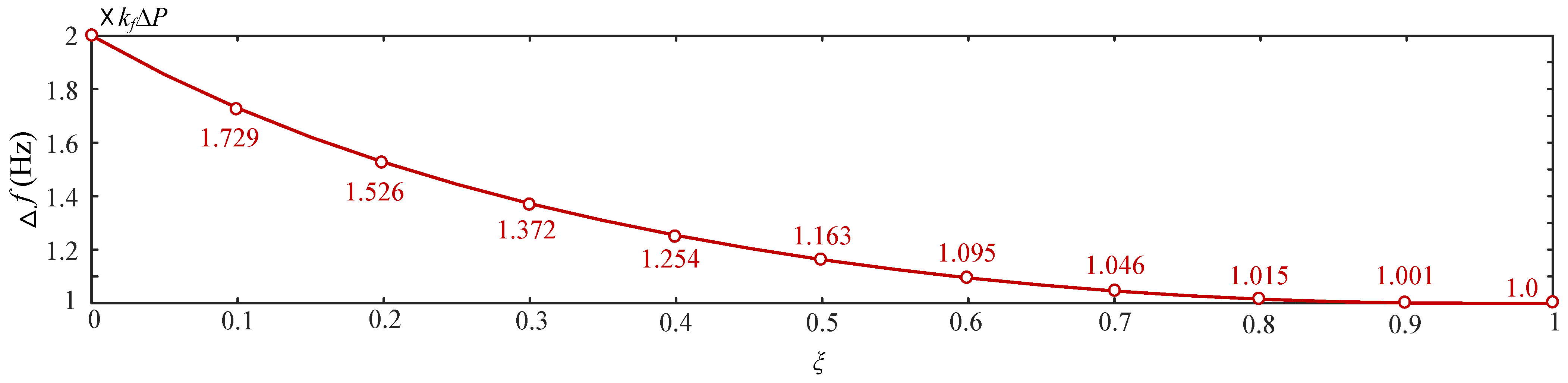
3. Relationship Between Inertia and Frequency Change

To demonstrate the correlation between virtual inertia and frequency variation, it is essential to first develop an analytical model [21,33]. In terms of the frequency regulation loop in Figure 2, which incorporates the f-P droop control and rotating function parts, its transfer function can be depicted as Figure 4, where ΔP is the load variation caused by the large-scale EVs. To obtain the relationship between the frequency change and inertia, assume that ΔP is the input and Δf is the output. The transfer function of the system G(s) can be derived as:

$$G(s)={\displaystyle \frac{\Delta f(s)}{\Delta P(s)}}={\displaystyle \frac{\frac{K}{{\omega }_{N}J}}{s^2+\frac{D}{J}s+\frac{K}{k_f{\omega }_{N}J}}}$$

(10)

where K is the gain factor of the inverter.

In (10), the rated angular speed ω_N, the frequency droop factor k_f, and the gain factor of invert K are determined by the system’s characteristics and remain constant in practical applications. Consequently, the system dynamics are only influenced by the parameters D and J. Furthermore, since our primary focus is on the impact of J on system performance, we assume D to be constant in this study. In theory, by adjusting the value of J in Equation (10), the second-order system can be designed to satisfy the desired performance. For clarity, let us define ω_a as the virtual natural frequency and ξ as the virtual damping ratio of the system as follows:

$${\omega }_a=\sqrt{{\displaystyle \frac{K}{k_f{\omega }_{N}J}}}$$

(11)

$$\xi ={\displaystyle \frac{D}{2}}\sqrt{{\displaystyle \frac{k_f{\omega }_N}{KJ}}}$$

(12)

And (10) can be rewritten as:

$$G(s)={\displaystyle \frac{\Delta f(s)}{\Delta P(s)}}={\displaystyle \frac{k_f{{\omega }_a}^2}{s^2+2\xi {\omega }_{a}s+{{\omega }_a}^2}}$$

(13)

Equation (13) is a standard second-order system. Based on the classic control theory [34], if ξ < 1, the system is undamped, while if ξ > 1, the system is overdamped. Practically, ξ should be well-designed to satisfy different requirements. Specifically, if the grid works stably and the frequency deviations are small, ξ needs to be less than 1 so as to guarantee the dynamics of the system. But, if the grid frequency deviations are large or experience unexpected sudden changes, ξ needs to be larger than 1, endowing the system with high-disturbance suppression capacity. These are the reasons why adaptive parameters can accommodate various operating conditions.

Given that the large-scale EVs need to be charged simultaneously, leading to a sudden load disturbance which can be described as (14):

$$\Delta P(s)={\displaystyle \frac{\Delta P}{s}}$$

(14)

The resulting frequency change can be calculated as:

$$\Delta f(s)=G(s)·{\displaystyle \frac{\Delta P}{s}}={\displaystyle \frac{k_f\Delta P{{\omega }_a}^2}{s^3+2\xi {\omega }_a{s}^2+{{\omega }_a}^{2}s}}$$

(15)

Relying on the inverse Laplace transformation applied to (15), the time-zone step response can be represented as:

$$\Delta f(t)=k_f\Delta P[1-{\displaystyle \frac{e^{-\xi {\omega }_{a}t}}{\sqrt{1-{\xi }^2}}}\sin (\sqrt{1-{\xi }^2}{\omega }_{a}t+\arctan {\displaystyle \frac{\sqrt{1-{\xi }^2}}{\xi }})]$$

(16)

For the sake of clarity, assume that the system is a standard second-order system. Based on [35], the maximum frequency deviation of this kind of system can be described as:

$$\Delta f_{\max }=k_f\Delta P(1+e^{-\xi \pi /\sqrt{1-{\xi }^2}})$$

(17)

where Δf_max is the maximum frequency deviation. And the time (t_max) when the frequency deviation reaches the maximum value is:

$$t_{\max }={\displaystyle \frac{\pi }{\sqrt{1-{\xi }^2}{\omega }_a}}$$

(18)

From (17), it can be noted that the maximum frequency deviation is only related to ξ and ΔP. In terms of ω_a, it influences the response time, and based on (18), the larger ω_a is, the faster the response speed becomes. In this paper, the relationship between Δf_max and ξ needs to be discussed more clearly. To achieve this goal, Figure 5 depicts the relationship between Δf_max and ξ. Intuitively, as ξ increases, the maximum frequency deviation decreases. This indicates that the system approaches overdamped behavior. However, for a second-order system, the response speed decreases in this process. Hence, in practice, if the real-time frequency deviation is significant, ξ should be small enough to ensure that the power grid frequency can be regulated quickly, maintaining stability. If the real-time frequency deviation is small, the stability margin is relatively large. In this case, ξ should be relatively large to slow down the system’s response speed, resulting in smaller frequency fluctuations. These reasons explain why the value of ξ should not remain constant in practice.

By carefully examining Equation (12), it becomes evident that ξ is inversely proportional to the virtual inertia J. Referring to Figure 5, when ξ is small, J is large, but the maximum frequency deviation is also large. Conversely, when ξ is large, J will be small, resulting in a smaller maximum frequency deviation. In practical terms, as the real-time frequency deviation approaches a critical level, J should be reduced to enhance the system’s dynamics. Conversely, if the real-time frequency deviation is small, increasing J can enhance steady-state performance. These guidelines are crucial when designing fuzzy controllers based on the magnitude of frequency deviation.

In addition to considering the magnitude of frequency deviation, the rate of frequency change is another essential factor for designing effective fuzzy controllers. Unlike the magnitude, the influence of frequency change rate is more intuitive. Specifically, when the frequency change rate is substantial, J should also be large to mitigate intense frequency changes that could lead to instability. Conversely, if the frequency change rate is small, J can be designed to be smaller. These guidelines are valuable when designing fuzzy controllers based on the frequency change rate.

4. Proposed Fuzzy Adaptive Inertia-Based VSG Technique

Figure 6 depicts the proposed fuzzy adaptive inertial controller, which is designed to meet the steady-state and dynamic performance demands of a power grid integrated with large-scale electric vehicles. This controller is implemented by carefully crafting fuzzy rules and membership functions to ensure optimal performance. The fuzzy controller consists of several components: input, fuzzification, fuzzy rules and membership functions, a fuzzy inference engine, defuzzification, and output. Each component of the controller is detailed as follows.

4.1. Input

Based on the adaptive control mechanisms presented in Section 3, the proposed fuzzy controller is designed to be a two-dimensional controller. The inputs include frequency deviation Δf and the frequency change rate, which can be represented as:

$$\Delta f=f-f_N$$

(19)

$$f_{der}={\displaystyle \frac{df}{dt}}$$

(20)

where f_der is the maximum frequency change rate. Δf represents the magnitude of frequency deviation. When it is large, the output virtual inertia needs to be small. As for f_der, if it is large, the virtual inertia should be large as well. These need to be well-balanced when designing the fuzzy rules and membership function.

4.2. Fuzzification

Fuzzification serves to transform the real input values into the input format required by the fuzzy inference engine. In this paper, we have defined the fuzzy domain’s range as [−1, 1]. Consequently, the fuzzy inputs for the inference engine, denoted as In1 and In2, can be characterized as follows:

$$In1=K_f·\Delta f$$

(21)

$$In2=K_{fd}·f_{der}$$

(22)

where K_f and K_fd are the scaling coefficients, which are equal to:

$$K_f={\displaystyle \frac{1}{\Delta f_{\max }}}, K_{fd}={\displaystyle \frac{1}{f_{der\_\max }}}$$

(23)

where Δf_max is the maximum frequency deviation, which can be set as the rated frequency, and f_{der_max} is the maximum frequency change rate, which is set as 1000 in this paper.

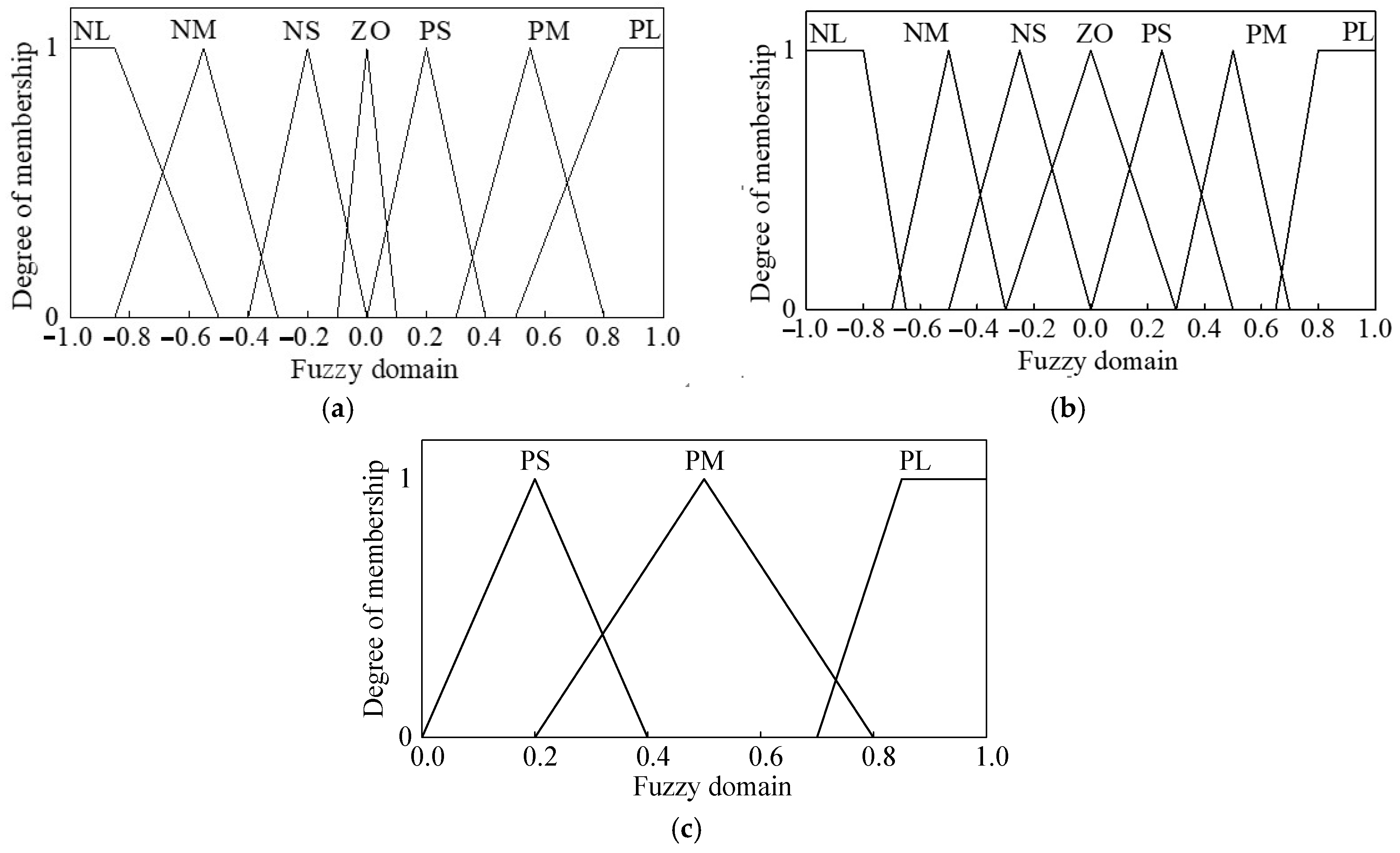
4.3. Fuzzy Rules and Mebership Function

Fuzzy rules are fundamental to the operation of a fuzzy controller, as they define the connections between input and output variables using linguistic expressions. These rules specify how the system should respond under various conditions and typically comprise two elements: the antecedent (the “IF” condition) and the consequent (the “THEN” response) [36]. The antecedent outlines the conditions using linguistic variables and fuzzy sets, while the consequent describes the corresponding actions. Fuzzy rules encapsulate expert knowledge or system behavior in a qualitative and easily comprehensible manner. Membership functions play a vital role in quantifying the degree of membership of an input value to a fuzzy set. They express how input values correspond to the fuzzy sets defined for each variable and are crucial for translating precise input values into fuzzy values that can be interpreted by fuzzy rules. Membership functions evaluate the extent to which an input belongs to a specific fuzzy set, assigning a membership value between 0 and 1. These functions can take various forms, such as triangular, trapezoidal, or Gaussian [37], depending on the application requirements and system characteristics. Practically, the rules for designing the fuzzy rules and membership functions are determined by expert knowledge, engineering experience, and theoretical analysis given in Section 3.

(a)

Fuzzy rules

Given that fuzzy rules and membership functions establish the foundational principles of the proposed adaptive inertia strategy, it is imperative that they are meticulously designed. Prior to formulating specific control rules, it is imperative to establish a set of seven linguistic variables to encapsulate the nuances of fuzzy variables. These variables are designated as follows: positive large (PL), positive medium (PM), positive small (PS), zero (ZO), negative small (NS), negative medium (NM), and negative large (NL). Given the nature of input variables, where both frequency deviation and frequency change rate can exhibit either positive or negative characteristics, the corresponding fuzzy subset encompasses {PL, PM, PS, ZO, NS, NM, NL}. It is noteworthy that the controller’s output will be designed to maintain a value greater than or equal to zero. Consequently, the descriptive subset for the controller’s output comprises {PL, PM, PS}. Within the realm of fuzzy control theory, the pivotal role is played by fuzzy control rules, serving as the foundational mechanism for mapping input signals to their corresponding output signals. Presented in

Table 1. Fuzzy rules.

		In1
		PL	PM	PS	ZO	NS	NM	NL
In2	PL	PM	PL	PL	PL	PL	PL	PM
	PM	PS	PM	PL	PM	PL	PM	PS
	PS	PS	PS	PM	PM	PM	PS	PS
	ZO	ZO	ZO	PM	PM	PM	ZO	ZO
	NS	PS	PS	PM	PM	PM	PS	PS
	NM	PS	PM	PL	PM	PL	PM	PS
	NL	PM	PL	PL	PL	PL	PL	PM

are 49 such rules, which have been derived from a synthesis of mechanisms derived from Section 3.

Utilizing the guidelines provided in Table 1, the formulated fuzzy rules are structured in the classical “if–then” format as delineated below:

If In1 is A and In2 is B, Then Out is C.

If In1 assumes the condition A and In2 assumes the condition B, then the resultant output, denoted as Out, is characterized by condition C. In this context, A, B, and C signify the respective fuzzy description subsets affiliated with each variable, while Out denotes the outcome produced by the fuzzy inference engine. It is imperative to underscore that these rules are inherently grounded in the theoretical framework elucidated in Section 3, thereby encompassing considerations pertaining to both the steady-state and dynamic performance attributes of the system under study.

(b)

Membership function

The membership functions for In1, In2, and Out are depicted in Figure 7. Two critical points should be highlighted. First, the membership functions for the input variables are designed to map normalized values of frequency deviation and power disturbance to corresponding membership degrees within the range of 0 to 1. In contrast, the membership functions for the output variable operate in reverse, ensuring that the output values remain within the range of 0 to 1. Secondly, in Figure 7a, the functions exhibit gentler slopes near ±1 compared to those near zero. This characteristic allows the fuzzy controller to effectively regulate virtual inertia levels with less sensitivity to significant frequency deviations, ensuring system stability. Conversely, in Figure 7b, the functions near ±1 feature steeper slopes, enabling the system to respond swiftly to abrupt changes in frequency change rates, ensuring rapid and agile system adjustments. Through the utilization of the provided membership functions, the virtual inertia value can be dynamically and autonomously adjusted to align with varying levels of frequency deviations and frequency change rates. This capability enables the system to exhibit self-adaptive behaviors, ensuring both steady-state and dynamic characteristics remain in accordance with the prevailing conditions and requirements.

4.4. Fuzzy Inference Engine

In a fuzzy controller, the fuzzy inference engine plays a pivotal role in determining the appropriate control actions or output values based on the fuzzy rules, membership function, and the input signals provided. Here is a more detailed explanation of the function of it [38,39,40]. (1) Processing fuzzy rules: The fuzzy inference engine takes the exact input values and evaluates them against the fuzzy rules defined in the system. These rules express how different combinations of input values relate to specific output actions in linguistic terms. The engine matches the input values to the conditions specified in the rules. (2) Fuzzy logic operations: After matching the input values to the fuzzy rules, the fuzzy inference engine performs fuzzy logic operations to determine the degree of applicability of each rule. These operations take into account the degree to which the input values belong to the linguistic variables and fuzzy sets defined in the rules. (3) Aggregation of rule outputs: The engine combines the results from all applicable rules by considering their degrees of applicability. It aggregates the output actions or control suggestions produced by each rule, taking into account the strengths of these rules in the current context.

4.5. Defuzzification

The output of the fuzzy inference engine undergoes a substantial transformation during the defuzzification process. Instead of being represented as a single numerical value or equation, it takes the form of a fuzzy set, embodying the degrees of membership across various linguistic variables or fuzzy sets. In engineering, the defuzzification step frequently relies on a widely embraced strategy known as centroid defuzzification. This strategy determines the center of gravity or centroid of the fuzzy set, skillfully summarizing the weighted contributions from different linguistic variables or fuzzy sets. This approach is favored in engineering applications for its pronounced intuitive and interpretable characteristics [21,41]:

$$J_d={\displaystyle \frac{{\displaystyle \sum _{i=1}^m{y}_i·u(y_i)}}{{\displaystyle \sum _{i=1}^{m}u(y_i)}}}$$

(24)

where J_d denotes the output obtained from the defuzzification process, and u(y_i) signifies the membership degree associated with a specific value y_i that corresponds to its degree of membership. The variable m represents the total number of membership functions being utilized. Usually, J_d maintains a range between 0 and 1. Consequently, a scaling coefficient becomes essential to fine-tune it to the desired level:

$$J_{dc}=K_J·J_d$$

(25)

where J_dc is the adjusted value for J_d. K_J is the scaling coefficient, which needs to be designed based on the desired maximum adjustment value of inertia. For example, if the desired maximum adjustment value is 4, K_J should be set to 4.

4.6. Output

As shown in Figure 6, the output of the fuzzy controller is the real-time virtual inertia that can be represented as:

$$J=J_{dc}+J_0$$

(26)

where J₀ is the initial value of the virtual inertia. Based on the above analysis, J_dc remains positive. Thus, J₀ should be small in practice. In this study, it is 0.25.

5. Verification Results

In order to evaluate the efficacy of the proposed fuzzy adaptive inertia-based VSG approach, this section presents simulation results. The key parameters characterizing the grid under examination are provided in

Table 2. Main parameters of the grid.

Variable	Description	Value	Unit
PN	Rated active power	10	kVA
QN	Rated reactive power	0	kVA
VN	Rated output voltage	220	V
fN	Rated frequency	50	Hz
VDC	EV DC-bus voltage	800	V
Pch	Test charging power of EVs	10, 12, 17	kVA
Lf	Filter inductance	0.18	H
Cf	Filter capacitance	10	μF
J0	Initial virtual inertia	0.25	kg·m2
kf	Frequency droop coefficient	−2π × 10−4	-
kV	Voltage droop coefficient	0.0001	-
D	Virtual damping	4	-
KJ	Scaling coefficient for output	4	-
Kf	Scaling coefficient for frequency	1/50	-
Kfd	Scaling coefficient for frequency change rate	1/1000	-
K	Inverter gain	1	-
kpv	Gain coefficient of voltage controller	0.5	-
kiv	Integral coefficient of voltage controller	0.002	-

, sourced from a reference [21]. The simulation model was constructed using MATLAB/Simulink 2022b. The simulation configurations are elaborated as follows: Firstly, the simulation replicated the EV charging load by adjusting the resistive load, where a lower resistance corresponds to higher EV charging loads, and conversely, higher resistance results in reduced charging loads. Charging patterns were modeled to peak (small resistance) between 6 p.m. and 9 p.m., reflecting typical residential charging behavior. Conversely, during off-peak (high resistance) hours, such as between 12 a.m. and 6 a.m., most EVs have completed charging, leading to a significant reduction in demand. Secondly, the power grid was represented as an AC source consisting of a DC source and an inverter. The inverter functions to convert DC voltage into AC voltage. Thirdly, the control period was defined as 2 × 10⁻⁶ s. For a comprehensive analysis, this study examined both the steady-state performance and dynamic characteristics of the proposed method, comparing it with traditional VSG employing constant parameters. Furthermore, the control performance of the commonly utilized droop control strategy is presented as a benchmark, illustrating the superior performance of the proposed method.

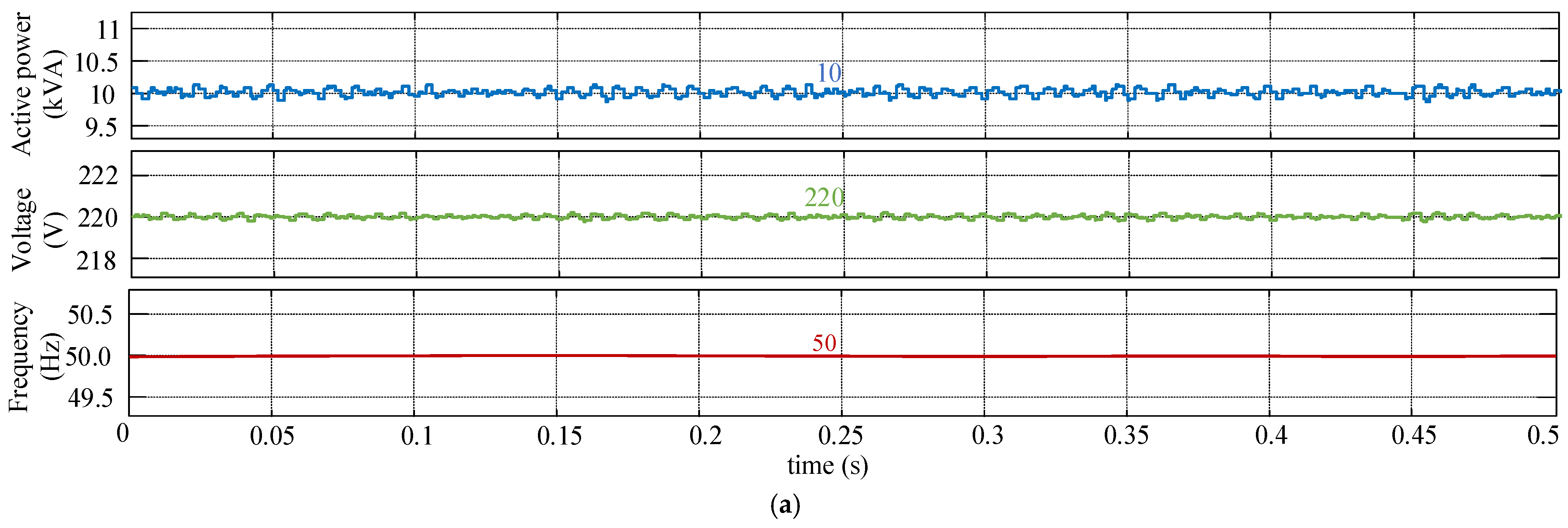
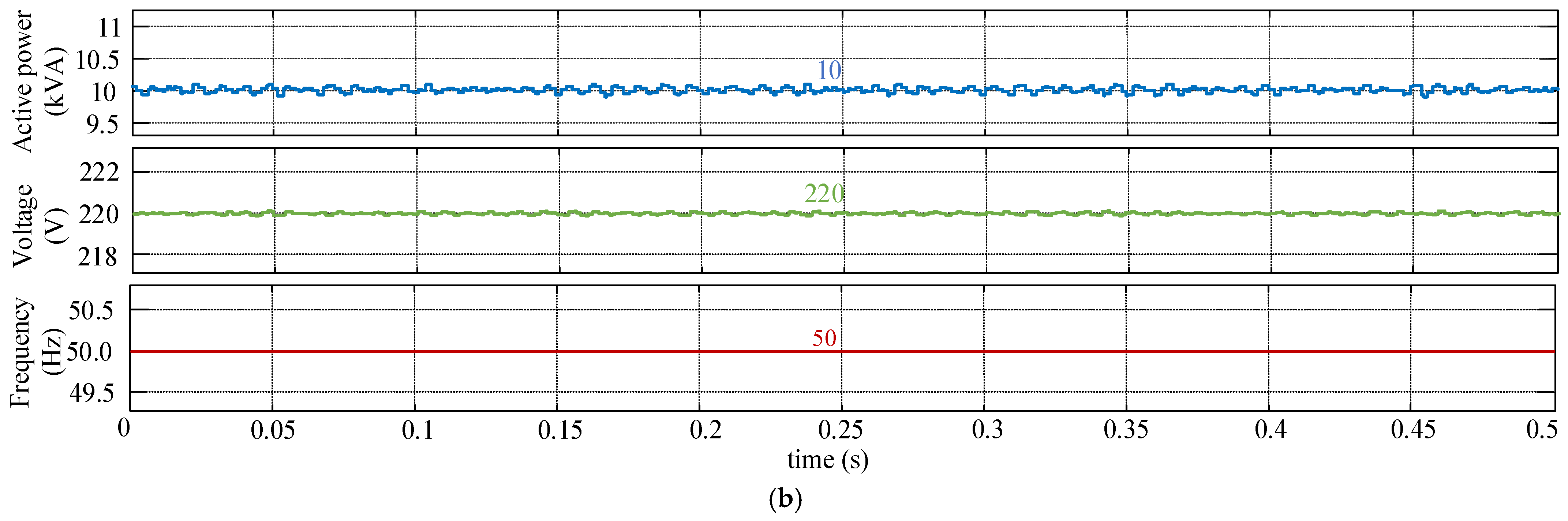
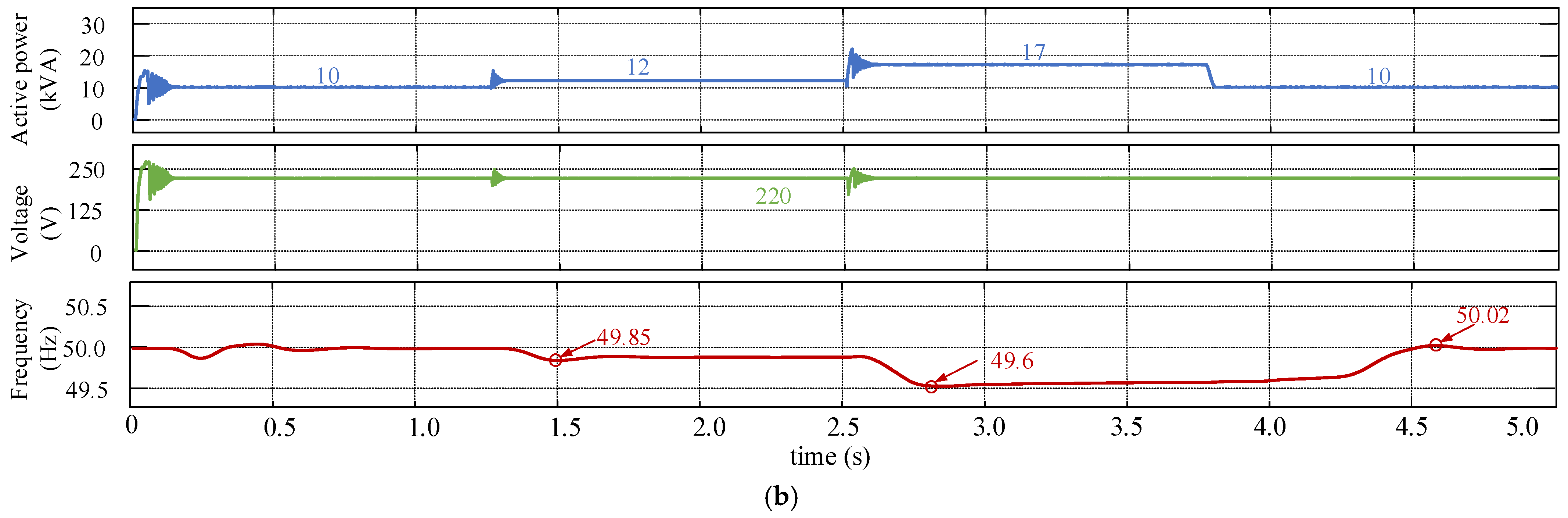
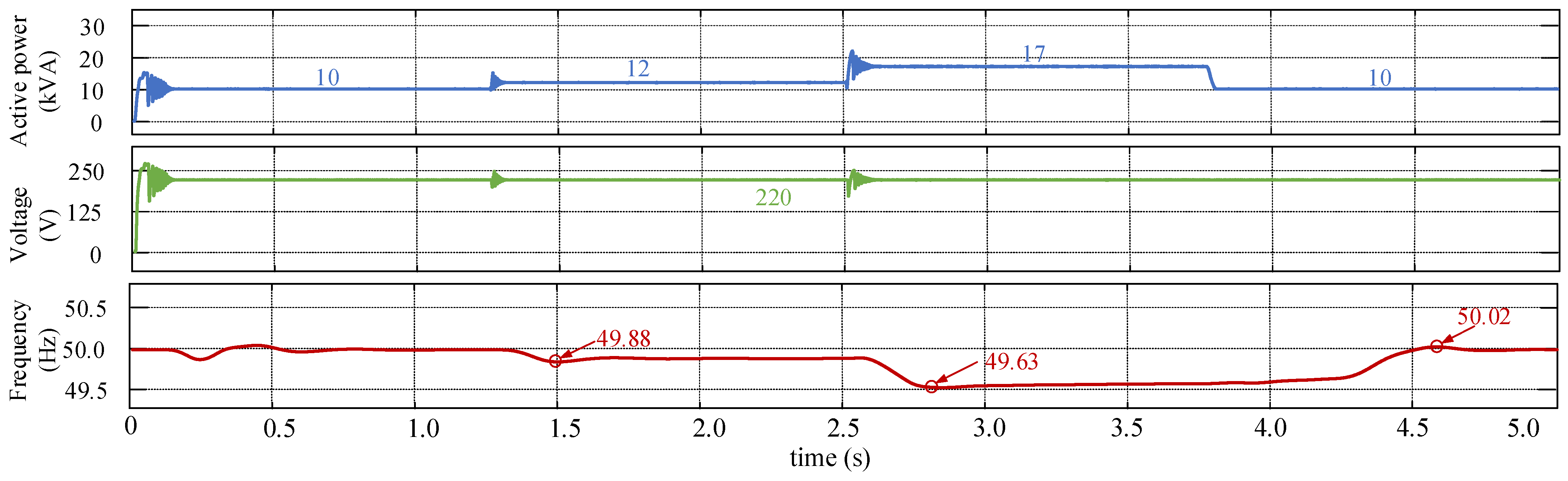
5.1. Simulation Results

(a)

Steady-state performance

Figure 8 shows the control performance of the traditional VSG with constant parameters and the proposed fuzzy adaptive inertia-based VSG method, respectively. First of all, both methods can maintain the power grid frequency at 50 Hz at the rated load. This illustrates that the VSG methods regardless of adaptive parameters can effectively control the power grid. Secondly, by carefully comparing Figure 8a,b, the active power and voltage fluctuations of the traditional method are slightly larger than those of the proposed method. These indicate that the proposed VSG method is able to make the system work stably. It is possible that the constant virtual inertia of the traditional VSG method is not tuned at the best level. In practice, if the higher control performance of the traditional VSG is needed, complex tuning process is required. This is the disadvantage of the traditional method compared to the proposed one.

(b)

Dynamic performance

Figure 9 compares the dynamic performance of the traditional and proposed VSG methods. The testing process was divided into four stages. At the first stage, the power grid worked at 10 kVA. Then, the load became heavy to 12 kVA, simulating that the EV charging demand increased. For the third stage, the load rose to 17 kVA. In this case, large-scale EVs will be charged simultaneously. Finally, the power load returned to the rated level suddenly. Firstly, both methods can maintain the power grid to stabilize at the desired output power. Secondly, when the load rose from 10 kVA to 12 kVA, the maximum frequency change reached 0.2 Hz for the traditional VSG, while it was 0.15 Hz for the proposed method. A similar phenomenon occurred when the load changed from 12 kVA to 17 kVA. The frequency change of the traditional method was about 0.3 Hz, which is about 20% higher than the proposed method. Thirdly, when the load decreased suddenly, the maximum frequency of the traditional method was 50.05 Hz, while it was 50.02 Hz for the proposed method. As shown in Figure 9b, obviously, this happens because the frequency change rate of the proposed method is much lower than that of the traditional method. Thirdly, the overall frequency change rate of the proposed method was lower than the traditional one. For example, between 2.5 s and 4.5 s, the response time of the system in Figure 9b is longer than that in Figure 9a. This represents that the proposed method is able to suppress sharp frequency changes. In summary, the proposed method shows better control performance than the traditional one, thereby being valuable in practice.

This paper focuses on developing a fuzzy inertia-based VSG method for grid frequency regulation, with the output scaling coefficient K_J being a critical parameter. To assess its impact, Figure 10 illustrates results with K_J set to 6, under the same conditions as Figure 9. Three key observations emerge. First, steady-state performance remained consistent, confirming system stability with K_J = 6. Second, during load increases (e.g., 10 kVA to 12 kVA), the frequency deviation reduced to 0.12 Hz compared to 0.15 Hz when K_J = 4, indicating improved dynamic response, a trend that persisted during further load increases to 17 kVA. Third, during load reductions, the frequency deviation remained at 0.02 Hz, identical to that with K_J = 4. These findings suggest that increasing K_J can moderately reduce frequency deviations, enhancing dynamic performance, but with diminishing returns, allowing for flexible tuning based on specific application needs.

(c)

Traditional droop control

The traditional droop control strategy is a well-established method for primary frequency control. However, its performance is often limited in scenarios involving significant frequency disturbances, such as those introduced by large-scale electric vehicle (EV) integration. To illustrate the quantitative differences, the dynamic performance of the droop control method was compared with the proposed fuzzy adaptive inertia-based VSG and traditional VSG methods using key performance metrics, including maximum frequency deviation, frequency recovery time, and frequency fluctuation range. The previous sections show that the dynamic performance of the proposed method shows more significant differences than the steady-state performance compared with the traditional control strategy. Hence, only the dynamic performance of the droop control method is given in Figure 11 in this part. It can be seen that when the load increased from 10 kVA to 12 kVA, the frequency deviation with droop control reached 0.24 Hz, compared to 0.20 Hz for traditional VSG and 0.15 Hz for the proposed method. This indicates that the droop control exhibits a 20% larger deviation than the traditional VSG and a 60% larger deviation than the proposed method. These prove that the droop control has a fast response speed but low frequency change suppression ability. Overall, the proposed method is superior in this aspect.

5.2. Discussion of Results

The results obtained in this study underscore the effectiveness of the proposed fuzzy adaptive inertia-based VSG method compared to traditional VSG and droop control strategies. Traditional VSG methods with fixed inertia and damping parameters, as noted in prior works such as [18], often fail to strike a balance between transient and steady-state performance, particularly during dynamic load changes. In contrast, the proposed method dynamically adjusts virtual inertia and damping through fuzzy control, resulting in notable improvements. For instance, during a load increase from 10 kVA to 12 kVA, the proposed method achieves a frequency deviation of 0.15 Hz, significantly lower than the 0.20 Hz observed with traditional VSG. This advantage persists during larger load transitions, such as from 12 kVA to 17 kVA, where the proposed method reduces frequency deviation by approximately 20% compared to the traditional approach. These results align with prior findings in [21], while offering enhanced adaptability through real-time parameter adjustments.

Compared to droop control, which is valued for its simplicity and rapid response, the proposed method demonstrates superior capability in suppressing frequency deviations during significant disturbances. Droop control, as seen in studies like [13,15], typically exhibits limited suppression capabilities, leading to larger frequency deviations under dynamic conditions. This limitation is evident in our findings, where droop control results in a frequency deviation of 0.24 Hz during a load increase from 10 kVA to 12 kVA, which is 60% higher than the 0.15 Hz achieved by the proposed method. Furthermore, the proposed method excels in maintaining stability during sudden load reductions. For example, when the load decreases from 17 kVA to 10 kVA, the maximum frequency deviation is limited to 0.02 Hz, demonstrating consistent and effective control under varying conditions. This performance surpasses results reported in [25,27], where traditional adaptive VSG designs often face challenges balancing dynamic and steady-state performance.

Additionally, the scalability of the proposed method is highlighted by its performance with varying output scaling coefficients K_J. Increasing K_J reduces frequency deviations further, as demonstrated in Figure 10, where a deviation of 0.12 Hz is observed during a load increase from 10 kVA to 12 kVA when K_J = 6, compared to 0.15 Hz when K_J = 4. This adaptability makes the proposed method versatile for a range of grid conditions, including weak grids or those with high renewable energy penetration.

6. Conclusions

This paper introduces a novel fuzzy adaptive inertia control strategy tailored to virtual synchronous generators (VSGs) for power grids integrating large-scale electric vehicles (EVs). By addressing the challenges of frequency instability and dynamic performance under high EV penetration, the proposed approach offers significant advancements over traditional methods. Key contributions of this study include the following:

• Establishing a robust theoretical framework to elucidate the critical relationship between virtual inertia and grid frequency stability, providing valuable insights for future investigations;
• Developing an innovative fuzzy inertia-based VSG methodology, designed to dynamically adjust to varying grid conditions and EV charging demands, ensuring stability without sacrificing transient performance;
• Incorporating adaptive output scaling factors, enhancing the control system’s responsiveness to both steady-state and dynamic scenarios;
• The empirical results demonstrated the proposed method’s superior performance in mitigating frequency fluctuations, achieving improved stability and responsiveness compared to traditional VSGs and droop control strategies. Specifically, the proposed method reduces the maximum frequency change by 25% during load transitions, with a peak variation of 0.15 Hz compared to 0.2 Hz for the traditional VSG. These findings underscore the practical value of the fuzzy adaptive inertia control strategy in addressing real-world grid challenges posed by the rapid adoption of EVs.

The results of this study provide a solid foundation for addressing the evolving challenges in power systems, paving the way for more sustainable and resilient energy infrastructures. Future work in this direction will contribute to optimizing the integration of EVs and renewable energy into modern grids, ensuring stability, efficiency, and sustainability in power distribution networks. For example, integrating the proposed VSG strategy with renewable energy sources, such as solar and wind power, can further enhance grid resilience while accommodating variable power generation.