Optimization Configuration of Leasing Capacity of Shared-Energy-Storage Systems in Offshore Wind Power Clusters
Abstract
1. Introduction
- (1)
- An overall framework for shared energy storage is established to provide capacity-leasing services and participate in spot market transactions, and the feasibility and superiority of leasing-service models in the current market environment in China are discussed.
- (2)
- To improve the universality and economy of the configuration results of shared energy storage, improved K-means-clustering and robust optimization methods are adopted to depict the uncertainty of the output power of wind power clusters and the clearing prices of spot markets at multiple time scales.
- (3)
- Considering the energy sharing and interactive game between wind farm clusters and shared energy storage, a double-layer robust optimization model for the capacity configuration of shared energy storage is constructed. The upper layer of the optimization model aims to minimize the annual cost of shared energy storage to develop a plan for energy storage capacity. It determines the leasing prices for each time period using leasing demand and leasing income and transmits them to the lower layer of the optimization model. At the same time, the plan for energy storage capacity is modified. The lower level of the optimization model aims to minimize the assessment cost of the wind farm cluster and updates the leasing capacity of each time period by utilizing the leasing prices of each time period and the leasing demand in the worst scenario of the output power of the wind farm cluster.
- (4)
- Multiple scenarios are set up for analysis and comparison to verify the effectiveness and rationality of the optimization results of capacity configuration of shared energy storage.
2. The Proposed Optimization Model
2.1. Uncertainties on Multiple Time Scales
2.2. SESO Model
2.2.1. The Pricing Mechanism of SESO Leasing Services
2.2.2. SESO Model
- (1)
- Power balance relationship of shared energy storage
- (2)
- Constraints on the charging and discharging power of shared energy storage
- (3)
- Constraints on the state of charge of shared energy storage
2.2.3. A Robust Optimization Model for SESO Considering Electricity Price Uncertainty
2.3. WFCO Model
2.3.1. WFCO Model
- (1)
- Constraints on the output power of wind farm clusters
- (2)
- Constraints on the output power of each member of the wind farm clusters
- (3)
- Constraints on the abandoned wind power of a wind farm cluster
2.3.2. A Robust Optimization Model for WFCO Considering Wind Power Uncertainty
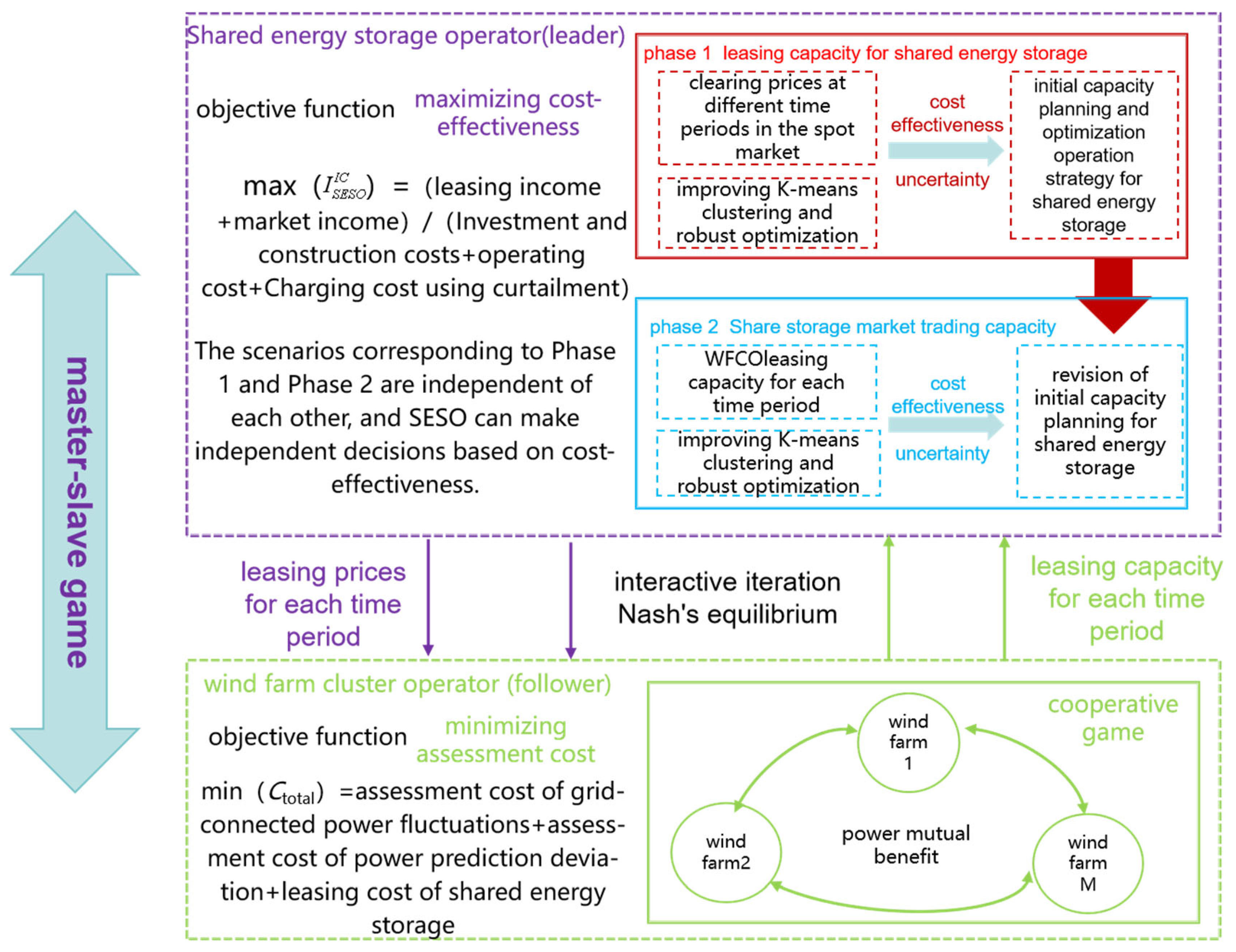
2.4. A Double-Layer Robust Optimization Model for Capacity Configuration in the Master–Slave Game of SESO
- (1)
- Participant: The participants in the master–slave game are wind farm clusters and shared energy storage, with a set of .
- (2)
- Strategy: The strategy for sharing energy storage among actors is the following:
- (3)
- Benefits: The benefits of SESO and WFCO are calculated using Equations (2), (12), and (22), respectively.
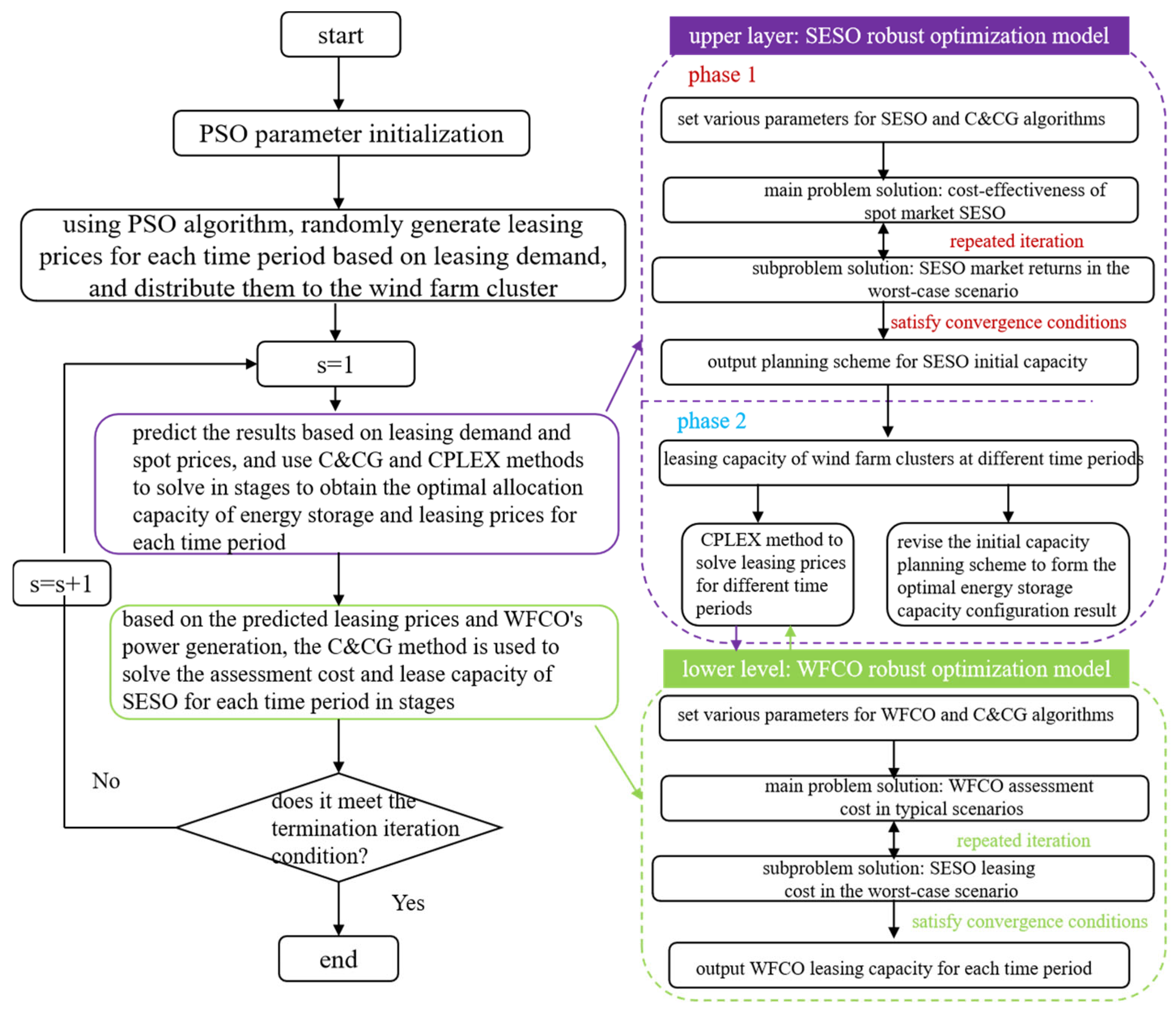
3. The Solving Steps
- (1)
- At the upper level of the two-layer optimization configuration model, multi-stage solutions are carried out based on diverse application scenarios. In the first stage, targeting the arbitrage scenario of price differences in the spot market, the C and CG algorithm is used to split the robust optimization model of shared energy storage into a main problem and a sub problem, achieving iterative solution of upper and lower bounds in two stages, forming an initial planning scheme for shared energy storage in the worst-case scenario of clearing prices in the spot market. In the second stage, aimed at providing leasing service scenarios, the initial planning scheme for shared energy storage formed in the first stage is utilized, combined with the leasing needs of wind farm clusters in different time periods. The CPLEX commercial solver is used to directly solve the leasing prices for shared energy storage in each time period, and the initial planning scheme for shared energy storage is modified to form the optimal capacity configuration for shared energy storage.
- (2)
- At the lower level of the two-layer optimization configuration model, the C and CG algorithm is used to split the robust optimization model of the wind farm cluster into a main problem and a sub problem, achieving two-stage iterative solution of upper and lower bounds, and forming leasing capacity for each time period in the worst output power scenario of the wind farm cluster.
4. Study Cases
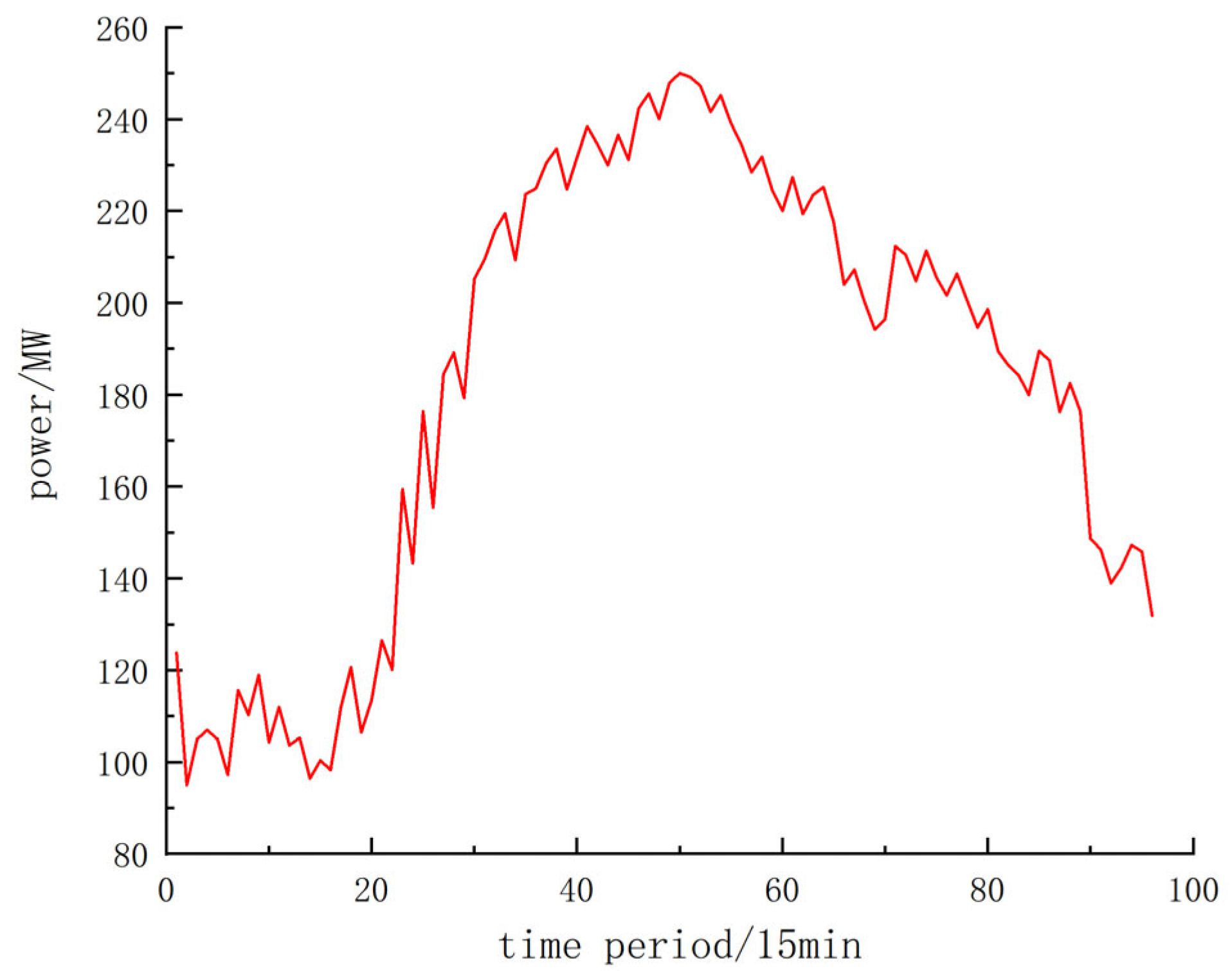
4.1. Data and Scene Settings
4.2. Optimization Results and Analysis
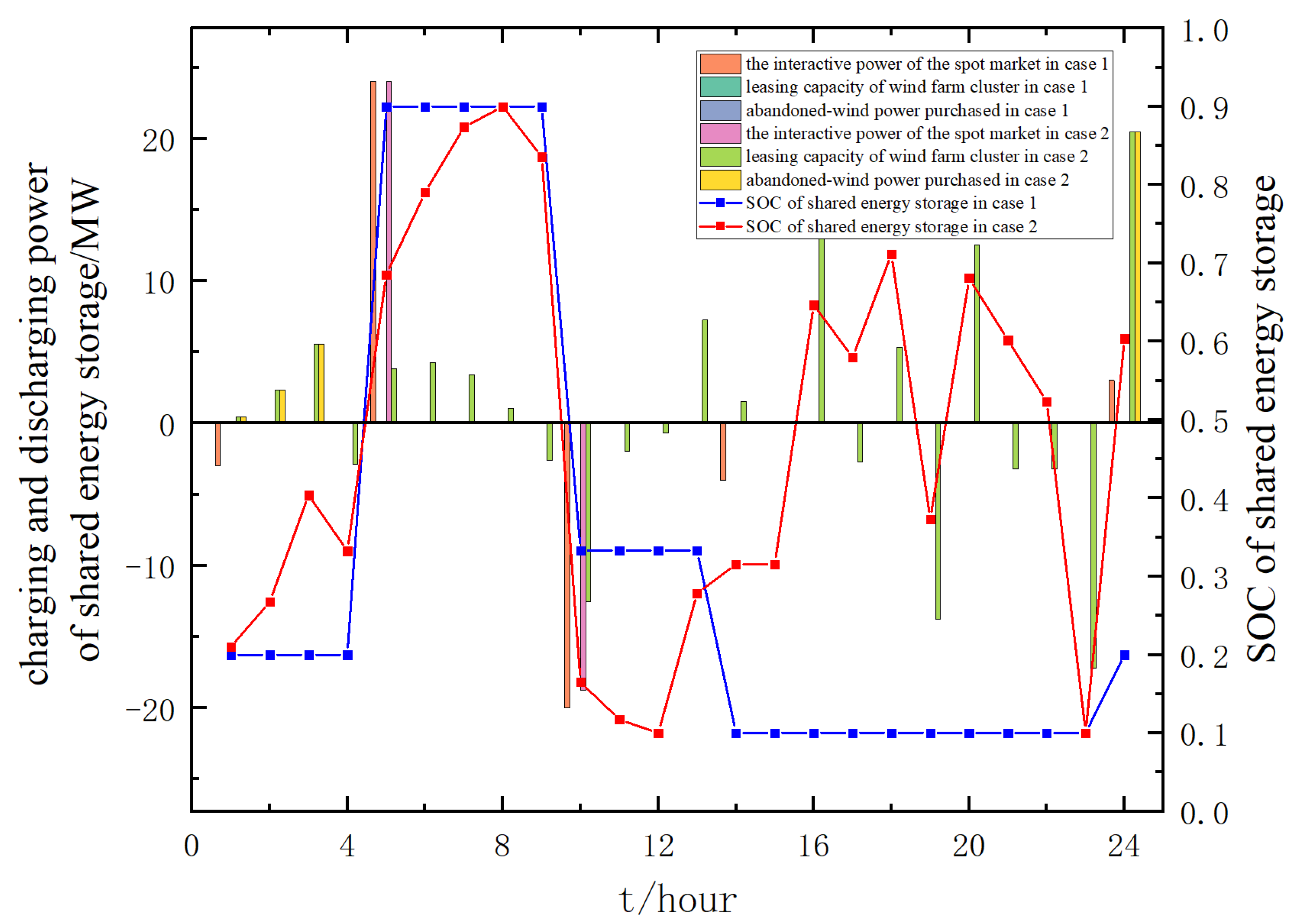
4.2.1. Impact Analysis of Leasing Models for Shared Energy Storage
4.2.2. Impact Analysis of Autonomous Decision-Making on Shared Energy Storage
4.2.3. Impact Analysis of Short-Term Uncertainty
4.2.4. Impact Analysis of Long-Term Uncertainty
5. Conclusions
- (1)
- A reasonable leasing price is the key to ensuring the continuous operation of shared-energy-storage-leasing services. By constructing a master–slave game model to depict the interactive game between the leasing demand of wind farm clusters and the capacity configuration of shared energy storage, the formation process of leasing prices reflects the supply–demand balance on both sides of the game. Compared with the fixed electric price of shared energy storage, the leasing income has increased by $1.46 million, which is conducive to guiding wind farm clusters to lease shared energy storage according to demand.
- (2)
- Fully considering the autonomy of shared energy storage, the setting of prioritizing shared energy storage to meet the leasing needs of wind farm clusters is canceled, and the clearing price of the spot market is included in the formation process of leasing prices. The configured capacity of shared energy storage is increased by 5.06 MWh, and the cost-effectiveness is significantly reduced by 8.6%. This is conducive to improving the independent decision-making ability of shared energy storage in multi coupling scenarios, thereby optimizing the rationality and economy of capacity configuration.
- (3)
- The capacity configuration of shared energy storage tends towards long-term planning, and the impact of uncertainty elements on the configuration results includes both long-term and short-term scales. The uncertainty on a long-term scale takes into account the limitations of optimizing typical scenarios, reducing cost-effectiveness by 8.7%. The uncertainty on a short-term scale takes into account the impact of accommodating extreme scenarios, resulting in more robust configuration results. Taking into account the uncertainty impact of key elements in multiple application scenarios at multiple time scales is beneficial for improving the response capacity and adequacy of shared energy storage in various potential scenarios, ensuring the effectiveness and economy of capacity configuration results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Definition |
| WFCO | Wind farm cluster operator |
| WF | Wind farm |
| SESO | Shared energy storage operator |
| SES | Shared energy storage |
| PG | Power grid |
| K-means | k-means clustering algorithm |
| SOC | State of Charge |
| C&CG | column-and-constraint generation |
| a typical scenario set of uncertainty in the joint clustering of wind power output and spot prices over a long time scale | |
| an uncertainty set | |
| the probability that the uncertainty scenario set of wind power output and spot prices in the joint clustering occurs in the i typical scenario | |
| robust parameters for the output power of the wind farm cluster | |
| robust parameters for the output power of the uncertainty set of spot prices | |
| the actual values of the output power of the wind farm cluster in the time period | |
| the actual values of the spot price in the time period | |
| the period during which shared energy storage provides leasing services to wind farm clusters, in hour, | |
| capacity leasing price for the shared energy storage of the wind farm cluster during the time period | |
| electricity leasing price for shared energy storage of the wind farm cluster in the time period | |
| the annual cost benefit of shared energy storage | |
| annual leasing income for shared energy storage leasing services | |
| the annual market trading income of price differences arbitrage in the spot market for shared energy storage | |
| the annual investment and construction cost of shared energy storage over its entire lifecycle | |
| the annual operating cost discount of shared energy storage | |
| the annual cost of purchasing electricity for wind farm cluster abandonment through shared energy storage | |
| the annual operating days of shared energy storage, and it is necessary to consider the maintenance status of shared energy storage | |
| the leasing capacity of shared energy storage of the wind farm cluster in the time period | |
| the total charging and discharging power of shared energy storage of the wind farm cluster in the time period | |
| the curtailment electricity purchased by shared energy storage from wind farm cluster during the time period | |
| the operator, indicating that at least one of the left and right parameters will be 0 | |
| the online power of the price difference arbitrage of shared energy storage participating in the spot market during the time period | |
| The charging power of the price difference arbitrage of shared energy storage participating in the spot market during the time period | |
| the on-grid electric price for price difference arbitrage of shared energy storage participating in the spot market during the time period | |
| the charging electric price for price difference arbitrage of shared energy storage participating in the spot market during the time period | |
| the unit capacity cost of shared energy storage | |
| the rated capacity of the configured shared energy storage | |
| the planning period for configured shared energy storage | |
| the discount rate | |
| the discounted cost per unit of charging and discharging power for shared energy storage | |
| the charging power of the shared energy storage in the time period | |
| the discharging power of the shared energy storage in the time period | |
| the purchasing price of wind power for shared energy storage during the time period | |
| the charging power of the shared energy storage leasing capacity called by the wind farm cluster during the time period | |
| The discharging power of the shared energy storage leasing capacity called by the wind farm cluster during the time period | |
| the charging power of the shared energy storage purchased from the wind farm cluster during the time period | |
| the state of charge values of shared energy storage during the time period, respectively | |
| the charging efficiency of shared energy storage | |
| the discharging efficiency of shared energy storage | |
| the initial state of charge values for shared energy storage | |
| the state of charge values at the end of one operating cycle (24 h) | |
| the worst-case scenario that considers the uncertainty of clearing prices in the spot market on a short-term scale (with the smallest price difference) |
Appendix A
Calculation of Assessment Costs and Leasing Needs for Wind Farm Clusters
Appendix B
Appendix C



References
- Zou, Y.; Xu, Y.; Li, J. Aggregator-Network Coordinated Peer-to-Peer Multi-Energy Trading via Adaptive Robust Stochastic Optimization. IEEE Trans. Power Syst. 2024, 1–13. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Y.; Li, Z.; Jiang, T.; Li, X. Two-stage robust operation of electricity-gas-heat integrated multi-energy microgrids considering heterogeneous uncertainties. Appl. Energy 2024, 371, 123690. [Google Scholar] [CrossRef]
- Wang, Z.; Ren, Y.; Meng, Q. A cooperative game-based strategy for the optimal operation of ELectricity-thermal-gas synergy in integrated energy systems. J. Sol. Energy 2022, 43, 20–29. [Google Scholar]
- Zhang, Z.; Kang, C. Challenges and prospects of constructing new power systems with carbon neutral goals. Proc. CSEE 2022, 42, 2806–2819. [Google Scholar]
- Li, R.; Hu, Y.; Wang, X.; Zhang, B.; Chen, H. Estimating the impacts of a new power system on electricity prices under dual carbon targets. J. Clean. Prod. 2024, 438, 140583. [Google Scholar] [CrossRef]
- Pei, M.; Ye, L.; Luo, Y. Inertia estimation method for new energy power systems considering spatiotemporal correlation of frequency response. Power Syst. Autom. 2024, 1–16. [Google Scholar]
- Si, J.; Wu, X.; Guo, Q. Wind farm group joint shared energy storage two-stage collaborative grid-connection optimization. Power Grid Technol. 2024, 1–18. [Google Scholar]
- Li, X.; Chen, L.; Sun, F.; Hao, Y.; Du, X.; Mei, S. Share or not share, the analysis of energy storage interaction of multiple renewable energy stations based on the evolution game. Renew. Energy 2023, 208, 679–692. [Google Scholar] [CrossRef]
- Song, M.; Meng, J.; Lin, G.; Cai, Y.; Gao, C.; Chen, T.; Xu, H. Applications of shared economy in smart grids: Shared energy storage and transactive energy. Electr. J. 2022, 35, 107128. [Google Scholar] [CrossRef]
- Yan, D.; Chen, Y. Review of shared energy storage business model and pricing mechanism. Power Syst. Autom. 2022, 46, 178–191. [Google Scholar]
- Qiu, W.; Zhou, S.; Yang, Y.; Lv, X.; Lv, T.; Chen, Y.; Huang, Y.; Zhang, K.; Yu, H.; Wang, Y.; et al. Application Prospect, Development Status and Key Technologies of Shared Energy Storage toward Renewable Energy Accommodation Scenario in the Context of China. Energies 2023, 16, 731. [Google Scholar] [CrossRef]
- Liu, L.; Yao, X.; Qi, X.; Han, Y. Low-carbon economy configuration strategy of electro-thermal hybrid shared energy storage in multiple multi-energy microgrids considering power to gas and carbon capture system. J. Clean. Prod. 2023, 428, 139366. [Google Scholar] [CrossRef]
- Xiao, J.W.; Yang, Y.B.; Cui, S.; Wang, Y.W. Cooperative online schedule of interconnected data center microgrids with shared energy storage. Energy 2023, 285, 129522. [Google Scholar] [CrossRef]
- Ma, K.; Yang, J.; Liu, P. Relaying-Assisted Communications for Demand Response in Smart Grid: Cost Modeling, Game Strategies, and Algorithms. IEEE J. Sel. Areas Commun. 2020, 38, 48–60. [Google Scholar] [CrossRef]
- Ma, K.; Yu, Y.; Yang, B.; Yang, J. Demand-Side Energy Management Considering Price Oscillations for Residential Building Heating and Ventilation Systems. IEEE Trans. Ind. Inform. 2019, 15, 4742–4752. [Google Scholar] [CrossRef]
- Chen, G.; Kuang, R.; Li, W.; Cui, K.; Fu, D.; Yang, Z.; Liu, Z.; Huang, H.; Yu, M.; Shen, Y. Numerical study on efficiency and robustness of wave energy converter-power take-off system for compressed air energy storage. Renew. Energy 2024, 232, 121080. [Google Scholar] [CrossRef]
- Li, L.; Sun, Y.; Han, Y.; Chen, W. Seasonal hydrogen energy storage sizing: Two-stage economic-safety optimization for integrated energy systems in northwest China. iScience 2024, 27, 110691. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, D.; Hu, J.; Zou, X.; Kang, Y.; Guerrero, J.M. Inertial PLL of Grid-connected Converter for Fast Frequency Support. CSEE J. Power Energy Syst. 2023, 9, 1594–1599. [Google Scholar]
- Meng, Q.; Tong, X.; Hussain, S.; Luo, F.; Zhou, F.; Liu, L.; He, Y.; Jin, X.; Li, B. Revolutionizing photovoltaic consumption and electric vehicle charging: A novel approach for residentialmdistribution systems. IET Gener. Transm. Distrib. 2024, 18, 2822–2833. [Google Scholar] [CrossRef]
- Li, P.; Hu, J.; Qiu, L.; Zhao, Y.; Ghosh, B.K. A Distributed Economic Dispatch Strategy for Power–Water Networks. IEEE Trans. Control Netw. Syst. 2022, 9, 356–366. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Y.; Xiao, Y.; Lan, X. Optimized configuration and operation model and economic analysis of shared energy storage based on master-slave game considering load characteristics of PV communities. J. Energy Storage 2024, 76, 109841. [Google Scholar] [CrossRef]
- Du, X.; Li, X.; Hao, Y.; Chen, L. Sizing of centralized shared energy storage for resilience microgrids with controllable load: A bi-level optimization approach. Front. Energy Res. 2022, 10, 954833. [Google Scholar] [CrossRef]
- Li, L.; Peng, K.; Yang, X.; Liu, K. Coordinated design of multi-stakeholder community energy systems and shared energy storage under uncertain supply and demand: A game theoretical approach. Sustain. Cities Soc. 2024, 100, 105028. [Google Scholar] [CrossRef]
- Han, X.; Li, J.; Zhang, Z. Dynamic game optimization control for shared energy storage in multiple application scenarios considering energy storage economy. Appl. Energy 2023, 350, 121801. [Google Scholar] [CrossRef]
- Liu, F.; Li, F.; Zhang, G. Optimization configuration of energy storage power stations in wind power gathering areas considering cycle life and operational strategies. Power Syst. Prot. Control 2023, 51, 127–139. [Google Scholar]
- Ju, Y.; Liu, W.; Zhang, Z.; Zhang, R. Distributed Three-Phase Power Flow for AC/DC Hybrid Networked Microgrids Considering Converter Limiting Constraints. IEEE Trans. Smart Grid 2022, 13, 1691–1708. [Google Scholar] [CrossRef]
- Shirkhani, M.; Tavoosi, J.; Danyali, S.; Sarvenoee, A.K.; Abdali, A.; Mohammadzadeh, A.; Zhang, C. A review on microgrid decentralized energy/voltage control structures and methods. Energy Rep. 2023, 10, 368–380. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Zhao, L.; Fu, H.L.; Yeatman, E.; Ding, H.; Chen, L.Q. Ocean wave energy harvesting with high energy density and self-powered monitoring system. Nat. Commun. 2024, 15, 6513. [Google Scholar] [CrossRef]
- Xu, X.; Lin, Z.; Li, X.; Shang, C.; Shen, Q. Multi-objective robust optimisation model for MDVRPLS in refined oil distribution. Int. J. Prod. Res. 2022, 60, 6772–6792. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, D.; Hu, J.; Liu, R.; Zou, X.; Kang, Y. Optimized Design of Demagnetization Control for DFIG-Based Wind Turbines to Enhance Transient Stability During Weak Grid Faults. IEEE Trans. Power Electron. 2024, 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Liao, H.; Zhou, Z.; Ma, X.; Yin, X.; Wang, Z.; Liu, Y.; Lu, Z.; Lv, G. Optimal capacity planning and operation of shared energy storage system for large-scale photovoltaic integrated 5G base stations. Int. J. Electr. Power Energy Syst. 2023, 147, 108816. [Google Scholar] [CrossRef]
- Dai, R.; Charkhgard, H.; Rigterink, F. A robust biobjective optimization approach for operating a shared energy storage under price uncertainty. Int. Trans. Oper. Res. 2020, 29, 1627–1658. [Google Scholar] [CrossRef]
- Jinrui, S. Collaborative optimal scheduling of shared energy storage station and building user groups considering demand response and conditional value-at-risk. Electr. Power Syst. Res. 2023, 224, 109769. [Google Scholar]
- Zhang, T.; Wu, Y. Collaborative allocation model and balanced interaction strategy of multi flexible resources in the new power system based on Stackelberg game theory. Renew. Energy 2024, 220, 119714. [Google Scholar]
- Yan, H.; Hou, H.; Deng, M.; Si, L.; Wang, X.; Hu, E.; Zhou, R. Stackelberg game theory based model to guide users’ energy use behavior, with the consideration of flexible resources and consumer psychology, for an integrated energy system. Energy 2024, 288, 129806. [Google Scholar] [CrossRef]
- Rehman, U.N.; Uzair, M.; Allauddin, U. An optical-energy model for optimizing the geometrical layout of solar photovoltaic arrays in a constrained field. Renew. Energy 2020, 14, 55–65. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H.; Song, J. Deep belief network based k-means cluster approach for short-term wind power forecasting. Energy 2018, 16, 840–852. [Google Scholar] [CrossRef]
- Li, X.; Fang, Z.; Li, F. Game optimization scheduling of distribution network with multi-microgrid rental shared energy storage. Proc. CSEE 2022, 42, 6611–6625. [Google Scholar]
- Lu, Q.; Yang, Y.; Xie, P. A two-stage optimization operation strategy for leasing and sharing energy storage in wind farm clusters. Power Grid Technol. 2024, 48, 1146–1165. [Google Scholar]
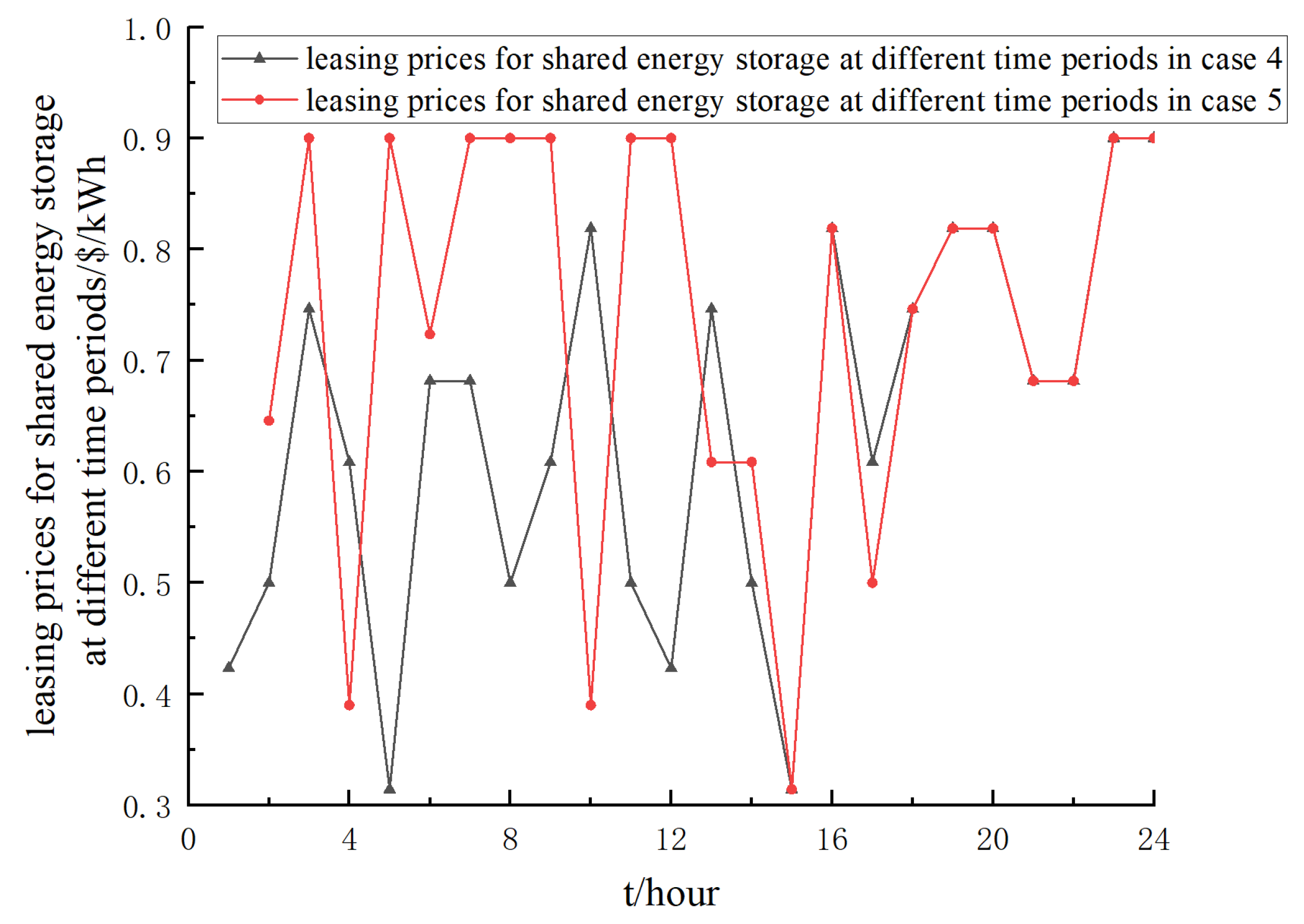
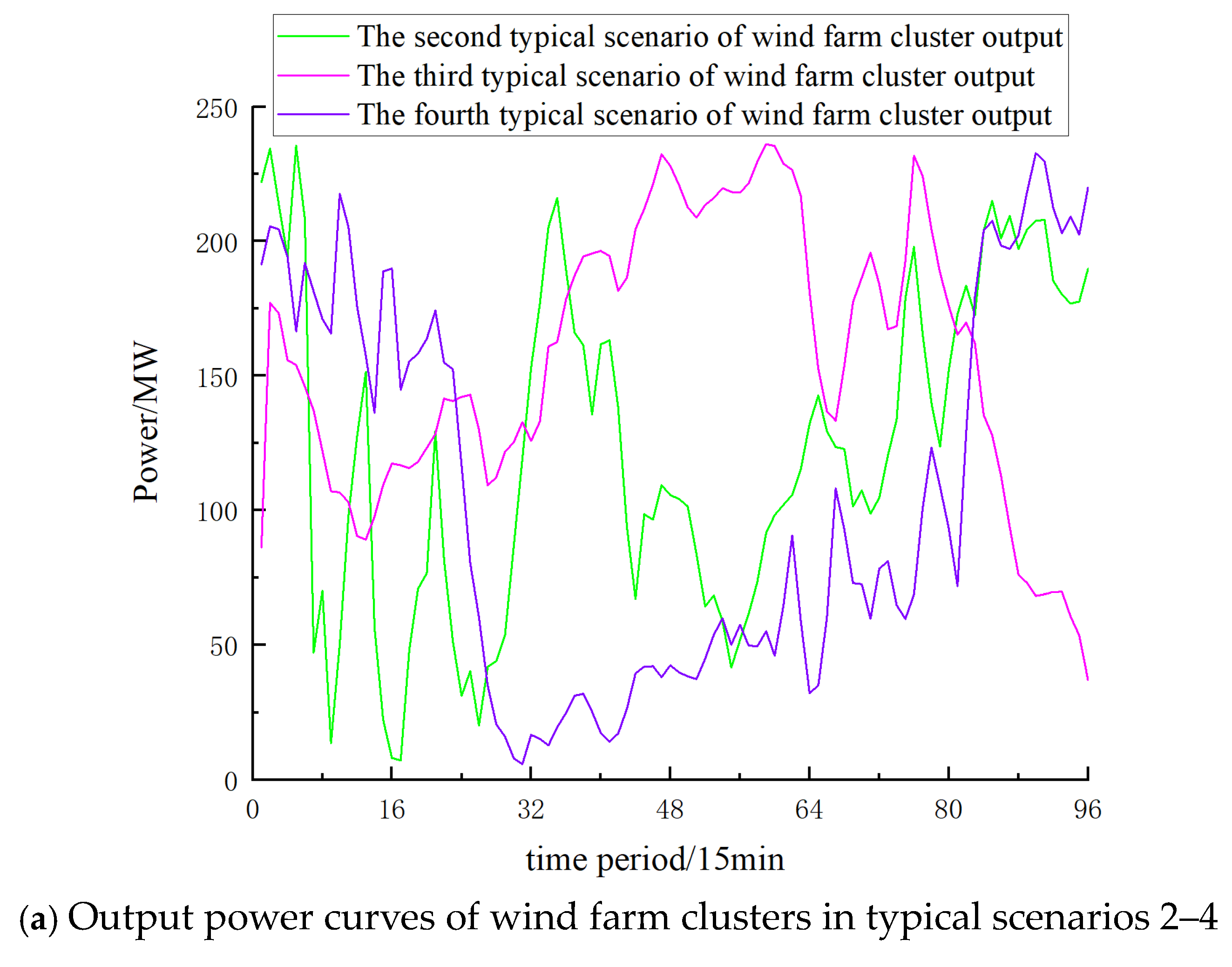
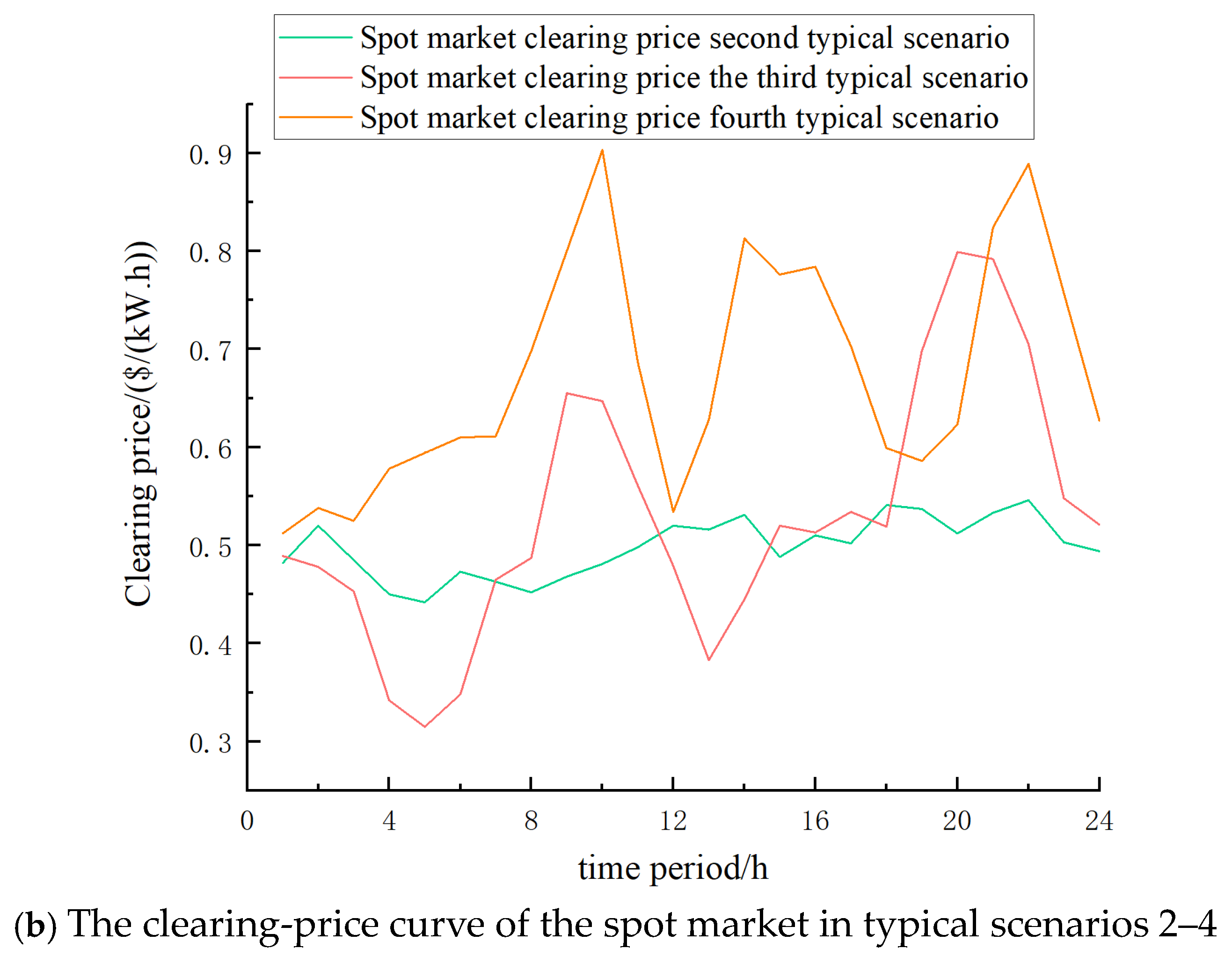
| Case Scenario | Leasing Services | Autonomous Decision-Making | Robust Optimization | Scene Reduction | Reference |
|---|---|---|---|---|---|
| Case1 | × | × | × | × | [31] |
| Case2 | √ | × | × | × | [38] |
| Case3 | √ | √ | × | × | [3,21] |
| Case4 | √ | √ | √ | × | [1,29,32] |
| Case5 | √ | √ | √ | √ | / |
| Case Scenario | The Configuration Results of Shared Energy Storage/MWh | The Cost-Effectiveness of Shared Energy Storage/$ | The Leasing Cost of Wind Power Gathering Stations/104$ | Assessment Costs for Wind Farm Clusters/104$ |
|---|---|---|---|---|
| Case1 | 30 | 0.1172 | / | 0.8988 |
| Case2 | 40.62 | 0.0402 | 0.3824 | 0.3824 |
| Case3 | 45.68 | 0.0368 | 0.3242 | 0.4223 |
| Case4 | 52.47 | 0.0414 | 0.3767 | 0.4756 |
| Case5 | 56.23 | 0.0378 | 0.4300 | 0.5477 |
| Typical Scenarios | Number | Probability |
|---|---|---|
| 1 | 119 | 32.60% |
| 2 | 68 | 18.63% |
| 3 | 94 | 25.75% |
| 4 | 84 | 23.02% |
| Case | The Cost-Effectiveness of Shared Energy Storage |
|---|---|
| 4–1 | 0.3127 |
| 4–2 | 0.2593 |
| Case Scenario | The Configuration Results of Shared Energy Storage/MWh | The Cost-Effectiveness of Shared Energy Storage |
|---|---|---|
| Case4 | 52.47 | 0.2943 |
| Case5–1 | 77.61 | 0.2409 |
| Case5–2 | 46.83 | 0.2845 |
| Case5–3 | 54.77 | 0.2781 |
| Case5 | 56.23 | 0.2686 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, Y.; Wu, J.; Lei, Z. Optimization Configuration of Leasing Capacity of Shared-Energy-Storage Systems in Offshore Wind Power Clusters. Processes 2025, 13, 138. https://doi.org/10.3390/pr13010138
Lou Y, Wu J, Lei Z. Optimization Configuration of Leasing Capacity of Shared-Energy-Storage Systems in Offshore Wind Power Clusters. Processes. 2025; 13(1):138. https://doi.org/10.3390/pr13010138
Chicago/Turabian StyleLou, Yuanyuan, Jiekang Wu, and Zhen Lei. 2025. "Optimization Configuration of Leasing Capacity of Shared-Energy-Storage Systems in Offshore Wind Power Clusters" Processes 13, no. 1: 138. https://doi.org/10.3390/pr13010138
APA StyleLou, Y., Wu, J., & Lei, Z. (2025). Optimization Configuration of Leasing Capacity of Shared-Energy-Storage Systems in Offshore Wind Power Clusters. Processes, 13(1), 138. https://doi.org/10.3390/pr13010138






