Tool Wear State Monitoring in Titanium Alloy Milling Based on Wavelet Packet and TTAO-CNN-BiLSTM-AM
Abstract
:1. Introduction
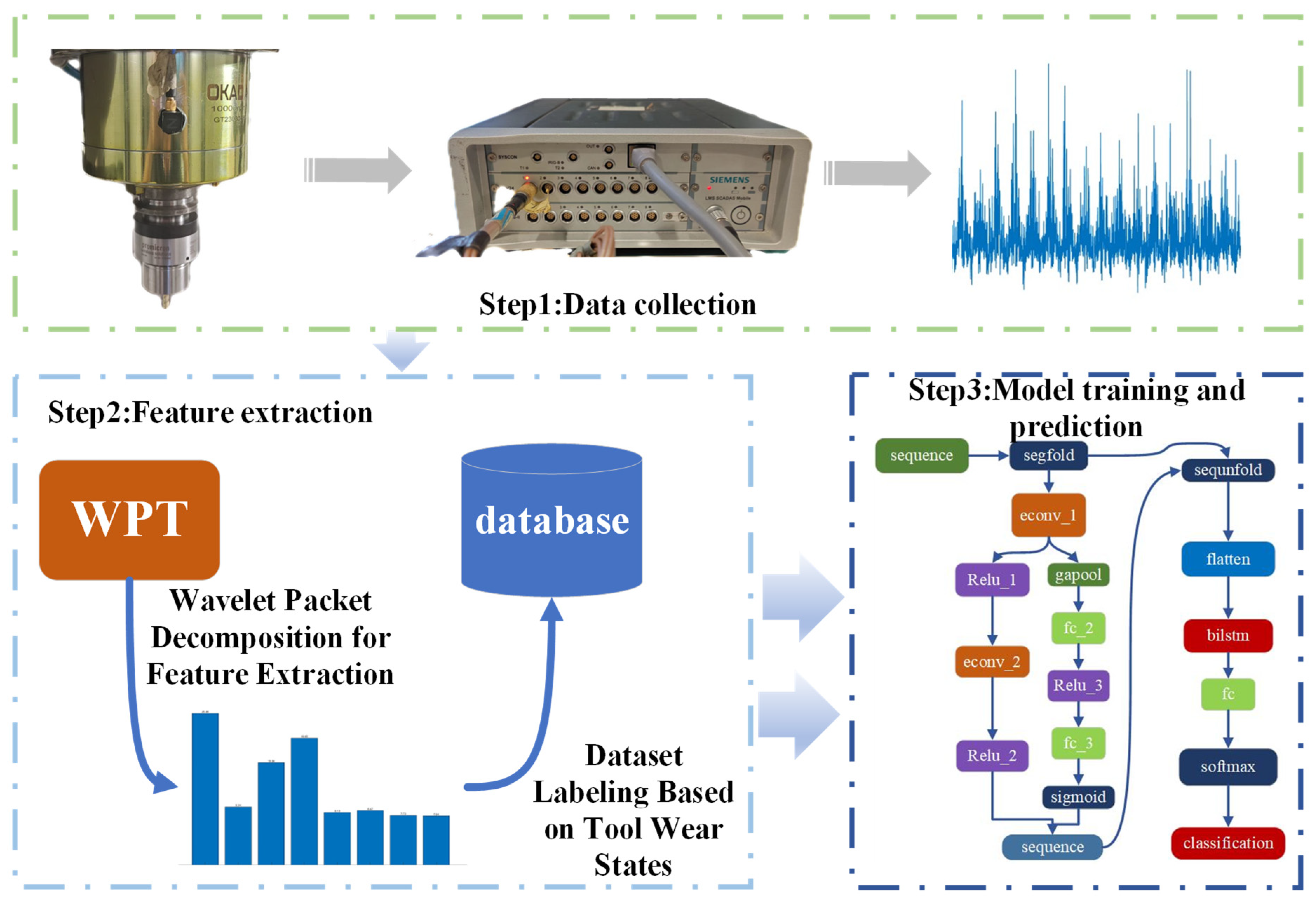
2. Materials and Methods
- (1)
- Data acquisition and preprocessing: Collect vibration signals during the tool cutting process using signal acquisition devices and perform noise reduction and segmentation to ensure data quality.
- (2)
- Feature extraction using WPT: Perform a three-layer WPT on the processed signals to extract energy distribution features.
- (3)
- Model training and classification prediction: Based on the eight extracted features from each signal group, divide the dataset into training and testing sets. Use the TTAO-CNN-BiLSTM-AM model to perform classification prediction and achieve fault type recognition.
2.1. Data Acquisition
2.2. Data Processing
2.3. The Proposed Improved Method
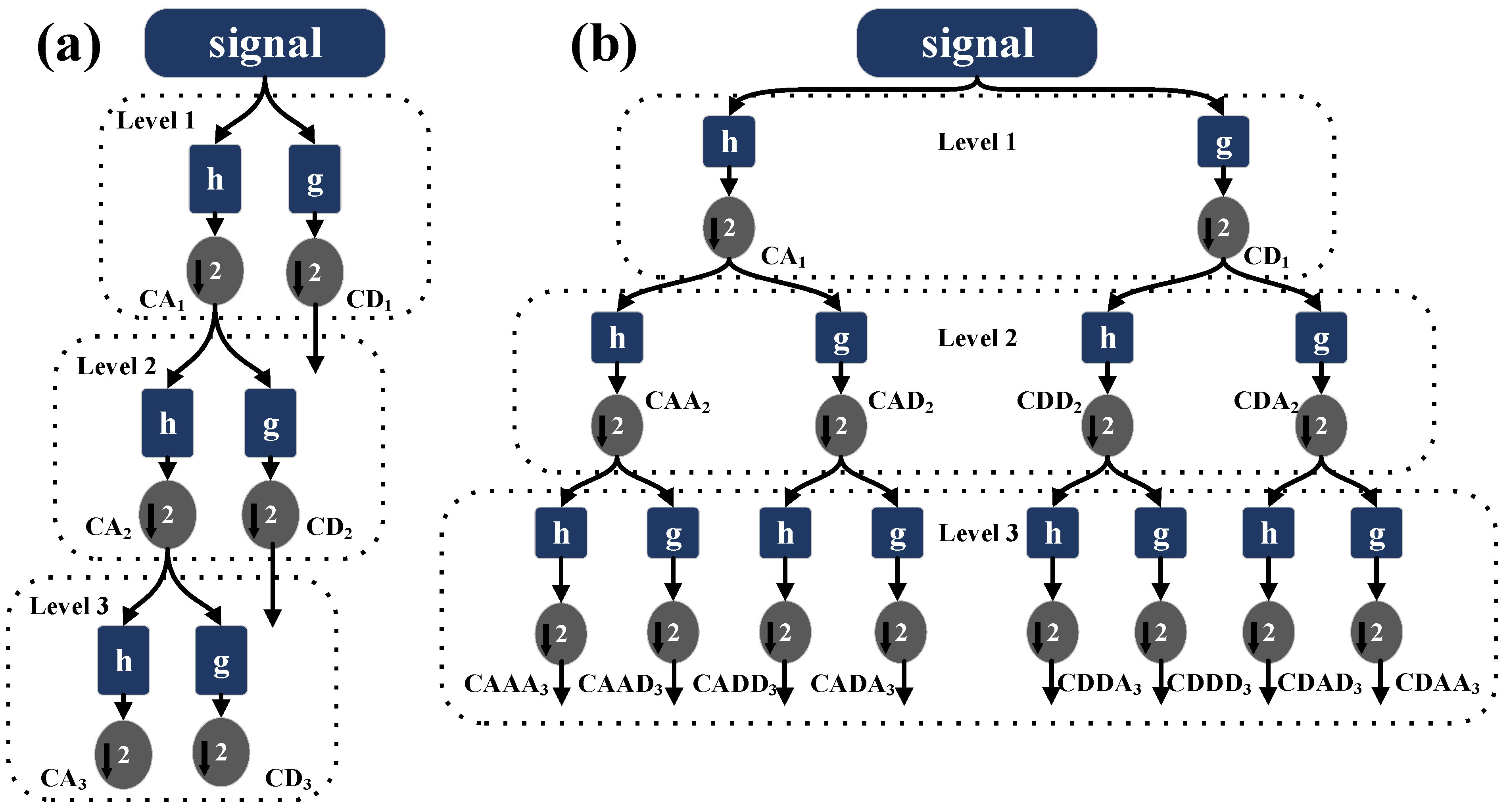
2.3.1. Multi-Scale Feature Extraction of Vibration Signals Based on Wavelet Packet Transform
- (1)
- Initial wear (a): In the first set of subfigures, the amplitude–frequency plots exhibit relatively lower amplitude peaks across all nodes. The frequency components seem to be distributed within a narrow range between 0 to 600 Hz, suggesting moderate vibration signals typical of early wear conditions.
- (2)
- Normal wear (b): As wear progresses to normal levels, the amplitude peaks increase in certain nodes, notably in Node 0 and Node 3. There is a broader distribution of frequency components, indicating that the mechanical system experiences higher vibrations and potentially a wider range of resonance frequencies.
- (3)
- Rapid wear (c): In the rapid wear stage, there is a significant rise in amplitude, especially in Node 0, where the amplitude exceeds 1.0. The broadening of frequency components across all nodes reflects a substantial increase in vibration intensity, suggesting that the system is undergoing critical wear or failure conditions.
2.3.2. Key Feature Extraction of Tool Wear States
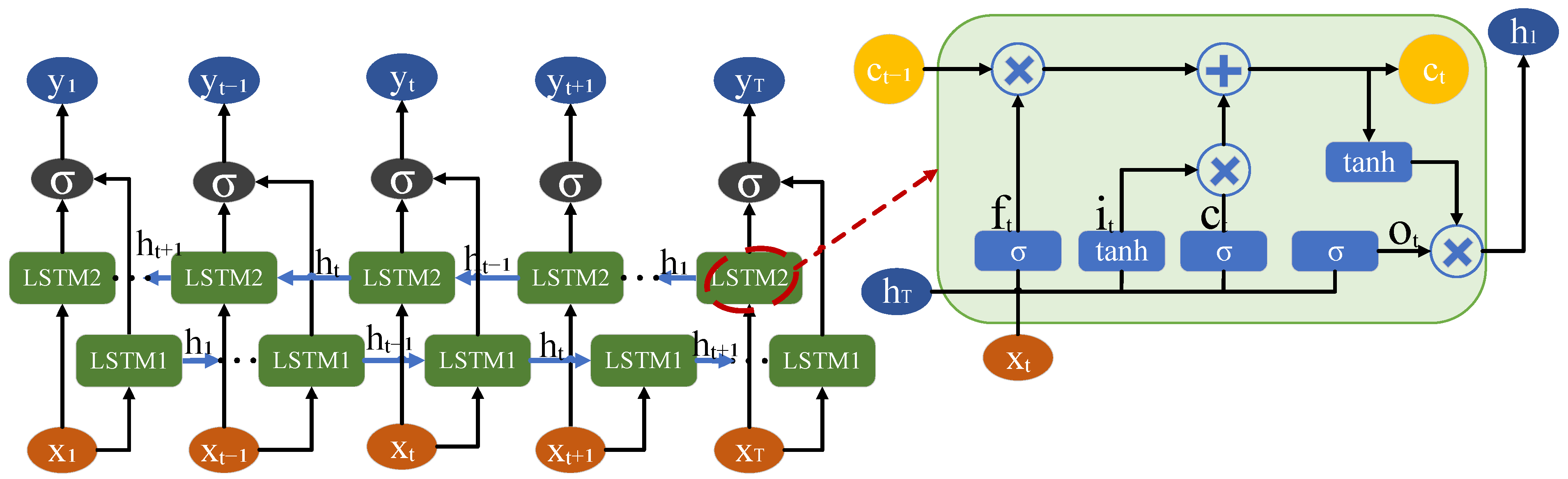
2.3.3. Temporal Feature Extraction in Tool Wear Monitoring
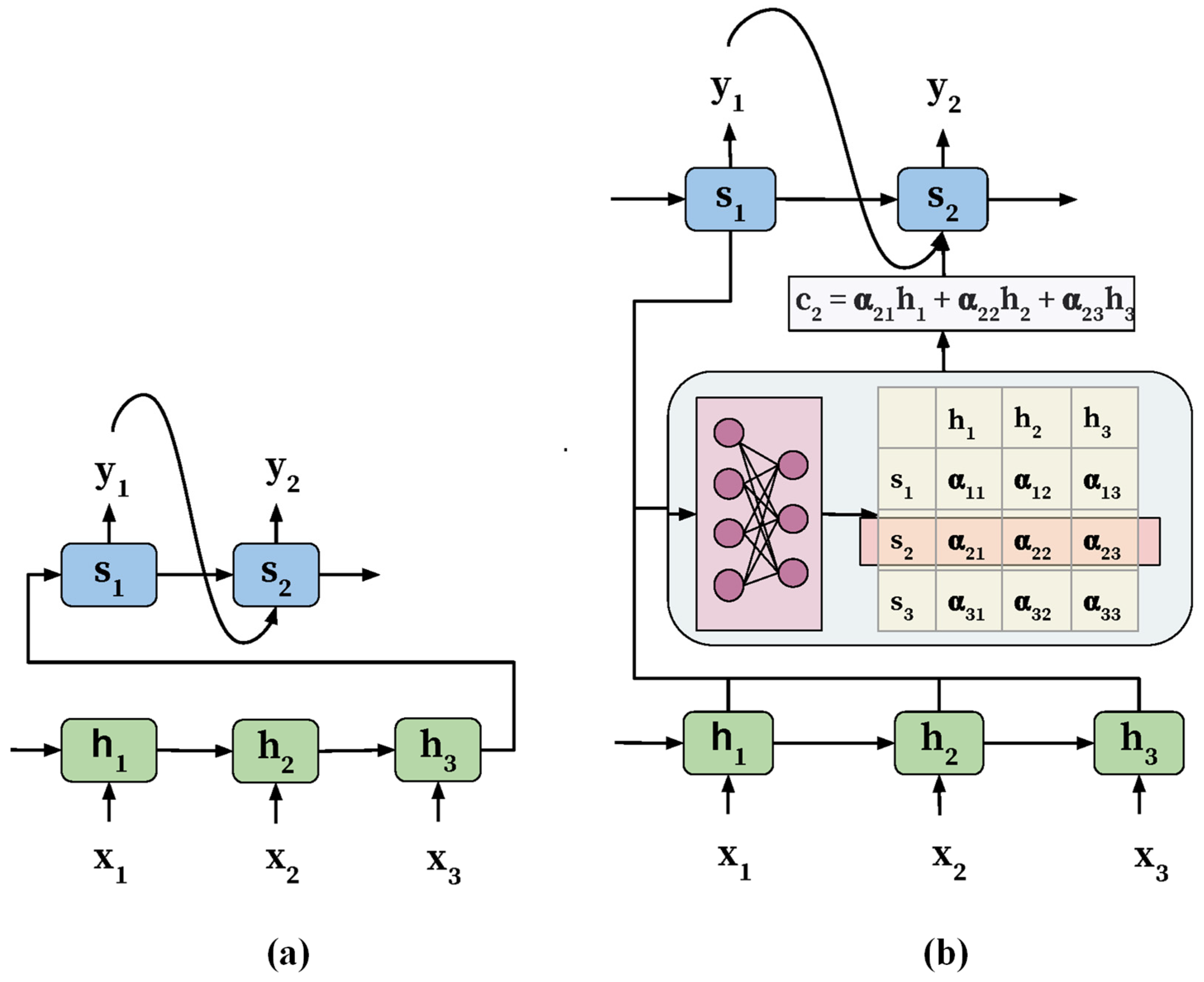
2.3.4. Introduction of AM
2.3.5. TTAO Optimization Algorithm for Multi-Scale Temporal Feature Extraction and Monitoring of Tool Wear
3. Results and Discussion
3.1. Model Training
3.1.1. Experimental Setup
3.1.2. Evaluation Metrics
3.2. Experimental Results and Analysis
3.2.1. Model Experimental Results
3.2.2. Comparison of Detection Results from Different Models
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Updated memory cell | ||
| Forget gate | |||
| VB | Flank wear land width (mm) | Input gate | |
| Sampling frequency (Hz) | Output gate | ||
| CA | Approximation coefficients | Cutting speed (m/min) | |
| CD | Detail coefficients | f | Feed rate (mm/min) |
| h | Low-pass filter coefficients | Cutting depth (mm) | |
| g | High-pass filter coefficients | Y | Output signal or prediction vector |
| n | Number of decomposition levels | Time interval | |
| Scaling function (low-frequency component) | Abbreviations | ||
| Wavelet function (high-frequency component) | AM | Attention Mechanism | |
| k | Down-sampling factor (set to 2 after subsampling) | BiLSTM | Bidirectional Long Short-Term Memory |
| E | Energy of the signal or wavelet coefficients | BP | Backpropagation |
| l | Size of the triangular topology unit | CNN | Convolutional Neural Network |
| X | Candidate solution or input signal vector | DWT | Discrete Wavelet Transform |
| Best solution in the current population | FN | False Negative | |
| Randomly selected solution from the population | FP | False Positive | |
| dir1 | First directional vector in TTAO | FPR | False Positive Rate |
| dir2 | Second directional vector in TTAO | MSE | Mean Squared Error |
| Directional angle | ROC | Receiver Operating Characteristic | |
| α | Aggregation range | RUC | Receiver Utility Curve |
| t | Current iteration number or time step | TCM | Tool Condition Monitoring |
| T | Total number of iterations | TN | True Negative |
| UB | Upper bound of the search space | TP | True Positive |
| LB | Lower bound of the search space | TPR | True Positive Rate |
| F | Fitness function value | TTAO | Triangulation Topology Aggregation Op-timizer |
| Candidate memory cell | WPT | Wavelet Packet Transform | |
References
- Wang, Q.; Chen, X.; An, Q.; Chen, M.; Guo, H.; He, Y. Research on cutting performance and tool life improvement methods of titanium alloy ultra-high speed milling tools. J. Manuf. Process. 2024, 131, 38–51. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, D.; Yao, C. Investigation of the grain refinement mechanism in machining Ti-6Al-4V: Experiments and simulations. J. Manuf. Process. 2023, 94, 479–496. [Google Scholar] [CrossRef]
- Cardoso, G.C.; Grandini, C.R.; Rau, J.V. Comprehensive review of PEO coatings on titanium alloys for biomedical implants. J. Mater. Res. Technol. 2024, 31, 311–328. [Google Scholar] [CrossRef]
- Nasir, V.; Sassani, F. A review on deep learning in machining and tool monitoring: Methods, opportunities, and challenges. Int. J. Adv. Manuf. Technol. 2021, 115, 2683–2709. [Google Scholar] [CrossRef]
- Guo, X.; Lee, C. Preliminary study of phase-shifting strobo-stereoscopy for cutting tool monitoring. J. Manuf. Process. 2021, 64, 1214–1222. [Google Scholar] [CrossRef]
- Fong, K.M.; Wang, X.; Kamaruddin, S.; Ismadi, M.-Z. Investigation on universal tool wear measurement technique using image-based cross-correlation analysis. Measurement 2021, 169, 108489. [Google Scholar] [CrossRef]
- Bergs, T.; Holst, C.; Gupta, P.; Augspurger, T. Digital image processing with deep learning for automated cutting tool wear detection. Procedia Manuf. 2020, 48, 947–958. [Google Scholar] [CrossRef]
- Du, M.; Wang, P.; Wang, J.; Cheng, Z.; Wang, S. Intelligent Turning Tool Monitoring with Neural Network Adaptive Learning. Complexity 2019, 2019, 8431784. [Google Scholar] [CrossRef]
- Rimpault, X.; Chatelain, J.-F.; Klemberg-Sapieha, J.; Balazinski, M. Tool wear and surface quality assessment of CFRP trimming using fractal analyses of the cutting force signals. CIRP J. Manuf. Sci. Technol. 2017, 16, 72–80. [Google Scholar] [CrossRef]
- Tiwari, K.; Shaik, A.; Arunachalam, N. Tool wear prediction in end milling of Ti-6Al-4V through Kalman filter based fusion of texture features and cutting forces. Procedia Manuf. 2018, 26, 1459–1470. [Google Scholar] [CrossRef]
- Klocke, F.; Döbbeler, B.; Pullen, T.; Bergs, T. Acoustic emission signal source separation for a flank wear estimation of drilling tools. Procedia CIRP 2019, 79, 57–62. [Google Scholar] [CrossRef]
- Niaki, F.A.; Michel, M.; Mears, L. State of health monitoring in machining: Extended Kalman filter for tool wear assessment in turning of IN718 hard-to-machine alloy. J. Manuf. Process. 2016, 24, 361–369. [Google Scholar] [CrossRef]
- Cao, X.-C.; Chen, B.-Q.; Yao, B.; He, W.-P. Combining translation-invariant wavelet frames and convolutional neural network for intelligent tool wear state identification. Comput. Ind. 2019, 106, 71–84. [Google Scholar] [CrossRef]
- Upase, R.; Ambhore, N. Experimental investigation of tool wear using vibration signals: An ANN approach. Mater. Today Proc. 2020, 24 Pt 2, 1365–1375. [Google Scholar] [CrossRef]
- Zhou, C.; Guo, K.; Sun, J. An integrated wireless vibration sensing tool holder for milling tool condition monitoring with singularity analysis. Measurement 2021, 174, 109038. [Google Scholar] [CrossRef]
- Yangue, E.; Ye, Z.; Kan, C.; Liu, C. Integrated deep learning-based online layer-wise surface prediction of additive manufacturing. Manuf. Lett. 2023, 35, 760–769. [Google Scholar] [CrossRef]
- Liu, C.; Wang, R.R.; Ho, I.; Kong, Z.J.; Williams, C.; Babu, S.; Joslin, C. Toward online layer-wise surface morphology measurement in additive manufacturing using a deep learning-based approach. J. Intell. Manuf. 2023, 34, 2673–2689. [Google Scholar] [CrossRef]
- Gouarir, A.; Martínez-Arellano, G.; Terrazas, G.; Benardos, P.; Ratchev, S. In-process Tool Wear Prediction System Based on Machine Learning Techniques and Force Analysis. Procedia CIRP 2018, 77, 501–504. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Gao, R.X. Enhanced particle filter for tool wear prediction. J. Manuf. Syst. 2015, 36, 35–45. [Google Scholar] [CrossRef]
- Wang, J.; Yan, J.; Li, C.; Gao, R.X.; Zhao, R. Deep heterogeneous GRU model for predictive analytics in smart manufacturing: Application to tool wear prediction. Comput. Ind. 2019, 111, 1–14. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, J.; Mo, R.; Zhang, X. In-process tool condition forecasting based on a deep learning method. Robot. Comput.—Integr. Manuf. 2020, 64, 101924. [Google Scholar] [CrossRef]
- Shi, C.; Luo, B.; He, S.; Li, K.; Liu, H.; Li, B. Tool Wear Prediction via Multidimensional Stacked Sparse Autoencoders with Feature Fusion. IEEE Trans. Ind. Inform. 2019, 16, 5150–5159. [Google Scholar] [CrossRef]
- Sick, B. On-line and indirect tool wear monitoring in turning with artificial neural networks: A review of more than a decade of research. Mech. Syst. Signal Process. 2002, 16, 487–546. [Google Scholar] [CrossRef]
- Zhu, K.; Wong, Y.S.; Hong, G.S. Wavelet analysis of sensor signals for tool condition monitoring: A review and some new results. Int. J. Mach. Tools Manuf. 2009, 49, 537–553. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, J.; Liu, X.; Ma, J.; Zhang, B. Based on domain adversarial neural network with multiple loss collaborative optimization for milling tool wear state monitoring under different machining conditions. Precis. Eng. 2024, 91, 692–706. [Google Scholar] [CrossRef]
- Mishra, D.; Pattipati, K.R.; Bollas, G.M. Gaussian mixture model for tool condition monitoring. J. Manuf. Process. 2024, 131, 1001–1013. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Z.; Wang, B.; Song, Q.; Wang, H.; Zhang, L. Leveraging artificial intelligence for real-time indirect tool condition monitoring: From theoretical and technological progress to industrial applications. Int. J. Mach. Tools Manuf. 2024, 202, 104209. [Google Scholar] [CrossRef]
- Hao, Y.; Zhu, L.; Wang, J.; Shu, X.; Yong, J.; Xie, Z.; Qin, S.; Pei, X.; Yan, T.; Qin, Q.; et al. Ball-end tool wear monitoring and multi-step forecasting with multi-modal information under variable cutting conditions. J. Manuf. Syst. 2024, 76, 234–258. [Google Scholar] [CrossRef]
- Qiang, B.; Shi, K.; Ren, J.; Shi, Y. Multi-source online transfer learning based on hybrid physics-data model for cross-condition tool health monitoring. J. Manuf. Syst. 2024, 77, 1–17. [Google Scholar] [CrossRef]
- Wen, D.L.W.; Soon, H.G.; Kumar, A.S. Micro-milling digital twin for real-time tool condition monitoring. Manuf. Lett. 2024, 41, 1231–1236. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Cai, L.; Yang, R. Triangulation topology aggregation optimizer: A novel mathematics-based meta-heuristic algorithm for continuous optimization and engineering applications. Expert Syst. Appl. 2023, 238 Pt B, 121744. [Google Scholar] [CrossRef]
- ISO-8688-1/1994; Cranes—Design Principles for Loads and Load Combinations—Part 1: General principles. ISO: Geneva, Switzerland, 2014.
- Zhang, B.; Liu, X.; Yue, C.; Liang, S.Y.; Wang, L. Meta-learning-based approach for tool condition monitoring in multi-condition small sample scenarios. Mech. Syst. Signal Process. 2024, 216, 111444. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, Y.; Jiao, F.; Cui, X.; Zhang, D.; Ren, L.; Zhao, B.; Pang, X. Dynamic milling force model considering vibration and tool flank wear width for monitoring tool states in machining of Ti-6AI-4V. J. Manuf. Process. 2024, 124, 1519–1540. [Google Scholar] [CrossRef]
- Liu, Z.; Lang, Z.-Q.; Gui, Y.; Zhu, Y.-P.; Laalej, H. Digital twin-based anomaly detection for real-time tool condition monitoring in machining. J. Manuf. Syst. 2024, 75, 163–173. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Sun, W.; Xiang, J. Multi-sensor signal fusion for tool wear condition monitoring using denoising transformer auto-encoder Resnet. J. Manuf. Process. 2024, 124, 1054–1064. [Google Scholar] [CrossRef]
- Abadia, J.J.P.; Zabaljauregui, M.C.; Barrenechea, F.L. A meta-learning strategy based on deep ensemble learning for tool condition monitoring of machining processes. Procedia CIRP 2024, 126, 429–434. [Google Scholar] [CrossRef]
- Gao, Z.; Chen, N.; Yang, Y.; Li, L. An innovative multisource multibranch metric ensemble deep transfer learning algorithm for tool wear monitoring. Adv. Eng. Inform. 2024, 62, 102659. [Google Scholar] [CrossRef]






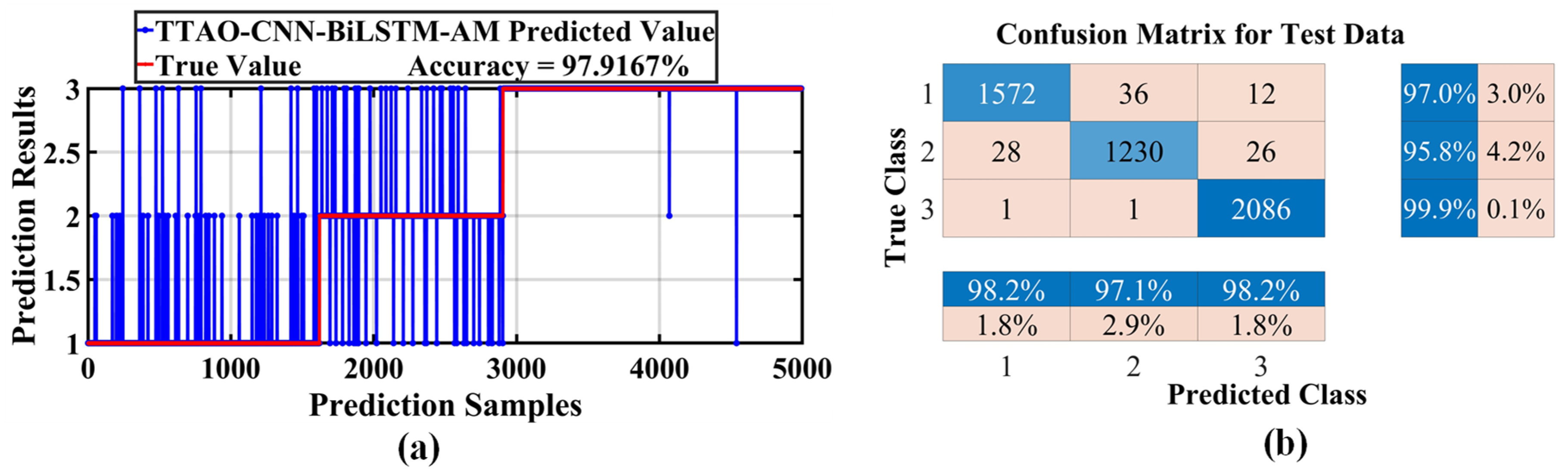
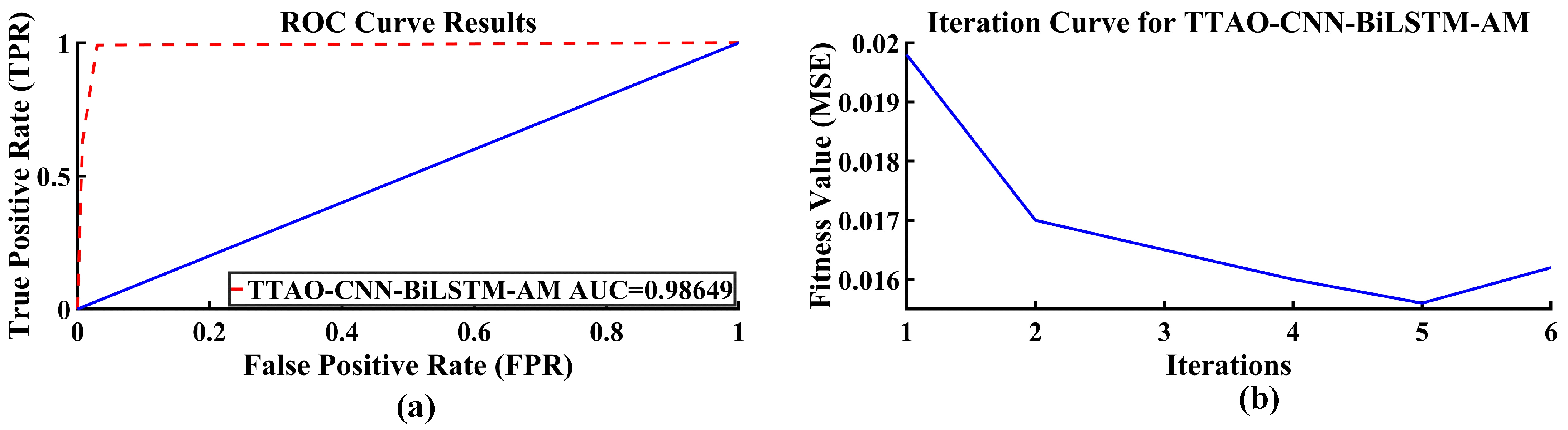
| Dataset | Training Set | Test Set |
|---|---|---|
| 1 | 3780 | 1620 |
| 2 | 2996 | 1284 |
| 3 | 4872 | 2088 |
| Total | 11,648 | 4992 |
| CPU | GPU | Deep Learning Framework | Operating System | Batch Size |
|---|---|---|---|---|
| 12th Gen Intel(R) Core(TM) i5-12600KF 3.70 GHz | Nvidia GeForce RTX 4060 | MATLAB R 2024a | Windows 11 | 64 |
| Model | Number of Feature Sets | Learning Rate | Average Accuracy (%) |
|---|---|---|---|
| BP | 16,640 | 0.001 | 91.428 |
| 1D CNN | 16,640 | 0.001 | 97.262 |
| CNN-BiLSTM-AM | 16,640 | 0.001 | 96.498 |
| TTAO-CNN-BiLSTM-AM | 16,640 | 0.001 | 98.649 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Li, L.; Zhang, Y.; Jiang, Z.; Liu, X. Tool Wear State Monitoring in Titanium Alloy Milling Based on Wavelet Packet and TTAO-CNN-BiLSTM-AM. Processes 2025, 13, 13. https://doi.org/10.3390/pr13010013
Yang Z, Li L, Zhang Y, Jiang Z, Liu X. Tool Wear State Monitoring in Titanium Alloy Milling Based on Wavelet Packet and TTAO-CNN-BiLSTM-AM. Processes. 2025; 13(1):13. https://doi.org/10.3390/pr13010013
Chicago/Turabian StyleYang, Zongshuo, Li Li, Yunfeng Zhang, Zhengquan Jiang, and Xuegang Liu. 2025. "Tool Wear State Monitoring in Titanium Alloy Milling Based on Wavelet Packet and TTAO-CNN-BiLSTM-AM" Processes 13, no. 1: 13. https://doi.org/10.3390/pr13010013
APA StyleYang, Z., Li, L., Zhang, Y., Jiang, Z., & Liu, X. (2025). Tool Wear State Monitoring in Titanium Alloy Milling Based on Wavelet Packet and TTAO-CNN-BiLSTM-AM. Processes, 13(1), 13. https://doi.org/10.3390/pr13010013






