Estimation of Multiple Parameters in Semitransparent Mediums Based on an Improved Grey Wolf Optimization Algorithm
Abstract
1. Introduction
2. GWO Algorithm
2.1. Original GWO Algorithm
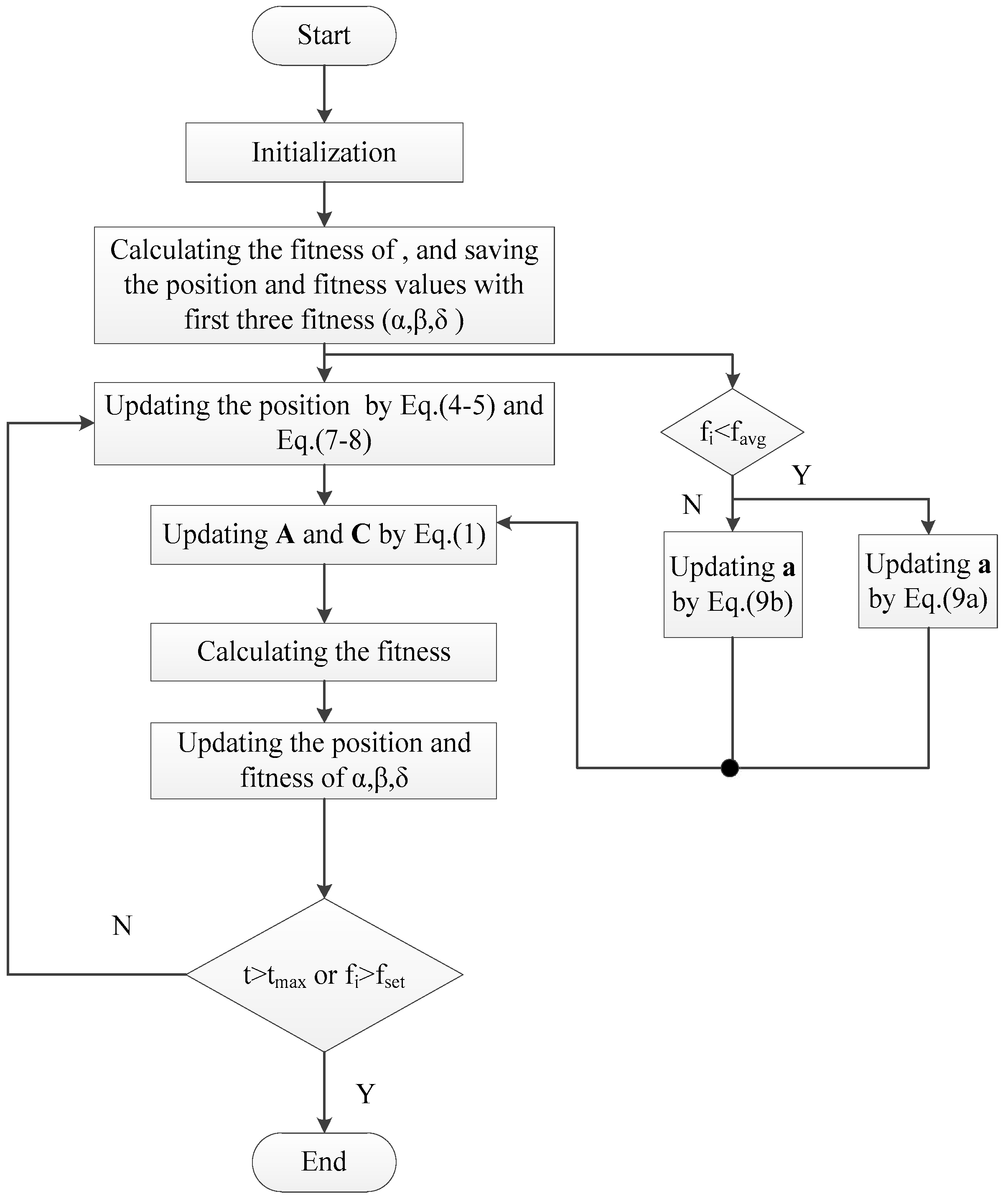
2.2. Improved GWO Algorithm
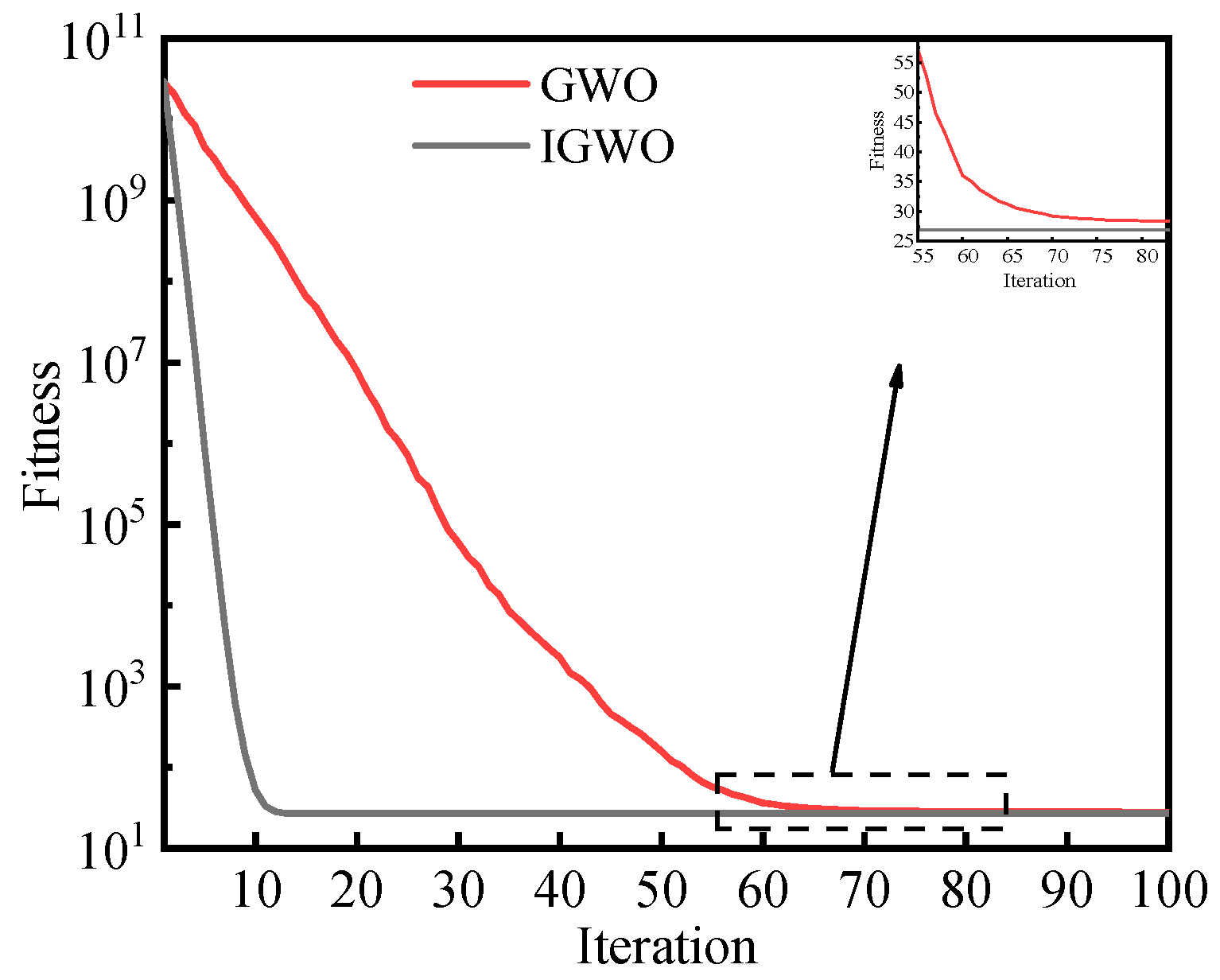
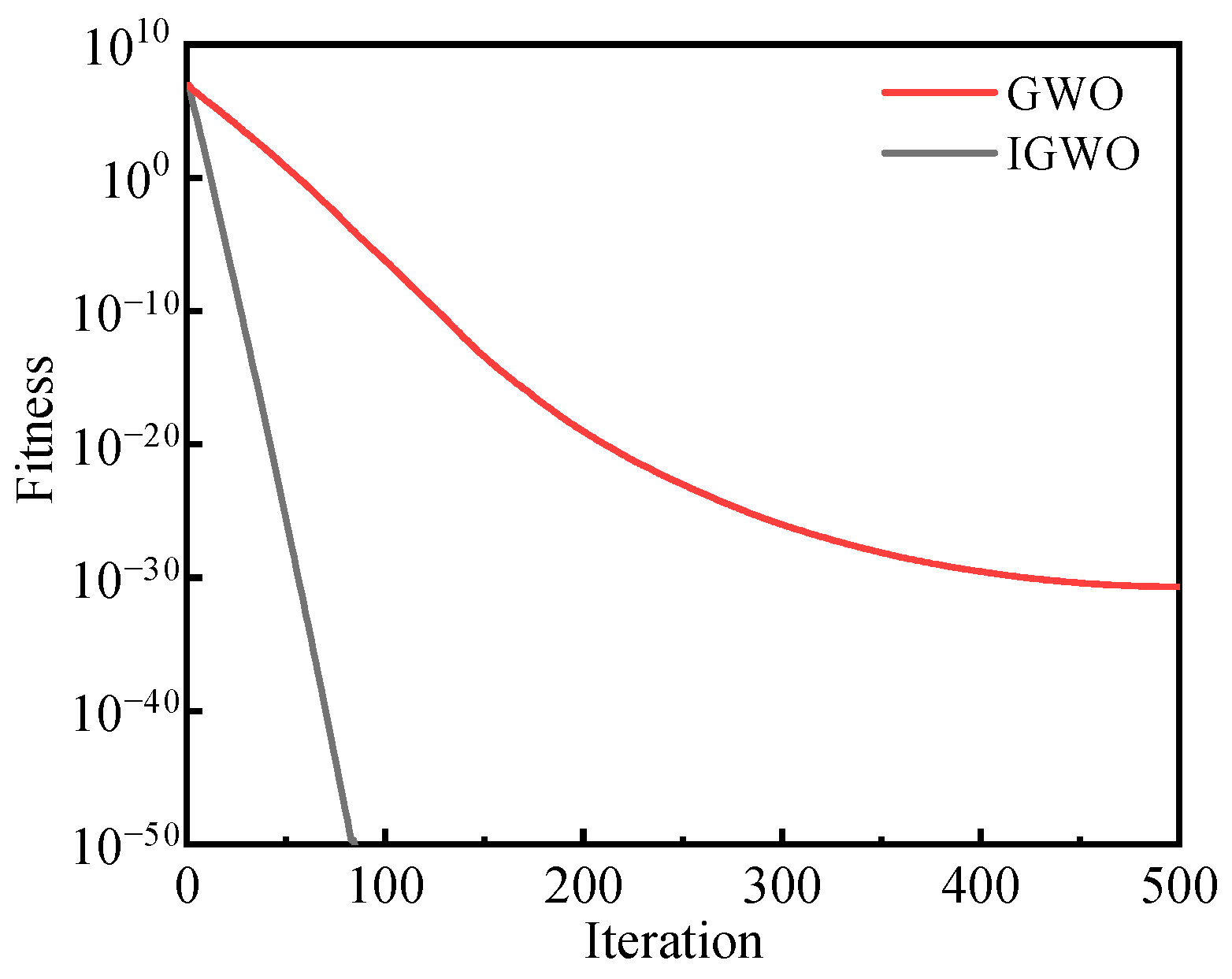
2.3. Performance Test of IGWO Algorithm
3. Results and Discussion
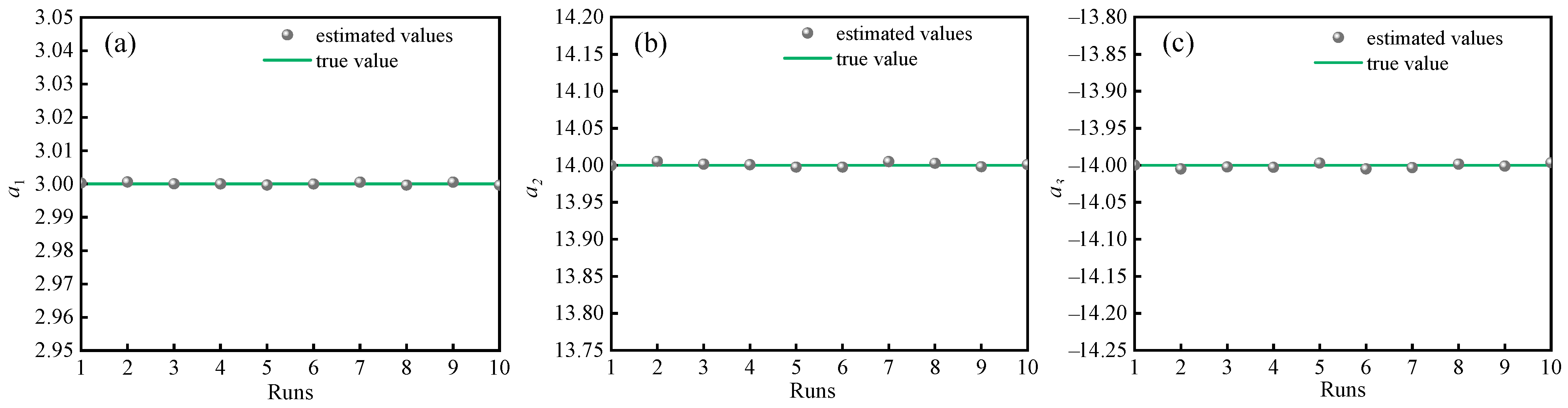
3.1. Inverse Estimation for Source Term Coefficients
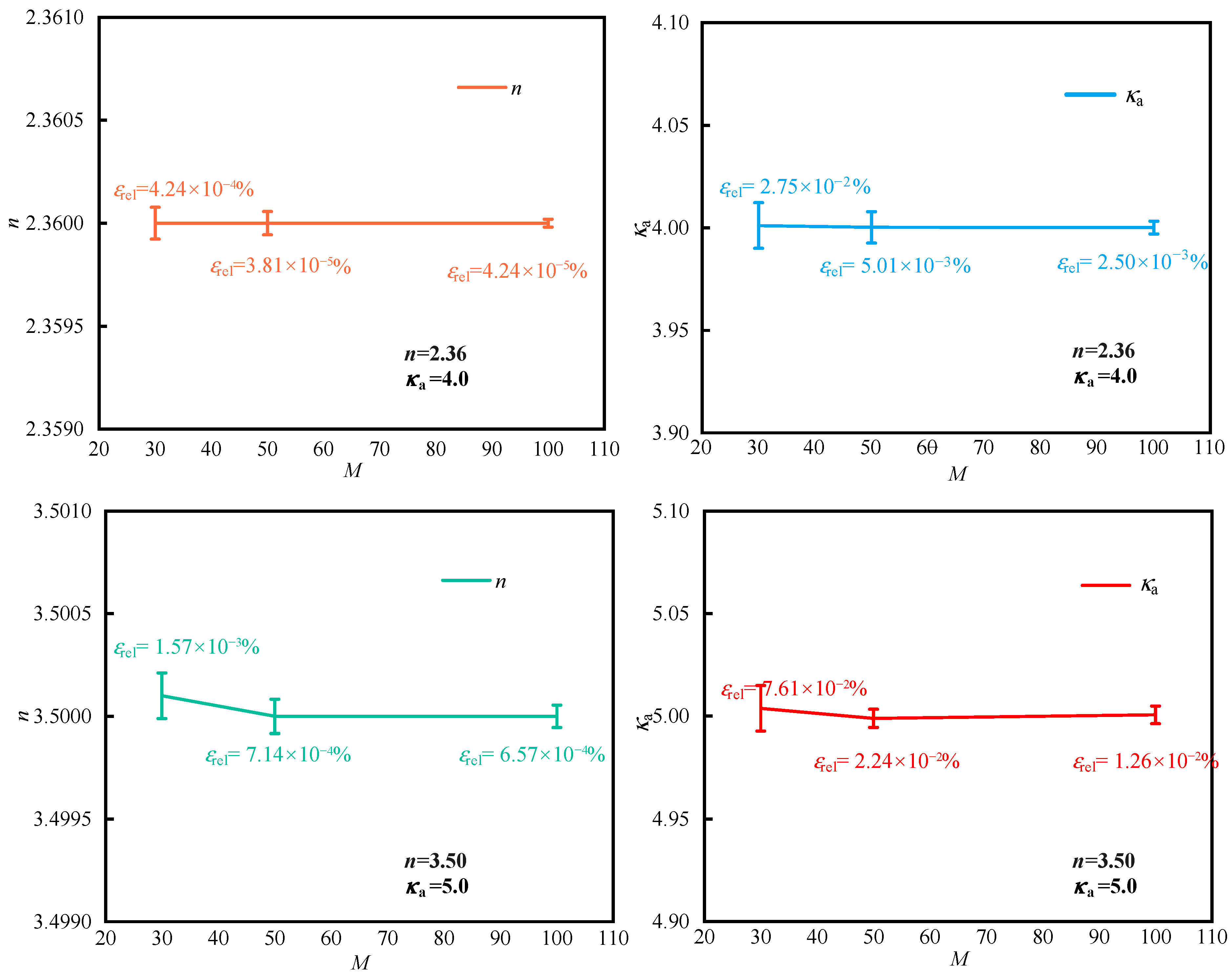
3.2. Simultaneous Inverse Estimation of Refractive Index and Absorption Coefficient
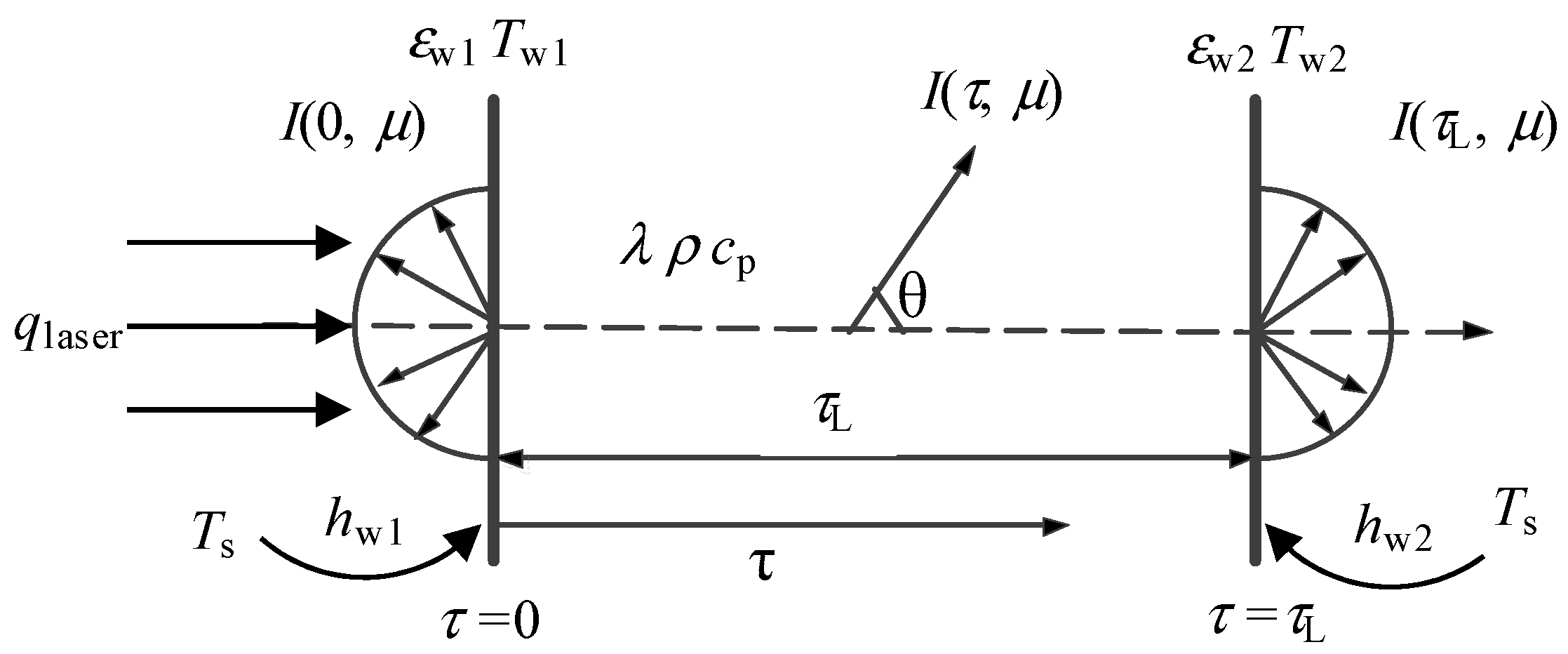
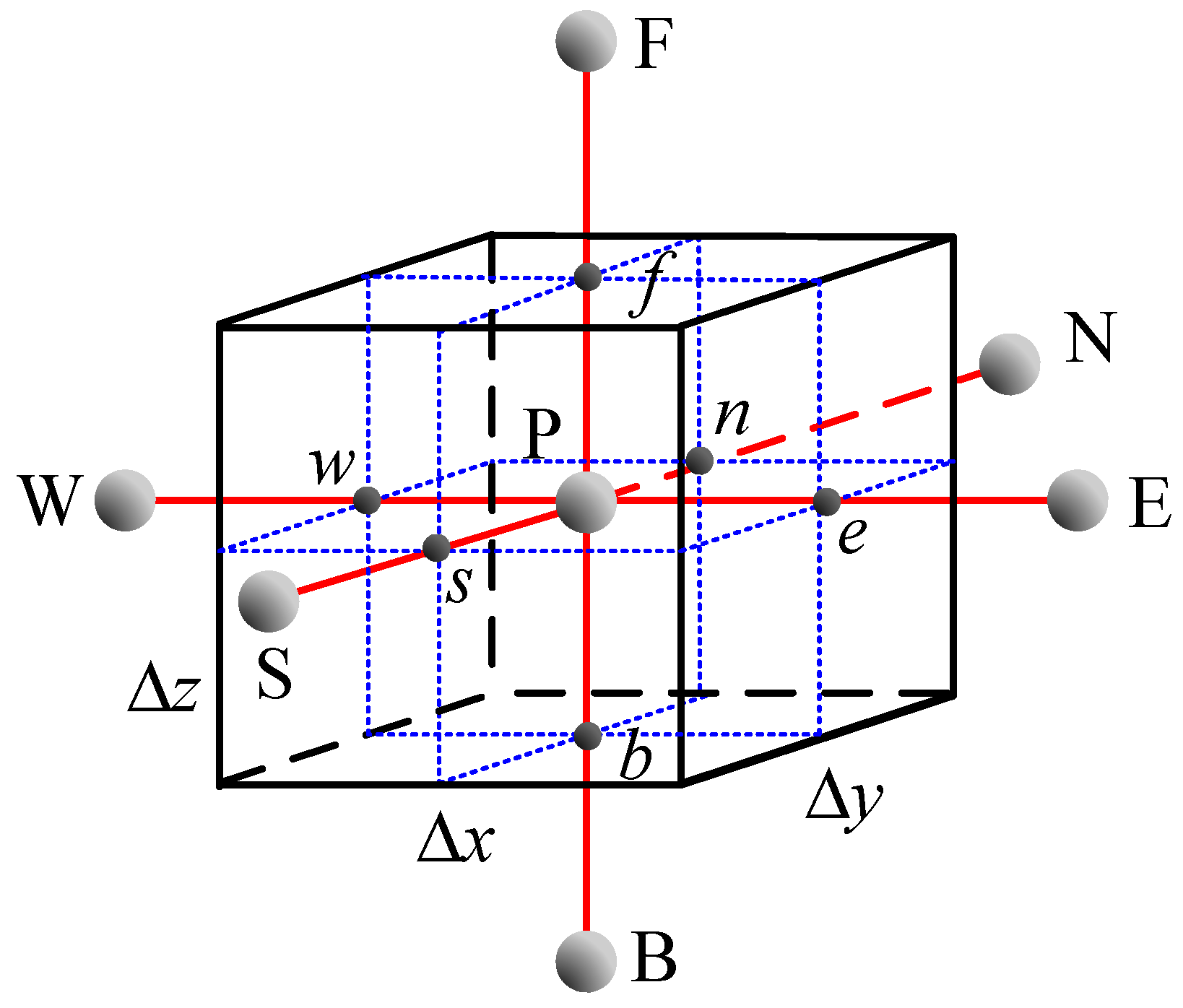
3.2.1. Physical Model
3.2.2. Inverse Estimation of the Refractive Index and Absorption Coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Nomenclature | Greek symbols | ||
| A | Coefficient vector | The scattering coefficient | |
| C | Coefficient vector | The polar angle | |
| D | Distance between grey wolf and prey | Absorption coefficient | |
| X | Grey wolf position | Optical thickness | |
| Xp | Prey position | Stefan- The wall emissivity | |
| t | Number of iterations | Stefan-Boltzmann constant | |
| a | Convergence factor | Thermal conductivity | |
| Random number within [0, 1] | Power density | ||
| Random number within [0, 1] | εrel | The relative error | |
| Radiative intensity | γ | The measurement error | |
| Refractive index | Subscripts | ||
| Temperature | mea | The measured value | |
| Array radiative | est | The estimated value | |
| Fobj | Objective function | exact | The exact value |
| Y | The estimated or exact values of refractive index, absorption coefficient, and source term | b | Black body |
| The source term | avg | Average value | |
| The source term coefficient | L2 | L2-type norm | |
| M | The population size of grey wolf | i | The ith iteration |
References
- Viskanta, R.; Mengüç, M.P. Radiation heat transfer in combustion systems. Prog. Energy Combust. Sci. 1987, 13, 97–160. [Google Scholar] [CrossRef]
- Lockwood, F.C.; Shah, N.G. A new radiation solution method for incorporation in general combustion prediction procedures. Symp. Combust. 1981, 18, 1405–1414. [Google Scholar] [CrossRef]
- Al-Gebory, L.; Mengüç, M.P.; Koşar, A.; Şendur, K. Effect of electrostatic stabilization on thermal radiation transfer in nanosuspensions: Photo-thermal energy conversion applications. Renew. Energy 2018, 119, 625–640. [Google Scholar] [CrossRef]
- Mätzler, C. Thermal Microwave Radiation: Applications for Remote Sensing; Institution of Engineering & Technology: Guwahati, India, 2006; pp. 52–584. [Google Scholar]
- Nordlund, Å.; Stein, R.F. Accurate radiation hydrodynamics and MHD modeling of 3-D stellar atmospheres. AIP Conf. Proc. 2009, 1171, 242–259. [Google Scholar]
- Wiscombe, W.J.; Ramanathan, V. The role of radiation and other renascent subfields in atmospheric science. Bull. Am. Meteorol. Soc. 2010, 66, 1278–1287. [Google Scholar] [CrossRef][Green Version]
- Tyshchenko, V.A.; Shabalina, T.N.; Sheikina, N.A.; Diskina, D.E. Radiation stability of low-viscosity base oils for aerospace engineering control systems. Chem. Technol. Fuels Oils 2003, 39, 141–144. [Google Scholar] [CrossRef]
- Song, X. Analysis of zirconium just jade nature fire-proof material by X-ray fluorescence spectrometry. Chin. J. Spectrosc. Lab. 2006, 23, 1314–1317. [Google Scholar]
- Cheng, Q.; Chai, J.; Zhang, Z. Investigation of double-layer coating pigmented with CuO particles of different concentrations on aesthetic and thermal aspects. Int. J. Therm. Sci. 2016, 105, 36–44. [Google Scholar] [CrossRef]
- Wang, Z.C.; Song, J.L.; Chai, J.L.; Cheng, Q.; Zhou, H.C. The effect of BRDF surface on radiative heat transfer within a one-dimensional graded index medium. Int. J. Therm. Sci. 2014, 77, 116–125. [Google Scholar] [CrossRef]
- Wei, L.Y.; Qi, H.; Niu, Z.T.; Wen, S.; Ren, Y.T. Inverse heat transfer analysis to determine the temperature or phase change-dependent refractive index of semitransparent materials. Inverse Probl. Sci. Eng. 2021, 29, 586–608. [Google Scholar] [CrossRef]
- Wang, J.Y.; Gao, Z.X.; Lee, C.H. An iterative technique for coupled conduction-radiation heat transfer in semitransparent media. Numer. Heat Transf. Part A Appl. 2015, 67, 1208–1231. [Google Scholar] [CrossRef]
- Lacroix, D.; Parent, G.; Asllanaj, F.; Jeandel, G. Coupled radiative and conductive heat transfer in a non-grey collimated radiation. J. Quant. Spectrosc. Radiat. Transf. 2002, 75, 589–609. [Google Scholar] [CrossRef]
- An, W.; Zhu, T.; Gao, N.P. Accelerative iteration for coupled conductive-radiative heat transfer computation in semitransparent media. Int. J. Heat Mass Transf. 2015, 82, 503–509. [Google Scholar] [CrossRef]
- Bai, D.; Fan, X.J. Transient coupled heat transfer in multilayer non-gray Radiative heat transfer in semitransparentsolidifying slab considering space-time dependent refractive index media with reflective foils. Int. J. Thermophys. 2006, 27, 647–664. [Google Scholar] [CrossRef]
- Li, H.Y. Inverse radiation problem in two-dimensional rectangular media. J. Thermophys. Heat Transf. 1997, 11, 556–561. [Google Scholar] [CrossRef]
- Menguc, M.P.; Manickavasagam, S. Inverse radiation problem in axisymmetric cylindrical scattering media. J. Thermophys. Heat Transf. 1993, 7, 479–486. [Google Scholar] [CrossRef]
- Chopade, R.P.; Agnihotri, E.; Singh, A.K.; Kumar, A.; Uppaluri, R.; Mishra, S.C.; Mahanta, P. Application of a particle swarm algorithm for parameter retrieval in a transient conduction-radiation problem. Numer. Heat Transf. Part A Appl. 2011, 59, 672–692. [Google Scholar] [CrossRef]
- Qi, H.; Niu, C.Y.; Gong, S.; Ren, Y.T.; Ruan, L.M. Application of the hybrid particle swam optimization algorithms for simultaneous estimation of multi-parameters in a transient conduction-radiation problem. Int. J. Heat Mass Transf. 2015, 83, 428–440. [Google Scholar] [CrossRef]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Swarm Intelligence: From Natural to Artificial Systems; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Stutzle, T.; Dorigo, M. Ant Colony Optimization; Bradford Company: Holland, MI, USA, 2004. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Kaipa, K.N.; Ghose, D. Glowworm Swarm Optimization: THEORY, Algorithms, and Applications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Madhiarasan, M.; Deepa, S.N. Long-Term Wind Speed Forecasting using Spiking Neural Network Optimized by Improved Modified Grey Wolf Optimization Algorithm. Int. J. Adv. Res. 2016, 4, 356–368. [Google Scholar] [CrossRef]
- Gholizadeh, S. Optimal design of double layer grids considering nonlinear behavior by sequential grey wolf algorithm. J. Optim. Civ. Eng. 2015, 5, 511–523. [Google Scholar]
- Long, W.; Liang, X.; Cai, S.; Jao, J.; Zhang, W. A Modified augmented Lagrangian with improved grey wolf optimization to constrained optimization problem. Neural Comput. Appl. 2016, 28, 421–438. [Google Scholar] [CrossRef]
- Zhang, S.; Luo, Q.F.; Zhou, Y.Q. Hybrid grey wolf optimizer using elite opposition-based learning strategy and simplex method. Int. J. Comput. Intell. Appl. 2017, 16, 1750012. [Google Scholar] [CrossRef]
- Zhu, A.; Xu, C.; Li, Z.; Wu, J.; Liu, Z. Hybridizing grey wolf optimization with differential evolution for glbal optimization and test scheduling for 3D stacked SoC. J. Syst. Eng. Electron. 2015, 26, 317–328. [Google Scholar] [CrossRef]
- Modest, M.F. Radiative Heat Transfer; McGraw-Hill: Now York, NY, USA, 2003. [Google Scholar]
- Wei, L.Y.; Qi, H.; Zhang, X.L.; Wen, S.; Islam, M.A.; Ruan, L.M. Reconstruction of radiative properties fields in participating media by using the sequential quadratic programing combined with regularization technique. J. Heat Transf. 2019, 141, 022702. [Google Scholar] [CrossRef]




| Function | Expression | Dimension | Space |
|---|---|---|---|
| Sphere | 30 | [−100, 100] | |
| Rosenbrock | 30 | [−100, 100] | |
| Griewank | 30 | [−100, 100] |
| Function | GWO | Iteration | IGWO | Iteration |
|---|---|---|---|---|
| F1 (Sphere) | 500 | 83 | ||
| F2 (Rosenbrock) | 500 | 500 | ||
| F3 (Griewank) | 500 | 86 |
| Algorithm | afin | aini | tmax | M |
|---|---|---|---|---|
| IGWO | 0 | 2 | 500 | 100 |
| Exact Value | Measure Error | a1 | εrel (%) | a2 | εrel (%) | a3 | εrel (%) |
|---|---|---|---|---|---|---|---|
| a1 = 3 | γ = 0% | 2.9998 ± 9.05 × 10−4 | 6.67 × 10−3 | 14.0010 ± 1.03 × 10−2 | 7.37 × 10−2 | −14.0016 ± 1.07 × 10−2 | 1.14 × 10−2 |
| a2 = 14 | γ = 3% | 3.0003 ± 8.11 × 10−4 | 1.00 × 10−2 | 13.9979 ± 9.81 × 10−3 | 6.46 × 10−2 | −13.9981 ± 8.89 × 10−3 | 1.36 × 10−2 |
| a3 = −14 | γ = 5% | 2.9995 ± 9.09 × 10−4 | 1.67 × 10−2 | 14.0039 ± 9.04 × 10−3 | 7.00 × 10−2 | −14.0039 ± 9.71 × 10−3 | 2.79 × 10−2 |
| a1 = 5 | γ = 0% | 4.9999 ± 1.30 × 10−3 | 1.18 × 10−3 | 12.0008 ± 1.57 × 10−2 | 6.58 × 10−3 | −12.0010 ± 1.56 × 10−2 | 8.13 × 10−3 |
| a2 = 12 | γ = 3% | 4.9997 ± 9.55 × 10−4 | 5.54 × 10−3 | 12.0033 ± 1.03 × 10−2 | 2.75 × 10−2 | −12.0032 ± 1.03 × 10−2 | 2.70 × 10−2 |
| a3 = −12 | γ = 5% | 4.9997 ± 9.76 × 10−4 | 6.24 × 10−3 | 12.0046 ± 1.11 × 10−2 | 3.80 × 10−2 | −12.0034 ± 1.09 × 10−2 | 2.83 × 10−2 |
| Physical Parameters | Symbol | Value |
|---|---|---|
| The thickness of the medium | τL | 0.01 m |
| The heat capacity | ρcp | 1.0 × 107 J/(m3·K) |
| The thermal conductivity | λ | 0.7 W/(m·K) |
| The convective heat transfer coefficient | 7.0 W/(m2·K) | |
| Initial or ambient temperature | Ts | 300 K |
| The laser intensity | qlaser | 500 W/m2 |
| The wall emissivity | 1 |
| Runs | Population Size = 30 | Population Size = 50 | Population Size = 100 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | εrel (%) | κa | εrel (%) | n | εrel (%) | κa | εrel (%) | n | εrel (%) | κa | εrel (%) | |
| 1 | 2.36002 | 0.000847 | 4.00245 | 0.06125 | 2.36001 | 0.000424 | 3.99422 | 0.1445 | 2.36000 | 0 | 4.00102 | 0.0255 |
| 2 | 2.35994 | 0.002542 | 3.98836 | 0.291 | 2.36006 | 0.002542 | 4.01019 | 0.25475 | 2.36003 | 0.001271 | 4.00204 | 0.051 |
| 3 | 2.36009 | 0.003814 | 4.00454 | 0.1135 | 2.35990 | 0.004237 | 3.99224 | 0.194 | 2.36000 | 0 | 3.99930 | 0.0175 |
| 4 | 2.36012 | 0.005085 | 4.01512 | 0.378 | 2.36009 | 0.003814 | 3.99118 | 0.2205 | 2.35996 | 0.001695 | 3.99352 | 0.162 |
| 5 | 2.35997 | 0.001271 | 3.98440 | 0.39 | 2.35997 | 0.001271 | 3.99861 | 0.03475 | 2.36000 | 0 | 4.00135 | 0.03375 |
| 6 | 2.36006 | 0.002542 | 4.00759 | 0.18975 | 2.36002 | 0.000847 | 4.00334 | 0.0835 | 2.36001 | 0.000424 | 3.99957 | 0.01075 |
| 7 | 2.35998 | 0.000847 | 3.99912 | 0.022 | 2.36001 | 0.000424 | 3.99651 | 0.08725 | 2.35999 | 0.000424 | 3.99912 | 0.022 |
| 8 | 2.36000 | 0 | 4.00418 | 0.1045 | 2.35999 | 0.000424 | 3.99807 | 0.04825 | 2.36000 | 0 | 4.00124 | 0.031 |
| 9 | 2.36008 | 0.00339 | 4.01289 | 0.32225 | 2.35996 | 0.001695 | 3.99805 | 0.04875 | 2.35998 | 0.000847 | 3.99898 | 0.0255 |
| 10 | 2.35986 | 0.005932 | 3.99270 | 0.1825 | 2.35999 | 0.000424 | 3.99844 | 0.039 | 2.36002 | 0.000847 | 4.00045 | 0.01125 |
| Exact Value | Measure Error | εn | εrel (%) | κa | εrel (%) |
|---|---|---|---|---|---|
| n = 2.36 κa = 4.0 | γ = 0% | ||||
| γ = 3% | |||||
| γ = 5% | |||||
| n = 3.50 κa = 5.0 | γ = 0% | ||||
| γ = 3% | |||||
| γ = 5% |
| Runs | Measure Error = 0% | Measure Error = 3% | Measure Error = 5% | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | εrel (%) | κa | εrel (%) | n | εrel (%) | κa | εrel (%) | n | εrel (%) | κa | εrel (%) | |
| 1 | 2.36002 | 0.000847 | 4.00245 | 0.06125 | 2.35943 | 0.024153 | 3.99901 | 0.02475 | 2.36083 | 0.035169 | 3.97479 | 0.63025 |
| 2 | 2.35994 | 0.002542 | 3.98836 | 0.291 | 2.35652 | 0.147458 | 4.00351 | 0.08775 | 2.37942 | 0.822881 | 4.01223 | 0.30575 |
| 3 | 2.36009 | 0.003814 | 4.00454 | 0.1135 | 2.37278 | 0.541525 | 3.99553 | 0.11175 | 2.38106 | 0.892373 | 3.99321 | 0.16975 |
| 4 | 2.36012 | 0.005085 | 4.01512 | 0.378 | 2.35075 | 0.391949 | 3.99687 | 0.07825 | 2.39463 | 1.467373 | 4.01683 | 0.42075 |
| 5 | 2.35997 | 0.001271 | 3.98440 | 0.39 | 2.35259 | 0.313983 | 3.99507 | 0.12325 | 2.34236 | 0.747458 | 3.99695 | 0.07625 |
| 6 | 2.36006 | 0.002542 | 4.00759 | 0.18975 | 2.36087 | 0.036864 | 4.00166 | 0.0415 | 2.37423 | 0.602966 | 3.99618 | 0.0955 |
| 7 | 2.35998 | 0.000847 | 3.99912 | 0.022 | 2.36178 | 0.075424 | 3.99703 | 0.07425 | 2.36949 | 0.402119 | 4.04793 | 1.19825 |
| 8 | 2.36000 | 0 | 4.00418 | 0.1045 | 2.37068 | 0.452542 | 3.99690 | 0.0775 | 2.37773 | 0.751271 | 4.00493 | 0.12325 |
| 9 | 2.36008 | 0.00339 | 4.01289 | 0.32225 | 2.36673 | 0.285169 | 4.00650 | 0.1625 | 2.36561 | 0.237712 | 3.90035 | 2.49125 |
| 10 | 2.35986 | 0.005932 | 3.99270 | 0.1825 | 2.35481 | 0.219915 | 3.98811 | 0.29725 | 2.34342 | 0.702542 | 3.97317 | 0.67075 |
| Exact Value | Thermal Conductivity | n | εrel (%) | κa | εrel (%) |
|---|---|---|---|---|---|
| n = 2.36 κa = 4.0 | λ = 0.5 | ||||
| λ = 0.7 | |||||
| λ = 0.9 | |||||
| n = 3.50 κa = 5.0 | λ = 0.5 | ||||
| λ = 0.7 | |||||
| λ = 0.9 |
| Runs | Thermal Conductivity = 0.5 | Thermal Conductivity = 0.7 | Thermal Conductivity = 0.9 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | εrel (%) | κa | εrel (%) | n | εrel (%) | κa | εrel (%) | n | εrel (%) | κa | εrel (%) | |
| 1 | 2.36 | 0 | 4.00141 | 0.03525 | 2.36002 | 0.000847 | 4.00245 | 0.06125 | 2.36005 | 0.002119 | 3.99955 | 0.01125 |
| 2 | 2.36006 | 0.002542 | 4.00936 | 0.234 | 2.35994 | 0.002542 | 3.98836 | 0.291 | 2.36012 | 0.005085 | 3.98836 | 0.291 |
| 3 | 2.36003 | 0.001271 | 4.00454 | 0.1135 | 2.36009 | 0.003814 | 4.00454 | 0.1135 | 2.36016 | 0.00678 | 4.01749 | 0.43725 |
| 4 | 2.35996 | 0.001695 | 4.0048 | 0.12 | 2.36012 | 0.005085 | 4.01512 | 0.378 | 2.36022 | 0.009322 | 4.01512 | 0.378 |
| 5 | 2.35999 | 0.000424 | 3.99879 | 0.03025 | 2.35997 | 0.001271 | 3.98440 | 0.39 | 2.36012 | 0.005085 | 4.01273 | 0.31825 |
| 6 | 2.35992 | 0.00339 | 3.99398 | 0.1505 | 2.36006 | 0.002542 | 4.00759 | 0.18975 | 2.36013 | 0.005508 | 4.02681 | 0.67025 |
| 7 | 2.35998 | 0.000847 | 3.99912 | 0.022 | 2.35998 | 0.000847 | 3.99912 | 0.022 | 2.36007 | 0.002966 | 4.00884 | 0.221 |
| 8 | 2.36 | 0 | 4.00418 | 0.1045 | 2.36000 | 0 | 4.00418 | 0.1045 | 2.35983 | 0.007203 | 3.9611 | 0.9725 |
| 9 | 2.35998 | 0.000847 | 3.99766 | 0.0585 | 2.36008 | 0.00339 | 4.01289 | 0.32225 | 2.36008 | 0.00339 | 4.01289 | 0.32225 |
| 10 | 2.36 | 0 | 3.99965 | 0.00875 | 2.35986 | 0.005932 | 3.99270 | 0.1825 | 2.36019 | 0.008051 | 4.05203 | 1.30075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Xie, L.; Zhou, J.; Wu, X.; Ding, D.; Li, C. Estimation of Multiple Parameters in Semitransparent Mediums Based on an Improved Grey Wolf Optimization Algorithm. Processes 2024, 12, 1445. https://doi.org/10.3390/pr12071445
Li K, Xie L, Zhou J, Wu X, Ding D, Li C. Estimation of Multiple Parameters in Semitransparent Mediums Based on an Improved Grey Wolf Optimization Algorithm. Processes. 2024; 12(7):1445. https://doi.org/10.3390/pr12071445
Chicago/Turabian StyleLi, Kefu, Lang Xie, Jianhua Zhou, Xiaofang Wu, Ding Ding, and Caibin Li. 2024. "Estimation of Multiple Parameters in Semitransparent Mediums Based on an Improved Grey Wolf Optimization Algorithm" Processes 12, no. 7: 1445. https://doi.org/10.3390/pr12071445
APA StyleLi, K., Xie, L., Zhou, J., Wu, X., Ding, D., & Li, C. (2024). Estimation of Multiple Parameters in Semitransparent Mediums Based on an Improved Grey Wolf Optimization Algorithm. Processes, 12(7), 1445. https://doi.org/10.3390/pr12071445





