Impact of Wellbore Cross-Sectional Elongation on the Hydraulic Fracturing Breakdown Pressure and Fracture Initiation Direction
Abstract
1. Introduction
2. Problem Definition, Mixed Criterion
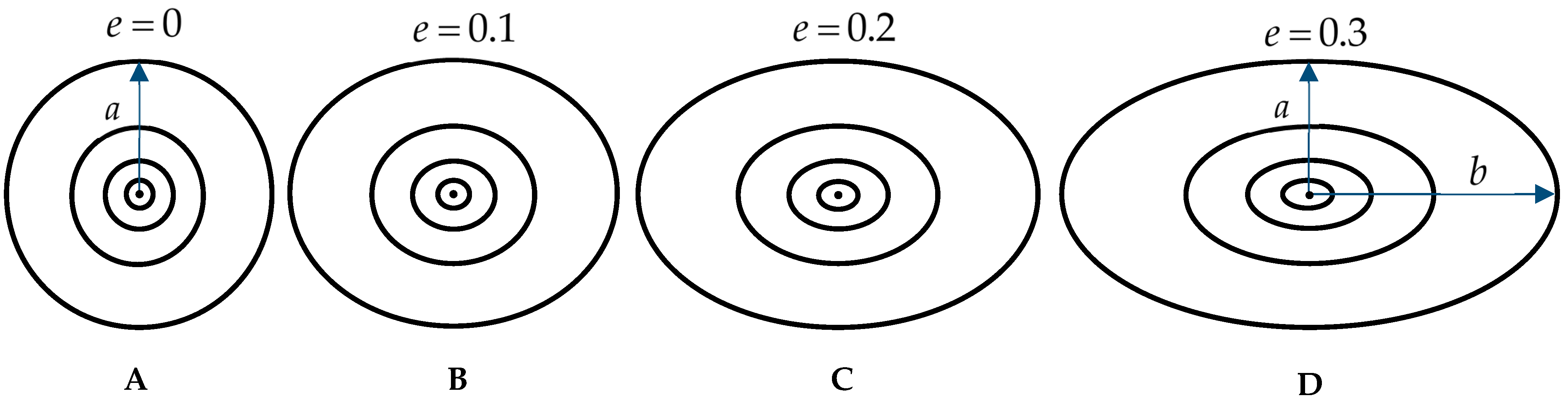
2.1. Elliptical Wellbores
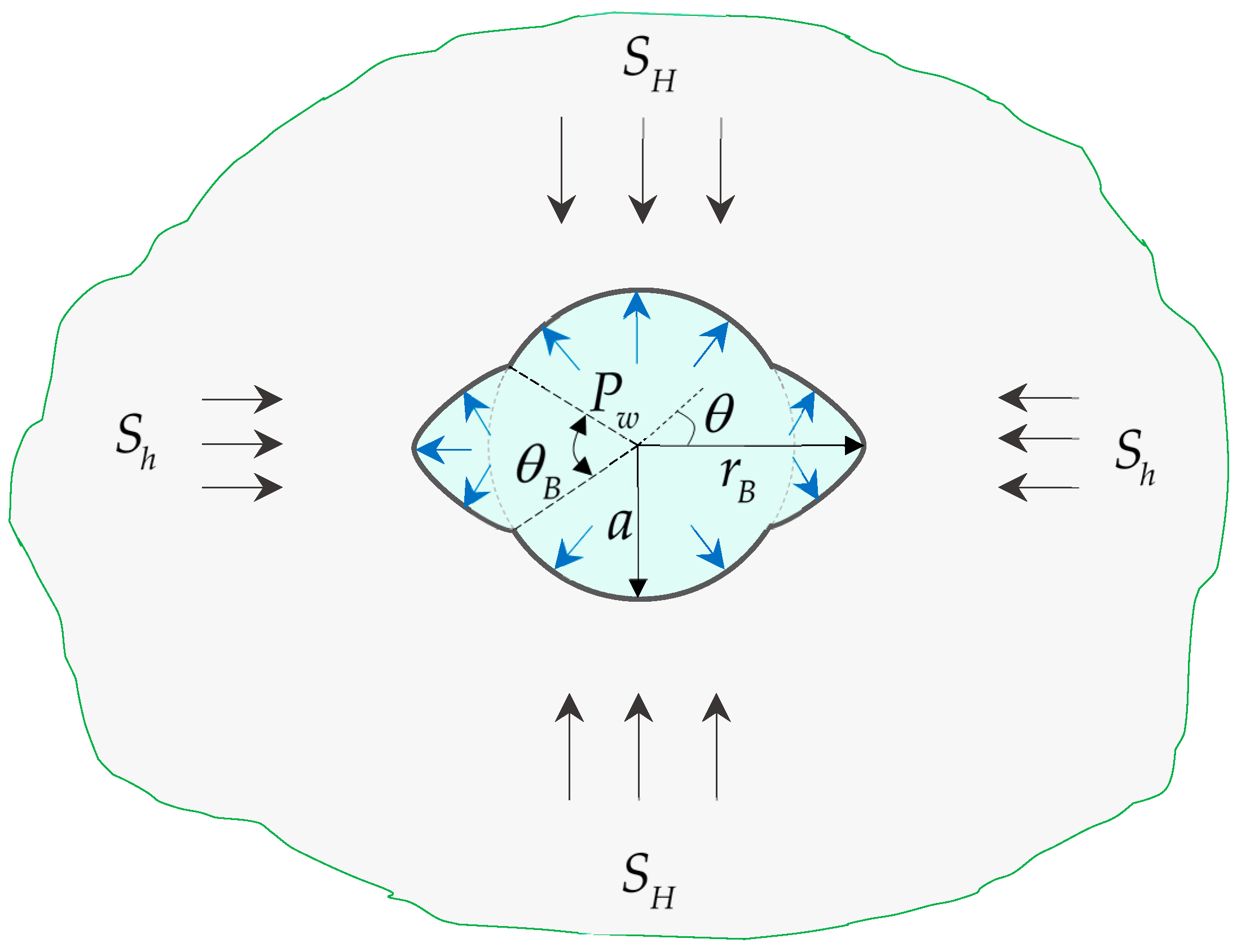
2.2. Breakout Wellbores
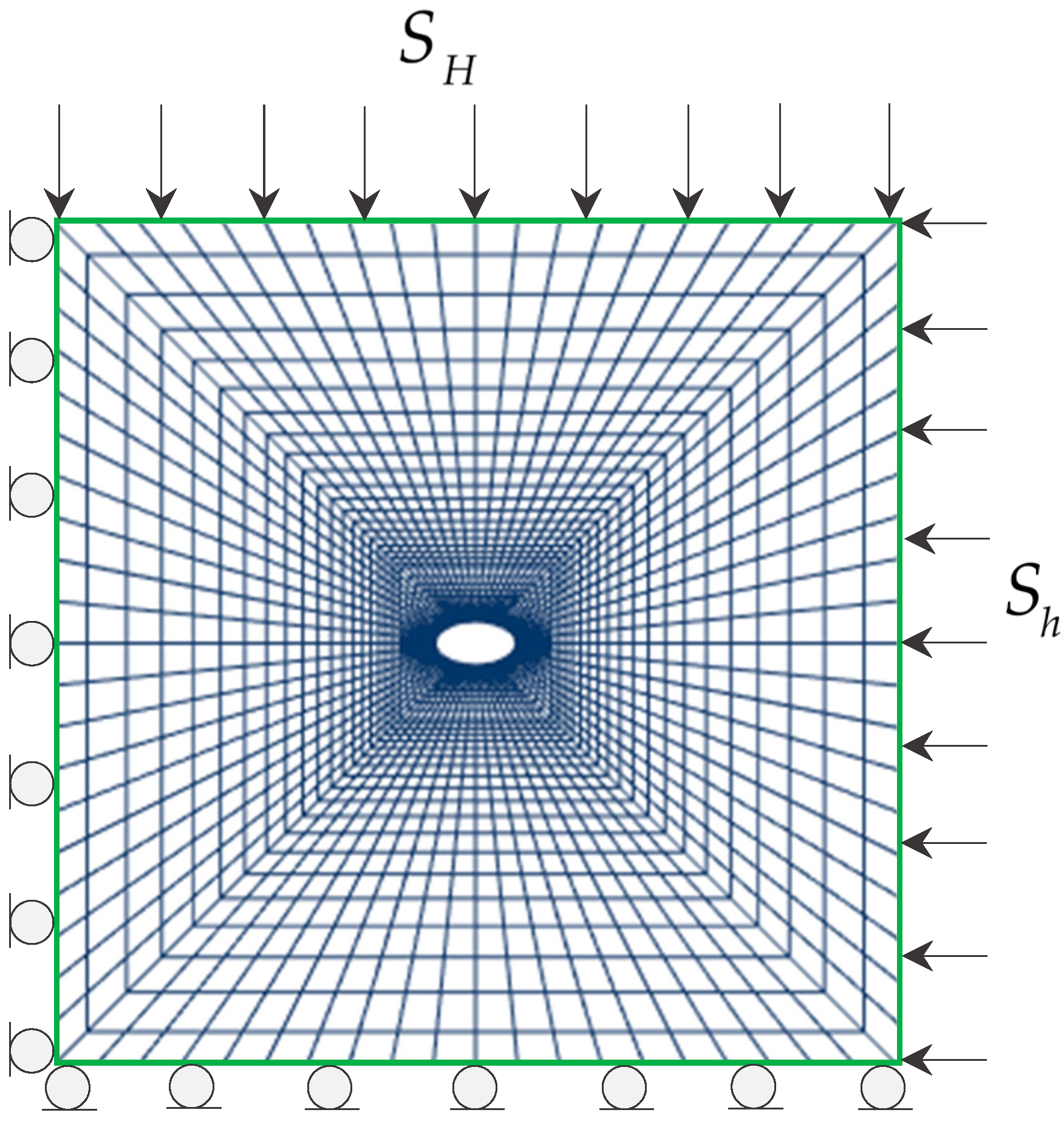
2.3. The Numerical Model
2.4. The Mixed Criterion, Procedure for Finding Hydraulic Fracture Breakdown Pressure and Initiation Length
3. Results for Elliptical Wells
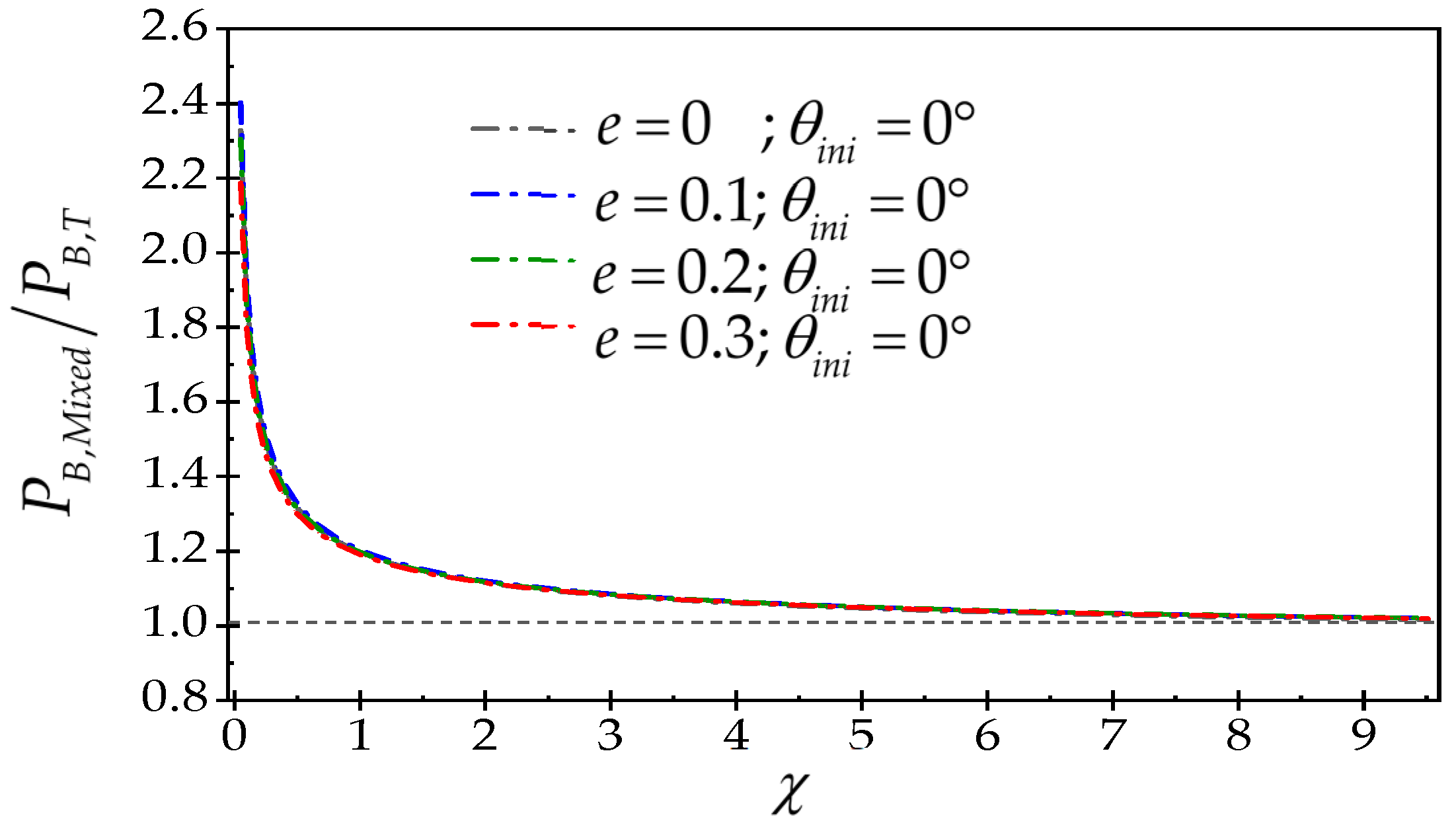
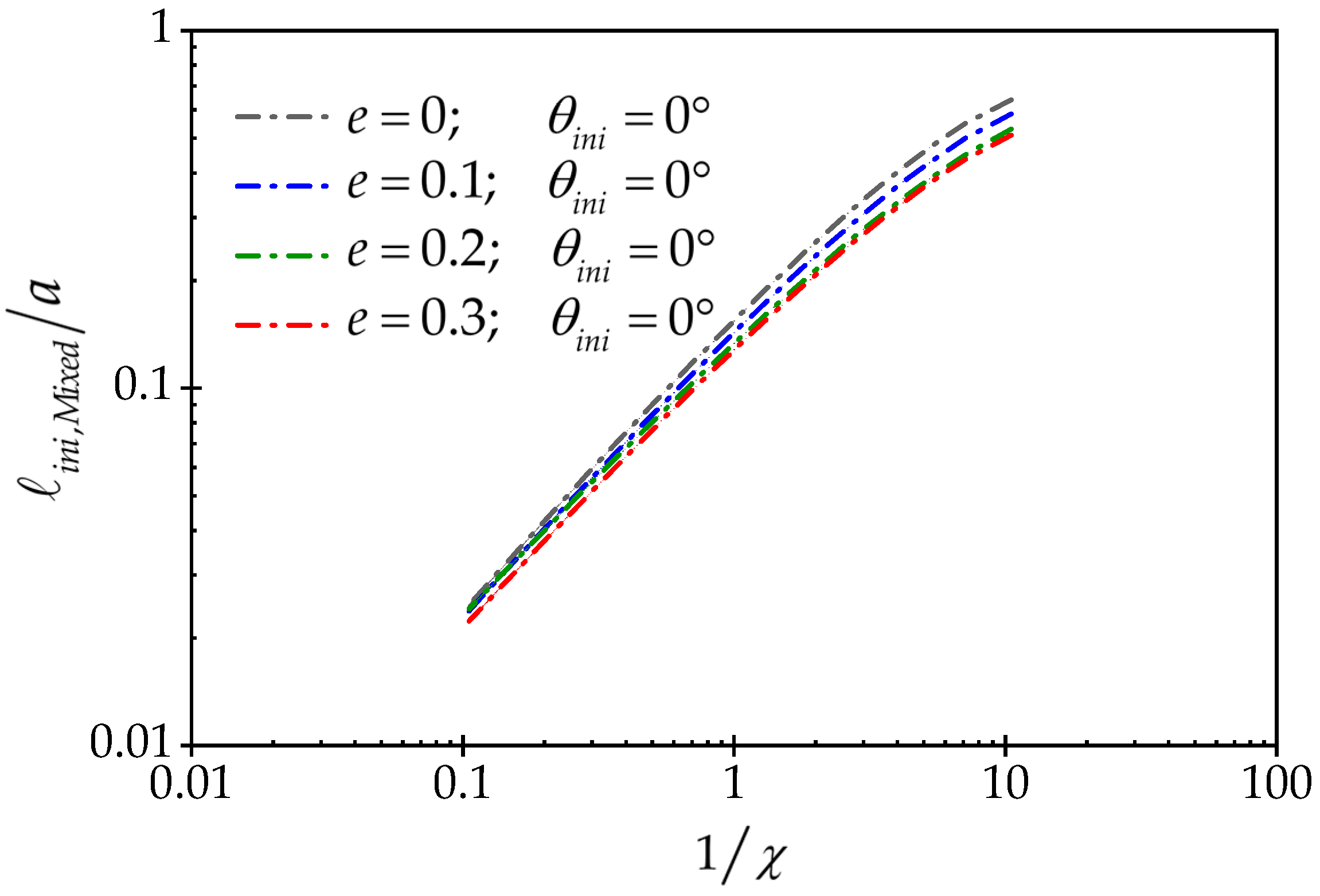
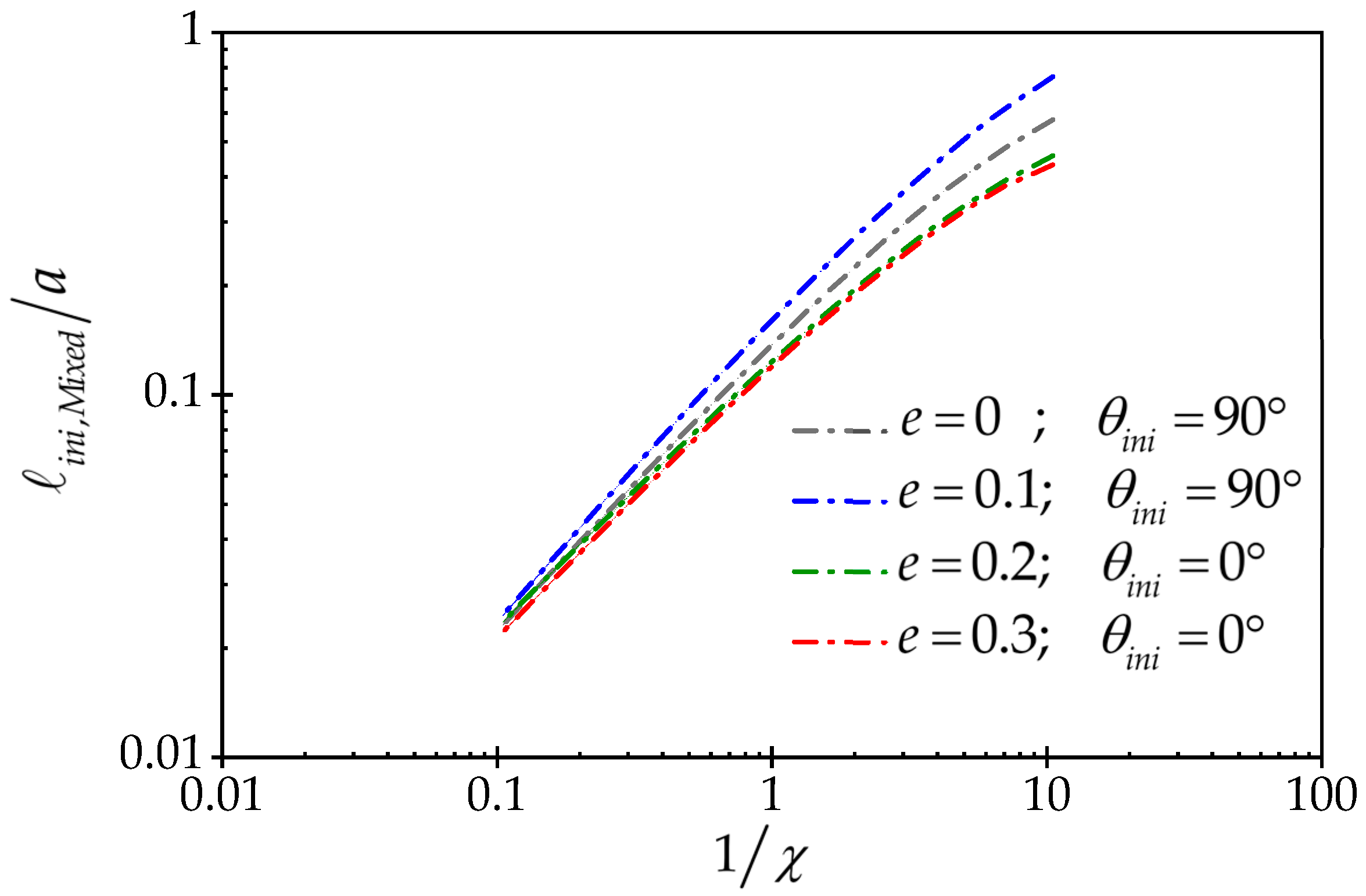
3.1. The Effect of the Wellbore Shape Parameter on Fracture Initiation Position and Breakdown Pressure
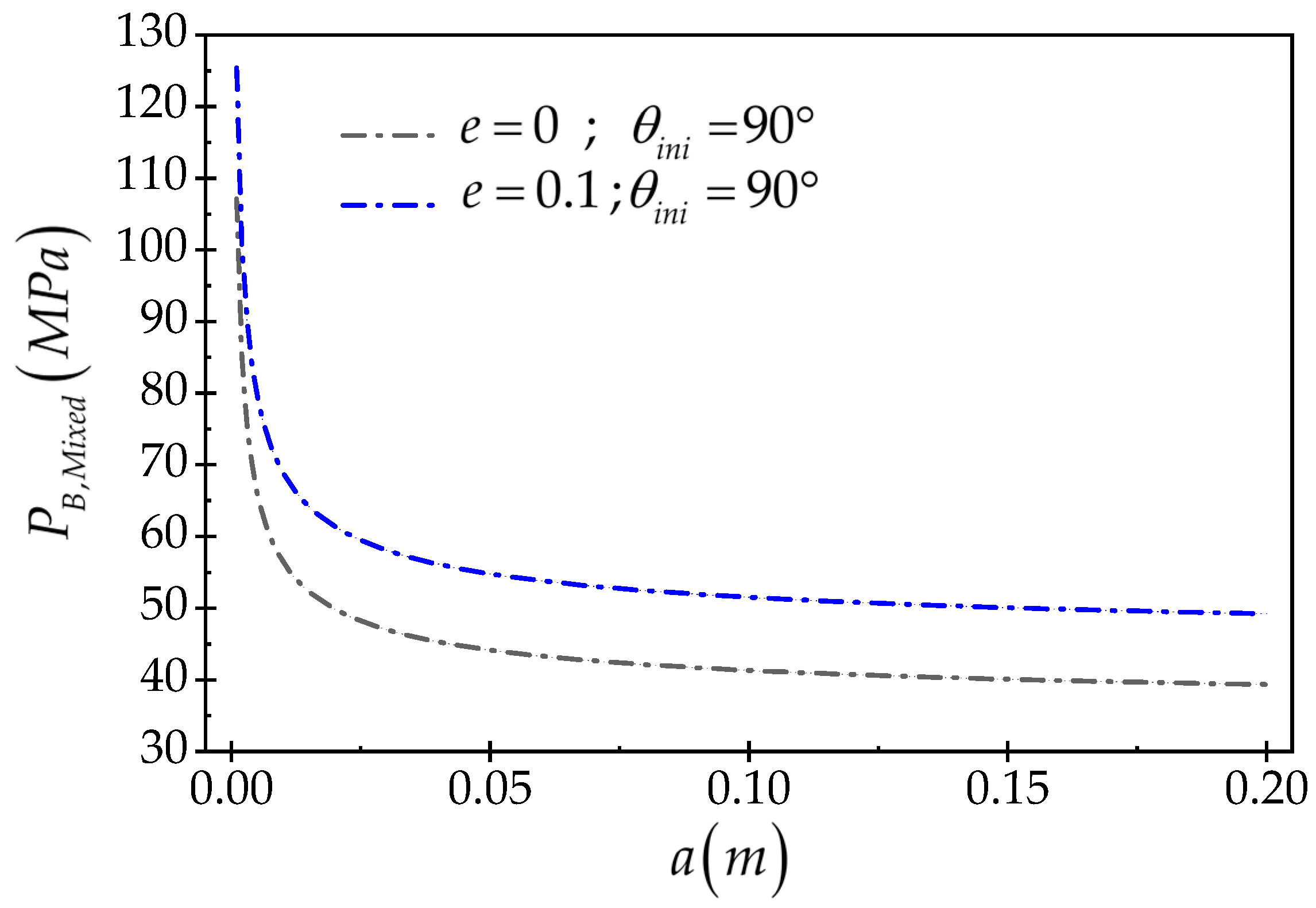
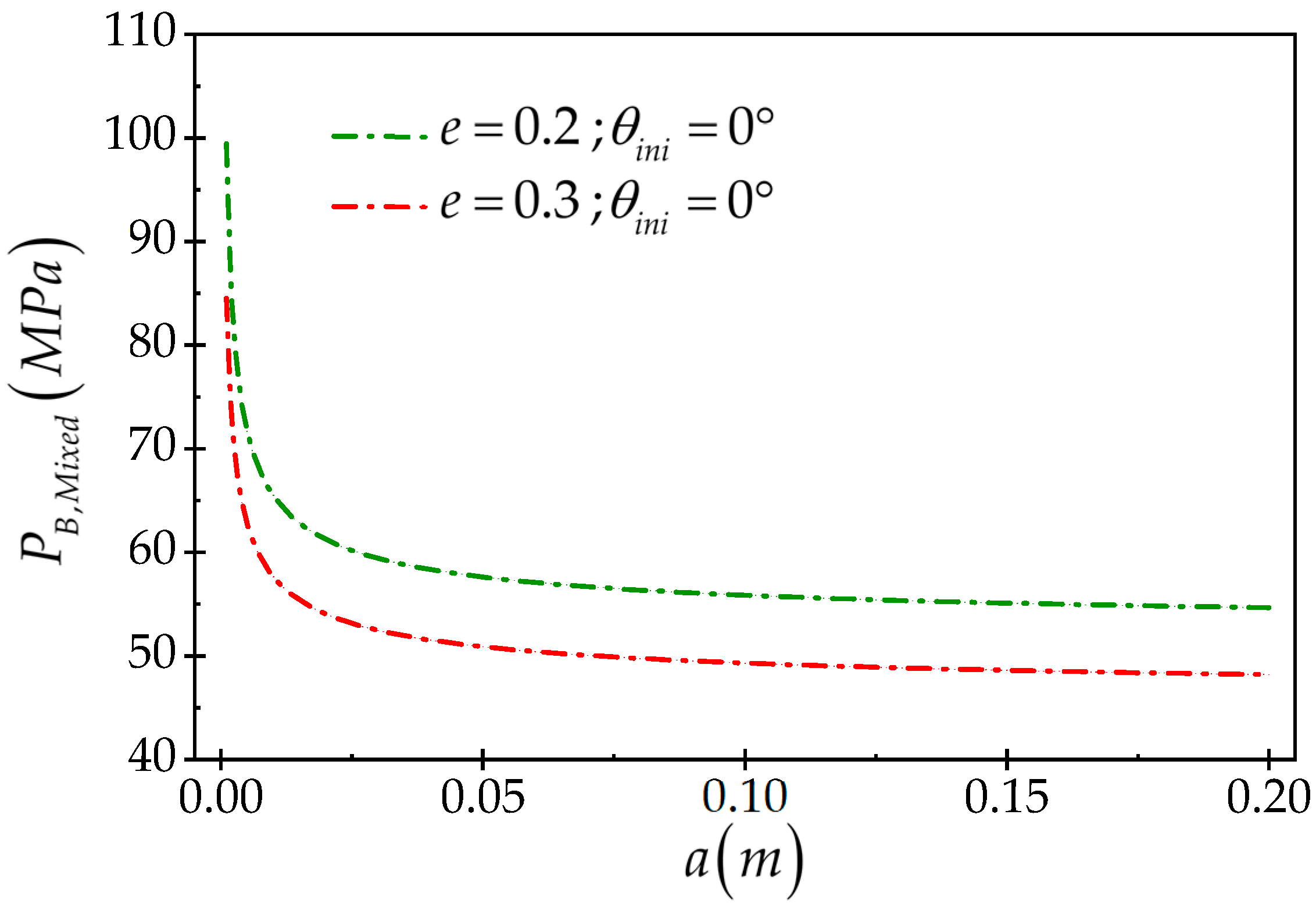
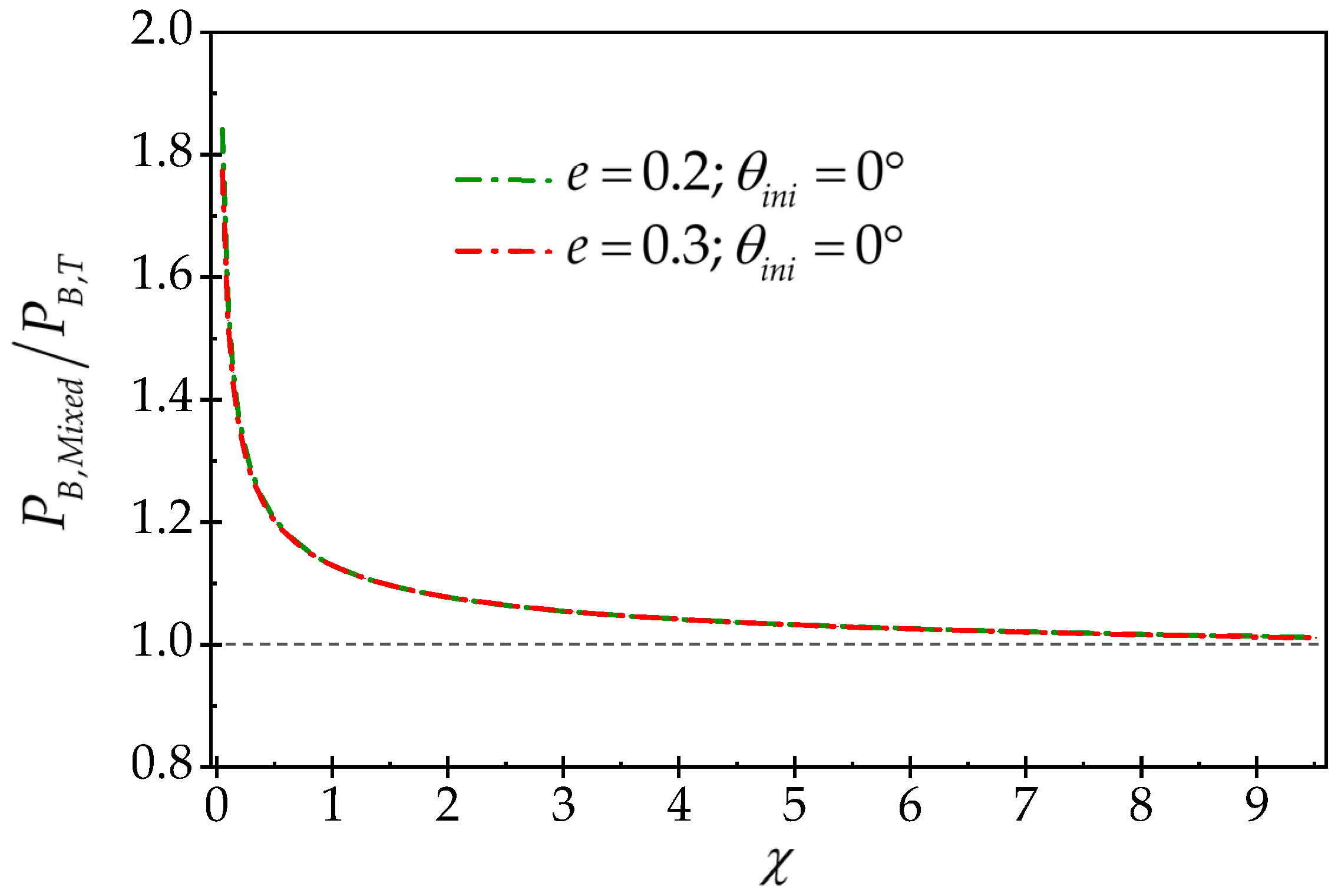
3.2. The Effect of Wellbore Size on Breakdown Pressure Behavior
3.2.1. The Isotropic Stress Field
3.2.2. The Anisotropic Stress Field
4. Results for Breakout Wellbores
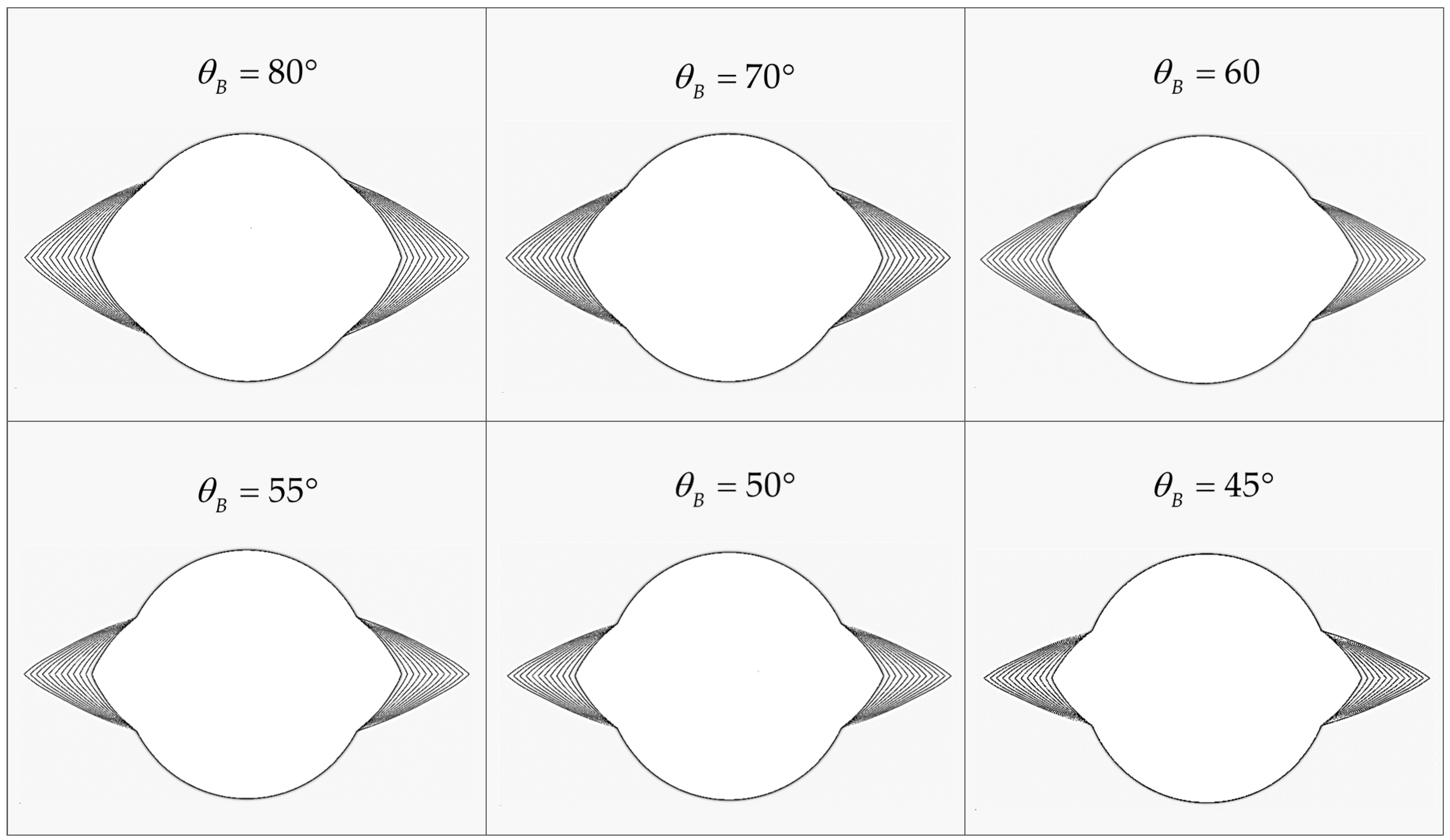
4.1. The Effect of Breakout Depth on Breakdown Pressure
4.2. The Effect of Breakout Width on Breakdown Pressure
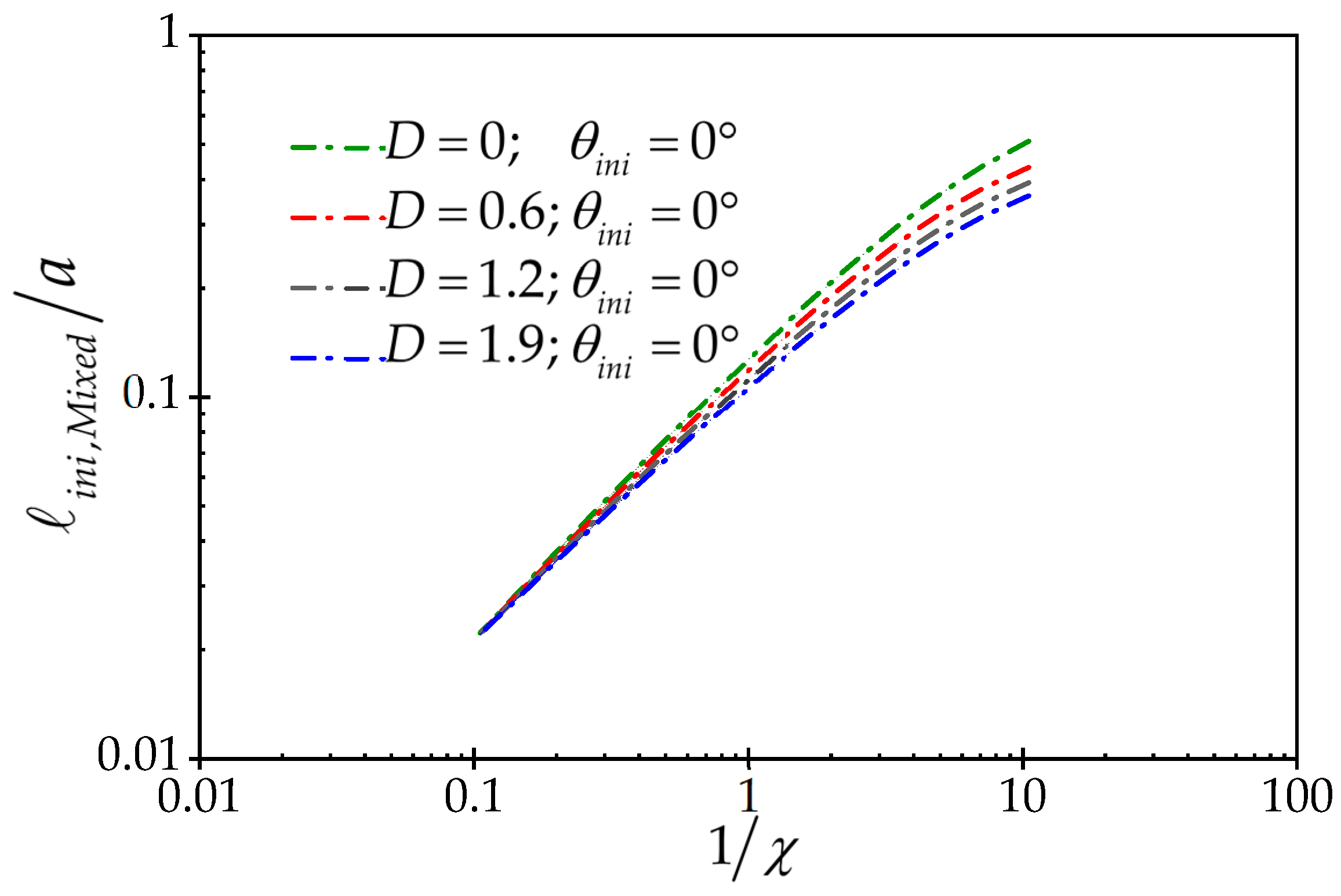
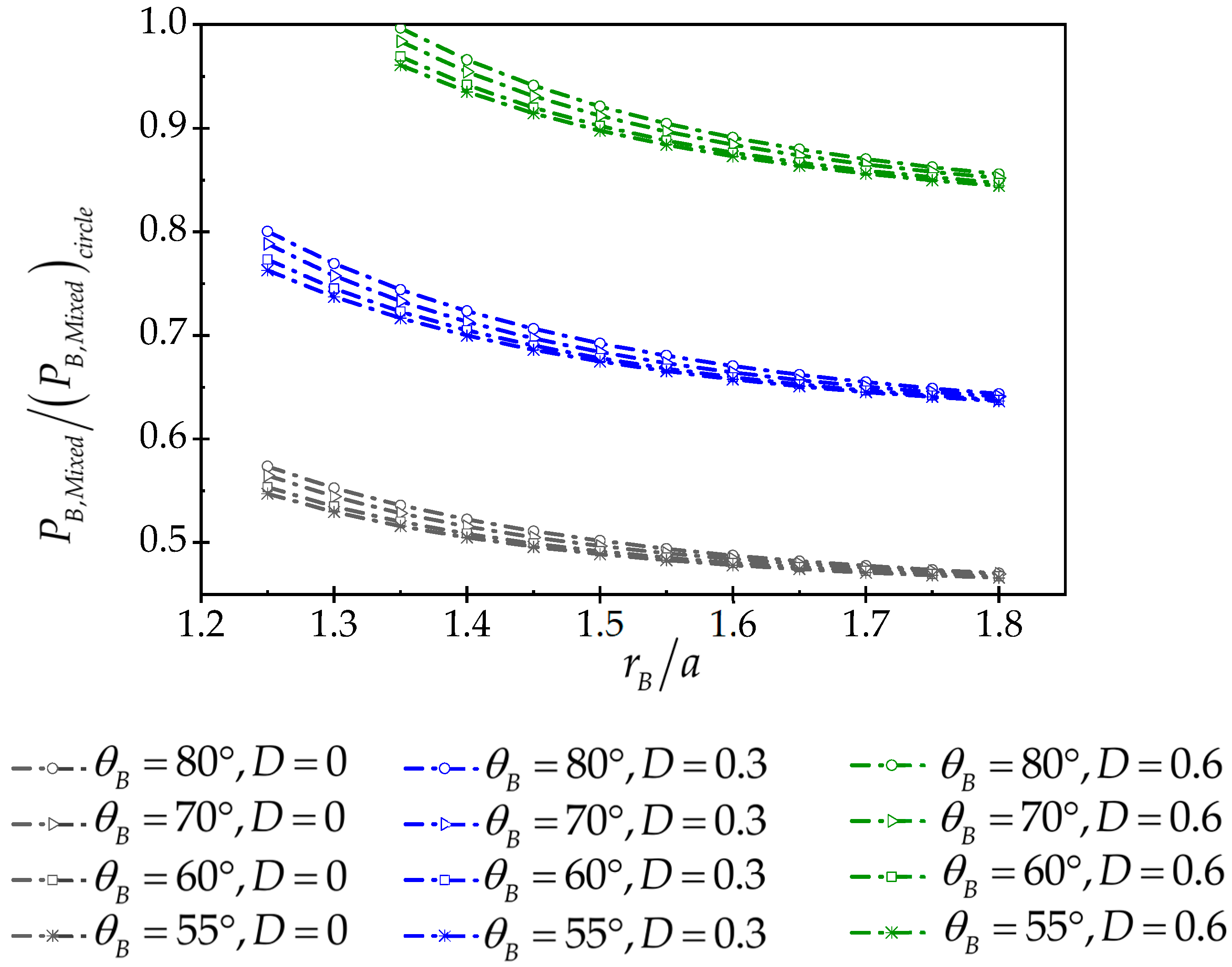
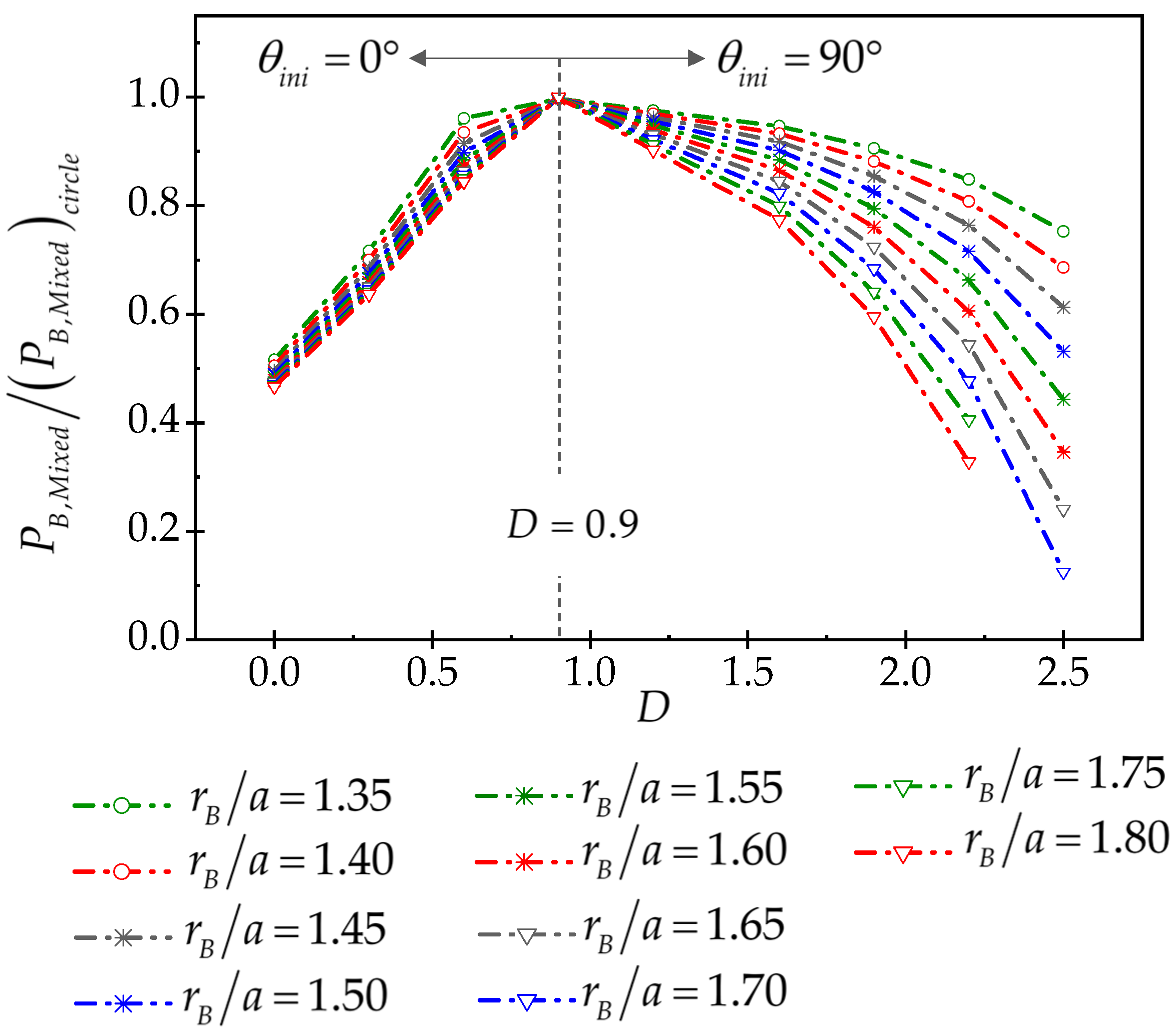
4.3. The Effect of Deviatoric In Situ Stress on Breakdown Pressure
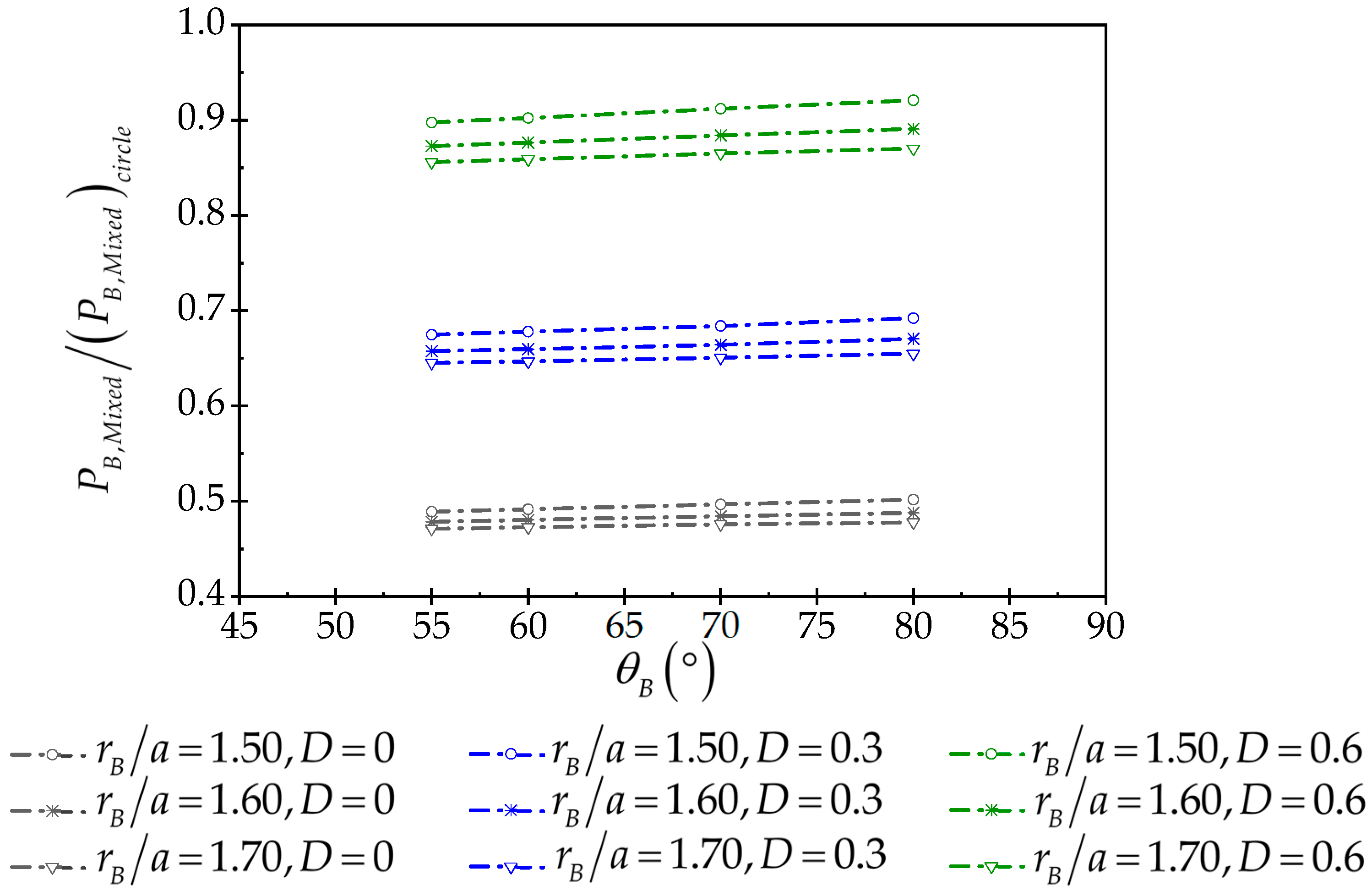
4.4. The Effect of Wellbore Size on Breakdown Pressure
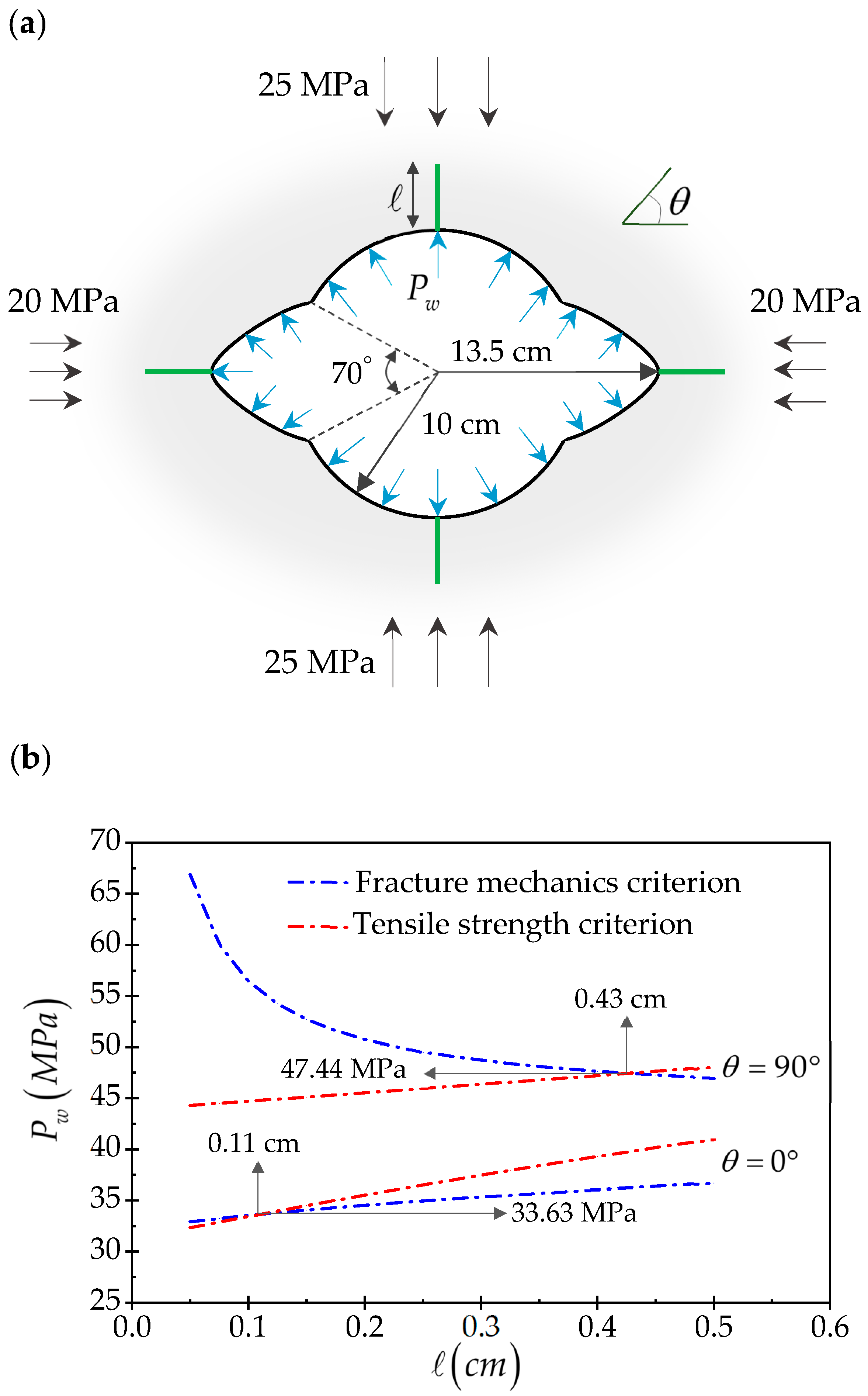
5. Discussion
6. Conclusions
- For each deviatoric stress, there is a critical shape factor. If the wellbore shape factor is less than the critical shape factor, the breakdown pressure increases with the increase in the shape factor; for this case, the fracture initiation site is aligned with the major principal stress (like circular wellbores) or minor diameter of the ellipse. If the wellbore shape factor is greater than the critical shape factor, the breakdown pressure will decrease as the shape factor increases, and in this situation, the fracture initiation site is aligned with the minor principal stress or major diameter of the wellbore, unlike the circular wellbores.
- According to Equation (6), the critical eccentricity is in control of the deviatoric stress and the rock tensile strength, it increases by increasing the deviatoric stress or decreasing the tensile strength of the rock.
- The mixed model strongly represents the impact of wellbore size on the breakdown pressure behavior. The analyses performed on elliptical wellbores with the same shape factor but different size show that in large wellbores, the tensile fracture mechanism and breakdown pressure are dominated by the rock tensile strength criterion, but in small wellbores, the fracture mechanism is dominated by fracture toughness.
- The main finding of the section of breakout wellbores is that it was observed that for a given in situ stress, the breakdown pressure in the breakout wellbore is always lower than that of the circular wellbore. As shown in the following results, wellbore elongation has a significant effect on both breakdown pressure and failure initiation position.
- Where , fracture initiation is aligned with the minor in situ stress or breakout tip, and the ratio of breakdown pressure in the breakout wellbore to the breakdown pressure of the circular wellbore is between 0.47 and 1, depending on the deviatoric stress and the width and depth of the breakout zone. In this case, with the rise of the dimensionless deviatoric stress, the breakdown pressure increases.
- Where , the initiation of fracture is aligned with the maximum in situ stress, while, the ratio of the breakdown pressure of the breakout wellbore to the breakdown pressure in the circular wellbore is between 1 and 0.04, depending on the deviatoric stress and the width and depth of the breakout zone. In this case, with the rise of the dimensionless deviatoric stress, the breakdown pressure declines.
- As the breakout depth increases, the breakdown pressure declines.
- The effect of wellbore size in breakout wellbores with the same breakout depth and width but different diameters was investigated and it was seen that similar to elliptical wellbores, the breakdown pressure in large-diameter wellbores is dominated by the tensile strength theory, while the breakdown pressure in small wellbores is dominated by the fracture toughness criterion.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Numerical Model Verification

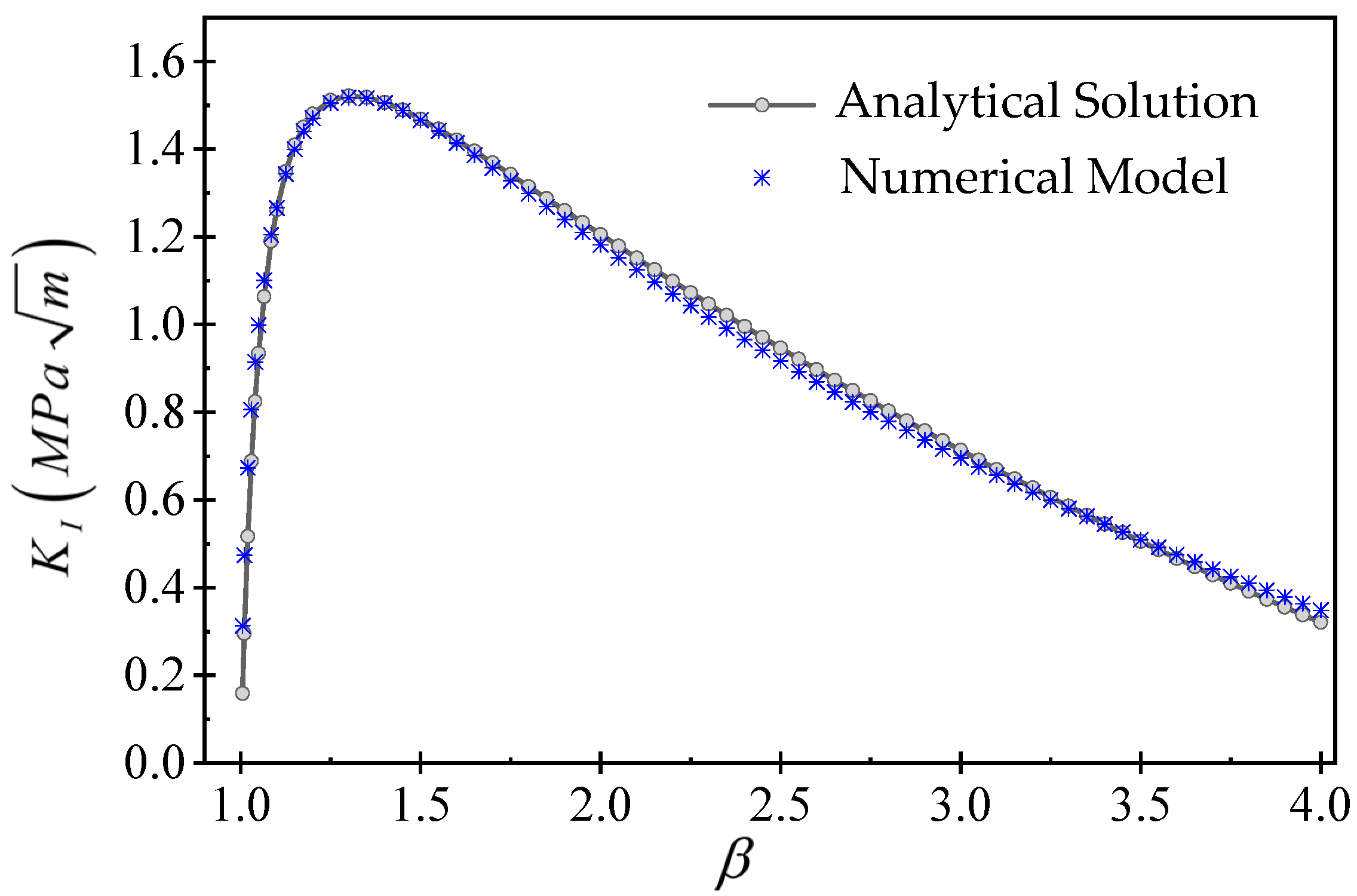

References
- Hubbert, M.K.; Willis, D.G. Mechanics of hydraulic fracturing. Trans. AIME 1957, 210, 153–168. [Google Scholar] [CrossRef]
- Haimson, B.; Fairhurst, C. Initiation and extension of hydraulic fractures in rocks. Soc. Pet. Eng. J. 1967, 7, 310–318. [Google Scholar] [CrossRef]
- Aadnoy, B.S.; Angell-Olsen, F. Some effects of ellipticity on the fracturing and collapse behavior of a borehole. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 621–627. [Google Scholar] [CrossRef]
- Akgun, F.; Yang, Z.; Crosby, D.G.; Rahman, S.S. Factors affecting hydraulic fracture initiation in high in-situ stress conditions: A wellbore stress modelling approach. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 5–8 October 1997; p. SPE-38631. [Google Scholar] [CrossRef]
- Zhang, X.; Jeffrey, R.G.; Bunger, A.P. Hydraulic fracture growth from a non-circular wellbore. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011; p. ARMA-11. [Google Scholar]
- Han, H.X.; Yin, S.; Aadnoy, B.S. Impact of elliptical boreholes on in situ stress estimation from leak-off test data. Pet. Sci. 2018, 15, 794–800. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, D.; Zhao, H.; Li, M.; Song, Z. Experimental study on hydraulic fracturing properties of elliptical boreholes. Bull. Eng. Geol. Environ. 2022, 81, 18. [Google Scholar] [CrossRef]
- Jolfaei, S.; Lakirouhani, A. Initiation Pressure and Location of Fracture Initiation in Elliptical Wellbores. Geotech. Geol. Eng. 2023, 41, 4487–4506. [Google Scholar] [CrossRef]
- Ito, T.; Hayashi, K. Physical background to the breakdown pressure in hydraulic fracturing tectonic stress measurements. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 285–293. [Google Scholar] [CrossRef]
- Garagash, D.; Detournay, E. An analysis of the influence of the pressurization rate on the borehole breakdown pressure. Int. J. Solids Struct. 1997, 34, 3099–3118. [Google Scholar] [CrossRef]
- Jin, X.; Shah, S.N.; Roegiers, J.C.; Hou, B. Breakdown pressure determination-a fracture mechanics approach. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013. [Google Scholar] [CrossRef]
- Lakirouhani, A.; Bunger, A.; Detournay, E. Modeling initiation of hydraulic fractures from a wellbore. In Proceedings of the ISRM International Symposium-Asian Rock Mechanics Symposium, Tehran, Iran, 24–26 November 2008; pp. 1101–1108. [Google Scholar]
- Bunger, A.P.; Lakirouhani, A.; Detournay, E. Modelling the effect of injection system compressibility and viscous fluid flow on hydraulic fracture breakdown pressure. In Proceedings of the ISRM International Symposium on In-Situ Rock Stress, Beijing, China, 25–27 August 2010; pp. ISRM–ISRS. [Google Scholar]
- Lakirouhani, A.; Jolfaei, S. Hydraulic fracturing breakdown pressure and prediction of maximum horizontal in situ stress. Adv. Civ. Eng. 2023, 2023, 8180702. [Google Scholar] [CrossRef]
- Haimson, B.C.; Zhao, Z. Effect of borehole size and pressurization rate on hydraulic fracturing breakdown pressure. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Norman, Oklahoma, 10–12 July 1991; p. ARMA–91. [Google Scholar]
- Schmitt, D.R.; Zoback, M.D. Diminished pore pressure in low-porosity crystalline rock under tensional failure: Apparent strengthening by dilatancy. J. Geophys. Res. Solid Earth 1992, 97, 273–288. [Google Scholar] [CrossRef]
- Schmitt, D.R.; Zoback, M.D. Infiltration effects in the tensile rupture of thin walled cylinders of glass and granite: Implications for the hydraulic fracturing breakdown equation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 289–303. [Google Scholar] [CrossRef]
- Zhao, Z.; Kim, H.; Haimson, B. Hydraulic fracturing initiation in granite. In Proceedings of the ARMA North America Rock Mechanics Symposium, Montreal, QC, Canada, 19–21 June 1996; p. ARMA–96. [Google Scholar]
- Lakirouhani, A.; Detournay, E.; Bunger, A.P. A reassessment of in situ stress determination by hydraulic fracturing. Geophys. J. Int. 2016, 205, 1859–1873. [Google Scholar] [CrossRef]
- Carter, B.J. Size and stress gradient effects on fracture around cavities. Rock Mech. Rock Eng. 1992, 25, 167–186. [Google Scholar] [CrossRef]
- Carter, B.J.; Lajtai, E.Z.; Yuan, Y. Tensile fracture from circular cavities loaded in compression. Int. J. Fract. 1992, 57, 221–236. [Google Scholar] [CrossRef]
- Leguillon, D. Strength or toughness? A criterion for crack onset at a notch. Eur. J. Mech. A/Solids 2002, 21, 61–72. [Google Scholar] [CrossRef]
- Leguillon, D.; Quesada, D.; Putot, C.; Martin, E. Prediction of crack initiation at blunt notches and cavities–size effects. Eng. Fract. Mech. 2007, 74, 2420–2436. [Google Scholar] [CrossRef]
- Lecampion, B. Modeling size effects associated with tensile fracture initiation from a wellbore. Int. J. Rock Mech. Min. Sci. 2012, 56, 67–76. [Google Scholar] [CrossRef]
- Chuprakov, D.; Melchaeva, O.; Prioul, R. Injection-sensitive mechanics of hydraulic fracture interaction with discontinuities. Rock Mech. Rock Eng. 2014, 47, 1625–1640. [Google Scholar] [CrossRef]
- Molnár, G.; Doitrand, A.; Estevez, R.; Gravouil, A. Toughness or strength? Regularization in phase-field fracture explained by the coupled criterion. Theor. Appl. Fract. Mech. 2020, 109, 102736. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Guo, Y.T.; Zhang, X.; Huang, G.T. Fracture initiation from oval boreholes. J. Pet. Sci. Eng. 2022, 218, 110994. [Google Scholar] [CrossRef]
- Lakirouhani, A.; Jolfaei, S. Assessment of Hydraulic Fracture Initiation Pressure Using Fracture Mechanics Criterion and Coupled Criterion with Emphasis on the Size Effect. Arab. J. Sci. Eng. 2023, 49, 5897–5908. [Google Scholar] [CrossRef]
- Gerolymatou, E.; Petalas, A. In situ stress assessment based on width and depth of brittle borehole breakouts. In Recent Developments of Soil Mechanics and Geotechnics in Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2020; pp. 297–319. [Google Scholar] [CrossRef]
- Lakirouhani, A.; Bahrehdar, M.; Medzvieckas, J.; Kliukas, R. Comparison of predicted failure area around the boreholes in the strike-slip faulting stress regime with Hoek-Brown and Fairhurst generalized criteria. J. Civ. Eng. Manag. 2021, 27, 346–354. [Google Scholar] [CrossRef]
- Haimson, B.C.; Song, I. Laboratory study of borehole breakouts in Cordova Cream: A case of shear failure mechanism. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 1047–1056. [Google Scholar] [CrossRef]
- Haimson, B. Micromechanisms of borehole instability leading to breakouts in rocks. Int. J. Rock Mech. Min. Sci. 2007, 44, 157–173. [Google Scholar] [CrossRef]
- Meier, T.; Rybacki, E.; Reinicke, A.; Dresen, G. Influence of borehole diameter on the formation of borehole breakouts in black shale. Int. J. Rock Mech. Min. Sci. 2013, 62, 74–85. [Google Scholar] [CrossRef]
- Setiawan, N.B.; Zimmerman, R.W. Semi-analytical method for modeling wellbore breakout development. Rock Mech. Rock Eng. 2022, 55, 2987–3000. [Google Scholar] [CrossRef]
- Sahara, D.P.; Schoenball, M.; Gerolymatou, E.; Kohl, T. Analysis of borehole breakout development using continuum damage mechanics. Int. J. Rock Mech. Min. Sci. 2017, 97, 134–143. [Google Scholar] [CrossRef]
- Leriche, A.; Kalenchuk, K.; Diederichs, M.S. Estimation of In Situ Stress from Borehole Breakout at KGHM’s Victoria Project, Canada. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018. [Google Scholar]
- Xiang, Z.; Moon, T.; Oh, J.; Li, X.; Si, G.; Canbulat, I. Numerical investigation of borehole breakout and rock spalling based on strain energy criteria. Int. J. Rock Mech. Min. Sci. 2023, 171, 105587. [Google Scholar] [CrossRef]
- Babcock, E.A. Measurement of subsurface fractures from dipmeter logs. AAPG Bull. 1978, 62, 1111–1126. [Google Scholar] [CrossRef]
- Gough, D.I.; Bell, J.S. Stress orientations from borehole wall fractures with examples from Colorado, east Texas, and northern Canada. Can. J. Earth Sci. 1982, 19, 1358–1370. [Google Scholar] [CrossRef]
- Zoback, M.D.; Moos, D.; Mastin, L.; Anderson, R.N. Well bore breakouts and in situ stress. J. Geophys. Res. Solid Earth 1985, 90, 5523–5530. [Google Scholar] [CrossRef]
- Jolfaei, S.; Lakirouhani, A. Sensitivity analysis of effective parameters in borehole failure, using neural network. Adv. Civ. Eng. 2022. [Google Scholar] [CrossRef]
- Rummel, F. Fracture mechanics approach to hydraulic fracturing stress measurements. In Fracture Mechanics of Rock; Elsevier: Amsterdam, The Netherlands, 1987; p. 217. [Google Scholar]
- Jaeger, J.C.; Cook, N.G.; Zimmerman, R. Fundamentals of Rock Mechanics; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]











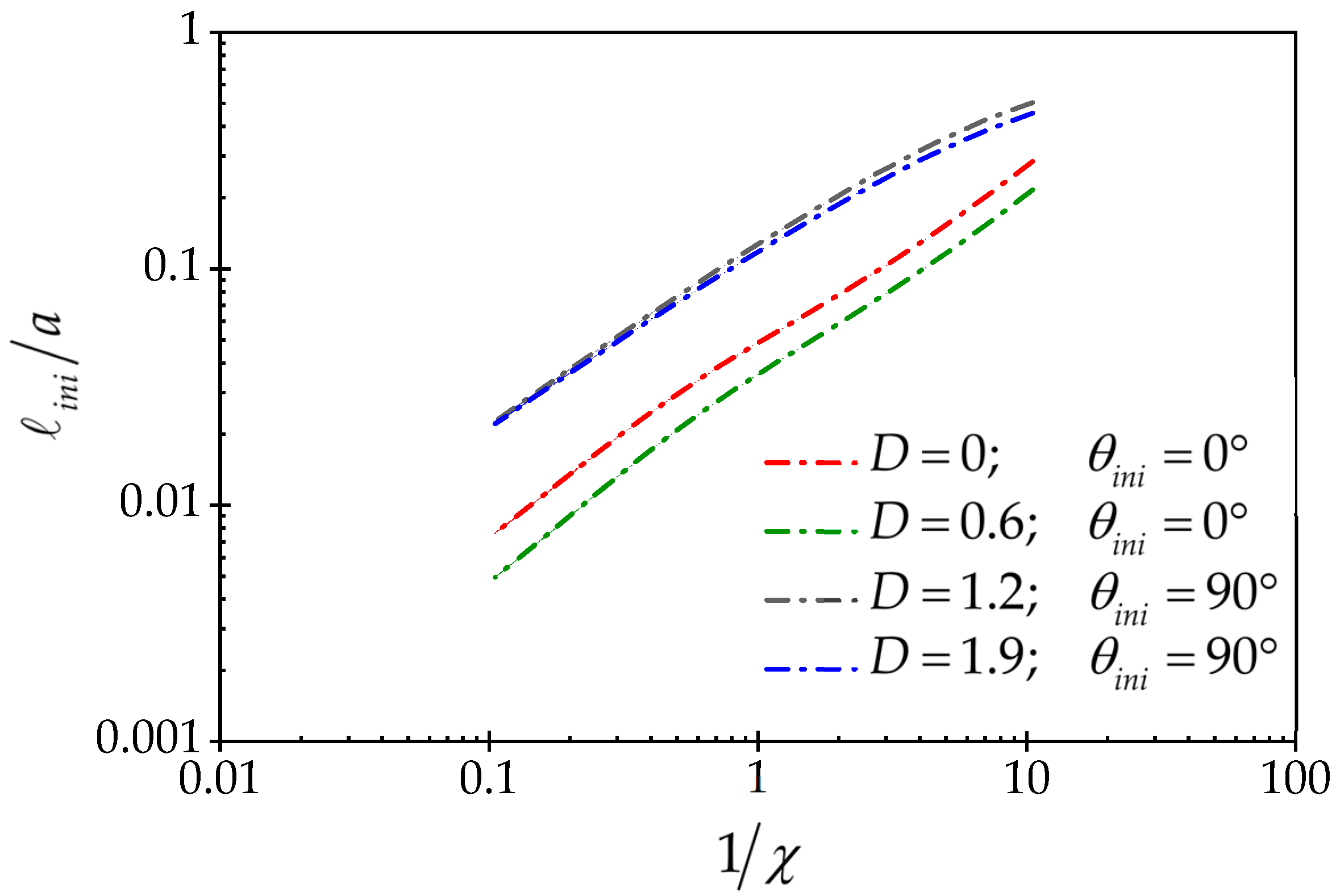
| --- | |||
| 59 | 0.25 | 8 | 1.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jolfaei, S.; Lakirouhani, A. Impact of Wellbore Cross-Sectional Elongation on the Hydraulic Fracturing Breakdown Pressure and Fracture Initiation Direction. Processes 2024, 12, 848. https://doi.org/10.3390/pr12050848
Jolfaei S, Lakirouhani A. Impact of Wellbore Cross-Sectional Elongation on the Hydraulic Fracturing Breakdown Pressure and Fracture Initiation Direction. Processes. 2024; 12(5):848. https://doi.org/10.3390/pr12050848
Chicago/Turabian StyleJolfaei, Somaie, and Ali Lakirouhani. 2024. "Impact of Wellbore Cross-Sectional Elongation on the Hydraulic Fracturing Breakdown Pressure and Fracture Initiation Direction" Processes 12, no. 5: 848. https://doi.org/10.3390/pr12050848
APA StyleJolfaei, S., & Lakirouhani, A. (2024). Impact of Wellbore Cross-Sectional Elongation on the Hydraulic Fracturing Breakdown Pressure and Fracture Initiation Direction. Processes, 12(5), 848. https://doi.org/10.3390/pr12050848






