Abstract
Coal seam pressure is an important parameter for production performance evaluation and prediction of coalbed methane (CBM). CBM production from undersaturated CBM reservoirs can be divided into two stages according to critical desorption pressure. At present, few prediction models of coal seam pressure performance consider the comprehensive influence of critical desorption pressure, dissolved gas, matrix shrinkage, and stress sensitivity. For the purpose of accurately predicting coal seam pressure during gas production for an undersaturated coalbed methane reservoir, the material balance principle is used to establish the analytical method for predicting coal seam pressure, considering the comprehensive influence of the critical desorption pressure, dissolved gas, matrix shrinkage, and stress sensitivity. Then, the proposed method is verified against a numerical simulation case using a computer modelling group (CMG) and two actual coalbed methane wells. Finally, the sensitivities of influencing factors on the coal seam pressure are analyzed. The results show that good agreements were obtained between the calculated coal seam pressures using the proposed method and those from the CMG-GEM simulation case and actual CBM wells, with the relative errors all being less than 1%. When ignoring the influence of critical desorption pressure and mistaking pd for pi as well as ignoring Cs, the relative error can reach as high as 31.3%. The main factors affecting the coal seam pressure are the critical desorption pressure and free gas saturation. The proposed method is simple to use, and without shutting-in the well, it can provide an important basis for production performance evaluation and development strategies.
1. Introduction
In 2020, coal output in China accounted for 49.7% of the coal output all over the world [1]. As one of the important unconventional resources, coalbed methane (CBM) is associated with coal. Its efficient production can not only alleviate the energy shortage but also ensure coal mine safety and environmental protection. Therefore, it has attracted widespread attention all over the world. As the main parameter during CBM production, coal seam pressure has very important theoretical and practical significance for methane desorption [2], pulverized coal blockage [3], gas well production performance analysis [4], well interference analysis [5,6,7], and productivity forecasting [8,9,10,11]. Coal seam pressure can reflect the enrichment of CBM, and it is also an important parameter for calculating CBM reserves and other parameters. The coal seam pressure is usually determined through actual measurements or calculated using models. The actual measurement of coal seam pressure requires shutting-in of the well for a period. Although the result is accurate, this condition is unrealistic for CBM wells pursuing continuous drainage and production. In addition, it cannot track the coal seam pressure for every producing time. Calculations using models can solve this problem, which are mainly based on the material balance principle [12,13,14,15,16,17].
Many researchers have conducted in-depth investigations on seam pressure predictions [18,19,20]. These can be interpreted by measuring the bottom hole pressure buildup after a stable production for some time, namely well test methods, which are mainly divided into Horner method [21], MBH method [22,23], MDH method [24], Dietz method [25], Chen’s method [26], and other methods [27,28,29]. In addition, the coal seam pressure can also be predicted based on dynamic production data using models, including material balance equations [30,31], energy conservation equations [32], and artificial intelligence models [33].
For coalbed methane reservoirs, many investigations have been conducted on the pressure distribution and propagation law of CBM reservoirs, and some have established models for the calculation of coal seam pressure. Zhao et al. [34] established a coal seam pressure distribution model based on the gas water two-phase seepage mechanism, revealing the propagation law of coal seam pressure. They then analyzed the sensitivities of the influencing factors. They concluded that seam compressibility would have a significant influence on the pressure propagation speed in the coal seam. Du et al. [35] studied the pressure propagation law under different boundaries and drainage schemes, They divided the pressure propagation process into two stages according the time when the pressure propagated to boundary and found that the dropping characteristics of the coal seam pressure in these two stages were different. Li et al. [36] revealed the pressure propagation mechanism, analyzed the influencing factors on pressure propagation in different production stages, and finally summarized a unified pressure propagation law. They found that the coal seam pressure propagation is related not only to reservoir porosity and permeability but also to fluid phase changes due to desorption of the adsorbed gas. Ge et al. [37] established a model for coal seam pressure calculation using the implicit difference method based on the fluid crossflow in a coal seam matrix and cleat. However, its applicable conditions are ideal, and the dissolved gas is ignored. Wang [38] and Zeng et al. [39] concluded that stress sensitivity needs to be considered when calculating the coal seam pressure based on their understanding from experiments that coal has a strong stress sensitivity which is prone to result in coal permeability damage. Su et al. [40] established a model for coal seam pressure calculations in different stages based on gas and water equations of state. However, dissolved gas and matrix shrinkage were not considered.
A sensitivity analysis is a commonly used method to quantify the relevant relationship between a model’s output and its inputs. The exploration degree for the space of input factors determines the credibility of the research results [41]. The one-at-a-time (OAT) approach, which changes only one factor value during each test, is commonly used for convenience to understanding and operation [42]. With increasing complexity of the models, the number of tests increases exponentially. As a result, in order to enhance the exploration efficiency for the space of input factors, researchers have proposed many global sensitivity analysis methods that can change multiple factors at one time, such as design of experiment (DOE), Monte Carlo analysis, Morris sensitivity analysis, DGSA, and Bayesian SA [43,44,45].
At present, few coal seam pressure prediction models consider the pressure difference between the initial reservoir pressure and the critical desorption pressure, free gas, dissolved gas, matrix shrinkage, and stress sensitivity at the same time. If these factors are ignored, the coal seam pressure will be misestimated with large error, especially for deep CBM reservoirs with a high initial formation pressure, low critical desorption pressure, and small Langmuir volume. In addition, the current methods for predicting coal seam pressure involve well testing or reservoir simulation, which affect the gas production continuity or calculation processes, which are complex. Furthermore, the commonly used numerical simulation software for the simulation of CBM production (CMG-GEM) not only cannot consider the pressure difference between the initial reservoir pressure and critical desorption pressure, but it also cannot consider the dissolved gas. In other words, with the incorrect original adsorbed gas in place Gai and original dissolved gas in place Gsi, the coal seam pressure of undersaturated CBM reservoirs cannot be predicted correctly using a commercial reservoir simulator. Thus, analytical models and corresponding methods for the timely prediction of coal seam pressure using dynamic production data during the whole CBM production process are necessary.
In this work, two models for real-time calculation of coal seam pressure before and after gas desorption are established based on the material balance principle in which pore compressibility, water compressibility, coal matrix shrinkage, dissolved gas precipitation, free gas expansion, and gas desorption are considered. Then, the proposed models and methods are verified against a numerical simulation case using computer modelling group (CMG) and two actual coalbed methane wells, A and B. Finally, a field application on well S is conducted, and the sensitivities of the influencing factors on coal seam pressure are analyzed.
2. Model Establishment
The development process of undersaturated CBM reservoirs can be divided into two stages, encompassing an early drainage stage and gas desorption stage. Methane desorption will not take place until the local formation pressure is less than the critical desorption pressure. During the early drainage stage, gas production occurs due to dissolved gas and free gas. A small amount of free gas may exist in coal cleats or larger pores of undersaturated CBM reservoirs because of the heterogeneity of coal seam and water blockage after drilling and completion [9]. As for the gas desorption stage, the produced gas is composed of adsorbed gas, dissolve gas, and free gas, but with adsorbed gas dominating. It is well-known in physics that the decline in the rate of formation pressure will be dramatically mitigated due to the gas desorption effect [5,10]. As a result, two different calculation models for coal seam pressure should be established based on the two mentioned production stages.
2.1. Assumptions
The models for calculating coal seam pressure of undersaturated CBM reservoirs are established based on the following assumptions:
- (1)
- The development process of undersaturated CBM reservoirs can be divided into an early drainage stage and gas desorption stage according to the critical desorption pressure; i.e., the influence of the critical desorption pressure is considered and two different models are established separately for these two stages.
- (2)
- The gas types include adsorbed gas, dissolved gas, and free gas in undersaturated CBM reservoirs. The special situation of the presence of free gas in undersaturated CBM reservoirs is also considered.
- (3)
- During the early drainage stage, the adsorbed gas cannot desorb, and the gas production occurs due to dissolved gas and free gas.
- (4)
- During the gas desorption stage, the produced gas is composed of adsorbed gas, dissolved gas, and free gas.
- (5)
- The desorption of the adsorbed gas is described by the Langmuir equation.
- (6)
- The dissolved gas in water conforms to Henry’s law.
- (7)
- The free gas conforms to the equation of state for real gas, i.e., the deviation factor Z is considered.
- (8)
- The stress sensitivity and matrix shrinkage effects on the porosity are considered.
- (9)
- The initial coal seam water expansion and water influx with decreasing coal seam pressure are considered.
- (10)
- The original gas in place remains constant during the whole production process.
2.2. Early Drainage Stage
Coalbed methane mainly exists in the adsorbed state in the coal matrix (more than 85%). A small amount of coalbed methane is in the free gas state (less than 10%), and a very small amount is dissolved in water (less than 5%) [36]. In the process of gas reservoir exploitation, the coal seam material balance equation considering free gas and dissolved gas at this stage [9,46] is as follows:
where Gp is the cumulative gas production, m3; A is the control area of single well, m2; h is the thickness of the reservoir, m; ϕi is the initial porosity, fraction; Swi is the initial water saturation, fraction; Zsc is the deviation factor under standard pressure, dimensionless; Tsc is the standard temperature, K; pi is the initial formation pressure, MPa; psc is the standard pressure, MPa; T is the coal seam temperature, K; Zi is the deviation factor under the initial formation pressure, dimensionless; Cs is the methane dissolubility coefficient in water, MPa−1; Cp is the pore compressibility factor, MPa−1; is the coal seam pressure, MPa; Sw is the coal seam water saturation, fraction; and is the deviation factor under the coal seam pressure, dimensionless.
The water saturation can be expressed as follows:
where Cw is the water compressibility factor, MPa−1; We is cumulative water influx, m3; Wp is the cumulative water production, m3; and Bw is the volume factor of formation water, m3/sm3.
Relevant research on the calculation model of water influx is relatively mature, including the Schilthuis steady state method, Van Everdingen–Hurst unsteady state method, Carter–Tracy unsteady state method, Fetkovich quasi-steady state method, and other material balance models [47,48,49,50,51].
Water influx We can be calculated using the Schilthuis steady state model [49]:
where (We)n is the cumulative water inflow, m3; Csw is water invasion constant, m3/(d·MPa); i is the coal seam pressure at ti time, MPa; and ∆ti is the time interval, d.
Actually, for coalbed methane wells, the water influx from the aquifer can be usually considered as zero. Because there are so many wells in a coalbed methane reservoir, separating the whole production zone into small pieces, for each single well-controlling area, the water influx We can be ignored. Thus, in the following derivation and field applications, We is assumed to be zero.
Substituting Equation (2) into Equation (1) gives the following:
The following four terms are defined as follows:
where Vpi is the initial pore volume, m3; Gfi is the original free gas in place, m3; and Gsi is the original dissolved gas in place, m3.
Equation (4) can be rewritten as the following expression:
According to the root-seeking formula, the calculation formula of the coal seam pressure is as follows:
where:
2.3. Gas Desorption Stage
When the CBM reservoir enters the gas desorption stage, the produced gas includes not only free gas and dissolved gas but also adsorbed gas. The CBM material balance equation incorporating gas desorption can be expressed as follows [52]:
where bL is the Langmuir pressure constant in MPa−1 and pd is the critical desorption pressure in MPa.
The water saturation and porosity model considering stress sensitivity and matrix shrinkage are as follows:
where Ca is the coal matrix shrinkage coefficient, which is dimensionless.
Here, ϕ is the coal seam porosity, expressed as a fraction.
Substituting Equations (15) and (16) into Equation (14), the material balance equation in the gas desorption stage can be expressed as follows:
where Gai is the original adsorbed gas in place, m3.
Equation (17) is an implicit function equation. The coal seam pressure can be solved using the Newton–Ralph method. According to this formula, the iterative equation is provided as follows:
The F function is as follows:
Derivation of both sides of Equation (20) based on the coal seam pressure at the same time gives the following:
2.4. Calculation Procedures
The calculation procedure of the coal seam pressure in the early drainage stage is as follows:
- (1)
- Collect the basic parameters of coal seam and the cumulative water and gas productions of the coalbed methane wells and substitute them into Equations (5)–(8) to calculate the M value, the initial pore volume, the original free gas in place, and original dissolved gas in place.
- (2)
- According to the gas specific gravity and coal seam temperature, the gas deviation factors at different pressures can be calculated using the DAK method [53,54]. Then, the relationship between the deviation factor and pressure can be obtained via data fitting.
- (3)
- Set the initial value 0 as the coal seam pressure, calculate the initial value of the deviation factor 0 corresponding to the pressure, then calculate the values of the coefficients a, b, and c according to the basic parameters and cumulative production data in the statistical table.
- (4)
- Substitute the coefficients into Equation (10) to obtain the calculated value of the coal seam pressure 1.
- (5)
- Replace the initial value 0 with the calculated value 1 and repeat steps (3)–(5) until the error between the current calculated value and the previous calculated value is less than the desirable engineering tolerance, then the current calculated value will be the coal seam pressure at the early drainage stage. When the final coal seam pressure is less than the critical desorption pressure determined through drainage and production data or isothermal adsorption experiments, the early drainage stage ends and the gas desorption stage starts.
The calculation procedure of the coal seam pressure in gas desorption stage is as follows:
- (1)
- Substitute the basic parameters of coal seam and the cumulative water and gas productions of the coalbed methane well into Equations (5)–(8) and Equation (18) to calculate the M value, the initial pore volume, the original free gas in place, the original dissolved gas in place, and the original adsorbed gas in place.
- (2)
- Set the initial value 0 as the coal seam pressure, calculate the initial value of the deviation factor 0 under the pressure 0 according to the fitted polynomial relationship between the deviation factor and the pressure, and substitute the above parameters into Equations (20) and (21) to calculate the F function and its derivative value F’.
- (3)
- Substitute the required parameters into Equation (19) for Newton iteration to obtain the calculated value of the coal seam pressure 1.
- (4)
- Replace the initial value 0 with the calculated value 1, and repeat steps (2)–(4) until the error between the current calculated value and the previous calculated value is less than the desirable engineering tolerance, then the current calculated value will be the coal seam pressure in the gas desorption stage.
The flowchart for calculating the coal seam pressure during coalbed methane production is shown in Figure 1.
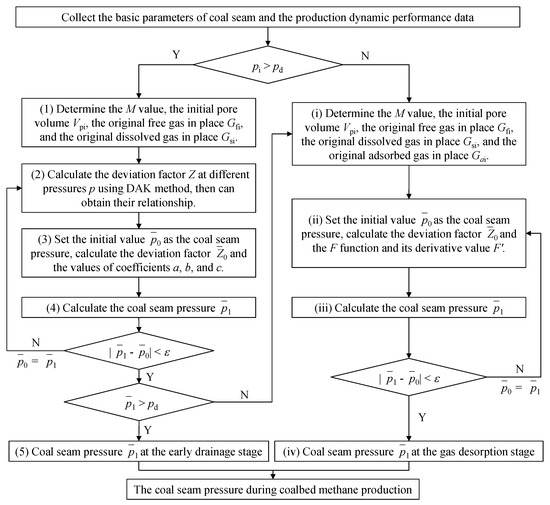
Figure 1.
The flowchart for calculating the average coal seam pressure during coalbed methane production.
3. Validation
3.1. Validation through a Synthetic Simulation Case
CMG-GEM is a commonly used numerical simulation software for coalbed methane. However, in GEM, the desorption pressure is equal to the initial reservoir pressure, and the characteristics of undersaturated coalbed methane reservoirs cannot be considered. In addition, the dissolved gas in water is ignored in GEM. In order to verify the reliability of the proposed model for the saturated CBM reservoir without considering dissolved gas, a synthetic model is established using the GEM component module in CMG software (CMG 2019.10) to simulate the production behavior of the saturated CBM reservoir without considering the dissolved gas. The model is divided into orthogonal uniform grids. The physical model is shown in Figure 2, and the basic parameters of the model are shown in Table 1.
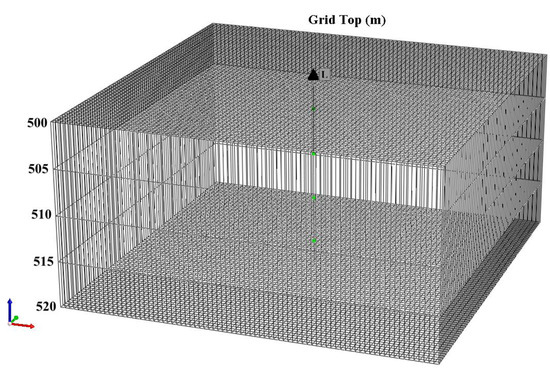
Figure 2.
3D stereogram of the synthetic simulation model of a coalbed methane reservoir.

Table 1.
Basic parameters of the CMG simulation model, well A and well B.
There is a vertical well in the center of the coalbed methane reservoir for production. Firstly, the daily water production of the well is set as 2 m3/d. When the bottom hole flow pressure is reduced to 1 MPa, the production scheme of the CBM reservoir switches to constant bottom-hole pressure. Ten years of dynamic data of the gas well are shown in Figure 3. Through numerical simulation, the coal seam pressure curve of the CBM reservoir in the production process can be output from the simulator, shown as the green points in Figure 3.
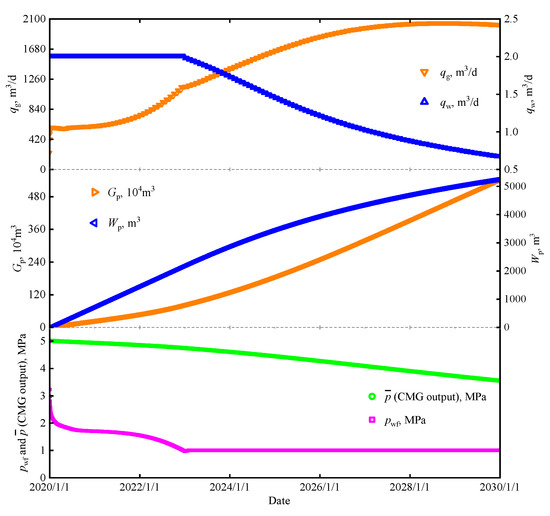
Figure 3.
Production performance curve and model prediction results of the CMG simulation model.
The cumulative gas production and water production of the coalbed methane well are substituted into the proposed model to calculate the coal seam pressure. The comparisons between the coal seam pressures calculated using the proposed method and those from the simulation results are displayed in Figure 4. It can be found that the error over the whole production process falls in the range of ± 1.00%, which meets the requirements of engineering applications. Thus, the established real-time calculation method of coal seam pressure is reasonable and reliable.
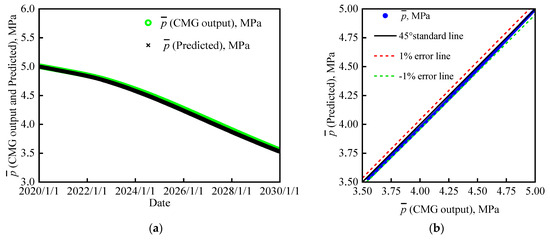
Figure 4.
Comparisons between coal seam pressures calculated using the proposed method and those from the simulation results: (a) coal seam pressure history comparison; (b) error analysis.
3.2. Validation through Field Cases
To further validate the effectiveness of this method, saturated coalbed methane well A, situated in the Hancheng block, and undersaturated coalbed methane well B, located in the Baode block, were selected for field applications.
3.2.1. Field Case I
Based on the reservoir parameters of well A, as shown in Table 1, the calculated original adsorbed gas in place Gai is 2.7 × 106 m3, the original free gas in place Gfi is 2.15 × 104 m3, and the original dissolved gas in place Gsi is 5.2 × 103 m3. The production performance history is depicted in Figure 5. At the beginning of well production, well A exhibits immediate gas production. During the production history, the average daily gas production was approximately 800 m3/day, and the average daily water production was less than 0.3 m3/day. By integrating the pertinent data of well A into both the complete model and the degraded model without Cs, the average reservoir pressure was calculated, as shown in Figure 5. Notably, the error of the average reservoir pressure derived from the complete model is −0.8027%. Conversely, the degradation model, by disregarding the presence of dissolved gas, engenders a little reduction in the gas reserve, consequently eliciting a larger error value of −4.87%.
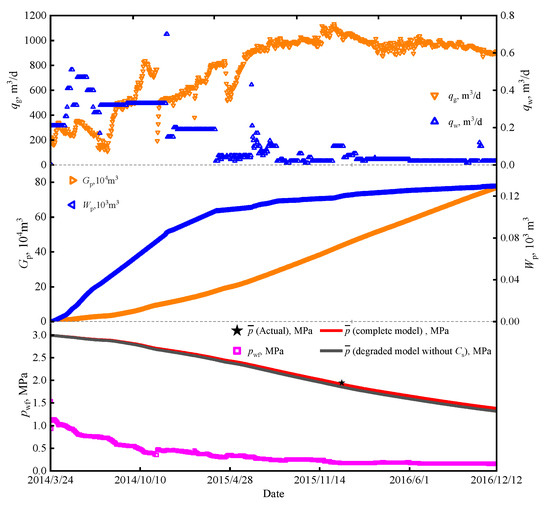
Figure 5.
Production performance curve and model prediction results of coalbed methane well A.
3.2.2. Field Case II
Based on the reservoir parameters of well B, as shown in Table 1, the calculated original adsorbed gas in place Gai is 3.8 × 107 m3, the original free gas in place Gfi is 9.4 × 105 m3, and the original dissolved gas in place Gsi is 5.1 × 105 m3. The production performance history is depicted in Figure 6. Well B began to produce gas after 500 days of operation, stabilizing at a daily gas production rate of approximately 1500 m3/day, coupled with an average daily water production rate of approximately 10 m3/day. By incorporating the pertinent data of well B into the complete model, the degradation model without considering Cs, and the degraded model without Cs and mistaking Pd for Pi, the average reservoir pressure dynamics were calculated, as shown in Figure 6. Notably, the error of the average reservoir pressure estimated by the complete model is only −0.9862%. However, the degradation model without considering Cs engenders an overall underestimation of the gas reserve, thereby manifesting a discernible error value of −11.45%. The degraded model without Cs and mistaking pd for pi overestimates the volume of adsorbed gas and consequently results in a markedly increased error value of 31.3%.
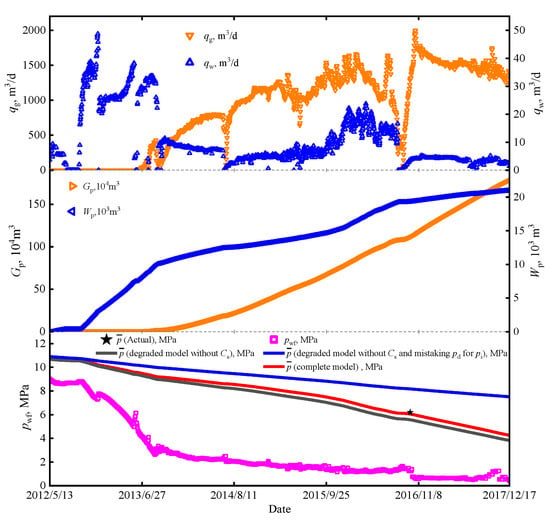
Figure 6.
Production performance curve and model prediction results of coalbed methane well B.
4. Sensitivity Analyses
In order to obtain the main factors affecting the coal reservoir pressure and accurately predict the coal reservoir pressure, sensitivity analyses of the influencing factors including pore compressibility, water compressibility, coal matrix shrinkage coefficient, methane dissolubility coefficient in water, initial free gas saturation, and critical desorption pressure on coal seam pressure were carried out based on the actual data of a coalbed methane well S. The basic parameters of the CBM reservoir where this coalbed methane well is located are shown in Table 2. The gas and water production data from this coalbed methane well are shown in Figure 7.

Table 2.
Basic parameters of the CBM reservoir where the coalbed methane well S is located.
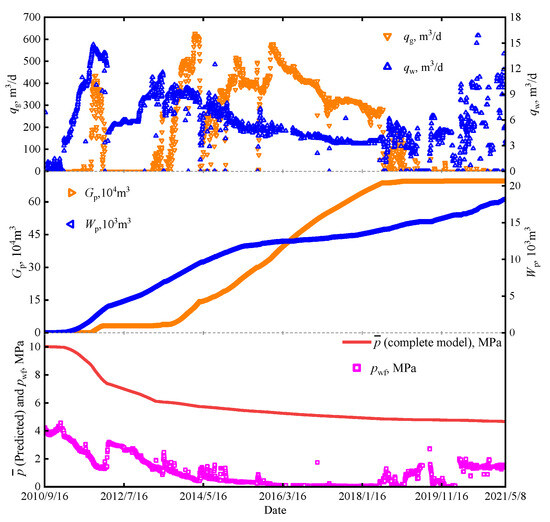
Figure 7.
Production performance curve of coalbed methane well S.
By using the proposed analytical method, the coal seam pressures controlled by this CBM well in the whole gas production history were calculated and are shown in Figure 7.
Next, the sensitivity analyses were conducted by changing any parameter in the last six lines and fixing the other parameters in Table 2. The ranges of Cp, Cw, Ca, Cs, Sgi, and pd are listed in Table 3.

Table 3.
The ranges of the basic parameters for well S.
The selection of the factor range selection, factor standardization, and formulation of evaluation criteria are the most important processes of sensitivity analyses that determine whether the analysis results are reasonable [50,51,52]. In this work, the sensitivities of the influencing factors on the coal seam pressure are analyzed as dimensionless. The range of each influencing factor f is determined using the actual production data, and the arithmetic mean between the maximum value fh and the minimum value fl is considered as the average value of each influence factor fa, which is taken as the benchmark value. The equation can be expressed as follows:
where fa is the average value of each influence factor, function; fh is the maximum value of each influence factor, function; fl is the minimum value of each influence factor, function.
The dimensionless variation spans of each influencing factor DVSf, defined as the ratio of its absolute difference from the average value fa versus the average value fa, can be expressed as follows:
where DVSf is the dimensionless variation span of each influencing factor, dimensionless; and f is the value of each influence factor, function.
Thus, the maximum dimensionless variation span of each influencing factor DVSfmax can be calculated by substituting fh or fl into Equation (24):
where DVSfmax is the maximum dimensionless variation span of each influencing factor, dimensionless.
For each day, for instance, the day i, three values of coal seam pressure can be calculated using the proposed method using fh, fa, and fl, which can be marked as i (fh), i (fa), and i (fl), respectively.
The maximum dimensionless variation span of the coal seam pressure DVSpmax is defined as follows:
where DVSpmax is the maximum dimensionless variation span of the coal seam pressure, dimensionless.
The sensitivity index of the factor f, marked as SIf, can be expressed as:
where SIf is the sensitivity index of factor f, dimensionless.
The sensitivity index can represent the sensitivity of a factor to coal seam pressure. Using this method, the sensitivity indexes for all the influencing factors can be determined based on this standard and ranked from highest to lowest. The results are shown in Table 4.

Table 4.
Sensitivity comparison among influencing factors.
It can be seen from Table 4 that the main factors affecting the real-time calculation of the coal seam pressure from strong to weak are the critical desorption pressure, initial free gas saturation, pore compressibility, methane dissolubility coefficient in water, water compressibility, and coal matrix shrinkage. In particular, the accuracies of the critical desorption pressure and initial free gas saturation directly affect the accuracy of the predicted coal seam pressure; thus, these two parameters should be determined with more attention in order to accurately predict the coal seam pressure. On the contrary, water compressibility and the coal matrix shrinkage coefficient rarely affect the coal seam pressure, so the accurate determination of these two parameters is not necessary.
5. Discussion
Normally, the development process of undersaturated CBM reservoirs has two stages: an early drainage stage and gas desorption stage. The presence of the critical desorption pressure pd and methane dissolubility coefficient in water Cs presents challenges to the analytical method for the timely prediction of coal seam pressure. In this research, for each production stage, considering the comprehensive influence of the critical desorption pressure, dissolved gas, matrix shrinkage, and stress sensitivity, the material balance principle is used to establish the analytical method for predicting the coal seam pressure.
As a commonly used numerical simulation software for coalbed methane, CMG-GEM can be used to simulate the CBM production from saturated CBM reservoirs in cases where dissolved gas can be ignored. Applying the proposed method to the simulation case from CMG-GEM for a saturated CBM reservoir without considering the dissolved gas, the relative errors of the proposed method (the outputs from the simulation case are considered as the real values) during the whole production process fall within the range of ±1.00%, verifying the effectiveness of the proposed method when ignoring the influence of pd and Cs.
Applying the proposed method to the saturated coalbed methane well A and the undersaturated coalbed methane well B, compared with actual measured coal seam pressure, the relative errors are also within 1% for both well A and well B. However, ignoring Cs can lead to a lack of Gsi, engendering a lower predicted pressure with relative error of −4.87% for well A and −11.45% for well B. Ignoring Cs and mistaking pd for pi for undersaturated CBM reservoirs can lead to overestimation of Gai, engendering a higher predicted pressure with very large relative error of 31.3% for well B. The results indicate that for undersaturated coalbed methane reservoirs, the proposed method has a higher prediction accuracy and superiority.
As shown in Table 4, the single-factor sensitivity analysis results indicate that for the undersaturated coalbed methane well S, pd is the most sensitive influencing factor, and Cs has a stronger sensitivity than Cw and Ca. It once again reveals the necessity of applying this pressure prediction method to undersaturated coalbed methane reservoirs.
One thing that needs to be mentioned is that the proposed method is established on the basis of the material balance principle. Thus, the formation and fluid properties as well as the coal seam pressure and water saturation are all the average values, and the geological uncertainty of coal formation is not considered in this work. Future research should focus on expanding its application in geological uncertainty to enhance the accuracy of the pressure prediction in undersaturated coalbed methane reservoirs.
6. Conclusions
Based on the material balance principle, analytical models and corresponding methods for predicting coal seam pressure in the whole process of coalbed methane production for undersaturated CBM reservoirs are established, considering the critical desorption pressure, dissolved gas, matrix shrinkage, and stress sensitivity. The method is simple and can be used to quickly determine the coal seam pressure without a shut-in operation.
The verifications in the CMG-GEM simulation case and field cases show that the coal seam pressure predicted using the new method in real time is very close to the actual measured pressure, with the relative errors all within 1%, which meets the requirements of engineering accuracy. However, if we ignore the comprehensive influence of the critical desorption pressure, dissolved gas, matrix shrinkage, and stress sensitivity, the relative error for the degraded method is very large, in some cases as high as 31.3%.
The main factors affecting coal seam pressure from strong to weak are the critical desorption pressure, initial free gas saturation, pore compressibility, methane dissolubility coefficient in water, water compressibility, and coal matrix shrinkage. The critical desorption pressure and initial free gas saturation are more sensitive to the coal seam pressure, while water compressibility and coal matrix shrinkage have little influence.
Author Contributions
Methodology, Y.J. and J.S.; validation, L.Z. and W.L.; analysis, Y.H. and Y.L.; writing—review and editing, J.C., C.J. and H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the State Key Program of the National Natural Science Foundation of China (No. 42230814) and Science and Technology Major Projects of Shanxi Province, China (No. 20201101002). The authors also acknowledge the Science Foundation of China University of Petroleum, Beijing (No. 2462020QNXZ003) for their support of part of this work.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The authors thank the Computer Modelling Group for giving them the authorization to use the CMG-GEM software (CMG-GEM 2019.10).
Conflicts of Interest
Authors Longlong Zhang and Yifan He were employed by the company Tianjin Branch of China National Offshore Oil Corporation Ltd. Author Wenbin Li was employed by the company Liaohe Oilfield of Petrochina. Author Hongxing Huang was employed by the company China United Coalbed Methane National Engineering Research Center Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Xu, F.-Y.; Wang, B.; Zhao, X.; Yun, J.; Zhang, S.-Y.; Wang, H.-Y.; Yang, Y. Thoughts and suggestions on promoting high quality development of China’s CBM business under the goal of “double carbon”. China Pet. Explor. 2021, 26, 9–18. [Google Scholar]
- Zeng, Q.; Wang, Z. Stress and temperature sensitivity of coal permeability in the Eastern Ordos Basin. Pet. Sci. Bull. 2020, 4, 512–519. [Google Scholar]
- Shi, J.; Wu, J.; Fang, Y.; Lu, J.; Hou, C.; Li, X.; Zhang, S.; Xiong, X. A new coal seam permeability model considering the influence of pulverized coal blockage and its application. Nat. Gas Ind. 2020, 40, 78–89. [Google Scholar]
- Qin, Y.; Wu, J.; Zhang, Z.; Yi, T.; Yang, Z.; Jin, J.; Zhang, B. Analysis of geological conditions for coalbed methane co-production based on production characteristics in early stage of drainage. J. China Coal Soc. 2020, 45, 241–257. [Google Scholar]
- Mora, C.A.; Wattenbarger, R.A. Comparison of computation methods for CBM production performance. J. Can. Pet. Technol. 2009, 48, 42–48. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Qanbari, F. A semi-analytical method for forecasting wells completed in low permeability, undersaturated CBM seams. J. Nat. Gas Sci. Eng. 2016, 30, 19–27. [Google Scholar] [CrossRef]
- Matteo, M.P.; Donald, L.; Dan, S.; Adrian, M. Advanced modeling of interwell-fracturing interference: An eagle ford shale-oil study. SPE J. 2016, 21, 1567–1582. [Google Scholar]
- Zhong, Z.; Wu, X.; Han, G. Pressure and saturation relationship in CBM seam and the semi-analytical production forecast model for the horizontal well. Pet. Sci. Bull. 2017, 2, 251–257. [Google Scholar]
- Shi, J.; Chang, Y.; Wu, S.; Xiong, X.; Liu, C.; Feng, K. Development of material balance equations for coalbed methane seams considering dewatering process, gas solubility, pore compressibility and matrix shrinkage. Int. J. Coal Geol. 2018, 195, 200–216. [Google Scholar] [CrossRef]
- Shi, J.; Jia, Y.; Wu, J.; Xu, F.; Sun, Z.; Liu, C.; Meng, Y.; Xiong, X.; Liu, C. Dynamic performance prediction of coalbed methane wells under the control of bottom-hole pressure and casing pressure. J. Pet. Sci. Eng. 2021, 196, 107799. [Google Scholar] [CrossRef]
- Shi, J.; Wu, J.; Sun, Z.; Xiao, Z.; Liu, C.; Sepehrnoori, K. Methods for simultaneously evaluating reserve and permeability of undersaturated coalbed methane seams using production data during the dewatering stage. Pet. Sci. 2020, 17, 1067–1086. [Google Scholar] [CrossRef]
- Mattar, L.; Mcneil, R. The “flowing” gas material balance. J. Can. Pet. Technol. 1998, 37, 52–55. [Google Scholar] [CrossRef]
- Mattar, L.; Anderson, D.; Stotts, G. Dynamic material balance-oil-or gas-in-place without shut-ins. J. Can. Pet. Technol. 2006, 45, 7–10. [Google Scholar] [CrossRef]
- Gonzalez, F.E.; Ilk, D.; Blasingame, T.A. A quadratic cumulative production model for the material balance of an abnormally pressured gas seam. In Proceedings of the SPE Western Regional and Pacific Section AAPG Joint Meeting 2008, SPE 114044, Bakersfield, CA, USA, 31 March–1 April 2008. [Google Scholar]
- Dusseault, M.B. Geomechanical challenges in petroleum reservoir exploitation. KSCE J. Civ. Eng. 2011, 15, 669–678. [Google Scholar] [CrossRef]
- Li, P.; Kong, X.; Lu, D. Calculating average gas seam pressure by integrating pseudo pressure distribution. Nat. Gas Ind. 2000, 20, 67–69. [Google Scholar]
- Zhang, L.; Wang, Y.; Ni, J.; Qiao, X.; Xin, C.; Zhang, T.; Kang, Y.; Shi, J.; Wu, K. A new method for tracking and calculating average formation pressure of gas seams. Acta Pet. Sin. 2021, 42, 492–499. [Google Scholar]
- Muskat, M. Use of data oil the build-up of bottom-hole pressures. Trans. AIME 1937, 123, 44–48. [Google Scholar] [CrossRef]
- Araps, J.J.; Smith, A.E. Practical use of bottom-hole pressure buildup curves. In Drilling and Production Practice; API: New York, NY, USA, 1949; pp. 155–165. [Google Scholar]
- Brons, F.; Miller, W.C. A simple method for correcting spot pressure readings. J. Pet. Technol. 1961, 13, 803–805. [Google Scholar] [CrossRef]
- Horner, D.R. Pressure build-up in wells. In Proceedings of the 3rd World Petroleum Congress, The Hague, The Netherlands, 28 May–6 June 1951; pp. 503–523. [Google Scholar]
- Matthews, C.S.; Brons, F.; Hazebroek, P. A method for determination of average pressure in a boundary seam. Trans. AIME 1954, 201, 182–191. [Google Scholar] [CrossRef]
- Kazemi, H. Determining average seam pressure from pressure buildup tests. Soc. Pet. Eng. J. 1974, 14, 55–62. [Google Scholar] [CrossRef]
- Miller, C.C.; Dyes, A.B.; Hutchinson, C.A. The estimation of permeability and seam pressure from bottom-hole pressure build-up characteristics. Trans. AIME 1950, 2, 91–104. [Google Scholar]
- Dietz, D.N. Determination of average seam pressure from build-up surveys. J. Pet. Technol. 1965, 17, 955–959. [Google Scholar] [CrossRef]
- Chen, Y. A method of determining seam pressure by match data of the type curve. Acta Pet. Sin. 1988, 9, 67–74. [Google Scholar]
- Lu, D.; Kong, X. By use of the integral of pressure distribution to calculate the average seam pressure. Acta Pet. Sin. 1993, 14, 81–91. [Google Scholar]
- Hu, J. A simple method for determining average formation pressure of oil and gas well by using MDH method. Pet. Geol. Oilfield Dev. Daqing 1995, 14, 39–42. [Google Scholar]
- Kambiz, R.; Abdolnabi, H.; Abdolhassan, R. A least squares approach to estimating the average seam pressure. Iran. J. Oil Gas Sci. Technol. 2013, 2, 22–32. [Google Scholar]
- Orozco, D.; Aguilera, R. Use of dynamic data and a new material-balance equation for estimating average seam pressure, original gas in place, and optimal well spacing in shale gas seams. SPE Seam Eval. Eng. 2018, 21, 1035–1044. [Google Scholar]
- Yin, H.; Wen, G.; Xing, C.; Fu, J.; Perapon, F. Average formation pressure calculation for the composite oil seam with multi-well system. Spec. Oil Gas Seams 2019, 26, 76–80. [Google Scholar]
- Huang, X.; Qi, Z.; Lei, D.; Li, J. Energy weighing method to calculate the average pressure of gas seam. J. Chongqing Univ. Sci. Technol. (Nat. Sci. Ed.) 2014, 16, 24–26. [Google Scholar]
- Hu, C.; Wang, F.; Ai, C. Calculation of average seam pore pressure based on surface displacement using image-to-image convolutional neural network model. Front. Earth Sci. 2021, 9, 712681. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, S. Study on pressure drop transmission law of coal bed methane drainage seam stratum. Coal Sci. Technol. 2012, 40, 65–68. [Google Scholar]
- Du, Y.; Wu, C.; Zou, M.; Wang, C.; Jiang, W.; Lei, B. Study on seam pressure transmission law during gas mining and drainage process of coal bed methane well. Coal Eng. 2011, 1, 87–89. [Google Scholar]
- Li, X.; Pu, Y.; Sun, C.; Ren, W.; Li, Y.; Zhang, Y.; Li, J.; Zang, J.; Hu, A.; Wen, S.; et al. Recognition of absorption/desorption theory in coalbed methane seam and shale gas seam. Acta Pet. Sin. 2014, 35, 1113–1129. [Google Scholar]
- Ge, J.; Bai, X.; Chen, L. Prediction of seam pressure changes during CBM exploitation. Seam Eval. Dev. 2014, 4, 62–65. [Google Scholar]
- Wang, L. Research on the pressure sensitivity for low permeability fractured coalbed methane seam. Miner. Explor. 2020, 11, 157–162. [Google Scholar]
- Zeng, Q.; Gao, Q.; Wang, Z. Experimental and modeling studies on high pressure methane adsorbed on coals. Pet. Sci. Bull. 2020, 01, 78–92. [Google Scholar]
- Su, X.; Zhang, L. Prediction of seam pressure for coalbed gas. Nat. Gas Ind. 2004, 24, 88–90. [Google Scholar]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, T.; MacBeth, C. Fast assimilation of frequently acquired 4D seismic data for reservoir history matching. Comput. Geosci. 2019, 128, 30–40. [Google Scholar] [CrossRef]
- Shin, M.-J.; Guillaume, J.H.A.; Croke, B.F.W.; Jakeman, A.J. Addressing ten questions about conceptual rainfall–runoff models with global sensitivity analyses in R. J. Hydrol. 2013, 503, 135–152. [Google Scholar] [CrossRef]
- Yin, Z.; Strebelle, S.; Caers, J. Automated Monte Carlo-based quantification and updating of geological uncertainty with borehole data (AutoBEL v1. 0). Geosci. Model Dev. 2020, 13, 651–672. [Google Scholar] [CrossRef]
- Da Veiga, S. Global sensitivity analysis with dependence measures. J. Stat. Comput. Simulat. 2015, 85, 1283–1305. [Google Scholar] [CrossRef]
- Shi, J.; Sun, Z.; Liu, C.; Lv, M.; Fang, J.; Jia, Y.; Wu, S.; Li, X. An analytical model for fast and accurate prediction of production performance of coalbed methane wells. Nat. Gas Ind. 2018, 38 (Suppl. S1), 43–49. [Google Scholar]
- Klins, M.A.; Bouchard, A.J.; Cable, C.L. A polynomial approach to the van Everdingen-Hurst dimensionless variables for water encroachment. SPE Reserv. Eng. 1988, 3, 320–326. [Google Scholar] [CrossRef]
- Carter, R.D.; Tracy, G.W. An improved method for calculating water influx. Trans. AIME 1960, 219, 415–417. [Google Scholar] [CrossRef]
- Schilthuis, R.J. Active oil and seam energy. Trans. AIME 1963, 118, 33–52. [Google Scholar] [CrossRef]
- Fetkovich, M.J.; Reese, D.E.; Whitson, C.H. Application of a general material balance for high-pressure gas seams. SPE J. 1998, 3, 3–13. [Google Scholar] [CrossRef]
- Yan, Z.; Shi, J.; Qin, F.; Hong, S.; Bai, M. A new method for calculating dynamic seam and water influx of water drive gas seams. China Offshore Oil Gas 2021, 33, 93–103. [Google Scholar]
- Shi, J.T.; Jia, Y.R.; Zhang, L.L.; Ji, C.J.; Li, G.F.; Xiong, X.Y.; Huang, H.X.; Li, X.F.; Zhang, S.A. The generalized method for estimating reserves of shale gas and coalbed methane reservoirs based on material balance equation. Pet. Sci. 2022, 19, 2867–2878. [Google Scholar] [CrossRef]
- Dranchuk, P.M.; Abou-Kassem, H. Calculation of Z Factors for natural gases using equations of state. J. Can. Pet. Technol. 1975, 14, 34–36. [Google Scholar] [CrossRef]
- Li, X.; Zhuang, X.; Gang, T.; Sui, X.; Xie, L. Comprehensive appraisal and selection for gas compressibility factor calculating model. Oil Drill. Prod. Technol. 2001, 2, 42–46. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).