Abstract
In order to investigate the rational utilization of energy in the fluid jet process, a free dual jet of parallel air is used as a research object. Simulation of turbulence was carried out based on the realizable k-epsilon equations with pressure-velocity coupling, PISO method, discrete method with second-order windward format, and first-order implicit transient solution. The energy separation phenomenon within the jet shear layer and its influencing factors were investigated under dual-jet Reynolds number differences of 12,800, 19,200, 25,600, 32,000, 41,500, and 51,100, respectively. The simulation is in transient format and the jet inlet velocity is given by udf. Calculations show that the pressure perturbation in the air shear layer, which gives rise to the pressure work exchange between the jet and the surroundings, is the main reason for the coexistence of high- and low-temperature regions formed within the jet shear layer, and the larger the Reynolds number, the stronger the energy separation effect. The center streamline path of a parallel air free dual jet can be fitted by a circular arc, whose radius of curvature increases with the Reynolds number, and the curvilinear development path of the dual jet can offset the energy separation effect to some extent. This paper confirms the existence of energy separation in the shear layer of a parallel air free double jet, reveals the mechanism of energy separation in the fluid domain, and explores the flow characteristics of two parallel jets.
1. Introduction
Energy separation refers to the phenomenon whereby a system spontaneously separates into a part of the high-temperature zone and a part of the low-temperature zone in the absence of external work or heat conduction. Since the French engineer Ranque first observed the energy separation phenomenon in the vortex tube in the 1930s [1], researchers have observed the energy separation phenomenon in other flow conditions, such as free jet, vortex, impinging jet, and flow around circular cylinder, and studied its laws. Currently, the research on energy separation [2,3,4,5,6,7] mainly focuses on the technical application level of vortex tubes and vortex plates based on the Ranque–Hilsch effect, which belongs to the engineering thermodynamics problem. Regarding the study of the operation mechanism of energy separation in the field of fluid mechanics such as free jet, impinging jet, blunt-body flow, etc., researchers have made some experimental and theoretical in-depth studies on this, but they also mainly focus on the single jet. Research on the combined jet is few and far between. However, multiple jets are also encountered in practical engineering applications, such as multiple jets impinging on downstream water cushion ponds in high head relief projects, and impinging jet on the fuselage and the ground during take-off and landing of aircraft in vertical take-off (landing) in aerospace projects. Therefore, understanding and mastering the characteristics of multiple jets are of great significance in guiding the solution of practical engineering problems.
In the 1940s, Eckert and Drewitz [8] discovered the existence of energy separation in the boundary layer by analyzing the temperature field in the air boundary layer along the direction of the flow pressure gradient. Subsequently, Eckert and Weise [9] found that energy separation also exists in turbulent vortex streets when they measured the recovery temperature of a high-velocity gas stream around a cylindrical flow. Goldstein et al. [10,11] first observed energy separation in shock jets in 1986 and 1990. The experimental results show that when the experimental nozzle and the adiabatic plate are not far away from each other, a significant minimum value in the radial recovery temperature distribution occurs. They suggest that this is due to the energy separation effect produced by the circular vortex motion in the jet. Another study [10,11,12,13] measured the temperature distribution of the flow field in free jets, confirming that both Reynolds number and acoustic excitation can enhance the energy separation effect within a certain range. Han [14] experimentally measured the instantaneous total temperature and velocity distributions of free jets under different Reynolds numbers and different acoustic excitation conditions. The results not only led to similar conclusions to those of the previous authors, but also showed there is a certain influence of Reynolds number on the energy separation phenomenon—the larger the Reynolds number is, the more obvious the energy separation phenomenon is—and also revealed that acoustic excitation enhances the process of the energy separation effect by influencing the vortex pair fusion motion. Fox and Kurosaka [15] were the first to investigate the energy separation phenomenon in supersonic jets. They experimentally measured the total temperature distribution of a free jet from subsonic to supersonic conditions, and found that when the speed of sound reaches supersonic, there are more low values in the temperature distribution, which indicates that the energy separation of supersonic free jet is more obvious. Leontiev et al. [16] experimentally investigated the heat transfer phenomena within two coaxial pipes, and the data verified that the energy separation effect of the compressible boundary layer enhanced the heat transfer process between the two pipes. Through these experiments, people have discovered, recognized, and tried to explain the generation mechanism of energy separation phenomenon under different flow conditions step by step, which has provided significant enlightenment and research direction for subsequent research.
In addition to experimental studies, numerical simulations provide researchers with a more intuitive and effective way to study energy separation effects. Fox and Kurosaka [17] numerically simulated the energy separation in free jets and impinging jets under inviscid and non-conducting conditions. The authors simulated the energy separation in free jets under different Mach number conditions. The simulation results are in good agreement with the experimentally obtained data, clearly indicating the existence of energy separation phenomena, and the process of vortex twinning was found to enhance the total temperature distribution. Han et al. [18] numerically simulated the energy separation of two parallel jets to obtain the distribution of instantaneous velocity, pressure, and temperature in a two-dimensional planar shear layer flow field, and the results can clearly show the energy separation effect. They found that the vortex development is accelerated and the energy separation is enhanced with the increase in the Reynolds number.
Scholars have carried out a large number of experimental and numerical simulation studies on the energy separation phenomenon in the field of fluids, but most of the numerical simulations for free jets are focused on single jets at lower Reynolds numbers and with less consideration of viscous effects. However, at lower Reynolds number conditions, the effect of viscous shear on energy separation cannot be neglected. In this paper, two parallel air free jets with different velocities are taken as the object of study to numerically simulate the energy separation phenomenon of the free jet when the inlet velocities are both subsonic. We study the effect of higher Reynolds number on its specificity by taking into account the viscous and thermal conductivity conditions. Adopting the dimensionless turbulence control equations, and on the basis of the previous theoretical and experimental methods, both theoretical analysis and numerical simulation are carried out to verify the existence of the free jet energy separation phenomenon in the subsonic range and the influence of high Reynolds number on the energy separation, and we investigate the formation mechanism of the energy separation of the two parallel free jets and the flow characteristics of the dual jet.
2. Theoretical Analyses
2.1. Analysis of the Causes of Energy Separation
To date, researchers have observed energy segregation under many flow conditions and generally agree with the formation mechanism proposed by Eckert [19]. Assuming a constant specific heat capacity of the fluid to its surroundings, the total energy conservation equation is as follows:
The left side of the equation represents the change in total fluid energy along its pathline; the first term on the right-hand side of the equation is the hydrostatic pressure fluctuation at a given point; k is fluid thermal conductivity; the second and third terms on the right-hand side of the equation represent the energy transfer resulting from heat transfer and viscous shear work.
For steady state boundary layer flow, Equation (1) can be simplified as follows:
This equation implies that the total temperature can be varied along the streamline by heat transfer or viscous work. The energy separation in the boundary layer flow is caused by an imbalance between these two terms. When the Prandtl number () of a fluid is less than unity including air, heat transfer is greater than viscous work. As a result, the total temperature of the interior region adjacent to the insulated wall will be less than the total temperature of the exterior region.
For unsteady flow without heat transfer and neglecting viscous effects, the second and third terms of Equation (1) are negligible and the conservation equation can be simplified as follows.
In Equation (3), the total fluid temperature fluctuation is only related to the hydrostatic pressure change, and the hydrostatic pressure change generally occurs together with the vortex motion, so that for free jets at subsonic speeds, the energy separation of the free jet is more caused by the pressure fluctuation accompanying the vortex motion when the consideration of the viscous force and the heat conduction effect is neglected.
Since energy separation in boundary layer flows is related to viscous work and heat transfer, entropy always increases due to the irreversibility of the fluid. Therefore, it is reasonable to use the second law of thermodynamics to explain energy separation. Consider the energy separation of inviscid and non-conducting ideal gases with constant properties. The equation for the conservation of total energy expressed in terms of total temperature can be rewritten in total form as follows.
The total enthalpy, can be expressed in terms of static melt () and velocity ():
After inserting Equation (5) into Equation (4), the total energy conservation can be simplified as follows:
Based on the relationship between entropy and enthalpy, the enthalpy can rewrite melting in terms of entropy and pressure.
Assuming that the gas is a non-viscous, non-conducting fluid, the momentum conservation equation can be simplified to the following Euler equation:
Combining Equations (7) and (8) with Equation (6) results in the following:
Move the pressure gradient term to the right-hand side of Equation (9):
The right-hand side of Equation (10) is defined in the same way as the material derivative of pressure, and thus yields the following:
Equation (8) can be simplified as follows:
This means that the entropy of the fluid remains constant along its path. Thus, the energy separation of an ideal gas is an isentropic process and follows the second law of thermodynamics.
2.2. Numerical Perturbation Stability Analysis
In order to simulate the experimental flow conditions, small disturbances were introduced in the inlet plane. The instability of incompressible mixed layers to small perturbations belongs to the Kelvin–Helmholtz instability. The perturbations were obtained from the stability analysis of the inviscid flow, and the most unstable frequency and its two subharmonic frequencies were chosen as the frequencies of the disturbances. The linear stability analysis of the fluid is based on the continuity equation and unsteady N-S equation.
The magnitude of the inlet velocity of the introduced free jet is as follows:
The energy separation phenomenon of the free jet at different velocities is realized by numerical simulation; the energy separation intensity is characterized by a dimensionless energy separation factor as follows:
Most of the energy separation occurs in the shear layer, so depending on the thickness of the initial shear layer (), the relative Reynolds number ∆Re is defined as follows:
2.3. Computational Domain, Boundary Conditions and Meshing
The computational domain is taken as a two-dimensional rectangle with a grid of 200 in x and 100 in y, inlet1 and linlet2 are respectively set up, and the diameters of the two outlets D are both 5 mm. The numerical model and boundary conditions are shown in Figure 1 and Table 1. The computational domain is bounded by no-slip wall boundary conditions at both the upper left and lower left ends. In the center are the two velocity inlets of the free jet of air, and the relationship between the upper and lower is maintained at a fixed ratio. The relative Reynolds numbers for each of the five free jet groups are 12,800, 19,200, 25,600, 32,000, 41,500, and 51,100. In this paper, the meshed model is imported into ANSYS FLUENT for the calculation parameters. Simulation of turbulence based on the realizable k-epsilon equations with pressure–velocity coupling, PISO method, discrete method with second-order windward format, and first-order implicit transient solution. The computational model opens the energy equation and does not account for gravity. Unsteady transient flow, and the maximum residual value is 0.001, calculated using a first-order implicit transient solution with a time step of s. The medium is air and all physical parameters are kept as default. A quadrilateral structured grid is used in gambit. In order to obtain the energy separation effect of the free jet flow field more clearly, the grid encryption process is carried out in the vicinity of the jet boundary layer. The number of grids is obtained to be 67,574.
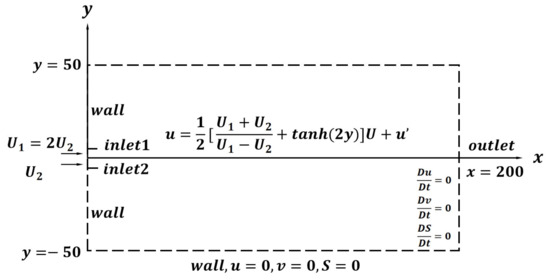
Figure 1.
Schematic diagram of the computational domain and boundary condition.

Table 1.
Boundary conditions.
The number of meshes has the potential to affect the accuracy of the calculations, so a mesh-independent analysis is performed. Calculate the static pressure difference in the free jet flow field at t = 240, , for five different grid accuracies. It can be seen from Figure 2 that the static differential pressure in the free jet flow field increases with the number of nodes. However, once the number of nodes reaches about 52,300, the tendency to continue to increase is not obvious. That is, the computational method under such conditions has satisfied the grid-independence. For economic considerations, a grid with a node count of 67,574 is chosen in this paper.
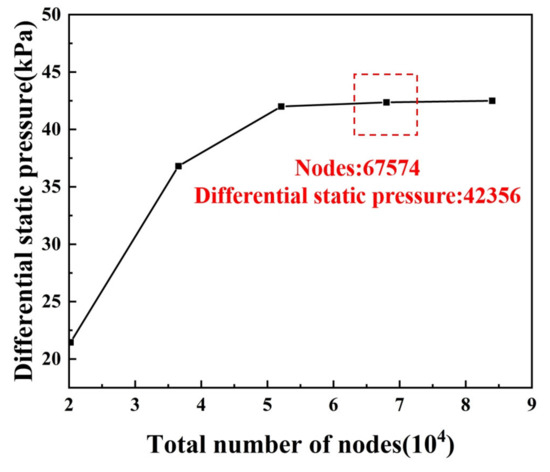
Figure 2.
Grid independence analysis.
3. Analysis of the Results
3.1. Energy Separation Phenomena in Free Jet
The energy separation factor for two free jets for at t = 120, t = 240 and t = 270 is shown in Figure 3. During this time period, the process from the appearance of significant energy separation within the jet field to the stabilization of the separation phenomenon is recorded. The fusion of the two adjacent vortices of the free jet is completed. Alternating high- and low-temperature regions can be seen in the free jet flow field at t = 120. Until t = 270, the energy separation effect tends to stabilize and is clearly divided into upper and lower high- and low-temperature regions. The total temperature separation is evident at x = 50. As the jet gets farther away from the nozzle exit, the energy separation region slowly becomes larger and the energy separation factor slowly increases. The maximum value of the energy separation factor occurs at x about 150 when t = 240, whose value is around 13. Thereafter, the energy separation factor becomes smaller and gradually diverges. The energy separation effect becomes weaker until it disappears. It can be seen that the location of the separation coincides essentially with the location of the vortex center, but the temperature distribution is asymmetric.
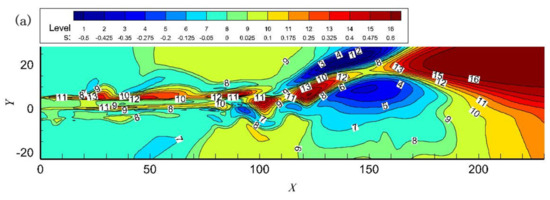
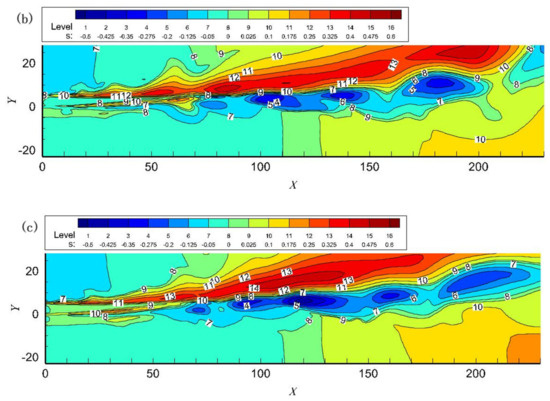
Figure 3.
Instantaneous total temperature distribution for when (a) t = 120; (b) t = 240; (c) t = 270.
Instantaneous pressure distribution in Figure 4 clearly shows alternating high- and low-pressure regions within the free jet flow field, with vortices distorting the pressure field. A distinct region of high and low pressure begins to appear near x = 50 from t = 240 to t = 270. When t = 120, the lowest-pressure zone occurs at x = 150 with a pressure rating of about 3. The adjacent high-pressure zone has a rating of about 18. The pressure fluctuation rating of about 15, after which the high- and low-pressure zones slowly become larger; When t = 240, the lowest-pressure zone occurs at x = 180 with a pressure rating of about 6. The adjacent high-pressure zone has a rating of about 18. When t = 270, the lowest-pressure zone occurs at x = 200 with a pressure rating of about 8. The adjacent high-pressure zone has a rating of about 17. The pressure fluctuation rating of about 9. The adjacent high- and low-pressure fluctuations can be seen to be weakened. It can be seen by comparing the energy separation factor cloud diagrams that the high-pressure region produces low temperatures, while the low-pressure region produces high temperatures. As the high- and low-pressure regions become larger and stronger, the corresponding resulting high- and low-temperature regions also become larger and stronger.
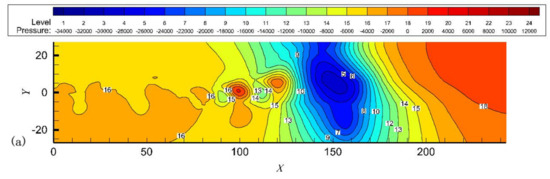
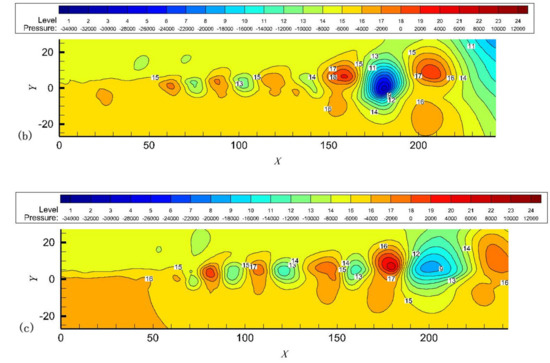
Figure 4.
Instantaneous pressure distribution for when (a) t = 120; (b) t = 240; (c) t = 270.
In Figure 5, the process of free-jet vortex generation, coiling and absorption, pairing and fusion, and weakening and disappearance can be clearly seen. In the region close to the inlet, the air free jet path is essentially straight. This region maintains the velocity at the exit of the nozzle. In the boundary layer of the jet at some distance from the nozzle, the high-velocity jet creates a shear layer, which, due to the rapid growth of the natural instability of the shear layer, forms a vortex, which leads to a swirling suction of the surrounding fluid, which draws the surrounding non-spinning fluid into the jet. Vortices continue to be created, expand, and develop, increasing the width of the jet and eventually breaking up into smaller vortices until they disappear.
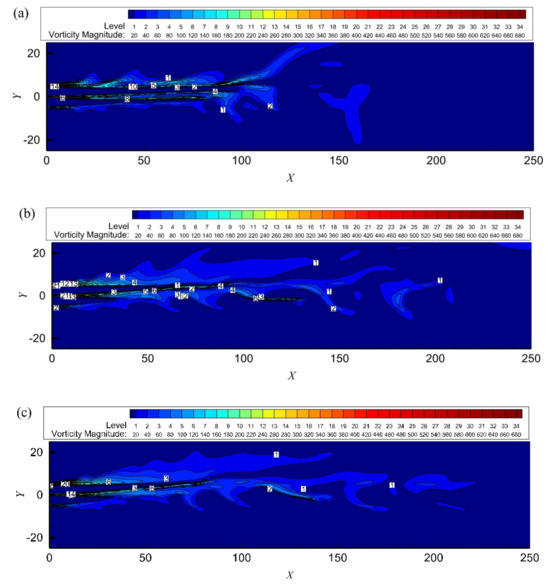
Figure 5.
Instantaneous vorticity distribution for when (a) t = 120; (b) t = 240; (c) t = 270.
Comparison of the instantaneous pressure distribution in Figure 4 shows that there is a low-pressure region near the center of the vortex and a high-pressure region between the vortices. Comparison of the energy separation factors in Figure 3 shows that the upper half of lower half produces a low-temperature region. These small vortices merge with neighboring vortices. The disturbance applied to the intake tract surface begins to increase and rolls up to form a vortex. The merging vortex moves downstream and combines with another merging vortex. After the vortices merged, the downward slowly weakened and disappeared, causing the pressure fluctuations to taper off and disappear. At the same time, the energy separation effect also weakens until it disappears.
As the vortex moves at a certain speed, so do the aberrations in the pressure field. As a result of the motion, the fluid in the first half of the vortex is subjected to a negative force (work is done on the surrounding fluid), while the fluid in the second half of the vortex is subjected to a positive force (pressure work is done on it by the surrounding fluid). Thus, the fluid loses energy through the first half of the vortex and gains energy through the second half.
Numerical simulation results confirm the significant energy separation effect produced by two parallel air free jets at subsonic speeds. Neglecting the effects of viscous forces and heat transfer, the energy separation of a free jet is generated more by the pressure fluctuations accompanying the vortex motion. In the jet, the second half of the vortex entraps the surrounding fluid and rolls it into the jet and moves with the lower half of the vortex, and the local pressure rises with time. This causes the jet to be compressed, gaining energy from the surrounding fluid and creating a high-temperature zone. In contrast, the first half of the vortex loses some of its energy by carrying out part of the jet, resulting in a pressure loss, thus creating a low-temperature zone. Through this process, the free jet exchanges pressure work with the surrounding fluid resulting in a separation of the total energy of the jet.
3.2. Influence of on the Energy Separation of Free Jet
In order to investigate the influence of the Reynolds number on the free jet energy separation, the distribution of the free jet energy separation factor is compared when 19,200, 25,600, 32,000, 41,500, and 51,100, respectively, and the results are shown in Figure 6.
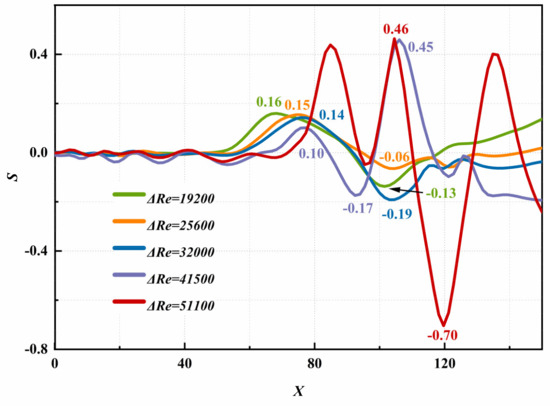
Figure 6.
Distribution of energy separation factors for five Reynolds numbers at different axial positions.
Comparison results found that the distribution trend of energy separation factor at different axial positions is essentially the same under the five numbers, indicating that the formation of free jet energy separation phenomenon is essentially the same under the five numbers.
We define the longitudinal distance between the peak and the trough of the energy separation factor as the width of the energy separation region. In the free jet direction from x = 0 to x = 160, as increases from 19,200 to 51,100, it can be seen that the larger , the farther the maximum value of the energy separation factor is from the exit of the jet nozzle, and the wider the width of the energy separation region. This is due to the increased vortex motion and enhanced pressure fluctuations as the inertial forces increase, which play major roles in the free jet energy separation. We note, however, that the situation is slightly different when = 19,200: the maximum energy separation factor value occurs at x = 68.18, whose width of the energy separation region is significantly larger than when = 25,600, reaching 0.2972. This suggests that when the Reynolds number is low, viscous shear plays a non-negligible role in energy separation compared to the pressure fluctuations generated by the vortex and facilitates the energy separation to some extent.
3.3. Streamwise Variation of
The results of the axial variation of the maximum () and minimum () values of the free jet energy separation factor are shown in Figure 7. The figure shows more clearly the effect of vortexing on the energy separation compared to when it is closer to the jet axis. It can be found that the trend is basically the same in all cases except when the velocity is small (at = 25,600), when the viscous shear dominates. When x is in the range of 0 to 25, a sharp increase in the rate of change of and is observed for vortex generation, indicating that the closer to the nozzle exit region, the faster the energy separation develops. The results confirm that the energy separation mechanism induced by pressure pulsation during vortex motion transport is much stronger than that induced by shear work and heat transfer imbalance. It is important to note that both the magnitude and amplitude of the change in is greater than . It is thought that this difference stems from the different path lines in the upper and lower parts of the clipping layer. This may be due to the three different types of fluid particle paths proposed by Breidenthal [20].
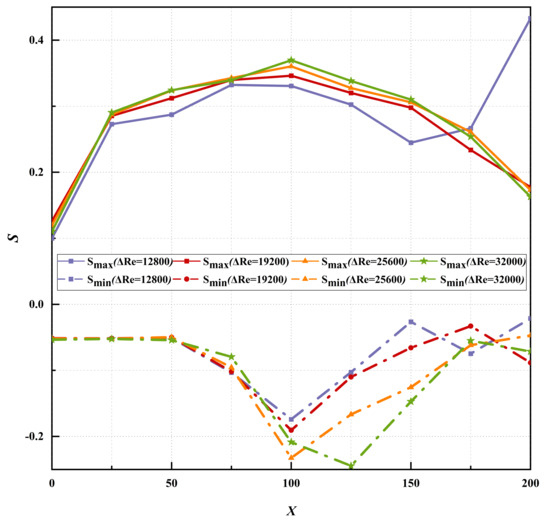
Figure 7.
Effect of on the variation of.
3.4. Flow Characteristics of Dual-Jet
The dual jets suck and interfere with each other, resulting in the formation of a negative pressure in the area surrounded by the dual jets (inside the cavity). An important feature of two-dimensional parallel dual jets is the presence of a negative-pressure region between the dual jets, which is due to the entrainment of the turbulent jet to the surrounding fluid. As a result, the dual jets are attracted to each other so that the axis of the jets bends and then the dual jets merge into one.
If the maximum velocity points in the convergence zone of the dual jets are connected, the center streamline of the curved jet can be derived. The center streamline can be fitted with a circular arc. This is the radius of curvature of the center streamline of the jet before the union of the dual jets. R2 is the square root of the sum of squares of the residuals between the output variable (Y) and the independent variable (X). The fitting function is as follows:
From Figure 8, the radius of curvature of the jet center streamlines of the dual jets becomes larger as the velocity increases in a certain range. In general, the deflection of the jets is caused by the asymmetry of the jet mixing and the pressure difference between its two sides. However, in this case, it is sufficient to consider only the pressure difference, which has a greater effect on the deflection than the random mixing between hot and cold fluids. When these dual jets are combined, the synthesized single jet will resemble a classical single jet.
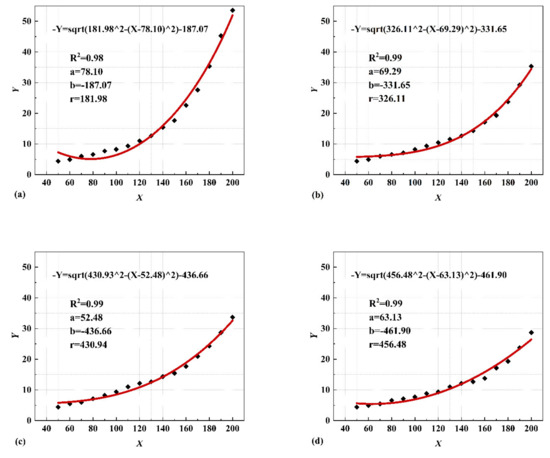
Figure 8.
Jet centerline fitting functions for dual jets for: (a) ∆Re = 12,800; (b) ∆Re = 19,200; (c) ∆Re = 25,600; (d) ∆Re = 32,000.
4. Conclusions
In this paper, the energy separation phenomenon of the free dual jet of parallel air at subsonic speeds is investigated through numerical simulations, and the flow characteristics within the flow field at five different relative Reynolds numbers are analyzed, leading to the following main conclusions:
- (a)
- There is air free jet energy separation in the subsonic range under viscous thermal conductivity conditions. Among them, the pressure fluctuation accompanying the vortex motion is the main cause of free jet energy separation. The flow field is perturbed by high- and low-pressure regions exchanging pressure work with the surroundings, forming high- and low-temperature regions.
- (b)
- When the relative Reynolds number is increased within a certain distance from the jet nozzle outlet, the vortex twinning and fusion process in the flow field is simultaneously enhanced. At the same time, the pressure fluctuation in the flow field is enhanced, thus enhancing the energy separation phenomenon. The larger the relative Reynolds number, the farther the maximum value of the energy separation factor is from the jet nozzle exit and the wider the width of the energy separation region, which may be used in practical situations such as oil-free ignition and air film cooling.
- (c)
- When the relative Reynolds number is small, viscous forces play a non-negligible role in the free jet energy separation phenomenon is seen, in addition to the pressure fluctuations accompanying the vortex.
- (d)
- The jet centerline of a dual jet can be fitted with a circular arc. In the subsonic range, the larger the relative Reynolds number, the larger the radius of curvature. When two jets are merged, the synthesized jet will resemble a classical single jet. At the same time, the center flow line offset is an entropy-increasing process, which, to some extent, counteracts the effect of energy separation.
5. Limitation and Future Work
Due to some limitations of experimental conditions and numerical methods, the research work in this thesis has certain deficiencies that need to be further explored, and the research outlook is as follows.
- (a)
- Since this thesis mainly develops the research content from both numerical simulation and theoretical analysis, namely the theoretical derivation as well as the numerical analysis of the energy separation mechanism in the parallel air free dual jet shear layer, it lacks the corresponding experimental verification. Therefore, it is necessary to experimentally verify the effects of various factors on the energy separation phenomenon of parallel air free dual jet shear layer step by step.
- (b)
- This thesis focuses on the numerical simulation of energy separation phenomena in the subsonic range of air free jet inlet velocities. The phenomenon of energy separation of velocities in the supersonic range as well as the difference and connection between the two different speed ranges need to be further investigated.
- (c)
- This thesis investigates the parallel air free jet in shear layer, and in the future, it is necessary to continue to study the energy separation phenomena of other single gas flows, mixed gas flows, and gas–solid mixing flows, such as the air boundary laminar flow and the pulverized coal tube flow.
Author Contributions
R.D. proposed the framework and methodology of this study. W.X. conducted numerical simulation experiments and validation with the assistance of S.L. W.X. analyzed the data using software and drafted the manuscript and editing from R.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Zhejiang Provincial Basic Public Welfare Research Program Project (grant no. LGG19A020002).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| D | nozzle diameter |
| specific heat at constant pressure | |
| the total temperature at the outlet of the free jet | |
| the instantaneous total fluid temperature at time t | |
| k | the fluid thermal conductivity |
| the magnitude of the disturbance magnitude | |
| kinematic viscosity of fluid | |
| the disturbance phase angle | |
| the frequency of the perturbation | |
| the distribution of disturbance at the disturbance frequency | |
| t | dimensionless time number, |
References
- Han, B.; Goldstein, R.J. A numerical study of energy separation in a jet flow. J. Heat Transfer. 2007, 129, 577–581. [Google Scholar] [CrossRef]
- Zhang, G.-Q.; Wu, Y.-T.; Ding, Y.; Ma, C.-F. Effect of various gases on the energy separation performance of vortex tube. J. Aerosp. Power 2008, 23, 4. [Google Scholar]
- Li, W. Study on Energy Separation Simulation Based on Vortex Tube. Pipeline Tech. Equip. 2018, 4, 50–52. [Google Scholar]
- Qi, H.; Huang, X.; Hu, Y.; Li, K.; Sun, X.; Wang, Z. Vacuum and energy separation characteristics of tornado like vortices. J. Tsinghua Univ. (Sci. Technol.) 2016, 56, 893–907. [Google Scholar]
- Tang, Z.; Yu, X.; Ding, Y. Research on the influence of nozzle structure on the performance of vortex tube. Refrigeration 2018, 46, 5. [Google Scholar]
- He, L.; Pan, P.; Huang, Y. Influence of Cold Orifice Diameter on Energy Separation Characteristics of Vortex Tube: A Simulation Study. Chin. J. Vac. Sci. Technol. 2018, 38, 252–257. [Google Scholar]
- Li, L.; Liu, X.; Zou, J. Gas Flow Characteristics of High Voltage SF, Circuit Breaker with Energy Separated Nozzle. High Volt. Eng. 2015, 41, 3123–3129. [Google Scholar]
- Eckert, E.R.G.; Drewitz, O. Die berechnung des temperaturfeldes in der laminaren grenzschicht schnell angeströmter, unbeheizter körper. Luftfahrtfordchung 1941, 19, 189–196. [Google Scholar]
- Eckert, E.R.G.; Weise, W. Messungen der temperaturverteilung auf der oberfläche schnell angeströmter unbeheizter körper. Forsch. Geb. Ingenieurwesens A 1942, 13, 246–254. [Google Scholar] [CrossRef]
- Goldstein, R.J.; He, B. Energy separation and acousticinteraction in flow across a circular cylinder. Acta Pathol. Microbiol. Scand. 2001, 62, 107–111. [Google Scholar]
- Seol, W.S.; Goldstein, R.J. Energy separation in a jet flow. J. Fluids Eng. 1997, 119, 74–82. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Behbahani, A.I.; Heppelmann, K.K. Streamwise distribution of the recovery factor and the local heat transfer coefficient to an impinging circular air jet. Int. J. Heat Mass Transfer. 1986, 29, 1227–1235. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Sobolik, K.A.; Seol, W.S. Effect of entrainment on the heat transfer to a heated circular air jet impinging on a flat surface. J. Heat Transf. 1990, 112, 608–611. [Google Scholar] [CrossRef]
- Han, B. Instantaneous Energy Separation in a Jet Flow; University of Minnesota: Minneapolis, MN, USA, 2001; pp. 52–62. [Google Scholar]
- Fox, M.D.; Kurosaka, M. Supersonic cooling by shock-vortex interaction. J. Fluid Mech. 1996, 308, 363–379. [Google Scholar] [CrossRef]
- Leontiev, A.I.; Zditovets, A.G.; Vinogradov, Y.A.; Strongin, M.M.; Kiselev, N.A. Experimental investigation of the machine-free method of temperature separation of air flows based on the energy separation effect in a compressible boundary layer. Exp. Therm. Fluid Sci. 2007, 88, 202–219. [Google Scholar] [CrossRef]
- Fox, M.D.; Kurosaka, M.; Hedges, L.; Hirano, K. The influence of vortical structures on the thermal fields of jets. J. Fluid Mech. 1993, 255, 447–472. [Google Scholar] [CrossRef]
- Han, B.; Goldstein, R.J.; Choi, H.G. Energy separation in shear layers. Int. J. Heat Mass Transfer. 2002, 45, 47–55. [Google Scholar] [CrossRef]
- Eckert, E.R.G. Energy separation in fluid streams. Int. Commun. Heat Mass Transfer. 1986, 13, 127–143. [Google Scholar] [CrossRef]
- Breidenthal, R. Structure in turbulent mixing layers and wakes using a chemical reaction. Fluid Mech. 1981, 109, 1–24. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).