Study on the Damping Performance of the Arrangement of Half-Bowl Spherical Structure Under Impact Velocity
Abstract
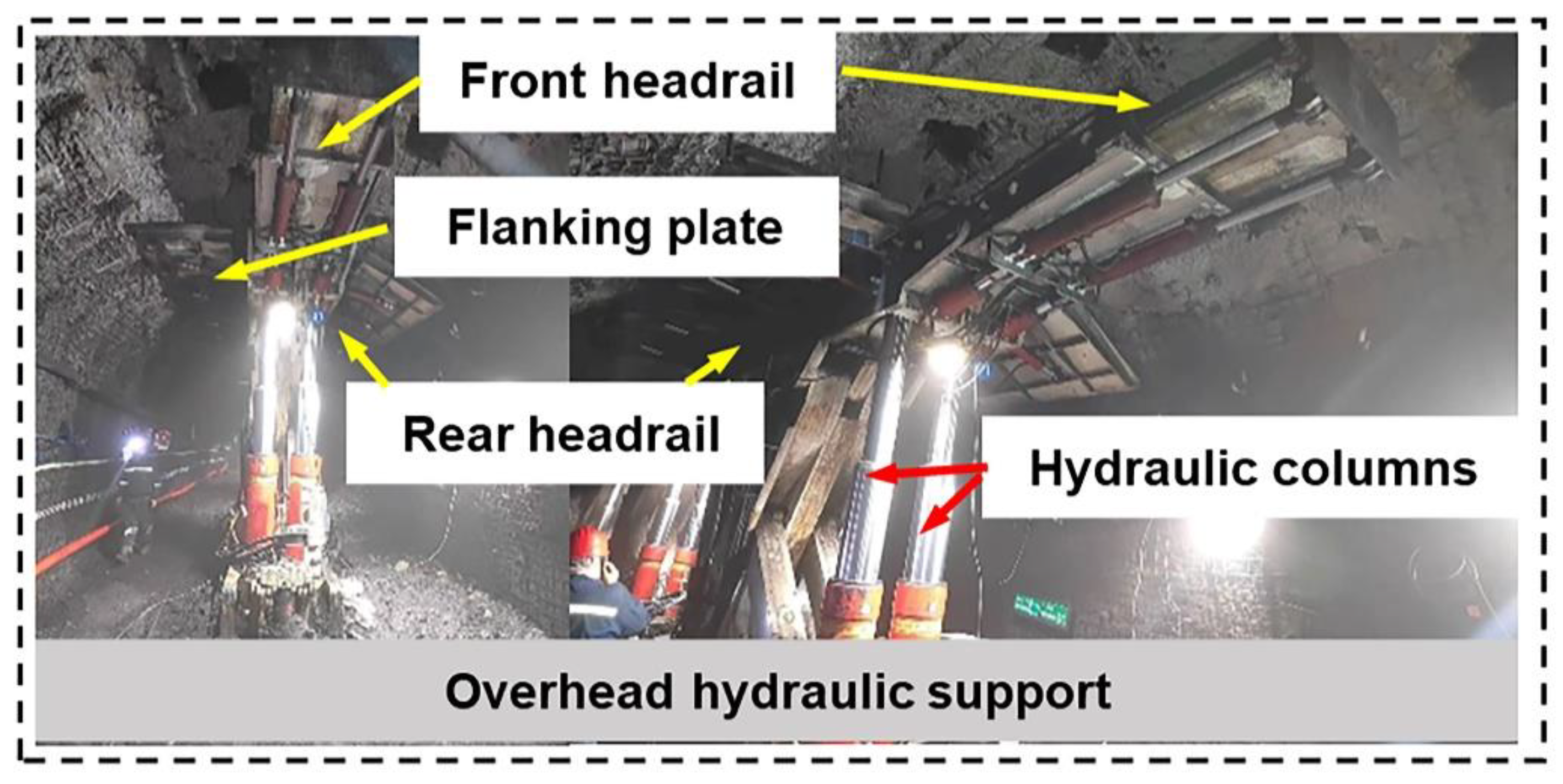
1. Introduction
2. Materials and Methods
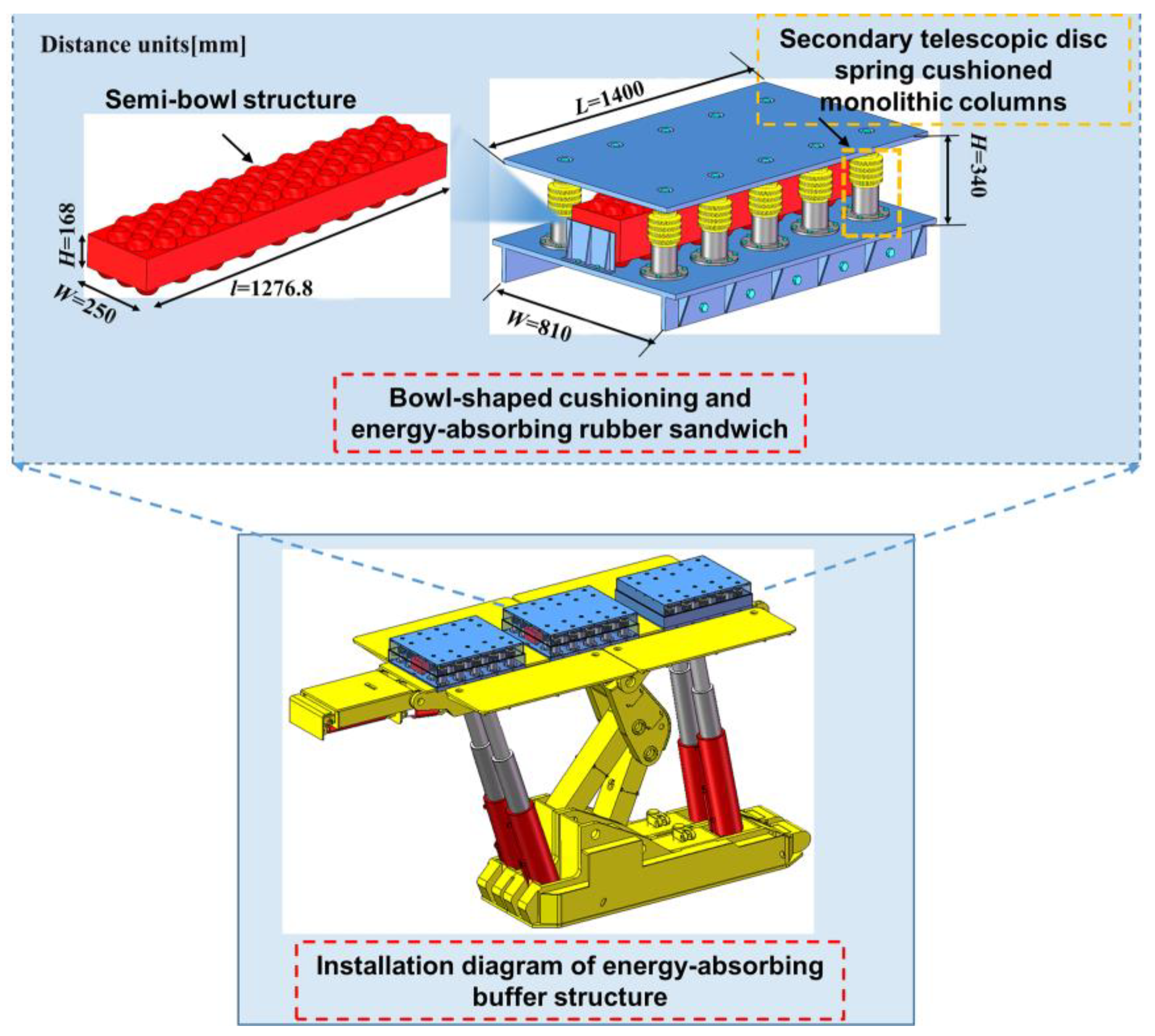
2.1. Bowl-Shaped Cushioning and Energy-Absorbing Rubber Sandwich
2.2. Dynamical Model
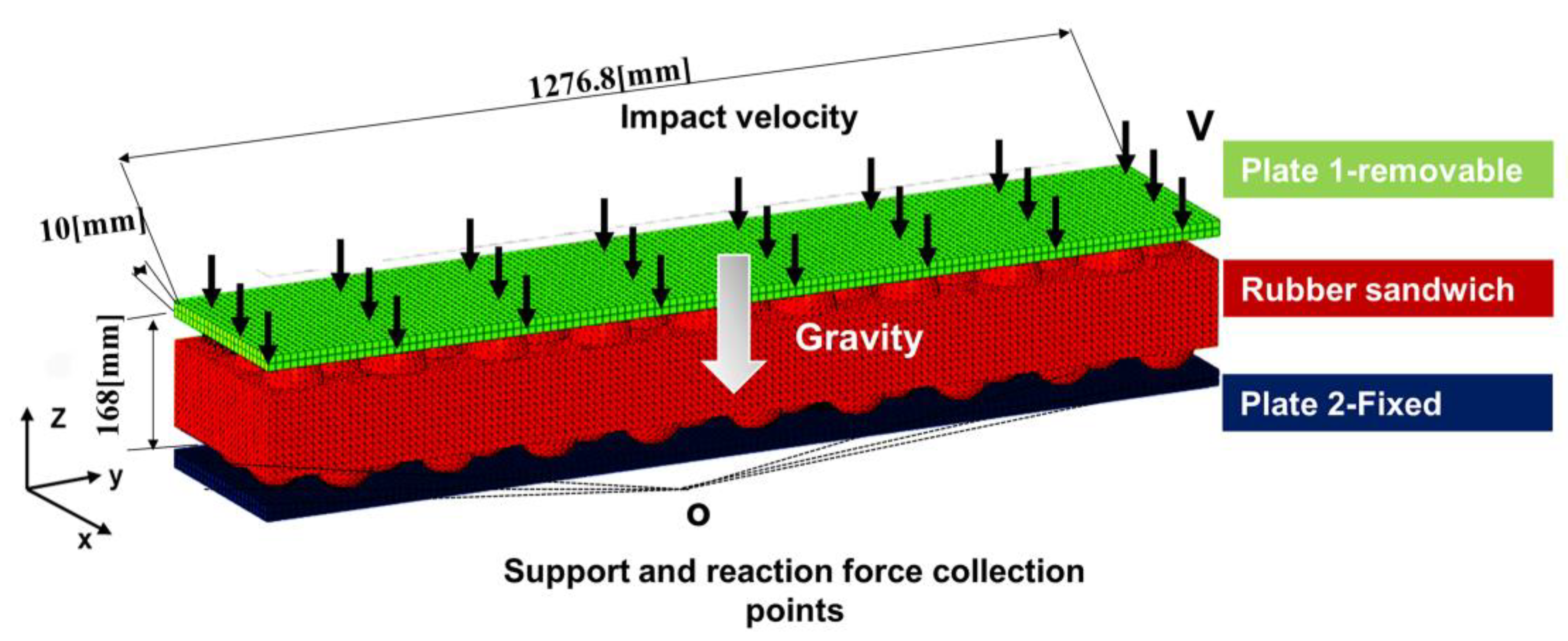
2.2.1. Finite Element Analysis (FEA)
2.2.2. Numerical Modeling
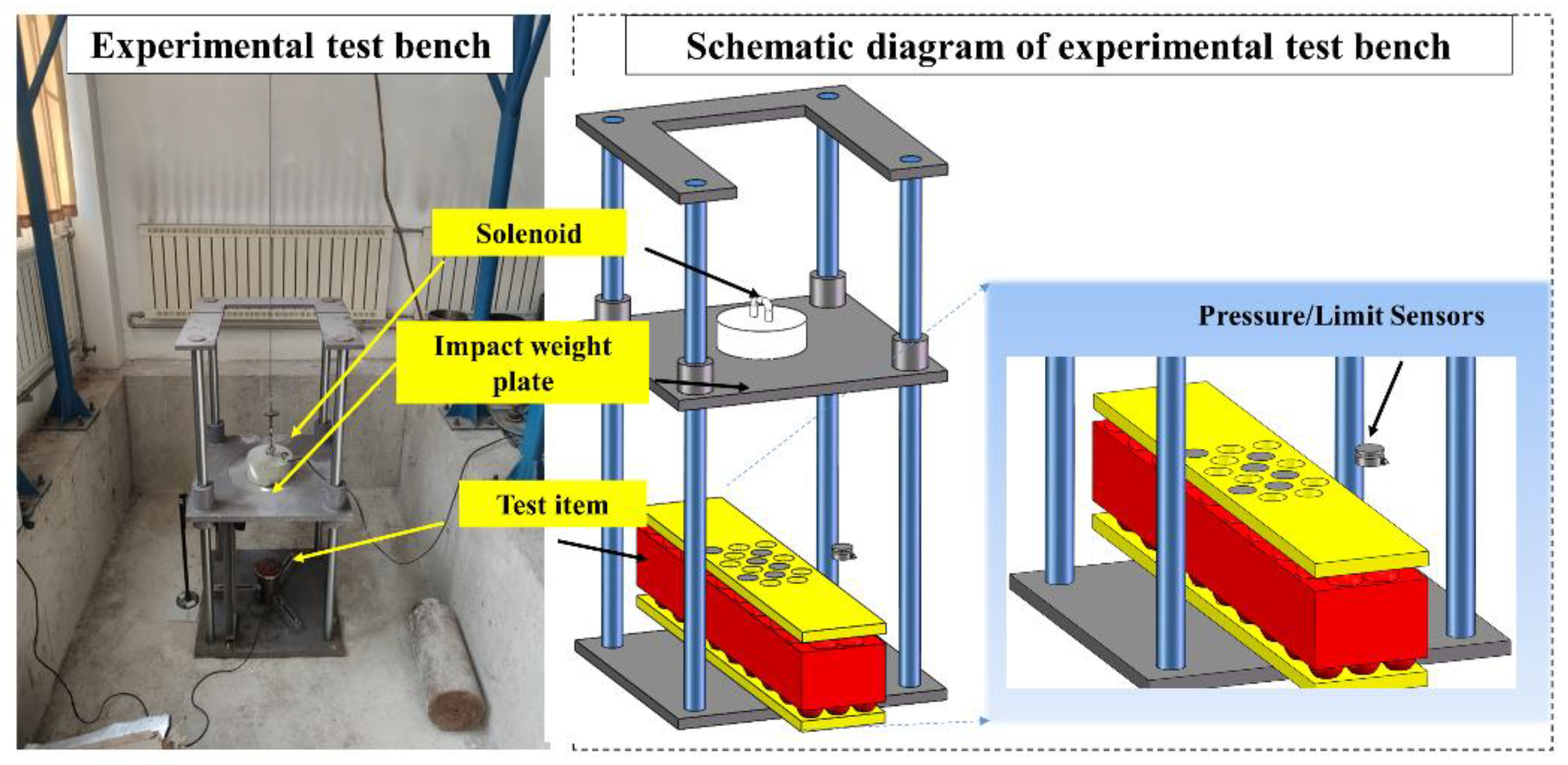
2.3. Impact Test
3. Results and Discussion
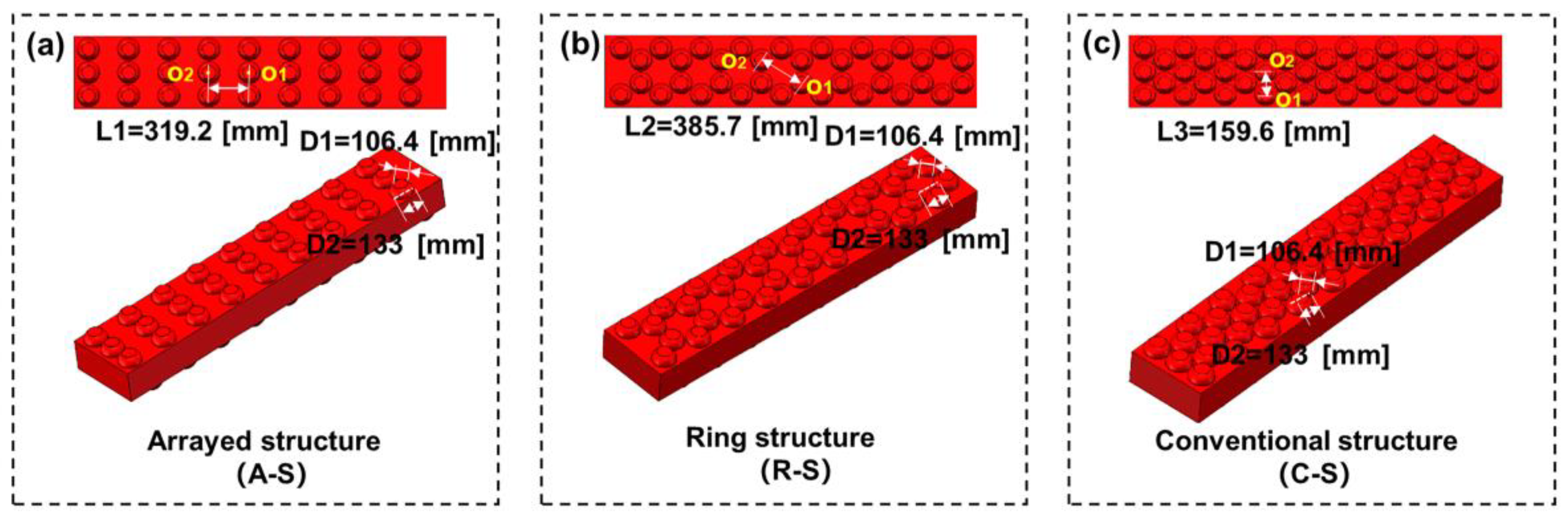
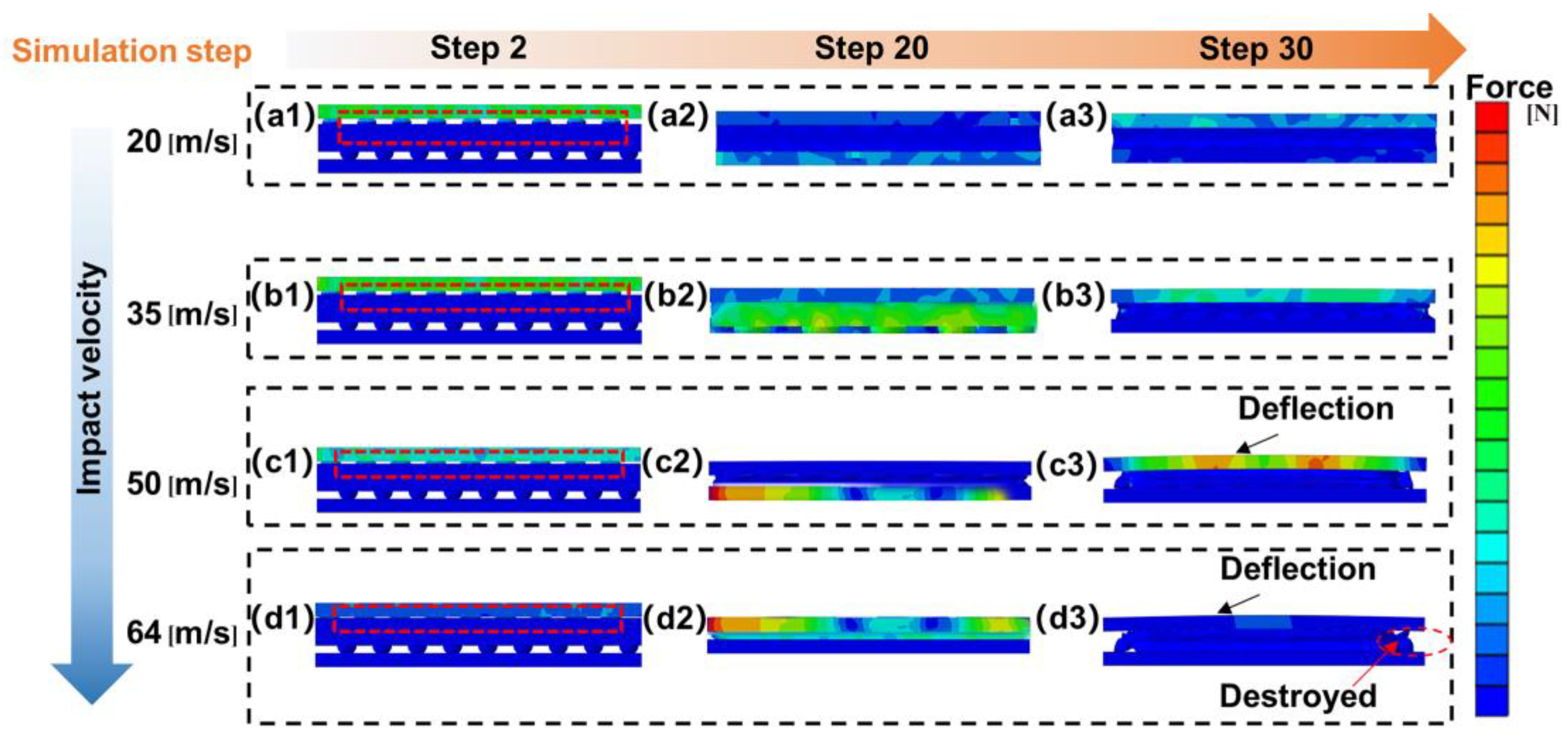
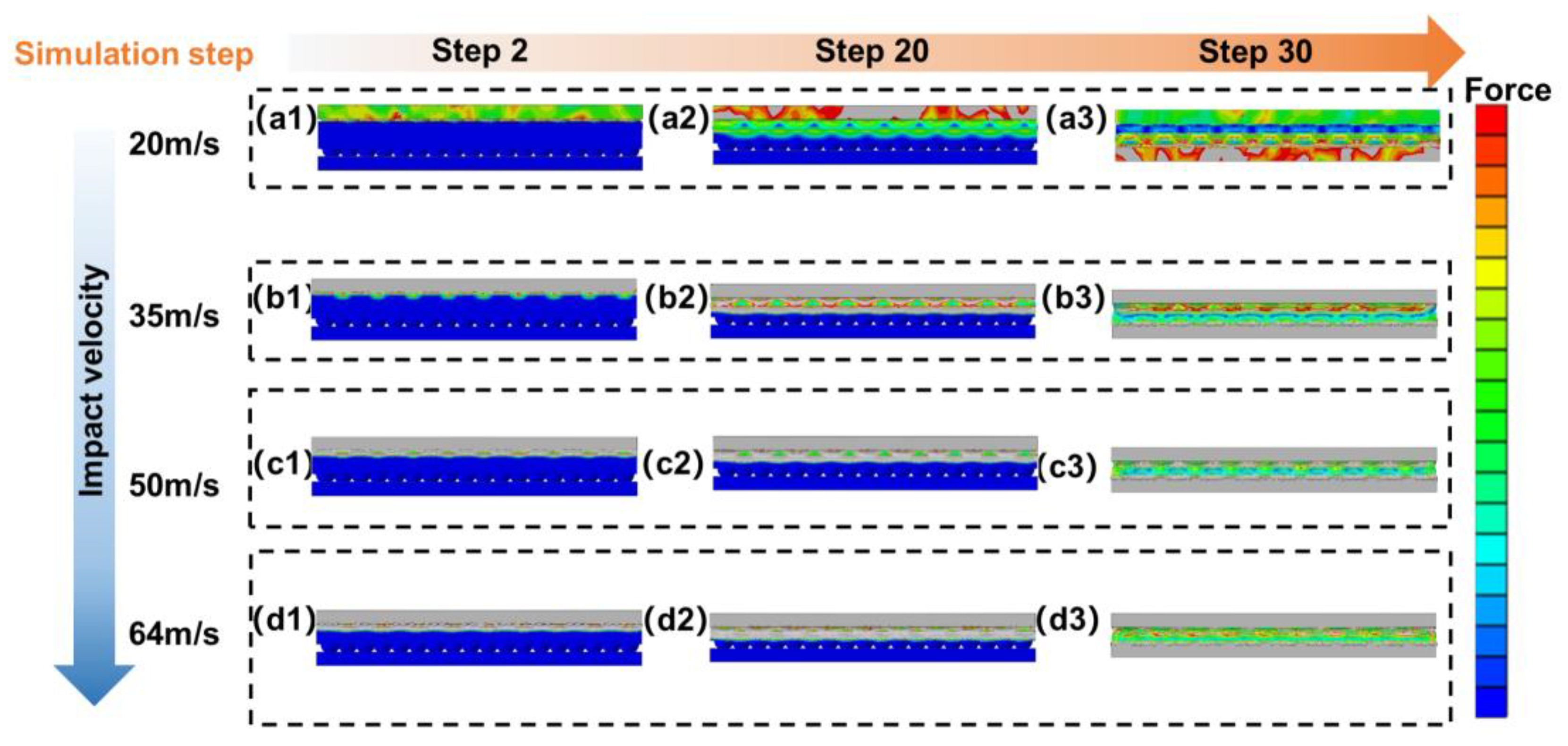
3.1. Simulation Analysis of Rubber Sandwich Under Different Impact Velocities
3.1.1. A-S Structural Analysis
3.1.2. R-S Structural Analysis
3.1.3. C-S Structural Analysis
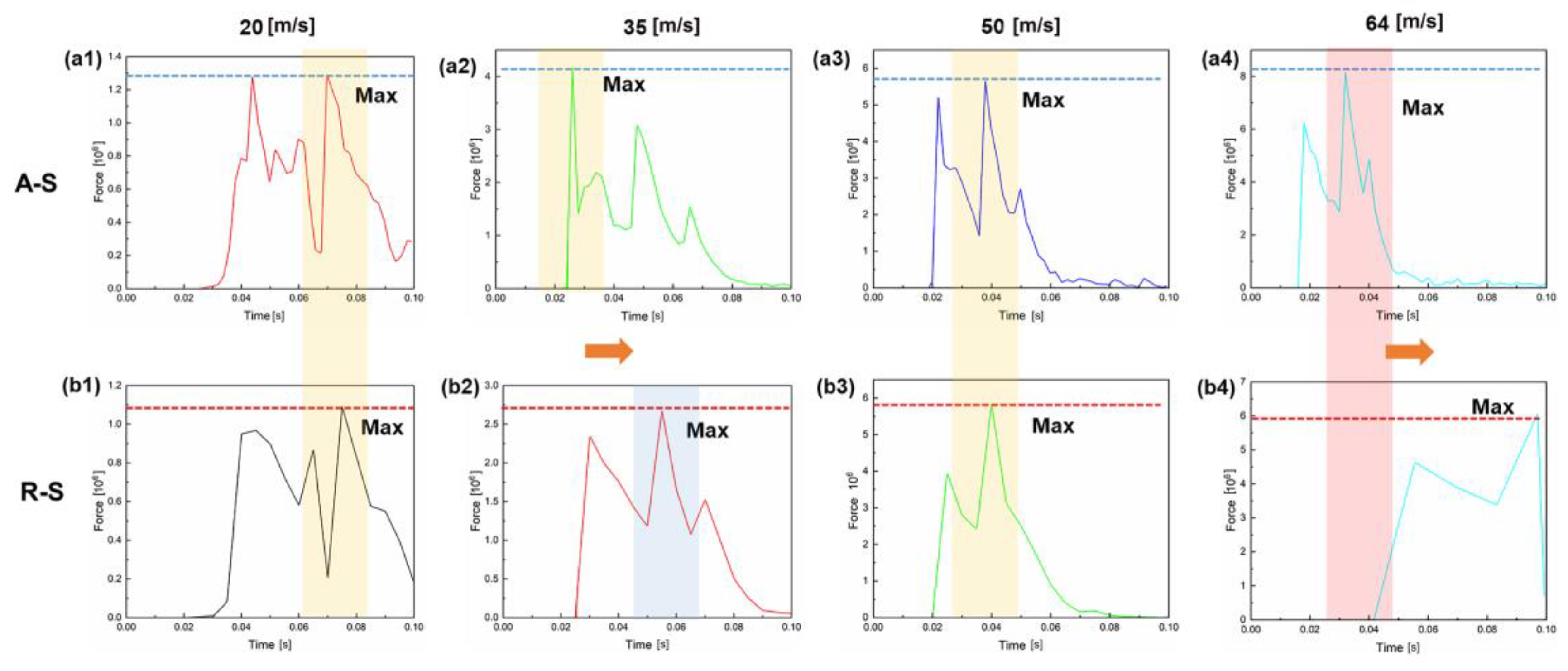
3.2. Analysis of Support and Reaction Forces in Energy-Absorbing Structures with Vibration Damping
3.3. Experimental Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols/Abbreviations | Connotation |
| A-S | Arranged structure |
| R-S | Ring structure |
| C-S | Conventional structure |
| M | Mass matrix |
| a | Phase displacement of the rubber material |
| fI | Internal force |
| fE | External force |
| w | Characteristic cell length of the finite element |
| v | Velocity of the energy wave |
| F() | Safety factor (≤1) |
| FEA | Finite element analysis |
| DEM | Discrete element analysis |
| R&D | Research and experimental development |
References
- Yang, Z.K.; Sun, Z.Y.; Jiang, S.B.; Mao, Q.H.; Liu, P.; Xu, C.Z. Structural analysis on impact-mechanical properties of ultra-high hydraulic support. Int. J. Simul. Model 2020, 19, 17–28. [Google Scholar] [CrossRef]
- Zhao, T.; Guo, W.; Tan, Y.; Lu, C.; Wang, C. Case histories of rock bursts under complicated geological conditions. Bull. Eng. Geol. Environ. 2018, 77, 1529–1545. [Google Scholar] [CrossRef]
- An, H.; Mu, X. Contributions to Rock Fracture Induced by High Ground Stress in Deep Mining: A Review. Rock Mech. Rock Eng. 2024, 1–49. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, N.; Chu, W. Key technologies and risk management of deep tunnel construction at Jinping II hydropower station. J. Rock Mech. Geotech. Eng. 2016, 8, 499–512. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, F.; Xing, Y.; Wang, H.; Liu, R. Design and Mechanical Properties Analysis of Variable Buffer-Force Planing Energy-Absorbing Device for Rail Vehicles. Appl. Sci. 2023, 13, 1596. [Google Scholar] [CrossRef]
- Yumrutas, H.I.; Ozcanan, S.; Apak, M.Y.; Anwer, M.J. Experimental and numerical comparative crashworthiness analysis of innovative renewable hybrid barrier with conventional roadside barriers. Int. J. Crashworthiness 2023, 28, 334–350. [Google Scholar] [CrossRef]
- Xiao, L.; Li, S.; Qian, Y.; Chen, D.; Jiang, T. An overview of OTFS for Internet of Things: Concepts, benefits, and challenges. IEEE Internet Things J. 2021, 9, 7596–7618. [Google Scholar] [CrossRef]
- Qi, C. Big data management in the mining industry. Int. J. Miner. Metall. Mater. 2020, 27, 131–139. [Google Scholar] [CrossRef]
- Cacciuttolo, C.; Guzmán, V.; Catriñir, P.; Atencio, E. Sensor Technologies for Safety Monitoring in Mine Tailings Storage Facilities: Solutions in the Industry 4.0 Era. Minerals 2024, 14, 446. [Google Scholar] [CrossRef]
- Ye, Z.; Yan, G.; Wei, Y.; Zhou, B.; Li, N.; Shen, S.; Wang, L. Real-time and efficient traffic information acquisition via pavement vibration IoT monitoring system. Sensors 2021, 21, 2679. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Wan, D.; Sheng, Q.; Fu, X.; Pang, X.; Xia, L.; Li, D. Risk assessment and support design optimization of a high slope in an open pit mine using the jointed finite element method and discontinuous deformation analysis. Bull. Eng. Geol. Environ. 2022, 81, 254. [Google Scholar] [CrossRef]
- Afzal, M.; Liu, Y.; Cheng, J.C.P.; Gan, V.J. Reinforced concrete structural design optimization: A critical review. J. Clean. Prod. 2020, 260, 120623. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Zhang, S.; Ren, J.; Zhang, L.; Zhang, R.; Cui, Y. Study on the energy evolution mechanism of coal and rock with impact tendency under different strain rates. Sci. Rep. 2023, 13, 13773. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, H.; Xie, J.; Xiao, S.; Zhu, T.; Zhou, G.; Xu, L. Energy absorption characteristics and parameter optimization of anti-climb energy-absorbing devices for subway vehicles under impact loads. Appl. Sci. 2024, 14, 5203. [Google Scholar] [CrossRef]
- Isaac, C.W.; Duddeck, F. Recent progress in 4D printed energy-absorbing metamaterials and structures. Virtual Phys. Prototyp. 2023, 18, e2197436. [Google Scholar] [CrossRef]
- Wang, S.; Su, S.; Zhao, Q.; An, D.; Xiao, Y.; Xu, H. Study on the Support Effect of Energy-Absorbing Support Structure in the Coal Mine Roadway and the Synergic Effect with Wall Rock. Shock Vib. 2023, 2023, 6673458. [Google Scholar] [CrossRef]
- Li, G.; Ma, F.; Guo, J.; Zhao, H.; Liu, G. Study on deformation failure mechanism and support technology of deep soft rock roadway. Eng. Geol. 2020, 264, 105262. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, Z.; Wan, L.; Ma, D. Study on Roof Instability Effect and Bearing Characteristics of Hydraulic Support in Longwall Top Coal Caving. Appl. Sci. 2023, 13, 8102. [Google Scholar] [CrossRef]
- Cao, D.; Chen, H.; Yuan, J. Inline force on human body due to non-impulsive wave overtopping at a vertical seawall. Ocean Eng. 2021, 219, 108300. [Google Scholar] [CrossRef]
- Ma, J.; Xiao, Y.; Ma, B.; Zheng, C.; Hu, X.; Tian, D.; Du, M.; Zhang, K. Research on the Energy-Absorbing and Cushioning Performance of a New Half-Bowl Ball Rubber Body in Tunnel Support. Processes 2024, 12, 1981. [Google Scholar] [CrossRef]
- Dai, K.; Fang, C.; Zhang, S.; Shi, Y. Conceptual design and numerical study on a cable-based energy dissipating system for the vibration reduction of tower-like structures. Eng. Struct. 2021, 237, 112034. [Google Scholar] [CrossRef]
- Bustamante, R.; Rajagopal, K.R. A new type of constitutive equation for nonlinear elastic bodies. Fitting with experimental data for rubber-like materials. Proc. R. Soc. A 2021, 477, 20210330. [Google Scholar] [CrossRef]
- Kowalczuk, Z.; Tatara, M.S. Analytical ‘steady-state’-based derivation and clarification of the courant-friedrichs-lewy condition for pipe flow. J. Nat. Gas Sci. Eng. 2021, 91, 103953. [Google Scholar] [CrossRef]
- Long, S.; Yao, X.; Wang, H.; Zhang, X. Failure analysis and modeling of foam sandwich laminates under impact loading. Compos. Struct. 2018, 197, 10–20. [Google Scholar] [CrossRef]
- Sabah, S.H.A.; Kueh, A.B.H.; Al-Fasih, M.Y. Bio-inspired vs. conventional sandwich beams: A low-velocity repeated impact behavior exploration. Constr. Build. Mater. 2018, 169, 193–204. [Google Scholar] [CrossRef]
- Almajhali, K.Y.M. Review on passive energy dissipation devices and techniques of installation for high rise building structures. Structures 2023, 51, 1019–1029. [Google Scholar] [CrossRef]
- Hu, S.; Zhu, S.; Wang, W.; Alam, M.S. Structural and nonstructural damage assessment of steel buildings equipped with self-centering energy-absorbing rocking core systems: A comparative study. J. Constr. Steel Res. 2022, 198, 107559. [Google Scholar] [CrossRef]
- Xu, G.; Guo, T.; Li, A.; Wang, S.; Zhang, R.; Zhu, R.; Xu, J. Review on self-centering damper for seismic resilient building structures. Structures 2023, 54, 58–77. [Google Scholar] [CrossRef]
- Dsouza, H.; Pastrana, J.; Figueroa, J.; Gonzalez-Afanador, I.; Davila-Montero, B.M.; Sepúlveda, N. Flexible, self-powered sensors for estimating human head kinematics relevant to concussions. Sci. Rep. 2022, 12, 8567. [Google Scholar] [CrossRef] [PubMed]
- Łupieżowiec, M.; Rybak, J.; Różański, Z.; Dobrzycki, P.; Jędrzejczyk, W. Design and construction of foundations for industrial facilities in the areas of former post-mining waste dumps. Energies 2022, 15, 5766. [Google Scholar] [CrossRef]


| Impact Energy [J] | 1 × 104 | 4 × 104 | 7 × 104 | 1 × 105 |
|---|---|---|---|---|
| Speed [m/s] | 20 | 35 | 50 | 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Zhang, K.; Meng, X.; Zheng, C.; Du, M.; Kong, X.; Tian, D.; Huang, L.; Yi, R. Study on the Damping Performance of the Arrangement of Half-Bowl Spherical Structure Under Impact Velocity. Processes 2024, 12, 2895. https://doi.org/10.3390/pr12122895
Ma J, Zhang K, Meng X, Zheng C, Du M, Kong X, Tian D, Huang L, Yi R. Study on the Damping Performance of the Arrangement of Half-Bowl Spherical Structure Under Impact Velocity. Processes. 2024; 12(12):2895. https://doi.org/10.3390/pr12122895
Chicago/Turabian StyleMa, Jian, Kun Zhang, Xiangjun Meng, Canguang Zheng, Mingchao Du, Xiangjun Kong, Dan Tian, Liangsong Huang, and Ran Yi. 2024. "Study on the Damping Performance of the Arrangement of Half-Bowl Spherical Structure Under Impact Velocity" Processes 12, no. 12: 2895. https://doi.org/10.3390/pr12122895
APA StyleMa, J., Zhang, K., Meng, X., Zheng, C., Du, M., Kong, X., Tian, D., Huang, L., & Yi, R. (2024). Study on the Damping Performance of the Arrangement of Half-Bowl Spherical Structure Under Impact Velocity. Processes, 12(12), 2895. https://doi.org/10.3390/pr12122895






