BetaSigmaSlurryFoam: An Open Source Code for the Numerical Simulation of Pseudo-Homogeneous Slurry Flow in Pipes
Abstract
1. Introduction
2. Key Features of the - Two-Fluid Model
2.1. Fluid-Dynamic Model
2.2. Wall Boundary Condition for the Solid Phase
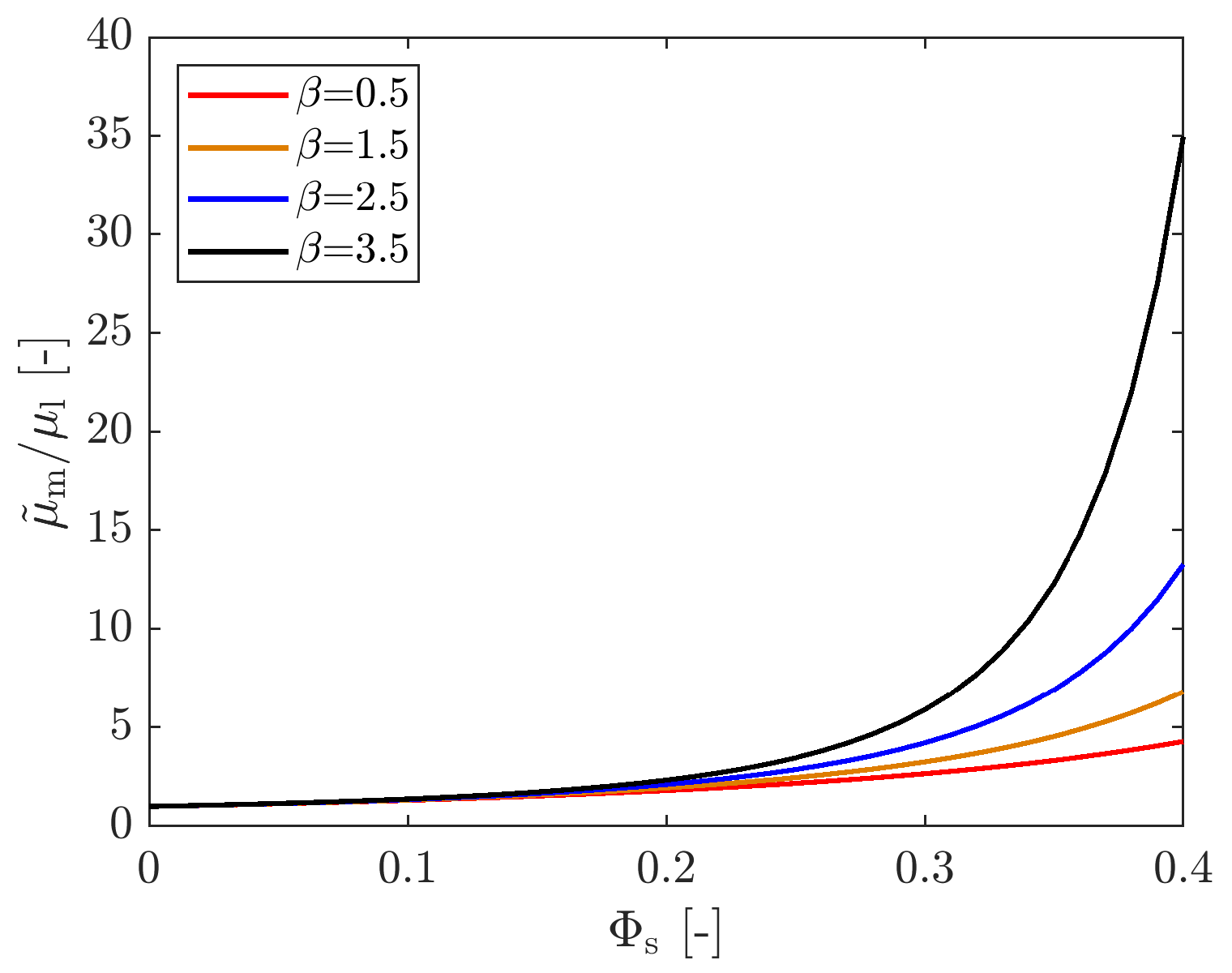
2.3. Applicability Conditions
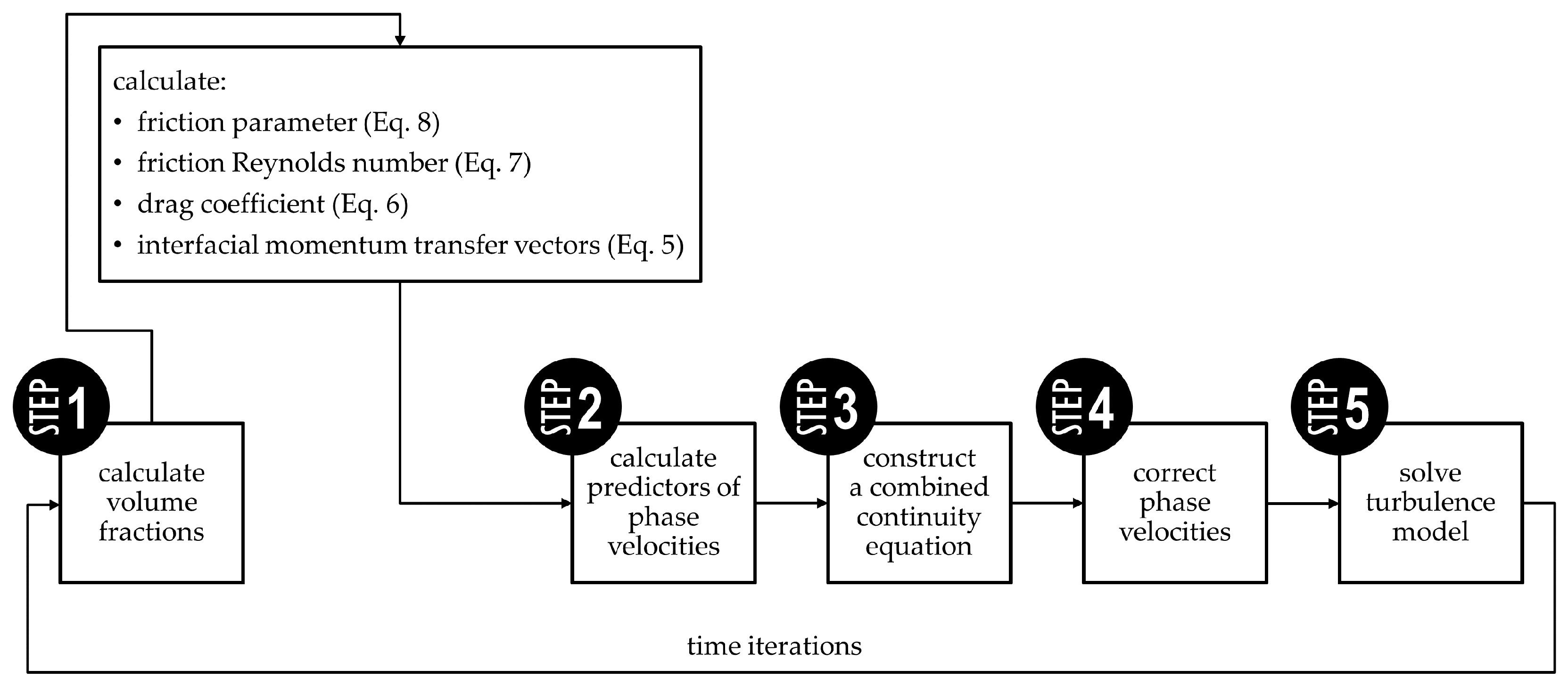
3. Key Implementation Details of betaSigmaSlurryFoam
4. Testing of betaSigmaSlurryFoam
4.1. Similarity Assessment Against the Previous - Two-Fluid Model for Horizontal Pipe Flow
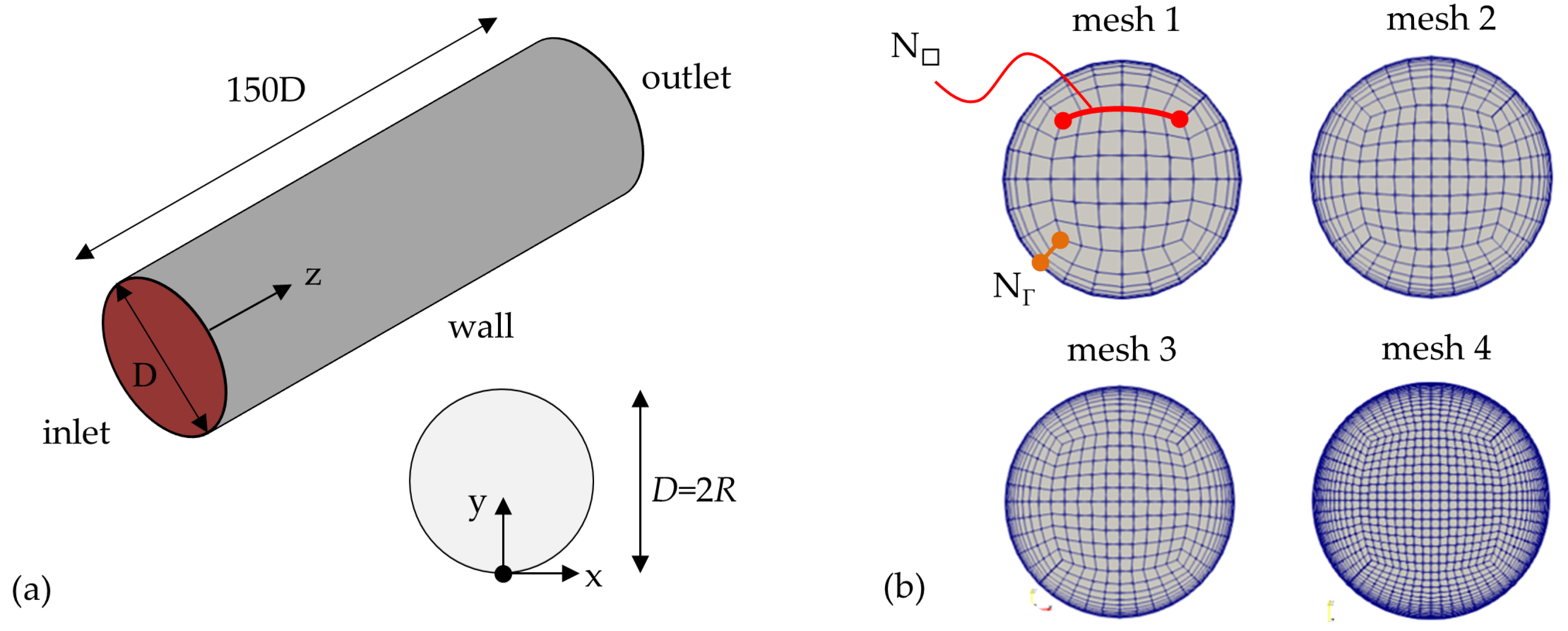
4.1.1. Numerical Set-Up
4.1.2. Control of the Numerical Sources of Uncertainty
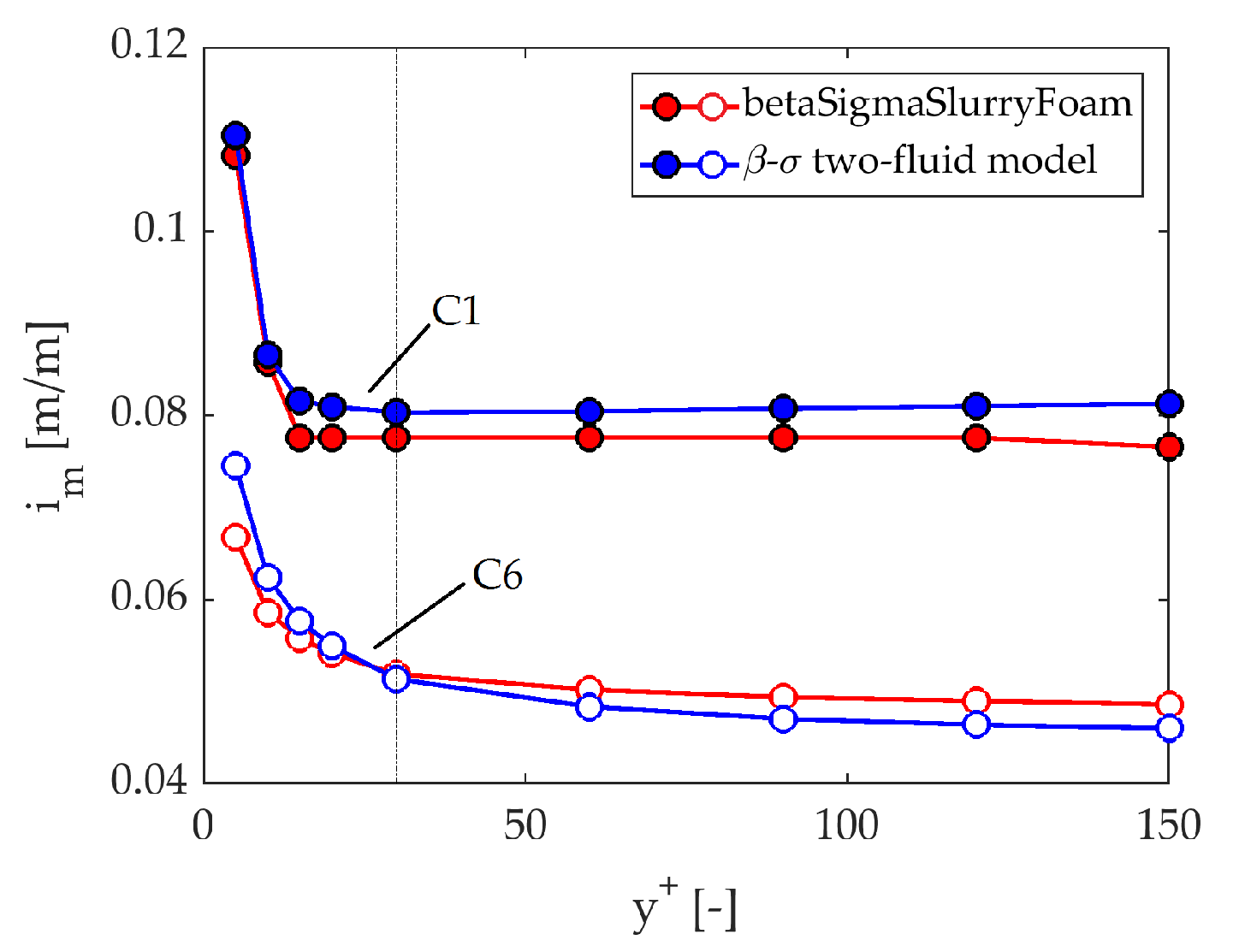
4.1.3. Results
4.2. Validation Against Slurry Flow Experiments in a Horizontal Pipe Bend
4.2.1. Description of the Test Case
4.2.2. Numerical Set-Up
4.2.3. Inspection of the CFD Results and Their Physical Interpretation
4.2.4. Control of the Numerical Sources of Uncertainty
4.2.5. Effect of the Calibration Coefficients and Comparison with Experiments
5. Conclusions
- We developed and shared with the scientific community betaSigmaSlurryFoam, a fully open source implementation of our earlier - two-fluid model for the simulation of fully suspended slurry transport in pipes within the OpenFOAM platform.
- We demonstrated the similarity between betaSigmaSlurryFoam, implemented in OpenFOAM, and the earlier - two-fluid model, implemented in PHOENICS, for horizontal slurry pipe transport in different testing conditions. We found not only that the two solutions are very close to each other, but also that the effects of and are the same for the two implementations, confirming that the same calibration procedures could be used.
- We successfully assessed the predictive capacity of betaSigmaSlurryFoam for the more complex case of slurry transport in a horizontal pipe bend, which was not considered in our previous works of the - two-fluid model, referring to some experimental tests carried out by Kaushal et al. [29]. Two features in particular made the results fully satisfactory. Firstly, betaSigmaSlurryFoam showed physical consistency and good agreement with the experimental data also for slightly coarser particles than those considered so far. Secondly, the suitable combination of and in the case of pipe bend flow was in line with the values obtained in previous studies on straight horizontal pipes with similar diameter and type of particles.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Visintainer, R.; Matoušek, V.; Pullum, L.; Sellgren, A. Slurry Transport Using Centrifugal Pumps; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Lareo, C.; Fryer, P.J.; Barigou, M. The fluid mechanics of two-phase solid-liquid food flows: A review. Food Bioprod. Process. 1997, 75, 73–105. [Google Scholar] [CrossRef]
- Jiang, Y.Y.; Zhang, P. Numerical investigation of slush nitrogen flow in a horizontal pipe. AIChE J. 2012, 59, 1762–1773. [Google Scholar] [CrossRef]
- Alvarado, J.L.; Marsh, C.; Sohn, C.; Phetteplace, G.; Newell, T. Thermal performance of microencapsulated phase change material slurry in turbulent flow under constant heat flux. Int. J. Heat Mass Transf. 2007, 50, 1938–1952. [Google Scholar] [CrossRef]
- Singh, M.K.; Kumar, S.; Ratha, D.; Kaur, H. Design of slurry transportation pipeline for the flow of muti-particulate coal ash suspension. Int. J. Hydrogen Energy 2017, 42, 19135–19138. [Google Scholar] [CrossRef]
- Quarini, G.; Aislie, E.; Ash, D.; Leiper, A.; McBryde, D.; Hebert, M.; Deans, T. Transient thermal performance of ice slurries pumped through pipes. Appl. Therm. Eng. 2021, 50, 743–748. [Google Scholar] [CrossRef]
- Messa, G.V.; Yang, Q.; Adedeji, O.E.; Chára, Z.; Duarte, C.A.R.; Matoušek, V.; Rasteiro, M.G.; Sanders, R.S.; Silva, R.C.; de Souza, F.J. Computational Fluid Dynamics Modelling of Liquid-Solid Slurry flows in Pipelines: State-of-the-Art and Future Perspectives. Processes 2021, 9, 1566. [Google Scholar] [CrossRef]
- Messa, G.V.; Matoušek, V. Analysis and discussion of two-fluid modelling of pipe flow of fully suspended slurry. Powder Technol. 2020, 360, 747–768. [Google Scholar] [CrossRef]
- Messa, G.V.; Malin, M.; Matoušek, V. Parametric study of the β-σ two-fluid model for simulating fully suspended slurry flow: Effect of flow conditions. Meccanica 2021, 56, 1047–1077. [Google Scholar] [CrossRef]
- Messa, G.V.; Yang, Q.; Rasteiro, M.G.; Faia, P.; Matoušek, V.; Silva, R.; Garcia, F. Computational fluid dynamic modelling of fully-suspended slurry flows in horizontal pipes with different solids concentrations. KONA Powder Part. J. 2023, 40, 219–235. [Google Scholar] [CrossRef]
- Ekambara, K.; Sanders, R.; Nandakumar, K.; Masliyah, J. Hydrodynamic Simulation of Horizontal Slurry Pipeline Flow Using ANSYS-CFX. Ind. Eng. Chem. Res. 2009, 48, 8159–8171. [Google Scholar] [CrossRef]
- Gopaliya, M.K.; Kaushal, D.R. Analysis of effect of grain size on various parameters of slurry flow through pipeline using CFD. Particul. Sci. Technol. 2015, 33, 369–384. [Google Scholar] [CrossRef]
- Gopaliya, M.K.; Kaushal, D.R. Modeling of sand-water slurry flow through horizontal pipe using CFD. J. Hydrol. Hydromech. 2016, 64, 261–272. [Google Scholar] [CrossRef]
- Kaushal, D.R.; Thinglas, T.; Tomita, Y.; Kuchii, S.; Tsukamoto, H. CFD modeling for pipeline flow of fine particles at high concentration. Int. J. Multiphase Flow 2012, 43, 85–100. [Google Scholar] [CrossRef]
- Singh, M.K.; Kumar, S.; Ratha, D. Computational analysis on disposal of coal slurry at high solid concentrations through slurry pipeline. Int. J. Coal Prep. Util. 2020, 40, 116–130. [Google Scholar] [CrossRef]
- Kumar, N.; Gopaliya, M.K.; Kaushal, D.R. Experimental investigations and CFD modeling for flow of highly concentrated iron ore slurry through horizontal pipeline. Part. Sci. Technol. 2018, 37, 232–250. [Google Scholar] [CrossRef]
- Krampa, F.N. Two-Fluid Modelling of Heterogeneous Coarse Particle Slurry Flows. Ph.D. Thesis, University of Saskatchewan, Saskatoon, Saskatchewan, 2009. [Google Scholar]
- Antaya, C.L.; Adane, K.F.K.; Sanders, R.S. Modelling concentrated slurry pipeline flows. In Proceedings of the ASME 2012 Fluids Engineering Summer Meeting, Rio Grande, Puerto Rico, 8–12 July 2012. [Google Scholar]
- Ofei, T.N.; Ismail, A.Y. Eulerian-Eulerian simulation of particle-liquid slurry flow in horizontal pipe. J. Pet. Eng. 2016, 37, 232–250. [Google Scholar] [CrossRef]
- Lapworth, L. Hydra-CFD: A framework for collaborative CFD development. In Proceedings of the International Conference on Scientific and Engineering Computation, Singapore, 30 June–2 July 2004. [Google Scholar]
- Fiorina, C.; Shriwise, P.; Dufresne, A.; Ragusa, J.; Ivanov, K.; Valentine, T.; Lindley, B.; Kelm, S.; Shwageraus, E.; Monti, S.; et al. An initiative for the development and application of open-source multi-physics simulation in support of R&D and E&T in nuclear science and technology. In Proceedings of the PHYSOR2020—International Conference on Physics of Reactors: Transition to a Scalable Nuclear Future, Cambridge, UK, 30 March–2 April 2020. [Google Scholar]
- Kodman, J.B.; Singh, B.; Murugaiah, M. A Comprehensive Survey of Open-Source Tools for Computational Fluid Dynamics Analyses. J. Adv. Res. Fluid Mech. Therm. Sci. 2024, 119, 123–148. [Google Scholar] [CrossRef]
- Shouten, T.D.; Keetels, G.H.; van Rhee, C. Suspended pipeflow with OpenFOAM. In Proceedings of the 19th International Conference on Transport and Sedimentation of Solid Particles, Cape Town, South Africa, 24–27 September 2019. [Google Scholar]
- Shouten, T.D.; van Rhee, C.; Keetels, G.H. Two-phase modelling for sediment water mixtures above the limit deposit velocity in horizontal pipelines. J. Hydrol. Hydromech. 2021, 3, 263–274. [Google Scholar] [CrossRef]
- Reyes, C.; Ihle, C.F. Numerical simulation of cation exchange in fine-coarse seawater slurry pipeline flow. Miner. Eng. 2018, 117, 14–23. [Google Scholar] [CrossRef]
- Mackenzie, A.; Stickland, M.T.; Dempster, W.M. Development of a Combined Euler-Euler Euler-Lagrange Slurry Model. In OpenFOAM: Selected Papers of the 11th Workshop; Nóbrega, J.M., Jasak, H., Eds.; Springer: Cham, Switzerland, 2019; pp. 77–92. [Google Scholar]
- Liu, X.; Yuan, A.; Li, Y.; Wang, Z.; Wang, Z.; Liu, Z.; Wang, W. Numerical simulation of hydrate slurry flow and deposit behavior based on openfoam-IATE. Fuel 2022, 310, 122426. [Google Scholar] [CrossRef]
- Ghoudi, Z.; Benckhaldoun, F.; Piscaglia, F.; Hajjaji, N. Towards the modeling of the effect of turbulent water batches on the flow of slurries in horizontal pipes using CFD. Eur. J. Mech. B Fluids 2023, 100, 208–222. [Google Scholar] [CrossRef]
- Kaushal, D.R.; Kumar, A.; Tomita, Y.; Kuchii, S.; Tsukamoto, H. Flow of mono-dispersed particles through horizontal bend. Int. J. Multiphase Flow 2013, 52, 71–91. [Google Scholar] [CrossRef]
- Spalding, D.B. Numerical computation of multi-phase fluid flow and heat transfer. In Recent Advances in Numerical Methods in Fluids; Taylor, C., Morgan, K., Eds.; Pineridge Press Limited: Swansea, UK, 1980; Volume 1, pp. 139–168. [Google Scholar]
- The PHOENICS Encyclopedia: Two-Phase Flows. Available online: https://www.cham.co.uk/phoenics/d_polis/d_lecs/ipsa/ipsa.htm (accessed on 6 December 2024).
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Meth. Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Models for Two-Phase Flow: Two-Equation k-ε Turbulence Model. Available online: https://www.cham.co.uk/phoenics/d_polis/d_enc/turmod/enc_tu74.htm (accessed on 6 December 2024).
- Schiller, L.; Naumann, A. A drag coefficient correlation. Z. Ver. Deutsch. Ing. 1935, 77, 318–320. [Google Scholar]
- Cheng, N.S.; Law, A.W.K. Exponential formula for computing effective viscosity. Powder Technol. 2003, 129, 156–160. [Google Scholar] [CrossRef]
- The PHOENICS Encyclopedia: Equilibrium Log-Law Wall Functions. Available online: https://www.cham.co.uk/phoenics/d_polis/d_enc/turmod/enc_tu82.htm (accessed on 6 December 2024).
- Massey, B.S.; Ward-Smith, J. Mechanics of Fluids; Taylor & Francis: London, UK, 2006. [Google Scholar]
- Thomas, A. A modification of the Wilson & Judge deposit velocity equation, extending its applicability to finer particles and larger pipe sizes. In Proceedings of the 17th International Conference of Transport and Sedimentation of Solid Particles, Delft, The Netherlands, 22–25 September 2015. [Google Scholar]
- Korving, A.C. High concentrated fine-sand slurry flow in pipelines: Experimental study. In Proceedings of the 15th International Conference on Hydrotransport, Banff, AB, Canada, 3–5 June 2002. [Google Scholar]
- Yang, Q.; Dong, J.; Xing, T.; Zhang, Y.; Guan, Y.; Liu, X.; Tian, Y.; Peng, Y. RANS-Based Modelling of Turbulent Flow in Submarine Pipe Bends: Effect of Computational Mesh and Turbulence Modelling. J. Mar. Sci. Eng. 2023, 11, 336. [Google Scholar] [CrossRef]
- Passalacqua, A.; Fox, R.O. Implementation of an iterative solution procedure for multi-fluid gas–particle flow models on unstructured grids. Powder Technol. 2011, 213, 174–187. [Google Scholar] [CrossRef]
- Sweby, P.K. High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Anal. 1984, 21, 995–1011. [Google Scholar] [CrossRef]
- Gillies, R.G. Pipeline Flow of Coarse Particle Slurries. Ph.D. Thesis, University of Saskatchewan, Saskatoon, Saskatchewan, 1993. [Google Scholar]
- Sudo, K.; Sumida, H.; Hibara, H. Experimental investigation on turbulent flow in a circular-sectioned 90-degree bend. Exp. Fluids 1998, 25, 42–49. [Google Scholar] [CrossRef]
- Thomas, T. Friction Factor in Internal Pipe Turbulent Flow; Internship Report; Indian Institute of Technology: Bombay, India, 2022. [Google Scholar]
- Yang, Q.; Messa, G.V.; Matoušek, V. Towards the assessment of the predictive capacity of the β-σ two-fluid model for pseudo-homogeneous slurry flow in pipes. In Proceedings of the 20th International Conference on Transport and Sedimentation of Solid Particles, Wroclaw, Poland, 26–29 September 2023. [Google Scholar]





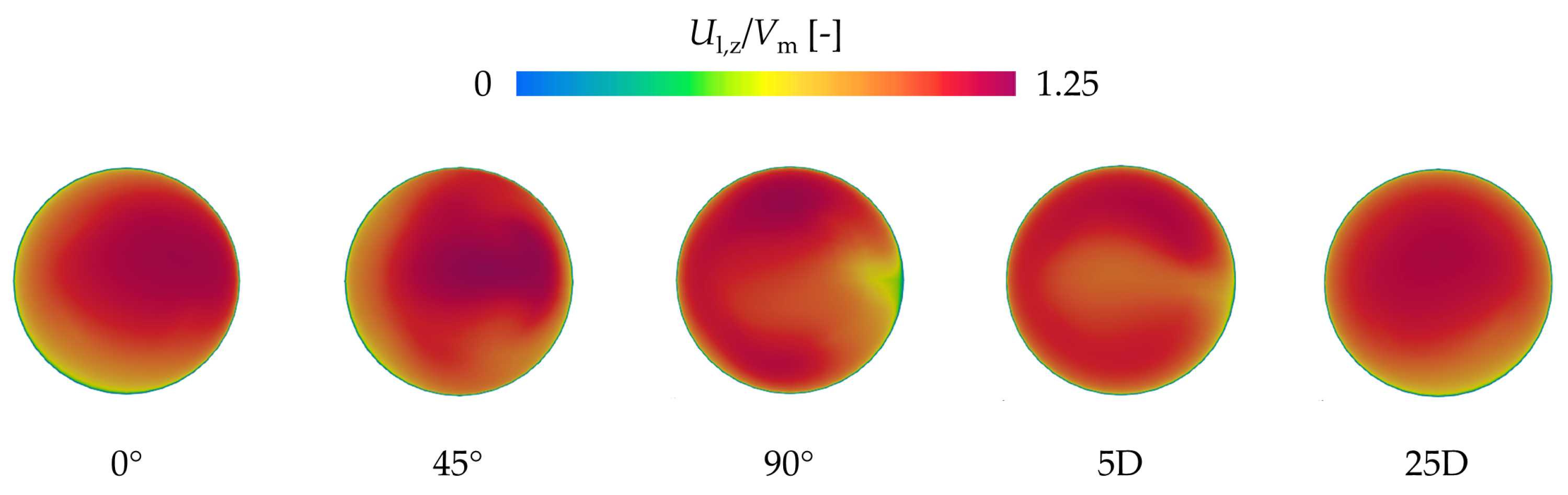



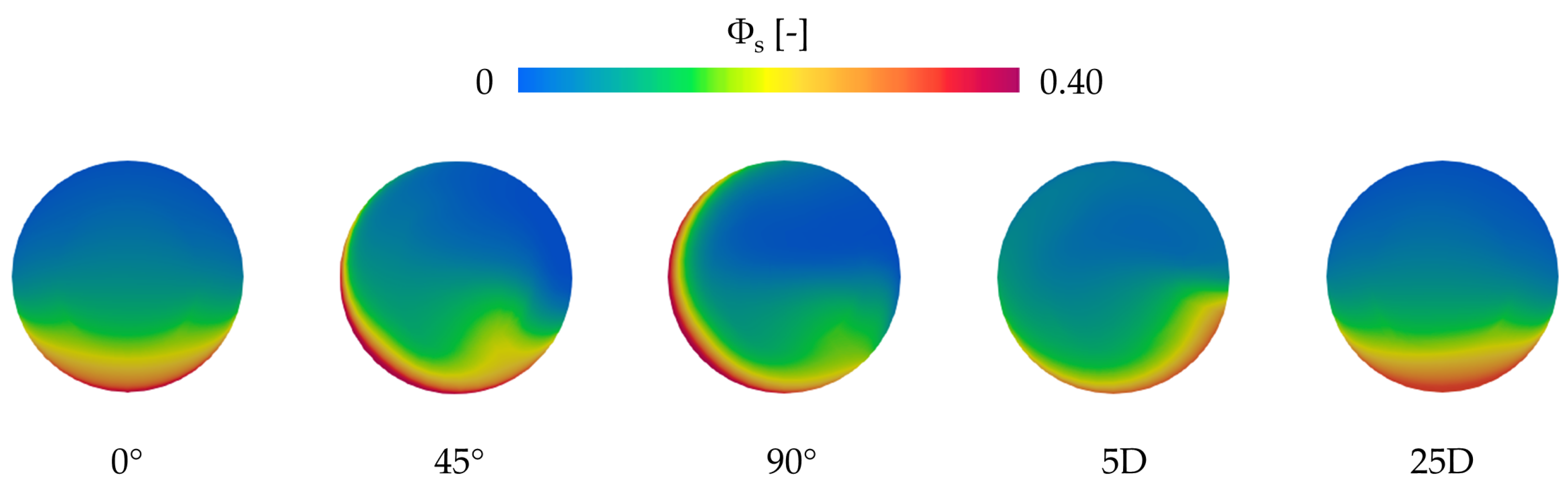






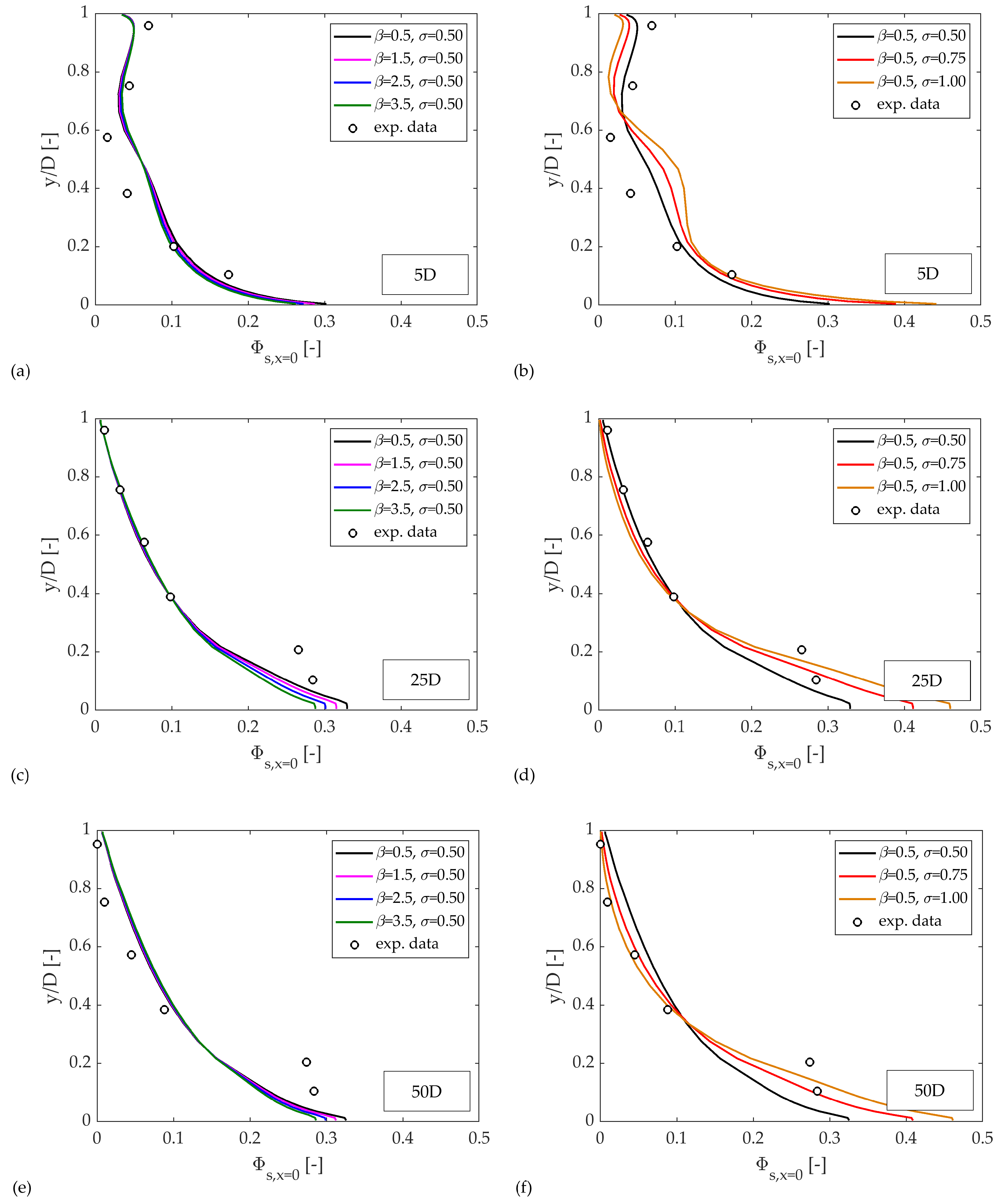

| Simulation ID | D [mm] | [m/s] | [−] | [kg/m3] | [m] | [m] |
|---|---|---|---|---|---|---|
| C1 | 50 | 2.0 | 0.05 | 2650 | 150 | 0 |
| C6 | 500 | 4.5 | 0.40 | 2650 | 150 | 0 |
| Mesh ID | ||||||
|---|---|---|---|---|---|---|
| mesh1 | 6 | 6 | 90 | 16,200 | 0.1251 | 1.790% |
| mesh2 | 8 | 8 | 110 | 35,200 | 0.1237 | 0.651% |
| mesh3 | 10 | 10 | 130 | 65,000 | 0.1231 | 0.163% |
| mesh4 | 16 | 14 | 180 | 207,360 | 0.1229 | - |
| betaSigmaSlurryFoam | - Model | ||||
|---|---|---|---|---|---|
| (OpenFOAM) | (PHOENICS) | ||||
| C1 | C6 | C1 | C6 | ||
| 0.5 | 0.75 | 0.0766 | 0.0402 | 0.0801 | 0.0396 |
| 1.5 | 0.0776 | 0.0443 | 0.0802 | 0.0435 | |
| 2.5 | 0.0776 | 0.0519 | 0.0803 | 0.0514 | |
| 3.5 | 0.0776 | 0.0698 | 0.0805 | 0.0712 | |
| 2.5 | 0.50 | 0.0766 | 0.0525 | 0.0789 | 0.0514 |
| 0.75 | 0.0776 | 0.0519 | 0.0803 | 0.0514 | |
| 1.00 | 0.0786 | 0.0517 | 0.0818 | 0.0513 | |
| Mesh ID | ||||||||
|---|---|---|---|---|---|---|---|---|
| mesh1 | 8 | 8 | 150 | 30 | 250 | 137,600 | 0.355 | 1.508% |
| mesh2 | 10 | 10 | 150 | 30 | 250 | 215,000 | 0.357 | 2.198% |
| mesh3 | 12 | 10 | 180 | 50 | 280 | 318,240 | 0.350 | 0.177% |
| mesh4 | 14 | 10 | 200 | 50 | 300 | 415,800 | 0.349 | - |
| = 0.0394 | = 0.0882 | = 0.1628 | |||||
|---|---|---|---|---|---|---|---|
| CFD | Exp. | CFD | Exp. | CFD | Exp. | ||
| 0.5 | 0.50 | 0.996 | 0.999 | 1.102 | 1.225 | 1.331 | 1.328 |
| 1.5 | 1.002 | 1.130 | 1.408 | ||||
| 2.5 | 1.009 | 1.161 | 1.500 | ||||
| 3.5 | 1.016 | 1.197 | 1.604 | ||||
| 0.50 | 0.50 | 0.996 | 0.999 | 1.102 | 1.225 | 1.331 | 1.328 |
| 0.75 | 1.035 | 1.185 | 1.442 | ||||
| 1.00 | 1.073 | 1.251 | 1.524 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Messa, G.V. BetaSigmaSlurryFoam: An Open Source Code for the Numerical Simulation of Pseudo-Homogeneous Slurry Flow in Pipes. Processes 2024, 12, 2863. https://doi.org/10.3390/pr12122863
Yang Q, Messa GV. BetaSigmaSlurryFoam: An Open Source Code for the Numerical Simulation of Pseudo-Homogeneous Slurry Flow in Pipes. Processes. 2024; 12(12):2863. https://doi.org/10.3390/pr12122863
Chicago/Turabian StyleYang, Qi, and Gianandrea Vittorio Messa. 2024. "BetaSigmaSlurryFoam: An Open Source Code for the Numerical Simulation of Pseudo-Homogeneous Slurry Flow in Pipes" Processes 12, no. 12: 2863. https://doi.org/10.3390/pr12122863
APA StyleYang, Q., & Messa, G. V. (2024). BetaSigmaSlurryFoam: An Open Source Code for the Numerical Simulation of Pseudo-Homogeneous Slurry Flow in Pipes. Processes, 12(12), 2863. https://doi.org/10.3390/pr12122863







