Estimation Model of Rockfall Trajectory Lateral Dispersion on Slopes with Loose Granular Cushion Layer Based on Three-Dimensional Discrete Element Method Simulations

Abstract

Rockfall is a typical successive hazard with a high incidence rate following primary geological disasters such as landslides, rock avalanches, and debris flows. The lateral dispersion of rockfall is significantly affected by the loose granular cushion layer deposited on slopes. This paper aims to develop a quick estimation model for this effect based on the 3D-DEM (discrete element method) numerical simulations. The DEM model employs particles with different bonding properties to create a modeling double-layer granular slope. The present model is also verified by comparing the data from the antecedent large-scale outdoor rockfall experiment with the numerical simulations. Accordingly, the influences of four factors: the initial horizontal release velocity, the size of the rock mass, the granular cushion thickness, and the slope angle on the lateral dispersion of the rockfall trajectory are analyzed, and the underlying physical mechanism is discussed thoroughly. Ultimately, we identify a nondimensional parameter that demonstrates a strong correlation with the evolution of the lateral dispersion ratio of the rockfall trajectory. Based on this insight, we propose an estimation model for predicting the lateral dispersion of the rockfall trajectory. This model can assist engineering and construction personnel in rapidly determining the lateral dispersion range of the rockfall.

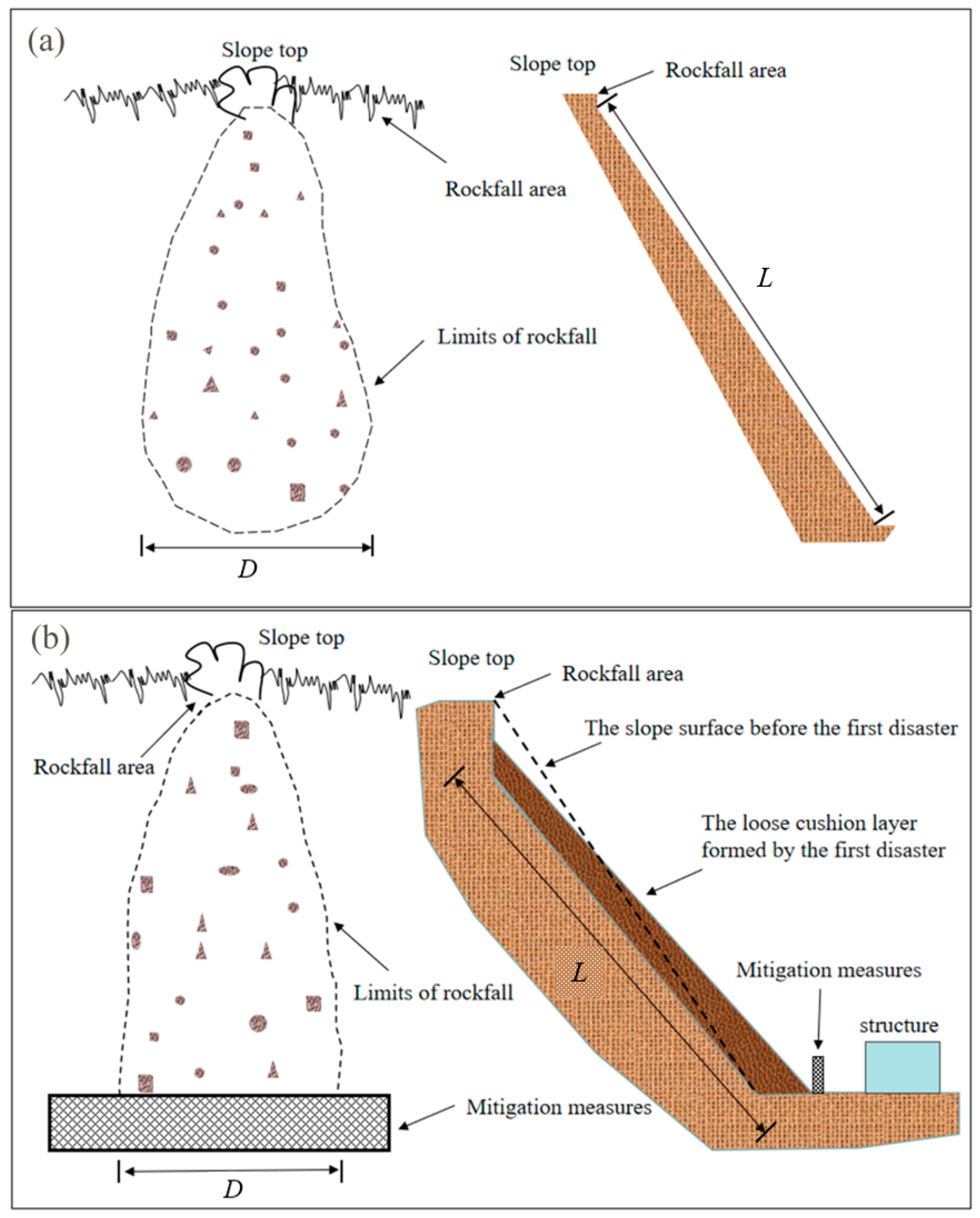
1. Introduction

Rockfall is one of the main disasters in mountainous areas and on engineering slopes, often resulting in severe economic and social losses [1,2,3]. Rockfall occurs when a dangerous rock mass detaches from a steep wall and moves downward with the combined motion of falling, sliding, rolling, or bouncing along the slope [4]. After experiencing a geological disaster (such as landslides, collapses and avalanches, and debris flow), the risk of rockfall disaster on high slopes is increased, posing a severe threat to on-site emergency rescue personnel and equipment as well as threatening the safety of buildings and traffic routes in the affected area [5,6]. As a result, assessing these rockfall hazards has become a significant issue in practice [7]. While traditional research has focused on rockfall hazards in coastal cliffs, engineering slopes, and unstable rock masses [8,9,10], the potential threat of rockfall on the loose granular deposit slopes produced by primary geological disasters has not received sufficient attention, with relatively little research conducted [5,6].

The motion of the rockfall on the side slope table is a three-dimensional motion with inherent randomness [11]. In addition to vertical and horizontal displacement, the rockfall exhibits offset movement along the strike direction of the slope. The magnitude of the offset determines the horizontal threat range of the rockfall perpendicular to the moving profile, which serves as the basis for determining the layout length and range of passive protection systems, such as shelter caves, stone barriers, and stone walls [12,13,14,15].

It is worth noting that on complex slopes, the trajectory of the rockfall is more susceptible to significant lateral deviation [16]. The formation of a loose granular cushion as a result of primary geological disasters often serves to complicate the situation of the slope in question. As a consequence, it is necessary to undertake a study of the trajectory of rockfalls on slopes comprising such a loose cushion. Previous studies using experiments or numerical simulations suggest that the trajectory deviation of rockfall is affected by factors such as the slope material, slope inclination, impact velocity, and the volume of rockfall [12,17,18,19]. Azzoni et al. gave a standardized representation of the maximum deviation of the trajectory from the direction of the steepest gradient and the ratio of the extreme fall path’s lateral distance to the slope length [14]. Their study indicates that the lateral dispersion typically accounts for approximately 20% of the slope length. Furthermore, the lateral dispersion of rockfall trajectories can be represented by a “shadow cone” with its vertex located in the rockfall source area [4]. However, the aperture angle of a shadow cone is typically evaluated subjectively. Consequently, it is essential to employ quantitative techniques to assess transverse dispersion, such as experimental or numerical methods [19]. The research objective of this paper is to study rockfall at rescue sites after disasters, and the main inducement factor is seismic activity. An important characteristic of earthquake-induced rockfall is the initial velocity in the horizontal direction [20]. To better relate this study to the real-world situation of earthquake-induced rockfall, we set a reference variable of initial horizontal velocity.

This study initially validates the feasibility of the three-dimensional DEM to simulate the motion trajectory of rockfall in conjunction with large-scale outdoor rockfall experiments. Subsequently, a rockfall model is constructed on a slope comprising a loose granular cushion with disaster residue. The simulation results are subjected to statistical analysis, including the radius of the rockfall block, the initial horizontal velocity, the slope angle on the rockfall trajectory, and the lateral dispersion of the rock slope covered by loose granular cushions. Finally, combined with the influence of characteristics of various factors, a fast prediction model of the lateral deviation ratio of the rockfall trajectory is proposed.

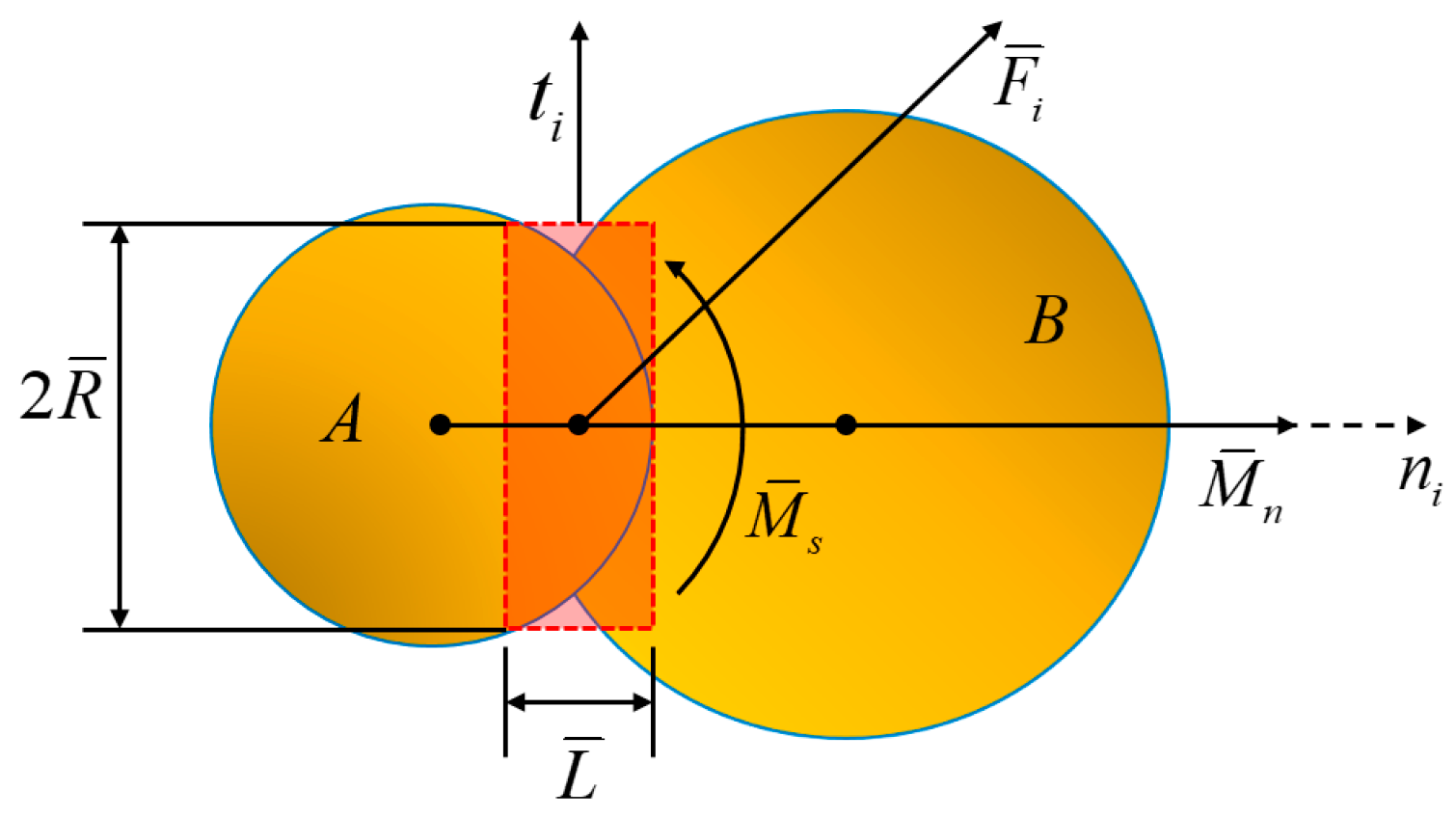
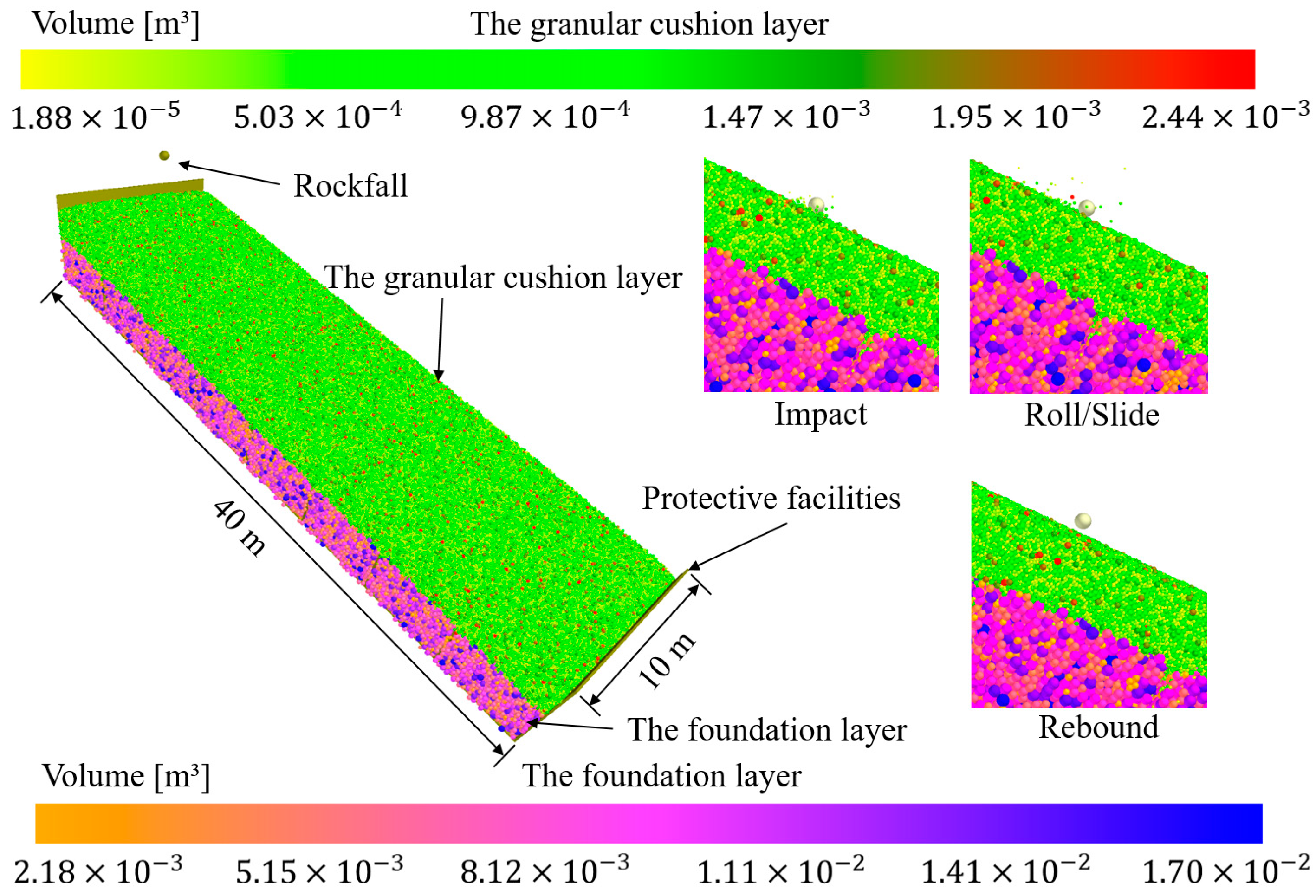
2. Construction and Verification of Discrete Element Model

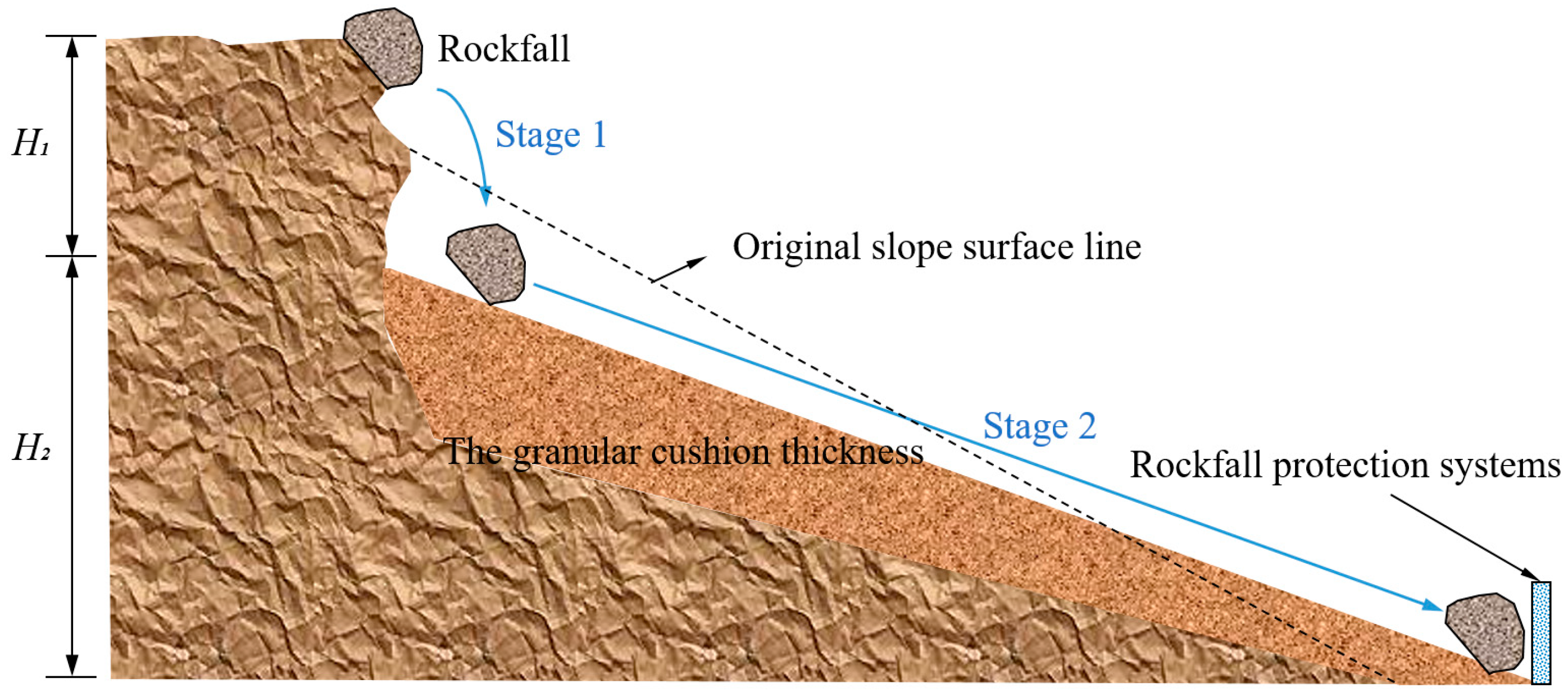
2.1. Construction of Discrete Element Model

The particle contact models involved in our 3D DEM model of rockfall on the granular cushion slope are the Hertz–Mindlin (no slip) model and the Bonding Particle Model (BPM) in EDEM software (Altair EDEM 2021.1). The former combines the Hertzian contact theory in the normal direction with the non-slip model in the tangential direction [21] (see Figure 1). It was applied to generate particles of the granular cushion layer in our DEM model. Specifically, the total force ($F_n$) on the particle is the sum of the elastic force and damping force components, given by Equation (1).

$$F_n=-K_n{\delta }_n+C_n{v}_n^{rel}$$

(1)

where $K_n$ is the normal spring stiffness [N/m], $C_n$ is the normal damping coefficient [Ns/m], ${\delta }_n$ is the normal overlap [m], and $v_n^{rel}$ is the normal component of the relative velocity [m/s].

The total tangential force ($F_t$) is limited by the Coulomb law of friction, and the specific equation is Equation (2).

$$F_t=\min \{{\mu }_s{F}_n;K_t{\delta }_t+C_t{v}_t^{rel}\}$$

(2)

where $K_t$ is the tangential spring stiffness [N/m], $C_t$ is the tangential damping coefficient [Ns/m], ${\delta }_t$ is the tangential overlap [m], ${\mu }_s$ is the static friction coefficient [-], and $v_t^{rel}$ is the tangential component of the relative velocity [m/s].

The rolling friction between the particles is explained by the torque on the contact surface and can be written as Equation (3).

$$T_i=-{\mu }_r{F}_n{R}_i{\omega }_i$$

(3)

where ${\mu }_r$ is the rolling friction coefficient [-], $R_i$ is the distance between the center of mass and the contact point [m], and ${\omega }_i$ is the unit angular velocity vector of the object at the contact point [rad/s].

The bonding contact model can bond particles with a finite-sized “glue” bond (see Figure 2). This bond can resist tangential and normal movement up to a maximum normal and tangential shear stress, at which point the bond breaks. After that, the particles interact as hard spheres. This model is based on the work of Potyondy and Cundall [22]. This model is particularly useful in modeling concrete and rock structures. If the bulk material active bonds are defined and the particles that comprise the bulk material are in contact at the formation start time, the bonds are formed according to the bond parameters. After bonding, the forces ($F_n$, $F_t$) and torques ($M_n$, $M_t$) on the particle are set to zero and are adjusted incrementally every time step according to Equations (4)–(7).

$$\delta F_n=-v_n{S}_{n}A\mathrm{\Delta }t$$

(4)

$$\delta F_t=-v_t{S}_{t}A\mathrm{\Delta }t$$

(5)

$$\delta M_n=-{\omega }_n{S}_{t}J\mathrm{\Delta }t$$

(6)

$$\delta M_t=-{\omega }_t{S}_n{\displaystyle \frac{J}{2}}\mathrm{\Delta }t$$

(7)

where $S_n$ and $S_t$ are the normal and shear stiffness, respectively [N/m], $\mathrm{\Delta }t$ is the time step [s], $v_n$ and $v_t$ are the normal and tangential velocities of the particles [m/s], ${\omega }_n$ and ${\omega }_t$ are the normal and tangential angular velocities [rad/s], $A$ is the cross-section of the parallel bonding bond [m²], and $J$ is the polar moment of inertia [kg·m²].

The bond is broken when the normal and tangential shear stresses exceed some predefined value (See Equations (8) and (9)).

$${\sigma }_{\max }<{\displaystyle \frac{-F_n}{A}}+{\displaystyle \frac{2M_t\overline{R}}{J}}$$

(8)

$${\tau }_{\max }<{\displaystyle \frac{-F_t}{A}}+{\displaystyle \frac{M_n\overline{R}}{J}}$$

(9)

After the bond breaks, the force and moment formed by the bond between small particles disappear. Subsequently, the tiny particles fall off from the large particles, and this induces the crushing of the particles.

It is worth noting that the two-particle coarser model adopted in this paper only considers the force interaction between the dry particles and does not consider the influence of rainfall and other conditions on the contact parameters between particles. For this study, they can be used for the current earthquake-induced rockfall, but the rain-induced rockfall needs to be newly selected or modified.

Figure 3 shows the three-dimensional DEM model of the double-grain layer slope rockfall proposed in this paper. The upper layer is the granular cushion to simulate the residual particle accumulation after a geological disaster, and the lower layer is the slope foundation composed of mutually bonded particles. The Hertz–Mindlin model generates the upper layer particles (no slip), and the lower layer particles are generated by the Hertz-Mindlin (no slip) model with the bonding model. It is difficult to predict the composition of loose deposit particles remaining in the slope after the geological disaster. So, the particle size of the two layers is generated randomly by the normal distribution to simulate the randomness of the natural particle size. The slope simplification model is widely adopted in many studies [23,24] as it simplifies the slope contour to a fixed angle and beveled plane. Moreover, the DEM slope model is composed of discrete element particles. Hence, the surface of the DEM slope model is rougher and more undulating than that of the ordinary simplified slope model, and there are certain micro-geomorphic features [25], so this simplification is acceptable. Similarly, this study ignores the shape effect of the particles, that is, the use of spherical particles of different radii to construct slope bodies and simulate rockfall blocks. Some scholars have proven that spherical blocks have higher energy restorer values than cubic blocks through the shape effect test [26]. In other words, if the motion characteristics of spherical rockfall are understood and corresponding preventive measures are taken, these measures can also effectively resist non-spherical rockfall. In addition, the simplified rock mass can be used in the rockfall trajectory simulation, which can significantly improve the calculation efficiency [27]. In the model, the slope length is set to 40 m, and the width is set to 10 m. Azzoni et al. [28] concluded through experiments that regardless of the slope length, the rockfall’s lateral dispersion is usually in a stable range. Therefore, due to the limitation of computing power, it is acceptable to set the slope length to 40 m. Considering the deterioration of the mechanical properties of slope soils caused by a geological disaster and the fact that the granular cushion layer has relatively weakened mechanical properties after primary disasters, the elastic modulus and bond stiffness of the particles in the slope model are moderately reduced compared with the corresponding values in Tan’s simulation [29]. Combined with the literature [25,30], the concrete parameters of the DEM model of the double granular layer slope rockfall are shown in

Table 1. The physical parameters and interparticle contact parameters used in the discrete element model.

DEM Parameter	Value	DEM Parameter	Value
Length of the slope L [m]	40	Particle density [kg/m3]	2700
Slope inclination angle β [°]	15/20/25	Young’s modulus [Pa]	1.00 × 108
Width of the slope W [m]	10	Poisson’s ratio [-]	0.25
Average particle radius of the foundation layer [m]	0.125	Normal bond stiffness [N/m3]	1.00 × 107
Particle bond radius of the foundation layer [m]	0.12	Tangential bond stiffness [N/m3]	1.00 × 107
Average particle radius of the granular cushion layer [m]	0.05	Normal tensile strength [Pa]	1.00 × 1010
Spherical rockfall radius R [m]	0.3/0.4/0.5/0.6/0.7	Tangential tensile strength [Pa]	1.00 × 1010
Coefficient of restitution e [-]	0.8	Coefficient of rolling friction ${\mu }_r$ [-]	0.1
Coefficient of static friction ${\mu }_s$ [-]	0.5	Gravitational acceleration [m/s2]	9.81
Initial horizontal velocities V0x [m/s]	1/3/5/7/9/11	The foundation layer’s thickness [m]	3.4
The granular cushion layer thickness [m]	0.35/0.5/0.65/0.8/1.1/1.4/1.7

. Among them, parameters such as Young’s modulus, Poisson’s ratio, and density of particles are mainly set according to the common values in the numerical simulation of particle media. The values of the rolling friction coefficient, sliding friction coefficient, and recovery coefficient refer to the research on the gravel slope in the monograph of Chen [30]. Since the solid particles simulated in this paper are all spherical, while the actual ones mostly rough particles with edges and surfaces that are not smooth, this paper attempted to restore the real particle situation as much as possible by increasing the static friction coefficient and reducing the rolling friction coefficient. Some investigations have shown that most secondary geological disasters occur between 0° and 50° [31]. However, when the slope angle of the discrete element numerical model is greater than 30°, the particles of the upper loose accumulation layer will slide. Therefore, the slope angle was selected within 30° in the current study.

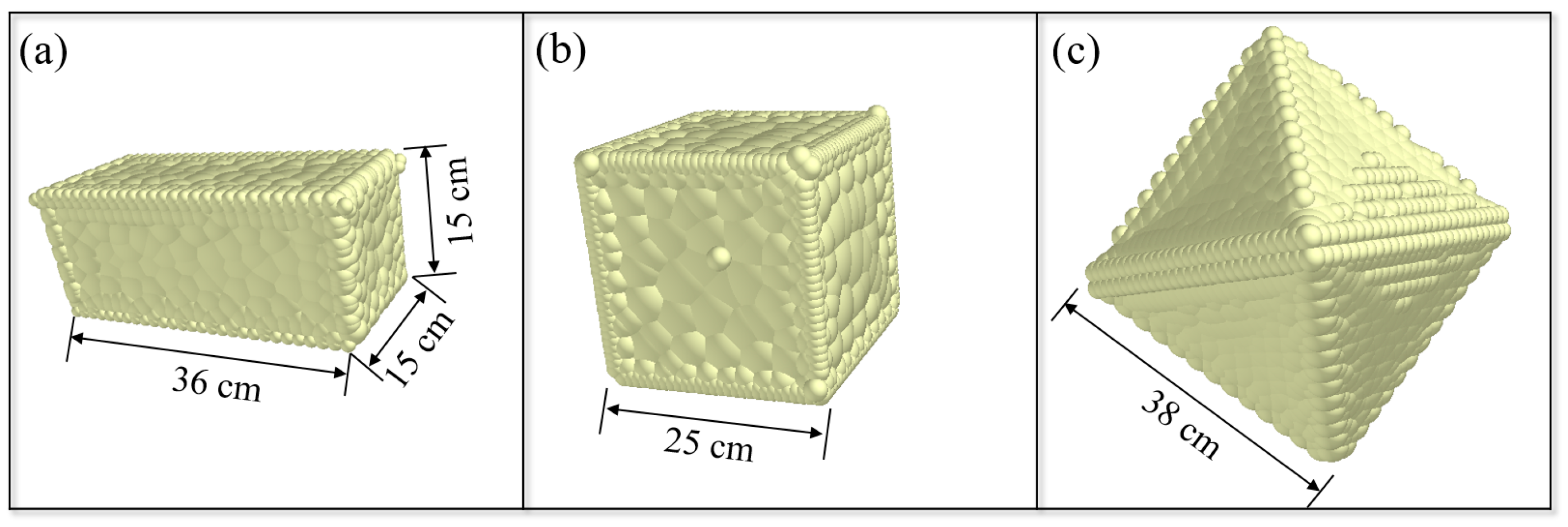
2.2. Feasibility Verification

In this study, the large-scale outdoor rockfall experiment conducted by Liu et al. [3] was used to verify the discrete element model, and the reliability of using the discrete element method to simulate rockfall motion trajectory was proven. According to the outdoor experiment conducted by Liu et al., rockfall blocks of different shapes are established in the DEM model, as shown in Figure 4. The rockfall blocks created in the DEM model are bonded by spherical particles of different sizes, and their surfaces are not entirely flat, which results in certain differences in mass between the rockfall blocks in DEM and those used in outdoor experiments. For details, see

Table 2. Comparison table of mass and size of rockfall blocks.

Block	Number	Dimension [cm]	Mass [kg] (Experiment)	Mass [kg] (DEM)
Cuboid	1−1	36 × 15 × 15	19.10	18.86
Cube	2−2	Edge length 25	41.20	40.81
Regular octahedron	3−3	Edge length 38	68.40	71.35

. Liu et al. used three different slopes to carry out rockfall experiments. Slope B was used in this section to verify the reliability of the simulation. Figure 5a shows the lateral deviations and resting positions at the slope foot, and Figure 5b shows the B slope (a rocky slope with an inclination of 45°) constructed using EDEM.

The constructed rockfall blocks 1−1, 2−2, and 3−3 are released on slope B in the DEM model. Figure 6a shows the variation in block lateral deviations over time. The lateral deviation results obtained by experiments and the DEM model follow the relationship of block 1−1 > block 2−2 > block 3−3. Figure 6b shows the variation in block kinetic energy over time, and the variation in kinetic energy obtained by experiments and the DEM model both follow the relationship of block 1−1 < block 2−2 < block 3−3. Figure 6c shows the maximum jumping height and average jumping height. They follow the relationship of block 1−1 > block 2−2 > block 3−3. Figure 6d shows the position of the rockfall resting positions at the slope foot. The horizontal coordinate (x) of the resting position obtained by the experiment and the DEM model both follow the relationship of block 1−1 > block 2−2 > block 3−3. Due to the difference in mass between the rockfall blocks created in the DEM model and those used in outdoor experiments, as well as certain errors between the particle contact parameters used in DEM and the experimental materials, the results obtained using the DEM simulation are not completely consistent with the results of outdoor experiments. However, the variation trend of the DEM simulation results is the same as that of the outdoor experiment results, and the lateral deviation, resting position, jumping height, and kinetic energy of different blocks obtained by both methods follow the same relationship. The reliability of using the DEM to study the motion characteristics of rockfall is verified.

The contact parameters between particles are also important factors affecting the reliability of the discrete element numerical simulation. The calibration of the contact model parameters (the recovery coefficient of particles, the coefficient of static friction, and the coefficient of rolling friction) is not easy for the proposed model since there has been no direct laboratory test or numerical model to study the influence of rocky granular cushion layer thickness on the rockfall motion characteristics to the best of our knowledge. In light of this reason, we can only verify simulation results with the closest investigation that a vertical spherical projectile impacts a horizontal soil bed [32].

Note that the research of Shen and Zhao et al. [32] on the projectile impacting a particle bed has indicated that the friction between particles affects the projectile dynamics more intensively; in comparison, the recovery coefficient changes as alterations in the damping ratio exerts little effect on the projectile velocity. The comparison and analysis of the simulation results in Figure 7, Figure 8 and Figure 9 are consistent with the above conclusions, indicating that the DEM model of rockfall of the slope containing cushion particles proposed in this paper is reasonable and reliable.

In addition, the size boundary condition of the model is a critical factor affecting the reliability of discrete element numerical simulation. When $T/D>2.6$, $L/D>5.0$, and $W/D>5.0$, the influence of lateral boundary constraints on the granular layer boundary can be ignored according to the results of the previous investigation [33]. Note that the diameter $D$ of the rockfall in the present DEM model is 0.8 m, 1 m, 1.2 m, and 1.4 m, respectively; when the particles are deposited and stabilized under the action of gravity, the total thickness $T$ of the particle layer is 3.75 m, 3.90 m, 4.05 m, 4.20 m, 4.50 m, 4.80 m, and 5.1 m, respectively; and the length $L$ is 40 m, and the width $W$ is 10 m; so it can be found that $T/D=2.68~6.38$, $L/D=28.57~50$, and $W/D=7.14~12.5$, and these dimensions can meet the above requirements. Therefore, the lateral boundary conditions and the size of the model slope adopted in this study are reasonable and valid.

3. Analysis of Numerical Simulation Results

To accurately describe the lateral deviation of rockfall on the double granular layer slope, we will analyze the lateral dispersion ratio of the rockfall trajectory as proposed by Azzoni et al. This ratio is defined as Equation (10) [28].

$$\eta ={\displaystyle \frac{D}{L}}$$

(10)

where $D$ is the distance between the two extreme fall paths of rockfall [m] and $L$ is the equivalent slope length [m]. See Figure 10a for details.

In the event of geological disasters such as landslides and collapses near slopes, particularly those related to buildings and highways, it is essential to implement passive protection measures at the slope’s bottom. These measures help prevent rockfall from damaging structures and endangering human activities (see Figure 10b). The increase in these protective measures will cause the rockfall to stop due to the blocking effect of the protective device. From another perspective, adding passive protection devices changes the effective slope length of the rockfall movement. Some rockfalls travel less distance than they would without a barrier, and the shorter trajectory of the rockfall may result in a non-maximum lateral dispersion (the maximum lateral dispersion in the natural state). At present, most of the lateral dispersion ratios for passive protection facilities are derived from natural slope rockfall experiments [28,34]. In practice, protective devices are installed according to the location of the building, which often makes the effective slope length of the rockfall moving on the slope shorter. Therefore, the reference value selected according to the experimental results may be too large. The effective slope length changed by the protective device is considered in the following research. It helps the designers of passive protection facilities to choose a more reasonable lateral dispersion ratio according to the actual situation and design a more appropriate length of protection facilities. Avoiding the waste of manpower, material resources, and time caused by the design of passive protection facilities is imperative.

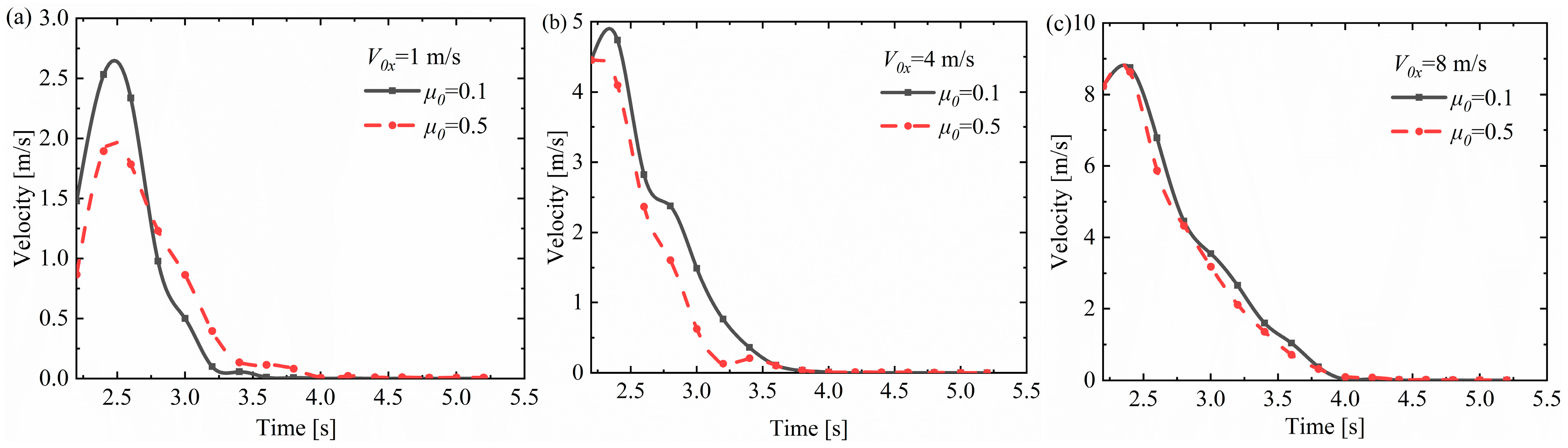
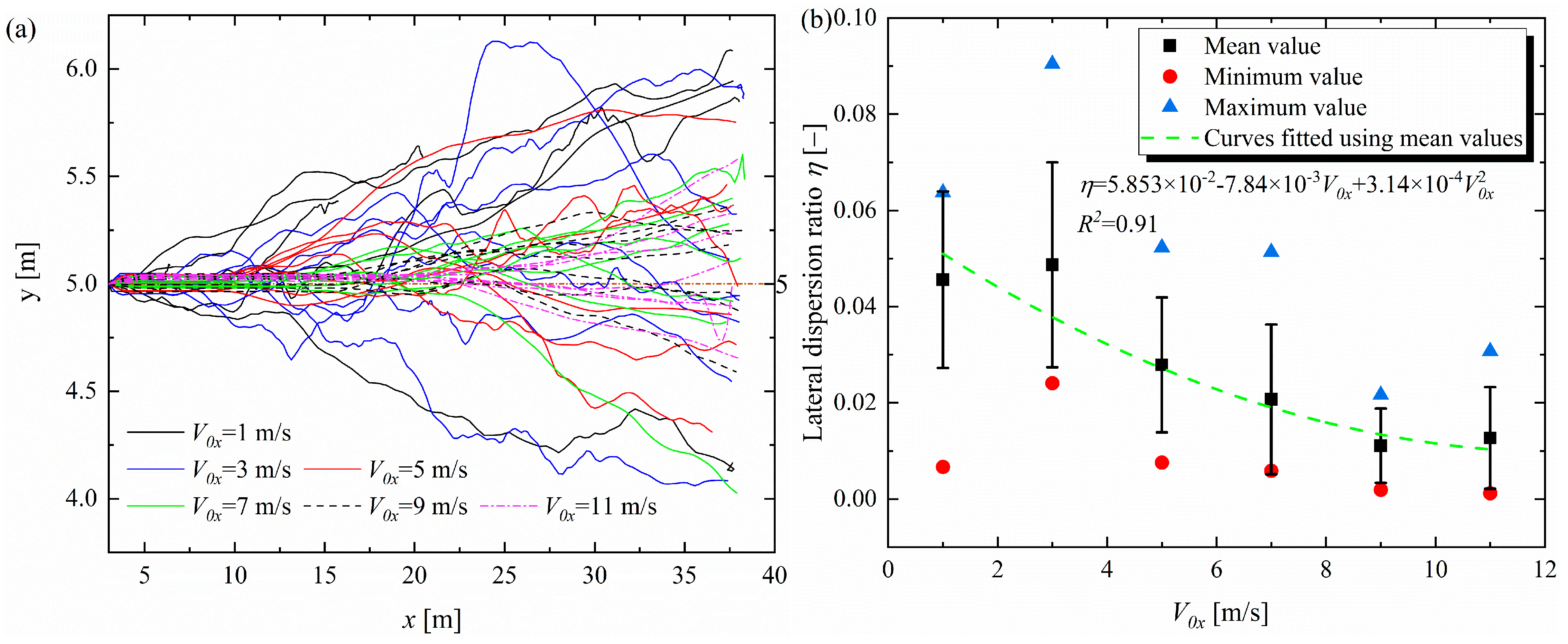
3.1. Effect of Horizontal Velocity

The elevation difference between the source area of rockfall and the double granular layer slope may be an essential factor affecting the lateral deviation, and the different elevation differences will lead to the different initial velocities of rockfall when it reaches the double granular layer slope. By releasing the rockfall with a radius of 0.5 m at six different horizontal velocities from a height of 4 m on the slope, we can simulate various elevation differences and effectively reduce the calculation domain of the discrete element model. Figure 11a illustrates the motion trajectory of the rockfall released with six different initial horizontal velocities. It can be observed that a decrease in the horizontal velocity at the point of release leads to a more dispersed motion path. In contrast, an increase in the horizontal velocity results in a decrease in the maximum lateral deviation. For example, the maximum lateral deviation of the rockfall released at 1 m/s is 1.08 m, whereas that of the rockfall released at 11 m/s is only 0.58 m.

Figure 11b presents the mean value and its fitted curve as well as other statistical results (the standard deviation, the maximum value, and the minimum value) of the rockfall lateral dispersion ratio with the change in $V_{0x}$. One can note that the maximum and minimum values of the rockfall lateral dispersion ratio increase first, then decrease rapidly with the ascending horizontal velocity, and finally tend to be stable. In addition, its mean value shows a similar evolution trend as the horizontal velocity increases. It can also be noted that according to the numerical simulation results, we fit the best functional relationship between the mean value of the lateral dispersion ratio and the horizontal velocity, which shows a trend of decreasing first and then stabilizing.

However, Liu [35] and Hu et al. [18] have concluded through the rockfall model experiment that the lateral dispersion ratio of the rockfall falling from the top of the slope has no clear rule, and the lateral dispersion ratio of other falling heights increases with the increase in the falling height. This differs from the conclusion obtained by the numerical simulation in this paper. The reason for this is that the experiment released the rockfall at different heights on the top of the slope, closer to the free fall to the slope. In the numerical simulation, the release of the rockfall at different horizontal speeds was more similar to the falling of dangerous rockfall along the slope and the ejection into the double granular layer slope after rolling, colliding, and other motion modes. According to the change curve fitted by the mean value of the lateral dispersion ratio, one can find that the changing trend of the mean value gradually decreases with the increasing horizontal velocity. It has an excellent nonlinear correlation with the initial horizontal velocity of the rockfall, and the correlation coefficient is 0.91.

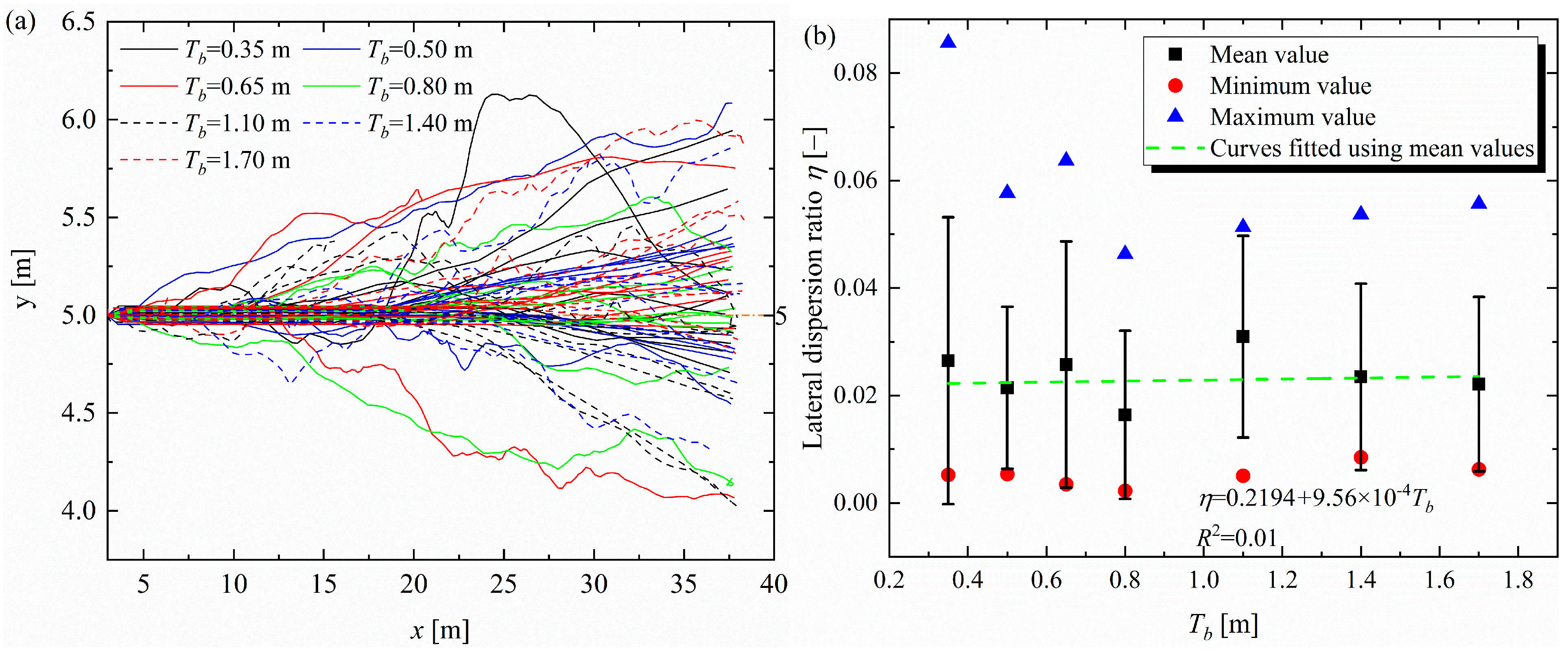
3.2. Effect of the Thickness of the Granular Cushion Layer

In this subsection, seven groups of loose cushion layers with different thicknesses are designed, and the rockfall with a 0.5 m radius is released at the same height from the top of the slope. Figure 12a shows the rockfall motion trajectories on the slope with seven different cushion layer thicknesses from the top–down view. The maximum lateral deviation of the rockfall is 1.13 m when the thickness of the cushion layer is 0.35 m. At the same time, the maximum lateral deviation of the rockfall is still close to 1 m when the thickness of the cushion layer increases to 1.7 m. The maximum lateral deviation of the rockfall under other thickness conditions is within the range of 0.9 m~1.08 m.

Figure 12b illustrates the mean value evolution of the rockfall lateral dispersion ratio at different $T_b$, along with its fitted curve and other statistical quantities (the standard deviation, the maximum value, and the minimum value). As can be seen from the figure, the average value of the rockfall lateral dispersion ratio of the slopes of seven kinds of cushion layer thicknesses is within the range of 0.02~0.03, and the relative fluctuations are minimal. As the thickness of the loose cushion layer decreases, the rockfall lateral dispersion ratio exhibits larger maximum values and standard deviations. This indicates that thinner cushion layers result in more dispersed rockfall trajectories. Therefore, the influence of cushion layer thickness should be taken into account when predicting the lateral dispersion ratio of rockfalls.

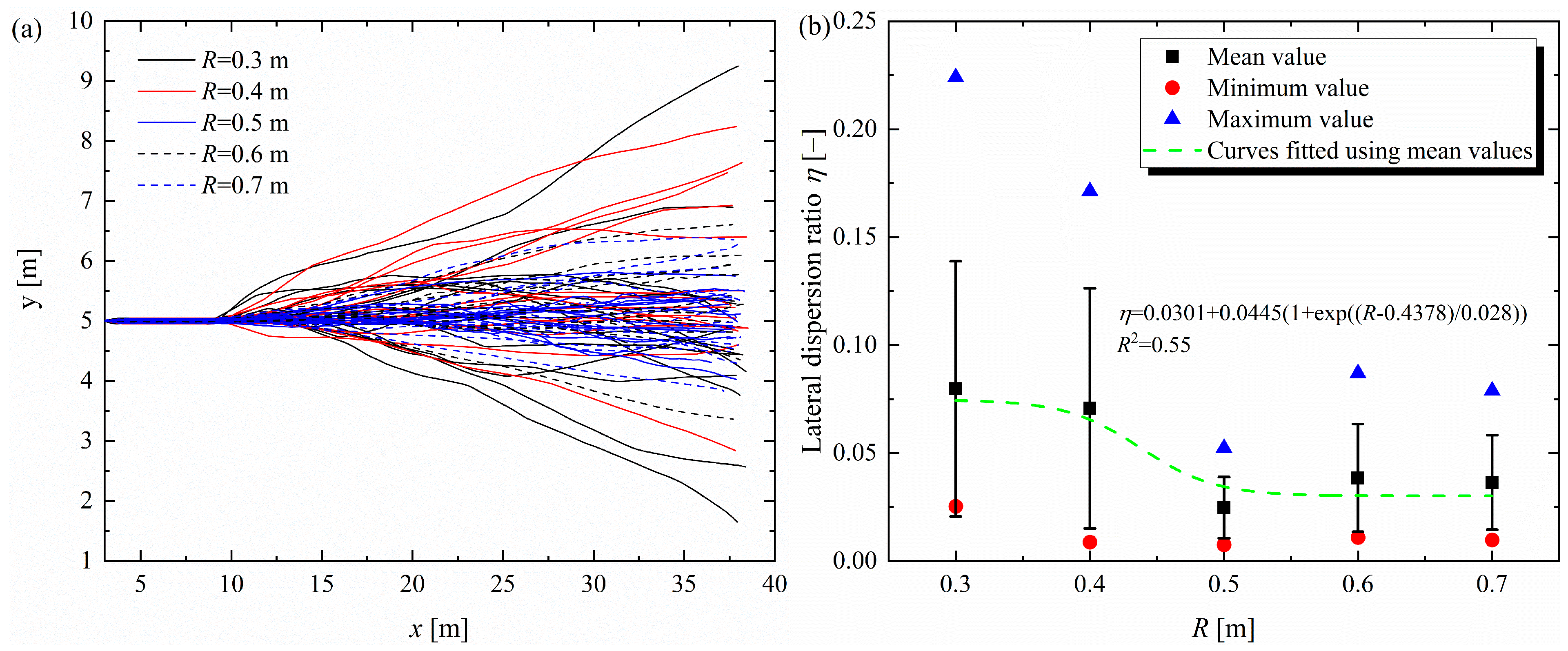
3.3. Effect of Rockfall Radius

This section simulates the rockfall motion with five different radii on the double-layer slope to study how the radius affects the lateral dispersion of the rockfall trajectory. Figure 13a shows the top view of the motion trajectories for the five different rockfall radii. As can be seen from this figure, the maximum lateral deviation of rockfall with a radius of 0.3 m can reach 4.25 m; the maximum lateral deviation of rockfall with a radius of 0.4 m is 3.24 m’ and the maximum lateral deviation of rockfall with a radius of 0.7 m is only 1.38 m. It can be concluded that a reduction in the rockfall radius results in an increase in the maximum lateral deviation of the rockfall trajectory.

Figure 13b shows the mean value evolution of the rockfall lateral dispersion ratio at different R, along with its fitted curve and other statistical quantities (the standard deviation, the maximum value, and the minimum value). One can notice that when the radius of the rockfall decreases, both the standard deviation and the maximum value of the rockfall lateral dispersion ratio increase, which indicates that the spread of the rockfall lateral dispersion ratio augments with the descending rockfall radius. It further verifies the conclusion above. Specifically, when the radius of the rockfall increases from 0.3 m to 0.5 m, the mean value of the lateral dispersion ratio is reduced by 68.9%; in comparison, when the rockfall radius increases from 0.6 m to 0.7 m, the mean value of the lateral dispersion ratio reduces by only 5.4%; this indicates that the lateral dispersion ratio decreases rapidly and then becomes stable with the increase in the volume of the rockfall, which is also proved by the curve variation trend fitted by the mean value of the lateral dispersion ratio. In addition, according to the change curve fitted by the mean value, it is found that the changing trend of the mean value decreases slowly with the increase in the radius of the rockfall at first, then decreases rapidly, and finally tends to be stable, with the correlation coefficient of 0.55.

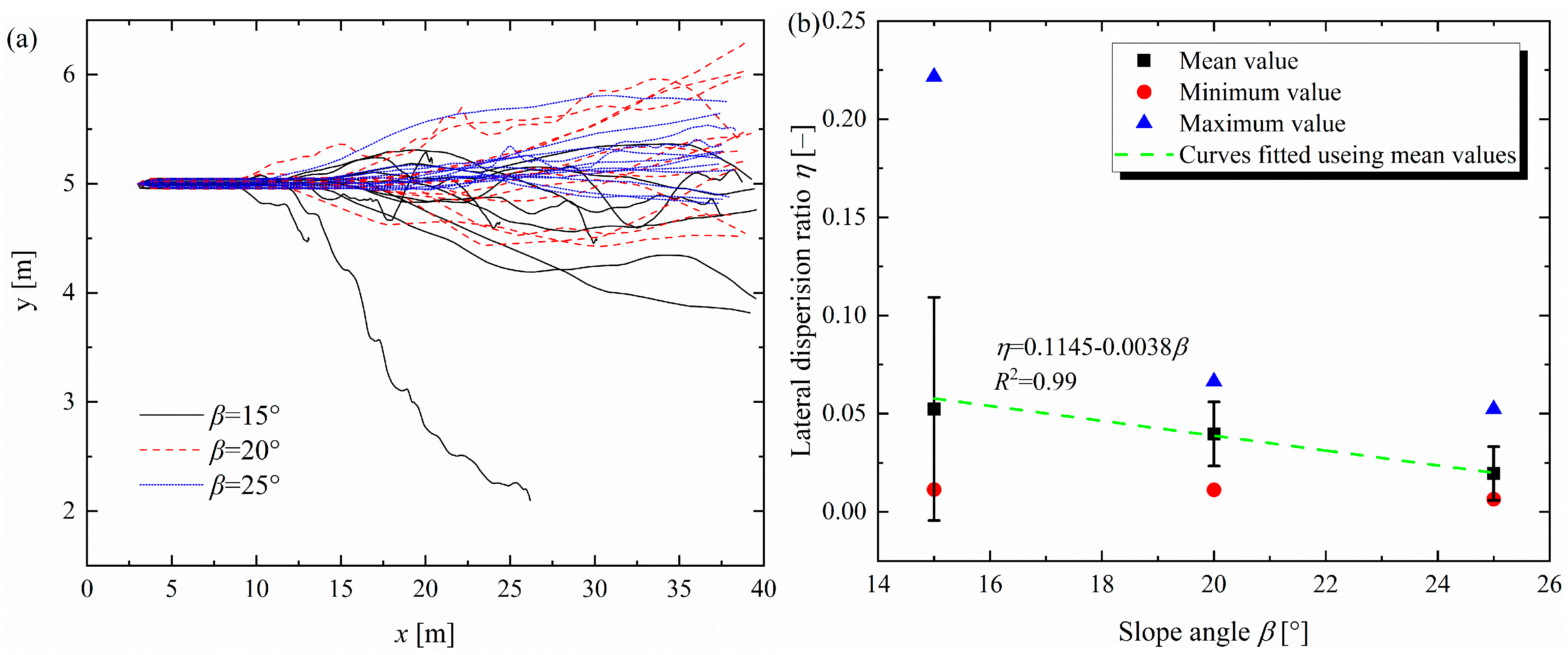
3.4. Effect of Slope Inclination

In this section, three different slope inclination angles are explored to study the influence of slope inclination on the rockfall trajectory lateral dispersion. Figure 14a shows the top view of the rockfall trajectory under different slope inclination conditions. One can note that as the inclination of the slope increases, the rockfall motion exhibits a more intensive lateral dispersion. Concretely, the maximum lateral deviation distance of the rockfall on the slope with the inclination of 15° is 2.9 m; for the inclination of 20°, the maximum lateral deviation distance decreases to 1.29 m; for the inclination of 25°, the maximum lateral deviation distance decreases to 0.81 m. This suggests that the smaller the inclination of the slope is, the larger the maximum lateral deviation of the rockfall trajectory.

Figure 14b shows the mean value and its fitting curve, standard deviation, maximum value, and minimum value of the trajectory lateral dispersion ratio of the rockfall on the double-layer slope with different inclination angles. Note that as the slope inclination declines, the standard deviation of the lateral dispersion ratio rises; this means that the dispersion degree of the lateral dispersion ratio increases with the declining slope inclination, which verifies the conclusion obtained according to Figure 14a. The average and maximum values of the lateral dispersion ratio decrease with the decrease in slope inclination, and the minimum values change little under different slope inclination conditions. According to the evolution curve fitted by the mean value, it can be seen that the lateral dispersion ratio of the trajectory has an excellent linear correlation with the slope inclination, and the correlation coefficient is 0.99.

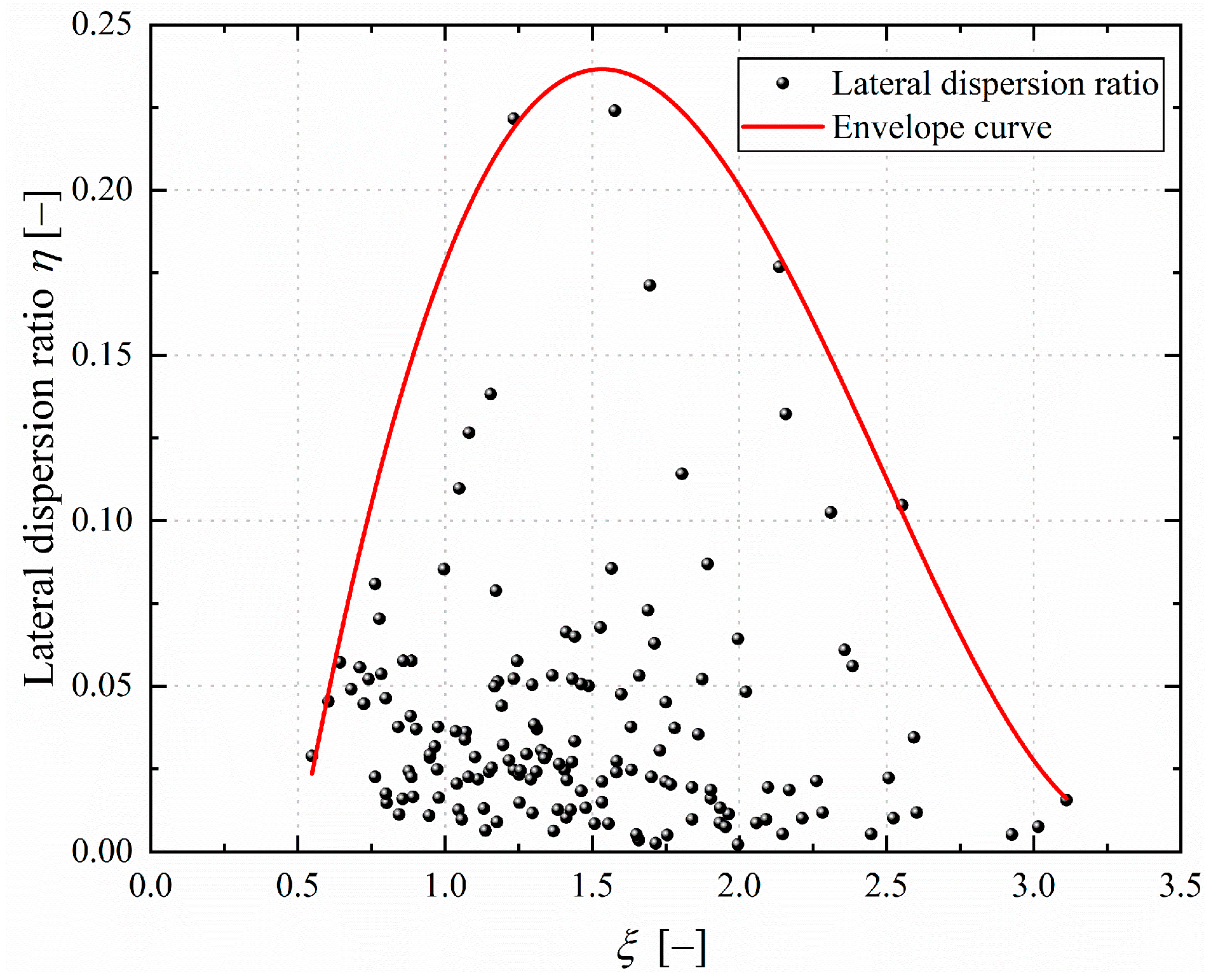
4. Rapid Estimation Model of the Lateral Dispersion Ratio of Rockfall

The influence of four factors on the lateral dispersion ratio of the double granular layer slope rockfall trajectory was analyzed in the previous section. It was found that the trajectory lateral dispersion ratio has a high correlation with $V_{0x}$. It is negatively correlated with slope inclination $\beta$. The combination of the natural constant and the rockfall radius $R$ strongly correlates with the lateral dispersion ratio. The cushion layer thickness also has an essential influence on the lateral dispersion of the rockfall trajectory. Taking these three factors into account, a rapid evaluation model of the rockfall trajectory lateral dispersion is proposed in this section.

Firstly, three reference variables $V_b/\sqrt{g{T}_b}$, $\tan \beta$ and $e^{-(R/R_0)}$ are introduced to construct the prediction model of the lateral dispersion ratio of double granular layer slope rockfall and ensure dimensional rationality. Herein, $V_b$ is the speed when the rockfall reaches the double granular layer slope, and it is employed to replace $V_{0x}$. Since the slope length of the present rockfall DEM model is limited and the height between the rockfall releasing position and the top of the slope is also limited, the horizontal release velocity $V_{0x}$ is set to make the rockfall have a bigger velocity $V_b$ when it reaches the slope surface. Moreover, the effect of the rockfall incidence angle with different $V_{0x}$ can be reflected indirectly by introducing $\tan \beta$ since the dependence of the rockfall incidence angle on the horizontal releasing velocity, and the slope inclination can be easily achieved by solving the trajectory equation of the rockfall flat throw combined with the geometric equation of the slope surface. For the sake of conciseness, we do not give them here.

The three reference variables are calculated based on the data obtained from the numerical simulation. They are listed as combination formulas in different fitting methods, and the relationship between different combination formulas and the lateral dispersion ratio is explored to construct the prediction model of the lateral dispersion ratio of double granular layer slope rockfall. After multiple combination tests, it was found that the scatter plot of the relation between the lateral dispersion ratio and the nondimensional parameter $\xi$ (see Equation (11)) is the most concentrated and has a relatively regular envelope curve (see Figure 15).

$$\xi ={\displaystyle \frac{V_b{e}^{(-R/R_0)}\tan \beta }{\sqrt{g{T}_b}}}$$

(11)

where $g$ is the acceleration of gravity [m/s²], $R_0$ is the rockfall relative radius [m], and the size is 1 m.

The specific equation of the envelope curve is Equation (12).

$$\eta =0.74\xi -0.24{\xi }^2-0.02{\xi }^3+0.01{\xi }^4-0.31$$

(12)

As aforementioned, considering that the slope length of the discrete element model is restricted, $V_{0x}$ is set to make the rockfall have a higher speed $V_b$ although $V_{0x}$ is not a natural variable in a real disaster relief scene. As shown in Figure 16, the double granular layer slope rockfall movement process is decomposed into two stages. However, ignoring the energy loss of the rockfall in the first stage, the speed of the rockfall reaching the double granular layer slope can be calculated according to the height $H_1$. The specific formula is given in Equation (13).

$$mg{H}_1={\displaystyle \frac{1}{2}}m{V}_b^2$$

(13)

where $m$ is the mass of the rockfall [kg]; $H_1$ is the elevation difference between the source area of the rockfall and the double granular layer slope [m].

Finally, the envelop of the lateral dispersion ratio of the rockfall on the double granular layer slope can be obtained with Equations (11)–(13). It is only necessary to know the rockfall radius $R$, the elevation difference between the source area of the rockfall and the double granular layer slope $H_1$, the slope inclination angle $\beta$, the loose cushion thickness $T_b$, and the local gravitational acceleration $g$, so that the maximum lateral dispersion ratio of double granular layer slope rockfall can be quickly estimated. Then, the relevant engineering design and construction personnel can be helped to quickly determine the lateral deviation range of the rockfall according to the specific situation and, thus, determine the scope of passive prevention.

According to the location information of the potential rockfall source and the radius of the rock mass, combined with the above fast prediction model, the maximum lateral dispersion ratio of the rock can be estimated. Then, the lateral length of the passive protection device can be quickly calculated by combining the formula $D=\eta L_1$. Here, $D$ is the distance from the source area of the rockfall to the passive protection facility [m].

The field of engineering often takes the lateral dispersion ratio of rockfall as a fixed value. For example, Azzoni et al. [28] proposed that on a single slope under a slope, the lateral dispersion ratio is within 0.1; Ye et al. [34] carried out the rockfall field test, and given the characteristics of road and railway, it was suggested that the rockfall lateral dispersion ratio should be 0.3. In this way, it is easy to cause an error between the lateral dispersion ratio used in the project and the actual project. If the lateral dispersion ratio is too large, the passive protection structure will be set up for too long, wasting a lot of time, manpower, and material resources. If the lateral dispersion ratio is too small, the protection range is too small, which is dangerous. In contrast, the advantage of the rapid prediction model of the lateral dispersion ratio of double granular layer slope rockfall constructed in this paper is that it can quickly determine the lateral dispersion ratio to be used in the project according to the actual conditions, which saves time and is more cost-effective for the related projects.

5. Conclusions

This paper presents a verification of the reliability of the DEM model for simulating rockfall disasters, which is achieved through a comparison with the results of large-scale outdoor rockfall tests. Subsequently, a double granular layer slope rockfall model was constructed using the DEM method. Based on the findings of numerical simulations, a model for predicting the quadratic trajectory lateral dispersion ratio of double granular layer slope rockfalls was developed. The main results of this study are as follows:

(1)

In order to construct the prediction model, the lateral dispersion ratio of rockfall trajectories under a variety of conditions is calculated based on the numerical simulation results. Furthermore, the variation rule of the lateral dispersion ratio of rockfall trajectories under the influence of a single factor is analyzed. We fit the curve equation and addressed the fact that the trajectory lateral dispersion ratio of rockfall varies with the influence factor.

(2)

Considering the influence of characteristics of each factor of change on the lateral dispersion ratio and the rationality of the formula dimension, a nondimensional parameter $\xi =V_b{e}^{(-R/R_0)}\tan \beta /\sqrt{g{T}_b}$ can be identified, and the envelope equation of the rockfall lateral dispersion ratio can be determined. It is only necessary to know limited parameters: the radius of the rockfall, the elevation difference between the source area of the rockfall and the cushion layer, the slope inclination, and the thickness of the particle cushion layer, which are easy to obtain so that the maximum of the rockfall dispersion ratio can be quickly estimated under the specified conditions. This prediction model can help the relevant engineering design and construction personnel to quickly determine the rockfall lateral dispersion ratio according to the specific situation, which is convenient for reasonably designing and planning rockfall protection measures.

(3)

The rockfall lateral dispersion model constructed in this paper is applied to the rapid placement of protection measures after a disaster at a site, so the parameters selected are obtained as quickly as possible. And because the number of particles in the model can reach up to 1,020,000, which leads to huge calculations, the shape of the rolling stone is simplified to a spherical shape. In future work, the current discrete element model can be improved to consider the influence of the shape of the rolling stone without increasing the amount of computation.