Study on the Influence of Heterogeneity of Low-Permeability Reservoirs on Wormhole Morphology and Acidizing Process Parameters
Abstract
:1. Introduction
2. Mathematical Models
- (1)
- Pressure equation:
- (2)
- Velocity equation [10]:
- (3)
- H+ concentration:
- (4)
- (5)
- Rock equation:
- (6)
- Chemical reaction:
- (7)
- Quantity update:
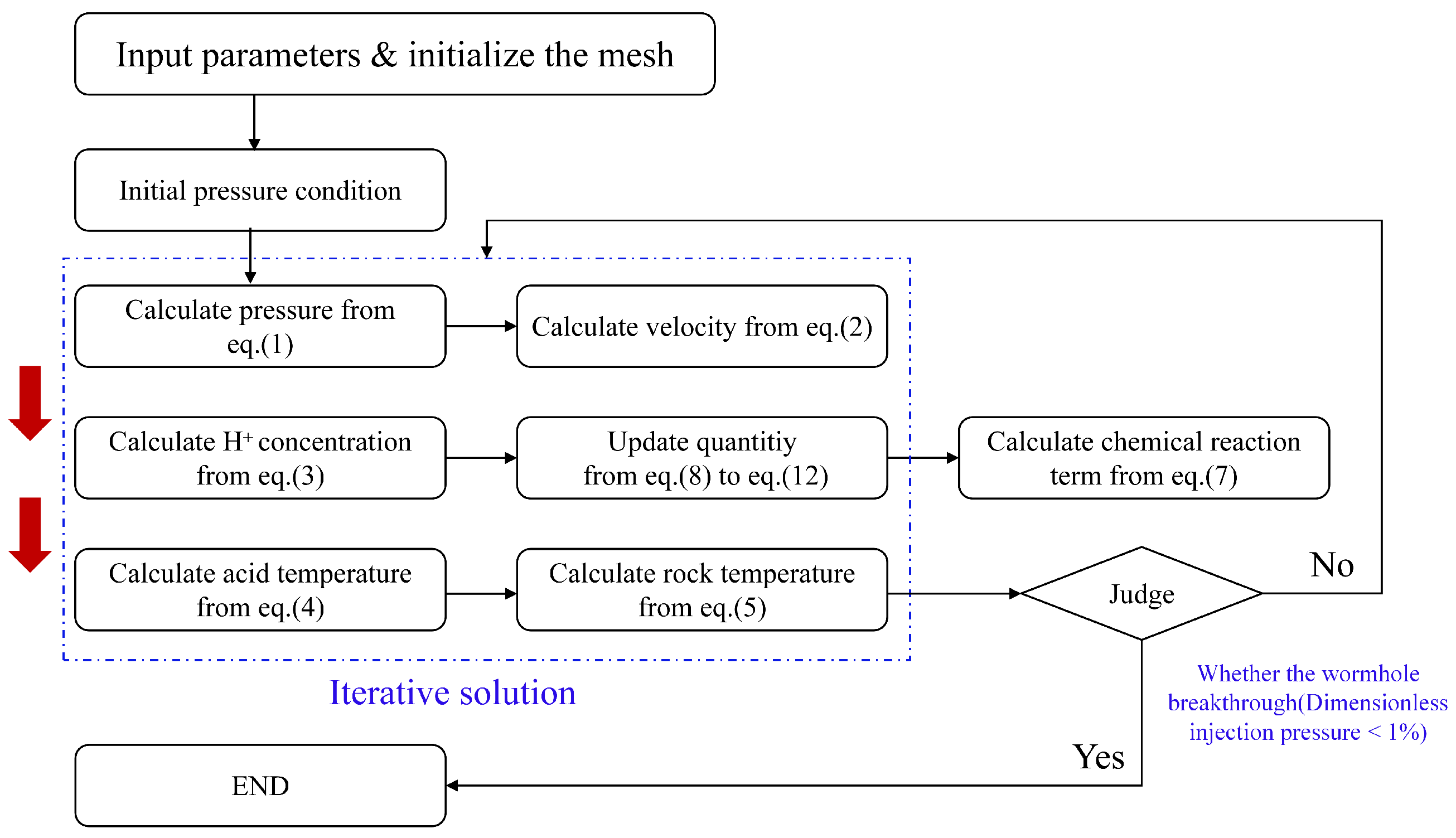
3. Numerical Methods
3.1. Discretization Method
3.2. Computational Methods and Simulation Parameters
3.3. Initial and Boundary Conditions
4. Results and Discussion
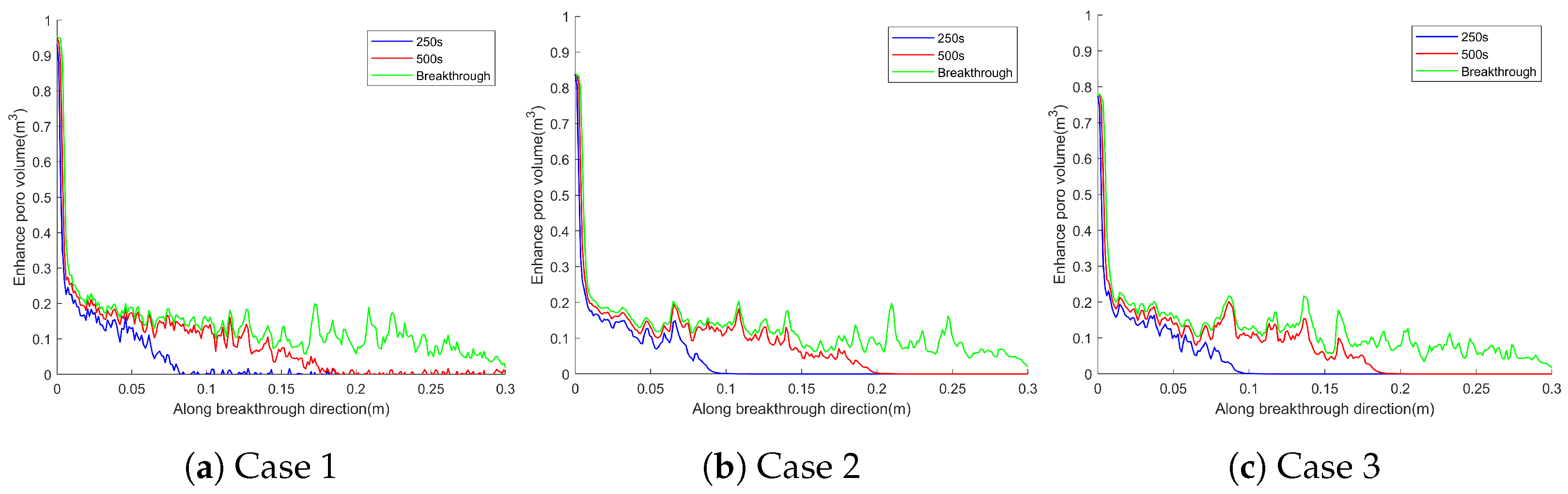
4.1. Effect of Different Heterogeneity Intensity on Wormhole Morphology
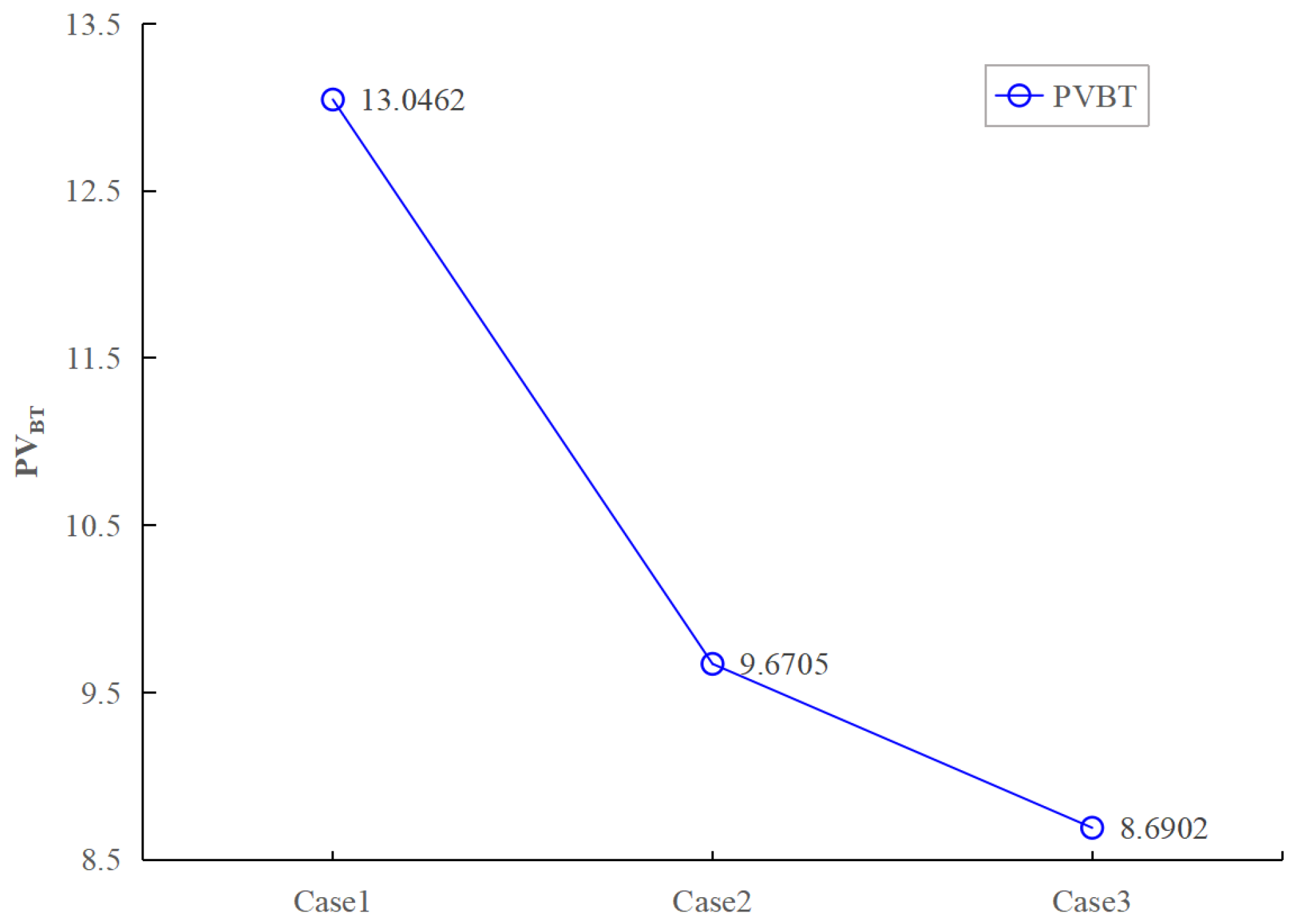
4.2. Effect of Different Heterogeneity Intensity on the Breakthrough Curve
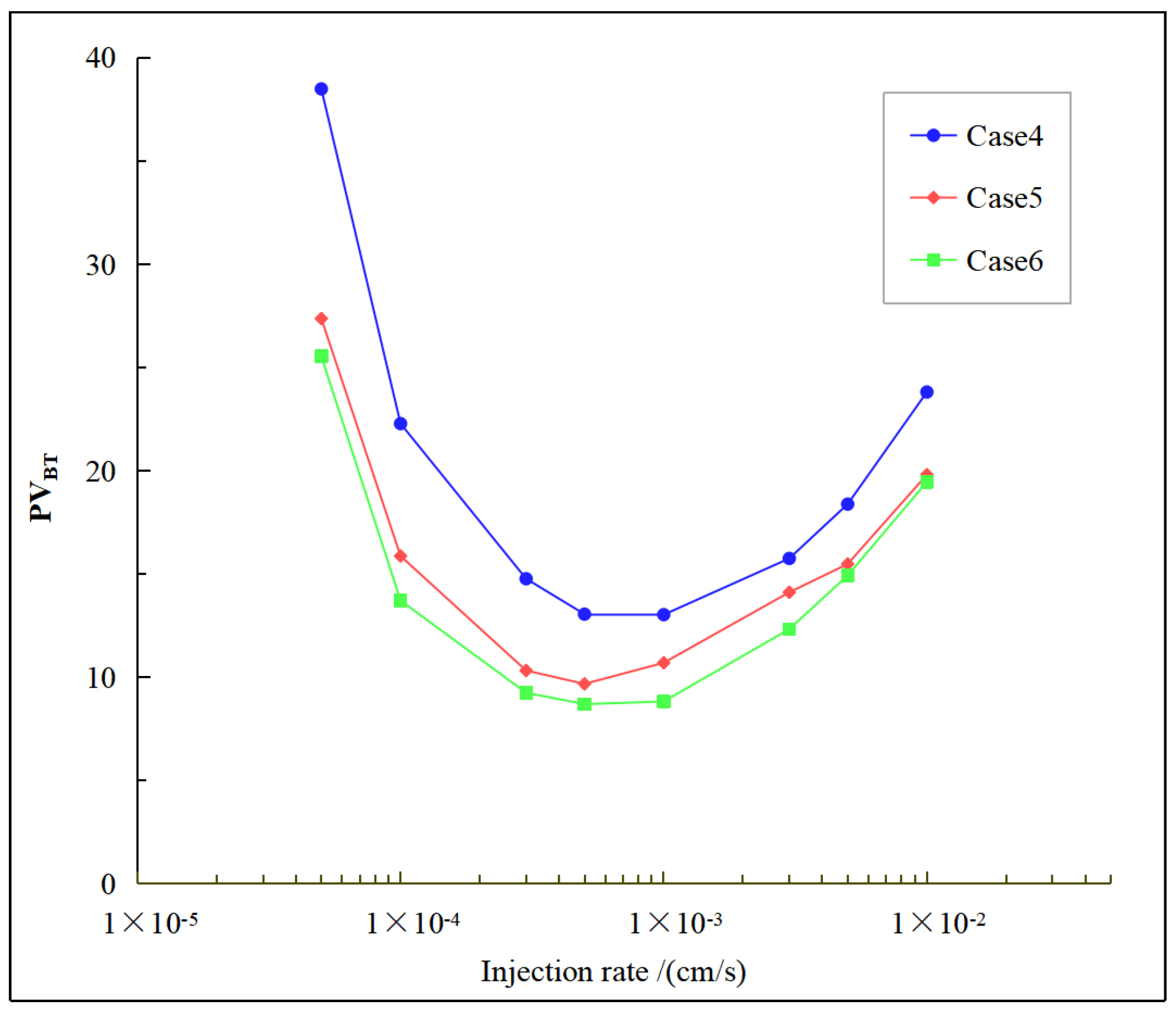
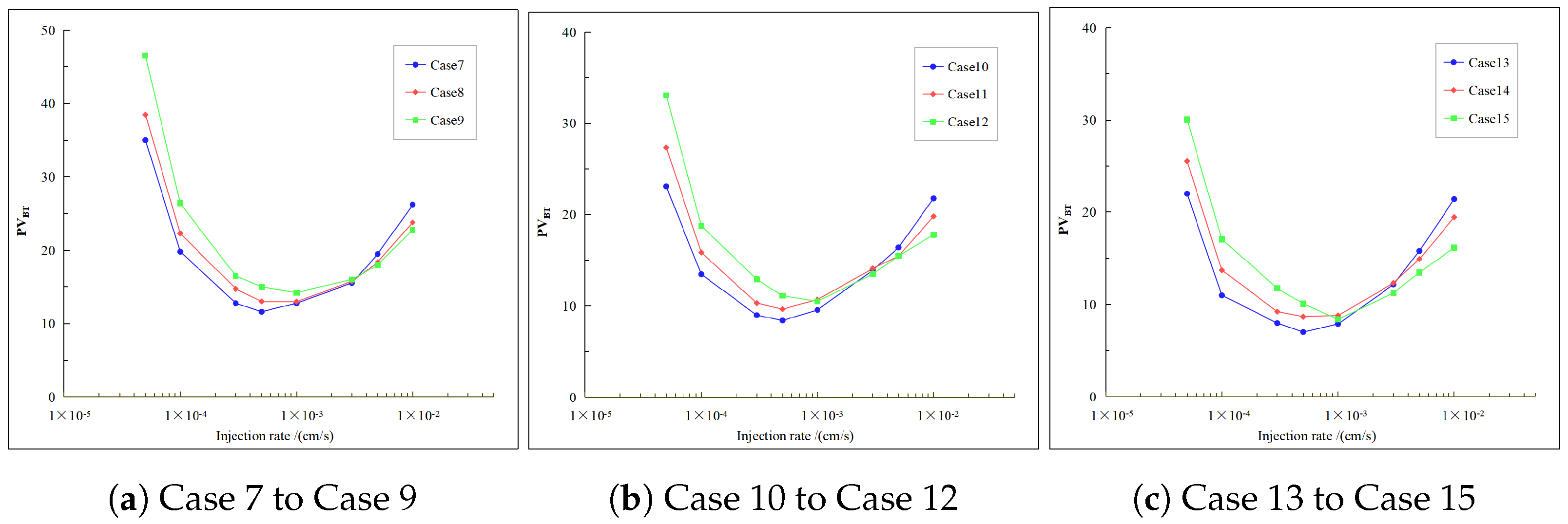
4.3. Effect of Different Inject Temperature on the Breakthrough Curve
5. Conclusions
- (1)
- The heterogeneity intensity has a significant impact on the development pattern of wormholes, when the heterogeneity intensity is low, the early stage of wormhole development is characterized by competition among multiple wormholes, and as the heterogeneity intensity increases, it gradually shifts to dominant wormhole development.
- (2)
- The wormhole morphology formed by different heterogeneous intensities during rock breakthrough also varies, mainly reflected in the branching wormholes on the main wormhole. When the heterogeneity intensity is low, the number of branch wormholes is small and the width is large. When the heterogeneity intensity is high, the number of branch wormholes is large, and the width is small.
- (3)
- The influence mechanism of heterogeneity intensity on the development pattern and morphology of wormholes mainly comes from the stronger heterogeneity, clearer preferential flow path, more obvious trend of acid solution forward development, lower PVBT, and higher acidification efficiency.
- (4)
- As heterogeneity intensity increases, the curve shows a downward trajectory characterized by a progressively diminishing rate of decline. A significant impact on reduction is particularly pronounced at low injection rates. However, this enhanced heterogeneity does not affect the optimal injection rate.
- (5)
- The optimal injection rate increases with the increase in the acid injection temperature. Under high heterogeneity conditions, the optimal injection rate increases more significantly with the increase in the inject temperature. Additionally, although there are typically increases with the rise in inject temperature, this trend reverses under high injection rates. This implies that in environments with high heterogeneity intensity and high temperatures, injecting colder acid helps to enhance the acidizing efficiency. This conclusion is only applicable within an appropriate injection rate range.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lungwitz, B.; Fredd, C.; Brady, M.; Miller, M.; Ali, S.; Hughes, K. Diversion and cleanup studies of viscoelastic surfactant-based self-diverting acid. SPE Prod. Oper. 2007, 22, 121–127. [Google Scholar] [CrossRef]
- Tian, H.; Quan, H.; Huang, Z. Investigation on rheological properties and thickening mechanism of a novel thickener based on hydrophobically associating water-soluble polymer during the acid rock reaction. J. Pet. Sci. Eng. 2020, 188, 106895. [Google Scholar] [CrossRef]
- Yavuz, H.; Demirdag, S.; Caran, S. Thermal effect on the physical properties of carbonate rocks. Int. J. Rock Mech. Min. Sci. 2010, 47, 94–103. [Google Scholar] [CrossRef]
- Murray, R.C. Origin of porosity in carbonate rocks. J. Sediment. Res. 1960, 30, 59–84. [Google Scholar] [CrossRef]
- Mostofizadeh, B.; Economides, M. Optimum injection rate from radial acidizing experiments. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 25–28 September 1994. [Google Scholar]
- Mahmoud, M.A.; Nasr-El-Din, H.A.; De Wolf, C.A.; LePage, J.N. Optimum injection rate of a new chelate that can be used to stimulate carbonate reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Wang, Y.; Hill, A.D.; Schechter, R.S. The optimum injection rate for matrix acidizing of carbonate formations. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993. [Google Scholar]
- Zhang, K.; Sang, S.; Liu, C.; Ma, M.; Zhou, X. Experimental study the influences of geochemical reaction on coal structure during the co2 geological storage in deep coal seam. J. Pet. Sci. Eng. 2019, 178, 1006–1017. [Google Scholar] [CrossRef]
- Dautriat, J.; Gl, N.; Dimanov, A.; Raphanel, J. Hydromechanical behavior of heterogeneous carbonate rock under proportional triaxial loadings. J. Geophys. Res. Solid Earth 2011, 116, 1–26. [Google Scholar] [CrossRef]
- Panga, M.K.; Ziauddin, M.; Balakotaiah, V. Two-scale continuum model for simulation of wormholes in carbonate acidization. AIChE J. 2005, 51, 3231–3248. [Google Scholar] [CrossRef]
- Kalia, N.; Balakotaiah, V. Modeling and analysis of wormhole formation in reactive dissolution of carbonate rocks. Chem. Eng. Sci. 2007, 62, 919–928. [Google Scholar] [CrossRef]
- Khormali, A.; Ahmadi, S.; Kazemzadeh, Y. Inhibition of barium sulfate precipitation during water injection into oil reservoirs using various scale inhibitors. Arab. J. Sci. Eng. 2023, 48, 9383–9399. [Google Scholar] [CrossRef]
- Kalia, N.; Balakotaiah, V. Effect of medium heterogeneities on reactive dissolution of carbonates. Chem. Eng. Sci. 2009, 64, 376–390. [Google Scholar] [CrossRef]
- Chierici, G.L. Principles of Petroleum Reservoir Engineering; Springer: Berlin/Heidelberg, Germany, 2012; Volume 2. [Google Scholar]
- Hollis, C.; Vahrenkamp, V.; Tull, S.; Mookerjee, A.; Taberner, C.; Huang, Y. Pore system characterisation in heterogeneous carbonates: An alternative approach to widely-used rock-typing methodologies. Mar. Pet. Geol. 2010, 27, 772–793. [Google Scholar] [CrossRef]
- Kalia, N.; Glasbergen, G. Wormhole formation in carbonates under varying temperature conditions. In Proceedings of the SPE European Formation Damage Conference and Exhibition, SPE, Scheveningen, The Netherlands, 27–29 May 2009; p. SPE-121803. [Google Scholar]
- Liu, M.; Zhang, S.; Mou, J. Effect of normally distributed porosities on dissolution pattern in carbonate acidizing. J. Pet. Sci. Eng. 2012, 94, 28–39. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, Y.; Cui, M.; Zhou, F.; Zhang, Y.; Liang, C.; Zou, H.; Yao, F. Effects of spent viscoelastic-surfactant acid flow on wormholes propagation and diverting performance in heterogeneous carbonate reservoir. Energy Rep. 2022, 8, 8321–8332. [Google Scholar] [CrossRef]
- Mahmoodi, A.; Javadi, A.; Sola, B.S. Porous media acidizing simulation: New two-phase two-scale continuum modeling approach. J. Pet. Sci. Eng. 2018, 166, 679–692. [Google Scholar] [CrossRef]
- Jafarpour, H.; Aghaei, H.; Litvin, V.; Ashena, R. Experimental optimization of a recently developed matrix acid stimulation technology in heterogeneous carbonate reservoirs. J. Pet. Sci. Eng. 2021, 196, 108100. [Google Scholar] [CrossRef]
- Bekibayev, T.T.; Beisembetov, I.K.; Assilbekov, B.K.; Zolotukhin, A.B.; Zhapbasbayev, U.K.; Turegeldieva, K.A. Study of the impact of reduced permeability due to near-wellbore damage on the optimal parameters of the matrix acidizing in carbonate rocks. In Proceedings of the SPE Annual Caspian Technical Conference & Exhibition, Baku, Azerbaijan, 4–6 November 2015. [Google Scholar]
- Cao, C.; Zhou, F.; Cheng, L.; Liu, S.; Lu, W.; Wang, Q. A comprehensive method for acid diversion performance evaluation in strongly heterogeneous carbonate reservoirs stimulation using ct. J. Pet. Sci. Eng. 2021, 203, 108614. [Google Scholar] [CrossRef]
- Dong, R.; Wheeler, M.F.; Su, H.; Ma, K. Modeling acid fracturing treatments in heterogeneous carbonate reservoirs. In Proceedings of the SPE International Conference on Oilfield Chemistry, The Woodlands, TX, USA, 6–7 December 2021. [Google Scholar]
- Mou, J.; Liu, M.; Zheng, K.; Zhang, S. Diversion conditions for viscoelastic-surfactant-based self-diversion acid in carbonate acidizing. SPE Prod. Oper. 2015, 30, 121–129. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Y.; Kerisit, S.; Zachara, J. Pore-scale process coupling and effective surface reaction rates in heterogeneous subsurface materials. Rev. Mineral. Geochem. 2015, 80, 191–216. [Google Scholar] [CrossRef]
- Ghommem, M.; Zhao, W.; Dyer, S.; Qiu, X.; Brady, D. Carbonate acidizing: Modeling, analysis, and characterization of wormhole formation and propagation. J. Pet. Sci. Eng. 2015, 131, 18–33. [Google Scholar] [CrossRef]
- Maheshwari, P.; Ratnakar, R.R.; Kalia, N.; Balakotaiah, V. 3-D simulation and analysis of reactive dissolution and wormhole formation in carbonate rocks. Chem. Eng. Sci. 2013, 90, 258–274. [Google Scholar] [CrossRef]
- de Paulo, F.L.; Surmas, R.; Tonietto, S.N.; da Silva, M.A.P.; Peçanha, R.P. Modeling reactive flow on carbonates with realistic porosity and permeability fields. Adv. Water Resour. 2020, 139, 103564. [Google Scholar] [CrossRef]
- Schwalbert, M.P.; Zhu, D.; Hill, A.D. Extension of an empirical wormhole model for carbonate matrix acidizing through two-scale continuum 3d simulations. In Proceedings of the SPE Europec Featured at 79th EAGE Conference and Exhibition, Paris, France, 12–15 June 2017. [Google Scholar]
- Liu, P.; Yao, J.; Couples, G.D.; Huang, Z.; Sun, H.; Ma, J. Numerical modelling and analysis of reactive flow and wormhole formation in fractured carbonate rocks. Chem. Eng. Sci. 2017, 172, 143–157. [Google Scholar] [CrossRef]
- Li, Y.; Mo, W.; Jiang, Y.; Chang, T. Influence of fractures and heat transmission on wormhole propagation in fractured carbonate rocks. Geoenergy Sci. Eng. 2024, 239, 212916. [Google Scholar] [CrossRef]
- Chang, T.; Jiang, Y.; Li, Y.; Chen, X.; Kang, X.; Mo, W. Study on the effect of natural fractures and temperature on the wormhole morphology formed by two-phase acidizing in carbonate rocks. Phys. Fluids 2024, 36, 083333. [Google Scholar] [CrossRef]
- Chang, T.; Jiang, Y.; Zhao, H.; Chen, X.; Mo, W. Effect of two-phase viscosity difference and natural fractures on the wormhole morphology formed by two-phase acidizing with self-diverting acid in carbonate rocks. Phys. Fluids 2024, 36, 093623. [Google Scholar] [CrossRef]
- Mo, W.; Jiang, Y.; Li, Y.; Chang, T.; Liu, K. Non-isothermal simulation of wormhole propagation in fractured carbonate rocks based on 3d-edfm. Geoenergy Sci. Eng. 2024, 244, 213453. [Google Scholar] [CrossRef]
- Jia, C.; Alkaabi, S.; Hu, J.; Sepehrnoori, K.; Yao, J.; Zhang, L. Impact of rock heterogeneity on reactive flow during acid stimulation process. Int. J. Heat Mass Transf. 2024, 227, 125560. [Google Scholar] [CrossRef]
- Kalia, N.; Glasbergen, G. Fluid temperature as a design parameter in carbonate matrix acidizing. In Proceedings of the SPE Production and Operations Conference and Exhibition, Tunis, Tunisia, 8–10 June 2010. [Google Scholar]
| Parameter | Symbol | Value |
|---|---|---|
| Core length [m] | L | 0.3 |
| Core diameter [H] | H | 0.1 |
| Acid injection concentration [kmol/m3] | 4.4178 (15wt%HCL) | |
| Acid injection velocity [m/s] | 1–1 cm/s | |
| Initial porosity of matrix [dimLess] | 0.01–0.5 | |
| Initial permeability of matrix [m2] | K | Calculated |
| Viscosity of acid at 20 °C [mPa·s] | 1 | |
| Acid specific heat capacity at 20 °C [J/(kg·°C)] | 4180 | |
| Rock specific heat capacity [J/(kg·°C)] | 999 | |
| Acid thermal conductivity at 20 °C [W/(m·°C)] | 0.6508 | |
| Solubility of acid [kg/kmol] | 50 | |
| Rock thermal conductivity [W/(m·°C)] | 5.2 | |
| Interfacial area of matrix [m2/m3] | 5000 | |
| Molecular diffusion coefficient [m2/s] | 3.6 | |
| Solubility of acid [kg/kmol] | 50 | |
| Rock convective heat transfer coefficient [W/(m2·°C)] | 600 |
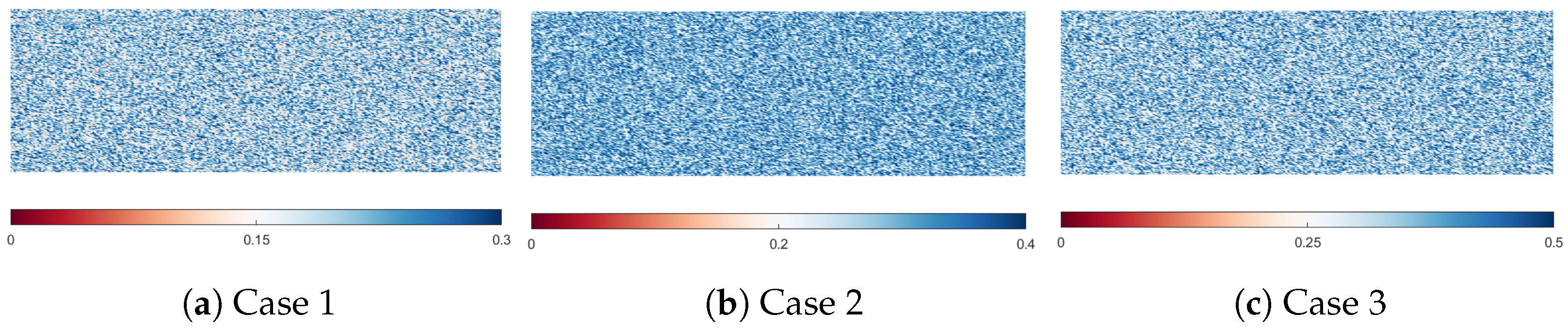
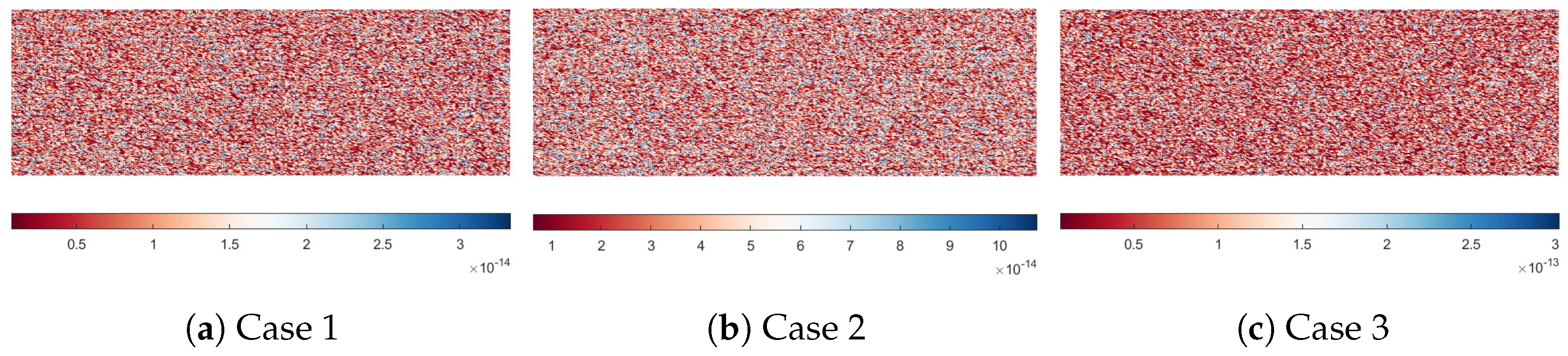
| Parameter | Symbol | Case 1 | Case 2 | Case 3 |
|---|---|---|---|---|
| Porosity [dimLess] | 0.1–0.3 | 0.05–0.4 | 0.01–0.5 | |
| Inject temperature [°C] | 333.15 | |||
| Inject velocity [m/s] | ||||
| Parameter | Symbol | Case 4 | Case 5 | Case 6 |
|---|---|---|---|---|
| Porosity [dimLess] | 0.1–0.3 | 0.05–0.4 | 0.01–0.5 | |
| Inject temperature [°C] | 333.15 | |||
| Inject velocity [m/s] | – | |||
| Parameter | Symbol | Case 7 | Case 8 | Case 9 |
| Porosity [dimLess] | 0.1–0.3 | |||
| Inject temperature [°C] | 293.15 | 333.15 | 373.15 | |
| Inject velocity [m/s] | – | |||
| Parameter | Symbol | Case 10 | Case 11 | Case 12 |
| Porosity [dimLess] | 0.05–0.4 | |||
| Inject temperature [°C] | 293.15 | 333.15 | 373.15 | |
| Inject velocity [m/s] | – | |||
| Parameter | Symbol | Case 13 | Case 14 | Case 15 |
| Porosity [dimLess] | 0.01–0.5 | |||
| Inject temperature [°C] | 293.15 | 333.15 | 373.15 | |
| Inject velocity [m/s] | – | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Wu, X.; Hou, J.; Zhou, F.; Nie, F. Study on the Influence of Heterogeneity of Low-Permeability Reservoirs on Wormhole Morphology and Acidizing Process Parameters. Processes 2024, 12, 2740. https://doi.org/10.3390/pr12122740
Yang G, Wu X, Hou J, Zhou F, Nie F. Study on the Influence of Heterogeneity of Low-Permeability Reservoirs on Wormhole Morphology and Acidizing Process Parameters. Processes. 2024; 12(12):2740. https://doi.org/10.3390/pr12122740
Chicago/Turabian StyleYang, Guobin, Xinwei Wu, Jingtao Hou, Fei Zhou, and Fajian Nie. 2024. "Study on the Influence of Heterogeneity of Low-Permeability Reservoirs on Wormhole Morphology and Acidizing Process Parameters" Processes 12, no. 12: 2740. https://doi.org/10.3390/pr12122740
APA StyleYang, G., Wu, X., Hou, J., Zhou, F., & Nie, F. (2024). Study on the Influence of Heterogeneity of Low-Permeability Reservoirs on Wormhole Morphology and Acidizing Process Parameters. Processes, 12(12), 2740. https://doi.org/10.3390/pr12122740





