DFT and TST Study of the Calcium Cyanamide Process for Synthesizing Cyanamide and Dicyandiamide
Abstract
1. Introduction
2. Computational Methods
2.1. Mechanism Method
2.2. Kinetics Calculation
3. Results and Discussion
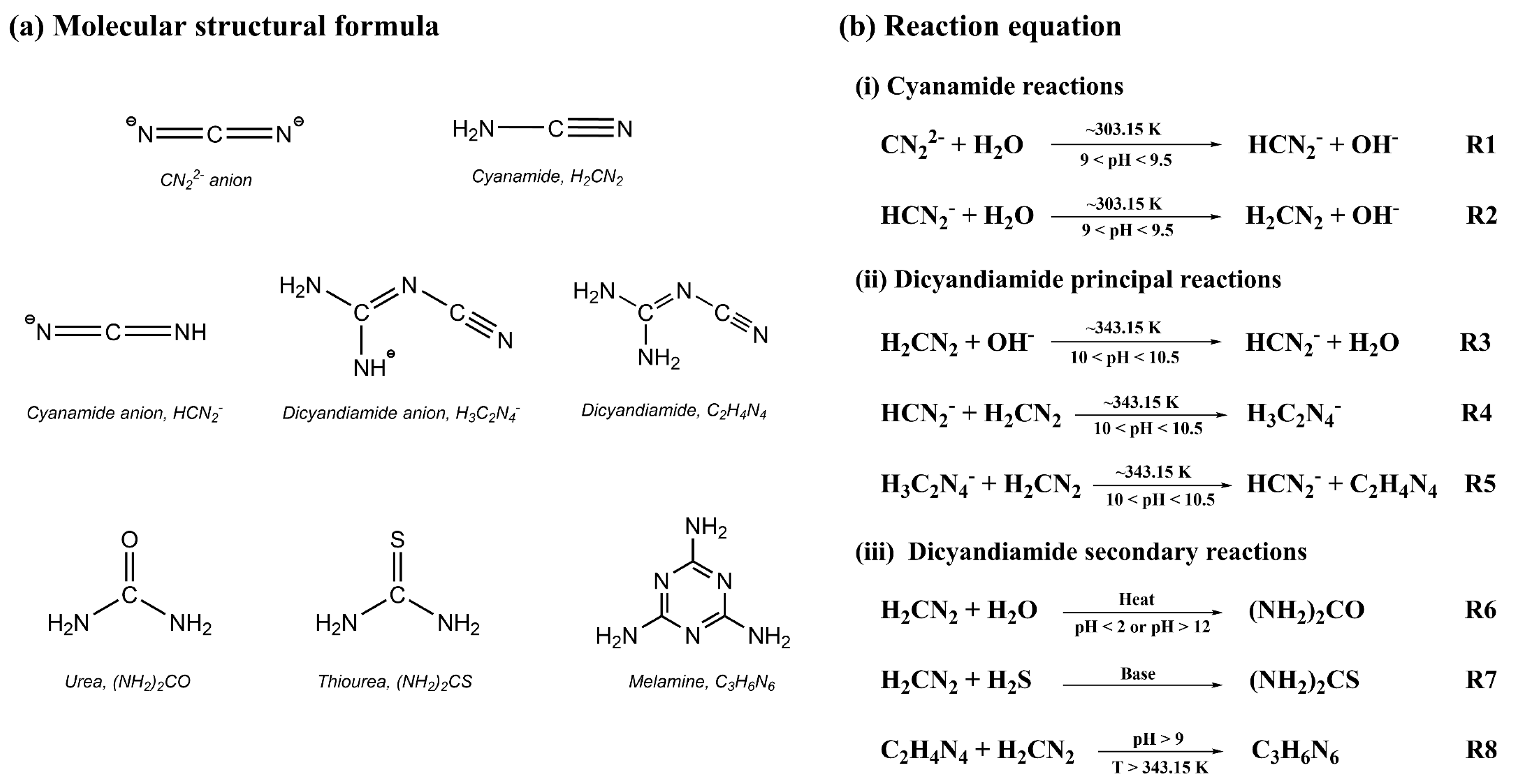
3.1. The Structure of Cyanamide and Dicyandiamide Structure
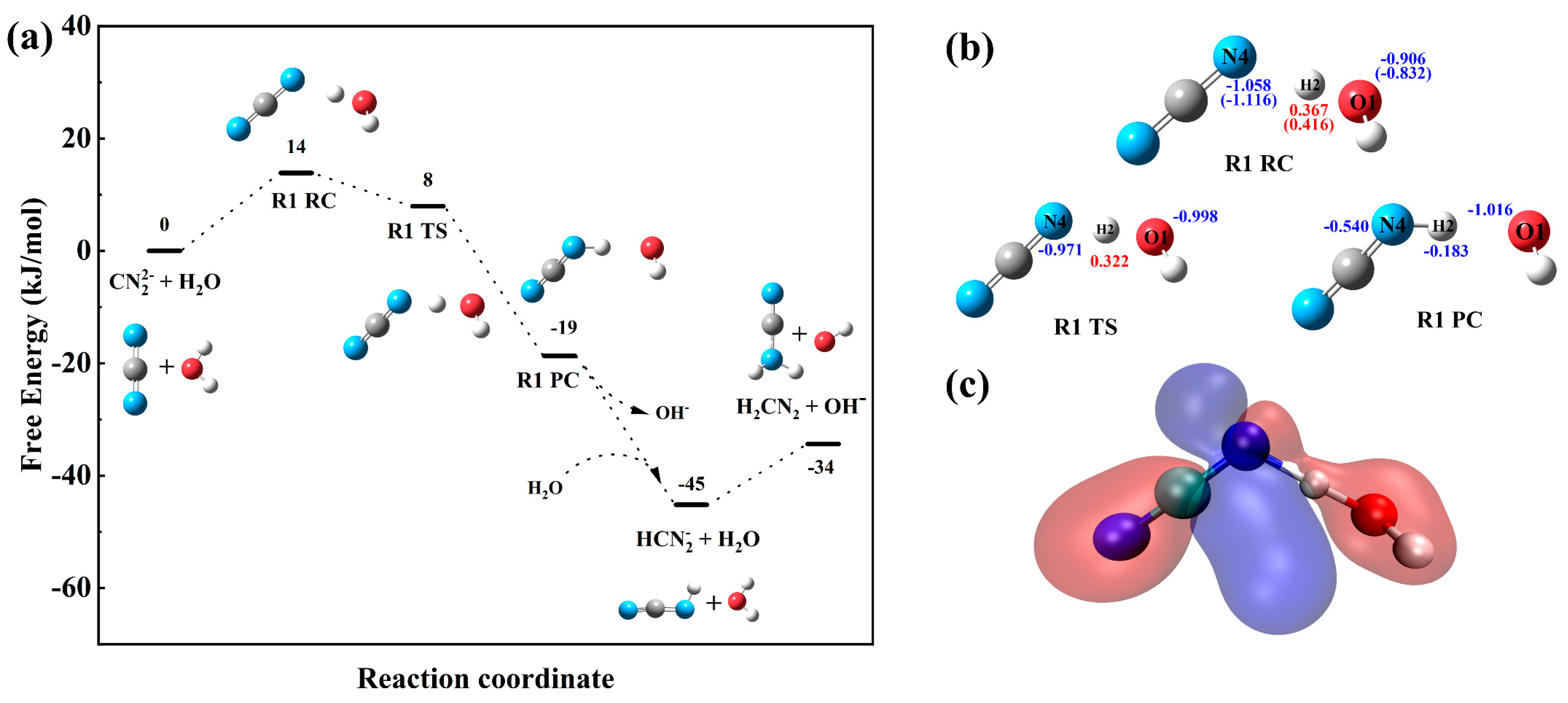
3.2. Reaction Mechanism Under the Implicit Solvent Model
3.3. Solvation Effect on the Reaction Mechanism
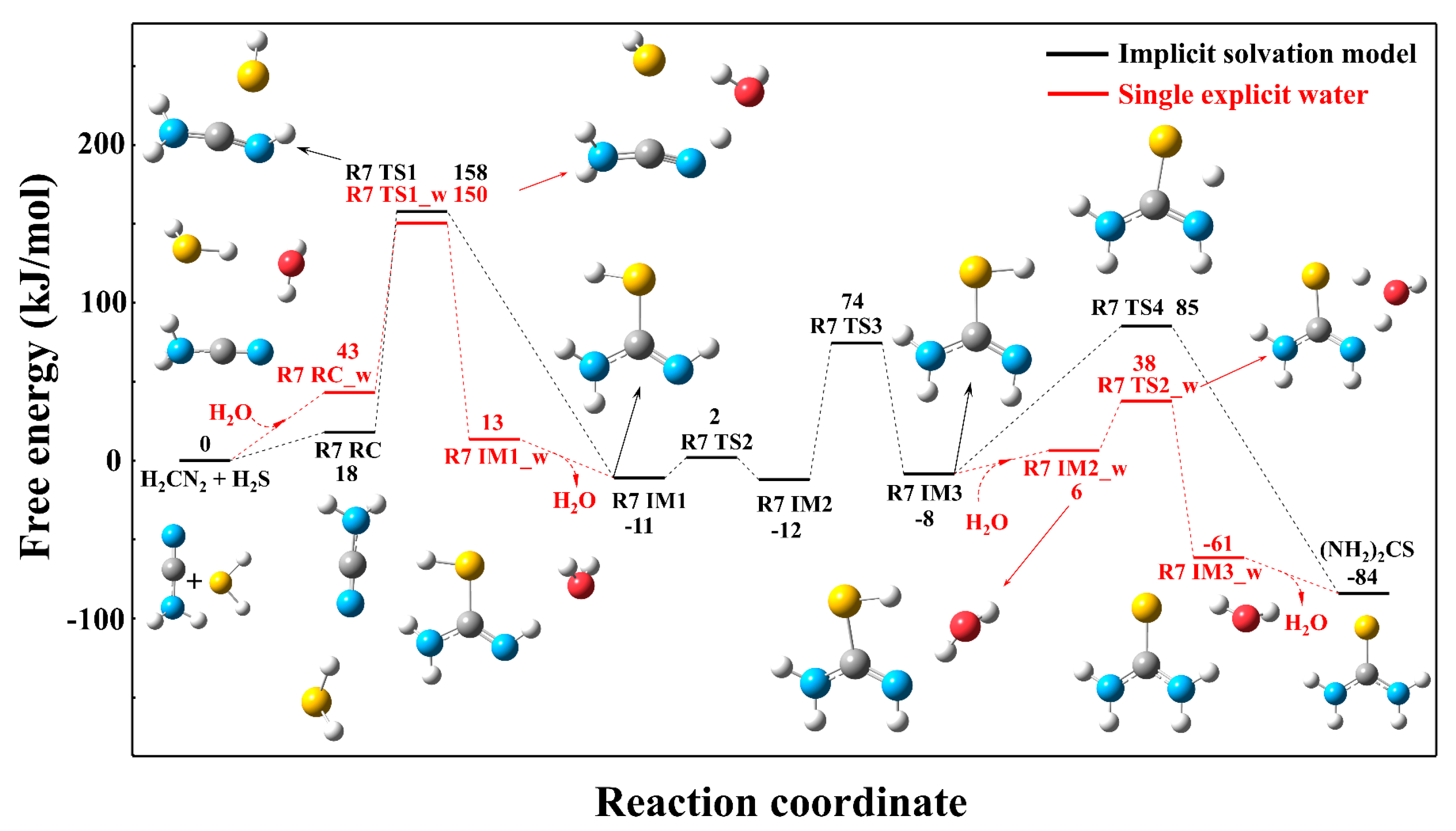
3.3.1. Reaction Mechanism Under the Single Explicit Water
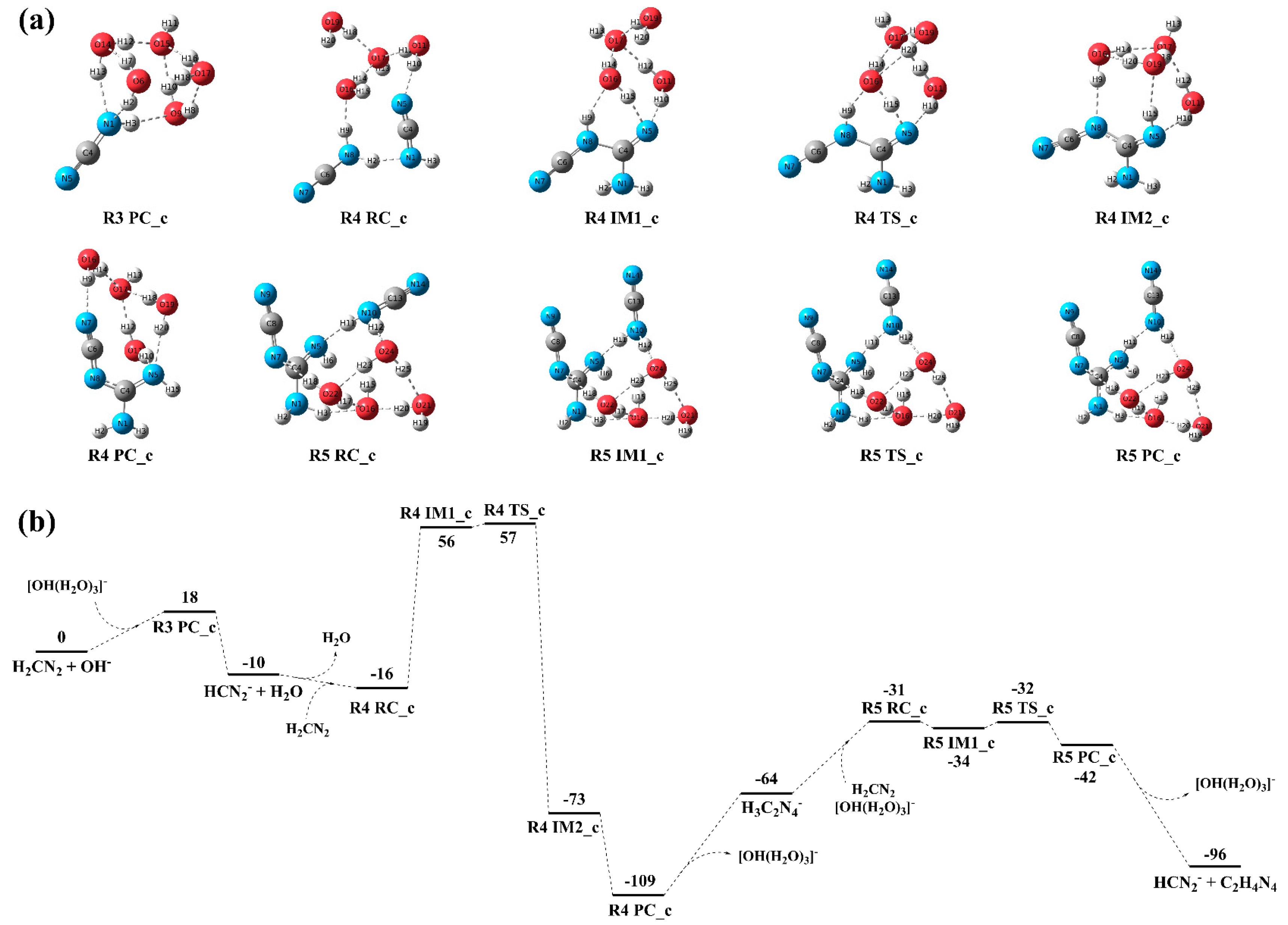
3.3.2. Reaction Mechanism and Kinetics Under the [OH(H2O)3]− Cluster
Reaction Mechanism
Reaction Kinetics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tanzer, K.; Pelc, A.; Huber, S.E.; Czupyt, Z.; Denifl, S. Low Energy Electron Attachment to Cyanamide (NH2CN). J. Chem. Phys. 2015, 142, 034301. [Google Scholar] [CrossRef] [PubMed]
- Lotsch, B.V.; Senker, J.; Schnick, W. Characterization of the Thermally Induced Topochemical Solid-State Transformation of NH4[N(CN)2] into NCNC(NH2)2 by Means of X-ray and Neutron Diffraction as Well as Raman and Solid-State NMR Spectroscopy. Inorg. Chem. 2004, 43, 895–904. [Google Scholar] [CrossRef] [PubMed]
- Güthner, T.; Mertschenk, B. Cyanamides; Wiley: Berlin, Germany, 2006. [Google Scholar]
- Shu, K.; Guan, B.; Guo, J.; Wu, X.; Chen, Y.; Ma, Z.; Zhang, J.; Chen, J.; Yao, S.; Bao, S.; et al. The Current Progresses and Future Perspectives of Photoreactors and Catalysts Used in Photocatalytic Reduction of CO2. Ind. Eng. Chem. Res. 2023, 62, 15699–15732. [Google Scholar] [CrossRef]
- Lin, Y.; Chien, T.; Li, K.; Lin, J. Comparison of the Thermal and Photochemical Reaction Pathways of Melamine on TiO2. J. Phys. Chem. C 2015, 119, 8645–8651. [Google Scholar] [CrossRef]
- Jürgens, B.; Irran, E.; Senker, J.; Kroll, P.; Müller, H.; Schnick, W. Melem (2,5,8-Triamino-tri-s-triazine), an Important Intermediate during Condensation of Melamine Rings to Graphitic Carbon Nitride: Synthesis, Structure Determination by X-ray Powder Diffractometry, Solid-State NMR, and Theoretical Studies. J. Am. Chem. Soc. 2003, 125, 10288–10300. [Google Scholar] [CrossRef]
- Cameron, W. Cyanamides; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Sugiuo, K.; Ku, S. Method of Producing Calcium-Free Crystalline Cyanamide. U.S. Patent 2982616, 2 May 1961. [Google Scholar]
- May, R.; Fall, N. Method for Manufacture of Cyanamide. U.S. Patent 3300281, 24 January 1967. [Google Scholar]
- Tao, Y.; Wang, H.; Wang, H.; Zhou, M. Pressure-Induced Phase and Isomer Transition of Dicyandiamide. Spectrosc. Spect. Anal. 2022, 42, 3046–3051. [Google Scholar]
- Bach, R.D.; McDouall, J.J.W.; Owensby, A.L.; Schlegel, H.B.; Holubka, J.W.; Ball, J.C. Structure and Dynamics of Dicyandiamide: A Theoretical Study. J. Phys. Org. Chem. 1991, 4, 125–134. [Google Scholar] [CrossRef]
- Zhang, X.; Quan, D.; Li, R.; Esimbek, J.; Chen, L.; Zhao, G.; Zhou, Y. Chemical Models of Adenine Precursors Cyanamide and Carbodiimide in the Interstellar Medium. Mon. Not. R. Astron. Soc. 2023, 521, 1578–1589. [Google Scholar] [CrossRef]
- Puzzarini, C.; Gambi, A. A Theoretical Study on CH2N2 Isomers: Structure and Energetics. Theor. Chem. Acc. 2012, 131, 1135. [Google Scholar] [CrossRef]
- Alıa, J.M.; Edwards, H.G.M.; Garcıa Navarro, F.J. The Imino–Amino Tautomeric Equilibrium in Cyanoguanidine Dissolved in Several Aprotic Solvents; An FT-Raman Spectroscopic Study. J. Mol. Struct. 2001, 597, 49–55. [Google Scholar] [CrossRef]
- Liang, L.; Zhong, Y.; Chen, J.; Zhang, J.; Zhang, T.; Li, Z. Energetic Bimetallic MOF: A Promising Promoter for Ionic Liquid Hypergolic Ignition. Inorg. Chem. 2022, 61, 14864–14870. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Yan, R.; Chen, L.; Lin, S. Five 3D Co(II)-MOFs Constructed from 5-(2-methylimidazol-1-yl) Isophthalic Acid and Different Bis(Imidazole) Ligands and One of their Derivatives as an Efficient Electrocatalyst for ORR. Dalton Trans. 2022, 51, 17481–17487. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, Y.; Yao, S.; Zhu, P. Selective Recognization of Dicyandiamide in Bovine Milk by Mesoporous Silica SBA-15 Supported Dicyandiamide Imprinted Polymer Based on Surface Molecularly Imprinting Technique. Food Chem. 2018, 240, 1262–1267. [Google Scholar] [CrossRef] [PubMed]
- Hussain, A.; Sun, D.; Pu, H. Bimetallic Core Shelled Nanoparticles (Au@AgNPs) for Rapid Detection of Thiram and Dicyandiamide Contaminants in Liquid Milk Using SERS. Food Chem. 2020, 317, 126429. [Google Scholar] [CrossRef]
- Ren, Q.; Wang, H.; Lu, X.; Tong, Y.; Li, G. Recent Progress on MOF-Derived Heteroatom-Doped Carbon-Based Electrocatalysts for Oxygen Reduction Reaction. Adv. Sci. 2018, 5, 1700515. [Google Scholar] [CrossRef]
- Zhou, H.; Xu, H.; Liu, Y. Aerobic Oxidation of 5-Hydroxymethylfurfural to 2,5-Furandicarboxylic Acid over Co/Mn-lignin Coordination Complexes-Derived Catalysts. Appl. Catal. B 2019, 244, 965–973. [Google Scholar] [CrossRef]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual Density Functional Theory. Chem. Rev. 2003, 103, 1793–1874. [Google Scholar] [CrossRef]
- Yang, K.; Park, Y.H.; Cho, S.G.; Lee, H.W.; Kim, C.K.; Koo, H. Theoretical Studies on the Formation Mechanism and Explosive Performance of Nitro-Substituted 1,3,5-Triazines. J. Comput. Chem. 2010, 31, 2483–2492. [Google Scholar] [CrossRef]
- Zhang, S.T.; Yan, H.; Wei, M.; Evans, D.G.; Duan, X. Hydrogenation Mechanism of Carbon Dioxide and Carbon Monoxide on Ru(0001) Surface: A Density Functional Theory Study. RSC Adv. 2014, 4, 30241–30249. [Google Scholar] [CrossRef]
- Wigner, E. Calculation of the Rate of Elementary Association Reactions. J. Chem. Phys. 1937, 5, 720–725. [Google Scholar] [CrossRef]
- Alemán, C. The Keto–Amino/Enol Tautomerism of Cytosine in Aqueous Solution. A Theoretical Study using Combined Discrete/Self-Consistent Reaction Field Models. Chem. Phys. 2000, 253, 13–19. [Google Scholar] [CrossRef]
- Alemán, C. Hydration of Cytosine using Combined Discrete/SCRF Models: Influence of the Number of Discrete Solvent Molecules. Chem. Phys. 1999, 244, 151–162. [Google Scholar] [CrossRef]
- Eckart, C. The Penetration of a Potential Barrier by Electrons. Phys. Rev. 1930, 35, 1303–1309. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, G.A.P.B.; Nakatsuji, H.; et al. Gaussian 09, Revision D.01, 2013. Available online: https://gaussian.com (accessed on 10 October 2024).
- Grimme, S. Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Becke, A.D. A New Mixing of Hartree–Fock and Local Density-Functional Theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Alecu, I.M.; Zheng, J.; Zhao, Y.; Truhlar, D.G. Computational Thermochemistry: Scale Factor Databases and Scale Factors for Vibrational Frequencies Obtained from Electronic Model Chemistries. J. Chem. Theory Comput. 2010, 6, 2872–2887. [Google Scholar] [CrossRef]
- Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H.R.; Truhlar, D.G. Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theory Comput. 2011, 7, 3027–3034. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, X.; Truhlar, D.G. Minimally Augmented Karlsruhe Basis Sets. Theor. Chem. Acc. 2011, 128, 295–305. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Ho, J.; Klamt, A.; Coote, M.L. Comment on the Correct Use of Continuum Solvent Models. J. Phys. Chem. A 2010, 114, 13442–13444. [Google Scholar] [CrossRef]
- Ribeiro, R.F.; Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Use of Solution-Phase Vibrational Frequencies in Continuum Models for the Free Energy of Solvation. J. Phys. Chem. B 2011, 115, 14556–14562. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Shermo: A General Code for Calculating Molecular Thermochemistry Properties. Comput. Theor. Chem. 2021, 1200, 113249. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Atomic Dipole Moment Corrected Hirshfeld Population Method. J. Theor. Comput. Chem. 2012, 11, 163–183. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Canneaux, S.; Bohr, F.; Henon, E. KiSThelP: A Program to Predict Thermodynamic Properties and Rate Constants from Quantum Chemistry Results. J. Comput. Chem. 2014, 35, 82–93. [Google Scholar] [CrossRef]
- Feyel, S.; Döbler, J.; Höckendorf, R.; Beyer, M.K.; Sauer, J.; Schwarz, H. Activation of Methane by Oligomeric (Al2O3)x+ (x = 3, 4, 5): The Role of Oxygen-Centered Radicals in Thermal Hydrogen-Atom Abstraction. Angew. Chem. Int. Ed. 2008, 47, 1946–1950. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wu, X.; Zhao, X.; Ding, X.; He, S. Methane Activation by V3PO10•+ and V4O10•+ Clusters: A Comparative Study. Phys. Chem. Chem. Phys. 2010, 12, 12223–12228. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Zhao, Y.; Xue, W.; Wang, Z.; He, S.; Ding, X. Active Sites of Stoichiometric Cerium Oxide Cations (CemO2m+) probed by Reactions with Carbon Monoxide and Small Hydrocarbon Molecules. Phys. Chem. Chem. Phys. 2010, 12, 3984–3997. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Dai, J.; Luo, Y.; Lau, K.K.; Lan, Y.; Shao, Z.; Zhao, Y. Desymmetrization of 1,3-Diones by Catalytic Enantioselective Condensation with Hydrazine. J. Am. Chem. Soc. 2021, 143, 4179–4186. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Wu, X.; Ma, J.; He, S.; Ding, X. Experimental and Theoretical Study of the Reactions between Vanadium−Silicon Heteronuclear Oxide Cluster Anions with n-Butane. J. Phys. Chem. C 2010, 114, 12271–12279. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics. Chem. Rev. 1999, 99, 2161–2200. [Google Scholar] [CrossRef]
- da Silva, E.F.; Svendsen, H.F.; Merz, K.M. Explicitly Representing the Solvation Shell in Continuum Solvent Calculations. J. Phys. Chem. A 2009, 113, 6404–6409. [Google Scholar] [CrossRef]
- Bankura, A.; Chandra, A. Hydration Structure and Dynamics of a Hydroxide ion in Water Clusters of Varying Size and Temperature: Quantum Chemical and ab initio Molecular Dynamics Studies. Chem. Phys. 2012, 400, 154–164. [Google Scholar] [CrossRef]
- Robertson, W.H.; Diken, E.G.; Price, E.A.; Shin, J.-W.; Johnson, M.A. Spectroscopic Determination of the OH− Solvation Shell in the OH−·(H2O)n Clusters. Science 2003, 299, 1367–1372. [Google Scholar] [CrossRef]
- Xantheas, S.S. Theoretical Study of Hydroxide Ion-Water Clusters. J. Am. Chem. Soc. 1995, 117, 10373–10380. [Google Scholar] [CrossRef]
- Galano, A.; Narciso-Lopez, M.; Francisco-Marquez, M. Water Complexes of Important Air Pollutants: Geometries, Complexation Energies, Concentrations, Infrared Spectra, and Intrinsic Reactivity. J. Phys. Chem. A 2010, 114, 5796–5809. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Yang, C.; Feng, X.; Kang, J.; Song, L.; Lu, Y.; Wang, Z.; Xu, Q.; Wang, W.; Wang, Z. The Catalytic Effect of Water, Water Dimers and Water Trimers on H2S + 3O2 Formation by the HO2 + HS Reaction under Tropospheric Conditions. Phys. Chem. Chem. Phys. 2016, 18, 17414–17427. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, Z.; Zhao, R.; Xu, T. The Effect of (H2O)n (n = 1–3) Clusters on the Reaction of HONO with HCl: A Mechanistic and Kinetic Study. Phys. Chem. Chem. Phys. 2022, 24, 10011–10024. [Google Scholar] [CrossRef] [PubMed]
- Zanuttini, D.; Gervais, B. Ground and Excited States Of OH–(H2O)n Clusters. J. Phys. Chem. A 2015, 119, 8188–8201. [Google Scholar] [CrossRef] [PubMed]
- Wei; Proynov, E.I.; Milet, A.; Salahub, D.R. Solvation of the Hydroxide Anion: A Combined DFT and Molecular Dynamics Study. J. Phys. Chem. A 2000, 104, 2384–2395. [Google Scholar] [CrossRef]
- Li, X.; Teige, V.E.; Iyengar, S.S. Can the Four-Coordinated, Penta-Valent Oxygen in Hydroxide Water Clusters Be Detected through Experimental Vibrational Spectroscopy? J. Phys. Chem. A 2007, 111, 4815–4820. [Google Scholar] [CrossRef]
- Ley, D.; Gerbig, D.; Schreiner, P.R. Tunnelling Control of Chemical Reactions—The Organic Chemist’s Perspective. Org. Biomol. Chem. 2012, 10, 3781–3790. [Google Scholar] [CrossRef]

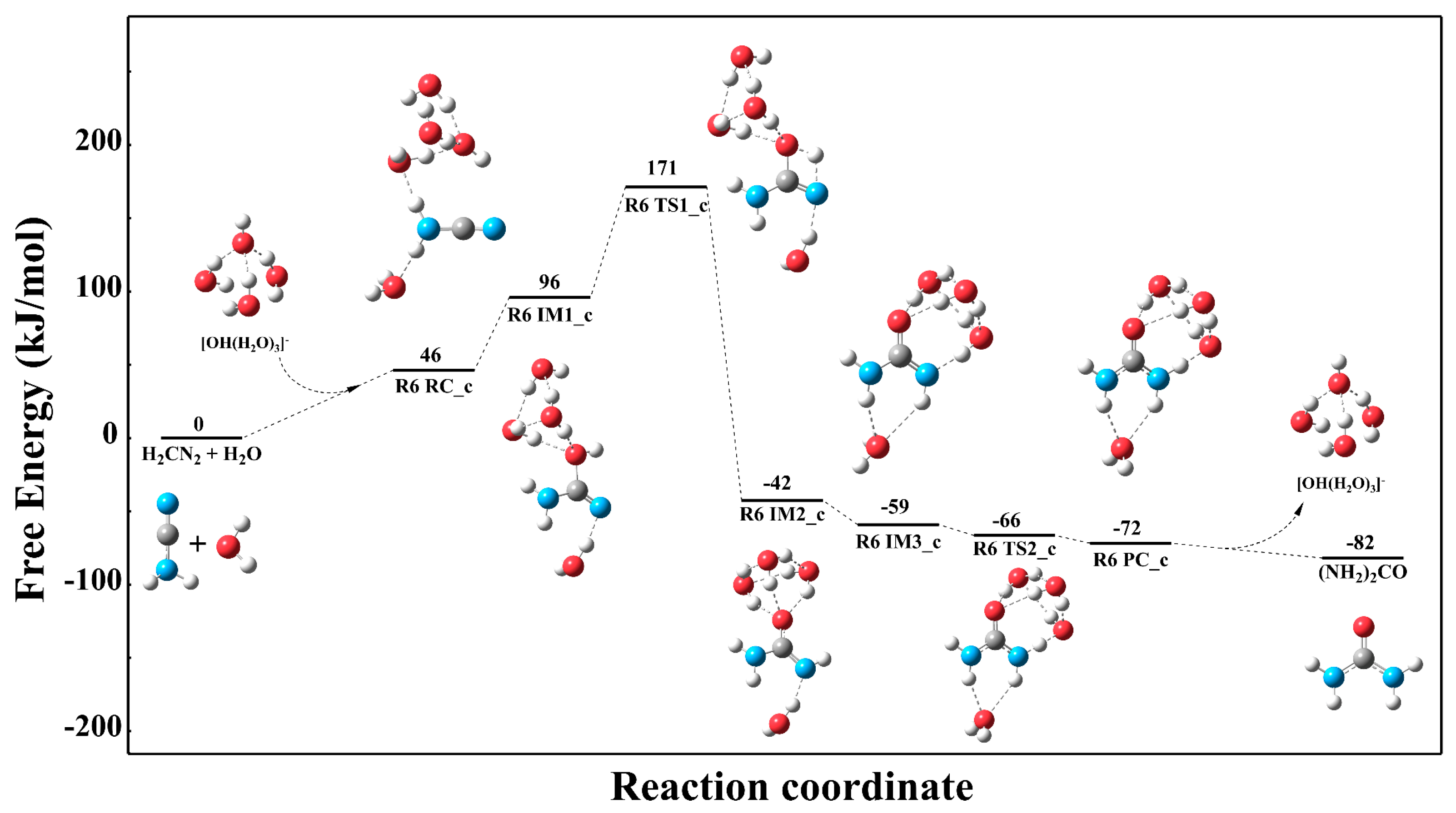
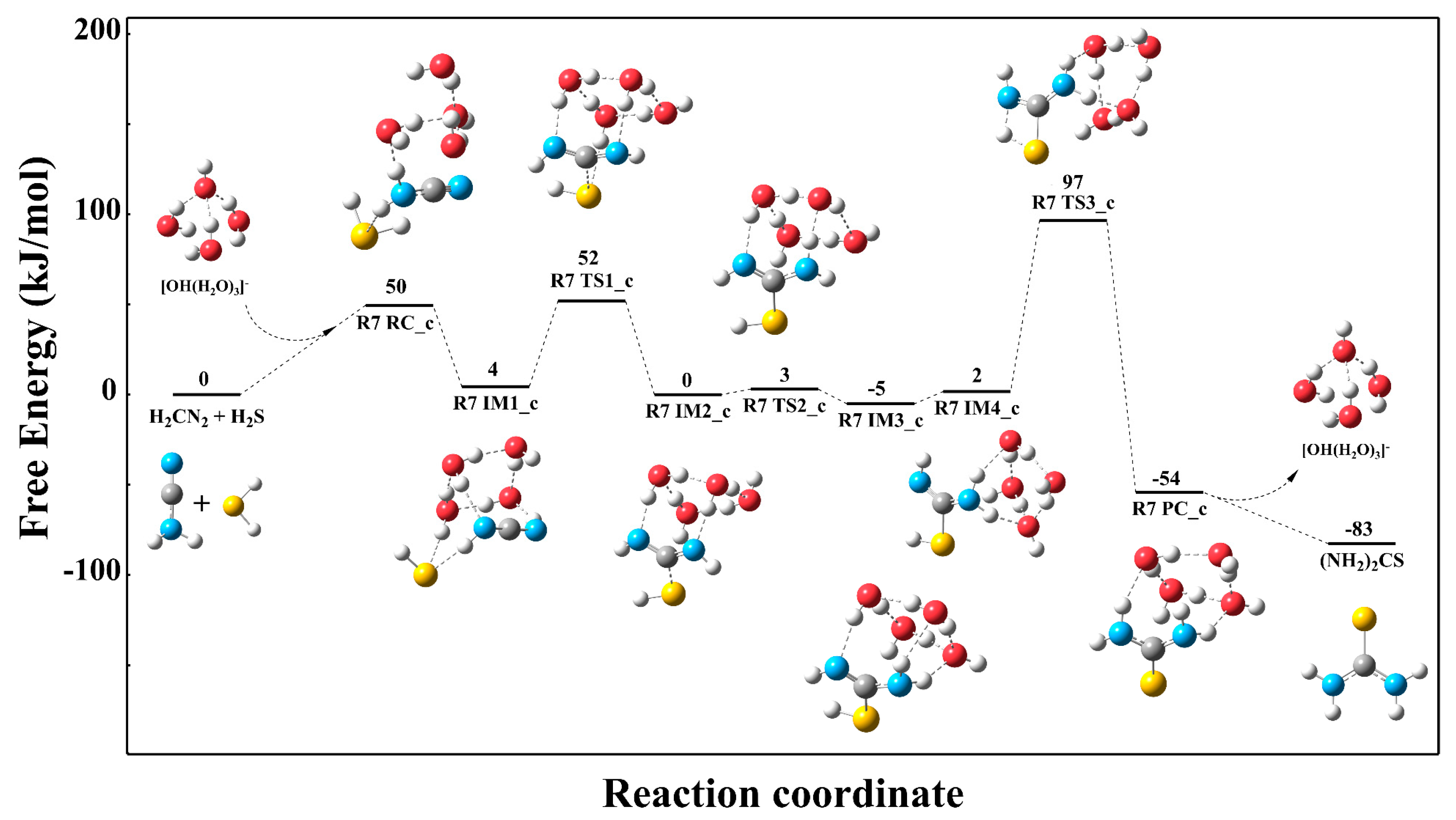
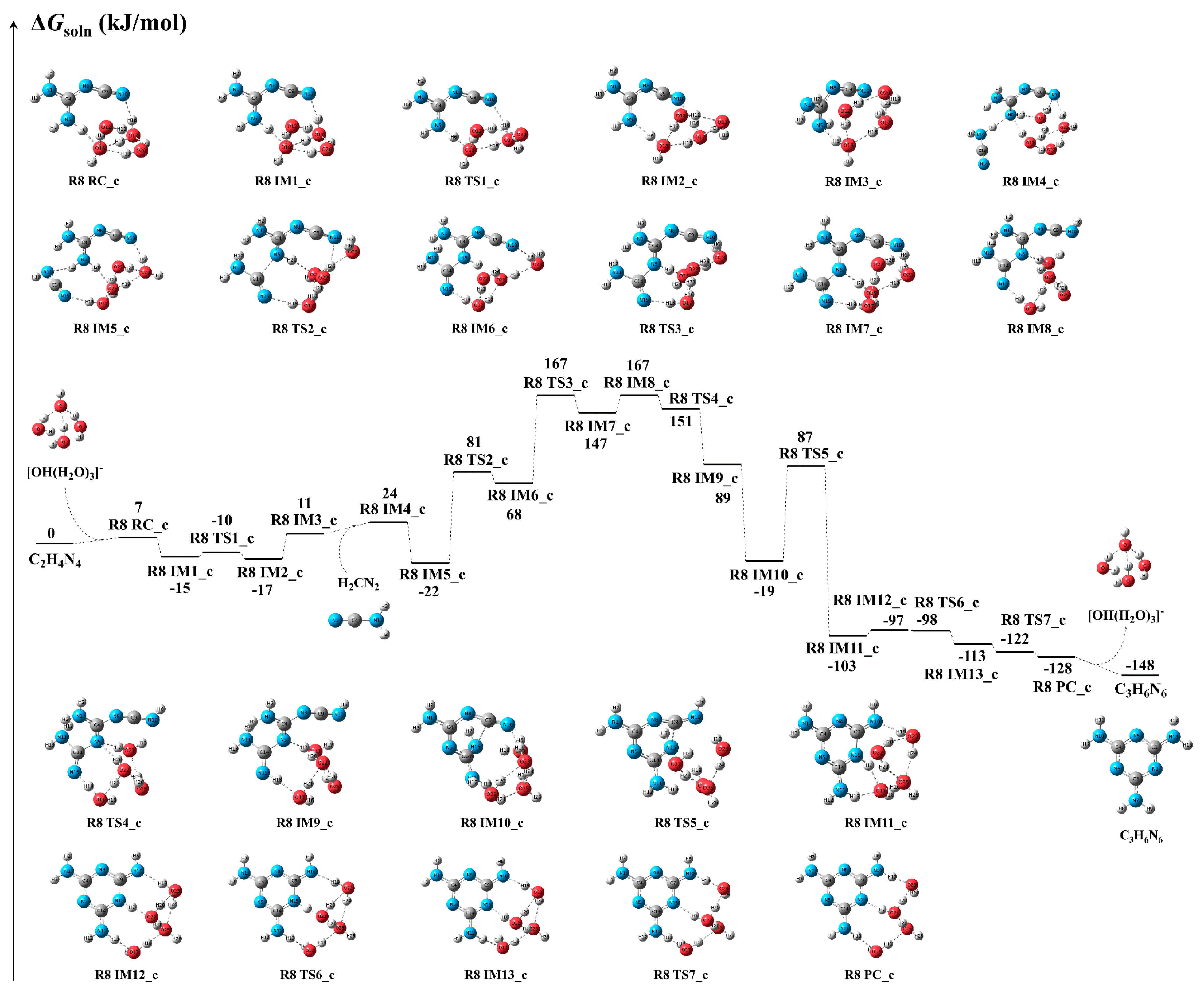
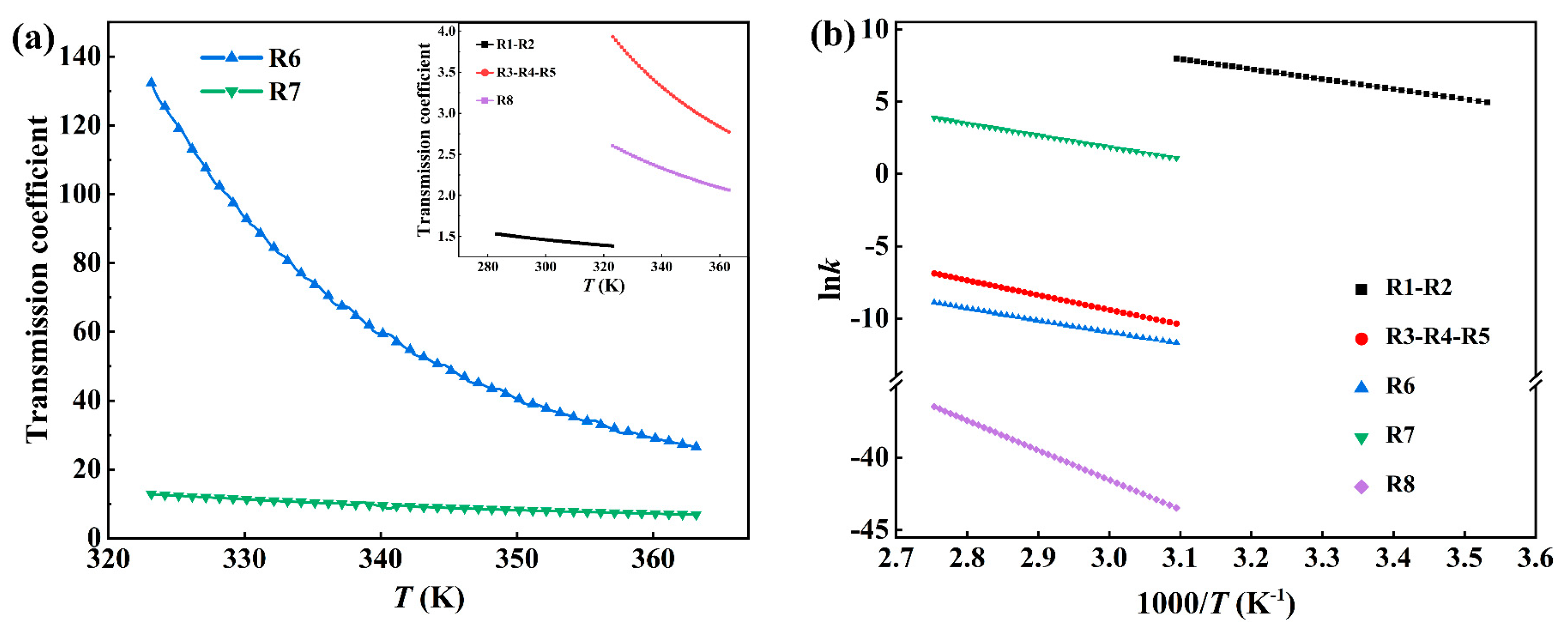

| Reaction | Reaction Type | κ | k (cm3 mol−1 s−1) |
|---|---|---|---|
| R1-R2 | Principal reaction | 1.447 | 7.117 × 102 |
| R3-R4-R5 | Principal reaction | 3.234 | 1.995 × 10−4 |
| R6 | Secondary reaction | 52.638 | 3.495 × 10−5 |
| R7 | Secondary reaction | 9.095 | 1.278 × 10 |
| R8 | Secondary reaction | 2.290 | 5.322 × 10−18 |
| Reaction | Slope | Intercept | A | Ea (kJ/mol) | Arrhenius Formula |
|---|---|---|---|---|---|
| R1-R2 | −6.91 | 29.36 | 5.62 × 1012 | 57.44 | k = (5.62 × 1012) exp(−6.91/T) |
| R3-R4-R5 | −10.18 | 21.15 | 1.53 × 109 | 84.64 | k = (1.53 × 109) exp(−10.18/T) |
| R6 | −8.20 | 13.66 | 8.53 × 105 | 68.17 | k = (8.53 × 105) exp(−8.20/T) |
| R7 | −8.16 | 26.34 | 2.75 × 1011 | 67.87 | k = (2.75 × 1011) exp(−8.16/T) |
| R8 | −20.53 | 20.06 | 5.17 × 108 | 170.73 | k = (5.17 × 108) exp(−20.53/T) |
| Reaction System | Hydrogen Dissociation Energy | Hydrogen Binding Energy |
|---|---|---|
| Dicyandiamide principal reactions (R3-R5) | 395 | −445 |
| Urea secondary reaction (R6) | 287 | −435 |
| Thiourea secondary reaction (R7) | 389 | −452 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Hong, Q.; Zhang, T.; Zhang, J.; Nian, Y.; Han, Y. DFT and TST Study of the Calcium Cyanamide Process for Synthesizing Cyanamide and Dicyandiamide. Processes 2024, 12, 2741. https://doi.org/10.3390/pr12122741
Huang J, Hong Q, Zhang T, Zhang J, Nian Y, Han Y. DFT and TST Study of the Calcium Cyanamide Process for Synthesizing Cyanamide and Dicyandiamide. Processes. 2024; 12(12):2741. https://doi.org/10.3390/pr12122741
Chicago/Turabian StyleHuang, Jiyong, Qin Hong, Tiantong Zhang, Jinli Zhang, Yao Nian, and You Han. 2024. "DFT and TST Study of the Calcium Cyanamide Process for Synthesizing Cyanamide and Dicyandiamide" Processes 12, no. 12: 2741. https://doi.org/10.3390/pr12122741
APA StyleHuang, J., Hong, Q., Zhang, T., Zhang, J., Nian, Y., & Han, Y. (2024). DFT and TST Study of the Calcium Cyanamide Process for Synthesizing Cyanamide and Dicyandiamide. Processes, 12(12), 2741. https://doi.org/10.3390/pr12122741






