Next Article in Journal
Deep Fat Frying Characteristics of Malpoa: Kinetics, Heat, and Mass Transfer Modeling
Next Article in Special Issue
Investigation of Coal Structure and Its Differential Pore–Fracture Response Mechanisms in the Changning Block
Previous Article in Journal
Introducing the Second-Order Features Adjoint Sensitivity Analysis Methodology for Neural Ordinary Differential Equations—I: Mathematical Framework
Previous Article in Special Issue
The Gas Generation Process and Modeling of the Source Rock from the Yacheng Formation in the Yanan Depression, South China Sea
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 12
Issue 12
10.3390/pr12122661
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Numerical Simulation of Coal’s Mechanical Properties and Fracture Process Under Uniaxial Compression: Dual Effects of Bedding Angle and Loading Rate

by
Jianchun Ou
1,
Jizhan Niu
2,
Bican Wang
1,*,
Wei Zhang
1,
Jing Zhao
3,
Benming Lyu
4,
Beihuai Zhan
5 and
Yue Ma
6
1
State Key Laboratory for Fine Exploration and Intelligent Development of Coal Resources, China University of Mining and Technology, Xuzhou 221116, China
2
No. 4 Mine of Pingdingshan Tian’an Coal Industry Co., Ltd., Pingdingshan 467000, China
3
Jiangsu Jufu Geological Engineering Co., Ltd., Xuzhou 221000, China
4
Dongtan Coal Mine, Yankuang Energy Group Co., Ltd., Jining 272000, China
5
Anhui Shenyuan Coal Chemical Co., Ltd., Huaibei 235000, China
6
State Grid Shandong Electric Power Company Jining Power Supply Company, Jining 272000, China
*
Author to whom correspondence should be addressed.
Processes 2024, 12(12), 2661; https://doi.org/10.3390/pr12122661
Submission received: 31 July 2024 / Revised: 13 September 2024 / Accepted: 28 October 2024 / Published: 25 November 2024
(This article belongs to the Special Issue Theoretical Progress in the Exploration and Development of Deep Coal-Measure Gas)
Browse Figures
Versions Notes

Abstract

In view of the significant influence of bedding structure on the mechanical characteristics and fracture behavior of coal, uniaxial compression discrete element numerical simulation experiments were carried out on coal samples with bedding angles of 0°, 30°, 60°, and 90°, and loading rates of 10−3/s, 10−2/s, 10−1/s, and 100/s, respectively, using PFC 6.0 software. The dual effects of bedding angle and loading rate on the mechanical properties of coal and its damage behavior were analyzed. The results show that (1) as the loading rate increases, the peak strength of the specimen increases, and the damage intensifies. The counts of the three types of cracks increased exponentially, while the crack growth rate was dramatic. (2) With the increase in loading rate, the density of the compressive stress force chain inside the specimen increases and gathers to the two ends, and the density of the tensile stress force chain is basically unchanged but gathers to the middle. The overall strength of the force chain changes according to the law of decreasing and then increasing. (3) With the increase in the bedding angle, the peak strength decreases and then increases, and the curve is approximately “V” shape. When the bedding angle is 60° and 90°, the peak stress is minimum and maximum, respectively. Shear cracks are dominant in the model, and the crack distribution shows a trend of increasing and then decreasing. (4) With the increase in the bedding angle, the density of the compressive stress force chain gradually decreases, and the density of the tensile stress force chain appears to be aggregated. The overall strength of the force chain changes according to the law of decreasing and then increasing.

1. Introduction

Coal is a non-homogeneous multiphase composite structural material containing many randomly distributed and various complex joints and weak planes, resulting in a strong anisotropic character. Coal as a sedimentary rock has obvious characteristics of a bedding structure (BS), and the anisotropy of a BS (especially bedding angle (BA)) has an important influence on the mechanical and fracture characteristics of coal [1]. The mechanical properties, deformation, and damage characteristics of coal seams become more complicated under the joint control of external forces and structurally weak surfaces such as a BS [2,3].
As the mining depth increases, the pressure and temperature in the coal seam change significantly, leading to variations in the mechanical properties of the coal bed. Such changes may trigger dynamic disasters, such as the coal seam impacts ground pressure and gas explosions. Specifically, deep mining may lead to fracture expansion or reactivation in the coal beds, increasing the stress concentration in the coal beds and thus raising the risk of disasters. Therefore, analyzing the evolution process of cracks in coal from initiation, development, and expansion to penetration under different BAs and portraying the evolution characteristics of crack expansion can help to better understand the destruction process of coal and help to further reveal the rupture and destruction mechanism of coal under different Bas; this is of great significance for the exploitation of deep coal bed methane, as well as the mechanism of dynamic disasters [4,5,6,7].
Many engineering practices show that coal has typical anisotropy and is rich in BS, and the initiation, expansion, and penetration of microscopic cracks are important factors leading to the destabilization and damage of the coal body, which plays a crucial role in the macro-mechanical behavior of the coal body [8,9]. Scholars have conducted numerous experimental studies. For example, Hao et al. [10] used conventional triaxial compression tests to explore the effects of BA and circumferential pressure on the mechanical behavior of shale. Duan et al. [11] discussed the effects of bedding and stress state on the deformation, seepage, energy, and fracture of coal using true triaxial tests. Liu et al. [12] studied the mechanical properties and fracture characteristics of rock masses with defective bedding planes by establishing pre-fracture models with different bedding plane properties (strength degradation factors, bedding plane angles, and spacing). Yuan et al. [13] quantitatively characterized the dynamic extension evolution process of the fissures before and after the rupture of the coal body using a uniaxial loading test and CT scanning test on the fissures of the original coal and the angle of the parapet. Fang et al. [14] established a coal physical strength model with a structural surface by conducting uniaxial compression tests on coal samples with different inclinations and analyzed the deformation and damage laws of coal seams with different inclinations. Huang et al. [15] revealed the mechanism of the influence of BS on the damage anisotropy of coal under loading by modeling the uniaxial damage evolution of seam-bearing coal rocks.
Although physical experiments have promoted the development of coal and rock mechanics to a certain extent, they can only be used to observe the crack development from a macroscopic perspective and obtain macroscopic mechanical parameters. Therefore, it is almost impossible to observe the initiation, expansion, and connection of microcracks in coal rocks by physical experiments. In addition, physical experiments require more human, material, and financial resources. So, many scholars have used numerical simulation to study the crack evolution process of coal rock. For example, Yin et al. [16] investigated the effect of BA on fracture toughness and fracture mode of specimens using ABAQUS. Huang et al. [17] used uniaxial compression and numerical simulation tests to investigate the extended fracture mode and different crack evolution processes in sandstone. Since the DEM method can comprehensively study local phenomena, such as sprouting and growth, local deformation, and rupture of microscopic mechanisms [18,19] the method is widely used by scholars. For example, Yue et al. [20] and Fan et al. [21] evaluated the mechanical behavior and damage characteristics of anisotropic specimens under compression conditions using PFC (2D and 3D). The obtained fracture modes were consistent with the experimental results of compressive strength. Xu et al. [22] used a DEM numerical method to investigate the crack extension mechanism and damage mode of coal samples containing two prefabricated fissures under biaxial compression conditions. BA has an important effect on the mechanical properties and crack extension of coal rock bodies. For example, Tomporowski et al. [23] used DEM to study the crack extension and aggregation process of marble at different angles. Li et al. [24] and Lei et al. [25] both used a combination of indoor experiments and numerical simulations to study the mechanical properties and rupture behaviors of coal by using BA.
Mechanical properties and the damage law of bedding coal (BC) are not only affected by BA but also by the loading rate (LR). For example, Li et al. [26] used a triaxial compression test to study the effect of different LR and confining pressures on the strength and deformation characteristics of the coal body. Gong et al. [27] adopted dynamic experiments to study the fracture mode and the difference between dynamic fracture toughness and quasi-static of coal samples with different bedding angles. It was concluded that the dynamic fracture mode of the coal samples with different bedding angles was tensile damage under their impact loads. The dynamic fracture toughness is 3.52–8.64 times of the quasi-static fracture toughness. Su et al. [28] believed that both dynamic compressive strength and fracture toughness increased with the change of joint angle. Under static loading, Type I indicates that the damage of specimens with small joint angles is caused by tensile cracks penetrating through the joints and local compression damage, and all tensile cracks penetrate through the joints with the same trajectory and expand along the diagonal. Under dynamic loading, the specimens with small joint angles are more likely to have fracture cracks across the joints, which are mainly tensile cracks and supplemented by shear cracks. The mechanical characteristics of coal rock materials are controlled by the LR, and it is generally recognized that the LR increases and the strength increases. For example, Liu et al. [29] used the uniaxial compression test and PFC2D numerical simulation method to study the crack extension process and macroscopic damage mode of coal under different LRs and determined that the compressive strength increases with the increase in the LR. Some scholars also studied the effect of LR coal damage from a dynamic point of view. For example, Chen et al. [30] and Tan et al. [31] used indoor dynamic loading experiments and numerical simulation tests to discuss the process of crack initiation and expansion of coal samples at different LRs with different BCs, respectively. However, there are few studies on the dual effects of BA and LR on coal samples.
Therefore, in this paper, the PFC2D 6.0 software was used to establish a dual-influence factor model of LR and BA and discrete element simulation was carried out. The stress–strain and strength, rupture mode crack evolution process, and force chain characteristics of BC under different LRs and BAs were investigated. The crack extension and damage pattern of the coal samples during the whole loading process were recorded from a microscopic point of view. It is of guiding significance for engineering practice.

2. Numerical Modeling and Micro Parameter Assignment

Particle flow theory focuses on explaining the damage and fracture mechanism of materials from the perspective of fine mechanics and analyzes the large deformation process of materials from the linear elasticity stage to the fracture damage stage. It can visually characterize the process of crack formation, expansion, and penetration and is suitable for the study of mechanical and engineering properties of rocks, concrete, and other materials [32,33]. In recent years, the PFC program based on particle flow theory has been widely used to simulate the generation and extension process of cracks inside the medium, which can simulate the macroscopic mechanical parameters of the computational model only by setting the fine mechanical parameters of the particles. Therefore, the PFC discrete element was selected for numerical study in this study. Laboratory 3D coal samples are damaged with very similar cracks on the front and back surfaces, and the crack merging behavior is essentially 2D, with only minor differences due to non-homogeneity. In addition, PFC3D simulations are computationally long, and the loading/boundary conditions are difficult to control. Therefore, in this study, a 2D plane stress model was used to numerically simulate the coal samples [32,33].
The modeling procedure is referenced in [34] with a model size of 100 mm × 50 mm. The particle sizes are uniformly distributed, ranging from 0.3 to 0.5 mm. Each complete numerical sample is discretized into 8266 particles, and the global damping coefficient is set to 0.1. The particle contact satisfies the parallel-bonded constitutive model. Drawing on Yang et al. [35], a discrete fracture network was invoked to determine the location of bedding and install a smooth joint model. This model allows slip deformation parallel to the contact surface, avoids the behavior of winding along the particle surface, and is widely used to simulate the mechanical behavior of structural surfaces in coal rock bodies. The PFC parallel bonding model was applied to simulate the contact behavior in granular materials. It assumes that the contact between particles is described by parallel bonding with elasticity and bond strength. The core of the model is to calculate the contact forces between the particles and predict the mechanical response of the material from these forces. It is suitable for simulating complex failure modes and material behavior. Eventually, numerical models were constructed for coal samples with BAs of 0°, 30°, 60°, and 90°, and LRs of 10−3/s, 10−2/s, 10−1/s, and 100/s, respectively, as shown in Figure 1.
In this study, the parameters of the contact model were calibrated by the “trial-and-error”. The micro-mechanical parameters in the parallel bond model were determined. As shown in Table 1.

3. Numerical Simulation Results

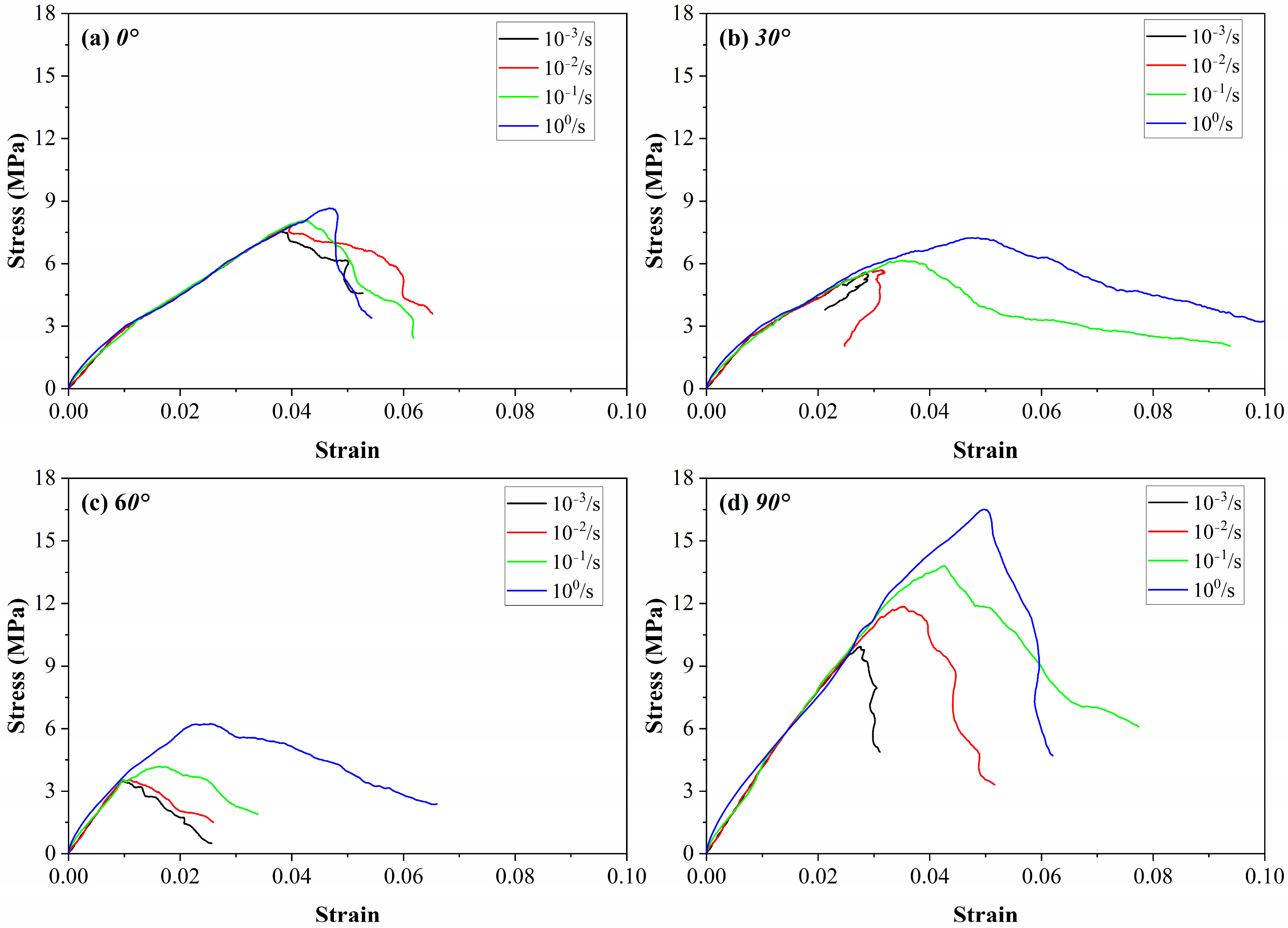
3.1. Stress–Strain and Strength

Understanding the mechanical properties of coal samples is essential in coal bed methane mining and coal mine engineering. The stress–strain curve of a coal sample is a key tool for describing its mechanical behavior, which demonstrates the deformation and strength characteristics of a coal sample under different loading conditions.
The stress–strain curves of coal samples under different BAs are shown in Figure 2, and the curves have obvious stages, which can be categorized into the compaction stage, elasticity stage, and destruction stage. After the specimen entered the destructive stage, the stress–strain curve decreased rapidly, showing obvious brittle damage. However, the time to achieve this transition varied at different LRs. When the LR was 10−3/s, the destruction time of coal samples was much larger than that of coal samples with other LRs. The degree of destruction of coal samples under different LRs was different. This may be related to this fracture extension penetration mode, which needs to be studied from a fine viewpoint.
There were differences in the change rule of stress–strain in coal samples with different BAs, which were divided into two categories. The first category was when the BA was 0° and 90°, and the second category was when the BA was 30° and 60°; the difference between the two was mainly the different rate of decline of the curve after the peak, which was greater than that of the latter. The reason for this difference may be that the angle between the normal direction of the damaged surface of the specimen and the loading direction is the same as the BA, which promotes the occurrence of shear damage in the coal samples. It matches the experimental phenomenon of Zhao et al. [36].
In actual coal bed methane mining projects, the strength parameters of coal samples, such as compressive strength and shear strength, directly affect the mining design and safety assessment. Therefore, an in-depth study of the peak strength (PS) of coal samples can help optimize the coal bed methane mining scheme and improve the safety and economy of the project. The highest point of the stress–strain curve was taken as PS of the BC sample, and the change curves of PS with different BAs and LRs were plotted, respectively, as shown in Figure 3.
As can be seen from Figure 3a, since the change rule of the PS with the BA of coal samples was similar under the condition of different LRs, an LR of 100/s was used as an example to describe the change rule of PS with the BA of coal samples. The PS of the coal samples gradually decreased from 8.66 MPa to 6.23 MPa and then increased to 16.5 MPa as the BA increased from 0° to 90°. The minimum PS was 6.23 MPa when the BA was 60°, and the maximum PS was 16.5 MPa when the BA was 90°. This law is the same as that of Zhou et al. [32]. It shows that the uniaxial compressive strength (UCS) of coal samples varies in a “V” shape with the increase in the BA.
As can be seen from Figure 3b, since the change rule of the PS with strain rate of coal samples was similar under the condition of different BAs, the change rule of the PS of coal samples increasing with strain rate was described by taking a BA of 90° as an example. As the LR increased from 10−3/s to 100/s, the PS of the coal samples gradually increased from 9.94 MPa to 16.5 MPa. It increased by 39.76%. It shows that the LR has a significant effect on the UCS of coal samples. There were differences in the rate of increase of different BAs, and the rate of increase was 12%, 22.79%, and 43.66% for BAs of 0°, 30°, and 60°, respectively. It shows that the UCS of coal samples is significantly affected by both the BA and LR. The conclusion obtained by Zhou et al. [34] is slightly different from the conclusions of this paper. This is mainly due to the consideration of the dual effects of the bedding angle and loading rate of bedding coal in this paper.
Therefore, when the LR of coal samples was the same, the UCS decreased and then increased with the increase in the BA, showing a “V” type. When the BA was the same, the UCS showed an increasing trend with the increase in the LR. The mechanical properties of coal samples control the safety and stability of the mining process during coal bed methane mining. When the BA was small, the LR could be appropriately increased to further improve the mining efficiency. When the BA was large, the LR was reduced, which enhanced the stability of mining.

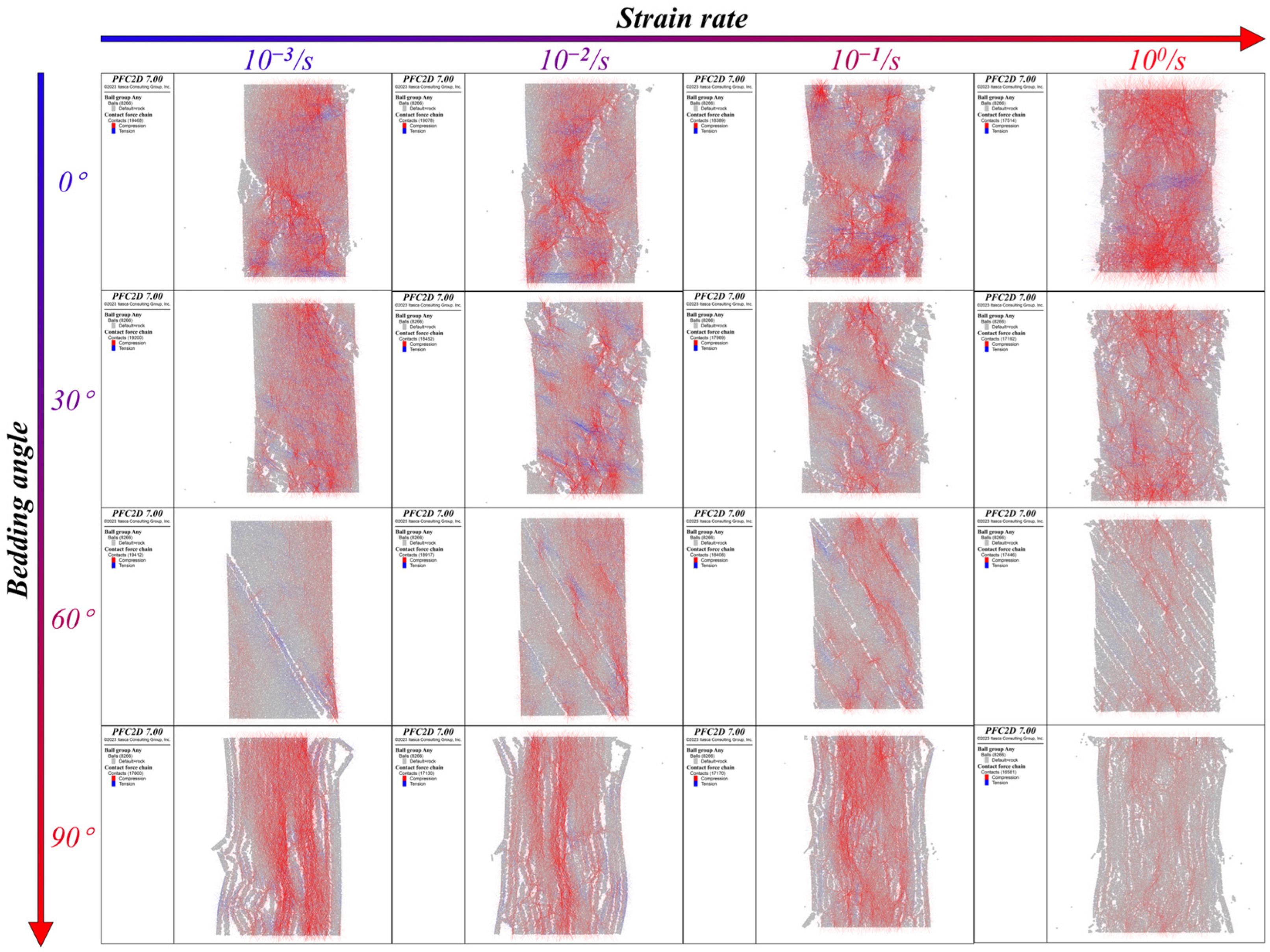
3.2. Failure Mode

The Plot window and the Edit Monitor Code command that comes with the PFC program were used to analyze the crack extension of coal samples. When the coal sample reached a certain strain increment, the crack distribution map of the corresponding state was output, which showed the crack generation process and counted the number of cracks. When the specimen reached peak strength, it started to enter the stress reduction phase. When the degree of stress drop reached 40% or more, the coal sample was considered to have reached destruction. Therefore, a stress drop of 40% or more can be used as a criterion for the failure of a coal sample. At this time, the failure modes exhibited by specimens containing different LRs and BAs were counted, as shown in Figure 4, where the red color represents shear cracking, and the blue color represents tensile cracking.
As seen in Figure 4, when α = 0°, multiple cracks were generated in the model, mainly concentrated in the upper right end with the middle part of the specimen tilted to damage. The shear cracks were distributed along the direction of the BA, and the tensile cracks were mainly distributed in the model damage region. As the LR increased from 10−3/s to 100/s, the damage degree of the model deepened and expanded to the middle. When the LR was 10−1/s, the upper part of the model showed a “V” type rupture area. When the LR was 100/s, the upper part of the model showed an “X” type rupture area.
When α = 30°, the cracks generated in the computational model were basically along the bedding surface, and a small number of cracks appeared in the left and right tips of the model when the LR was 10−3/s. With the increase in the LR, the extension of the cracks in the tips intensified and extended to the middle. When the LR was 10−1/s, the middle part of the model was tilted and ruptured. When the LR was 100/s, the model was strewn with shear cracks and tensile cracks, and the rupture was intensified. It shows that the LR has a significant effect on the damage pattern of coal samples.
When α = 60°, the rupture surface developed mainly along the bedding surface with an inclination angle of 60°, and there were no longer any obvious cracks at the loading end. The number of micro-fractures was minimized. The model damage cracks were mainly shear cracks with a small number of tensile cracks along the damaged surface. As the LR increased, the damaged surface intensified along the bedding surface. When α = 90°, the cracks were at a smaller angle to the loading direction. A small number of cracks appeared at the loading tip and in the middle and lower part of the specimen, with tensile cracks predominating. Model damage was greater at a BA of 90° compared to others. When the LR was 10−1/s, the model rupture was dominated by tensile cracks. When the LR was 100/s, the model was littered with shear and tensile cracks, and the model rupture increased. As the BA increased, the model was dominated by shear cracks, and the crack distribution showed a tendency to increase and then decrease.
In conclusion, there were significant differences in the rupture patterns and crack distributions of coal samples with different BAs and LRs under uniaxial compression conditions. With the increase in the LR, the PS of the specimen increased, and the degree of damage intensified. With the increase in the BA, shear cracks dominated in the model, and the crack distribution showed a trend of increasing first and then decreasing. The dual coupling effects of the BA and LR on the damage mode of the model were reflected from the side. To reduce the aggregation of shear cracks, the BA and LR are minimized during coal bed methane extraction, thus improving the stability and safety of the project.

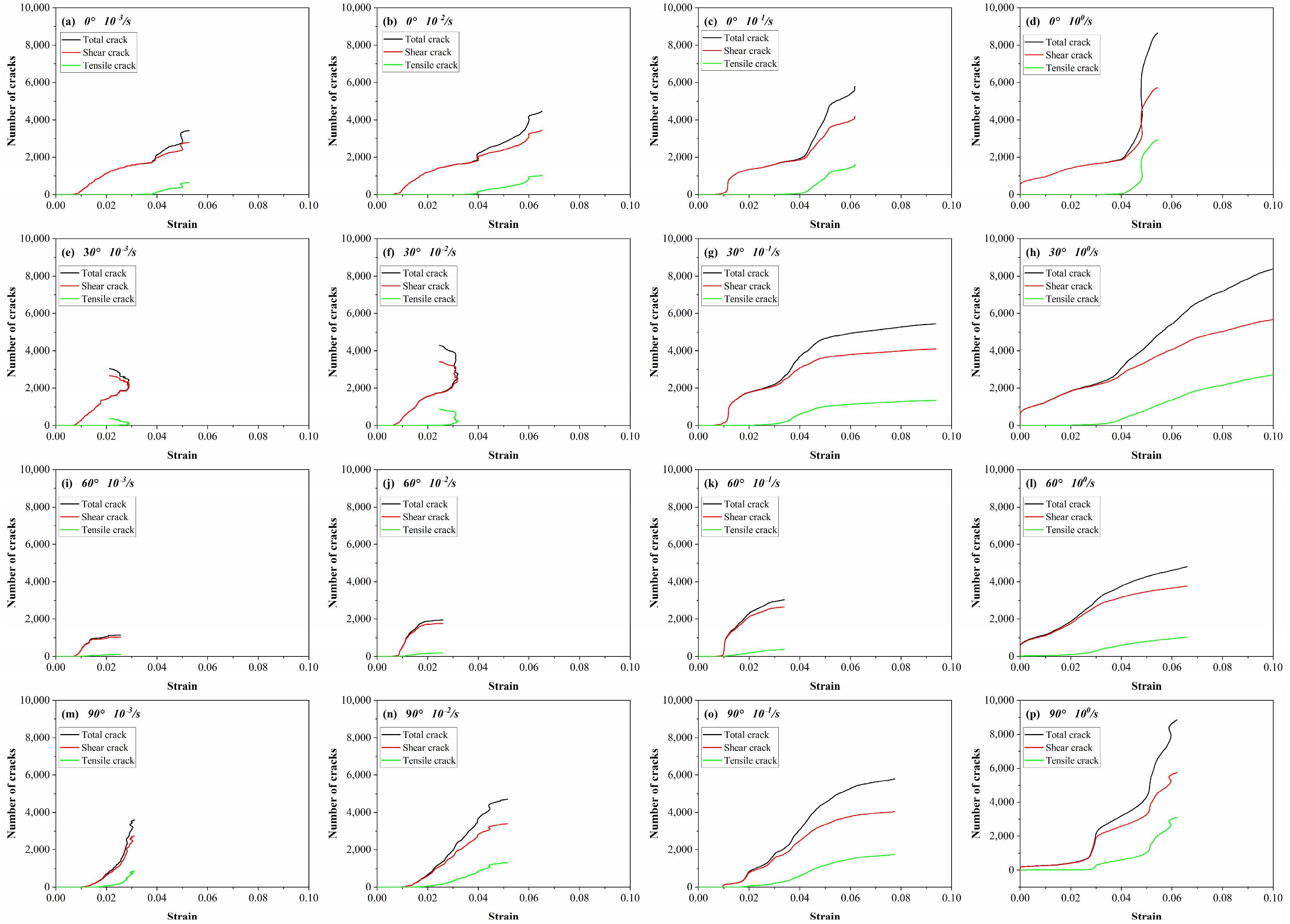
3.3. Evolution of Microcracks

To further analyze the crack distribution evolution laws during uniaxial compression of coal samples with different BAs and LRs, the evolution laws of total cracks, tensile cracks, and shear cracks and the distribution of the number of different types of cracks at the PS were compiled, as shown in Figure 5 and Figure 6.
From Figure 5, the distribution pattern of total, shear, and tensile cracks in coal samples with the increase in strain can be divided into three stages: Stage I (quiet period), Stage II (crack stable expansion stage), and Stage III (crack accelerated expansion stage). The black, red, and green curves represent total, shear, and tensile cracks, respectively.
As shown in Figure 5a, due to the compression effect of the structure of the coal samples, microcracks did not appear in the coal samples at the beginning with the increase in axial strain, and shear cracks appeared in the coal samples for the first time when the axial strain increased to 6.63 × 10−3. As the axial strain increased, the shear crack count gradually increased, and an inflection point occurred when the peak strain was reached. It shows that when the peak strain is reached, the coal samples have reached macroscopic rupture, making the crack counts increase. Tensile cracks first appeared in the coal samples when the axial strain increased to 0.027. An inflection point occurred until the peak strain was reached. The rate of shear crack counts then increased further.
As shown in Figure 5b–d, the total, shear, and tensile cracks followed the same trend as the LR gradually increased, but the counts of each type of crack increased exponentially while the crack growth rate intensified. This indicates that the larger the LR is, the more favorable the crack extension is, i.e., the LR and the crack count are positively correlated. When the BA was 90°, the change rule of crack count with the LR was the same as this.
As shown in Figure 5i, the crack curve increased gradually with increasing strain, where the total and shear crack curves were significantly higher than the tensile crack curve. When the strain reached the peak strain, the number of cracks varied in near horizontal direction. When the LR gradually increased, the number of cracks doubled, and the damage to the coal samples increased. It shows that the LR seriously affects the damage of coal samples. When the BA was 30°, it had a similar law. Therefore, the appropriate LR should be selected for the project.
When the LR was constant, the crack counts were significantly lower at 60° than in coal samples with other BAs as the BA varied. It shows that the BA plays an important role in the crack extension of coal samples, and a 60° BA is favorable for slowing down the extension of cracks. In general, when the BA was 0°–60°, the cracks inside the sample became easier to break due to the influence of the BA (decomposition of axial stresses), resulting in a smaller axial stress required for the final breakage of the specimen, with a consequent reduction in the PS of the sample. Ultimately, when a macroscopic rupture was developed, the internal yield region decreased, and the energy required for damage was smaller (axial stress and strain are smaller). This, in turn, led to lower fragmentation of the coal samples and a lower number of cracks. When the BA was 60°–90°, it had the opposite law.
So, the higher the LR, the more favorable the crack extension, i.e., the LR and crack count are positively correlated. When the BA was 0°–60°, the degree of coal sample crushing was lower, and the number of cracks was also lower. When the BA was 60°–90°, it had the opposite law. In the coal bed methane mining project, when the BA is large, the LR should be reduced to improve the safety of coal bed methane mining. When BA is small, the LR can be increased appropriately to achieve the purpose of efficient coal bed methane mining.
To further investigate the double influence law of the BA and LR on the coal samples, the variation curves of the number of cracks within the coal samples with the LR and BA were organized at the peak stress moment, as shown in Table 2 and Figure 6.
Figure 6a shows that the number of total cracks, shear cracks, and tensile cracks in the coal samples increased with an increasing LR. Figure 6b shows that with the increase in the BA, the cracks of the coal samples showed the characteristic of “increase–decrease–increase”. The minimum number of total, shear, and tensile cracks was 285, 282, and 3, respectively, when the BA was 60°. This suggests that specimen damage occurs in the 60° direction of bedding, resulting in a small number of newly generated cracks and a tendency for specimen damage to occur easily. This corresponds to the PS and damage pattern of the specimens.
To clearly identify the tendency of internal crack expansion in coals with different BAs and LRs, PFC2D simulation experiments were used to monitor them. Since this paper uses 2D simulation software for numerical experiments, the crack tendency was between 0° and 180°. The rosette diagram of the microcrack tendency of the coal sample after damage is shown in Figure 7.
As shown in Figure 7, taking a BA of 0° as an example, the variation of the crack tendency of coal samples with the LR is illustrated. With the LR gradually increasing from 10−3/s to 100/s, the microcrack tendency was mainly distributed in the range of 40°–140°, and the crack tendency was transformed from dispersed distribution to concentrated aggregation. There were differences in the distribution range of microcracks in the coal samples with different BAs. It indicates that the LR, which favors the increase in the strength of the BC and the enhancement of the rupture rate, contributes to the development and accumulation of crack tendencies.
When the BA and LR were 0° and 10−3/s, respectively, the crack inclination was mainly distributed in the range of 40°–140°. Figure 7, from top to bottom, shows that as the BA gradually increased from 30° to 60°, the microcrack tendency was concentrated from 40°–60° to 60°–80°. When the BA was 90°, the extension direction of microcracks was the same as the BA, and the microcrack damage tendency was highly concentrated in the 90° range, which makes the damage of coal samples require greater strength and more energy to be absorbed. It shows that the range of cracking tendency of coal samples is more concentrated as BA increases.
In conclusion, the crack tendency of coal samples increases with the LR, and the microcrack tendency changes from scattered distribution to concentrated aggregation. The range of crack tendency of coal samples is more concentrated as the BA increases. When the BA was 90°, the microcrack damage tendency was highly concentrated in the 90° range. It is shown that the tendency to concentrate the tendency of microcracks in coal samples is not only affected by the LR, but also by the BA, i.e., the tendency of cracks is affected by both. In coal bed methane mining, we should attempt to avoid an excessive BA and LR.

3.4. Force Chain Characteristics

In particle aggregates, a backbone force chain is defined as a chain-like structure consisting of neighboring particles with a contact force greater than the average contact force. The periphery of the skeletal force chain is constrained by the particles of the weak contact system to maintain the stability of the skeletal force chain structure [37,38] Macroscopic cracking occurs when many strong force chains concentrate and break. The force chain distribution describes the internal force transfer pattern between particles and reveals the mechanical sensitivity of coal samples to damage. In addition, it clarified the evolution of macroscopic cracks [39,40]. Figure 8 shows the variation of the contact force chain of coal samples at different BAs and LRs, respectively, where the red color is compressive stress, and the blue color is tensile stress.
Figure 8 shows the force chain distribution characteristics of coal samples under different BAs and LRs. The force chain distribution was dominated by compressive stress, with a small amount of tensile stress, which was quite different from each other. The internal rupture zones of the model were mainly located in areas of compressive stress concentration, with a small amount of tensile stress concentration. We took a BA of 0° and a loading rate of 10−3/s as an example to analyze the evolution law of the force chain in the model. When the specimen reached the PS, more compressive stress force chains along the rupture surface appeared inside the model, and a small concentration of tensile stress force chains appeared at the bottom and upper right corners. As the LR increased sequentially from left to right, the density of the compressive stress force chain inside the specimen increased and aggregated toward the ends, and the density of the tensile stress chain remained basically unchanged but aggregated toward the middle. It shows that the increase in the LR favors the aggregation of compressive stress force chains in coal samples and changes the aggregation location. This result is different from the conclusion of Yan et al. [41]. The reason for this phenomenon may be that the effect of the bedding angle on the stress chain was not considered in the Yan et al. experiment.
As the BA increased sequentially from top to bottom, the density of compressive stress force chains was gradually smaller, and tensile stress force chains appeared to be aggregated with increased density. When the BA was 60°, the compressive stress force chain was mainly concentrated on the left and right sides of the model. The rupture surface appeared along the direction of the BA, and a small amount of tensile stress force chain appeared. When the BA was 90°, there were many compressive stress force chains along the BA in the middle of the model, but there were almost no tensile stress force chains.
Therefore, as the LR increased, the density of compressive stress force chains inside the specimen increased and aggregated toward the ends. The density of the tensile stress force chain was basically unchanged but aggregated towards the center. As the BA increased, the density of compressive stress force chains became progressively smaller, and tensile stress force chains appeared to aggregate with increased density. In coal bed methane mining, when the BA is large, a smaller LR is selected to avoid an increase in compressive stress chains. When the BA is small, a larger LR is selected to reduce the tensile stress chains inside the coal samples.
Macroscopic cracks appear in the weak parts of the coal body when the density of force chain aggregation increases in the coal samples. The larger the force chain, the more intense the macroscopic damage, and the force chain acts as a bridge connecting the microscopic and macroscopic damage of the model. Analyzing the influence law of the LR and BA on the size of the force chain from the microscopic point of view is of great significance for understanding the macroscopic damage process of coal samples. To further analyze the size distribution characteristics of the force chain, PFC2D 6.0 software was used to derive the size distribution characteristics of the force chain for different LRs and different BAs as shown in Figure 9.
In Figure 9, the red color represents generated strong chains, the green color represents highly stressed particles, and the blue color represents free particles. During the model compression simulation, neighboring particles contact each other to form a force chain, and the force chains are glued to each other to form a force chain contact force network. The intricate mechanical response of the contact force network determines the mechanical properties of the modeled macroscopic particle system [42]. The coarseness of the force chain reflects the magnitude of the forces acting on the particles, and the level of aggregation represents the developmental characteristics of the model. When the BA was 0°, the maximum values of the contact force of the force chain at different LRs were 2.36 × 104 N, 2.34 × 104 N, 1.57 × 104 N, and 3.31 × 104 N, respectively. As the LR increased, the maximum contact force of the force chain showed a pattern of decreasing and then increasing. The laws obtained were the same as those of the laboratory tests conducted by Liu et al. [43] and Feng et al. [44]. When the LR was 10−3/s, the maximum values of the contact force of the force chain at different BAs were 2.36 × 104 N, 2.36 × 104 N, 1.88 × 104 N, and 2.15 × 104 N, respectively. The maximum value of the contact force of the force chain decreased and then increased as the BA increased. Therefore, the overall strength of the force chain network varied according to the law of decreasing and then increasing as both the LR and the BA increased. In coal bed methane mining, the BA and LR influence the expansion of macroscopic cracks in coal samples by influencing the magnitude of the contact force in the internal force chain of the coal samples, which ultimately leads to changes in mining efficiency and stability.

4. Conclusions and Prospects

In this paper, the mechanical properties and fracture characteristics of bedding coal are studied by numerical methods, and the following conclusions are obtained by analyzing the stress–strain curves and crack evolution laws of bedding coal:
(1)
The loading rate significantly increased the destruction rate of the coal samples and greatly increased the extent of coal sample destruction. The bedding angle divides the failure of coal samples into two categories, which makes the post-peak failure rate of coal samples different. The UCS tends to increase with an increasing loading rate. As the bedding angle increased, UCS decreased and then increased, and the curve was approximately “V” shaped. The minimum peak stress was 6.23 MPa when the bedding angle was 60°. The maximum peak strength was 16.5 MPa when the bedding angle was 90°;
(2)
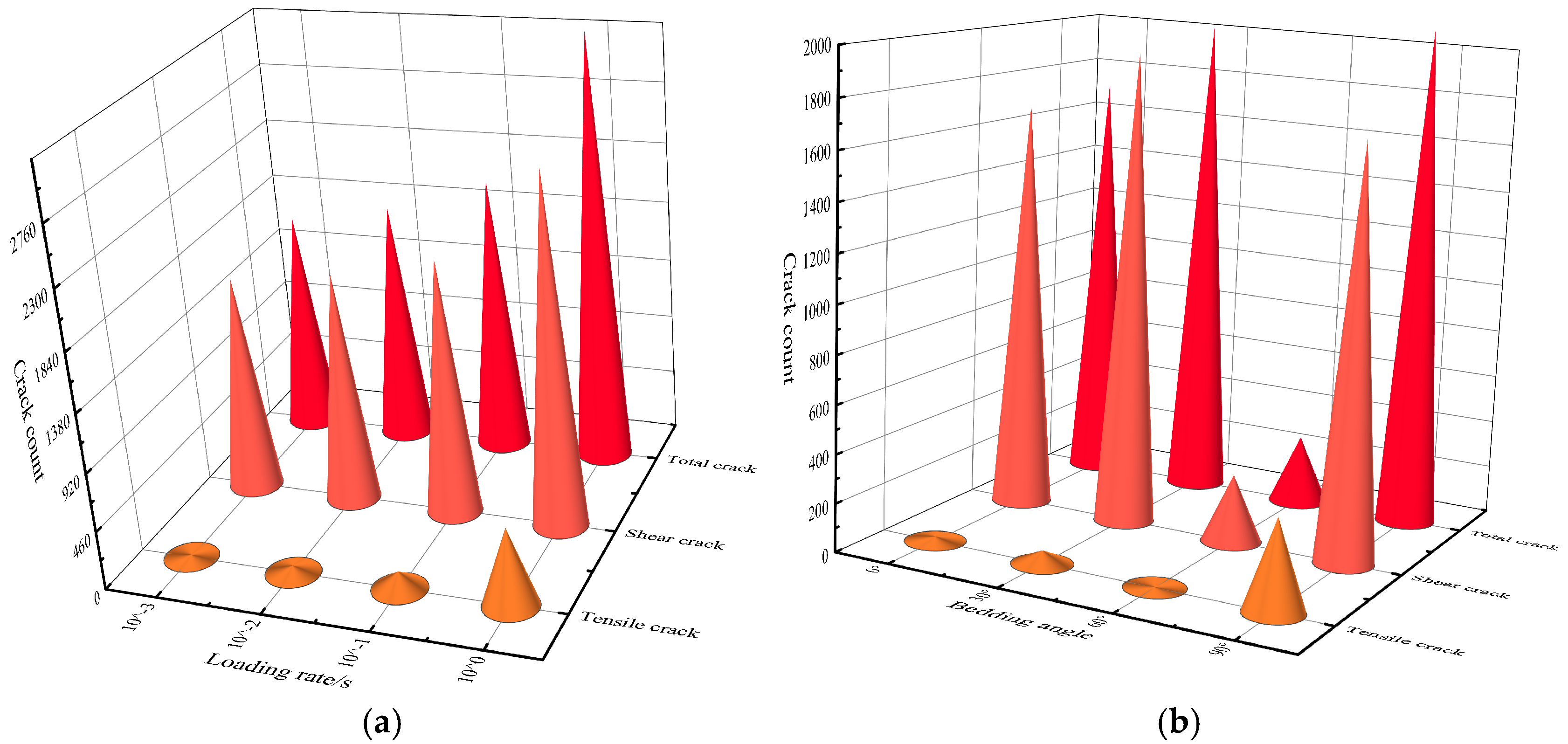
Significant differences in rupture patterns and crack distributions were observed in coal samples with different bedding angles and loading rates under uniaxial compression conditions. As the loading rate increased, the peak strength of the specimen increased, and the damage intensified. As the bedding angle increased, shear cracks dominated in the model, and the crack distribution showed a trend of increasing and then decreasing. Loading rate and crack counts were positively correlated. When the bedding angle was 0°–60°, the degree of coal sample crushing was lower, and the number of cracks was also lower. When the bedding angle was 60°–90°, it had the opposite law;
(3)
The number of cracks increased with the increase in the loading rate. With the increase in the bedding angle, the cracks of the coal samples showed the characteristic of “increase–decrease–increase”. The crack tendency of coal samples increased with the loading rate, and the microcrack tendency changed from scattered distribution to concentrated aggregation. The range of the crack tendency of coal samples was more concentrated as the bedding angle increased. When the bedding angle was 90°, the microcrack damage tendency was highly concentrated in the 90° range;
(4)
As the loading rate increased, the density of compressive stress force chains inside the specimen increased and aggregated toward the ends. The density of the tensile stress force chain was basically unchanged but aggregated towards the center. As the bedding angle increased, the density of compressive stress force chains became progressively smaller, and tensile stress force chains appeared to aggregate with increased density. The overall strength of the force chain network varied according to the law of decreasing and then increasing as both the loading rate and the bedding angle increased.
In addition, in this paper, the dual effects of the BA and LR on coal samples were investigated, and the results are of great reference significance for coal bed methane mining. From the microscopic point of view, the concentration of both tensile and compressive stress chains is unfavorable to the stability of the coal sample structure. Therefore, the selection of a smaller BA and LR can avoid the concentration of force chains as much as possible, and then reduce the contact force of internal force chains, which is conducive to the overall stability of the coal body structure. From the macroscopic point of view, the shear cracks of the coal body structure are concentrated when the BA and LR are larger, which is unfavorable to the overall stability of coal samples. Thus, when the BA is larger, a smaller LR is selected to avoid increased crack aggregation. When the BA is small, a larger LR is selected to improve the efficiency of coal bed methane mining. Although the laws obtained in this paper have some reference significance in engineering, these conclusions are qualitative descriptions and lack quantitative indicators. In future research, we will increase the quantitative parameter selection in coal bed methane mining, such as the BA and LR value range and method. Meanwhile, we also apply the conclusions obtained in this paper to the practice of coal bed methane mining and continuously improve the parameter scale in engineering practice to achieve safe and efficient coal bed methane mining.

Author Contributions

Conceptualization, J.O. and J.N.; software, B.W.; resources, W.Z.; writing—original draft preparation, J.O.; writing—review and editing, B.W., J.Z., B.L., B.Z. and Y.M.; funding acquisition, J.O. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (NO. 51974305 and NO. 52227901).

Data Availability Statement

Data are contained within this article.

Conflicts of Interest

Author Jizhan Niu was employed by the company Pingdingshan Tian’an Coal Industry Co., Ltd. Author Jing Zhao was employed by the company Jiangsu Jufu Geological Engineering Co., Ltd. Author Benming Lyu was employed by the company Yankuang Energy Group Co., Ltd. Author Beihuai Zhan was employed by the company Anhui Shenyuan Coal Chemical Co., Ltd. Author Yue Ma was employed by the company State Grid Shandong Electric Power Company Jining Power Supply Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The Pingdingshan Tian’an Coal Industry Co., Ltd., Jiangsu Jufu Geological Engineering Co., Ltd., Yankuang Energy Group Co., Ltd., Anhui Shenyuan Coal Chemical Co., Ltd. and State Grid Shandong Electric Power Company Jining Power Supply Company had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Duan, M.; Jiang, C.; Gan, Q.; Zhao, H.; Yang, Y.; Li, Z. Study on permeability anisotropy of bedded coal under true triaxial stress and its application. Transp. Porous Med. 2020, 131, 1007–1035. [Google Scholar] [CrossRef]
  2. Wang, R.; Pan, J.; Wang, Z.; Li, G.; Ge, T.; Zheng, H.; Wang, X. Influence of in situ stress on well test permeability and hydraulic fracturing of the Fanzhuang Block, Qinshui Basin. Energy Fuels 2021, 35, 2121–2133. [Google Scholar] [CrossRef]
  3. Xia, Z.-G.; Liu, S.; Bian, Z.; Song, J.; Feng, F.; Jiang, N. Mechanical properties and damage characteristics of coal/rock combination with different dip angles. KSCE J. Civ. Eng. 2021, 25, 1687–1699. [Google Scholar] [CrossRef]
  4. Hu, J.; He, M.C.; Li, H.R.; Tao, Z.G.; Liu, D.Q.; Cheng, T.; Peng, D. Rockburst hazard control using the excavation compensation method (ECM): A case study in the Qinling water conveyance tunnel. Engineering 2024, 34, 154–163. [Google Scholar] [CrossRef]
  5. Hu, J.; He, M.C.; Li, H.R.; Cheng, T.; Tao, Z.G.; Liu, D.Q.; Peng, D. Control effect of negative Poisson’s ratio (NPR) cable on impact-induced rockburst with different strain rates: An experimental investigation. Rock. Mech. Rock. Eng. 2023, 56, 5167–5180. [Google Scholar] [CrossRef]
  6. Li, H.R.; He, M.C.; Qiao, Y.F.; Cheng, T.; Xiao, Y.M.; Gu, Z.J. Mode I fracture properties and energy partitioning of sandstone under coupled static-dynamic loading: Implications for rockburst. Theor. Appl. Fract. Mech. 2023, 127, 104025. [Google Scholar] [CrossRef]
  7. Li, H.R.; Qiao, Y.F.; He, M.C.; Shen, R.X.; Gu, Z.J.; Cheng, T.; Xiao, Y.M.; Tang, J. Effect of water saturation on dynamic behavior of sandstone after wetting-drying cycles. Eng. Geol. 2023, 319, 107105. [Google Scholar] [CrossRef]
  8. Bésuelle, P.; Desrues, J.; Raynaud, S. Experimental characterisation of the localisation phenomenon inside a Vosges sandstone in a triaxial cell. Int. J. Rock. Mech. Min. Sci. 2000, 37, 1223–1237. [Google Scholar] [CrossRef]
  9. Wong, R.H.C.; Chau, K.T.; Tang, C.A.; Lin, P. Analysis of crack coalescence in rock-like materials containing three flaws- part I: Experimental approach. Int. J. Rock Mech. Min. Sci. 2001, 38, 909–924. [Google Scholar] [CrossRef]
  10. Hao, X.; Wang, S.; Xu, Q.; Yang, D.; Zhang, Q.; Jin, D.; Wei, Y. Influences of confining pressure and bedding angles on the deformation, fracture and mechanical characteristics of slate. Constr. Build. Mater. 2020, 243, 118255. [Google Scholar] [CrossRef]
  11. Duan, M.; Jiang, C.; Guo, X.; Yang, K.; Tang, J.; Yin, Z.; Hu, X. Experimental study on mechanics and seepage of coal under different bedding angle and true triaxial stress state. Bull. Eng. Geol. Environ. 2022, 81, 1–16. [Google Scholar] [CrossRef]
  12. Liu, L.; Li, H.; Chen, S.; Shao, Z.; Zhou, C.; Fu, S. Effects of bedding planes on mechanical characteristics and crack evolution of rocks containing a single pre-existing flaw. Eng. Geol. 2021, 293, 106325. [Google Scholar] [CrossRef]
  13. Yuan, T.; Wei, Y.; Chen, S.; Liu, W.; Zhao, L.; Zhang, X. Study on Mechanical Properties and Crack Propagation of Raw Coal with Different Bedding Angles based on CT Scanning. ACS Omega 2022, 7, 27185–27195. [Google Scholar] [CrossRef] [PubMed]
  14. Fang, X.; Wu, C.; Zhang, H.; Jiang, X.; Li, G.; Zhang, Z.; Liu, N. Energy Evolution of Coal During Uniaxial Compression under Different Bedding Intersection Angles and its Controlling Effect on the Failure Process. Nat. Resour. Res. 2024, 33, 813–830. [Google Scholar] [CrossRef]
  15. Huang, L.; Li, B.; Li, C.; Wu, B.; Wang, J. Research on anisotropic characteristics and energy damage evolution mechanism of bedding coal under uniaxial compression. Energy 2024, 301, 131659. [Google Scholar] [CrossRef]
  16. Yin, Q.; Wu, S.; Meng, Y.; Wu, J.; Zhang, Q.; Jing, H. Experimental and numerical investigation on mode I fracture properties of bedded rocks. Theor. Appl. Fract. Mech. 2023, 124, 103807. [Google Scholar] [CrossRef]
  17. Huang, Y.-H.; Yang, S.-Q.; Tian, W.; Wu, S. Experimental and DEM study on failure behavior and stress distribution of flawed sandstone specimens under uniaxial compression. Theor. Appl. Fract. Mech. 2022, 118, 103266. [Google Scholar] [CrossRef]
  18. Wong, L.N.Y.; Einstein, H.H. Crack coalescence in molded gypsum and Carrara marble: Part 2-microscopic observations and interpretation. Rock Mech. Rock. Eng. 2009, 42, 513–545. [Google Scholar] [CrossRef]
  19. Ge, R.; Ghadiri, M.; Bonakdar, T.; Zheng, Q.; Zhou, Z.; Larson, I.; Hapgood, K. Deformation of 3D printed agglomerates: Multiscale experimental tests and DEM simulation. Chem. Eng. Sci. 2020, 217, 115526. [Google Scholar] [CrossRef]
  20. Yue, Z.; Meng, F.; Zhou, X.-L.; Wang, X.; Zhang, L.; Wang, Z.-Q. Influence of non-persistent joint aperture and inclination angle on the shear behavior and fracture mode of solid rock and concrete material. Constr. Build. Mater. 2022, 316, 125892. [Google Scholar] [CrossRef]
  21. Xiang, F.; Kulatilake, P.H.W.; Chen, X. Mechanical behavior of rock-like jointed blocks with multi-non-persistent joints under uniaxial loading: A particle mechanics approach. Eng. Geol. 2015, 190, 17–32. [Google Scholar]
  22. Xu, H.; Qin, Y.; Wang, G.; Fan, C.; Wu, M.; Wang, R. Discrete element study on meso-mechanical behavior of crack propagation in coal samples with two prefabricated fissures under biaxial compression. Powder Technol. 2020, 375, 42–59. [Google Scholar] [CrossRef]
  23. Tomporowski, D.; Nitka, M.; Tejchman, J. Application of the 3D DEM in the modelling of fractures in pre-flawed marble specimens during uniaxial compression. Eng. Fract. Mech. 2023, 277, 108978. [Google Scholar] [CrossRef]
  24. Li, H.R.; He, M.C.; Qiao, Y.F.; Cheng, T. Burst behavior and its proneness evaluation of bedding coal. Chin. J. Rock. Mech. Eng. 2024, 43, 2178–2188. [Google Scholar]
  25. Lei, B.; Zuo, J.; Liu, H.-Y.; Wang, J.; Xu, F.; Li, H.-T. Experimental and numerical investigation on shale fracture behavior with different bedding properties. Eng. Fract. Mech. 2021, 245, 107639. [Google Scholar] [CrossRef]
  26. Li, Y.; Yang, S.-Q.; Liu, Z.-L.; Sun, B.-W.; Yang, J.; Xu, J. Study on mechanical properties and deformation of coal specimens under different confining pressure and strain rate. Theor. Appl. Fract. Mech. 2022, 118, 103287. [Google Scholar] [CrossRef]
  27. Gong, S.; Wang, Z.; Zhou, L. Dynamic fracture mechanics and energy distribution rate response characteristics of coal containing bedding structure. PLoS ONE 2021, 16, e0247908. [Google Scholar] [CrossRef]
  28. Su, Q.; Ma, Q.; Ma, D.; Yuan, P. Dynamic mechanical characteristic and fracture evolution mechanism of deep roadway sandstone containing weakly filled joints with various angles. Int. J. Rock. Mech. Min. Sci. 2021, 137, 104552. [Google Scholar] [CrossRef]
  29. Liu, X.; Chen, H.; Liu, B.; Deng, W.; Liu, Q.; Zhang, Z. Experimental and numerical study on failure characteristics and mechanism of coal under different quasi-static loading rates. Theor. Appl. Fract. Mech. 2022, 121, 103478. [Google Scholar] [CrossRef]
  30. Chen, Z.; Yuan, Y.; Qin, Z.; Wang, W.; Li, H. The mechanism of crack propagation under dynamic loading stress at different rates. Comp. Part. Mech. 2024. [Google Scholar] [CrossRef]
  31. Tan, L.; Ren, T.; Yang, X.; He, X. A numerical simulation study on mechanical behaviour of coal with bedding planes under coupled static and dynamic load. Int. J. Min. Sci. Technol. 2018, 28, 791–797. [Google Scholar] [CrossRef]
  32. Yang, S.Q.; Huang, Y.H.; Jing, H.W.; Liu, X.R. Discrete element modeling on fracture coalescence behavior of red sandstone containing two unparallel fissures. Eng. Geol. 2014, 178, 28–48. [Google Scholar] [CrossRef]
  33. Debecker, B.; Vervoort, A. Two-dimensional discrete element simulations of the fracture behaviour of slate. Int. J. Rock. Mech. Min. Sci. 2013, 61, 161–170. [Google Scholar] [CrossRef]
  34. Zhou, Y.; Li, C.; Wang, W.L.; Xian, Z. A meso-level study on mechanical properties of bedding coal under uniaxial compression. J. Cent. South Univ. (Sci. Technol.) 2022, 53, 4036–4047. [Google Scholar]
  35. Yang, S.Q.; Sun, B.W.; Tian, W.L. Discrete element simulation of the mechanical properties of shale with different bedding inclinations under conventional triaxial compression. Chin. J. Eng. 2022, 44, 430–439. [Google Scholar]
  36. Zhao, H.; Hou, J.C.; Zhang, L.; Zhao, M.H. Towards concrete-rock interface shear containing similar triangular asperities. Int. J. Rock. Mech. Min. 2021, 137, 104547. [Google Scholar] [CrossRef]
  37. Ma, G.; Chang, X.-L.; Zhou, W.; Ng, T.-T. Mechanical response of rockfills in a simulated true triaxial test: A combined FDEM study. Geomech. Eng. 2014, 7, 317–333. [Google Scholar] [CrossRef]
  38. Nie, Z.H.; Qi, Q.; Wang, X.; Zhu, Y.G. DEM investigation of strain behaviour and force chain evolution of gravel–sand mixtures subjected to cyclic loading. Particuology 2022, 68, 13–28. [Google Scholar] [CrossRef]
  39. Huang, Y.; Li, J.; Teng, Y.; Dong, X.; Wang, X.; Kong, G.; Song, T. Numerical simulation study on macroscopic mechanical behaviors and micro-motion characteristics of gangues under triaxial compression. Powder Technol. 2017, 320, 668–684. [Google Scholar] [CrossRef]
  40. Li, H.R.; Qiao, Y.F.; Shen, R.X.; He, M.C.; Cheng, T.; Xiao, Y.M.; Tang, J. Effect of water on mechanical behavior and acoustic emission response of sandstone during loading process: Phenomenon and mechanism. Eng. Geol. 2021, 294, 106386. [Google Scholar] [CrossRef]
  41. Yan, Y.T.; Li, J.C.; Li, X. Dynamic viscoelastic model for rock joints under compressive loading. Int. J. Rock. Mech. Min. Sci. 2022, 154, 105123. [Google Scholar] [CrossRef]
  42. Li, Z.; Gao, Y.H.; Liu, P.; Li, L.; De, X. Discrete element study on evolution of force-chain during salix grains dense molding. Acta Energiae Solaris Sin. 2019, 40, 3186–3195. [Google Scholar]
  43. Liu, W.; Cheng, W.; Liu, X.; Zhang, Z.; Yue, Z.; Yang, L.; Shen, A. Effects of Loading Rate and Notch Geometry on Dynamic Fracture Behavior of Rocks Containing Blunt V-Notched Defects. Rock. Mech. Rock. Eng. 2024, 57, 2501–2521. [Google Scholar] [CrossRef]
  44. Feng, P.; Xu, Y.; Dai, F. Effects of dynamic strain rate on the energy dissipation and fragment characteristics of cross-fissured rocks. Int. J. Rock. Mech. Min. Sci. 2021, 138, 104600. [Google Scholar] [CrossRef]
Processes 12 02661 g001
Figure 1. Numerical modeling of bedding coal.
Figure 1. Numerical modeling of bedding coal.
Processes 12 02661 g001
Processes 12 02661 g002
Figure 2. Stress–strain curves (a–d).
Figure 2. Stress–strain curves (a–d).
Processes 12 02661 g002
Processes 12 02661 g003
Figure 3. Uniaxial compressive strength of bedding coal: (a) Different bedding angle; (b) Different strain rates.
Figure 3. Uniaxial compressive strength of bedding coal: (a) Different bedding angle; (b) Different strain rates.
Processes 12 02661 g003
Processes 12 02661 g004
Figure 4. Failure mode.
Figure 4. Failure mode.
Processes 12 02661 g004
Processes 12 02661 g005
Figure 5. Evolution of microcracks (a–p).
Figure 5. Evolution of microcracks (a–p).
Processes 12 02661 g005
Processes 12 02661 g006
Figure 6. Distribution of the number of different types of cracks at the peak stress (a,b).
Figure 6. Distribution of the number of different types of cracks at the peak stress (a,b).
Processes 12 02661 g006
Processes 12 02661 g007
Figure 7. Crack Inclination Distribution.
Figure 7. Crack Inclination Distribution.
Processes 12 02661 g007
Processes 12 02661 g008
Figure 8. Force Chain Attribute Characterization.
Figure 8. Force Chain Attribute Characterization.
Processes 12 02661 g008
Processes 12 02661 g009
Figure 9. Force chain magnitude characteristics.
Figure 9. Force chain magnitude characteristics.
Processes 12 02661 g009
Table 1. Micro-mechanical parameters of PFC2D.
Table 1. Micro-mechanical parameters of PFC2D.
Micro-ParametersValues
Minimum radius of the particle, Rmin/mm0.28
Ratio of maximum to minimum of radius, Rrat1.66
Density of the particle, ρ/(kg·m−3)1400
Friction coefficient, μ0.5
Young’s modulus of the particle, EC/GPa2.25
Ratio of normal to shear stiffness of the particle, kn/ks3.0
Parallel bonding radius factor, λ1.0
Young’s modulus of the parallel bond, E ¯ C /GPa2.25
Ratio of normal to shear stiffness of the parallel bond, K ¯ n / K ¯ s 3.0
Average bond normal strength, σn,mean/MPa12.5
Standard deviation of bond normal strength, σn,dev/MPa1.25
Average bond tangential strength, τs,mean/MPa12.5
Standard deviation of bond tangential strength, τs,dev/MPa1.25
Table 2. Cracking statistics for different bedding angles and loading rates.
Table 2. Cracking statistics for different bedding angles and loading rates.
Bedding Angle α/°Loading Rate/s
10−310−210−1100
Total CrackShear CrackTensile CrackTotal CrackShear CrackTensile CrackTotal CrackShear CrackTensile CrackTotal CrackShear CrackTensile Crack
0172217031918671810572122198513733082706602
302017196255246723111562760252923140623309753
602852823702680221793168111224582287171
90208517103752800223856235122757755429032631027
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ou, J.; Niu, J.; Wang, B.; Zhang, W.; Zhao, J.; Lyu, B.; Zhan, B.; Ma, Y. Numerical Simulation of Coal’s Mechanical Properties and Fracture Process Under Uniaxial Compression: Dual Effects of Bedding Angle and Loading Rate. Processes 2024, 12, 2661. https://doi.org/10.3390/pr12122661

AMA Style

Ou J, Niu J, Wang B, Zhang W, Zhao J, Lyu B, Zhan B, Ma Y. Numerical Simulation of Coal’s Mechanical Properties and Fracture Process Under Uniaxial Compression: Dual Effects of Bedding Angle and Loading Rate. Processes. 2024; 12(12):2661. https://doi.org/10.3390/pr12122661

Chicago/Turabian Style

Ou, Jianchun, Jizhan Niu, Bican Wang, Wei Zhang, Jing Zhao, Benming Lyu, Beihuai Zhan, and Yue Ma. 2024. "Numerical Simulation of Coal’s Mechanical Properties and Fracture Process Under Uniaxial Compression: Dual Effects of Bedding Angle and Loading Rate" Processes 12, no. 12: 2661. https://doi.org/10.3390/pr12122661

APA Style

Ou, J., Niu, J., Wang, B., Zhang, W., Zhao, J., Lyu, B., Zhan, B., & Ma, Y. (2024). Numerical Simulation of Coal’s Mechanical Properties and Fracture Process Under Uniaxial Compression: Dual Effects of Bedding Angle and Loading Rate. Processes, 12(12), 2661. https://doi.org/10.3390/pr12122661

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop