Advanced Emission Reduction Strategies: Integrating SSSC and Carbon Trading in Power Systems
Abstract
:1. Introduction
2. Global Carbon-Trading Mechanisms: Evolution and Key Drivers
2.1. Evolution and Drivers of Global Carbon-Trading Mechanisms
2.2. Taiwan’s Carbon-Trading System and Market Challenges
2.3. Power Market Dynamics
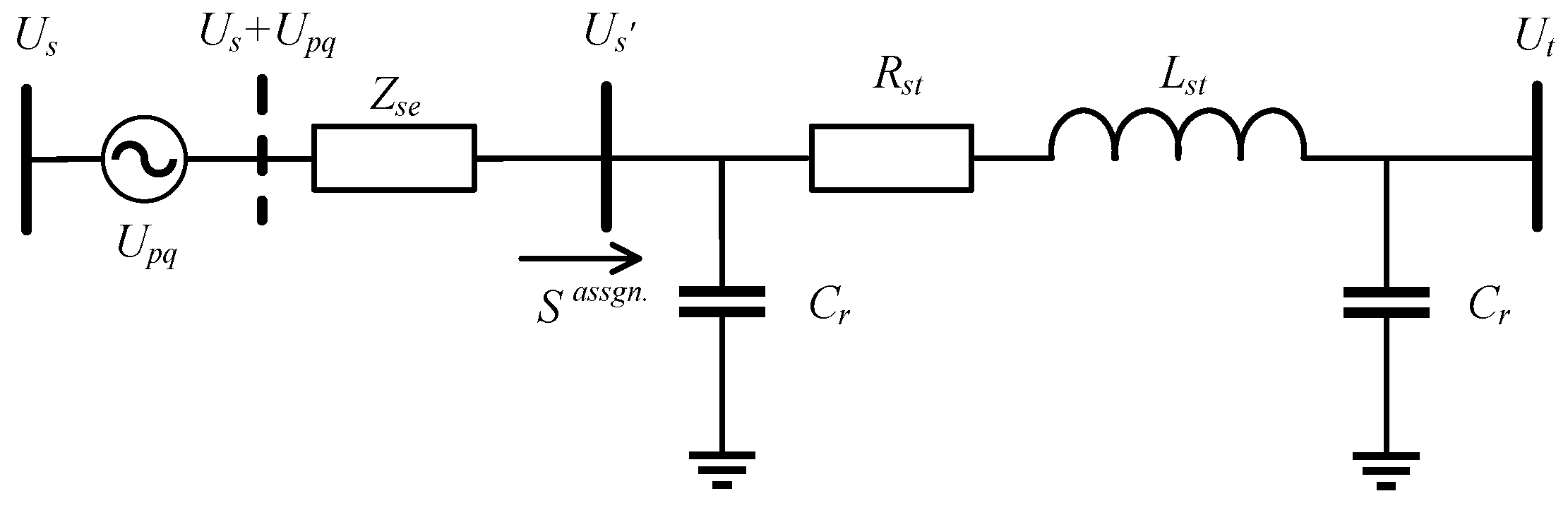
3. Integration of the SSSC into the Power Market Load Flow Model
3.1. Power Flow Calculation Using the ECI Approach
3.2. Derivation of a ECI Model Incorporating SSSC
3.3. Installation Principles of the SSSC
- Each transmission line or bus is limited to one SSSC installation.The SSSC regulates power flow, but adding more than one per line offers little benefit and increases reactive power demand, limiting installations to one per line.
- The SSSC should not be installed on lines with significantly low impedance.Low-impedance lines naturally carry higher power flow, making rerouting to under-utilized lines more effective than installing the SSSC for congestion reduction.
- Buses with existing generators or synchronous machines are unsuitable for SSSC installation.Generators and synchronous machines can address congestion, reducing SSSC need. In Taiwan, separate generation and transmission may still warrant SSSCs for optimization.
3.4. Max Profit Model for Power Generators in Carbon Markets
- Equality constraints:
- (1)
- Power balance constraint
- (2)
- OPF equality constraint
- (3)
- Reserve capacity constraint
- Inequality constraints:
- (1)
- Carbon dioxide emission limits
- (2)
- Volume constraints on transactions
- (3)
- SSSC voltage magnitude and phase angle constraints
3.5. The Mathematical Model of Taipower’s CO2 Emissions
4. Solving Market Problems with the Adaptive Time-Varying Gravitational Algorithm (ATGA)
4.1. Gravitational Search Algorithm (GSA)
- (1)
- Initialization
- (2)
- Calculation of mass
- (3)
- Calculation of gravitational force
- (4)
- Acceleration and velocity updates
- (5)
- Position update
- (6)
- Dynamic adjustment of the gravitational constant
- (7)
- Convergence and stopping criteria
4.2. The ATGA for Dynamic Economic Dispatch Problems Involving Optimal Power Flow
- Step 1: Input system parameters and initialize time interval.
- Step 2: Initialize population and set iteration count.
- Step 3: Perform load flow calculations using the ECI method.
- Step 4: Fitness evaluation and update of pbest and gbest
- Step 5: GA stage
- (1)
- Selection
- (2)
- Crossover operation
- (3)
- Mutation operation
- Step 6: GSA stage
- (1)
- Initialize particle position.
- (2)
- Calculate gravitational force between particles.
- (3)
- Update particle velocity and position.
- (4)
- Adjust time-varying acceleration coefficient.
- Step 7: Check global best update.
- Step 8: Check iteration termination conditions.
- Step 9: Check 24-h calculation progress.
| Algorithm 1. Pseudocode of the ATGA algorithm |
| Initialize parameters: Set population size (N), max iterations (T), gravitational constant (G0), decay factor (φ) Initialize positions Xi (control variables: generator power outputs, bus voltages) and velocities Vi for all particles Set initial pbest and gbest t = 0 //iteration counter While t < T: For each particle i in population: //fitness evaluation Perform ECI-based power flow calculation for particle i: For each bus m: Inject equivalent current Im based on generator output and SSSC effect Update bus voltage Um using power flow equations Ensure system constraints (voltage limits, line capacities) are satisfied Calculate fitness Fitness(Xi) based on power flow results (profit, emission) //update personal best (pbest) If Fitness(Xi) < Fitness(pbesti): pbesti = Xi //update global best (gbest) If Fitness(Xi) < Fitness(gbest): gbest = Xi For each particle i: Mi = Compute mass(Fitness(Xi)) //calculate particle mass based on fitness For each particle j ≠ i: Compute distance Rij between i and j //gravitational force between i and j //acceleration update For each particle i: //update velocity //update position (control variables: power output, voltage) //update gravitational constant Adjust inertia and acceleration(t) //optional: time-varying adjustments t = t + 1 //increment iteration counter Output gbest as the optimal solution |
5. System Testing and Result Analysis
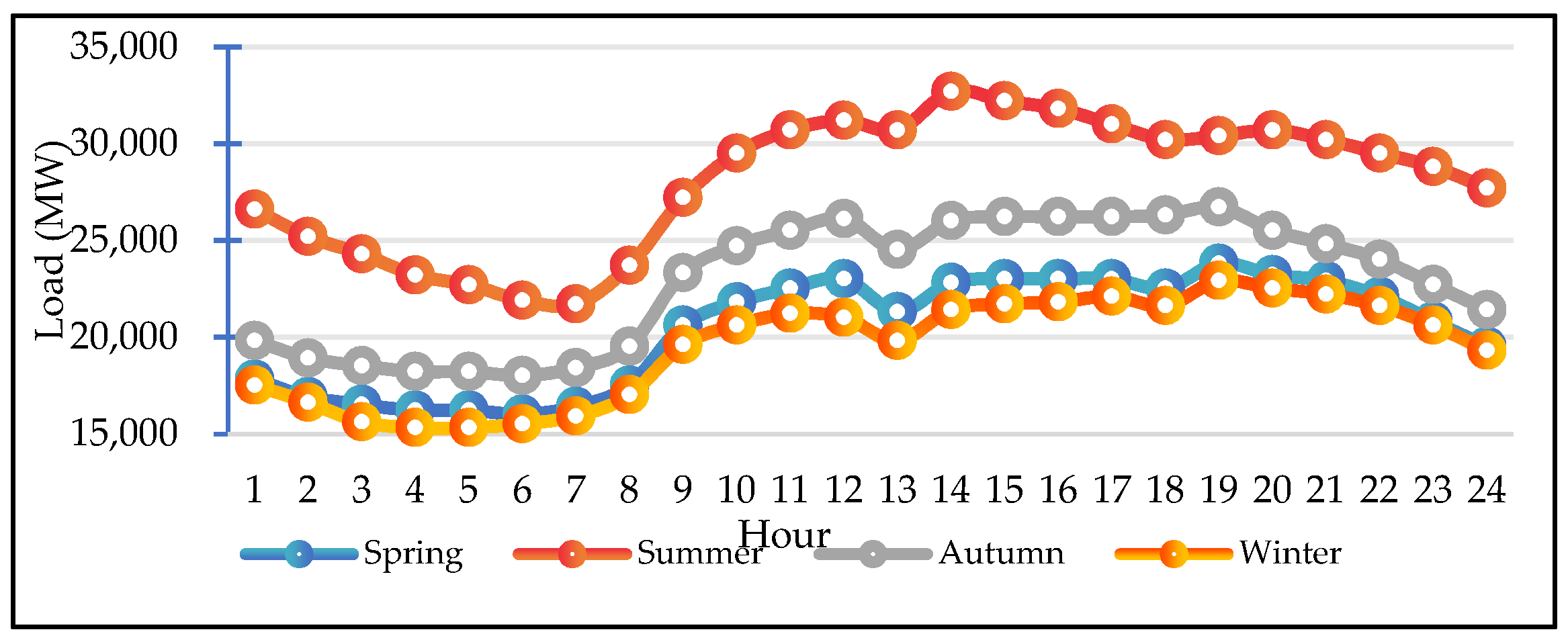
- Case 1: Based on the annual average daily load data of Taiwan’s power system.
- Case 2: Full-year simulation and testing of Taiwan’s power system.
- Test 1: An evaluation of optimal power flow in the power system.
- Test 2: A profit-oriented carbon reduction analysis achieved through fuel-mix adjustments at the power company.
- Test 3: A detailed profit analysis of the power company’s participation in the carbon-trading market.
- Test 4: A profit analysis examining the joint participation of the power company and transmission operators (utilizing SSSC technology) in the carbon-trading market.
5.1. Convergence Testing of the ATGA
5.2. Case 1: Based on the Annual Average Daily Load Data
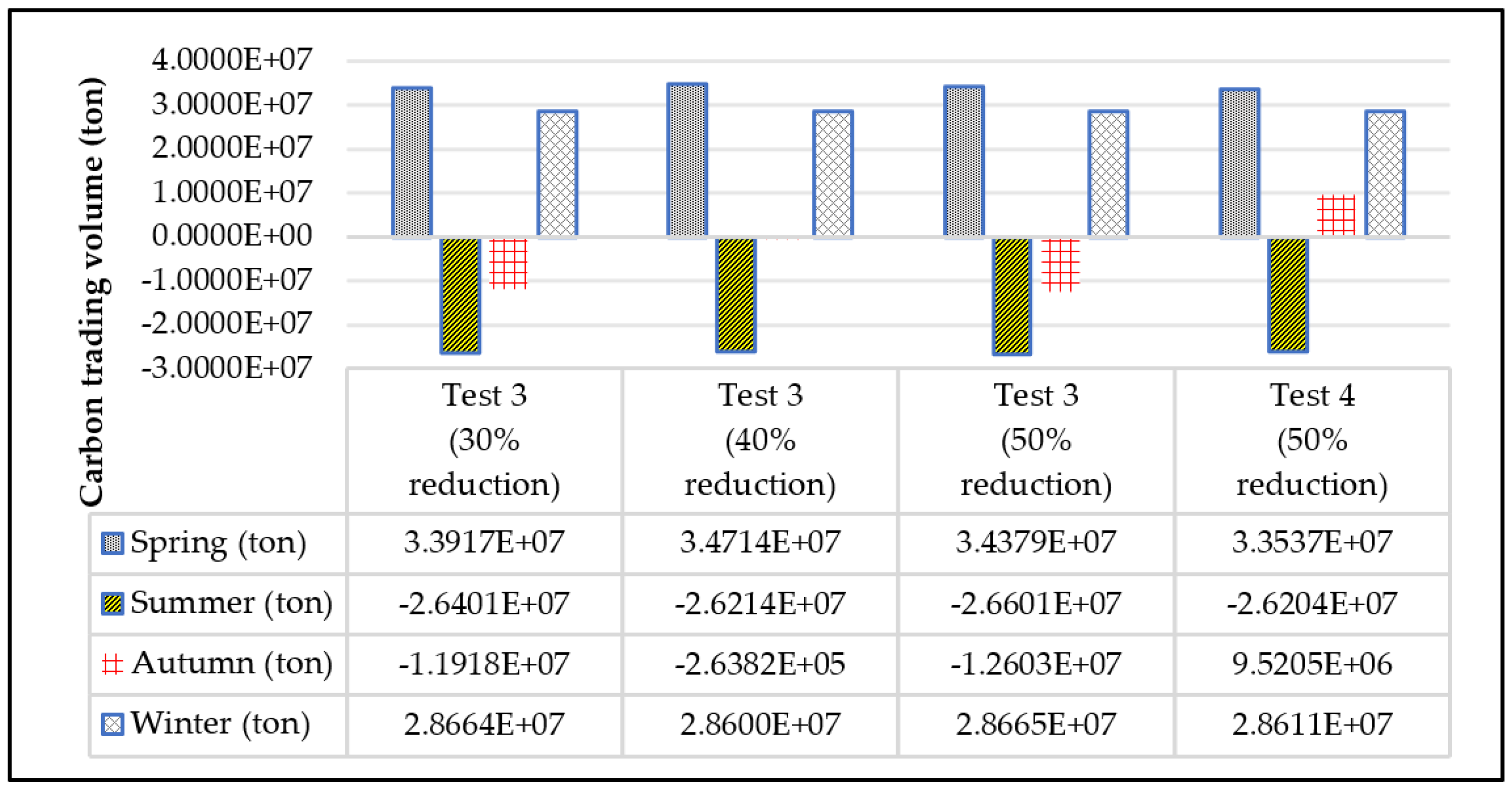
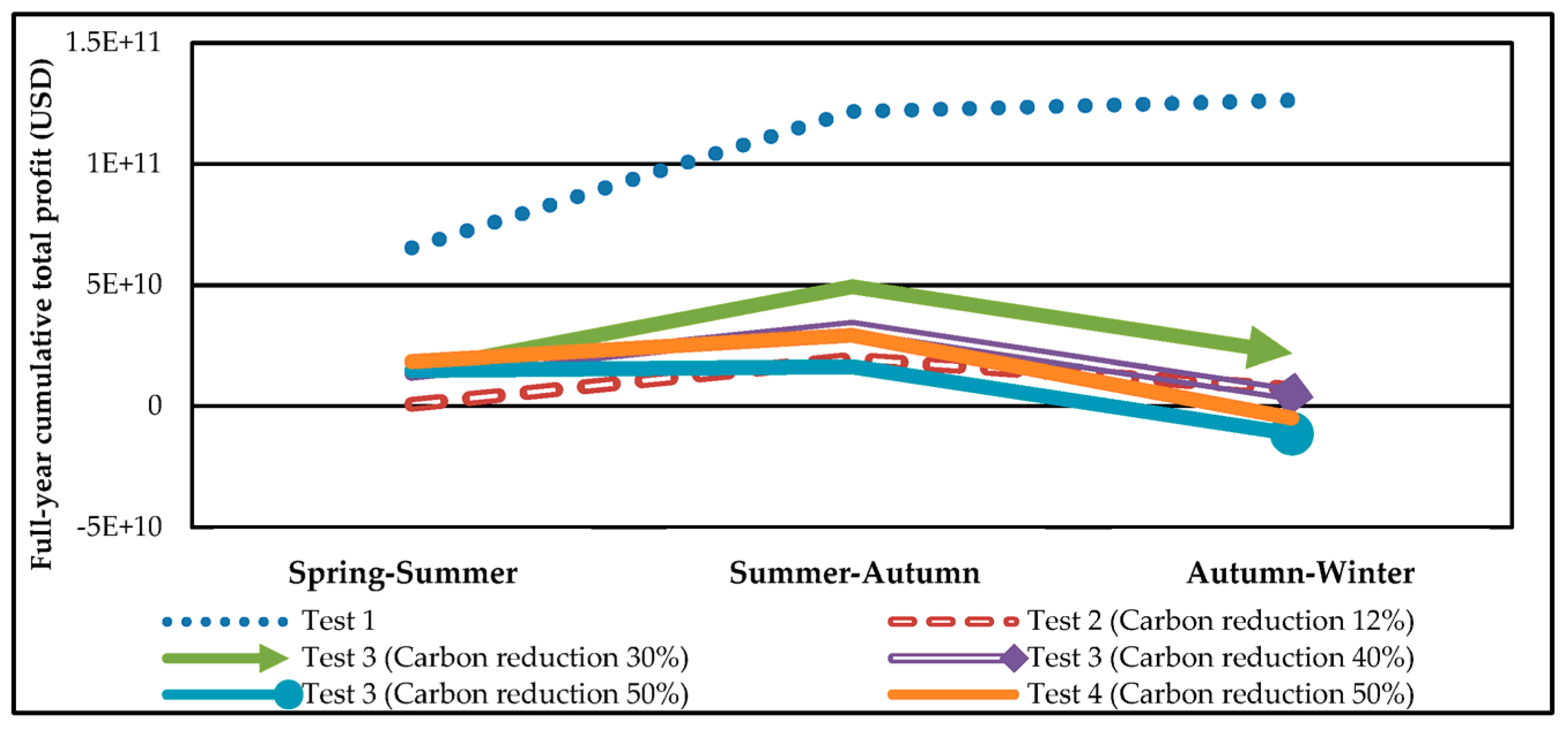
5.3. Case 2: Full-Year Simulation and Testing
6. Conclusions
- (1)
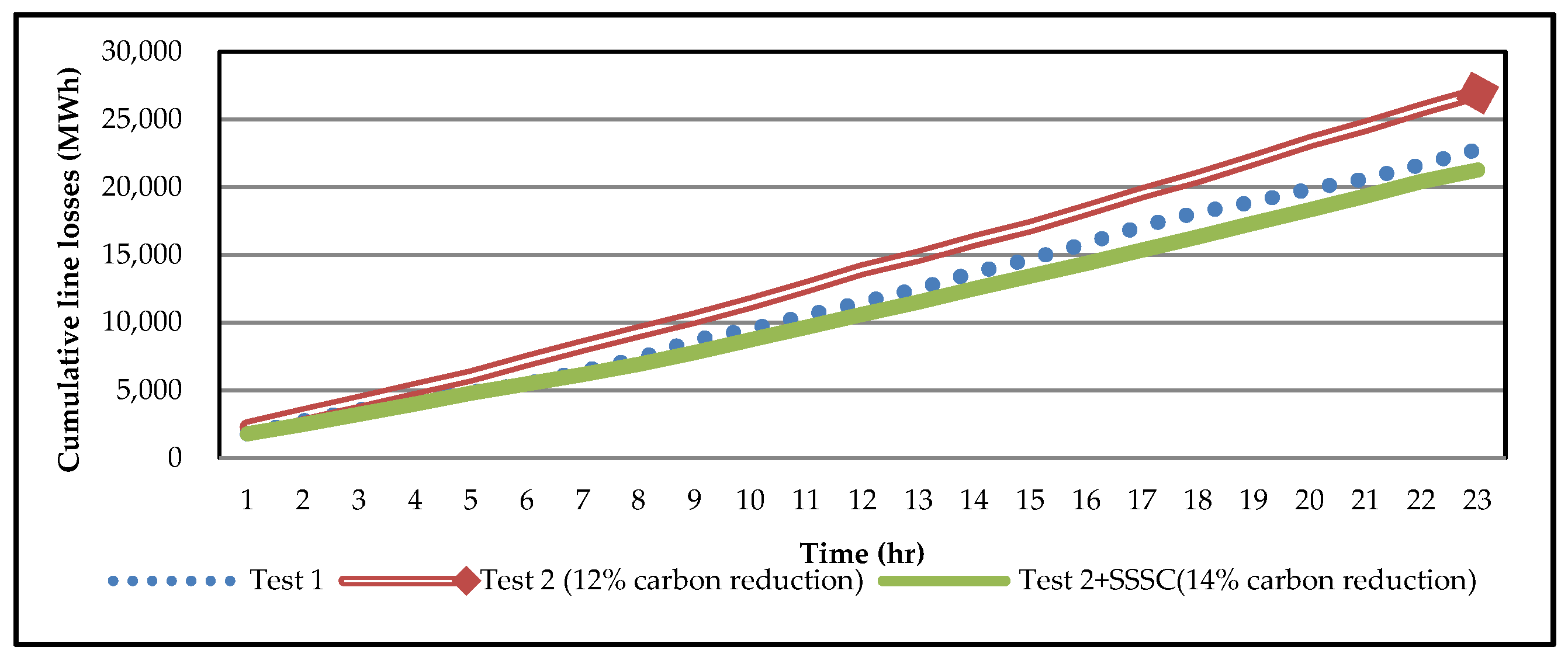
- Enhanced emissions reduction: Test 4 demonstrated a 50% reduction in carbon emissions, with total emissions reduced from 113.8 million tons (Test 3) to 109.9 million tons. This was achieved through the SSSC technology’s ability to reduce transmission losses and improve efficiency.
- (2)
- Improved economic performance: The integration of SSSC-enabled power generators to reduce carbon credit purchases resulted in a TWD 4.118 billion rebate for transmission operators. This collaborative mechanism minimized financial losses while supporting environmental goals.
- (3)
- Increased system profitability: Compared with Test 3, Test 4 showed improved profitability for both sectors. Transmission operator profits increased from TWD 5.26 million to TWD 12.63 million, illustrating the financial benefits of advanced transmission technologies.
- (4)
- Scalable and adaptable framework: The proposed model provides a replicable framework for other regions, offering a balance between economic and environmental objectives. By combining market-based carbon solutions with advanced optimization algorithms, it addresses the challenges in constrained power markets.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency (IEA). Global Energy Review: CO2 Emissions in 2021; IEA: Paris, France, 2021. [Google Scholar]
- International Renewable Energy Agency (IRENA). Renewables Readiness Assessment: 2021; IRENA: Abu Dhabi, United Arab Emirates, 2021. [Google Scholar]
- European Commission. EU Emissions Trading System (EU ETS); European Commission: Brussels, Belgium, 2022. [Google Scholar]
- Liu, Z.-F.; Li, L.-L.; Liu, Y.-W.; Liu, J.-Q.; Li, H.-Y.; Shen, Q. The role of FACTS devices in enhancing power system stability. Energy 2021, 235, 121407. [Google Scholar] [CrossRef]
- Alajrash, B.H.; Salem, M.; Swadi, M.; Senjyu, T.; Kamarol, M.; Motahhir, S. A comprehensive review of FACTS devices in modern power systems: Addressing power quality, optimal placement, and stability with renewable energy penetration. Energy Rep. 2024, 11, 5350–5371. [Google Scholar] [CrossRef]
- Bordignon, M.; Gamannossi degl’Innocenti, D. Third Time’s a Charm? Assessing the Impact of the Third Phase of the EU ETS on CO2 Emissions and Performance. Sustainability 2023, 15, 6394. [Google Scholar] [CrossRef]
- Cao, C.; Han, W.; Liu, Y. Impact of carbon trading market on photovoltaic power generation under grid parity policy. In Proceedings of the 2022 Power System and Green Energy Conference (PSGEC), Shanghai, China, 25–27 August 2022. [Google Scholar]
- Hawkes, A.D. Long-Run Marginal CO2 Emissions Factors in National Electricity Systems. Appl. Energy 2014, 125, 197–205. [Google Scholar] [CrossRef]
- Kung, S.-S.; Li, H.; Kung, C.-C. Prospects of Taiwan’s solar energy development and policy formulation. Heliyon 2024, 10, e23811. [Google Scholar] [CrossRef] [PubMed]
- Sen, S.; Ganguly, S. Opportunities, Barriers and Issues with Renewable Energy Development: A Discussion. Renew. Sustain. Energy Rev. 2017, 69, 1170–1181. [Google Scholar] [CrossRef]
- Rashed, G.I.; Otuo-Acheampong, D.; Mensah, A.A.; Haider, H. Fault Analysis of Power System Transient Stability with Thyristor-Controlled Series Capacitor (TCSC). Electrica 2023, 23, 475–491. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Li, Y.; Chang, D.; Ren, X. Low-Carbon Optimal Dispatch of Integrated Energy System Considering Demand Response under the Tiered Carbon Trading Mechanism. Electr. Power Constr. 2024, 45, 102–114. [Google Scholar]
- Hu, C.; Cai, X.; Zhao, X.; Luo, S.; Lu, H.; Li, X. Carbon trading-based layered operation optimization of the electric–thermal multi-energy-flow coupling system with photothermal power stations. Front. Energy Res. 2023, 11, 1252414. [Google Scholar] [CrossRef]
- Zhang, W.; Ji, C.; Liu, Y.; Hao, Y.; Song, Y.; Cao, Y.; Qi, H. Dynamic interactions of carbon trading, green certificate trading, and electricity markets: Insights from System Dynamics Modeling. PLoS ONE 2024, 19, e0304478. [Google Scholar] [CrossRef]
- Hong, Q.; Cui, L.; Hong, P. The impact of carbon emissions trading on energy efficiency: Evidence from quasi-experiment in China’s carbon emissions trading pilot. Energy Econ. 2022, 110, 106025. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, H.; Wang, D.; Dong, F.; Feng, T.; Xiong, R. Low-Carbon Economic Dispatch of Integrated Energy System Considering Expanding Carbon Emission Flows. IEEE Access 2024, 12, 104755–104769. [Google Scholar] [CrossRef]
- Li, J.; Xiang, Y.; Gu, C.; Sun, W.; Wei, X.; Cheng, S.; Liu, J. Formulation of Locational Marginal Electricity-Carbon Price in Power Systems. CSEE J. Power Energy Syst. 2023, 9, 1968–1972. [Google Scholar]
- Liu, X.; Chen, W.; Han, D. Carbon pricing and its impact on power sector transition. Energy Rep. 2022, 8, 3341–3351. [Google Scholar]
- Ellerman, A.D.; Buchner, B.K.; Carraro, C. The European Union Emissions Trading Scheme: Origins, allocation, and early results. Rev. Environ. Econ. Policy 2016, 10, 89–112. [Google Scholar] [CrossRef]
- Deb, S.; Houssein, E.H.; Said, M. Performance of turbulent flow optimization on economic load dispatch. IEEE Access 2021, 9, 77882–77893. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J.; Bi, L.; Jiang, Y. Does China’s Carbon Trading Pilot Policy Reduce Carbon Emissions? Empirical Analysis from 285 Cities. Int. J. Environ. Res. Public Health 2023, 20, 4421. [Google Scholar] [CrossRef]
- Wang, G.; Ma, H.; Wang, B.; Alharbi, A.M.; Wang, H.; Ma, F. Multi-Objective Optimal Power Flow Calculation Considering Carbon Emission Intensity. Sustainability 2023, 15, 16953. [Google Scholar] [CrossRef]
- Fang, J.; Li, Y.; Zou, H.; Ma, H.; Wang, H. Optimal Scheduling of Microgrids Considering Offshore Wind Power and Carbon Trading. Processes 2024, 12, 1278. [Google Scholar] [CrossRef]
- Khan, T.A.; Ling, S.H. An Improved Gravitational Search Algorithm for Solving an Electromagnetic Design Problem. J. Comput. Electron. 2020, 19, 773–779. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Tian, J.; Yang, G.; Wu, H.; Ha, R.; Wang, P. Low-Carbon Economic Dispatch of Integrated Electricity-Gas Energy System Considering Carbon Capture, Utilization and Storage. IEEE Access 2023, 11, 25077–25089. [Google Scholar] [CrossRef]
- Alghamdi, H.; Guanghua, L.; Riaz, M.; Hafeez, G.; Ullah, S. An Optimal Power Flow Solution for a Power System Integrated with Renewable Generation. AIMS Math. 2024, 9, 6603–6627. [Google Scholar] [CrossRef]
- Nagarajan, K.; Rajagopalan, A.; Bajaj, M.; Sitharthan, R.; Mohammadi, S.A.D.; Blazek, V. Optimizing Dynamic Economic Dispatch through an Enhanced Cheetah-Inspired Algorithm for Integrated Renewable Energy and Demand-Side Management. Sci. Rep. 2024, 14, 3091. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wang, B.; Wei, J. The Robust Optimization of Low-Carbon Economic Dispatching for Regional Integrated Energy Systems Considering Wind and Solar Uncertainty. Electronics 2024, 13, 3480. [Google Scholar] [CrossRef]
- Chou, K.-T.; Liou, H.-M. Carbon Tax in Taiwan: Path Dependence and the High-Carbon Regime. Energies 2023, 16, 513. [Google Scholar] [CrossRef]
- Ma, X.; Pan, Y.; Zhang, M.; Ma, J.; Yang, W. Impact of Carbon Emission Trading and Renewable Energy Development Policy on the Sustainability of Electricity Market: A Stackelberg Game Analysis. Energy Econ. 2024, 129, 107199. [Google Scholar] [CrossRef]
- Tu, C.-S.; Yang, C.-Y.; Tsai, M.-T. An Optimal Phase Arrangement of Distribution Transformers under Risk Assessment. Energies 2020, 13, 5852. [Google Scholar] [CrossRef]
- Gbadeyan, O.J.; Muthivhi, J.; Linganiso, L.Z.; Deenadayalu, N. Decoupling Economic Growth from Carbon Emissions: A Transition toward Low-Carbon Energy Systems—A Critical Review. Clean Technol. 2024, 6, 1076–1113. [Google Scholar] [CrossRef]
- Luo, S.; Li, Q.; Pu, Y.; Xiao, X.; Chen, W.; Liu, S.; Mao, X. A Carbon Trading Approach for Heat-Power-Hydrogen Integrated Energy Systems Based on a Vickrey Auction Strategy. J. Energy Storage 2023, 72, 108613. [Google Scholar] [CrossRef]
- Chang, C.-C.; Chang, K.-C.; Lin, Y.-L. Policies for Reducing the Greenhouse Gas Emissions Generated by the Road Transportation Sector in Taiwan. Energy Policy 2024, 191, 114171. [Google Scholar] [CrossRef]
- Sofia, D.; Giuliano, A.; Gioiella, F.; Barletta, D.; Poletto, M. Modeling of an air quality monitoring network with high space-time resolution. Comput. Aided Chem. Eng. 2018, 43, 193–198. [Google Scholar]
- Taiwan Power Company. Available online: http://www.taipower.com.tw/ (accessed on 1 November 2024).
- Ekinci, S.; Can, Ö.; Ayas, M.Ş.; Izci, D.; Salman, M.; Rashdan, M. Automatic Generation Control of a Hybrid PV-Reheat Thermal Power System Using RIME Algorithm. IEEE Access 2024, 12, 26919–26930. [Google Scholar] [CrossRef]
- European Commission. Energy, Climate Change, Environment. Available online: https://commission.europa.eu/energy-climate-change-environment_en (accessed on 2 November 2024).
- Sood, Y.R.; Padhy, N.P.; Gupta, H.O. Assessment for feasibility and pricing of wheeling transactions under deregulated environment of power industry. Int. J. Electr. Power Energy Syst. 2004, 26, 163–171. [Google Scholar] [CrossRef]









| Algorithm | Profit Min. (TWD) | Profit Avg. (TWD) | Profit Max. (TWD) | Execution Time (s) |
|---|---|---|---|---|
| GA | 15,294,475 | 16,325,800 | 17,357,124 | 61.24 |
| PSO | 16,541,734 | 17,292,533 | 18,043,332 | 37.02 |
| PSO_TVAC | 17,333,620 | 18,453,572 | 19,573,524 | 32.71 |
| ATGA | 19,122,016 | 19,867,601 | 20,613,186 | 36.88 |
| Algorithm | Emissions Min. (TWD) | Emissions Avg. (TWD) | Emissions Max. (TWD) | Execution Time (s) |
|---|---|---|---|---|
| GA | 18,934.18 | 19,043.83 | 19,153.48 | 54.16 |
| PSO | 18,246.75 | 18,339.69 | 18,152.90 | 38.27 |
| PSO_TVAC | 18,049.78 | 18,152.90 | 18,256.02 | 33.74 |
| ATGA | 17,857.36 | 17,961.87 | 18,066.38 | 37.31 |
| Candidate Lines No. | From | To |
|---|---|---|
| 1 | #9 Longtan | #10 Tatan |
| 2 | #14 Emei | #21 Zhongliao |
| 3 | #9 Longtan | #15 Tianlun |
| 4 | #25 Mailiao | #21 Zhongliao |
| 5 | #32 Renwu | #37 Gaogang |
| 6 | #27 Longqi | #30 Xingda |
| 7 | #42 Jiahui | #21 Zhongliao |
| 8 | #23 Fenglin | #40 Taitung |
| ⋮ | ⋮ | ⋮ |
| 52 | #29 Lubei | #31 Xingda |
| Candidate Lines | Profit Min. (TWD) | Profit Avg. (TWD) | Profit Max. (TWD) |
|---|---|---|---|
| No. 1 + No. 2 | 208,433,240.5 | 222,543,792 | 236,654,344.0 |
| No. 3 + No. 4 | 195,582,427.2 | 208,754,136 | 221,925,845.0 |
| No. 5 + No. 6 | 156,682,469.5 | 182,977,425 | 209,272,380.3 |
| No. 7 + No. 8 | 156,682,469.5 | 182,977,425 | 209,272,380.3 |
| Metrics | Test 1 | Test 2 (Carbon Reduction 12%) | Test 3 (Carbon Reduction 30%) | Test 3 (Carbon Reduction 40%) | Test 3 (Carbon Reduction 50%) | Test 4 (Carbon Reduction 50%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Total profit of power generators (TWD) | 271,300,849 | 20,262,449 | 53,709,861 | 6,124,002 | −28,027,552 | −2,595,366 | |||||
| Total revenue of power generators (TWD) | 1,774,734,960 | 1,774,734,960 | 1,774,734,960 | 1,774,734,960 | 1,774,734,960 | 1,774,734,960 | |||||
| Total expenditure of power generators (TWD) | 1,503,434,111 | 1,754,472,511 | 1,720,961,032 | 1,768,546,891 | 1,802,762,512 | 1,777,330,326 | |||||
| Cost of Taipower generation (TWD) | 828,419,472 | 1,035,019,927 | 1,035,019,927 | 1,035,019,927 | 1,035,019,927 | 1,004,719,118 | |||||
| Expenditure of power trading (TWD) | 669,921,495 | 714,191,978 | 714,127,911 | 714,127,911 | 714,127,911 | 717,846,322 | |||||
| Carbon trading expenditure (TWD) | −33,447,412 | 14,138,447 | 48,354,068 | 42,130,030 | |||||||
| Total profit of transmission operators (TWD) | 5,093,144 | 5,260,606 | 5,260,606 | 5,260,606 | 5,260,606 | 12,634,856 | |||||
| Transmission fee (TWD) | 5,093,144 | 5,260,606 | 5,260,606 | 5,260,606 | 5,260,606 | 5,272,011 | |||||
| Refund (TWD) | 7,362,845 | ||||||||||
| Total generation (MWh) | 568,531.71 | 572,179.31 | 572,179.31 | 572,179.31 | 572,179.31 | 567,026.92 | |||||
| Taipower generation (MWh) | 380,351.51 | 371,581.58 | 371,581.58 | 371,581.58 | 371,581.58 | 365,384.69 | |||||
| Power purchased from IPP (MWh) | 188,180.2 | 200,597.73 | 200,597.73 | 200,597.73 | 200,597.73 | 201,642.23 | |||||
| Line losses (MWh) | 22,786.71 | 26,959.03 | 26,959.03 | 26,959.03 | 26,959.03 | 21,281.92 | |||||
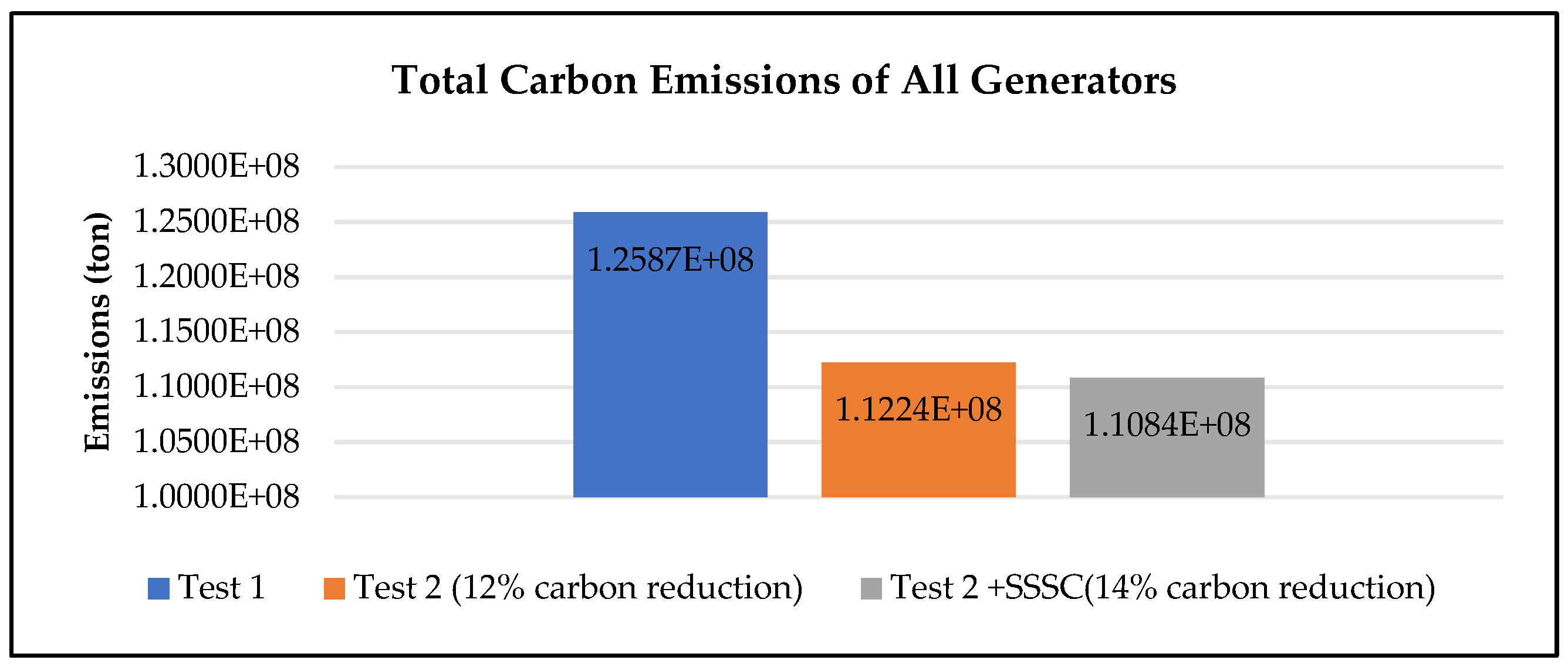
| Total pollution emissions (ton) | 343,073.29 | 300,822.27 | 240,170.89 | 205,920.66 | 171,601.23 | 171,538.56 | |||||
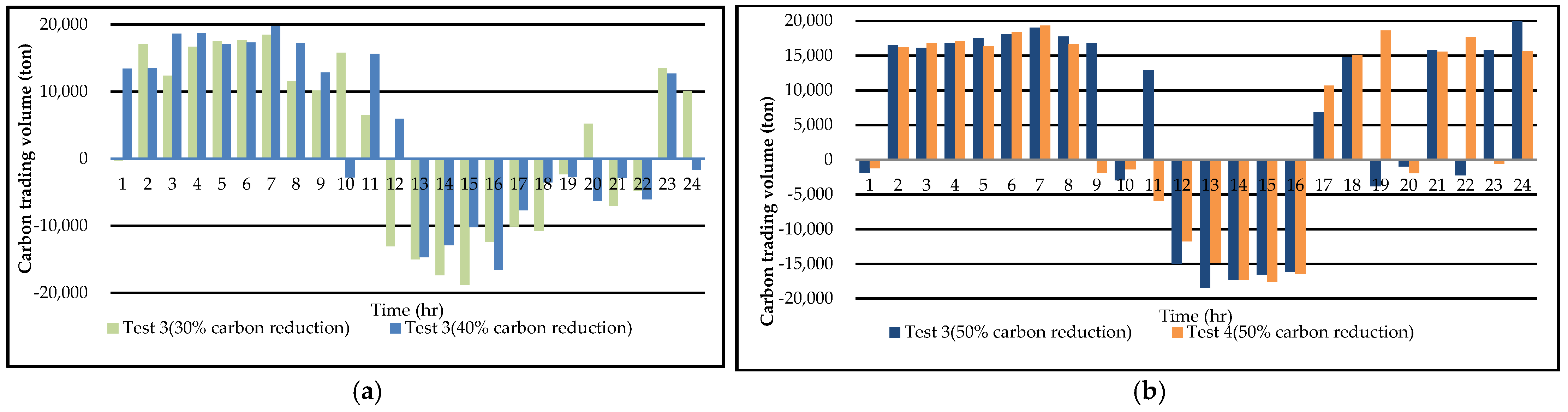
| Total carbon emissions of all generators (ton) | 343,073.29 | 300,822.27 | 300,822.27 | 300,822.27 | 300,822.27 | 294,527.7 | |||||
| Carbon trading volume (ton) | 60,651.38 | 94,901.61 | 129,221.04 | 129,221.04 | 122,989.14 | ||||||
| Coal (MWh) | 144,426.59 | 57,862.95 | 57,862.95 | 57,862.95 | 57,862.95 | 55,092.26 | |||||
| Oil (MWh) | 6781.75 | 13,174.15 | 13,174.15 | 13,174.15 | 13,174.15 | 10,724.63 | |||||
| Gas (MWh) | 43,254.6 | 115,167.45 | 115,167.45 | 115,167.45 | 115,167.45 | 113,680.91 | |||||
| Test Study | Total Carbon Emissions (ton) | Carbon Emission Difference (ton) | Carbon Price (TWD/ton) | Rebate Formula | Rebate Amount (TWD) |
|---|---|---|---|---|---|
| Test 3 (Carbon reduction 50%) | 300,822.27 | – | – | – | – |
| Test 4 (Carbon reduction 50%) | 294,527.7 | 300,822.27–294,527.7 | 5849 | 5849 × (300,822.27 − 294,527.70) × 20% | 7,362,845 |
| Metrics | Test 1 | Test 2 (Carbon Reduction 12%) | Test 3 (Carbon Reduction 30%) | Test 3 (Carbon Reduction 40%) | Test 3 (Carbon Reduction 50%) | Test 4 (Carbon Reduction 50%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Total profit of power generators (109 TWD) | 126.43 | 7.4913 | 21.798 | 5.0132 | −11.396 | −4.9236 | |||||
| Total revenue of power generators (1011 TWD) | 6.3890 | 6.3890 | 6.3890 | 6.3890 | 6.3890 | 6.3890 | |||||
| Total expenditure of power generators (1011 TWD) | 5.1247 | 6.3141 | 6.1711 | 6.3389 | 6.5030 | 6.4383 | |||||
| Cost of Taipower generation (1011 TWD) | 2.8417 | 3.6701 | 3.6701 | 3.6701 | 3.6701 | 3.6056 | |||||
| Expenditure of power trading (1011 TWD) | 2.2646 | 2.6252 | 2.6252 | 2.6252 | 2.6252 | 2.6235 | |||||
| Carbon trading expenditure (109 TWD) | 2.4781 | 18.887 | 14.592 | −14.306 | |||||||
| Total profit of transmission operators (109 TWD) | 1.8429 | 1.8804 | 1.8804 | 1.8804 | 1.8804 | 6.3301 | |||||
| Transmission fee (109 TWD) | 1.8429 | 1.8804 | 1.8804 | 1.8804 | 1.8804 | 1.9111 | |||||
| Refund (109 TWD) | 4.4190 | ||||||||||
| Total generation (108 MWh) | 2.0415 | 2.0609 | 2.0609 | 2.0609 | 2.0609 | 2.0366 | |||||
| Taipower generation (108 MWh) | 1.4054 | 1.3235 | 1.3235 | 1.3235 | 1.3235 | 1.2997 | |||||
| Power purchased from IPP (107 MWh) | 6.3613 | 7.3742 | 7.3742 | 7.3742 | 7.3742 | 7.3693 | |||||
| Line losses (106 MWh) | 7.6810 | 9.6251 | 9.6251 | 9.6251 | 9.6251 | 7.1905 | |||||
| Total pollution emissions (107 ton) | 12.587 | 11.239 | 8.8128 | 7.5552 | 6.3198 | 6.2934 | |||||
| Total carbon emissions of all generators (108 ton) | 1.2587 | 1.1224 | 1.1224 | 1.1224 | 1.1224 | 1.0840 | |||||
| Carbon trading volume (107 ton) | 2.4261 | 3.6837 | 4.9045 | 2.4261 | 4.5464 | ||||||
| Coal (106 MWh) | 56.401 | 12.385 | 12.385 | 12.385 | 12.385 | 9.4874 | |||||
| Oil (106 MWh) | 2.2094 | 6.8665 | 6.8665 | 6.8665 | 6.8665 | 6.0631 | |||||
| Gas (106 MWh) | 15.010 | 47.980 | 47.980 | 47.980 | 47.980 | 47.494 | |||||
| Test Study | Total Carbon Emissions (ton) | Carbon Emission Difference (ton) | Carbon Price (TWD/ton) | Rebate Formula | Rebate Amount (TWD) |
|---|---|---|---|---|---|
| Test 3 (carbon reduction 50%) | 113,801,849.9 | – | – | – | – |
| Test 4 (carbon reduction 50%) | 109,903,518.5 | 113,801,849.9– 109,903,518.5 | 5667 | 5667 × (113,801,849.9 − 109,903,518.5) × 20% | 4,117,992,957 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.-H.; Lian, J.; Liu, T.-W. Advanced Emission Reduction Strategies: Integrating SSSC and Carbon Trading in Power Systems. Processes 2024, 12, 2639. https://doi.org/10.3390/pr12122639
Lu K-H, Lian J, Liu T-W. Advanced Emission Reduction Strategies: Integrating SSSC and Carbon Trading in Power Systems. Processes. 2024; 12(12):2639. https://doi.org/10.3390/pr12122639
Chicago/Turabian StyleLu, Kai-Hung, Junfang Lian, and Ting-Wei Liu. 2024. "Advanced Emission Reduction Strategies: Integrating SSSC and Carbon Trading in Power Systems" Processes 12, no. 12: 2639. https://doi.org/10.3390/pr12122639
APA StyleLu, K.-H., Lian, J., & Liu, T.-W. (2024). Advanced Emission Reduction Strategies: Integrating SSSC and Carbon Trading in Power Systems. Processes, 12(12), 2639. https://doi.org/10.3390/pr12122639






