A Multi-Step Furnace Temperature Prediction Model for Regenerative Aluminum Smelting Based on Reversible Instance Normalization-Convolutional Neural Network-Transformer
Abstract
1. Introduction
2. Regenerative Aluminum Smelting Process Analysis
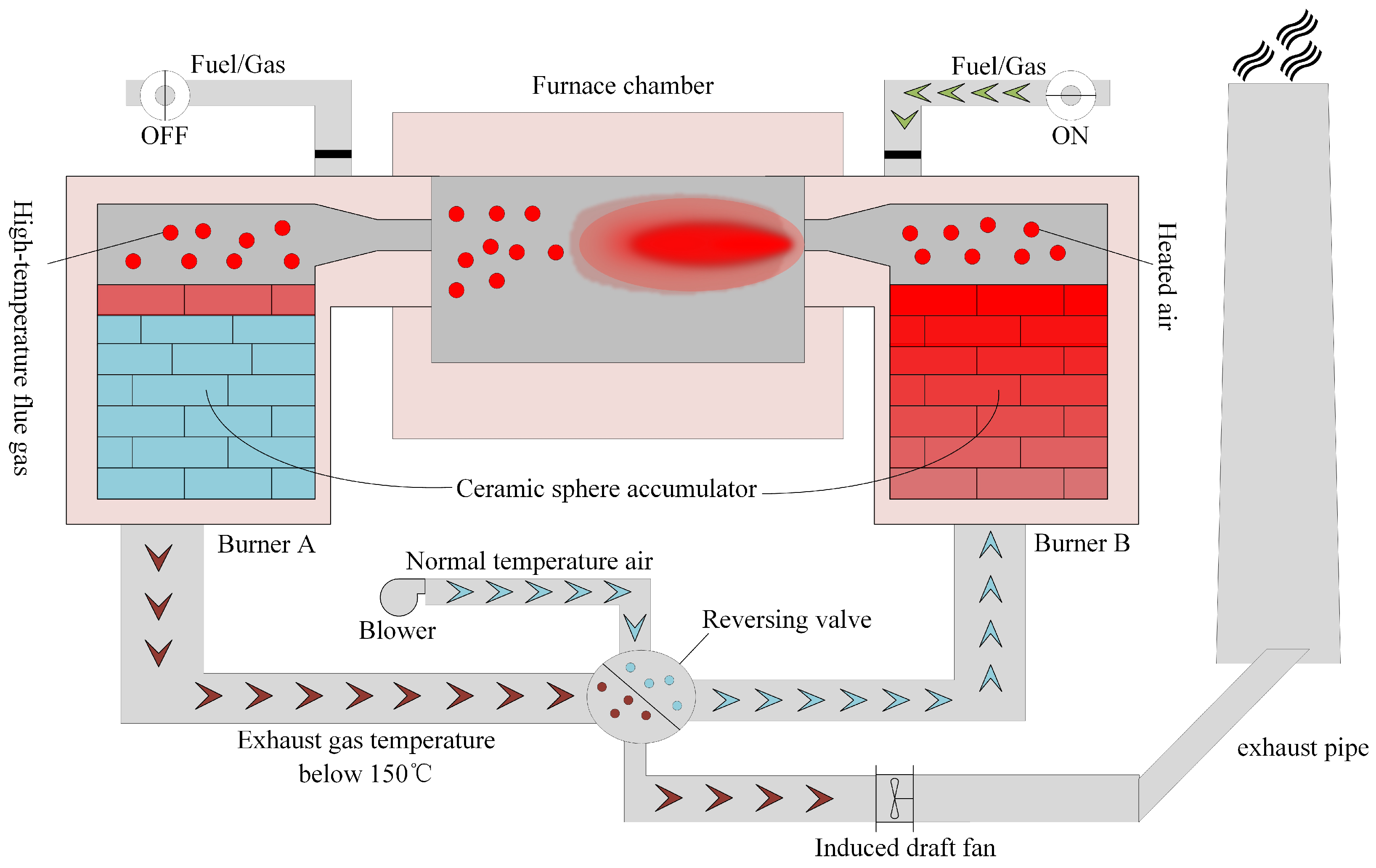
2.1. Structure and Working Principle of Regenerative Aluminum Smelting Furnace
2.2. Analysis of Factors Affecting Furnace Temperature
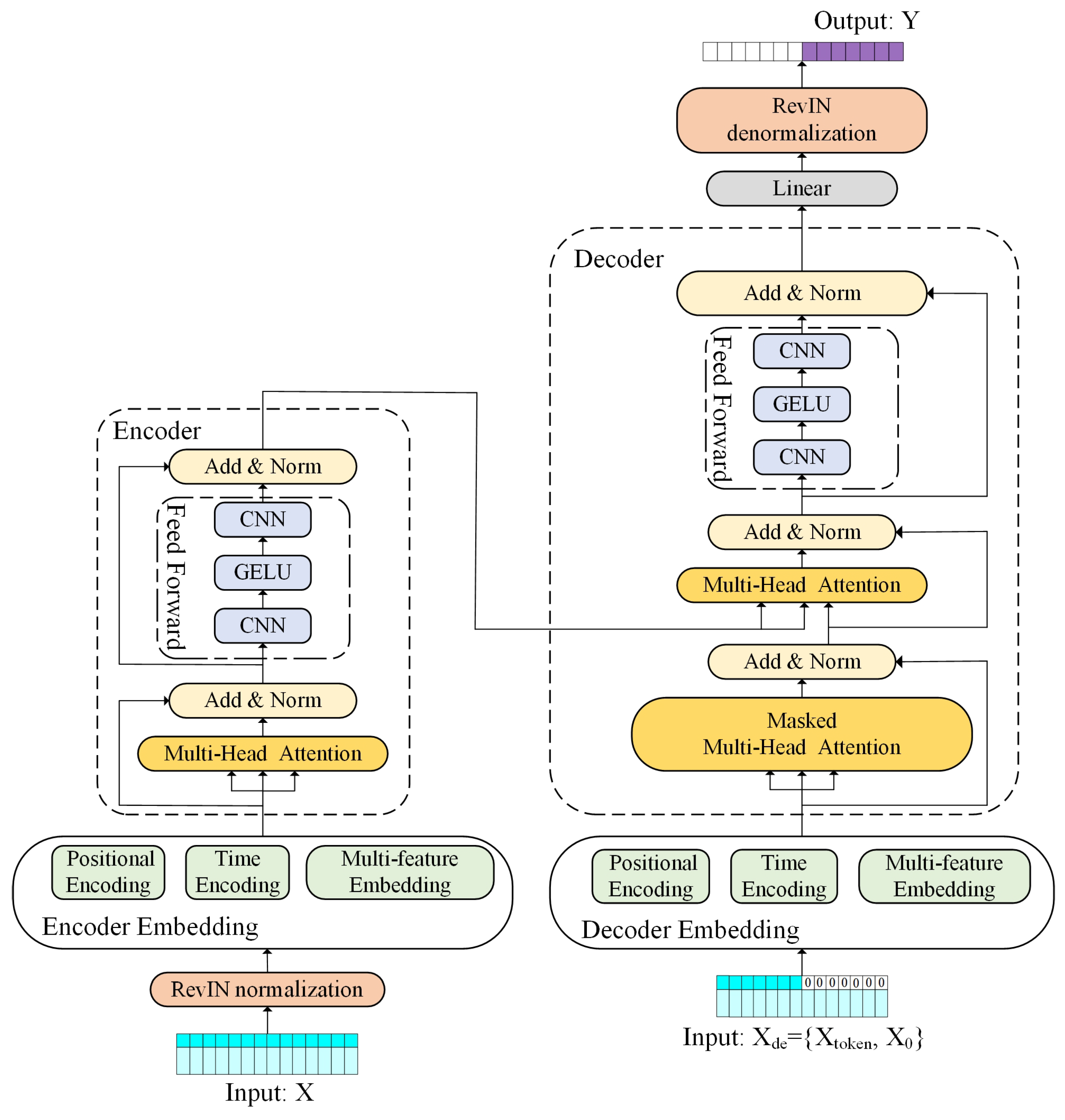
3. The RevIN-CNN-Transformer Prediction Model
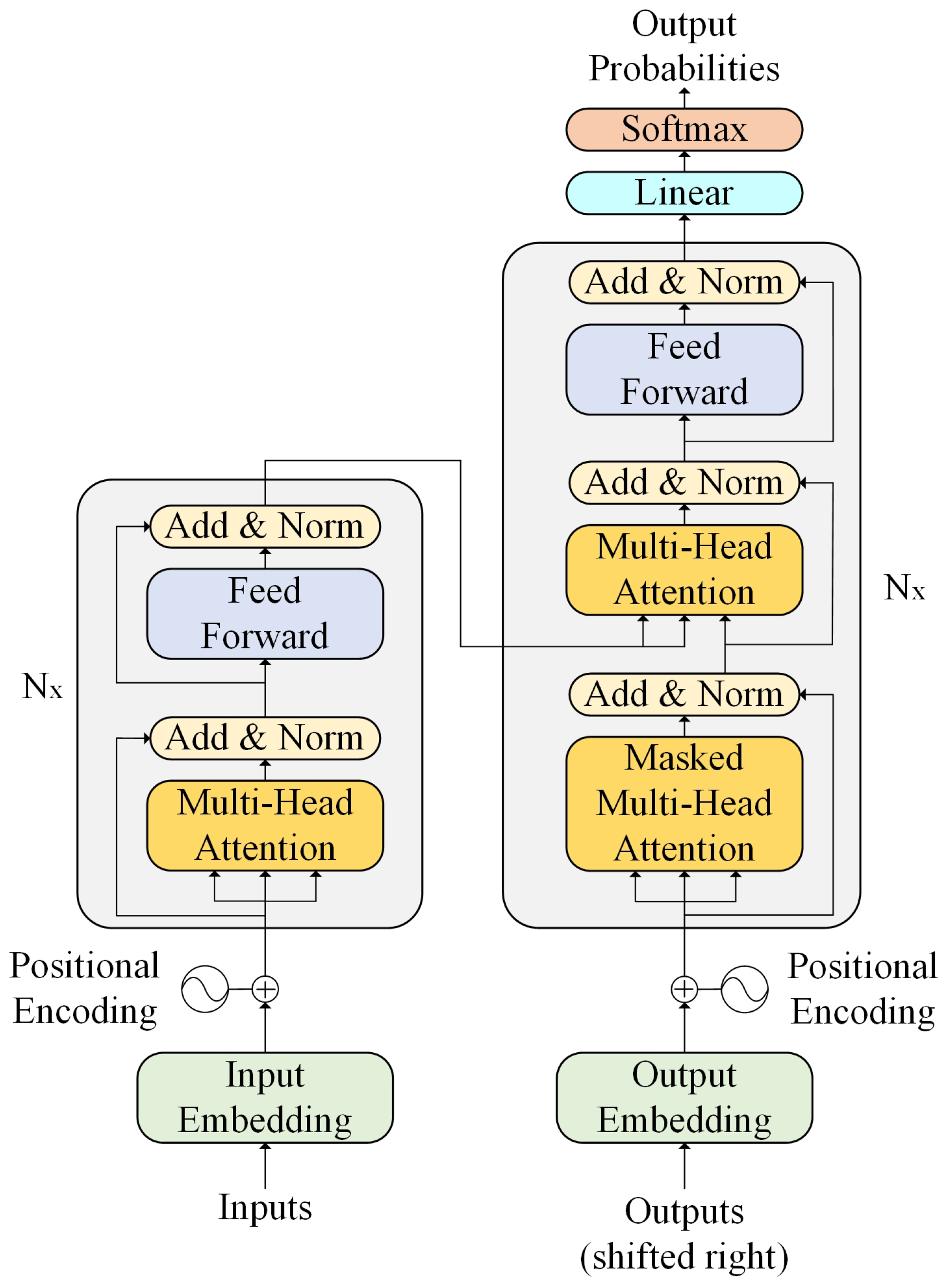
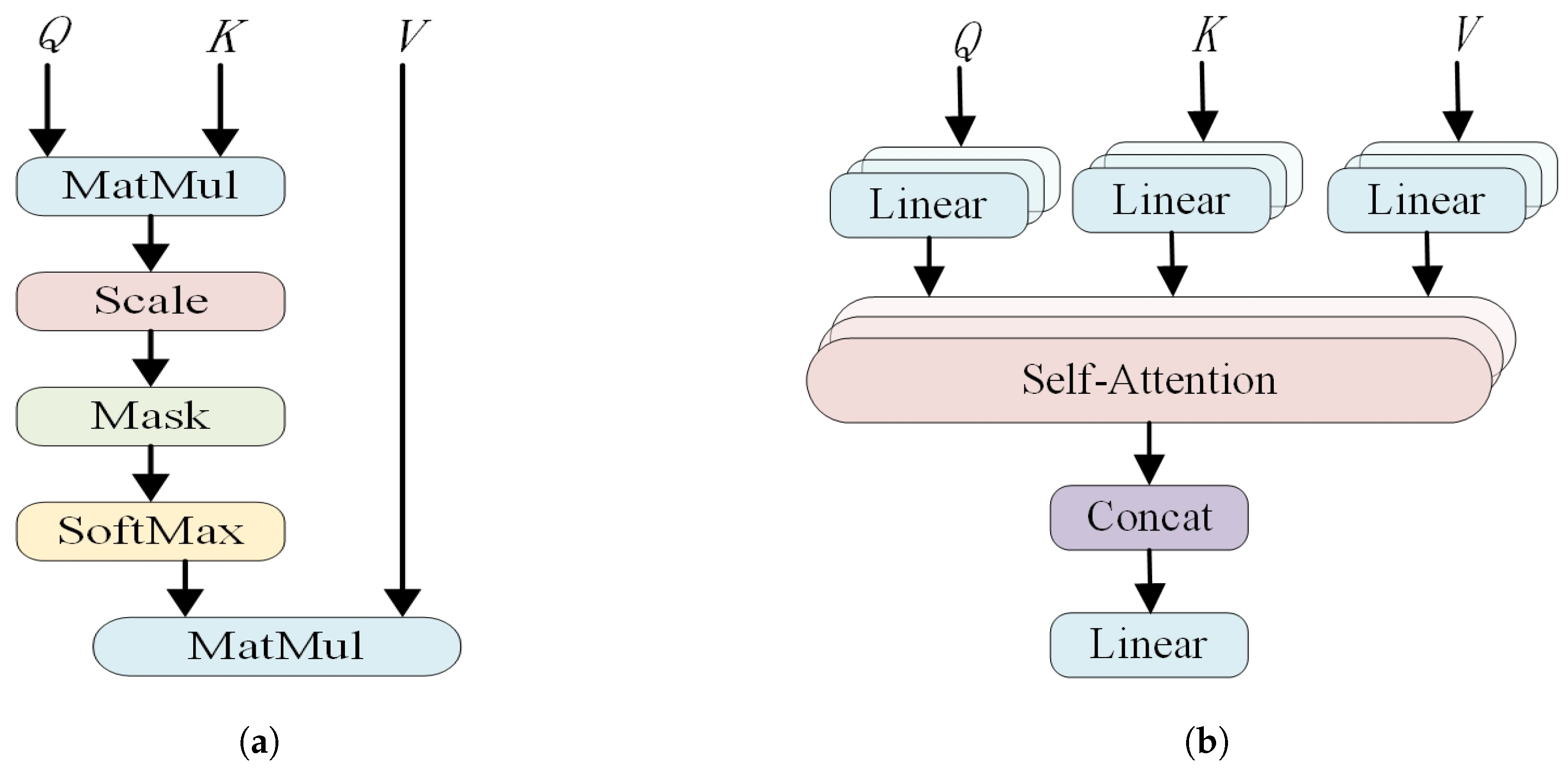
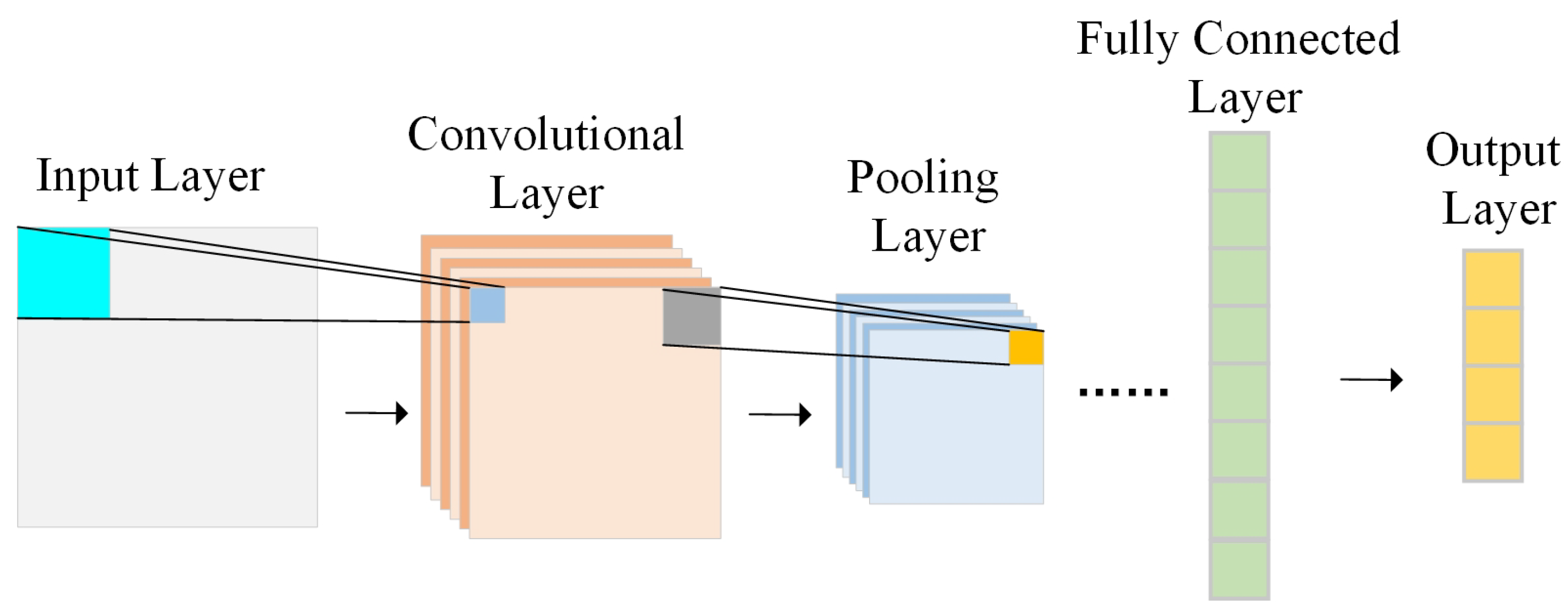
3.1. Time Coding Based CNN-Transformer
3.2. Reversible Instance Normalization
- (a)
- By applying positional encoding to through Equation (4), is obtained, where represents the dimensions of the prediction model.
- (b)
- By applying time coding to through Equation (5), is obtained.
- (c)
- By applying multi-feature embedding to through Equation (6), is obtained.
- (a)
- By applying positional encoding to through Equation (4), is obtained.
- (b)
- By applying time coding to through Equation (5), is obtained.
- (c)
- By applying multi-feature embedding to through Equation (6), is obtained.
4. Industrial Case
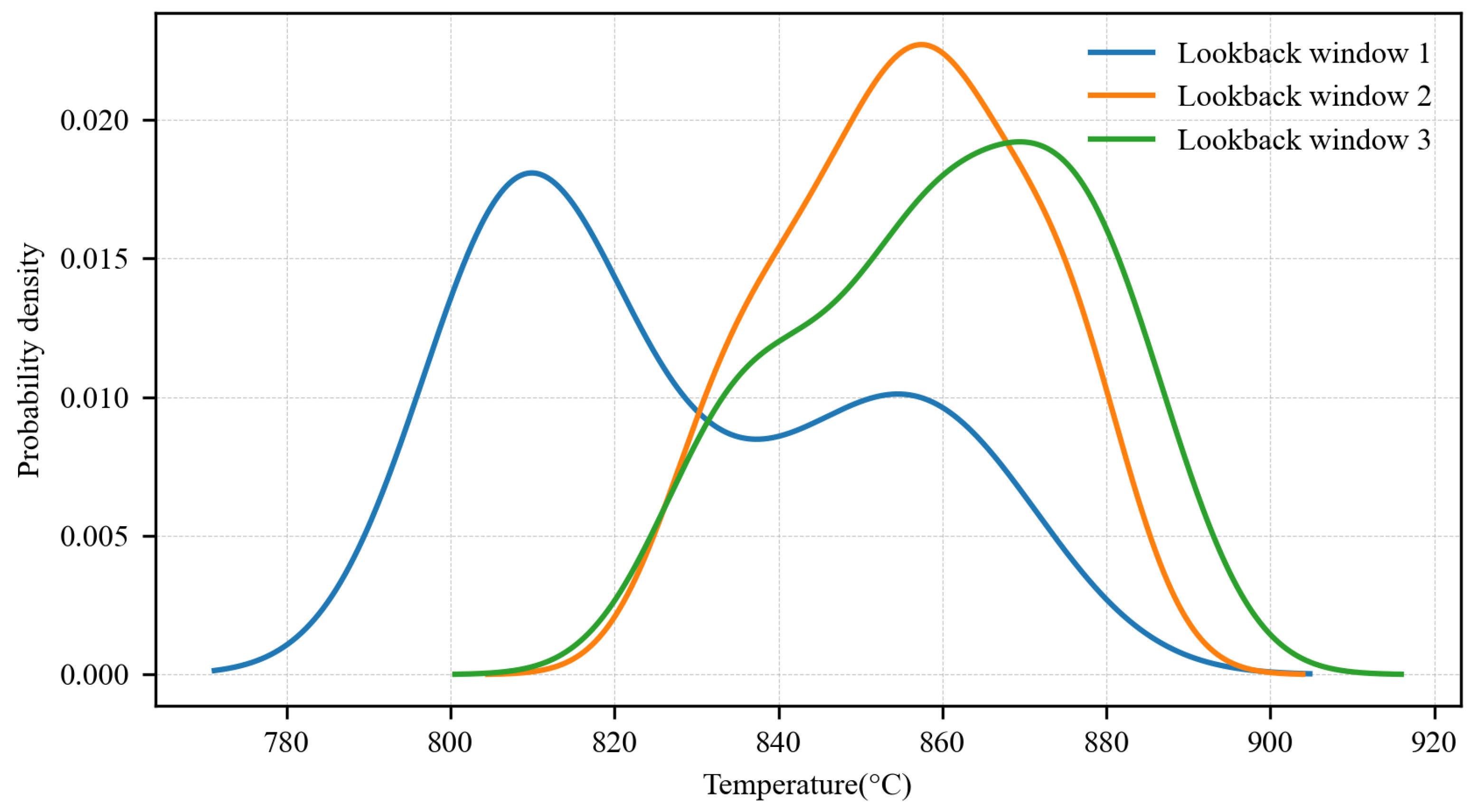
4.1. Dataset and Data Preprocessing
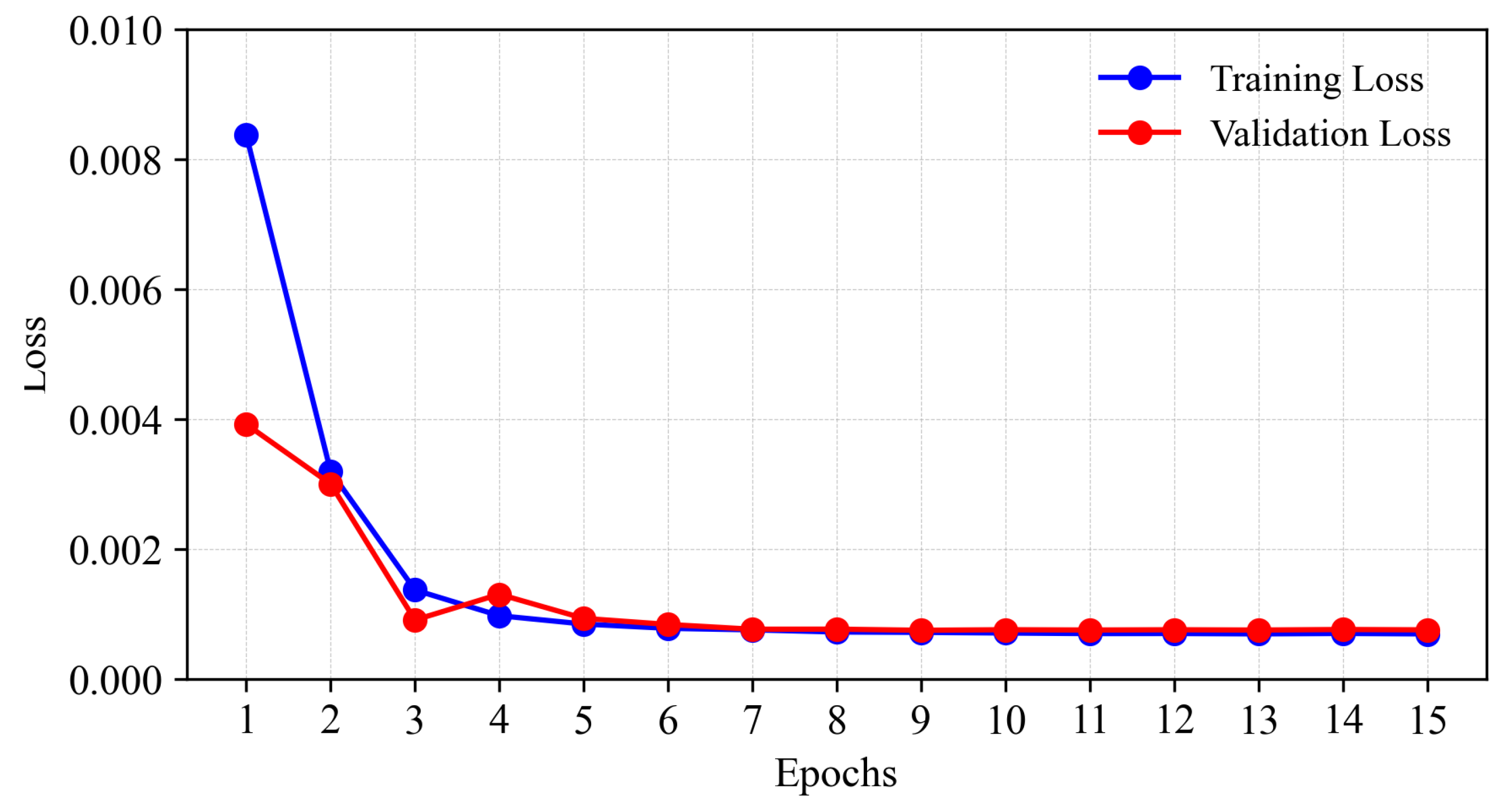
4.2. Results and Analysis
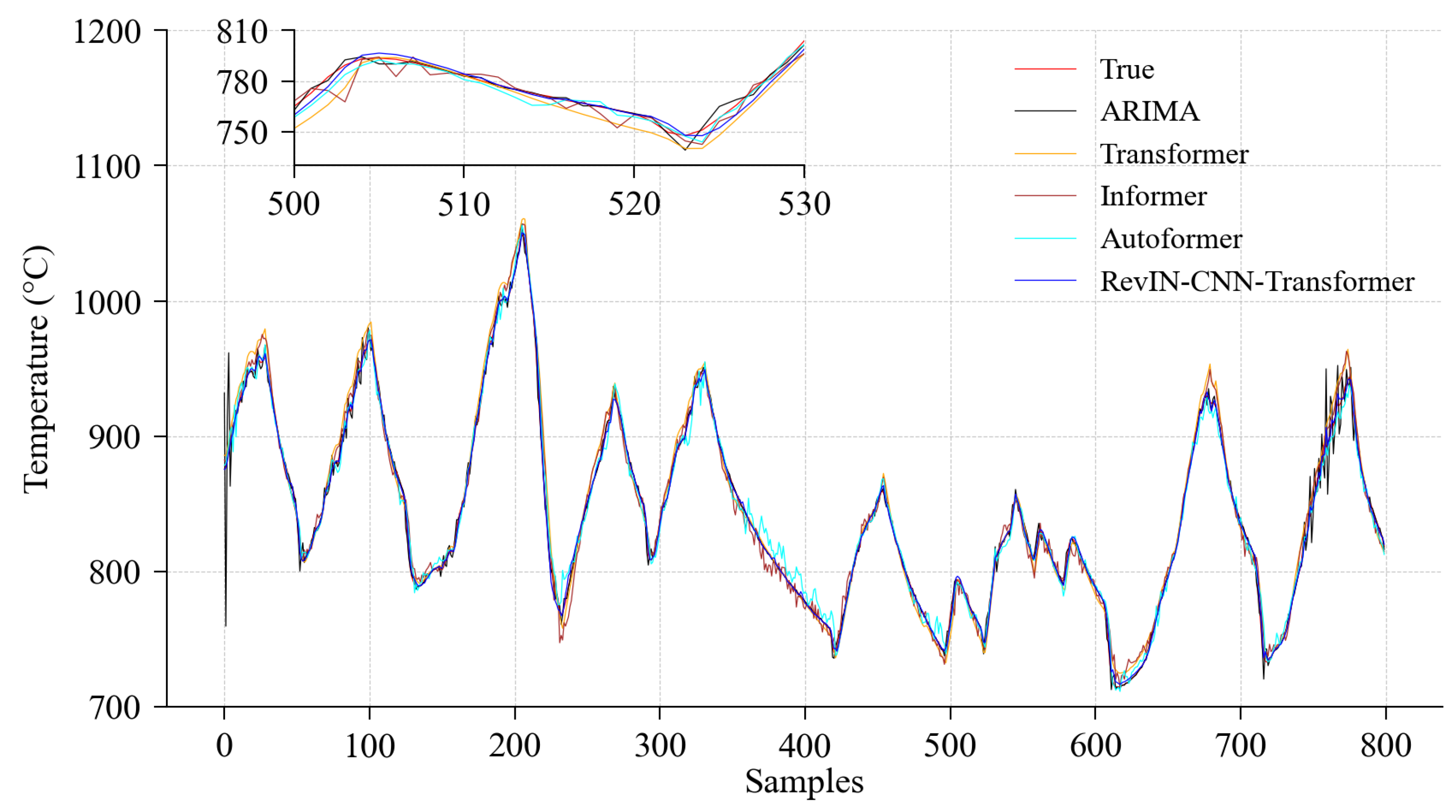
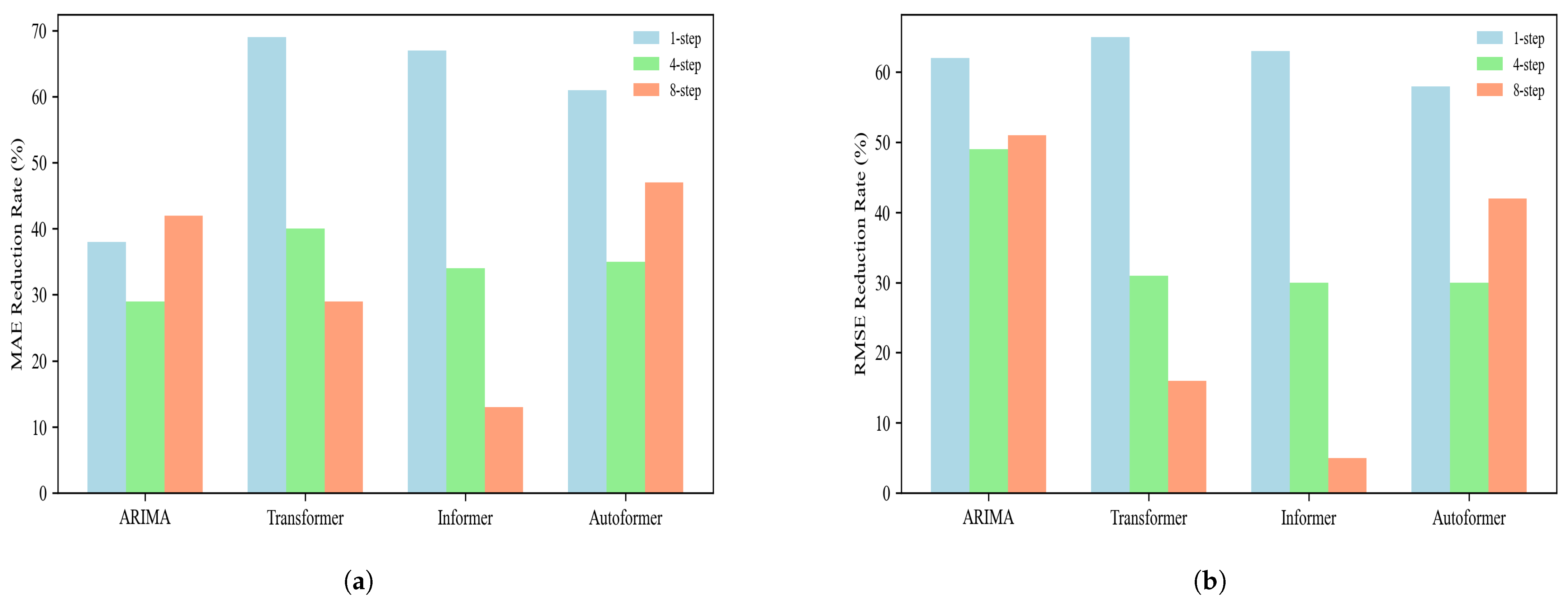
4.2.1. Comparative Experiments
4.2.2. Ablation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qiu, L.; Feng, Y.; Chen, Z.; Li, Y.; Zhang, X. Numerical simulation and optimization of the melting process for the regenerative aluminum melting furnace. Appl. Therm. Eng. 2018, 145, 315–327. [Google Scholar] [CrossRef]
- Bozkurt, Ö.; Kaya, M.F. A CFD Assisted Study: Investigation of the Transformation of A Recuperative Furnace to Regenerative Furnace For Industrial Aluminium Melting. Eng. Mach. Mag. 2021, 62, 245–261. [Google Scholar] [CrossRef]
- Chen, X.; Dai, J.; Luo, Y. Temperature prediction model for a regenerative aluminum smelting furnace by a just-in-time learning-based triple-weighted regularized extreme learning machine. Processes 2022, 10, 1972. [Google Scholar] [CrossRef]
- Yin, L.; Zhou, H. Modal decomposition integrated model for ultra-supercritical coal-fired power plant reheater tube temperature multi-step prediction. Energy 2024, 292, 130521. [Google Scholar] [CrossRef]
- Xue, P.; Jiang, Y.; Zhou, Z.; Chen, X.; Fang, X.; Liu, J. Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms. Energy 2019, 188, 116085. [Google Scholar] [CrossRef]
- Khosravi, K.; Golkarian, A.; Barzegar, R.; Aalami, M.T.; Heddam, S.; Omidvar, E.; Keesstra, S.D.; López-Vicente, M. Multi-step ahead soil temperature forecasting at different depths based on meteorological data: Integrating resampling algorithms and machine learning models. Pedosphere 2023, 33, 479–495. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, Z.; Han, X. Research on multi-step mixed predictiom model of coal gasifier furnace temperature based on machine learning. Proc. J. D Conf. Ser. 2022, 2187, 012070. [Google Scholar] [CrossRef]
- Yan, M.; Bi, H.; Wang, H.; Xu, C.; Chen, L.; Zhang, L.; Chen, S.; Xu, X.; Chen, Q.; Jia, Y.; et al. Advanced soft-sensing techniques for predicting furnace temperature in industrial organic waste gasification. Process. Saf. Environ. Prot. 2024, 190, 1253–1262. [Google Scholar] [CrossRef]
- Dai, J.; Chen, N.; Yuan, X.; Gui, W.; Luo, L. Temperature prediction for roller kiln based on hybrid first-principle model and data-driven MW-DLWKPCR model. ISA Trans. 2020, 98, 403–417. [Google Scholar] [CrossRef]
- Rasul, K.; Seward, C.; Schuster, I.; Vollgraf, R. Autoregressive denoising diffusion models for multivariate probabilistic time series forecasting. In Proceedings of the 38th International Conference on Machine Learning, Online, 18–24 July 2021; Volume 139, pp. 8857–8868. [Google Scholar]
- Magadum, R.B.; Bilagi, S.; Bhandarkar, S.; Patil, A.; Joshi, A. Short-term wind power forecast using time series analysis: Auto-regressive moving-average model (ARMA). In Recent Developments in Electrical and Electronics Engineering: Select Proceedings of ICRDEEE 2022; Springer: Singapore, 2023; Volume 979, pp. 319–341. [Google Scholar]
- Kumar, R.; Kumar, P.; Kumar, Y. Multi-step time series analysis and forecasting strategy using ARIMA and evolutionary algorithms. Int. J. Inf. Technol. 2022, 14, 359–373. [Google Scholar] [CrossRef]
- Lin, W.; Zhang, B.; Li, H.; Lu, R. Multi-step prediction of photovoltaic power based on two-stage decomposition and BILSTM. Neurocomputing 2022, 504, 56–67. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Song, X.; Sun, Q.; Zhang, J.; Liu, Z. Novel method for temperature prediction in rotary kiln process through machine learning and CFD. Powder Technol. 2024, 439, 119649. [Google Scholar] [CrossRef]
- Kong, X.; Du, X.; Xue, G.; Xu, Z. Multi-step short-term solar radiation prediction based on empirical mode decomposition and gated recurrent unit optimized via an attention mechanism. Energy 2023, 282, 128825. [Google Scholar] [CrossRef]
- Hu, Y.; Man, Y.; Ren, J.; Zhou, J.; Zeng, Z. Multi-step carbon emissions forecasting model for industrial process based on a new strategy and machine learning methods. Process. Saf. Environ. Prot. 2024, 187, 1213–1233. [Google Scholar] [CrossRef]
- Aljuaydi, F.; Wiwatanapataphee, B.; Wu, Y.H. Multivariate machine learning-based prediction models of freeway traffic flow under non-recurrent events. Alex. Eng. J. 2023, 65, 151–162. [Google Scholar] [CrossRef]
- Feng, K.; Yang, L.; Su, B.; Feng, W.; Wang, L. An integration model for converter molten steel end temperature prediction based on Bayesian formula. Steel Res. Int. 2022, 93, 2100433. [Google Scholar] [CrossRef]
- Huang, Q.; Lei, S.; Jiang, C.; Xu, C. Furnace temperature prediction of aluminum smelting furnace based on KPCA-ELM. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 1454–1459. [Google Scholar]
- Liu, Q.; Wei, J.; Lei, S.; Huang, Q.; Zhang, M.; Zhou, X. Temperature prediction modeling and control parameter optimization based on data driven. In Proceedings of the 2020 IEEE Fifth International Conference on Data Science in Cyberspace (DSC), Hong Kong, China, 27–30 July 2020; pp. 8–14. [Google Scholar]
- Zhang, Z.; Dai, H.; Jiang, D.; Yu, Y.; Tian, R. Multi-step ahead forecasting of wind vector for multiple wind turbines based on new deep learning model. Energy 2024, 304, 131964. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Dettori, S.; Matino, I.; Colla, V.; Speets, R. A deep-learning-based approach for forecasting off-gas production and consumption in the blast furnace. Neural Comput. Appl. 2022, 34, 911–923. [Google Scholar] [CrossRef]
- Duan, Y.; Dai, J.; Luo, Y.; Chen, G.; Cai, X. A Dynamic Time Warping Based Locally Weighted LSTM Modeling for Temperature Prediction of Recycled Aluminum Smelting. IEEE Access 2023, 11, 36980–36992. [Google Scholar] [CrossRef]
- Chen, C.J.; Chou, F.I.; Chou, J.H. Temperature prediction for reheating furnace by gated recurrent unit approach. IEEE Access 2022, 10, 33362–33369. [Google Scholar] [CrossRef]
- Ji, Z.; Tao, W.; Ren, J. Boiler furnace temperature and oxygen content prediction based on hybrid CNN, biLSTM, and SE-Net models. Appl. Intell. 2024, 54, 8241–8261. [Google Scholar] [CrossRef]
- Ma, S.; Li, Y.; Luo, D.; Song, T. Temperature Prediction of Medium Frequency Furnace Based on Transformer Model. In Proceedings of the International Conference on Neural Computing for Advanced Applications, Jinan, China, 8–10 July 2022; Volume 1637, pp. 463–476. [Google Scholar]
- Han, Y.; Han, L.; Shi, X.; Li, J.; Huang, X.; Hu, X.; Chu, C.; Geng, Z. Novel CNN-based transformer integrating Boruta algorithm for production prediction modeling and energy saving of industrial processes. Expert Syst. Appl. 2024, 255, 124447. [Google Scholar] [CrossRef]
- Tan, P.; Zhu, H.; He, Z.; Jin, Z.; Zhang, C.; Fang, Q.; Chen, G. Multi-step ahead prediction of reheat steam temperature of a 660 MW coal-fired utility boiler using long short-term memory. Front. Energy Res. 2022, 10, 845328. [Google Scholar] [CrossRef]
- Wan, Z.; Kang, Y.; Ou, R.; Xue, S.; Xu, D.; Luo, X. Multi-step time series forecasting on the temperature of lithium-ion batteries. J. Energy Storage 2023, 64, 107092. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Xu, A.; Sun, Q.; Peng, X. A hybrid CNN-Transformer model for ozone concentration prediction. Air Qual. Atmos. Health 2022, 15, 1533–1546. [Google Scholar] [CrossRef]
- Fan, W.; Wang, P.; Wang, D.; Wang, D.; Zhou, Y.; Fu, Y. Dish-ts: A general paradigm for alleviating distribution shift in time series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 7522–7529. [Google Scholar]
- Du, Y.; Wang, J.; Feng, W.; Pan, S.; Qin, T.; Xu, R.; Wang, C. Adarnn: Adaptive learning and forecasting of time series. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Queensland, Australia, 1–5 November 2021; pp. 402–411. [Google Scholar]
- Kim, T.; Kim, J.; Tae, Y.; Park, C.; Choi, J.H.; Choo, J. Reversible instance normalization for accurate time-series forecasting against distribution shift. In Proceedings of the Tenth International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Chen, M.; Peng, H.; Fu, J.; Ling, H. Autoformer: Searching transformers for visual recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 12270–12280. [Google Scholar]



| Variable | Unit | Description |
|---|---|---|
| Gas flow rate | Nm3/h | Volume flow rate of the gas entering the furnace |
| Combustion air flow rate | Nm3/h | Volume flow rate of air entering the furnace for combustion |
| Combustion air pressure differential | Pa | The pressure differential between the air before entering the furnace and the pressure in the furnace |
| Combustion air valve opening | % | Valve opening for adjusting the air flow rate |
| Exhaust temperature | °C | Temperature of the flue gas upon exit from the furnace |
| Index | Auxiliary Variable |
|---|---|
| 1 | 12 # Gas flow rate |
| 2 | 34 # Gas flow rate |
| 3 | 12 # Combustion air flow rate |
| 4 | 34 # Combustion air flow rate |
| 5 | 12 # Combustion air pressure differential |
| 6 | 34 # Combustion air pressure differential |
| 7 | 12 # Combustion air valve opening |
| 8 | 34 # Combustion air valve opening |
| 9 | B3 # Exhaust temperature |
| Sensor Type | Measurement Range | Accuracy | Response Time |
|---|---|---|---|
| Flow Meter | 0–15 m3/h | ±1% | 0.2 s |
| Differential Pressure Gauge | 0–10,000 Pa | ±0.5% | 0.1 s |
| Valve Position Indicator | 0–100% | ±1% | 0.1 s |
| Thermocouple | 0–1200 °C | ±0.5% | 0.5 s |
| Learning Rate | MAE | RMSE | R2 |
|---|---|---|---|
| 0.01 | 44.612 | 52.854 | 0.415 |
| 0.001 | 2.487 | 3.570 | 0.997 |
| 0.0001 | 1.984 | 2.865 | 0.998 |
| 0.00001 | 3.041 | 4.188 | 0.996 |
| Prediction Step | Evaluation Metrics | ARIMA | Transformer | Informer | Autoformer | RevIN-CNN-Transformer |
|---|---|---|---|---|---|---|
| 1-step | MAE | 3.181 | 6.312 | 6.061 | 5.107 | 1.984 |
| RMSE | 7.592 | 8.283 | 7.810 | 6.889 | 2.865 | |
| R2 | 0.988 | 0.986 | 0.987 | 0.990 | 0.998 | |
| 4-step | MAE | 8.063 | 9.648 | 8.691 | 8.897 | 5.755 |
| RMSE | 16.249 | 12.126 | 11.849 | 11.892 | 8.351 | |
| R2 | 0.949 | 0.969 | 0.971 | 0.970 | 0.985 | |
| 8-step | MAE | 18.376 | 14.872 | 12.129 | 19.943 | 10.600 |
| RMSE | 32.735 | 19.112 | 16.766 | 27.491 | 15.998 | |
| R2 | 0.810 | 0.924 | 0.941 | 0.842 | 0.946 |
| Prediction Model | MAE | RMSE | R2 |
|---|---|---|---|
| CNN-Transformer | 8.118 | 10.681 | 0.976 |
| RevIN-Transformer | 6.856 | 9.743 | 0.980 |
| RevIN-CNN-Transformer (without time coding) | 6.317 | 9.268 | 0.982 |
| RevIN-CNN-Transformer | 5.755 | 8.351 | 0.985 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Ling, P.; Shi, H.; Liu, H. A Multi-Step Furnace Temperature Prediction Model for Regenerative Aluminum Smelting Based on Reversible Instance Normalization-Convolutional Neural Network-Transformer. Processes 2024, 12, 2438. https://doi.org/10.3390/pr12112438
Dai J, Ling P, Shi H, Liu H. A Multi-Step Furnace Temperature Prediction Model for Regenerative Aluminum Smelting Based on Reversible Instance Normalization-Convolutional Neural Network-Transformer. Processes. 2024; 12(11):2438. https://doi.org/10.3390/pr12112438
Chicago/Turabian StyleDai, Jiayang, Peirun Ling, Haofan Shi, and Hangbin Liu. 2024. "A Multi-Step Furnace Temperature Prediction Model for Regenerative Aluminum Smelting Based on Reversible Instance Normalization-Convolutional Neural Network-Transformer" Processes 12, no. 11: 2438. https://doi.org/10.3390/pr12112438
APA StyleDai, J., Ling, P., Shi, H., & Liu, H. (2024). A Multi-Step Furnace Temperature Prediction Model for Regenerative Aluminum Smelting Based on Reversible Instance Normalization-Convolutional Neural Network-Transformer. Processes, 12(11), 2438. https://doi.org/10.3390/pr12112438









