Research on Oil–Water Two-Phase Flow Patterns in Wellbore of Heavy Oil Wells with Medium-High Water Cut
Abstract
1. Introduction
2. Mathematical Model for Heavy Oil–Water Two-Phase Flow
2.1. Multiphase Flow Calculation Model
2.2. Turbulence Model
3. Solution of Mathematical Models for Heavy Oil–Water Two Phase Flow
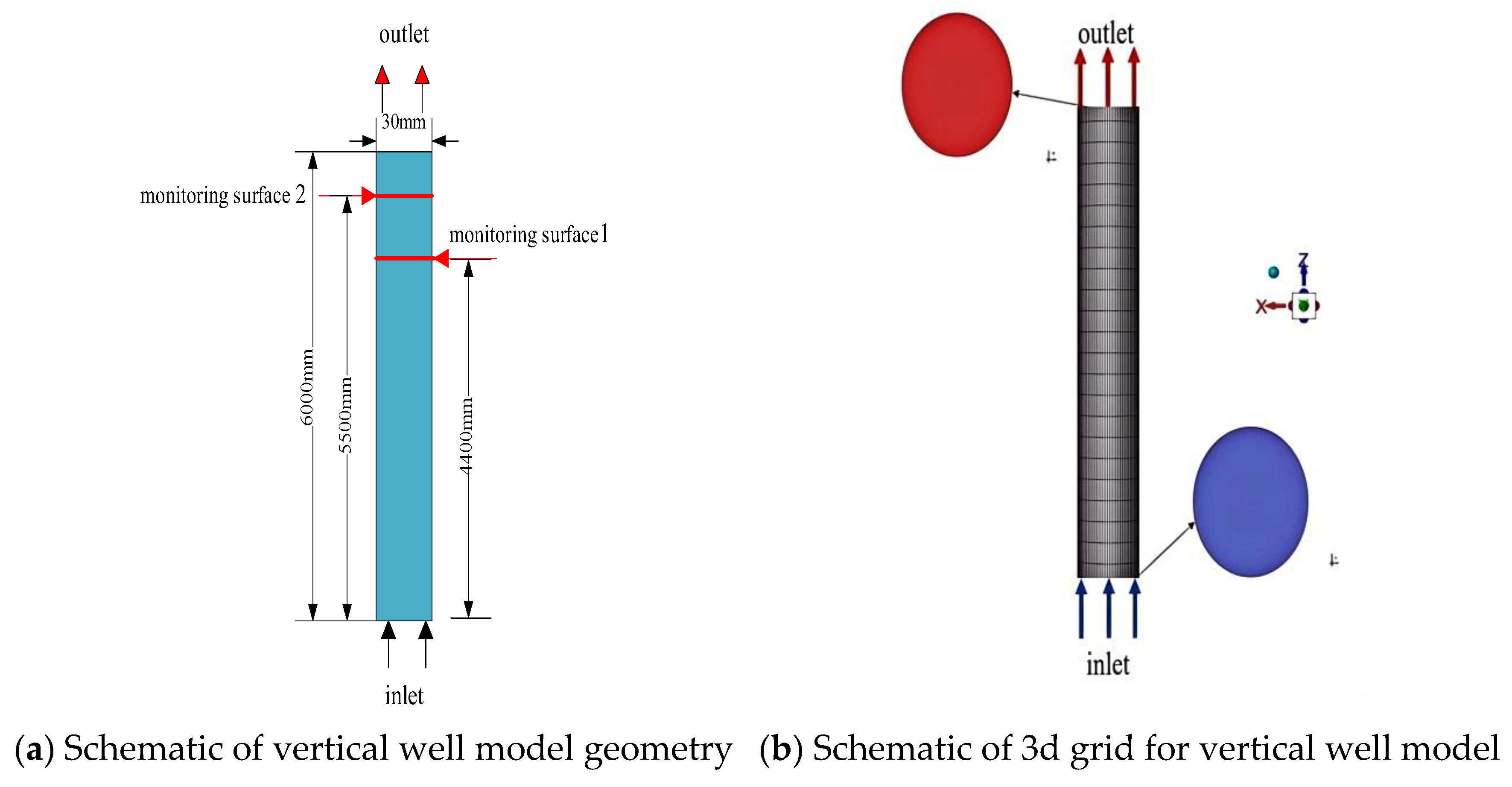
3.1. Geometric Model and Grid Generation
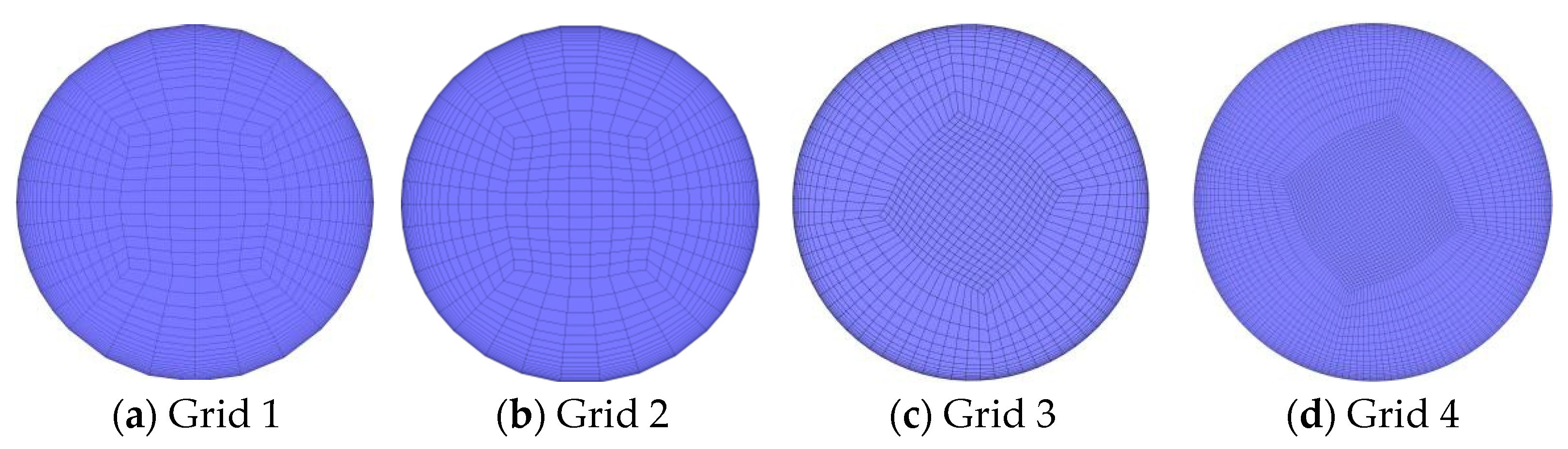
3.2. Boundary Conditions and Grid Independence Verification
3.3. Model Validation
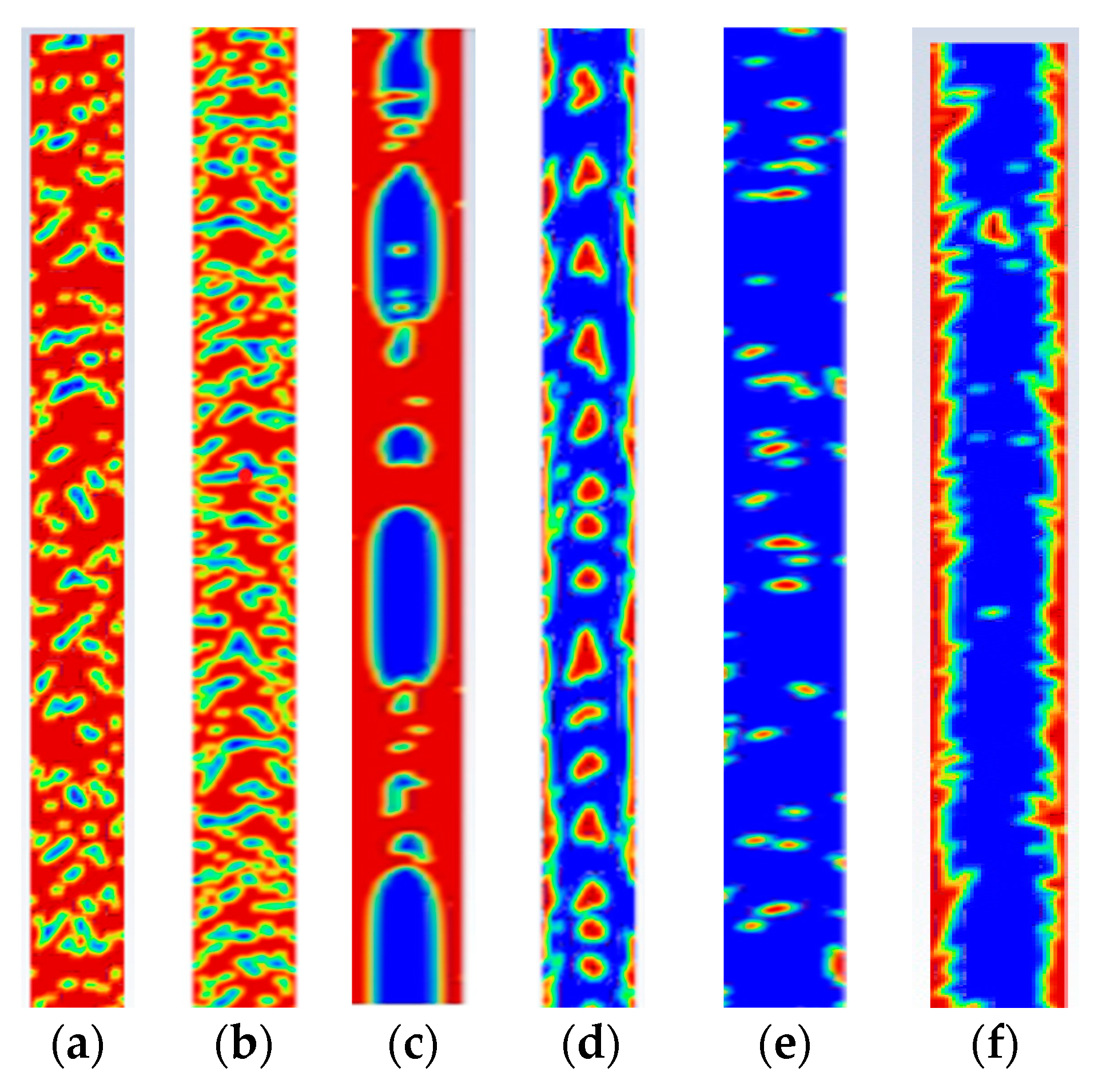
4. Research on the Identification of Flow Patterns in Heavy Oil–Water Two-Phase Flow
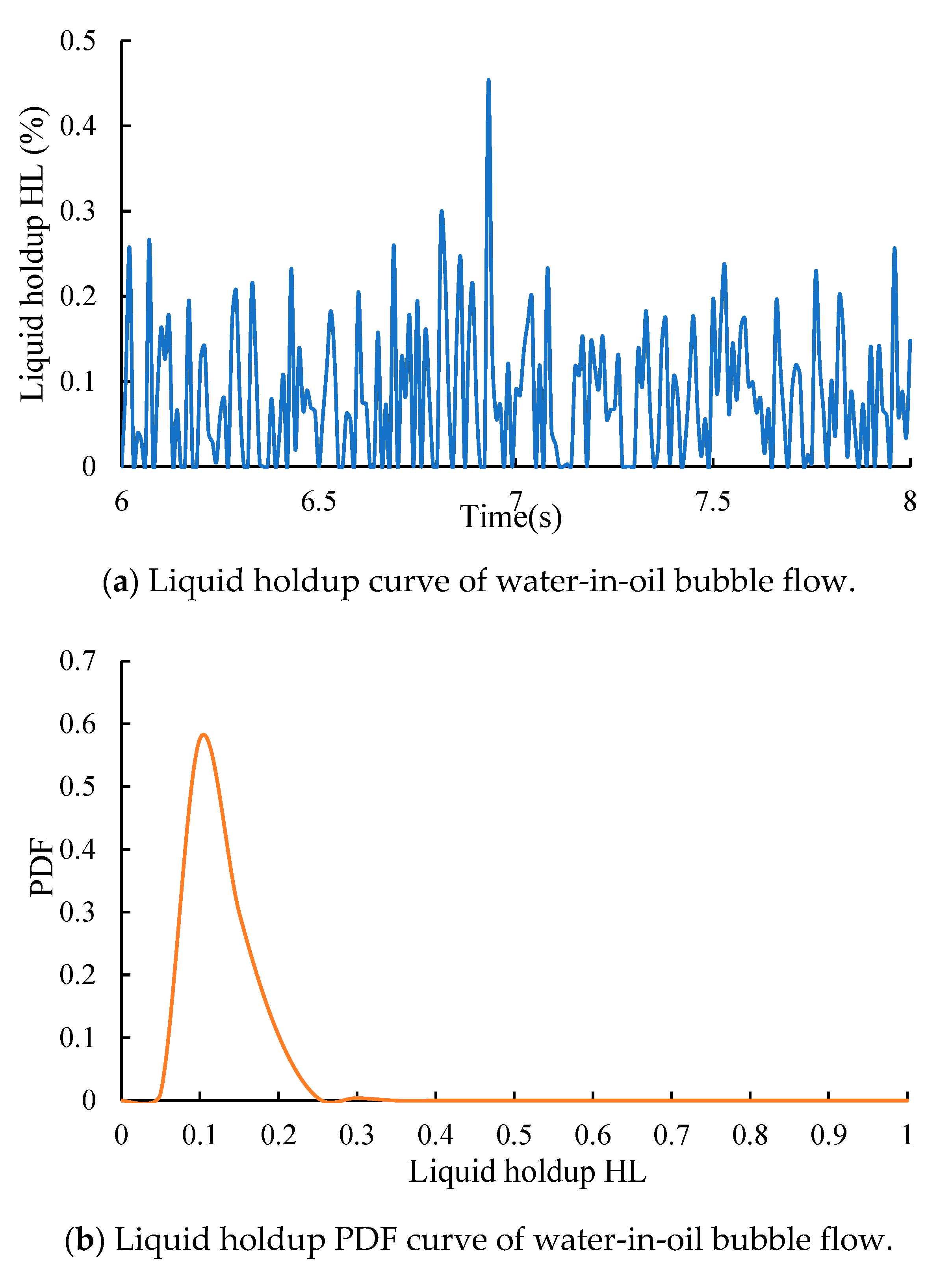
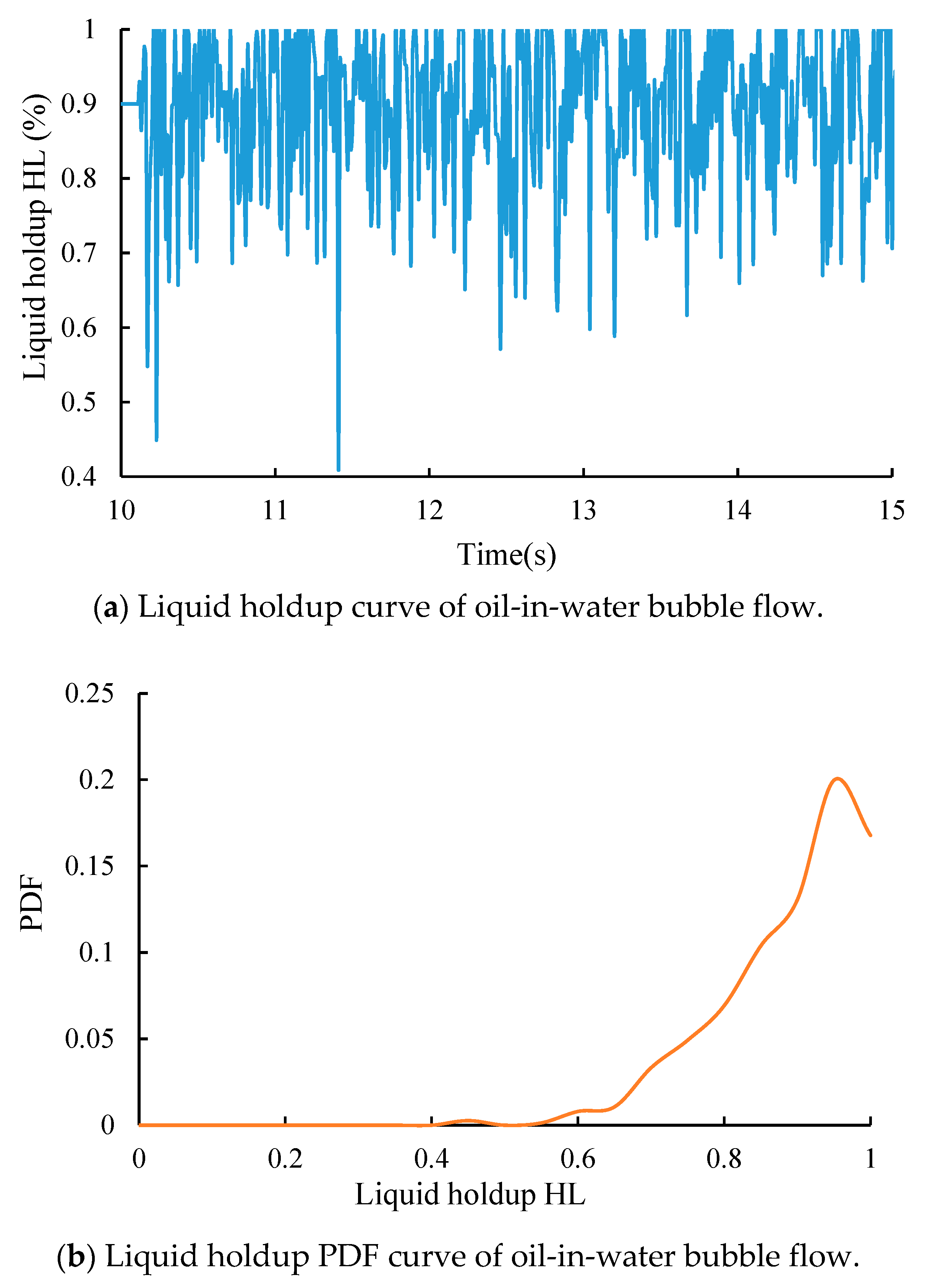
4.1. Water-in-Oil Bubble Flow (B W/O)
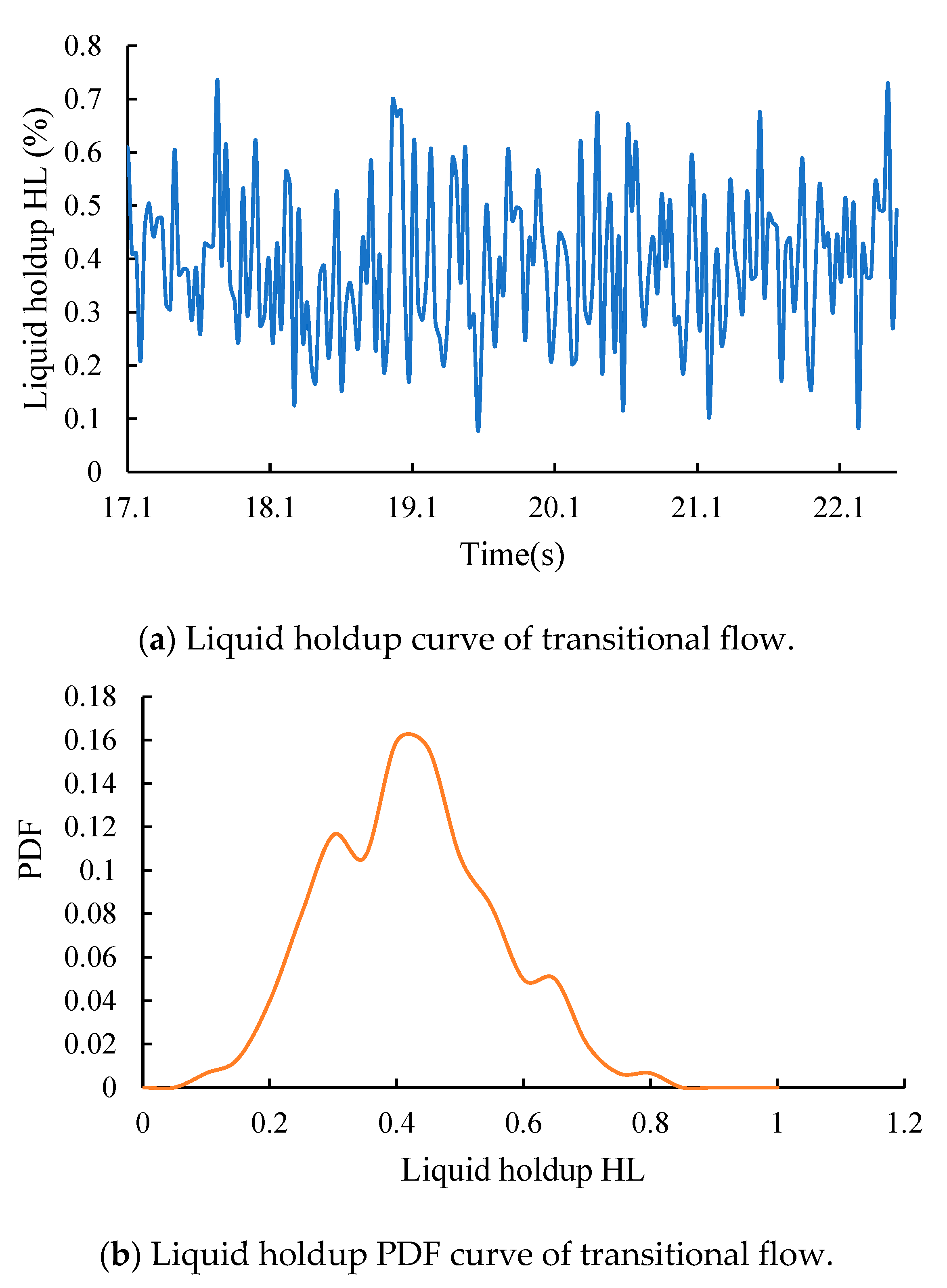
4.2. Transitional Flow (TF)
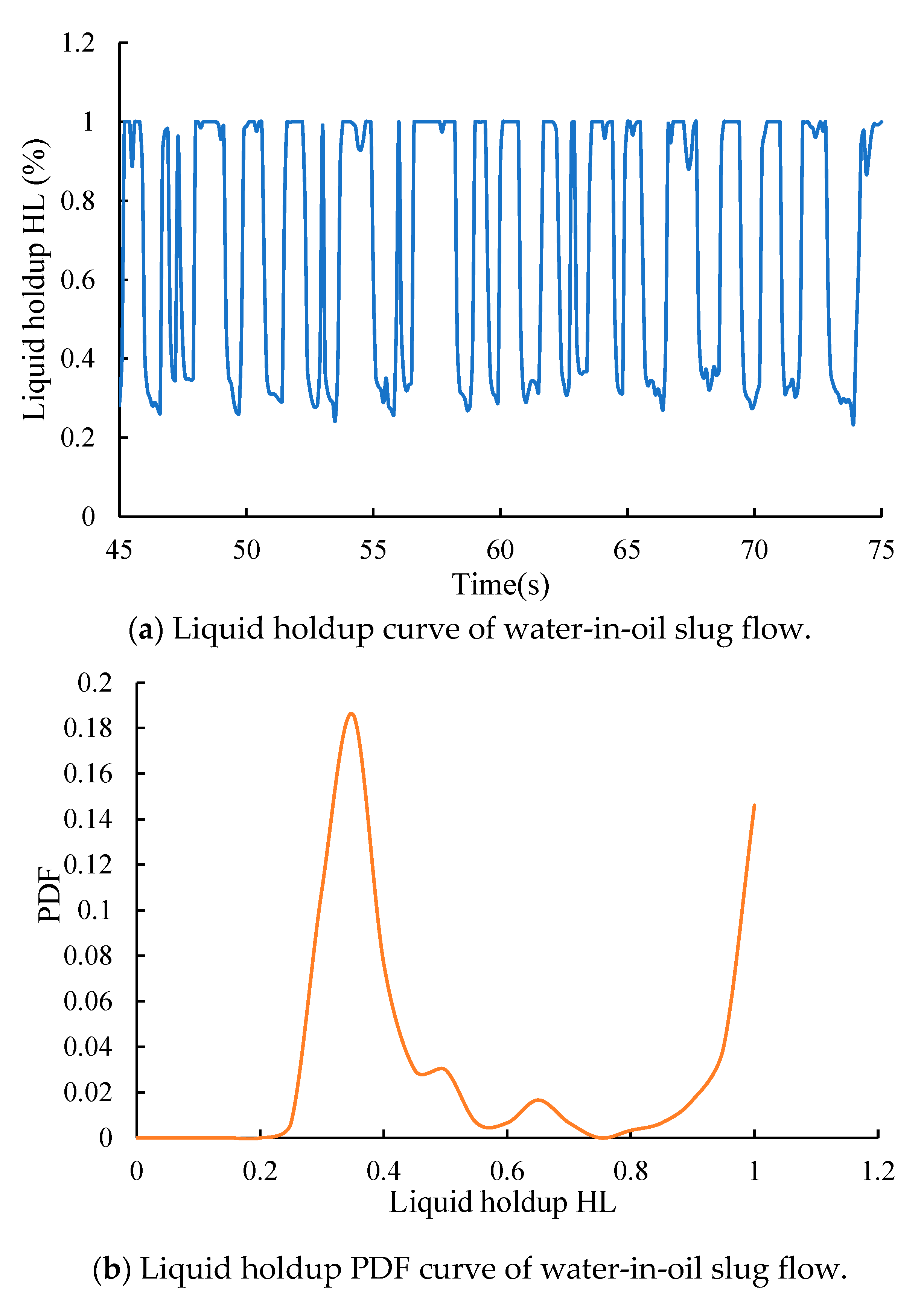
4.3. Water-in-Oil Slug Flow (S W/O)
4.4. Oil-in-Water Bubble Flow (B O/W)
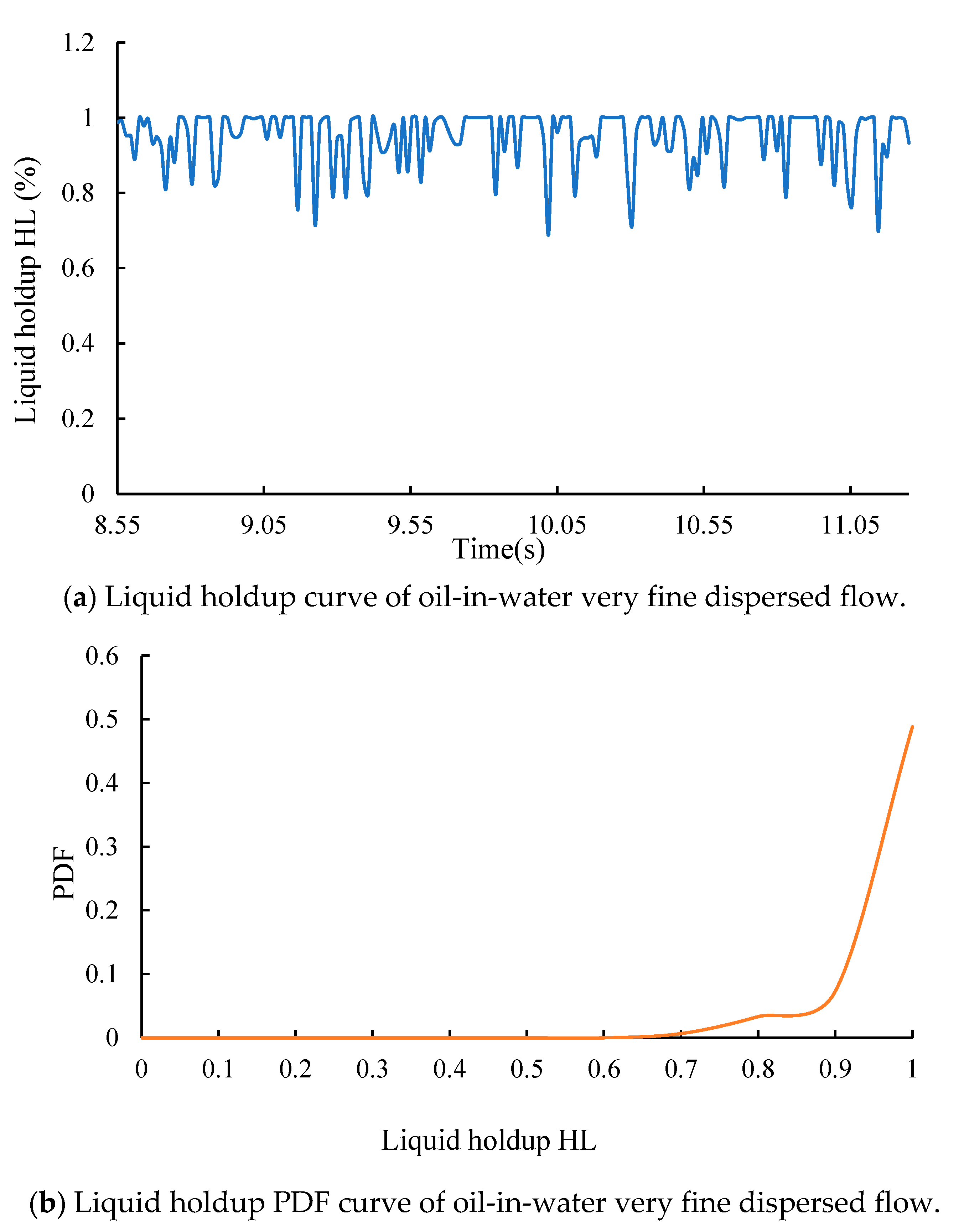
4.5. Oil-in-Water Very Fine Dispersed Flow (VFD O/W)
4.6. Water-in-Oil Core-Annular Flow (Core-Annular W/O)
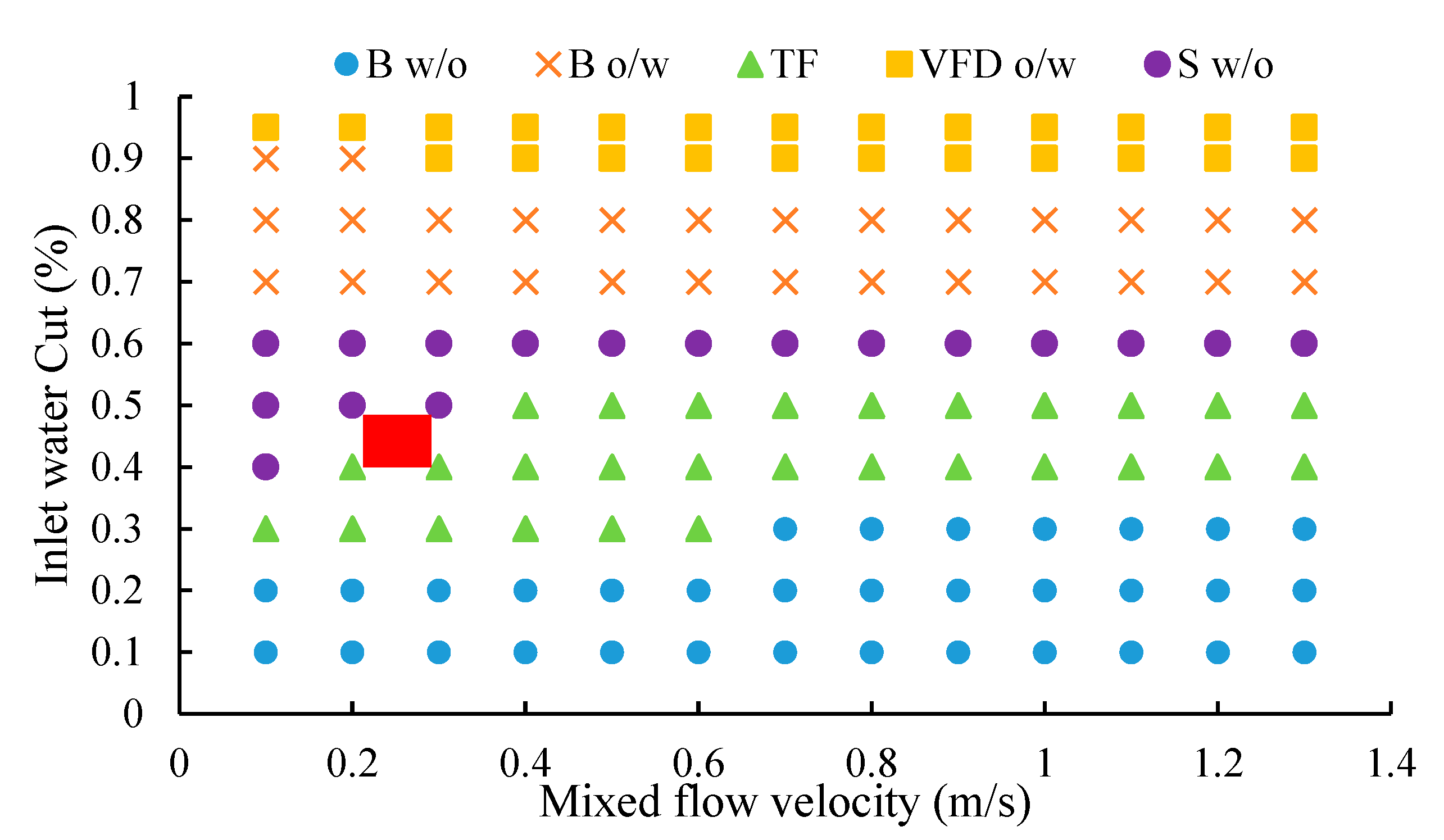
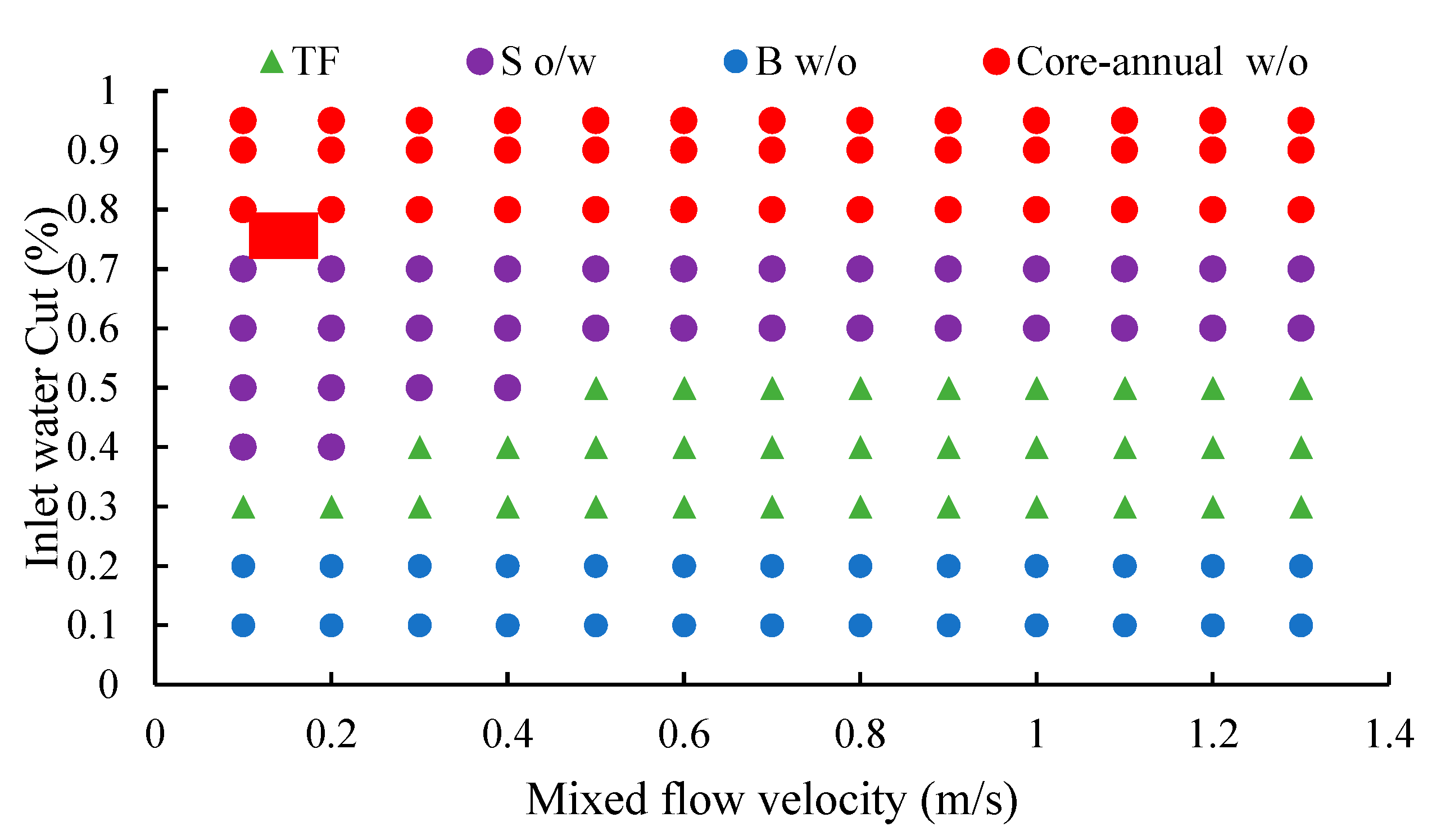
5. Study on the Flow Patterns of Heavy Oil–Water Two-Phase Flow
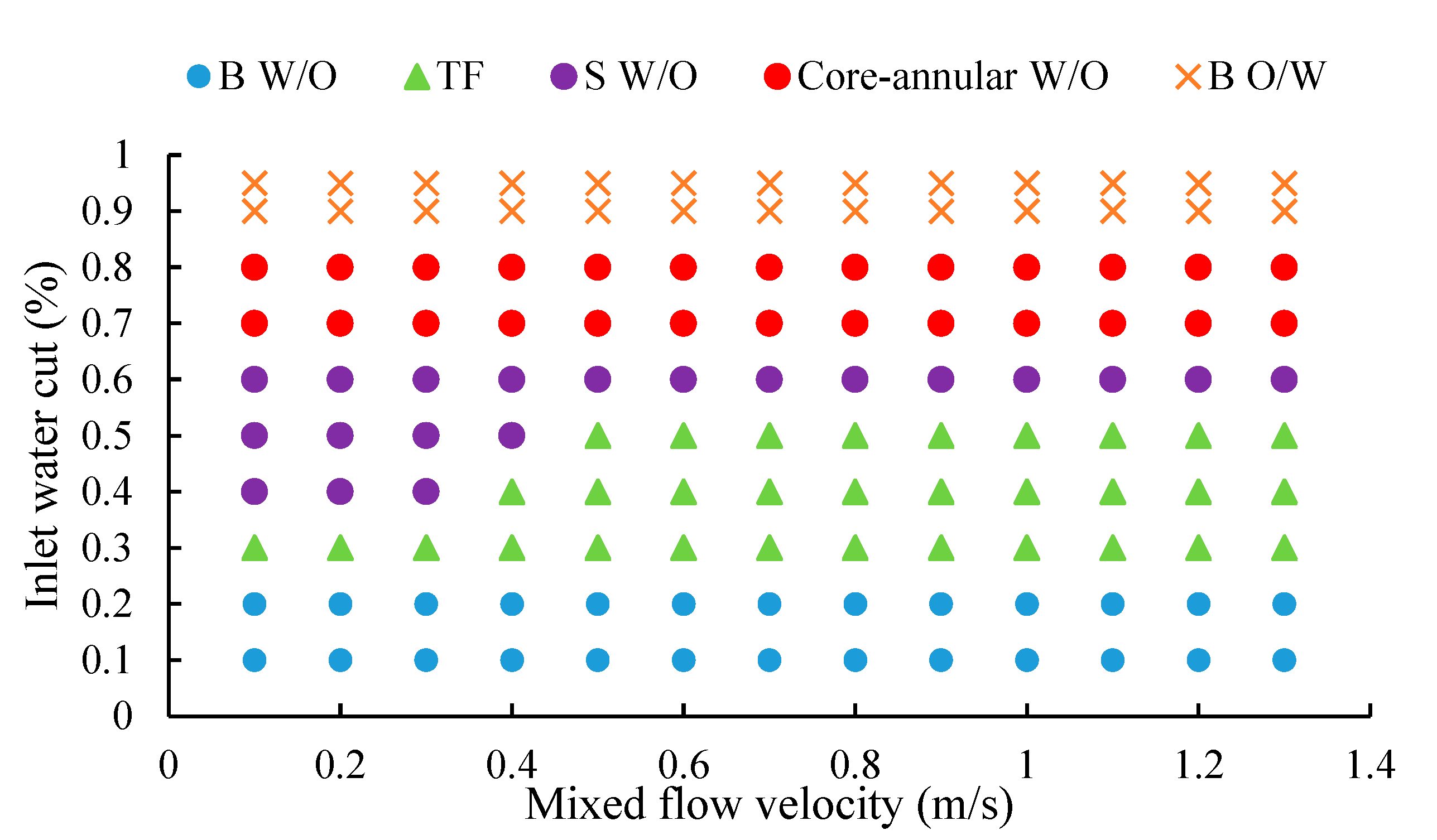
5.1. Development of Flow Pattern Maps
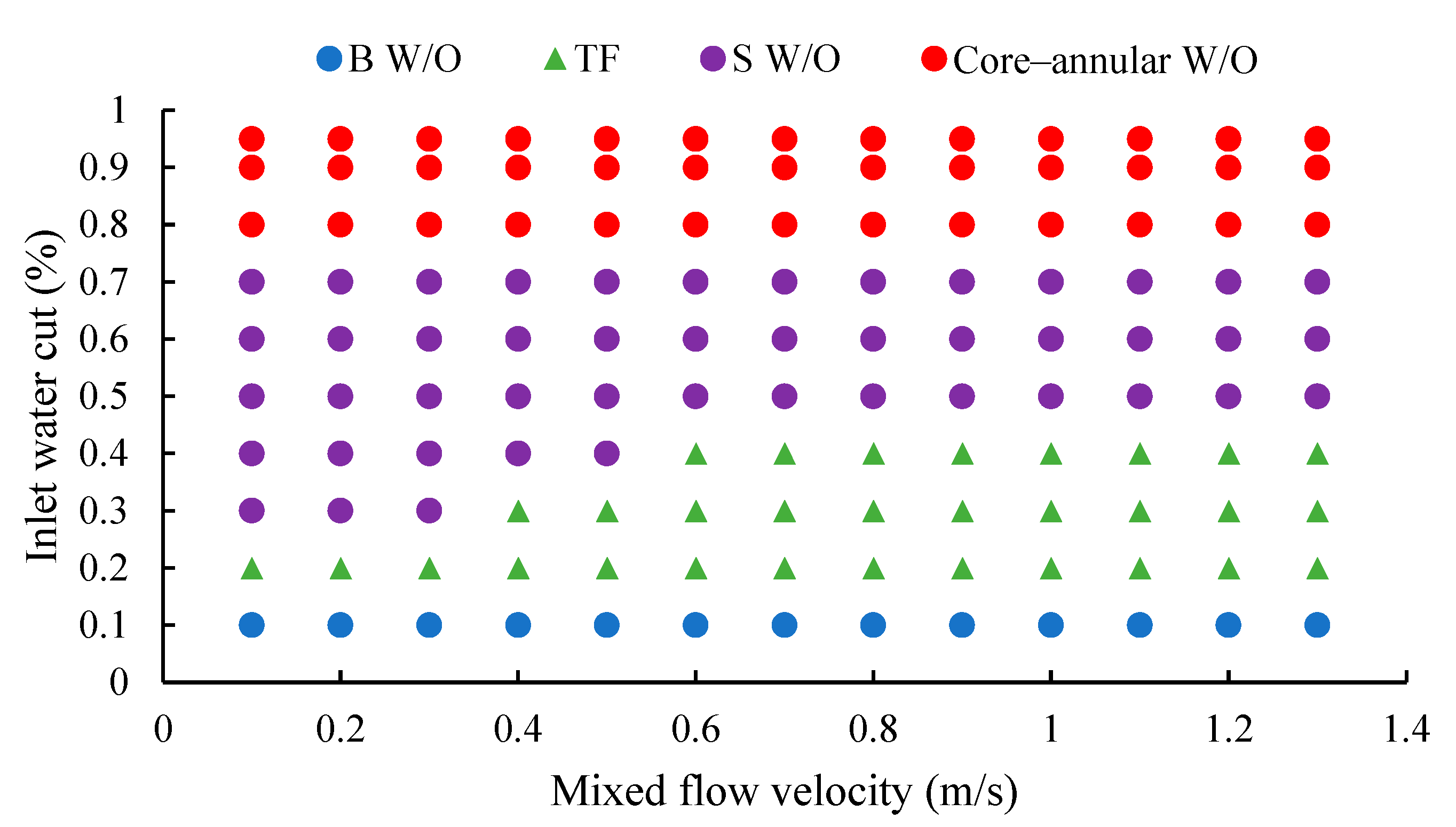
5.2. Verification of Flow Pattern Maps
6. Conclusions
- (1)
- There are six typical flow patterns for heavy oil–water two-phase flow: water-in-oil bubble flow (B W/O), transitional flow (TF), water-in-oil slug flow (S W/O), oil-in-water bubble flow (B O/W), oil-in-water very fine dispersed flow (VFD O/W), and water-in-oil core-annular flow (Core-annular W/O).
- (2)
- When the viscosity of heavy oil reaches 600 mPa·s, Core-annular W/O appears. However, flow patterns with water as the continuous phase (B O/W and VFD O/W) completely disappear when the viscosity increases to 1100 mPa·s.
- (3)
- S W/O tends to occur in low-velocity regions. When the viscosity remains unchanged, the larger the flow velocity, the smaller the S W/O region; conversely, the higher the viscosity of heavy oil, the larger the area where S W/O appears.
- (4)
- As the viscosity of the oil phase increases, the water phase is more likely to aggregate, and B W/O is more prone to transition to TF.
- (5)
- Based on the comparison and verification of the measured data from the W1 well with the heavy oil–water two-phase flow pattern map, the chart predicts that the flow pattern above the blending point of the well belongs to S W/O, and the flow pattern below the blending point belongs to Core-annular W/O, which is basically consistent with the actual measured flow pattern.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | Greek Symbols | ||
| v | Velocity m/s | τ | Shear stress tensor Pa |
| p | Static pressure Pa | μ | Dynamic viscosity Pa·s |
| g | Gravitational acceleration m/s2 | μq | Viscosity of phase q Pa·s |
| ρ | Density kg/m3 | αq | Volume fraction of phase q |
| F | External body force N | ε | Dissipation m2/s3 |
| mpq, mqp | Alternate mass transfer | μ, | Viscosity coefficient |
| ρq | Density of phase q kg/m3 | μt | Turbulent viscosity |
| k | Turbulent kinetic energy m2/s2 | ||
| Gk | Turbulent kinetic energy production item m2/s3 | Subscripts | |
| σk | Plrandte number of turbulent momentum | q | Phase q |
| C1ε, C2, Cμ, | Default constants with values | pq | Phase p to phase q |
| σε | Plentor number of the dissipation rate | qp | Phase q to phase p |
| xi | i-th coordinate direction | k | Turbulent kinetic energy |
| xj | j-th coordinate direction | t | Turbulent |
| A, Aw, Ao | Monitored surface m2; | w | Water phase |
| I | Identity tensor | o | Oil phase |
References
- Liu, X.; Wu, T.; Ge, T.; Du, C.; Wang, D.; Geng, Z. In-situ Enhanced Oil Recovery Techniques for Heavy and Super-Heavy Oil. Contemp. Chem. Ind. 2023, 52. [Google Scholar] [CrossRef]
- Hua, W.; Cai, L.; Xu, R.; Liu, T.; Yue, Y. Study on Flow Characteristics of Oil-Water Two-Phase Flow. Pet. Ind. Technol. Superv. 2022, 38, 28–31. [Google Scholar]
- Charles, M.E.; Lilleleht, L.V. Correlation of pressure gradients for the stratified laminar-turbulent pipeline flow of two immiscible liquids. Can. J. Chem. Eng. 1966, 44, 47–49. [Google Scholar] [CrossRef]
- Govier, G.W.; Sullivan, G.A.; Wood, R.K. The upward vertical flow of oil-water mixtures. Can. J. Chem. Eng. 1961, 39, 67–75. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. A new model for two-phase oil/water flow: Production log interpretation and tubular calculations. SPE Prod. Eng. 1990, 5, 193–199. [Google Scholar] [CrossRef]
- Zavareh, F.; Hill, A.D.; Podio, A.L. Flow regimes in vertical and inclined oil/water flow in pipes. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 2–5 October 1988; SPE: Kuala Lumpur, Malaysia, 1988. SPE-18215-MS. [Google Scholar]
- Zhong, X.; Huang, Z.; Lv, P.; Xie, R.; Li, H. Study on Flow Pattern Identification of Oil-Water Two-Phase Flow in a 125 mm Vertical Circular Pipe. Acta Pet. Sin. 2001, 5, 89–94. [Google Scholar]
- Jana, A.K.; Das, G.; Das, P.K. Flow regime identification of two-phase liquid–liquid upflow through vertical pipe. Chem. Eng. Sci. 2006, 61, 1500–1515. [Google Scholar] [CrossRef]
- Mydlarz-Gabryk, K.; Pietrzak, M.; Troniewski, L. Study on oil–water two-phase upflow in vertical pipes. J. Pet. Sci. Eng. 2014, 117, 28–36. [Google Scholar] [CrossRef]
- Hamidi, M.J.; Karimi, H.; Boostani, M. Flow Patterns and heat transfer of oil-water two-phase upward flow in vertical pipe. Int. J. Therm. Sci. 2018, 127, 173–180. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, J.; Ren, B.; Zhang, S.; Xiong, R.; Zhang, D.; Cao, C.; Liao, Z.; Zhang, S.; Fu, S.; et al. Oil-Water flow Patterns, holdups and frictional pressure gradients in a vertical pipe under high temperature/pressure conditions. Exp. Therm. Fluid Sci. 2019, 100, 271–291. [Google Scholar] [CrossRef]
- Huang, L.; Wang, Y.; Cheng, X.; Wen, M.; Kang, X.; Lv, R.; Zhang, H.; He, J.; Yang, Y. Prediction Model of Water Holdup and Pressure Drop Based on the Flow Patterns of Heavy Oil-Water Two-Phase Flow in Vertical Pipelines. Sci. Technol. Eng. 2021, 21, 14908–14917. [Google Scholar]
- Mazza, R.A.; Suguimoto, F.K. Experimental investigations of kerosene-water two-phase flow in vertical pipe. J. Pet. Sci. Eng. 2020, 184, 106580. [Google Scholar] [CrossRef]
- Ganat, T.; Hrairi, M.; Gholami, R.; Abouargub, T.; Motaei, E. Experimental investigation of oil-water two-phase flow in horizontal, inclined, and vertical large-diameter pipes: Determination of flow Patterns, holdup, and pressure drop. SPE Prod. Oper. 2021, 36, 946–961. [Google Scholar] [CrossRef]
- Farrar, B.; Bruun, H.H. A computer based hot-film technique used for flow measurements in a vertical kerosene-water pipe flow. Int. J. Multiph. Flow 1996, 22, 733–751. [Google Scholar] [CrossRef]
- Descamps, M.; Oliemans, R.; Ooms, G.; Mudde, R.; Kusters, R. Influence of gas injection on phase inversion in an oil–water flow through a vertical tube. Int. J. Multiph. Flow 2006, 32, 311–322. [Google Scholar] [CrossRef]
- Abduvayt, P.; Manabe, R.; Watanabe, T.; Arihara, N. Analysis of oil/water-flow tests in horizontal, hilly terrain, and vertical pipes. SPE Prod. Oper. 2006, 21, 123–133. [Google Scholar] [CrossRef]
- Zhao, D.; Guo, L.; Hu, X.; Zhang, X.; Wang, X. Experimental study on local characteristics of oil–water dispersed flow in a vertical pipe. Int. J. Multiph. Flow 2006, 32, 1254–1268. [Google Scholar] [CrossRef]
- Xu, J.; Li, D.; Guo, J.; Wu, Y. Investigations of phase inversion and frictional pressure gradients in upward and downward oil–water flow in vertical pipes. Int. J. Multiph. Flow 2010, 36, 930–939. [Google Scholar] [CrossRef]
- Du, M.; Jin, N.D.; Gao, Z.K.; Wang, Z.Y.; Zhai, L.S. Flow Pattern and water holdup measurements of vertical upward oil–water two-phase flow in small diameter pipes. Int. J. Multiph. Flow 2012, 41, 91–105. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, J.; Wu, Y.; Li, D.; Li, H. Experimental validation of the calculation of phase holdup for an oil–water two-phase vertical flow based on the measurement of pressure drops. Flow Meas. Instrum. 2013, 31, 96–101. [Google Scholar] [CrossRef]
- Han, Y.; Jin, N.; Ren, Y.; He, Y. Measurement of pressure drop and water holdup in vertical upward oil-in-water emulsions. IEEE Sens. J. 2017, 18, 1703–1713. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Zhang, L. Experimental Study and Transient Numerical Calculation of Gas-Liquid Two-Phase Flow in Pipelines. Ph.D. Thesis, Wuhan University, Wuhan, China, 2020. [Google Scholar]
- Ma, Y. Research on Flow Pattern Identification Method of Oil-Water Two-Phase Capacitance Tomography. Master’s Thesis, Northeast Petroleum University, Daqing, China, 2020. [Google Scholar]
- Feng, N. Numerical Simulation of Gas-Liquid Two-Phase Stirred Flow in a Vertical Rising Pipe. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2019. [Google Scholar]
- Ye, W. Reconstruction of a Multi-functional Experimental Device for Downward Flow of Gas-Liquid Two-Phase in Wellhead Injection. Master’s Thesis, Southwest Petroleum University, Daqing, China, 2019. [Google Scholar]
- Chen, L.; Yin, J.; Sun, Z.; Yao, F.; Zhou, T. Flow Pattern Identification of Bluff Body Flow around Gas-Liquid Two-Phase Flow Based on EEMD-Hilbert Spectrum. Chin. J. Sci. Instrum. 2017, 38, 2536–2546. [Google Scholar]
- Zhang, X.; Li, L.; Hu, H. Flow Pattern Identification of Gas-Solid Two-Phase Flow Based on EEMD and Fractal Box Dimension. J. Northwest Univ. (Nat. Sci. Ed.) 2016, 46, 178–183. [Google Scholar]
- Yu, H. Ultrasonic Echo Attenuation Characteristics of Gas-Liquid Two-Phase Flow Pipe Wall and Its Application. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2015. [Google Scholar]

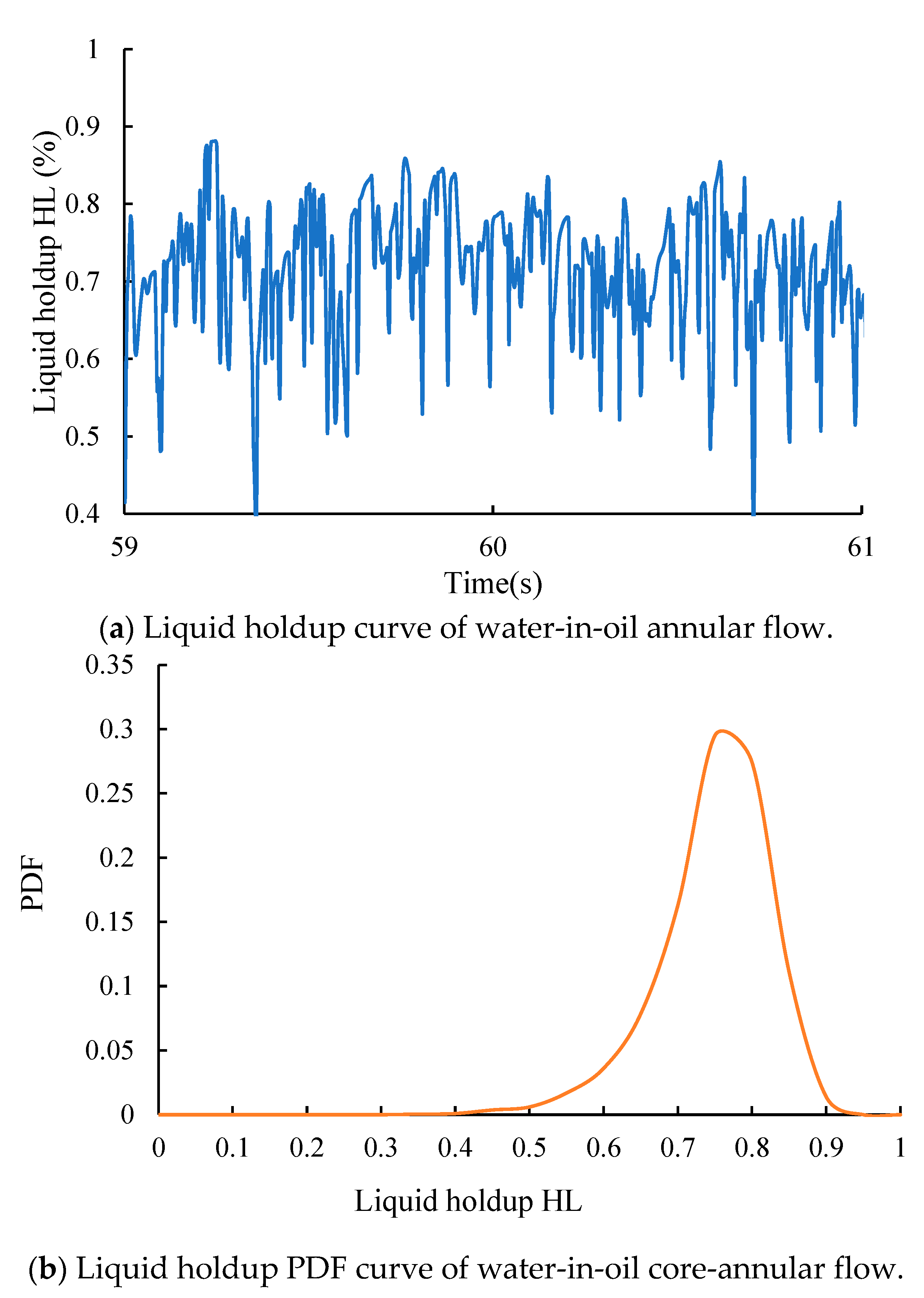




| Author | Experimental Medium | Oil Viscosity (mPa·s) | Pipe ID (mm) | Pipe Length (m) | Temperature (°C) | Flow Pattern |
|---|---|---|---|---|---|---|
| G.W. Govier (1961) [4] | Oil, Water | 0.936~20.1 | 26.4 | 11.3 | 22 | Bubbly O/W, Slug O/W, Transitional Flow, Bubbly W/O |
| Farrar (1996) [15] | Kerosene, Water | N/A | 77.8 | 1.5 | N/A | Bubble O/W |
| Zhong (2001) [7] | Oil, Water | 3 | 125 | 8 | Room Temperature | Bubbly O/W, Churn, VFD O/W, Bubbly W/O |
| Descamps (2006) [16] | Brine, Vitrea No. 10 Oil | 7.5 (40 °C) | 8.28 | 15.5 | 40 | Bubbly O/W, Bubbly W/O |
| P. Abduvayt (2006) [17] | Kerosene, Water | 1.88 ± 0.19 (35 ± 5 °C) | 106.4 | 11.95 | 35 ± 5 | D O/W, VFD O/W, O/W F, DW/O, VFD W/O, W/O F |
| Zhao (2006) [18] | Water, White Oil No. 5 | 4.1 | 40 | 3.8 | 40 | VFD O/W, DO/W, O/W CF |
| Jana (2006) [8] | Kerosene, Water | 1.37 (30 °C) | 2.54 | 1.4 | 30 | VFD O/W, B O/W, Churn Turbulent, Core-Annular O/W |
| Xu (2010) [19] | White Oil, Water | 44 (20 °C) | 50 | 3.5 | 20 | B O/W, D O/W, Churn, D W/O, D O/W |
| Du (2012) [20] | Industrial White Oil No. 15, Water | 11.984 (40 °C) | 2.0 | 4 | N/A | VFD O/W, D O/W, D OS/W, D W/O, TF |
| Zhang (2013) [21] | White Oil, Water | 60 (27 °C) | 2.5 | 1.2 | Room Temperature | N/A |
| Kamila [9] (2014) | Engine Oil, Water | 29.20 (20 °C) | 30 | 7.12 | N/A | Dr W/O, Transition, Dr PO/W, Dr O/W |
| Han (2017) [22] | Industrial White Oil, Water | N/A | 20 | 2.86 | Room Temperature | D OS/W, D O/W, VFD O/W, TF |
| Mohammad J. Hamidi (2018) [10] | Kerosene, Water | 1.49 (20 °C) 1.1 (40 °C) | 11 | 3.55 | 25 | SL, CH, DO/W, D W/O |
| Yang (2020) [11] | Industrial White Oil, Water | 97.32 (30 °C) | 20 | N/A | 30 | BW/O, SW/O, PW/O, TF, PO/WSO/W, BO/W, VFD O/W |
| RicardoA. Mazza (2020) [13] | Kerosene, Water | 1.1 | 26 | 3.1 | N/A | DB, CA, B, CT, EWD |
| Ganat (2022) [14] | Synthetic Oil, Water | 2 (40 °C) | 106.4 | 15 | 40 | DW/O, VFD W/O, W/O F, O/W F, D O/W, VFD O/W |
| Content | Parameters | |
|---|---|---|
| Inlet | Velocity inlet | 0.8 m/s |
| Outlet | Pressure outlet | Standard atmospheric pressure |
| Wall boundary conditions | No-slip wall | Standard wall function |
| Grid | Total Grid Count |
|---|---|
| 1 | 220,518 |
| 2 | 326,118 |
| 3 | 507,285 |
| 4 | 1,027,431 |
| Medium | Density | Dynamic Viscosity (30 °C) | Oil–Water Interfacial Tension |
|---|---|---|---|
| Water | 1.14 g/cm3 | 1.003 mPa·s | / |
| Oil | 1.027 g/cm3 | 100 mPa·s | 30 m N/m |
| Temperature (°C) | Water Density (g/cm3) | Oil Density (g/cm3) | Water Viscosity (mPa·s) | Oil Viscosity (mPa·s) | Oil–Water Interfacial Tension (m N/m) |
|---|---|---|---|---|---|
| 30 | 1.014 | 0.857 | 0.8 | 97.32 | 32.8 |
| No. | Mixing Flow Rate (m/s) | Water Content (%) | Flow Patterns | Consistency | |
|---|---|---|---|---|---|
| Experimental Data | Simulation Results | ||||
| 1 | 0.2 | 10 | Bubble Flow | Bubble Flow | Yes |
| 2 | 0.1 | 30 | Slug Flow | Slug Flow | Yes |
| 3 | 0.5 | 45 | Slug Flow | Slug Flow | Yes |
| 4 | 0.5 | 35 | Slug Flow | Slug Flow | Yes |
| 5 | 0.5 | 20 | Bubble Flow | Bubble Flow | Yes |
| 6 | 0.9 | 10 | Bubble Flow | Bubble Flow | Yes |
| 7 | 1 | 40 | Slug Flow | Bubble Flow | No |
| 8 | 1.2 | 15 | Bubble Flow | Bubble Flow | Yes |
| 9 | 1.4 | 95 | Bubble Flow | Bubble Flow | Yes |
| 10 | 1.8 | 10 | Bubble Flow | Bubble Flow | Yes |
| 11 | 0.5 | 55 | Transitional Flow | Slug Flow | No |
| 12 | 0.5 | 60 | Slug Flow | Slug Flow | Yes |
| 13 | 0.7 | 85 | Bubble Flow | Bubble Flow | Yes |
| 14 | 0.7 | 70 | Slug Flow | Slug Flow | Yes |
| 15 | 0.9 | 30 | Bubble Flow | Bubble Flow | Yes |
| 16 | 0.9 | 60 | Slug Flow | Slug Flow | Yes |
| 17 | 1.4 | 40 | Slug Flow | Bubble Flow | No |
| 18 | 1.4 | 70 | Bubble Flow | Bubble Flow | Yes |
| 19 | 1.8 | 30 | Slug Flow | Slug Flow | Yes |
| 20 | 1.8 | 70 | Bubble Flow | Bubble Flow | Yes |
| Tube ID (mm) | 76 mm | |
|---|---|---|
| Test Instrument Dia (mm) | 38.0 mm | |
| Explanation of test values | Pure oil: 30,159 CPS | Pure water: 11,636 CPS |
| Parameter | Numerical Value |
|---|---|
| Production | 97 t/d |
| Pipe ID | 76 mm |
| Diluent density | 910 kg/m3 |
| Heavy oil density | 1020 kg/m3 |
| Water density | 1140 kg/m3 |
| Flow rate | 39.64 m3/d |
| Viscosity of heavy oil after dilution | 136 mPa·s |
| Flow velocity | 0.25 m/s |
| Water cut | 45% |
| Parameter | Numerical Value |
|---|---|
| Production | 44 t/d |
| Pipe ID | 62 mm |
| Heavy oil density | 1020 kg/m3 |
| Water density | 1140 kg/m3 |
| Undiluted flow rate | 39.64 m3/d |
| Viscosity of undiluted heavy oil | 632 mPa·s |
| Flow velocity | 0.152 m/s |
| Water cut | 78% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Han, G.; Ren, Z.; Su, H.; Jia, S.; Cheng, T.; Li, M.; Liang, J. Research on Oil–Water Two-Phase Flow Patterns in Wellbore of Heavy Oil Wells with Medium-High Water Cut. Processes 2024, 12, 2404. https://doi.org/10.3390/pr12112404
Song Z, Han G, Ren Z, Su H, Jia S, Cheng T, Li M, Liang J. Research on Oil–Water Two-Phase Flow Patterns in Wellbore of Heavy Oil Wells with Medium-High Water Cut. Processes. 2024; 12(11):2404. https://doi.org/10.3390/pr12112404
Chicago/Turabian StyleSong, Zhengcong, Guoqing Han, Zongxiao Ren, Hongtong Su, Shuaihu Jia, Ting Cheng, Mingyu Li, and Jian Liang. 2024. "Research on Oil–Water Two-Phase Flow Patterns in Wellbore of Heavy Oil Wells with Medium-High Water Cut" Processes 12, no. 11: 2404. https://doi.org/10.3390/pr12112404
APA StyleSong, Z., Han, G., Ren, Z., Su, H., Jia, S., Cheng, T., Li, M., & Liang, J. (2024). Research on Oil–Water Two-Phase Flow Patterns in Wellbore of Heavy Oil Wells with Medium-High Water Cut. Processes, 12(11), 2404. https://doi.org/10.3390/pr12112404





