The Influence of Structure Optimization on Vortex Suppression and Energy Dissipation in the Draft Tube of Francis Turbine
Abstract
1. Introduction
2. Prototype Model and Numerical Calculation Method
2.1. Francis Turbine Geometrical Model
2.2. The Fluid Governing Equations and Turbulent Model
2.2.1. The Fluid Governing Equation
2.2.2. Turbulence Model
2.2.3. Entropy Production Theory
2.3. Computational Domain and Grid Generation
3. Results and Discussions
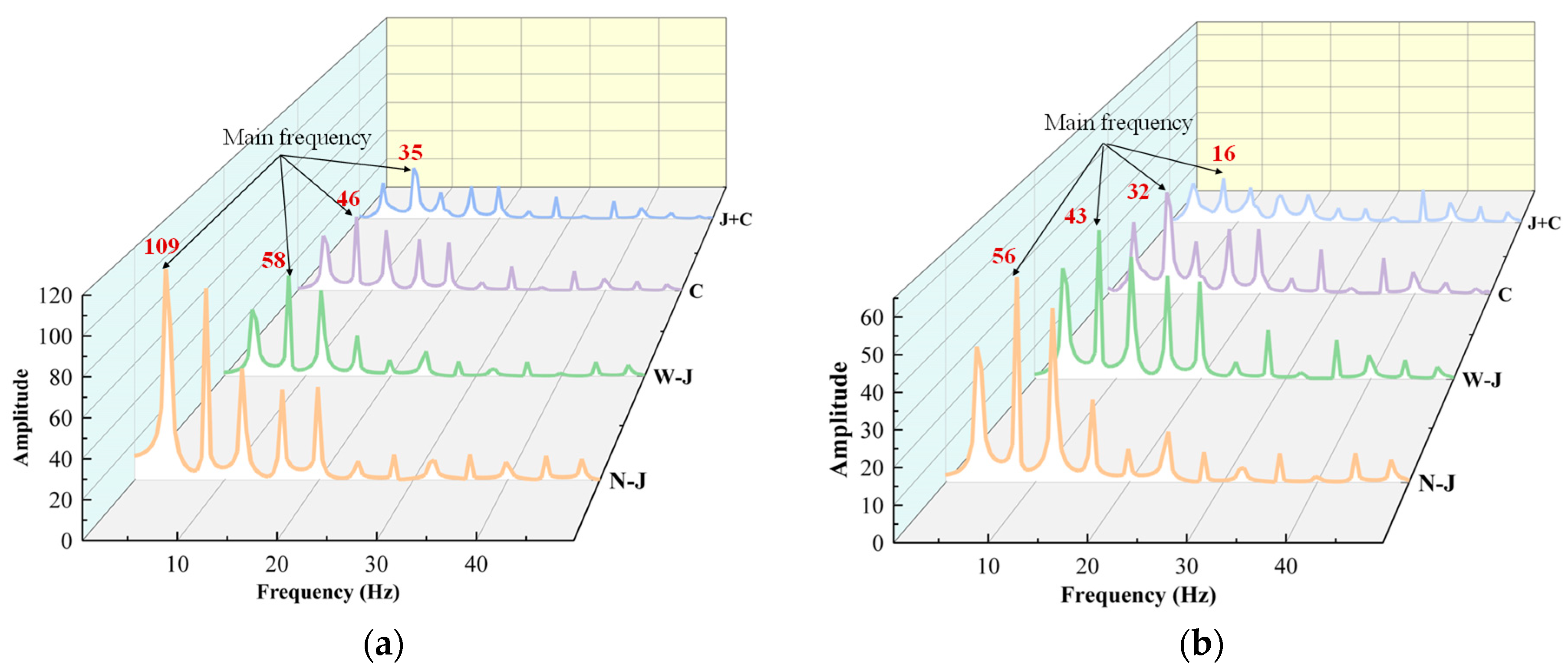
3.1. Pressure Fluctuation Analysis
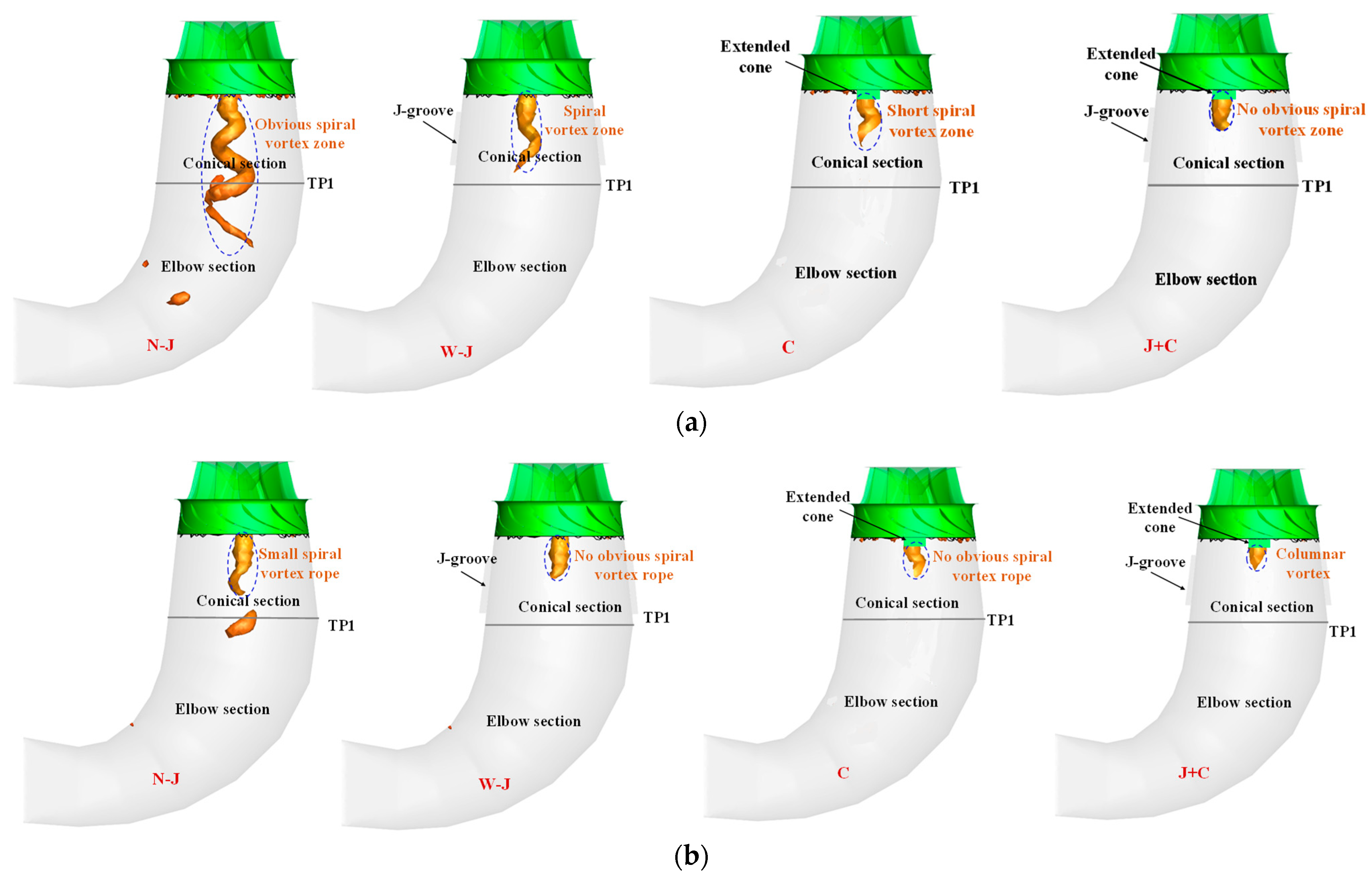
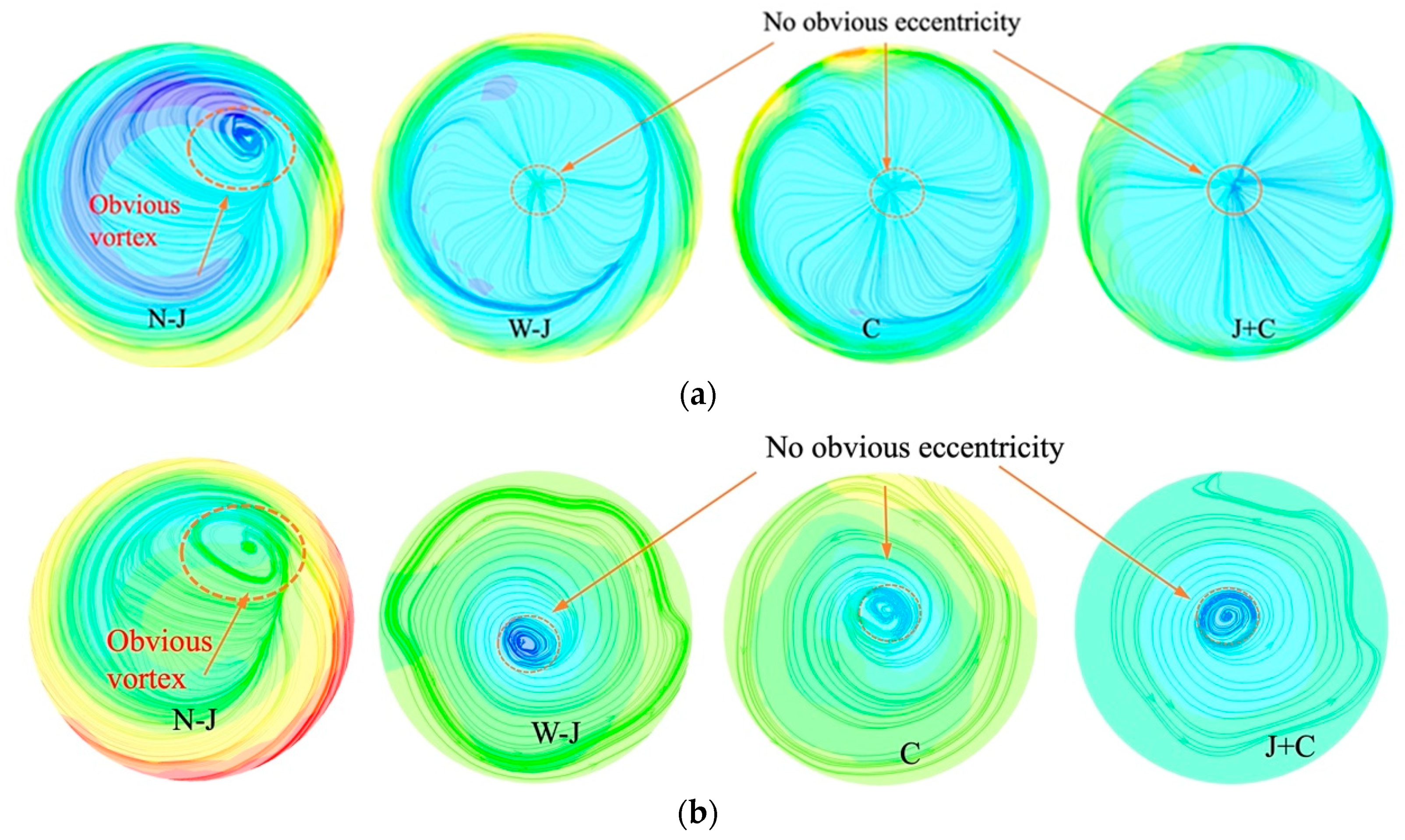
3.2. Analysis of Vortex Rope Morphology
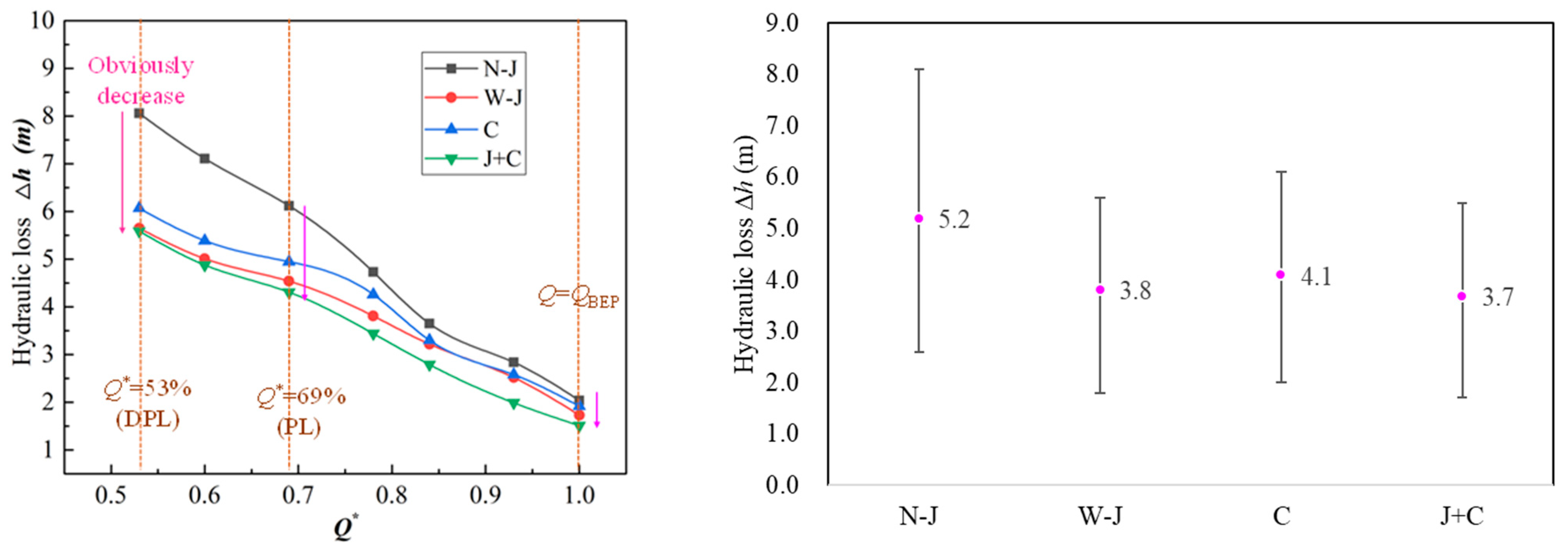
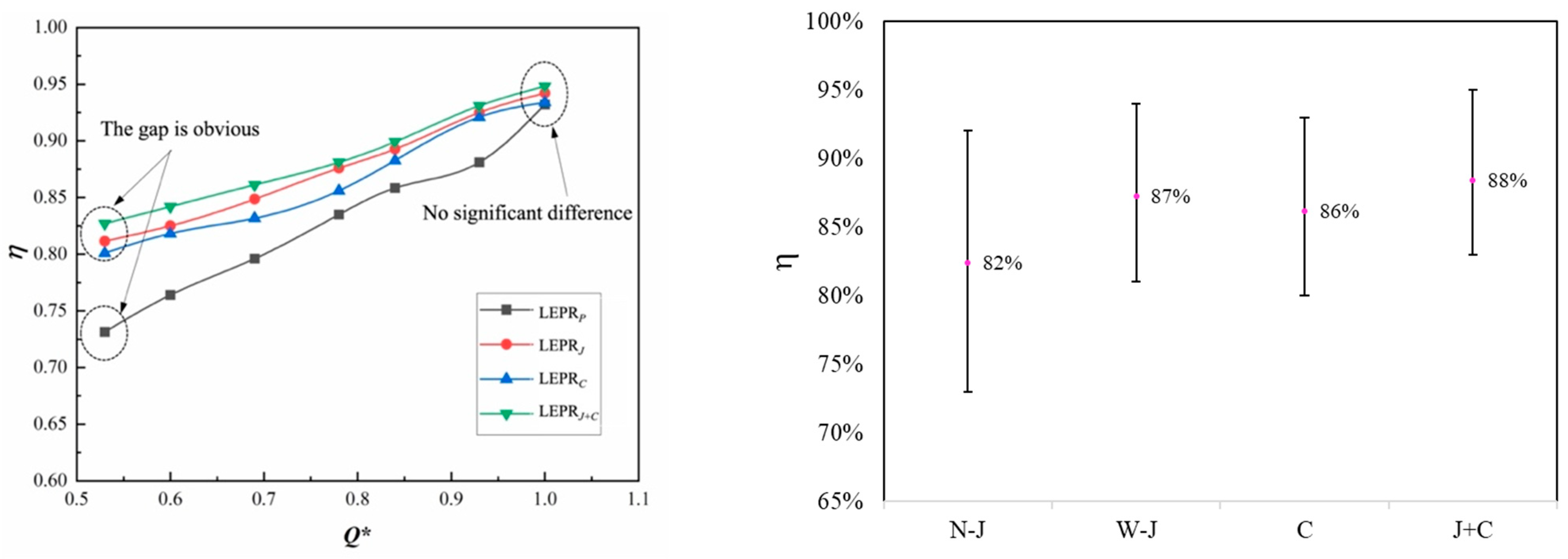
3.3. Analysis of Energy Loss
4. Conclusions
- (1)
- The draft tube pressure’s fluctuation amplitudes in the three optimized turbines, W-J, C, and J+C, can be effectively reduced. The J+C optimized structure adopted in the two modification methods can significantly decrease the pressure pulsation amplitude from 109 to 35. Thus, the eccentric vortex was effectively weakened, and the stable operation range of the hydro unit was expanded;
- (2)
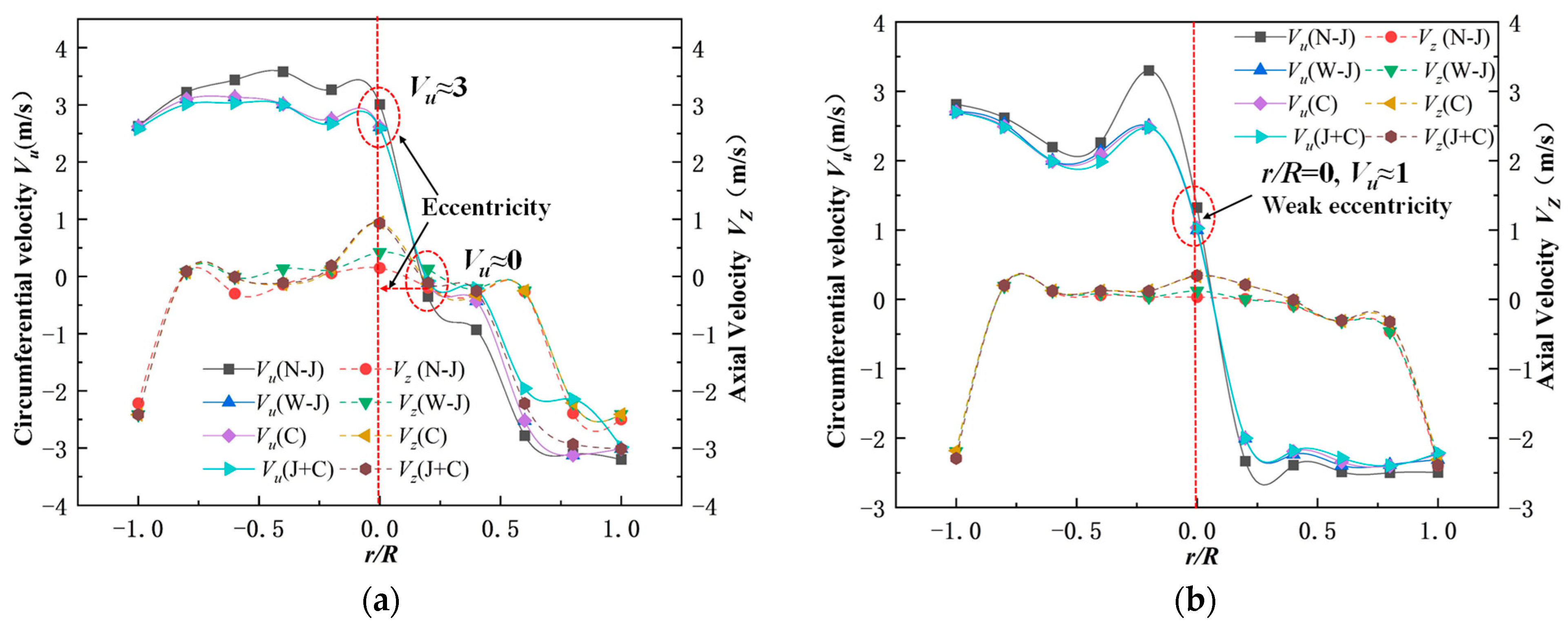
- Comparing the vortex morphologies of different modification measures, the J+C optimized structure with J-grooves and runner cone extension can reduce the circumferential velocity at the runner outlet under partial load conditions and increase the axial velocity. The diameter and length of the vortex rope are significantly suppressed. Therefore, the eccentric vortex in the draft tube is notably reduced. The optimization structure J+C can have a pronounced effect on vortex suppression;
- (3)
- By comparing the entropy production losses in the prototype and under the modification measures, it can be found that the structure optimization measure J+C can most notably minimize the pressure pulsation induced by the eddy current at the runner outlet and the hydraulic loss associated with the pressure pulsation. The energy dissipation effect is the most obvious under deep partial load conditions. The efficiency of the turbine with a J+C optimized structure was increased by 13.7% compared to the prototype turbine. Therefore, the entropy production theory can be used to locate the high hydraulic loss position in hydraulic machinery accurately, and also can be used to evaluate the energy loss accompanying the vortex rope’s generation in the draft tube of the water turbine.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| N-J | No J-grooves |
| W-J | With J-grooves |
| C | Extending runner cone |
| J+C | With J-grooves and extending runner cone simultaneously |
| BEP | Best efficiency point |
| QBEP | Discharge on the best efficiency point (m3/s) |
| DPL | Deep partial load condition |
| PL | Partial load condition |
| CFD | Computational Fluid Dynamics |
| RNG | Renormalization Group |
| k | Turbulent kinetic energy (m2/s2) |
| ε | Dissipation rate (m2/s3) |
| DES | Detached Eddy Simulation |
| LEPR | Local Entropy Production Ratio |
| nr | Rated revolution (r/min) |
| Qr | Design flow (m3/s) |
| Hr | Design head (m) |
| kW | Kilowatt |
| vˆ | Effective viscosity ratio |
| Viscous dissipation function | |
| Local entropy generation rate (W·m−3·K−1) | |
| Direct entropy production rate (W·m−3·K−1) | |
| Turbulent entropy production rate (W·m−3·K−1) | |
| Dynamic viscosity coefficient of flow | |
| η | Turbine efficiency (%) |
| y+ | Non-dimensional wall distance |
| L | Length of J-grooves (mm) |
| W | Width of J-grooves (mm) |
| D3 | Inlet diameter of draft tube (m) |
| D | Diameter of the runner cone’s extended section (mm) |
| L1 | Length of the runner cone’s extended section (mm) |
| Velocity of the spiral case’s inlet (m/s) | |
| Pressure of the draft tube’s outlet (Pa) | |
| Q* | Corresponding flow ratio |
| r | The position from the origin in the x-direction (m) |
| R | The radius of reference radius (m) |
| Vu | Circumferential speed (m/s) |
| VZ | Axial speed (m/s) |
| Δh | Hydraulic loss (m) |
References
- Zhou, J.P.; Du, X.H.; Zhou, X.B. Innovating ideas to promote the sustainable development of hydropower development—Forecast of hydropower development situation and analysis of countermeasures in the 14th Five-Year. China Electr. Power 2021, 8, 34–37. [Google Scholar]
- Tang, W. “Carbon Neutrality” aimed electric power development in the 14th Five-Year. Pet. New Energy 2021, 33, 13–17. [Google Scholar]
- Su, X.; Cao, Z.; Li, Y.; Jin, Y.; Tang, Z. Research on Flow Stability and Vibration of an Industrial Hydraulic Turbine. Processes 2021, 9, 311. [Google Scholar] [CrossRef]
- Zhang, S.Q. Study of hydraulic stability on large-scale the Francis turbine. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2008. [Google Scholar]
- Goyal, R.; Gandhi, B.K. Review of hydrodynamics instabilities in Francis turbine during off-design and transient operations. Renew. Energy 2018, 116, 697–709. [Google Scholar]
- Li, Q.F.; Wang, Y.K.; Liu, C.; Zhang, J.X.; Zhang, Z.J.; Wang, R.B. Pressure fluctuation characteristics of Francis pump turbine in Hump zone. J. Drain. Irrig. Mach. Eng. 2018, 36, 488–493. [Google Scholar]
- Wang, G. Study on vibration and stability of hydraulic turbine and associated test technology. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2002. [Google Scholar]
- Rheingans, W.J. Power swings in hydroelectric power plants. Trans. ASME 1940, 62, 171–177. [Google Scholar] [CrossRef]
- Rudolf, P.; Martin, J. Decomposition of the Swirling Flow Fields. In Proceedings of the 4-th International Meeting on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, Belgrade, Serbia, 26–28 October 2011. [Google Scholar]
- Liu, W.J.; Liu, G.N.; Wei, X.Z.; Han, X.L. Stability Research for Zhouba Hydraulic Power Station. Large Electr. Mach. Hydraul. Turbine 2006, 1, 49–52. [Google Scholar]
- Ma, Y.; Geng, Q.H.; Qian, B.; Feng, Z.G. Model test research on air supply for tail water pipe of Gongzui Hydropower Station. Yangtze River 2016, 47, 102–104. [Google Scholar]
- Sun, J.P.; Xiong, H.; Ao, J.P.; Zheng, L.Y. Influence of gas-supply on the stability of operating in low head of left bank units at three gorges hydropower station. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2006, 34, 75–77. [Google Scholar]
- Susan-Resiga, R.; Ciocan, G.D.; Anton, I.; Avellan, F. Analysis of the Swirling Flow Downstream a Francis Turbine Runner. J. Fluids Eng. 2006, 128, 177–189. [Google Scholar] [CrossRef]
- Anup, K.C.; Thapa, B.; Lee, Y.H. Transient numerical analysis of rotor–stator interaction in a Francis turbine. Renew. Energy 2014, 65, 227–235. [Google Scholar]
- Tiwari, G.; Kumar, J.; Prasad, V.; Patel, V.K.; Tiwari, G. Utility of CFD in the design and performance analysis of hydraulic turbines -A review. Energy Rep. 2020, 6, 2410–2429. [Google Scholar] [CrossRef]
- Wang, Z.W.; Zhou, L.J.; Huang, Y.F. Simulation of unsteady flow induced by in vortices the draft tube of a Francis turbine. J. Tsinghua Univ. (Sci. Technol.) 2002, 42, 1647–1650. [Google Scholar]
- Li, Z.C.; Chang, S.J.; Xin, Z. Numerical Simulation of Elimination of Pressure Fluctuation in Francis Turbine Draft Tube Using Water Jet. Trans. Chin. Soc. Agric. Mach. 2013, 44, 53–57. [Google Scholar]
- Su, W.T.; Zheng, Z.Y.; Li, X.B.; Lan, C.F. Verification of large eddy simulation (LES) applied in Francis hydro-turbine under partial flow conditions. J. Harbin Inst. Technol. 2015, 47, 90–97. [Google Scholar]
- Ye, S.; Li, X.; Zhu, Z.; Li, L.; Lin, T. Numerical Study of the Energy Flow Characteristics of Multi-Stage Pump as Turbines. Processes 2022, 10, 2488. [Google Scholar] [CrossRef]
- Mulu, B.G.; Jonsson, P.P.; Cervantes, M.J. Experimental investigation of a Kaplan draft tube—Part I: Best efficiency point. Appl. Energy 2012, 94, 71–83. [Google Scholar] [CrossRef]
- Foroutan, H.; Yavuzkurt, S. Flow in the Simplified Draft Tube of a Francis Turbine Operating at Partial Load—Part I: Simulation of the Vortex Rope. J. Appl. Mech. 2014, 81, 061010. [Google Scholar] [CrossRef]
- Kc, A.; Lee, Y.H.; Thapa, B. CFD study on prediction of vortex shedding in draft tube of Francis turbine and vortex control techniques. Renew. Energy 2016, 86, 1406–1421. [Google Scholar] [CrossRef]
- Cheng, H.; Zhou, L.; Liang, Q.; Guan, Z.; Liu, D.; Wang, Z.; Kang, W. A method of evaluating the vortex rope strength in draft tube of Francis turbine. Renew. Energy 2020, 152, 770–780. [Google Scholar] [CrossRef]
- Li, R.F.; Zhao, Y.; Liu, D.F.; Shi, Q. Study on the Influence of Cone with Holes on the Vortex Zone of Vortex Rope of the Francis Turbine. Large Electr. Mach. Hydraul. Turbine 2020, 2, 55–60. [Google Scholar]
- Daniel, B.M.; Zhao, Y.; Zhang, Y.M. Geometric shape optimization of turbine draft tube. Extern. Big Mot. 2005, 5, 64–68. [Google Scholar]
- Xin, Q.; Wu, J.; Du, J.; Ge, Z.; Huang, J.; Yu, W.; Yuan, F.; Wang, D.; Yang, X. Study of Draft Tube Optimization Using a Neural Network Surrogate Model for Micro-Francis Turbines Utilized in the Water Supply System of High-Rise Buildings. Processes 2024, 12, 1128. [Google Scholar] [CrossRef]
- Zhou, L.; Hang, J.; Bai, L.; Krzemianowski, Z.; El-Emam, M.A.; Yasser, E.; Agarwal, R. Application of entropy production theory for energy losses and other investigation in pumps and turbines: A review. Appl. Energy 2022, 318, 119211. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Hou, H.C.; Xu, C.; He, W.; Li, Z. Application of entropy production method to centrifugal pump energy loss evaluation. J. Drain. Irrig. Mach. Eng. 2017, 35, 277–282, 288. [Google Scholar]
- Nan, X.; Liu, L.; Ma, N.; Lu, Q.; Lin, F. Numerical investigation of entropy generation distribution in a transonic compressor. In Proceedings of the ASME Turbo Expo: Turbomachinery Technical Conference & Exposition, Seoul, Republic of Korea, 13–17 June 2016. [Google Scholar]
- Xu, L.H.; Guo, T.; Wang, W.Q. Effects of Vortex Structure on Hydraulic Loss in a Low Head Francis Turbine under Overall Operating Conditions Base on Entropy Production Method. Renew. Energy 2022, 198, 367–379. [Google Scholar]
- Wang, F.J. The Analysis of Computational Fluid Dynamic; Tsinghua University Press: Beijing, China, 2004; pp. 2–15. [Google Scholar]
- Favrel, A.; Müller, A.; Landry, C.; Yamamoto, K.; Avellan, F. Study of the vortex-induced pressure excitation source in a Francis turbine draft tube by particle image velocimetry. Exp. Fluids 2015, 56, 1–15. [Google Scholar] [CrossRef]
- Zhang, N. Research on the Evolution Mechanism of Cavitation Vortex in Draft Tube of Francis Turbine. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Zuo, Z.; Liu, S.; Liu, D.; Qin, D.; Wu, Y. Numerical analyses of pressure fluctuations induced by inter blade vortices in a model Francis turbine. Hydrodynamics 2015, 27, 513–521. [Google Scholar] [CrossRef]
- Demirel, G.; Acar, E.; Celebioglu, K.; Aradag, S. CFD-driven surrogate-based multi-objective shape optimization of an elbow type draft tube. Int. J. Hydrogen. Energy 2017, 42, 17601–17610. [Google Scholar] [CrossRef]
- Bilicki, Z.; Giot, M.; Kwidzinski, R. Fundamentals of two-phase flow by the method of irreversible thermodynamics. Int. J. Multiph. Flow 2002, 28, 1983–2005. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Hou, H.; Zhang, J.; Xu, C. Entropy production diagnostic analysis of energy consumption for cavitation flow in a two-stage LNG cryogenic submerged pump. Int. J. Heat Mass Transf. 2019, 129, 342–356. [Google Scholar] [CrossRef]
- Herwig, H.; Kock, F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problem. Heat Mass Transf. 2007, 43, 207–215. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Qin, Y.; Han, L.; Wei, X.; Qin, D. Entropy production analysis of hysteresis characteristic of a pump-turbine model. Energy Convers. Manag. 2017, 149, 175–191. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Mathieu, J.; Scott, J. An Introduction to Turbulent Flow; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Viet, L.V.; Chen, Z.M.; Choi, Y.D. Optimum design of J-groove for a bulb turbine model to suppress swirl flow in the draft tube. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 022030. [Google Scholar]
- Muhirwa, A.; Cai, W.H.; Su, W.T.; Liu, Q.; Binama, M.; Li, B.; Wu, J. A review on remedial attempts to counteract the power generation compromise from draft tubes of hydropower plants. Renew. Energy 2020, 150, 743–764. [Google Scholar] [CrossRef]
- Egusquiza, E.; Estevez, A.; Cabrera, J.; Vega, R. Vibration behavior in Hydro Power Plants Field Data Analysis. In Proceedings of the 20nd IAHR Symposium, Charlotte, NC, USA, 6–9 August 2000. [Google Scholar]
- Skoták, A.; Mikulasek, J.; Troubil, P. Unsteady flow in the draft tube with elbow. Part A–Experimental investigation. In Proceedings of the 10th International Meeting of the Work Group on The Behavior on hydraulic machinery under steady oscillatory conditions, Trondheim, Norway, 26–28 June 2001. [Google Scholar]
- Sotoudeh, N.; Maddahian, R.; Cervantes, M.J. Investigation of Rotating Vortex Rope formation during load variation in a Francis turbine draft tube. Renew. Energy 2020, 151, 238–254. [Google Scholar] [CrossRef]
- Luo, Z.; Nie, C.; Lv, S.; Guo, T.; Gao, S. The Effect of J-Groove on Vortex Suppression and Energy Dissipation in a Draft Tube of Francis Turbine. Energies 2022, 15, 1707. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Y.; Li, Z.; Jiang, T.; Zhang, J.; Xu, C. Numerical analysis of entropy production on a LNG cryogenic submerged pump. J. Nat. Gas Sci. Eng. 2016, 36, 87–96. [Google Scholar] [CrossRef]
- Yu, Z.F.; Wang, W.Q.; Yan, Y.; Liu, X.S. Energy loss evaluation in a Francis turbine under overall operating conditions using entropy production method. Renew. Energy 2021, 169, 982–999. [Google Scholar] [CrossRef]

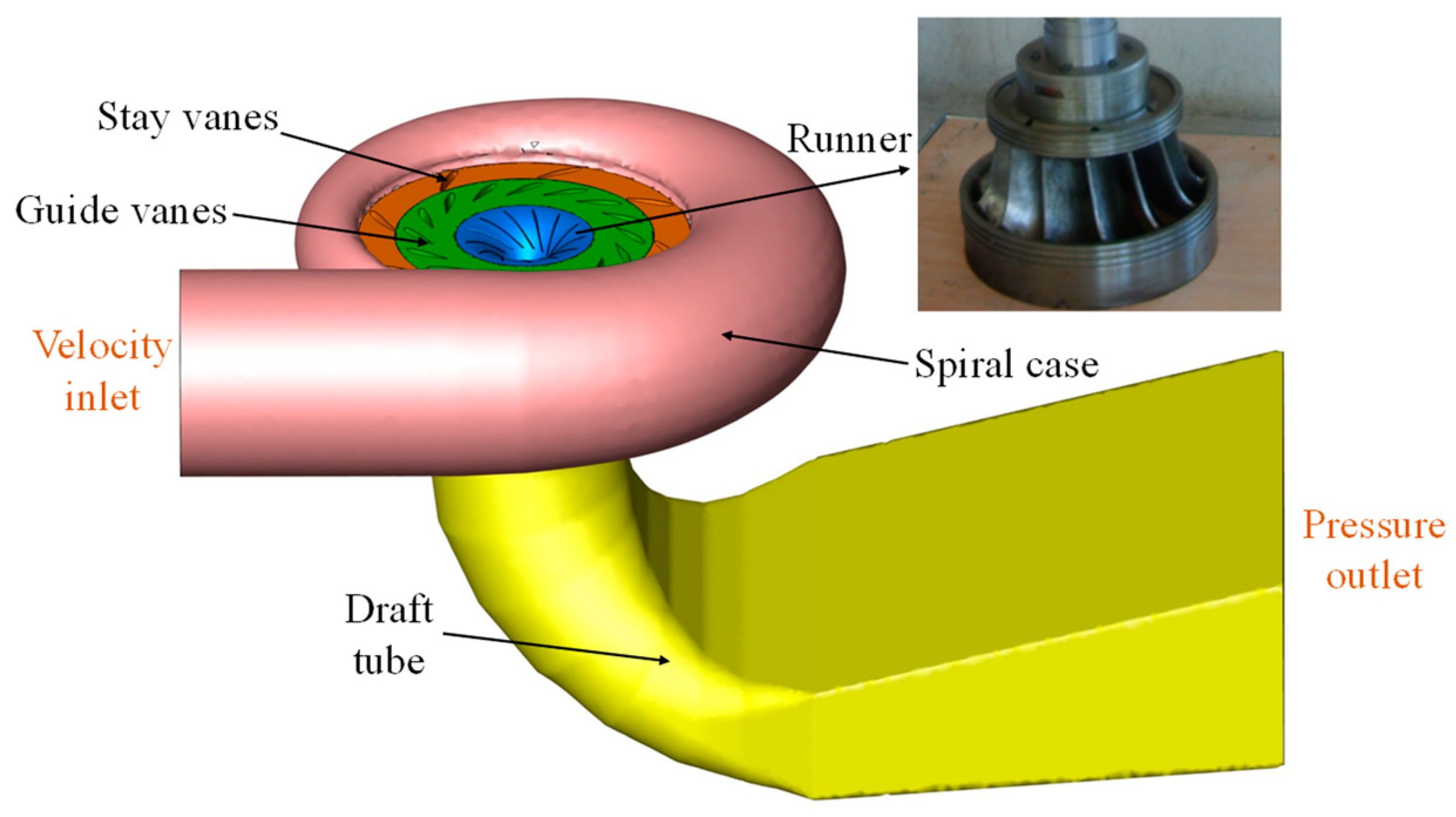
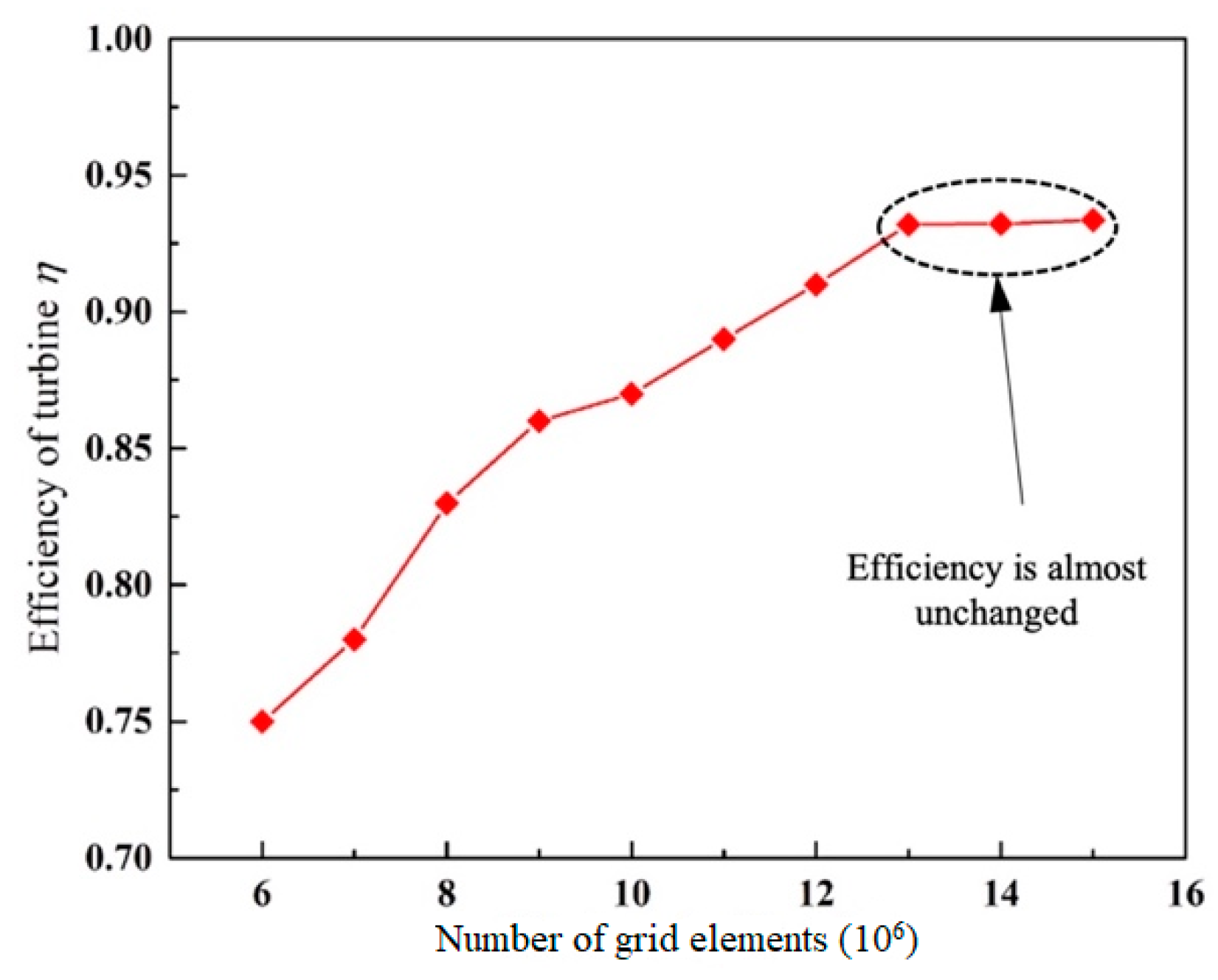
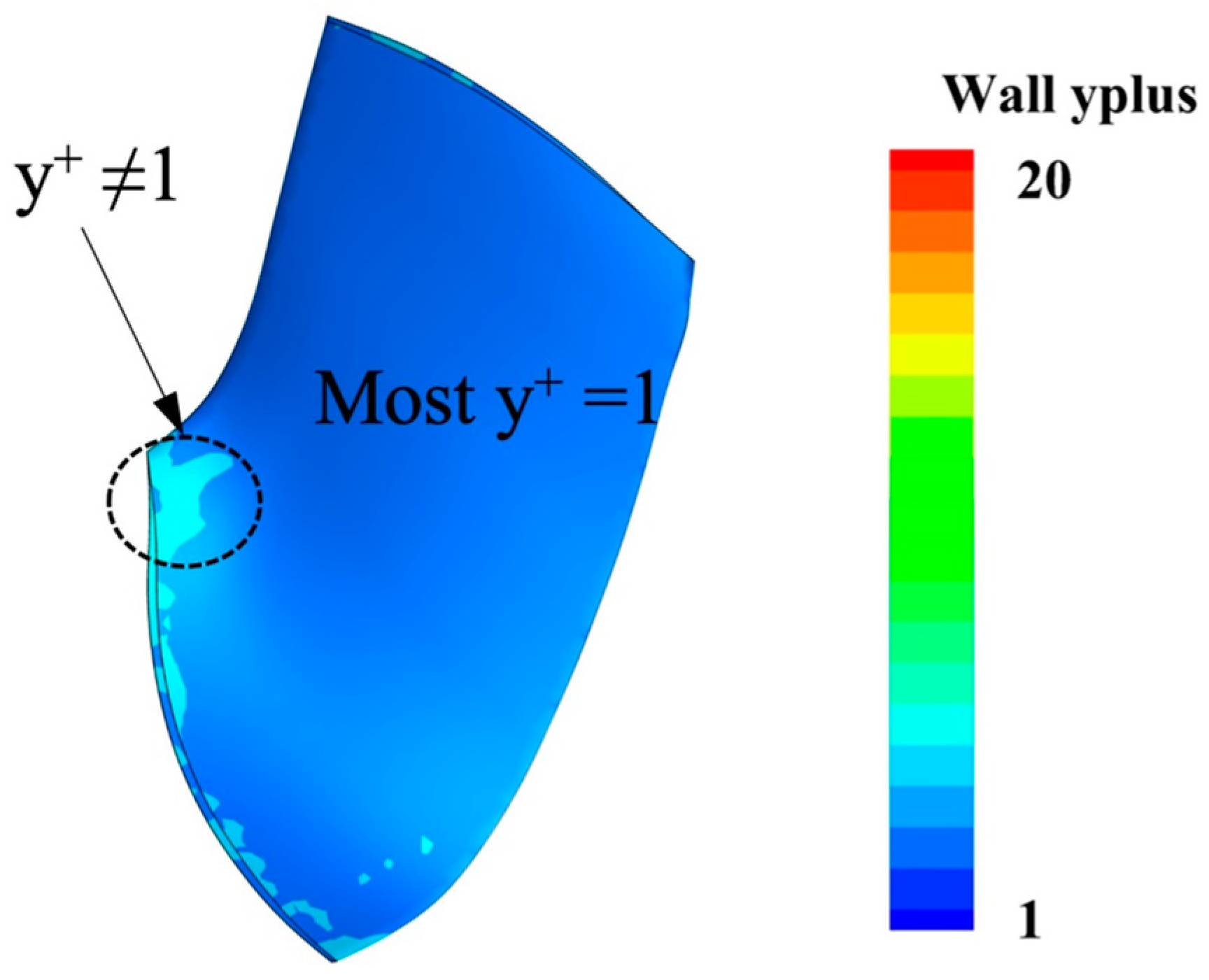

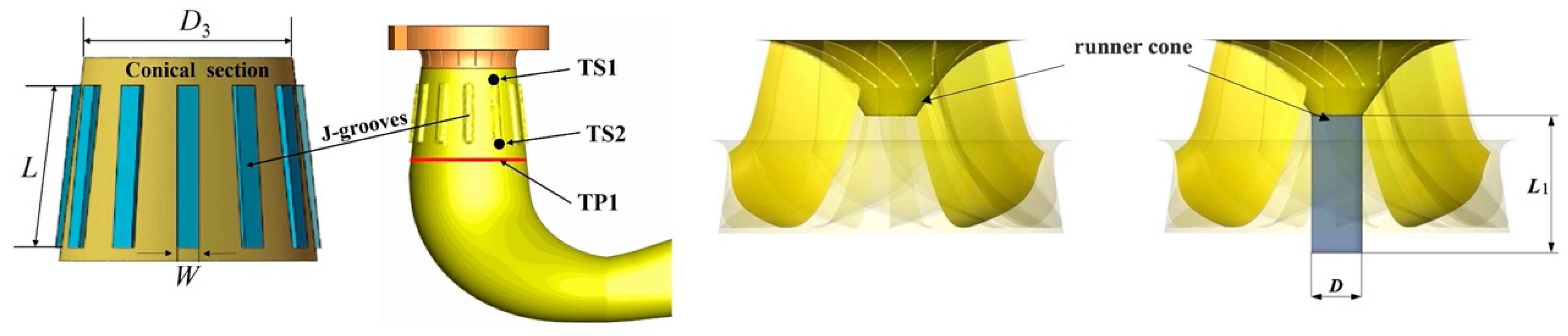


| Parameter | Value | Symbol |
|---|---|---|
| Runner diameter | 0.43 m | D1 |
| Unit speed | 81.587 r/min | n11 |
| Unit discharge | 1.064 m3/s | Q11 |
| Runner blades number | 13 | Zr |
| Stay vanes number | 16 | ZT |
| Guide vanes number | 8 | Zs |
| Entrance diameter of spiral casing | 0.547 m | D0 |
| Design head | 10 m | Hr |
| Rated revolution | 600 rpm | nr |
| Design flow | 0.7 m3/s | Qr |
| Rated output power | 55 kW | Pr |
| Turbine efficiency on design operating condition | 92% | ηr |
| Turbine Component | Spiral Case | Distributer | Runner | Draft Tube |
|---|---|---|---|---|
| elements (×104) | 380 | 210 | 474 | 232 |
| nodes (×104) | 354 | 200 | 445 | 221 |
| Optimized Structure Type | Installing J-Grooves on Conical Section of Draft Tube | Extending the Runner Cone | ||||
|---|---|---|---|---|---|---|
| Abbreviation of Model Name | Number | Length | Width | Diameter | Length | |
| 12 | 120 mm | 10 mm | 30 mm | 88 mm | ||
| N-J | No | No | ||||
| W-J | Yes | No | ||||
| C | No | Yes | ||||
| J+C | Yes | Yes | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Nie, C.; Luo, Z. The Influence of Structure Optimization on Vortex Suppression and Energy Dissipation in the Draft Tube of Francis Turbine. Processes 2024, 12, 2249. https://doi.org/10.3390/pr12102249
Zhang X, Nie C, Luo Z. The Influence of Structure Optimization on Vortex Suppression and Energy Dissipation in the Draft Tube of Francis Turbine. Processes. 2024; 12(10):2249. https://doi.org/10.3390/pr12102249
Chicago/Turabian StyleZhang, Xiaoxu, Cong Nie, and Zhumei Luo. 2024. "The Influence of Structure Optimization on Vortex Suppression and Energy Dissipation in the Draft Tube of Francis Turbine" Processes 12, no. 10: 2249. https://doi.org/10.3390/pr12102249
APA StyleZhang, X., Nie, C., & Luo, Z. (2024). The Influence of Structure Optimization on Vortex Suppression and Energy Dissipation in the Draft Tube of Francis Turbine. Processes, 12(10), 2249. https://doi.org/10.3390/pr12102249






