Modeling and Optimization of the Inland Container Transportation Problem Considering Multi-Size Containers, Fuel Consumption, and Carbon Emissions
Abstract
1. Introduction
- (1)
- We propose a simple but effective graph modeling approach to represent the problem on a directed network. The graph model not only simplifies the handling of capacity-related constraints arising from multiple container sizes but also enables the linear representation of the constraints posed by the limited empty containers, thereby facilitating the development of a mathematical formulation for the problem.
- (2)
- A tailored branch-and-price algorithm is presented for the problem. For efficient resolution of the pricing subproblems, we suggest a hybrid algorithm which integrates an exact label-setting algorithm, improved through the decremental state-space relaxation, with its heuristic counterpart. Besides, an upper bounding scheme is proposed to prune nodes.
- (3)
- Numerical tests are performed to verify the effectiveness of the proposed algorithm. Furthermore, a sensitivity analysis is performed to examine the effects of various factors, providing valuable insights for managerial decision making.
2. Literature Review
2.1. ICT with Multi-Size Containers
2.2. Ict with Limited Empty Containers
2.3. Ict Considering Fuel Consumption and Carbon Emissions
3. Problem Description and Models
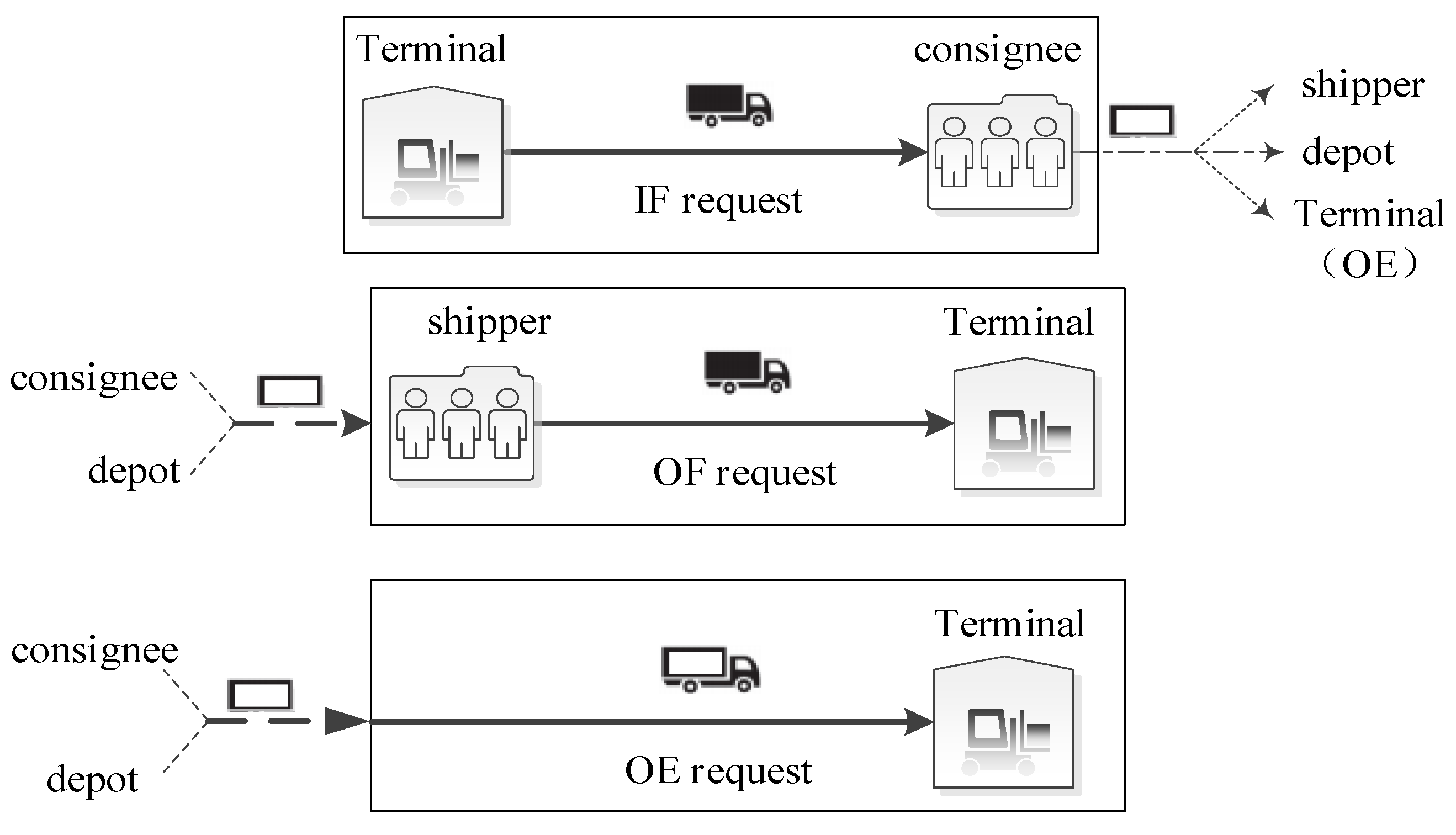
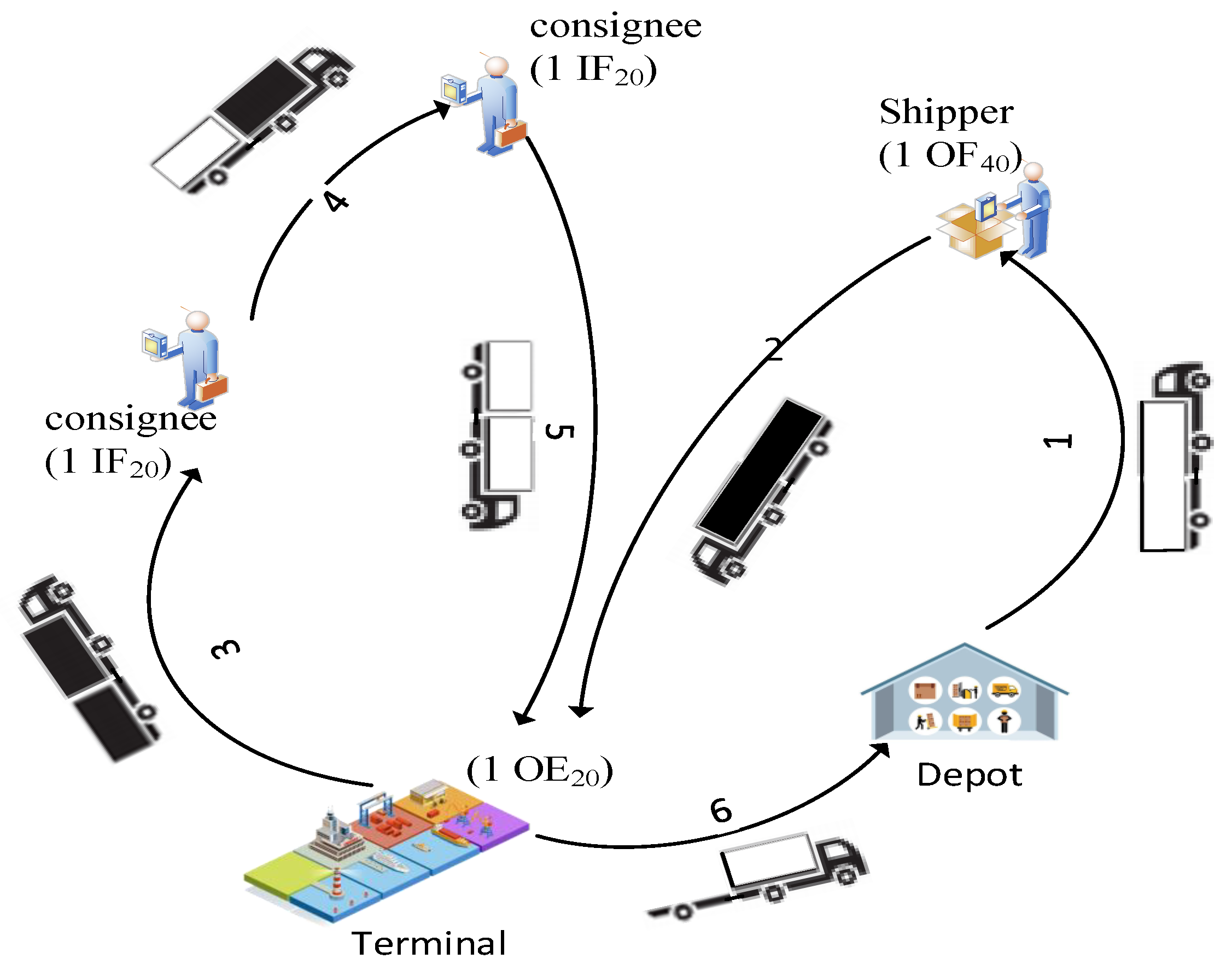
3.1. Problem Description
- (1)
- OF container transportation request. A truck transports an empty container to the shipper (origin). The container, once filled with goods, is then delivered by the truck to the terminal (destination) for export purposes.
- (2)
- OE container transportation request. Due to trade imbalances between regions, a certain quantity of empty containers needs to be transported to the terminal (destination) for export. It is worth mentioning that an OE request is not tied to a specific origin, as the empty container can be sourced from either the depot or a consignee;
- (3)
- IF container transportation request. A truck picks up a full container from the terminal (origin) and transports it to the designated consignee (destination). Once the container is emptied, the truck has several options: it can return the empty container to the depot, deliver it to another export customer for repacking, or transport it back to the terminal as an outbound empty (OE) container.
3.2. Graphic Representation
3.2.1. Source and Sink Nodes
3.2.2. Nodes for Container Transportation Requests
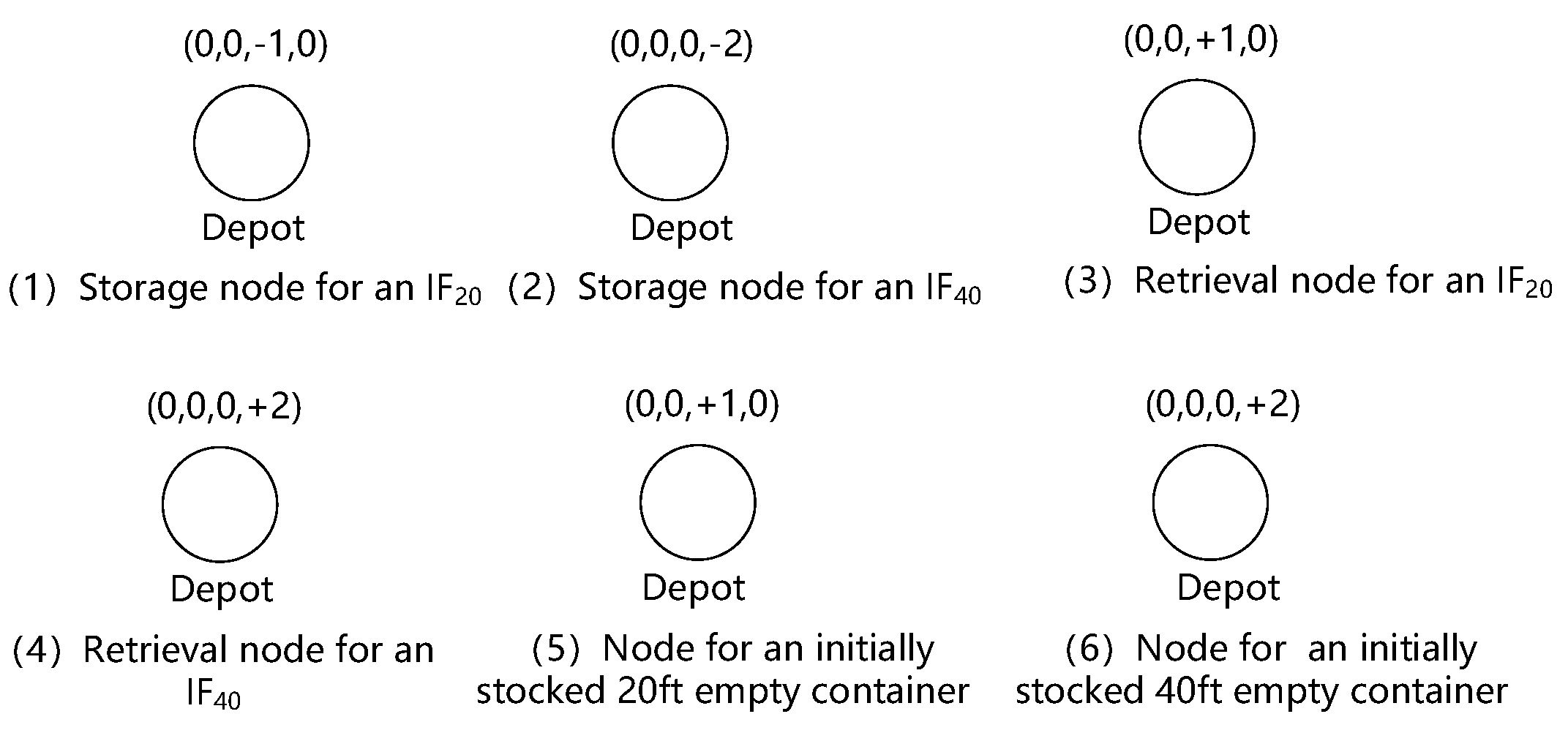
3.2.3. Node Representing Storage and Retrieval of an Empty Container from the Depot
3.3. Mathematical Formulation
4. Branch-and-Price Algorithm
4.1. Dantzig–Wolfe Decomposition
4.1.1. Master Problem
4.1.2. Pricing Subproblem
4.2. Label-Setting Algorithms for Solving Subproblems
4.2.1. Exact Label-Setting Algorithm
- (1)
- Label structure
- (2)
- Label extension
- (3)
- Dominance rule
- (4)
- Decremental state-space relaxation
| Algorithm 1: Pseudocode of the label-setting algorithm with decremental state-space relaxation |
 |
4.2.2. Heuristic Label-Setting Algorithm
4.2.3. The Framework of Algorithms for the Pricing Subproblems
| Algorithm 2: The algorithmic framework for solving the pricing subproblems |
 |
4.3. Initial Solution to the RLMP
4.4. Branching Schemes
4.4.1. Arc Branching
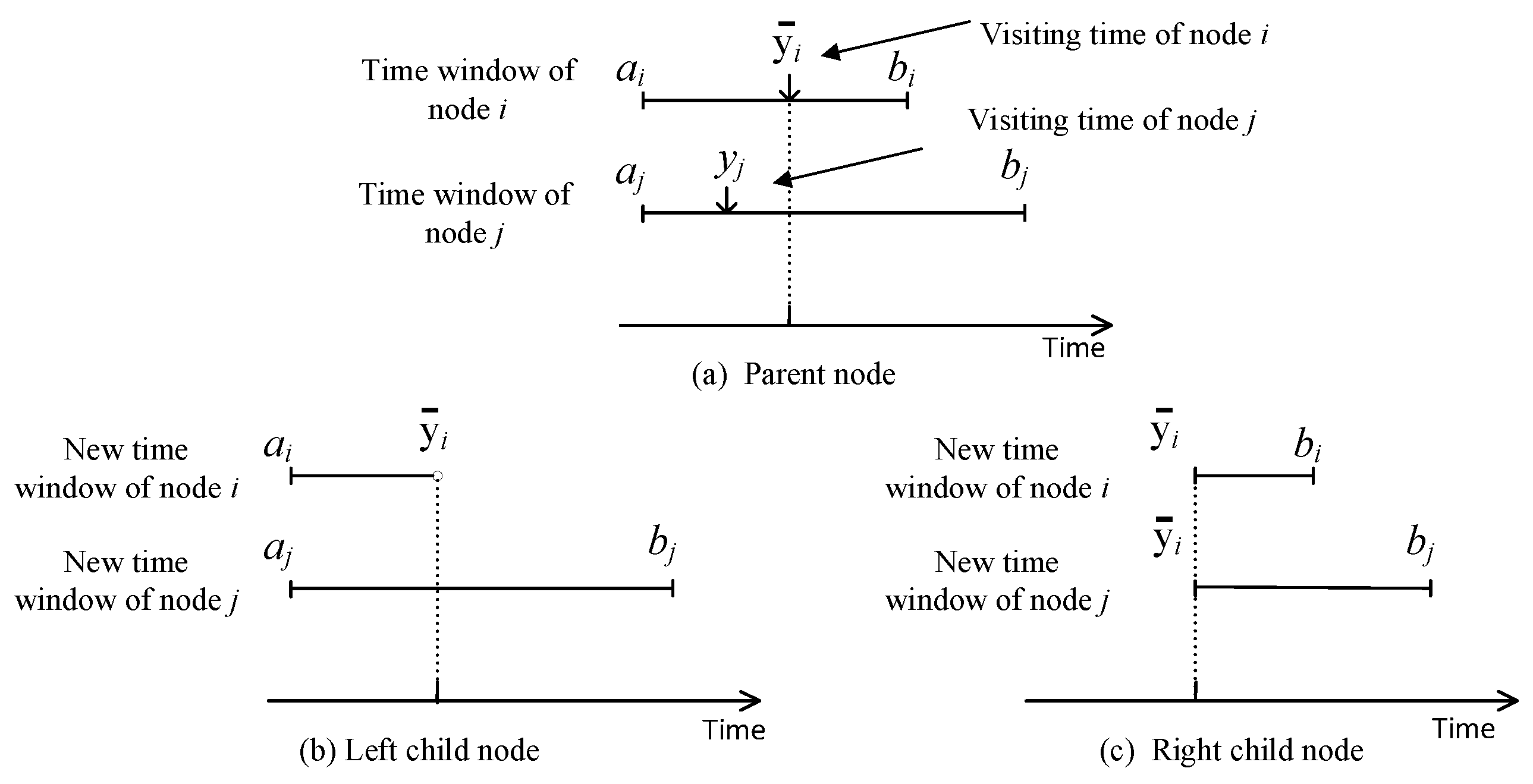
4.4.2. Time Window Branching
4.5. Bounding Strategy
5. Numerical Simulations
5.1. Test Instance Generation and Experimental Configuration
5.2. Computational Results
5.2.1. Results of Small- and Medium-Scale Instances
5.2.2. Results of Large-Scale Instances
5.3. Effectiveness of the Enhancement Strategies
5.4. Sensitivity Analysis
5.4.1. Impact of the Initial Number of Empty Containers at the Depot
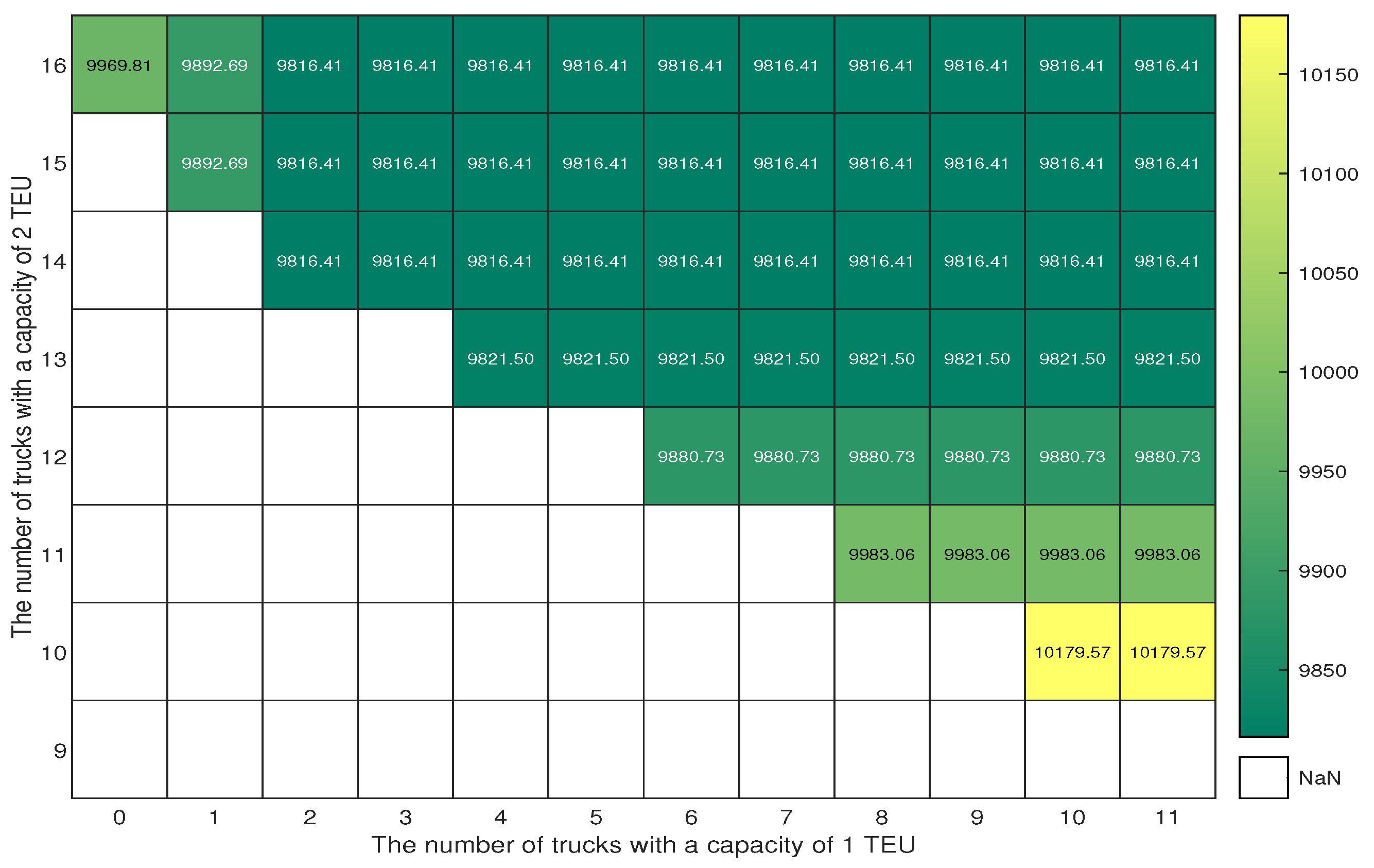
5.4.2. Impact of Truck Fleet Configuration
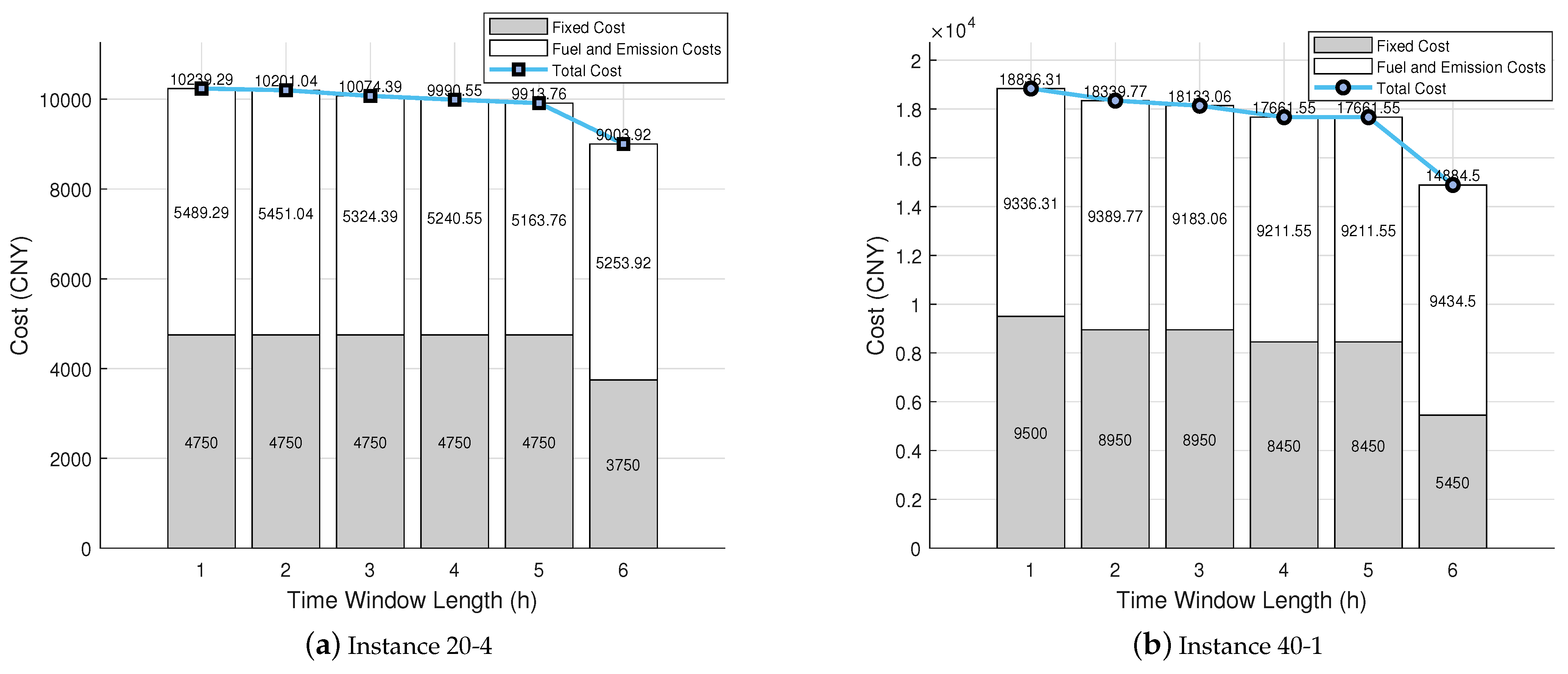
5.4.3. Impact of Time Window Length
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Springel, K. Network externality and subsidy structure in two-sided markets: Evidence from electric vehicle incentives. Am. Econ. J. Econ. Policy 2021, 13, 393–432. [Google Scholar] [CrossRef]
- Pan, X.; Wang, M.; Li, M. Low-carbon policy and industrial structure upgrading: Based on the perspective of strategic interaction among local governments. Energy Policy 2023, 183, 113794. [Google Scholar] [CrossRef]
- Available online: https://ww2.arb.ca.gov/resources/fact-sheets/advanced-clean-fleets-regulation-detailed-drayage-truck-requirements (accessed on 2 October 2024).
- Johanson, G.; Svedberg, U. A novel method for pre-ventilation of shipping containers. Int. J. Hyg. Environ. Health 2020, 230, 113626. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.boomandbucket.com/blog/how-much-storage-is-a-container-costs (accessed on 3 October 2024).
- Chung, K.H.; Ko, C.S.; Shin, J.Y.; Hwang, H.; Kim, K.H. Development of mathematical models for the container road transportation in Korean trucking industries. Comput. Ind. Eng. 2007, 53, 252–262. [Google Scholar] [CrossRef]
- Vidović, M.; Radivojević, G.; Raković, B. Vehicle routing in containers pickup up and delivery processes. Procedia Soc. Behav. Sci. 2011, 20, 335–343. [Google Scholar] [CrossRef][Green Version]
- Bruglieri, M.; Mancini, S.; Peruzzini, R.; Pisacane, O. The multi-period multi-trip container drayage problem with release and due dates. Comput. Oper. Res. 2021, 125, 105102. [Google Scholar] [CrossRef]
- Bustos-Coral, D.; Costa, A.M. Drayage routing with heterogeneous fleet, compatibility constraints, and truck load configurations. Transp. Res. Part E Logist. Transp. Rev. 2022, 168, 102922. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, W.Y.; Kopfer, H. Multi-size container transportation by truck: Modeling and optimization. Flex. Serv. Manuf. J. 2015, 27, 403–430. [Google Scholar] [CrossRef]
- Funke, J.; Kopfer, H. A model for a multi-size inland container transportation problem. Transp. Res. Part E Logist. Transp. Rev. 2016, 89, 70–85. [Google Scholar] [CrossRef]
- Moghaddam, M.; Pearce, R.H.; Mokhtar, H.; Prato, C.G. A generalised model for container drayage operations with heterogeneous fleet, multi-container sizes and two modes of operation. Transp. Res. Part E Logist. Transp. Rev. 2020, 139, 101973. [Google Scholar] [CrossRef]
- Chen, R.; Chen, S.; Cui, H.; Meng, Q. The container drayage problem for heterogeneous trucks with multiple loads: A revisit. Transp. Res. Part E Logist. Transp. Rev. 2021, 147, 102241. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, W.Y.; Moon, I.K. Modeling and optimization of a container drayage problem with resource constraints. Int. J. Prod. Econ. 2011, 133, 351–359. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, C.; Wang, J. A novel mathematical model and a large neighborhood search algorithm for container drayage operations with multi-resource constraints. Comput. Ind. Eng. 2020, 139, 106143. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Y.; He, C.; Liu, C. Modeling and Optimization of Container Drayage Problem with Empty Container Constraints across Multiple Inland Depots. Sustainability 2024, 16, 5090. [Google Scholar] [CrossRef]
- Fazi, S.; Choudhary, S.K.; Dong, J.X. The multi-trip container drayage problem with synchronization for efficient empty containers re-usage. Eur. J. Oper. Res. 2023, 310, 343–359. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, R.; Huang, M.; Shi, H. Modeling and analyses of container drayage transportation problem with the objective of low carbons. In Proceedings of the The 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 4654–4658. [Google Scholar]
- Konstantzos, G.E.; Saharidis, G.K.; Loizidou, M. Development of a model for assessing Greenhouse Gas (GHG) emissions from terminal and drayage operations. Oper. Res. 2017, 17, 807–819. [Google Scholar] [CrossRef]
- Shiri, S.; Huynh, N. Assessment of US chassis supply models on drayage productivity and air emissions. Transp. Res. Part D Transp. Environ. 2018, 61, 174–203. [Google Scholar] [CrossRef]
- He, W.; Jin, Z.; Huang, Y.; Xu, S. The inland container transportation problem with separation mode considering carbon dioxide emissions. Sustainability 2021, 13, 1573. [Google Scholar] [CrossRef]
- Chen, R.; Meng, Q.; Jia, P. Container port drayage operations and management: Past and future. Transp. Res. Part E Logist. Transp. Rev. 2022, 159, 102633. [Google Scholar] [CrossRef]
- Barth, M.; Younglove, T.; Scora, G. Development of a Heavy-Duty Diesel Modal Emissions and Fuel Consumption Model; Institute of Transportation Studies, UC Berkeley: Berkeley, CA, USA, 2005. [Google Scholar]
- Barth, M.; Boriboonsomsin, K. Energy and emissions impacts of a freeway-based dynamic eco-driving system. Transp. Res. Part D Transp. Environ. 2009, 14, 400–410. [Google Scholar] [CrossRef]
- Boland, N.; Dethridge, J.; Dumitrescu, I. Accelerated label setting algorithms for the elementary resource constrained shortest path problem. Oper. Res. Lett. 2006, 34, 58–68. [Google Scholar] [CrossRef]
- Righini, G.; Salani, M. New dynamic programming algorithms for the resource constrained elementary shortest path problem. Netw. Int. J. 2008, 51, 155–170. [Google Scholar] [CrossRef]
- Li, J.; Qin, H.; Baldacci, R.; Zhu, W. Branch-and-price-and-cut for the synchronized vehicle routing problem with split delivery, proportional service time and multiple time windows. Transp. Res. Part E Logist. Transp. Rev. 2020, 140, 101955. [Google Scholar] [CrossRef]
- Huang, N.; Li, J.; Zhu, W.; Qin, H. The multi-trip vehicle routing problem with time windows and unloading queue at depot. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102370. [Google Scholar] [CrossRef]
- Luo, Z.; Qin, H.; Lim, A. Branch-and-price-and-cut for the multiple traveling repairman problem with distance constraints. Eur. J. Oper. Res. 2014, 234, 49–60. [Google Scholar] [CrossRef]
- Nossack, J.; Pesch, E. A truck scheduling problem arising in intermodal container transportation. Eur. J. Oper. Res. 2013, 230, 666–680. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L.; Van Woensel, T.; Gross, J.P. Time-dependent vehicle routing problem with path flexibility. Transp. Res. Part B Methodol. 2017, 95, 169–195. [Google Scholar] [CrossRef]
- Fan, H.; Ren, X.; Guo, Z.; Li, Y. Truck scheduling problem considering carbon emissions under truck appointment system. Sustainability 2019, 11, 6256. [Google Scholar] [CrossRef]





| Paper | Feature | Objective | Model | Solution Method | |||||
|---|---|---|---|---|---|---|---|---|---|
| Multi-Size | Empty Con. | Heter. | Carbon | Solver | Exact | Heuristic | |||
| [6] | ✓ | ✓ | Minimal Cost | Non-linear | ✓ | ||||
| [7] | ✓ | Minimal Cost | Linear | ✓ | |||||
| [8] | ✓ | Minimal Distance | Linear | ✓ | |||||
| [9] | ✓ | ✓ | Minimal Cost | Linear | ✓ | ||||
| [10] | ✓ | Minimal Time | Non-linear | ✓ | |||||
| [11] | ✓ | Minimal Distance/Time | Linear | ✓ | |||||
| [12] | ✓ | Minimal Time | Linear | ✓ | |||||
| [13] | ✓ | ✓ | Minimal Cost | Linear | ✓ | ✓ | |||
| [14] | ✓ | Minimal Time | Non-linear | ✓ | |||||
| [15] | ✓ | Minimal Time/Truck | Non-linear | ✓ | |||||
| [16] | ✓ | ✓ | Minimal Cost | Non-linear | ✓ | ||||
| [17] | ✓ | Minimal Cost | Linear | ✓ | |||||
| [18] | ✓ | Minimal Emissions | Linear | ✓ | |||||
| [19] | ✓ | Minimal Emissions | Non-linear | ✓ | |||||
| [20] | ✓ | Minimal Time | Linear | ✓ | |||||
| [21] | ✓ | Minimal Fuel/Emissions | Non-linear | ✓ | |||||
| Our study | ✓ | ✓ | ✓ | ✓ | Minimal Fuel/Emissions | Linear | ✓ | ✓ | |
| Parameter | Description |
|---|---|
| N | Set of all nodes |
| K | Set of all trucks |
| S | Source node |
| Sink node | |
| Set of first nodes used to represent IF20, IF40, OF20, and OF40 requests | |
| Set of second nodes used to represent IF20, IF40, OF20, and OF40 requests | |
| The corresponding second node for node | |
| Set of nodes used to represent OE20 and OE40 requests | |
| D | Set of nodes representing storage of empty containers released by IF requests to the depot |
| P | Set of nodes representing retrieval of empty containers released by IF requests and returned back to the depot |
| Set of nodes representing retrieval of empty containers initially stationed at the depot | |
| Change in the number of 20 ft full containers when visiting node i, | |
| Change in the number of 40 ft full containers when visiting node i, | |
| Change in the number of 20 ft empty containers when visiting node i, | |
| Change in the number of 40 ft empty containers when visiting node i, | |
| Change in the payload of a truck when it visits node i, which can be determined based on associated handling operations and the weight of the empty container and its contents | |
| Unladen weight of truck k, i.e., the total weight of the tractor and the trailer for truck k | |
| Coefficient of the engine module | |
| Coefficient of the weight module | |
| Coefficient of the speed module | |
| Time window of node i | |
| Time consumed by loading and unloading operations associated with node i | |
| Distance from node i to node j | |
| v | The average travel speed of trucks |
| Traveling time from node i to node j, which can be computed by /v | |
| Grams of CO2 emitted per liter of fuel | |
| Capacity of truck k (measured in TEUs), | |
| The fixed cost of truck k | |
| Set of pairwise storage node and the corresponding retrieval node introduced for IF requests for which a temporal constraint exists | |
| The cost tax per unit of carbon emissions | |
| The price of fuel | |
| H | The planning horizon |
| M | A sufficiently large positive number |
| Variable | Description |
| The quantity of 20 ft full containers on truck k upon visiting node i | |
| The quantity of 40 ft full containers on truck k upon visiting node i | |
| The quantity of 20 ft empty containers on truck k upon visiting node i | |
| The quantity of 40 ft empty containers on truck k upon visiting node i | |
| One if truck k travels through arc(i, j), zero otherwise | |
| The time when truck k arrives at node i | |
| The payload weight of truck k on arc(i, j), i.e., the weight of full or empty containers carried by truck k |
| Parameter | Value |
|---|---|
| Fuel cost per liter | 8 CNY/L |
| Carbon emissions per liter | 2.23 kg/L |
| The carbon tax | 0.05 CNY/kg |
| Engine-specific coefficient | 0.00021 L/s |
| Speed-specific coefficient | Ls2/m3 |
| Weight-specific coefficient | L/(m * kg) |
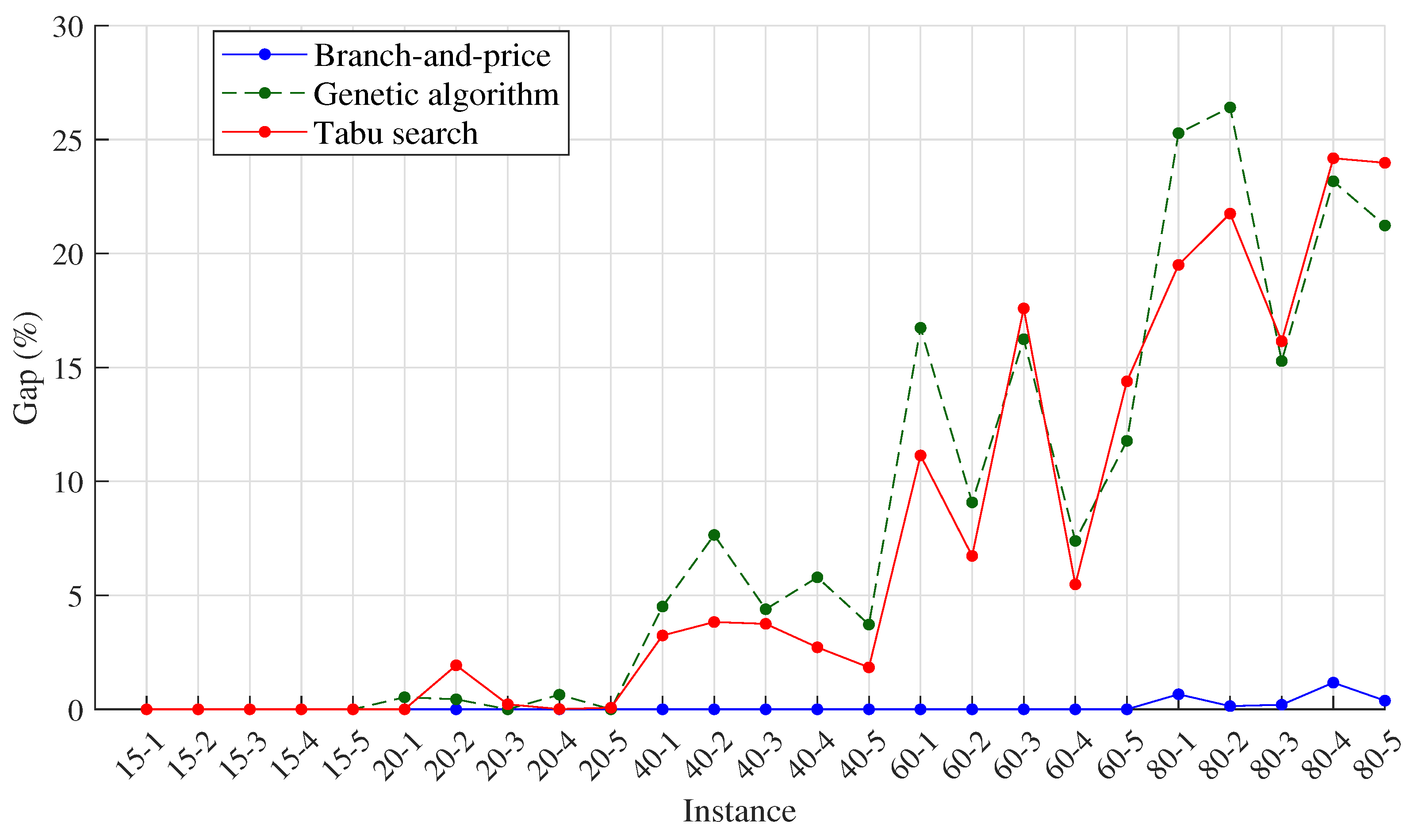
| Ins | LB | Branch-and-Price | Genetic Algorithm | Tabu Search | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Obj (CNY) | CPU (s) | Gap (%) | Obj (CNY) | CPU (s) | Gap (%) | Obj (CNY) | CPU (s) | Gap (%) | ||
| 15-1 | 8005.54 | 8005.54 | 2.2 | 0 | 8005.54 | 153.1 | 0 | 8005.54 | 100.3 | 0 |
| 15-2 | 6990.45 | 6990.45 | 1.4 | 0 | 6990.45 | 126.2 | 0 | 6990.45 | 88.4 | 0 |
| 15-3 | 7573.85 | 7573.85 | 1.1 | 0 | 7573.85 | 111.3 | 0 | 7573.85 | 85.5 | 0 |
| 15-4 | 7991.12 | 7991.12 | 0.9 | 0 | 7991.12 | 160.5 | 0 | 7991.12 | 80.4 | 0 |
| 15-5 | 6762.68 | 6762.68 | 2.2 | 0 | 6762.68 | 148.0 | 0 | 6762.68 | 86.3 | 0 |
| Average | 7464.73 | 7464.73 | 1.6 | 0 | 7464.73 | 139.8 | 0 | 7464.73 | 88.2 | 0 |
| 20-1 | 11,068.27 | 11,068.27 | 3.3 | 0 | 11,126.67 | 219.7 | 0.53 | 11,068.27 | 199.9 | 0 |
| 20-2 | 8485.57 | 8485.57 | 12.1 | 0 | 8523.27 | 220.1 | 0.44 | 8649.01 | 154.9 | 1.93 |
| 20-3 | 9961.17 | 9961.17 | 4.4 | 0 | 9961.17 | 212.2 | 0 | 9982.62 | 158.2 | 0.22 |
| 20-4 | 10,074.39 | 10,074.39 | 15.2 | 0 | 10,138.66 | 206.0 | 0.64 | 10,075.77 | 153.1 | 0.01 |
| 20-5 | 8876.97 | 8876.97 | 67.3 | 0 | 8876.97 | 199.3 | 0 | 8883.50 | 166.4 | 0.07 |
| Average | 9693.27 | 9693.27 | 20.5 | 0 | 9725.35 | 211.5 | 0.32 | 9731.83 | 166.5 | 0.45 |
| 40-1 | 18,133.06 | 18,133.06 | 81.3 | 0 | 18,950.32 | 830.5 | 4.51 | 18,720.71 | 556.2 | 3.24 |
| 40-2 | 16,692.86 | 16,692.86 | 122.9 | 0 | 17,969.90 | 749.3 | 7.65 | 17,331.51 | 519.8 | 3.83 |
| 40-3 | 19,205.73 | 19,205.73 | 119.6 | 0 | 20,048.78 | 687.6 | 4.39 | 19,926.12 | 467.1 | 3.75 |
| 40-4 | 17,958.27 | 17,958.27 | 113.5 | 0 | 18,997.52 | 673.9 | 5.79 | 18,446.95 | 491.9 | 2.72 |
| 40-5 | 19,684.70 | 19,684.70 | 274.7 | 0 | 20,417.10 | 628.2 | 3.72 | 20,046.11 | 491.1 | 1.84 |
| Average | 18,334.92 | 18,334.92 | 142.4 | 0 | 19,276.72 | 713.9 | 5.21 | 18,894.28 | 505.2 | 3.07 |
| 60-1 | 27,357.29 | 27,357.29 | 312.1 | 0 | 31,936.90 | 1439.5 | 16.74 | 30,404.16 | 1167.2 | 11.14 |
| 60-2 | 25,625.43 | 25,625.43 | 141.5 | 0 | 27,952.67 | 1338.1 | 9.08 | 27,349.41 | 1201.1 | 6.73 |
| 60-3 | 25,623.82 | 25,623.82 | 820.2 | 0 | 29,785.62 | 1416.8 | 16.24 | 30,130.46 | 1105.5 | 17.59 |
| 60-4 | 24,820.74 | 24,820.74 | 1032.7 | 0 | 26,655.37 | 1590.5 | 7.39 | 26,182.11 | 1134.8 | 5.48 |
| 60-5 | 25,846.78 | 25,846.78 | 1593.2 | 0 | 28,892.49 | 1421.6 | 11.78 | 29,566.73 | 1001.0 | 14.39 |
| Average | 25,854.81 | 25,854.81 | 779.9 | 0 | 29,044.61 | 1441.3 | 12.2 | 28,726.57 | 1121.9 | 11.07 |
| 80-1 | 31,348.31 | 31,554.81 | 3600.0 | 0.66 | 39,272.93 | 3375.7 | 25.28 | 37,459.72 | 1943.7 | 19.50 |
| 80-2 | 30,166.71 | 30,208.79 | 3600.0 | 0.14 | 38,134.08 | 2437.9 | 26.41 | 36,727.26 | 1887.2 | 21.75 |
| 80-3 | 29,774.46 | 29,834.54 | 3600.0 | 0.20 | 34,324.77 | 2351.6 | 15.28 | 34,583.22 | 1717.2 | 16.15 |
| 80-4 | 30,359.36 | 30,715.00 | 3600.0 | 1.17 | 37,393.83 | 2191.6 | 23.17 | 37,699.13 | 1637.3 | 24.18 |
| 80-5 | 33,303.11 | 33,429.26 | 3600.0 | 0.38 | 40,374.00 | 2234.6 | 21.23 | 41,288.75 | 1610.6 | 23.98 |
| Average | 30,990.39 | 31,148.48 | 3600.0 | 0.51 | 37,899.92 | 2518.3 | 22.28 | 37,551.61 | 1759.2 | 21.11 |
| Ins | Branch-and-Price | Genetic Algorithm | Tabu Search | |||||
|---|---|---|---|---|---|---|---|---|
| Obj (CNY) | CPU (s) | Obj (CNY) | CPU (s) | Gap (%) | Obj (CNY) | CPU (s) | Gap (%) | |
| 100-1 | 41,235.11 | 3600.0 | 48,204.36 | 2627.0 | 16.90 | 48,051.17 | 2534.5 | 16.53 |
| 100-2 | 38,424.29 | 3600.0 | 49,189.31 | 2790.5 | 28.02 | 47,151.14 | 2282.7 | 22.71 |
| 100-3 | 39,112.85 | 3600.0 | 46,052.86 | 2856.1 | 17.74 | 44,103.13 | 2421.2 | 12.76 |
| 100-4 | 45,983.66 | 3600.0 | 48,937.88 | 2708.4 | 6.42 | 51,213.51 | 2233.4 | 11.37 |
| 100-5 | 40,316.55 | 3600.0 | 48,937.88 | 2654.0 | 21.38 | 48,153.26 | 2266.5 | 19.44 |
| Average | 41,014.49 | 3600.0 | 48,264.46 | 2727.2 | 18.09 | 47,734.44 | 2347.7 | 16.56 |
| 120-1 | 46,961.14 | 3600.0 | 56,308.80 | 4092.8 | 19.91 | 55,994.75 | 3104.3 | 19.24 |
| 120-2 | 47,503.36 | 3600.0 | 59,026.46 | 3769.5 | 24.26 | 55,800.31 | 3263.8 | 17.47 |
| 120-3 | 47,436.77 | 3600.0 | 57,838.13 | 3511.6 | 21.93 | 56,490.31 | 3157.0 | 19.09 |
| 120-4 | 47,667.23 | 3600.0 | 57,335.73 | 3233.8 | 20.28 | 56,553.33 | 3251.5 | 18.64 |
| 120-5 | 51,068.30 | 3600.0 | 62,473.83 | 2833.3 | 22.33 | 60,457.96 | 3183.0 | 18.39 |
| Average | 48,127.36 | 3600.0 | 58,596.59 | 3488.2 | 21.74 | 57,059.33 | 3191.9 | 18.56 |
| 160-1 | 61,929.31 | 3600.0 | 79,455.31 | 6590.3 | 28.30 | 74,171.63 | 5227.3 | 19.77 |
| 160-2 | 63,367.66 | 3600.0 | 77,391.17 | 5267.4 | 22.13 | 75,331.57 | 5457.8 | 18.88 |
| 160-3 | 64,555.89 | 3600.0 | 83,217.71 | 8071.4 | 28.91 | 80,944.50 | 5130.9 | 25.39 |
| 160-4 | 61,750.05 | 3600.0 | 79,482.28 | 7853.2 | 28.72 | 75,365.98 | 5311.9 | 22.05 |
| 160-5 | 67,466.78 | 3600.0 | 85,316.26 | 8210.3 | 26.46 | 81,807.78 | 5289.2 | 21.26 |
| Average | 63,813.94 | 3600.0 | 80,972.54 | 7198.5 | 26.90 | 77,524.29 | 5283.4 | 21.47 |
| Ins | Proposed Exact Branch-and-Price | Basic Branch-and-Price | ||||
|---|---|---|---|---|---|---|
| Obj (CNY) | CPU (s) | Node | Obj (CNY) | CPU (s) | Node | |
| 15-1 | 8005.54 | 2.2 | 1 | 8005.54 | 18.3 | 1 |
| 15-2 | 6990.45 | 1.4 | 1 | 6990.45 | 23.2 | 1 |
| 15-3 | 7573.85 | 1.1 | 1 | 7573.85 | 6.9 | 1 |
| 15-4 | 7991.12 | 0.9 | 1 | 7991.12 | 14.9 | 1 |
| 15-5 | 6762.68 | 2.2 | 1 | 6762.68 | 22.2 | 1 |
| 20-1 | 11,068.27 | 3.3 | 1 | 11,068.27 | 328.9 | 1 |
| 20-2 | 8485.57 | 12.1 | 1 | 8485.57 | 135.2 | 1 |
| 20-3 | 9961.17 | 4.4 | 1 | 9961.17 | 136.9 | 1 |
| 20-4 | 10,074.39 | 15.2 | 9 | 10,074.39 | 412.8 | 9 |
| 20-5 | 8876.97 | 67.3 | 31 | 8876.97 | 2617.2 | 35 |
| 40-1 | 18,133.06 | 81.3 | 1 | - | - | - |
| 40-2 | 16,692.86 | 122.9 | 3 | - | - | - |
| 40-3 | 19,205.73 | 119.6 | 3 | - | - | - |
| 40-4 | 17,958.27 | 113.5 | 1 | - | - | - |
| 40-5 | 19,684.70 | 274.7 | 1 | - | - | - |
| Number of Empty Containers | Total Transportation Cost (CNY) | |||
|---|---|---|---|---|
| Ins 15-5 | Ins 20-4 | Ins 40-1 | Ins 60-4 | |
| 0 | 6779.16 | 10,154.07 | 18,211.60 | 24,954.44 |
| 1 | 6762.68 | 10,074.39 | 18,133.06 | 24,905.60 |
| 2 | 6762.68 | 10,074.39 | 18,103.62 | 24,858.94 |
| 3 | 6762.68 | 10,074.39 | 18,103.62 | 24,820.74 |
| 4 | 6762.68 | 10,074.39 | 18,103.62 | 24,820.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Zhang, Y. Modeling and Optimization of the Inland Container Transportation Problem Considering Multi-Size Containers, Fuel Consumption, and Carbon Emissions. Processes 2024, 12, 2231. https://doi.org/10.3390/pr12102231
Song Y, Zhang Y. Modeling and Optimization of the Inland Container Transportation Problem Considering Multi-Size Containers, Fuel Consumption, and Carbon Emissions. Processes. 2024; 12(10):2231. https://doi.org/10.3390/pr12102231
Chicago/Turabian StyleSong, Yujian, and Yuting Zhang. 2024. "Modeling and Optimization of the Inland Container Transportation Problem Considering Multi-Size Containers, Fuel Consumption, and Carbon Emissions" Processes 12, no. 10: 2231. https://doi.org/10.3390/pr12102231
APA StyleSong, Y., & Zhang, Y. (2024). Modeling and Optimization of the Inland Container Transportation Problem Considering Multi-Size Containers, Fuel Consumption, and Carbon Emissions. Processes, 12(10), 2231. https://doi.org/10.3390/pr12102231







