Experimental and CFD Analysis of Hydrodynamics in Dual-Impeller Crystallizer at Different Off-Bottom Clearances
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Determination of the Crystallization Parameters and Final Product Properties
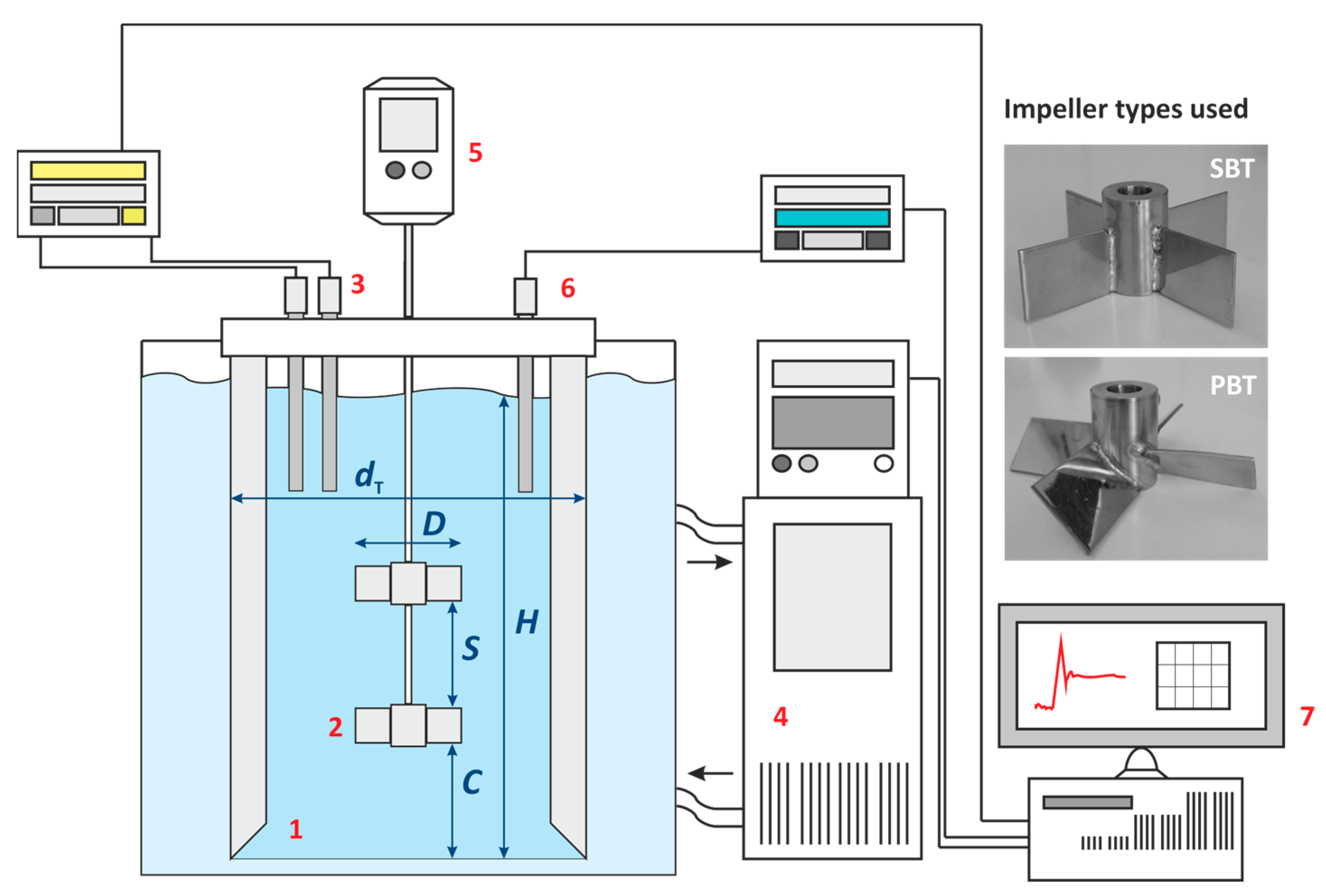
2.2. Experimental and Numerical Analyses of Hydrodynamics in the Crystallizer
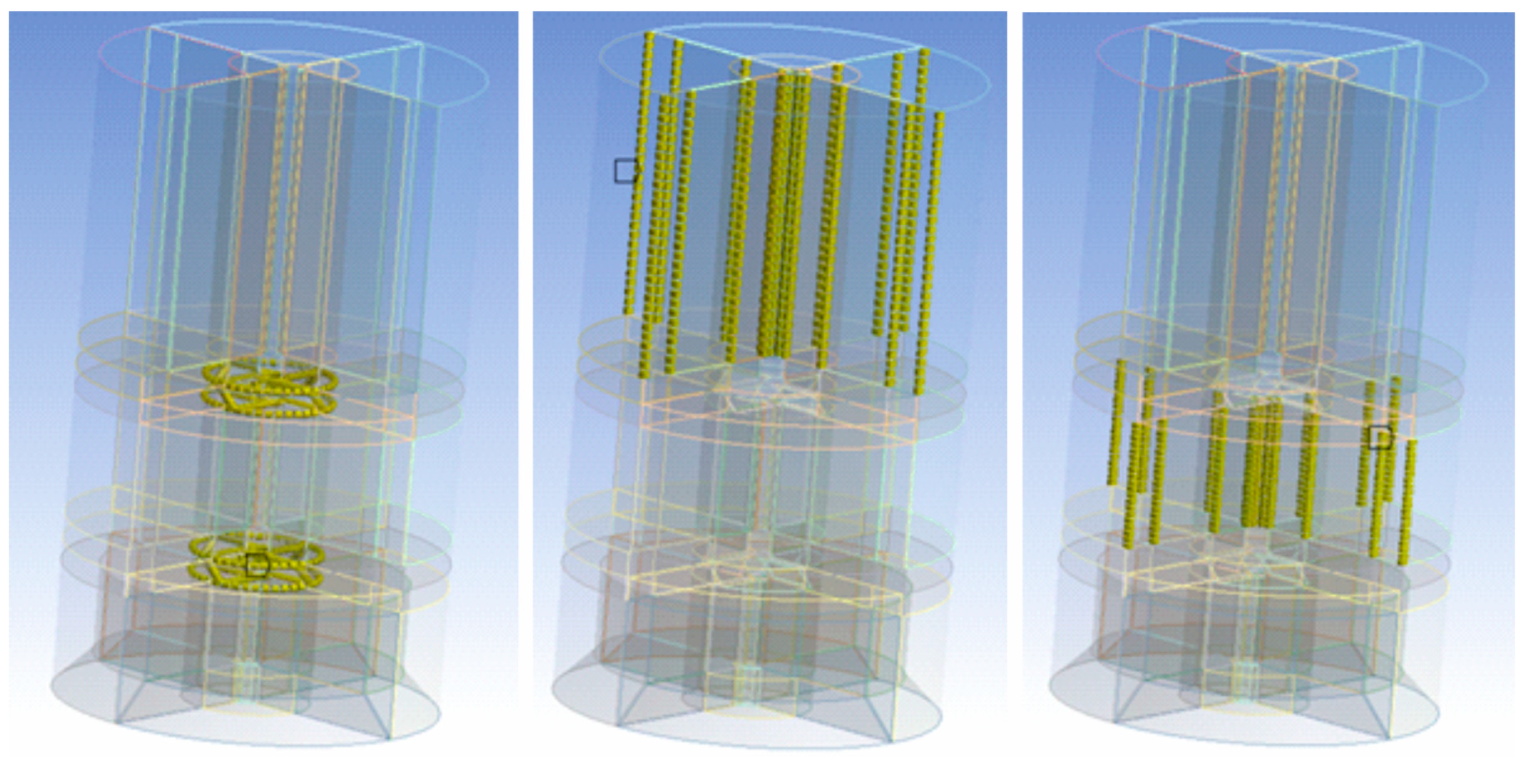
2.3. Experimental and Numerical Determinations of Mixing Time
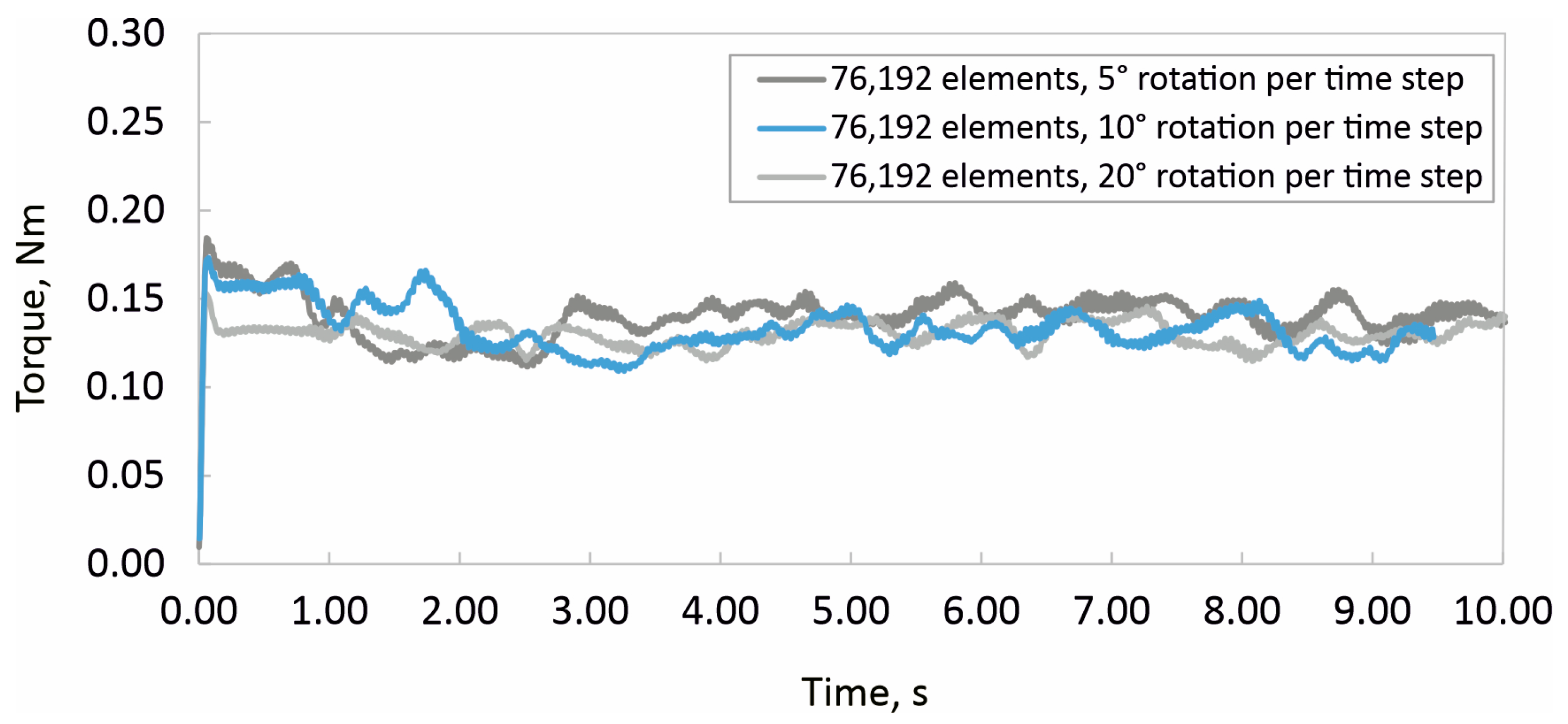
2.4. Experimental and Numerical Determinations of Power Input
3. Results and Discussion
3.1. Hydrodynamic Conditions in the Vessel
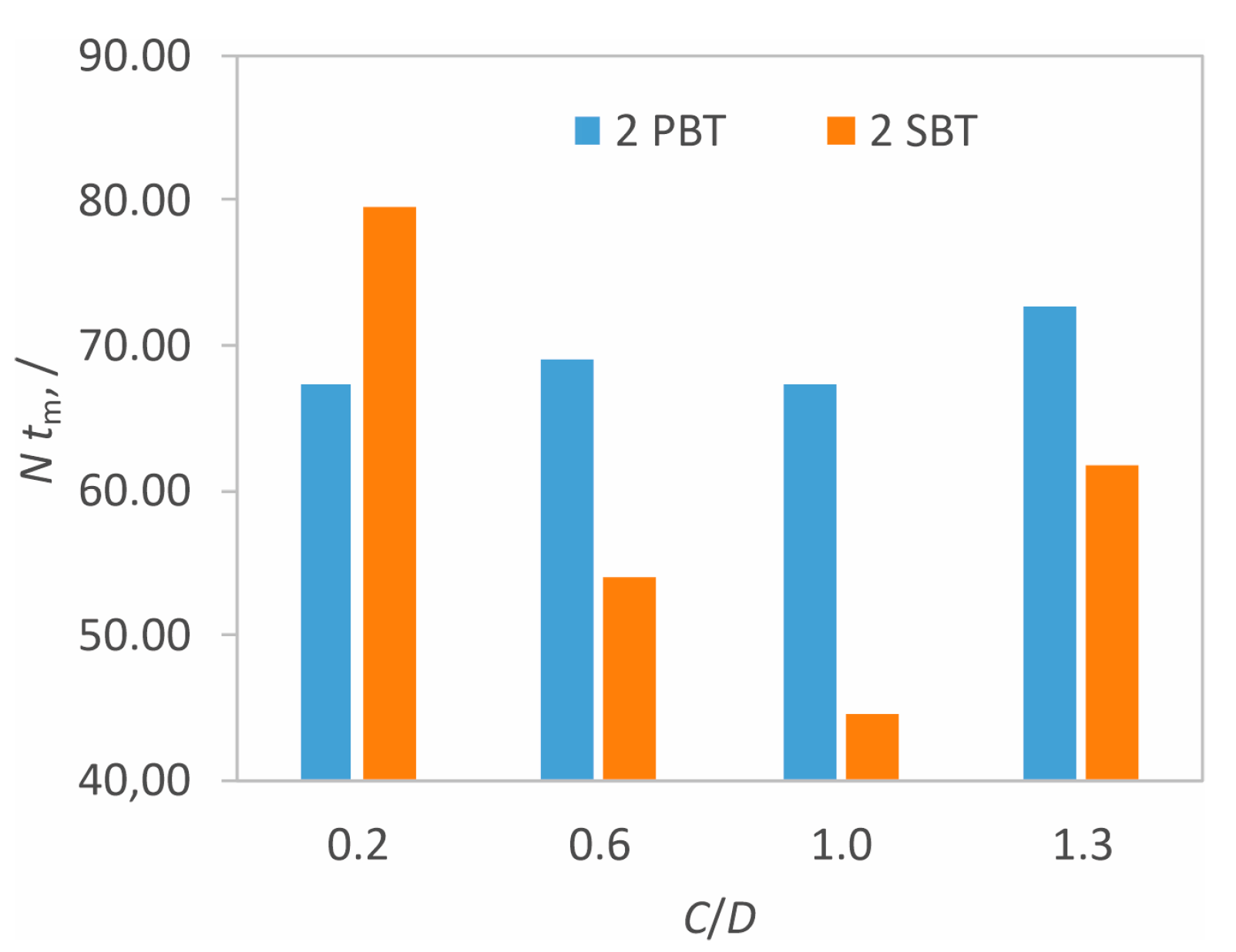
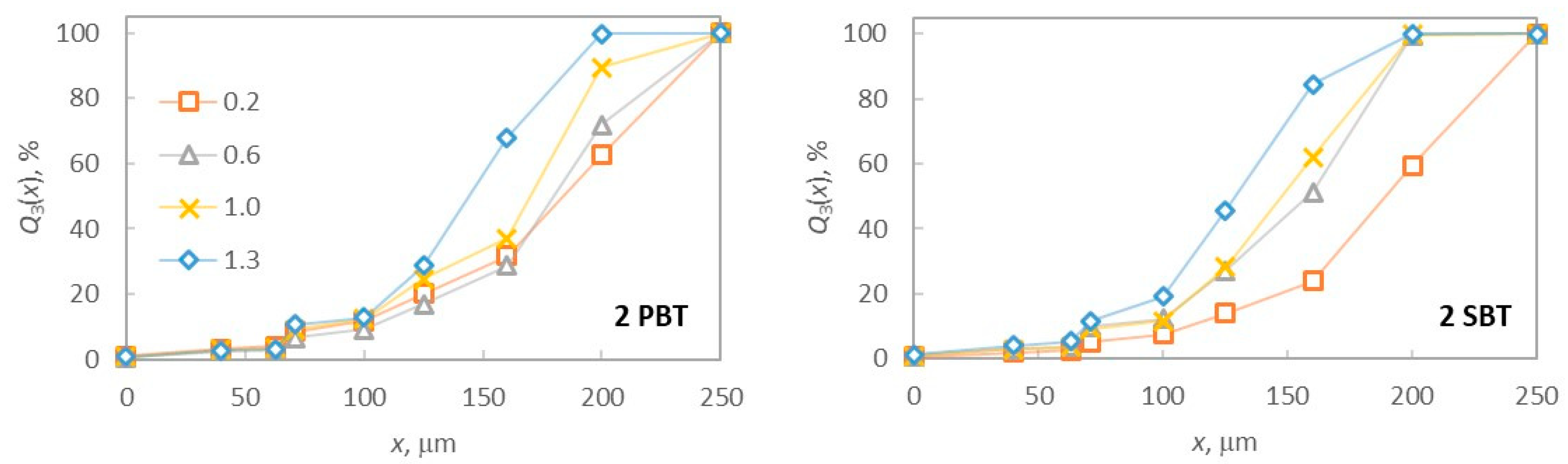
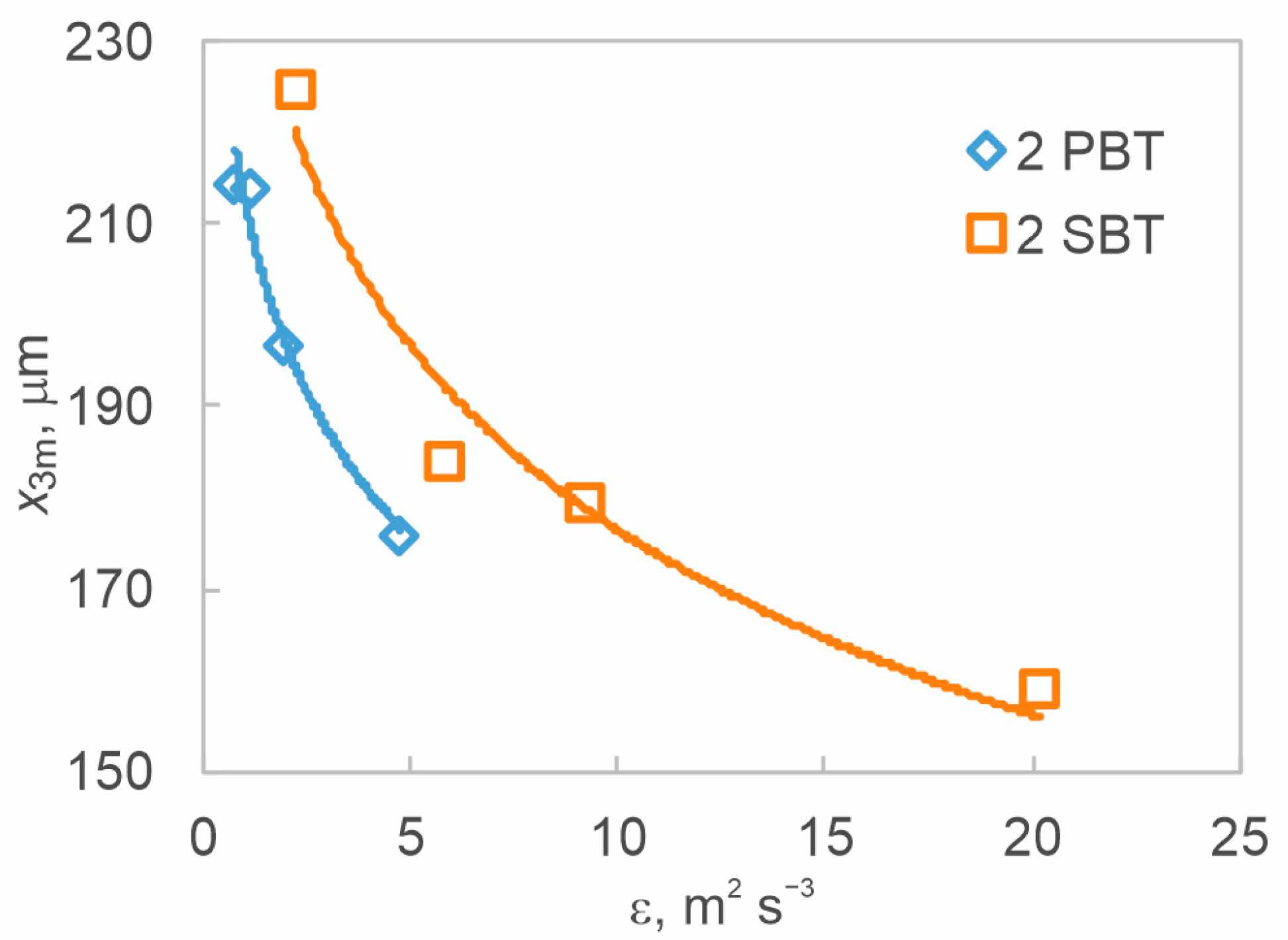
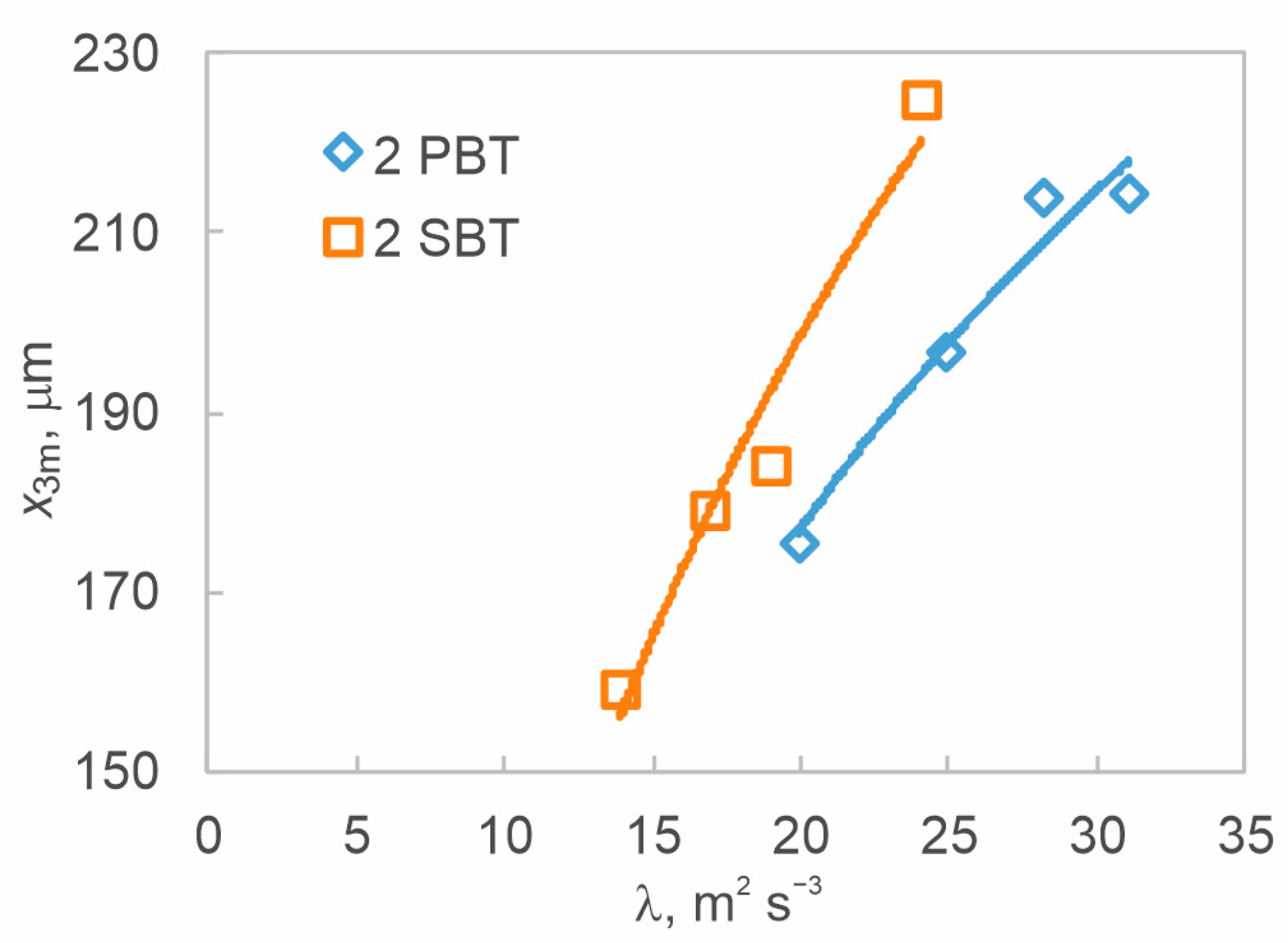
3.2. The Effect of Hydrodynamics on Nucleation Kinetics at Different Off-Bottom Clearances
3.3. The Effect of Hydrodynamics on Final Product Properties at Different Off-Bottom Clearances
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Montante, G.; Maluta, F.; Alberini, F.; Iwasawa, S.; Takenaka, K.; Paglianti, A. Large blade impeller application for turbulent liquid–liquid and solid–liquid mixing. Can. J. Chem. Eng. 2022, 100, 2230–2244. [Google Scholar] [CrossRef]
- Yao, Z.; Alberini, F.; Montante, G.; Paglianti, A. A new approach to evaluate 3D flow fields using an off-axis 2D PIV system: Investigation of a tubular reactor equipped with Kenics static mixers. Exp. Tech. 2023, 47, 1229–1245. [Google Scholar] [CrossRef]
- Nikku, M.; Myöhänen, K.; Ritvanen, J.; Hyppänen, T. Evaluation of mixing of a secondary solid phase in a circulating fluidized bed riser. Chem. Eng. Sci. 2023, 269, 118503. [Google Scholar] [CrossRef]
- Torotwa, I.; Ji, C. A Study of the Mixing Performance of Different Impeller Designs in Stirred Vessels Using Computational Fluid Dynamics. Designs 2018, 2, 10. [Google Scholar] [CrossRef]
- Avazpour, R.; Latifi, M.; Chaouki, J.; Fradette, L. A cleaner recovery of rare earth bearing minerals by Pickering emulsification: Improvement of processing conditions toward an economic operation. J. Environ. Chem. Eng. 2021, 9, 105449. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H.; Zhang, Z.; Liu, Y.; Zhang, T. Numerical optimization for blades of Intermig impeller in solid–liquid stirred tank. Chin. J. Chem. Eng. 2021, 29, 57–66. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, C.; Wan, L.; Liu, B. Numerical investigation on the intensification of coaxial slurry mixing systems. Chem. Eng. Process. 2023, 192, 109514. [Google Scholar] [CrossRef]
- Yang, C.; Sun, N.; Zhang, Z.; Liu, B. Experimental Study on Micromixing Characteristics of Coaxial Mixer in Solid–Liquid Systems. Ind. Eng. Chem. Res. 2021, 60, 14318–14328. [Google Scholar] [CrossRef]
- Xu, Z.; Wan, L.; Li, Z.; Liu, B. Numerical Study on the Synergistic Mechanism of Coaxial Mixers in Dense Solid–Liquid Mixing Systems. Ind. Eng. Chem. Res. 2023, 62, 11744–11755. [Google Scholar] [CrossRef]
- MS, A.; Hazra, D.; Steele, G.; Pal, S. Crystallization process modifications to address polymorphic and particle size challenges in early-stage development of an API salt. Chem. Eng. Res. Des. 2020, 164, 400–411. [Google Scholar] [CrossRef]
- Pukkella, A.K.; Vysyaraju, R.; Tammishetti, V.; Rai, B.; Subramanian, S. Improved mixing of solid suspensions in stirred tanks with interface baffles: CFD simulation and experimental validation. Chem. Eng. J. 2019, 358, 621–633. [Google Scholar] [CrossRef]
- Jacqueline, R.d.A.; Fabienne, E.; Letourneau, J.-J.; Inês, R.M. Antisolvent crystallization of a cardiotonic drug in ionic liquids: Effect of mixing on the crystal properties. J. Cryst. Growth 2017, 472, 29–34. [Google Scholar] [CrossRef]
- Li, X.; Heng, J.Y.Y. The critical role of agitation in moving from preliminary screening results to reproducible batch protein crystallisation. Chem. Eng. Res. Des. 2021, 173, 81–88. [Google Scholar] [CrossRef]
- Lenka, M.; Sarkar, D. Combined cooling and antisolvent crystallization of l-asparagine monohydrate. Powder Technol. 2018, 334, 106–116. [Google Scholar] [CrossRef]
- Camacho Corzo, D.M.; Ma, C.Y.; Mahmud, T.; Roberts, K.J. Digital Design of Batch Cooling Crystallization Processes: Computational Fluid Dynamics Methodology for Modeling Free-Surface Hydrodynamics in Agitated Crystallizers. Org. Process Res. Dev. 2020, 24, 2565–2582. [Google Scholar] [CrossRef]
- Oh, D.-H.; Jeon, R.-Y.; Adams, D.; Jung, W.-Y.; Shim, H.M.; Lee, C.-H.; Kim, K.-J. Software Platform for Computation Fluid Dynamics Simulation of Mixing and Crystallization in a Stirred Vessel. Cryst. Growth Des. 2020, 20, 1172–1185. [Google Scholar] [CrossRef]
- Tsuchioka, K.; Hayashi, K.; Misumi, R. Method for predicting the size of Ni1/3Mn1/3Co1/3(OH)2 particles precipitated in a stirred-tank semi-batch crystallizer using CFD and particle agglomeration models. Heliyon 2024, 10, e28710. [Google Scholar] [CrossRef]
- Shiea, M.; Querio, A.; Buffo, A.; Boccardo, G.; Marchisio, D. CFD-PBE modelling of continuous Ni-Mn-Co hydroxide co-precipitation for Li-ion batteries. Chem. Eng. Res. Des. 2022, 177, 461–472. [Google Scholar] [CrossRef]
- Szilagyi, B.; Eren, A.; Quon, J.L.; Papageorgiou, C.D.; Nagy, Z.K. Application of Model-Free and Model-Based Quality-by-Control (QbC) for the Efficient Design of Pharmaceutical Crystallization Processes. Cryst. Growth Des. 2020, 20, 3979–3996. [Google Scholar] [CrossRef]
- Čelan, A.; Ćosić, M.; Penga, Ž.; Kuzmanić, N. Connection of Hydrodynamics and Nucleation Kinetics in Dual-Impeller Crystallizers. Chem. Eng. Technol. 2021, 44, 914–923. [Google Scholar] [CrossRef]
- Nývlt, J. Kinetics of nucleation in solutions. J. Cryst. Growth 1968, 3–4, 377–383. [Google Scholar] [CrossRef]
- Harnby, N.; Edwards, M.F.; Nienow, A.W. Mixing in the Process Industries, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1992. [Google Scholar] [CrossRef]
- Čelan, A.; Ćosić, M.; Pehnec, I.; Kuzmanić, N. Influence of impeller diameter on crystal growth kinetics of borax in mixed dual impeller batch cooling crystallizer. Chem. Eng. Technol. 2019, 42, 788–796. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F. Zonal Two Equation k-w Turbulence Models for Aerodynamic Flows. AIAA J. 1993, 32, 1598–1605. [Google Scholar] [CrossRef]
- Jahoda, M.; Moštĕk, M.; Kukuková, A.; Machoň, V. CFD Modelling of Liquid Homogenization in Stirred Tanks with One and Two Impellers Using Large Eddy Simulation. Chem. Eng. Res. Des. 2007, 85, 616–625. [Google Scholar] [CrossRef]
- Green, D. Crystallizer Mixing. In Handbook of Industrial Crystallization, 3rd ed.; Myerson, A.S., Deniz, E., Lee, A.Y., Eds.; Butterworth-Heinemann: Boston, MA, USA, 2002; pp. 290–312. [Google Scholar]
- Amari, S.; Takahashi, R.; Hosokawa, M.; Takiyama, H. Improving the quality of crystalline particles and productivity during anti-solvent crystallization through continuous flow with high shear stress under low supersaturation condition. Adv. Powder Technol. 2024, 35, 104493. [Google Scholar] [CrossRef]
- Battaglia, G.; Romano, S.; Raponi, A.; Volpe, F.; Bellanca, L.; Ciofalo, M.; Marchisio, D.; Cipollina, A.; Micale, G.; Tamburini, A. Mixing phenomena in circular and rectangular cross-sectional T-mixers: Experimental and numerical assessment. Chem. Eng. Res. Des. 2024, 201, 228–241. [Google Scholar] [CrossRef]
- Tamburini, A.; Gagliano, G.; Micale, G.; Brucato, A. Direct numerical simulations of creeping to early turbulent flow in unbaffled and baffled stirred tanks. Chem. Eng. Sci. 2018, 192, 161–175. [Google Scholar] [CrossRef]
- Doran, P.M. Bioprocess Engineering Principles, 2nd ed.; Academic Press: Waltham, MA, USA; Oxford, UK, 2013; pp. 255–332. [Google Scholar]
- Mullin, J.W.; Söhnel, O. Expressions of supersaturation in crystallization studies. Chem. Eng. Sci. 1977, 32, 683–686. [Google Scholar] [CrossRef]
- Ćosic, M.; Pažin, A.; Čelan, A.; Kuzmanić, N. Influence of Cooling Rate on Crystallization of Borax in Stirred Batch Crystallizer. Chem. Eng. Trans. 2019, 74, 451–456. [Google Scholar]
- Yang, G.; Louhi-Kultanen, M.; Sha, Z.; Kubota, N.; Kallas, J. A Model for the Prediction of Supersaturation Level in Batch Cooling Crystallization. J. Chem. Eng. Jpn. 2006, 39, 426–436. [Google Scholar] [CrossRef]
- Ulrich, J.; Strege, C. Some aspects of the importance of metastable zone width and nucleation in industrial crystallizers. J. Cryst. Growth 2002, 237–239 Pt 3, 2130–2135. [Google Scholar] [CrossRef]
- Akrap, M.; Kuzmanić, N.; Prlić-Kardum, J. Effect of mixing on the crystal size distribution of borax decahydrate in a batch cooling crystallizer. J. Cryst. Growth 2010, 312, 3603–3608. [Google Scholar] [CrossRef]
- Schubert, H.; Mersmann, A. Determination of heterogeneous nucleation rates. Trans IChemE 1996, 74, 821–827. [Google Scholar]





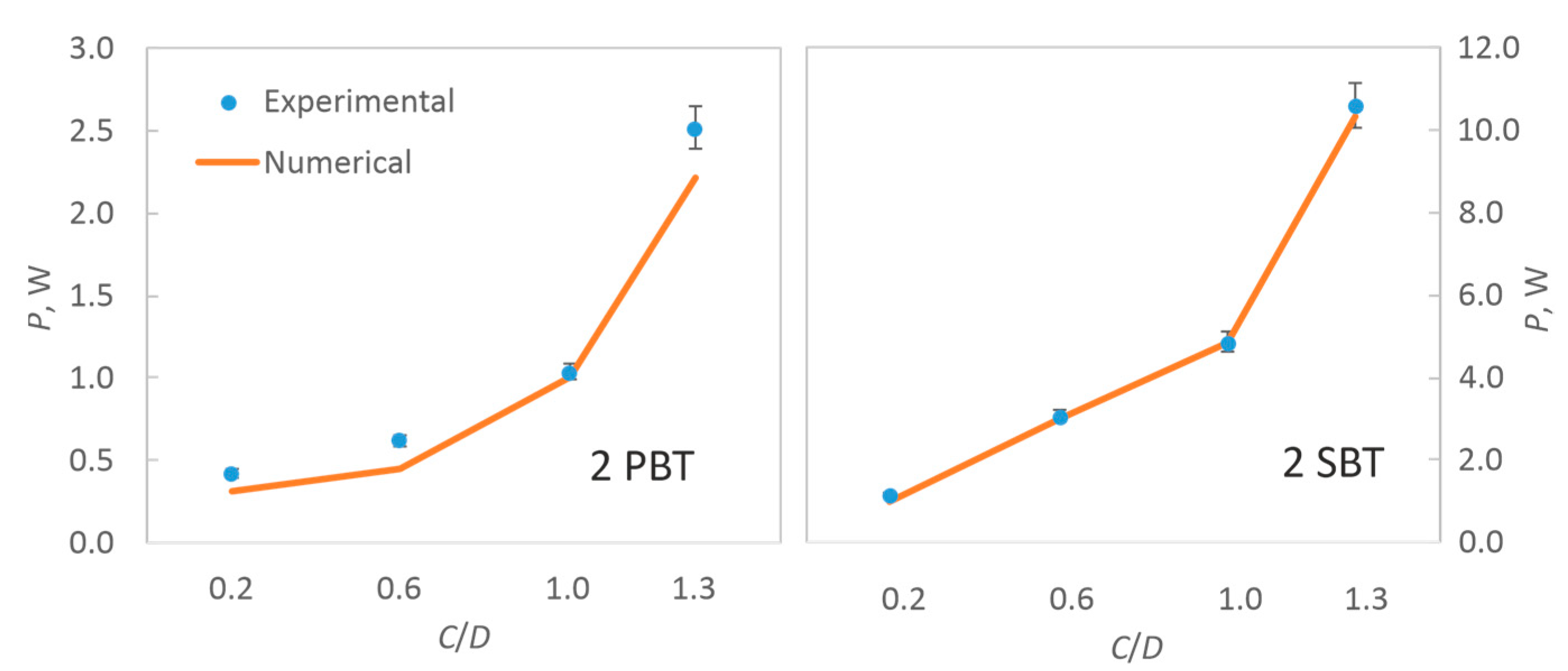
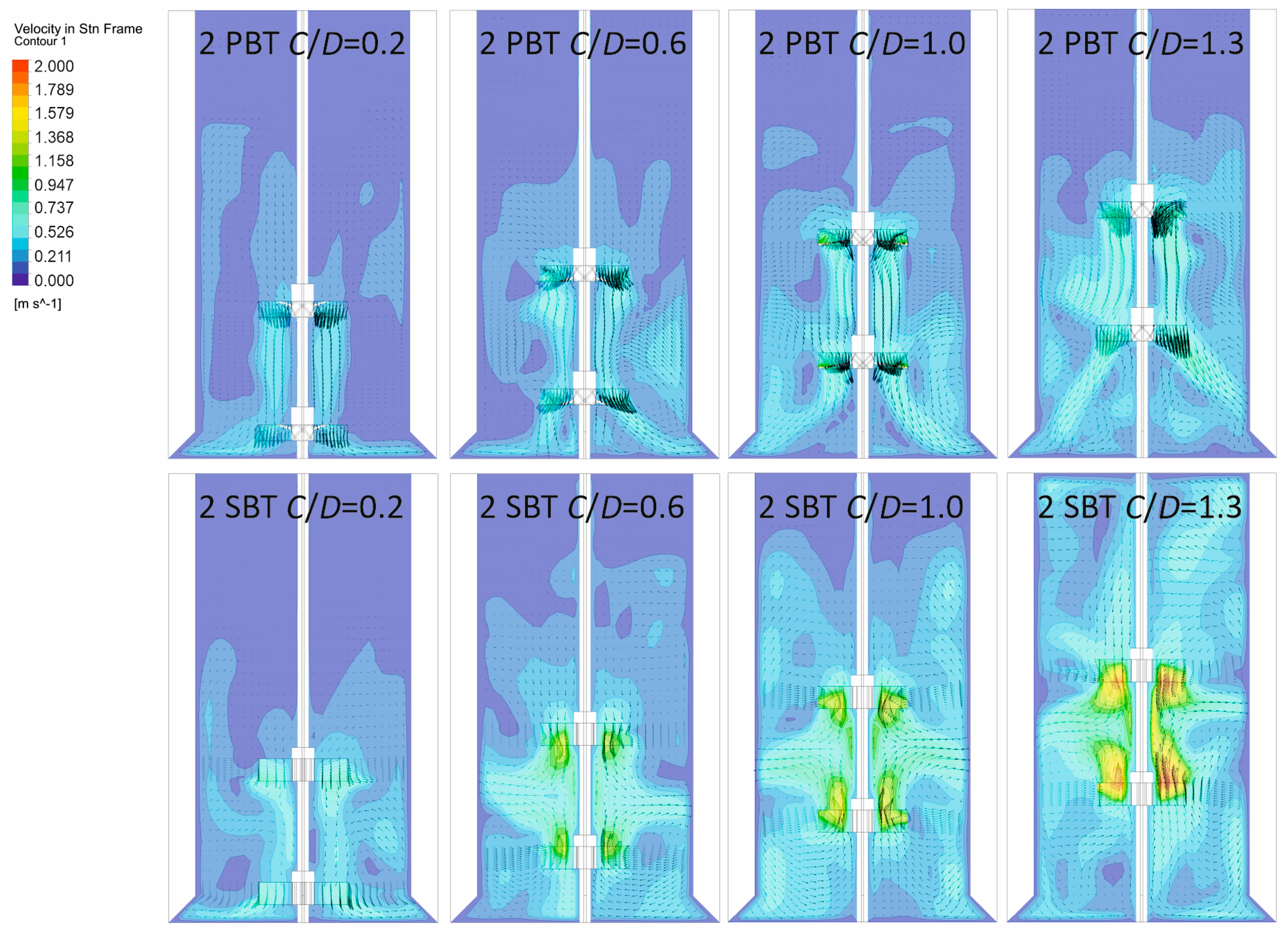
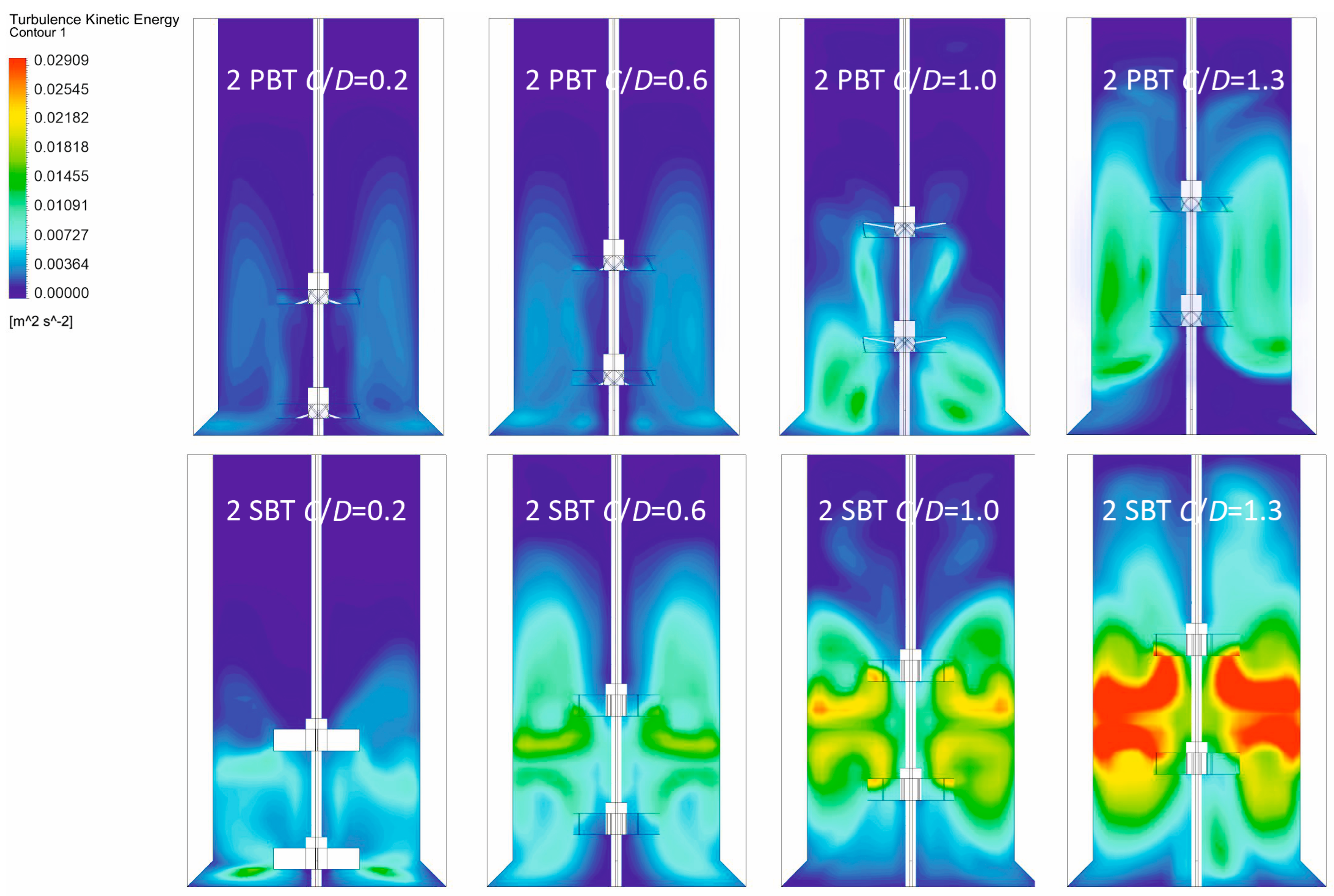



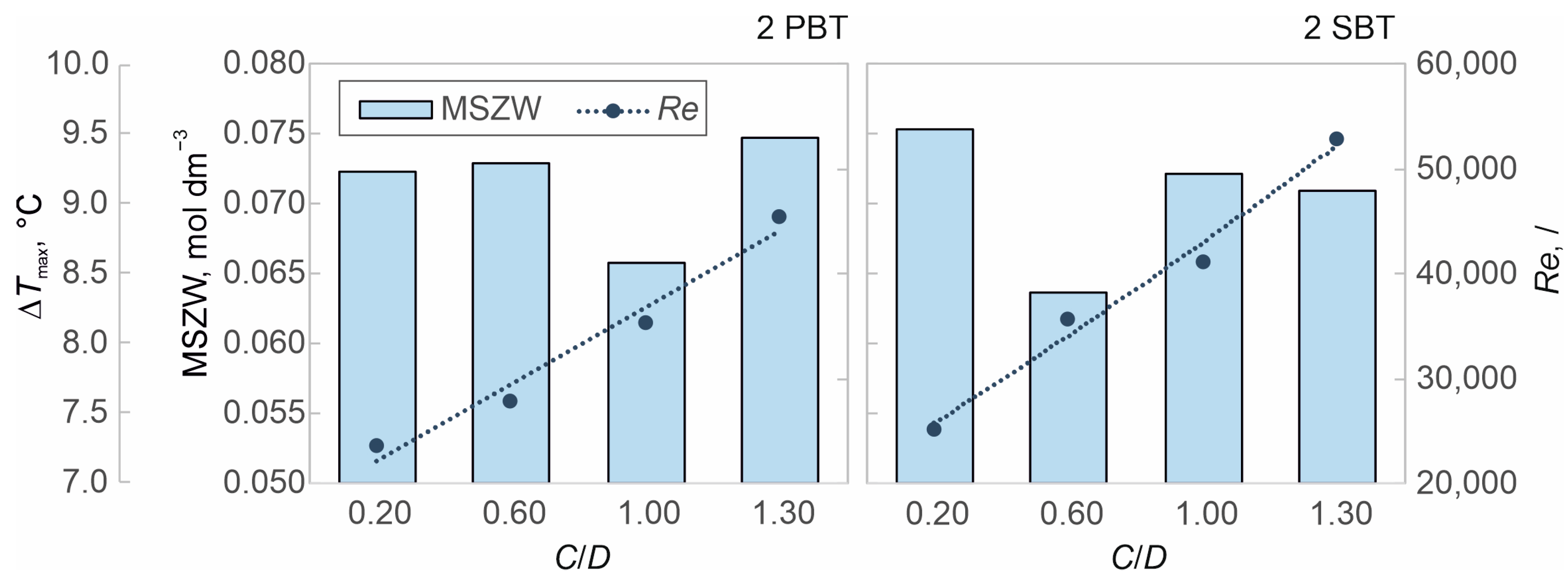
| Impeller Configuration | C/D | NJS, rpm | Re,/ |
|---|---|---|---|
| 2 PBT | 0.20 | 202 | 23715 |
| 0.60 | 238 | 27942 | |
| 1.00 | 301 | 35338 | |
| 1.30 | 388 | 45552 | |
| 2 SBT | 0.20 | 215 | 25242 |
| 0.60 | 306 | 35925 | |
| 1.00 | 352 | 41326 | |
| 1.30 | 451 | 52949 |
| Impeller Configuration | C/D | Nhet ∙ 1019, m−3 s−1, |
|---|---|---|
| 2 PBT | 0.20 | 4.9864 |
| 0.60 | 5.3865 | |
| 1.00 | 2.0930 | |
| 1.30 | 6.6177 | |
| 2 SBT | 0.20 | 7.0794 |
| 0.60 | 1.5287 | |
| 1.00 | 4.9864 | |
| 1.30 | 4.2733 |
| Impeller Configuration | C/D | Mean Crystal Size, μm | σ, μm | Y, % |
|---|---|---|---|---|
| 2 PBT | 0.20 | 214.43 | 64.83 | 87.68 |
| 0.60 | 214.08 | 57.73 | 87.94 | |
| 1.00 | 196.82 | 56.47 | 89.18 | |
| 1.30 | 175.71 | 47.02 | 88.84 | |
| 2 SBT | 0.20 | 224.70 | 57.13 | 87.08 |
| 0.60 | 184.20 | 50.33 | 89.5 | |
| 1.00 | 179.33 | 47.86 | 90.47 | |
| 1.30 | 159.07 | 45.79 | 89.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čelan, A.; Ćosić, M.; Penga, Ž.; Kuzmanić, N. Experimental and CFD Analysis of Hydrodynamics in Dual-Impeller Crystallizer at Different Off-Bottom Clearances. Processes 2024, 12, 2183. https://doi.org/10.3390/pr12102183
Čelan A, Ćosić M, Penga Ž, Kuzmanić N. Experimental and CFD Analysis of Hydrodynamics in Dual-Impeller Crystallizer at Different Off-Bottom Clearances. Processes. 2024; 12(10):2183. https://doi.org/10.3390/pr12102183
Chicago/Turabian StyleČelan, Antonija, Marija Ćosić, Željko Penga, and Nenad Kuzmanić. 2024. "Experimental and CFD Analysis of Hydrodynamics in Dual-Impeller Crystallizer at Different Off-Bottom Clearances" Processes 12, no. 10: 2183. https://doi.org/10.3390/pr12102183
APA StyleČelan, A., Ćosić, M., Penga, Ž., & Kuzmanić, N. (2024). Experimental and CFD Analysis of Hydrodynamics in Dual-Impeller Crystallizer at Different Off-Bottom Clearances. Processes, 12(10), 2183. https://doi.org/10.3390/pr12102183







