Optimizing Mass Transfer in Multiphase Fermentation: The Role of Drag Models and Physical Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement of Diffusion Coefficient
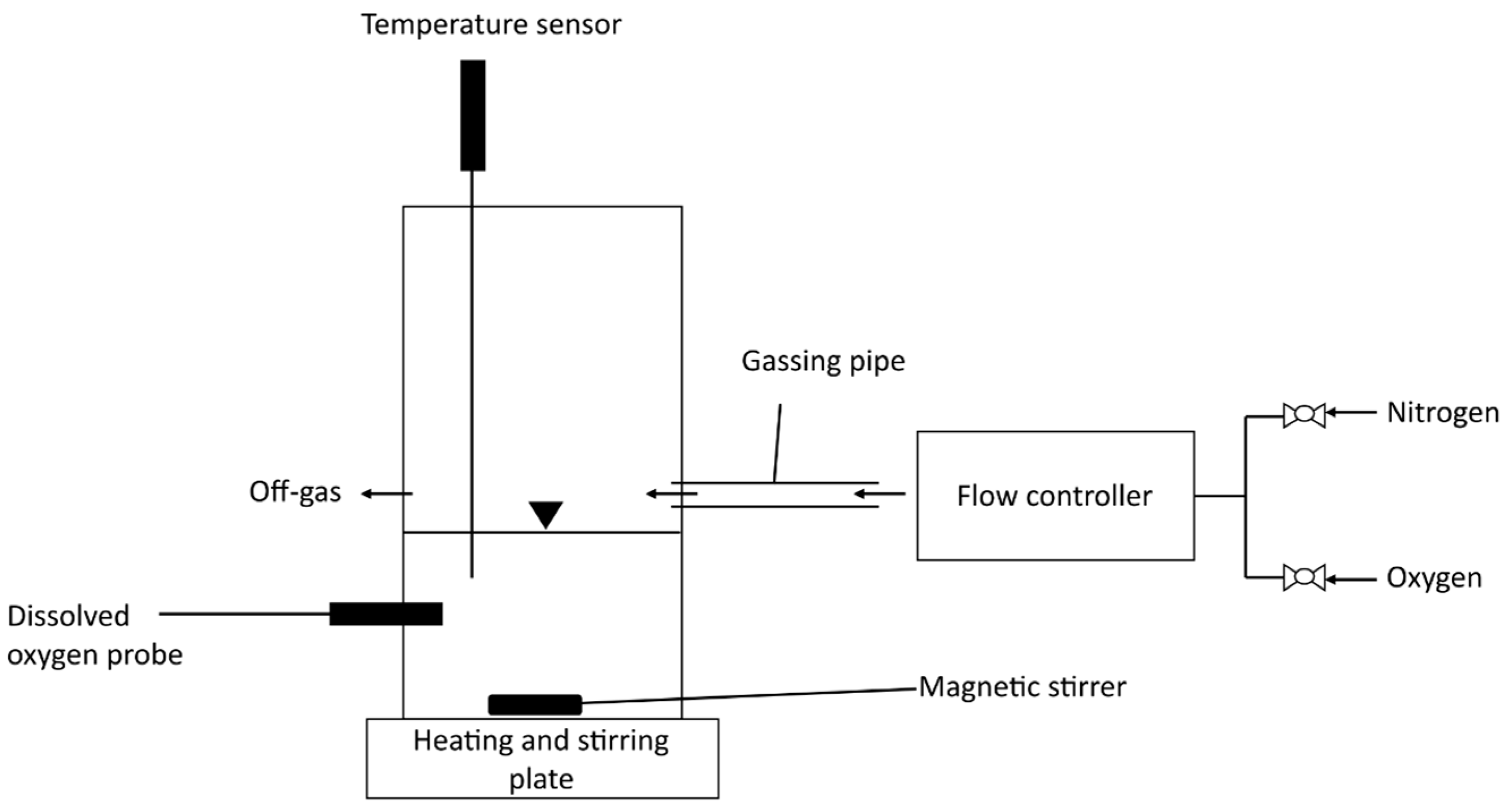
2.2. Measurement of Oxygen Transfer Coefficient
2.3. Measurement of Gas Hold-Up
2.4. Measurement of Bubble Size Distribution
2.5. Media Composition
2.6. Mathematical Model Description
| Models based on Re | ||
| Schiller and Naumann [12] | (13) | |
| Dalla Valle [32] | (14) | |
| Lapple [33] | (15) | |
| Mei and Klausner [34] | (16) | |
| Zhang and van der Heyden [35] | (17) | |
| Models based on Eo | ||
| Grevskott et al. [36] | (18) | |
| Models based on both Re and Eo | ||
| Tomiyama [10] (pure water) | (19) | |
| Tomiyama [10] (slightly contaminated water) | (20) | |
| Tomiyama [10] (fully contaminated water) | (21) | |
| Kelbaliyev and Ceylan [37] | (22) | |
| The Morton (Mo) number is defined as follows: | ||
| (23) | ||
| Dijkhuizen et al. [11] | (24) | |
| (25) | ||
| (26) | ||
2.7. Computer Fluid Dynamic Simulation Set-Up
3. Results and Discussion
3.1. Identification of Diffusion Coefficients in Aqueous Solutions
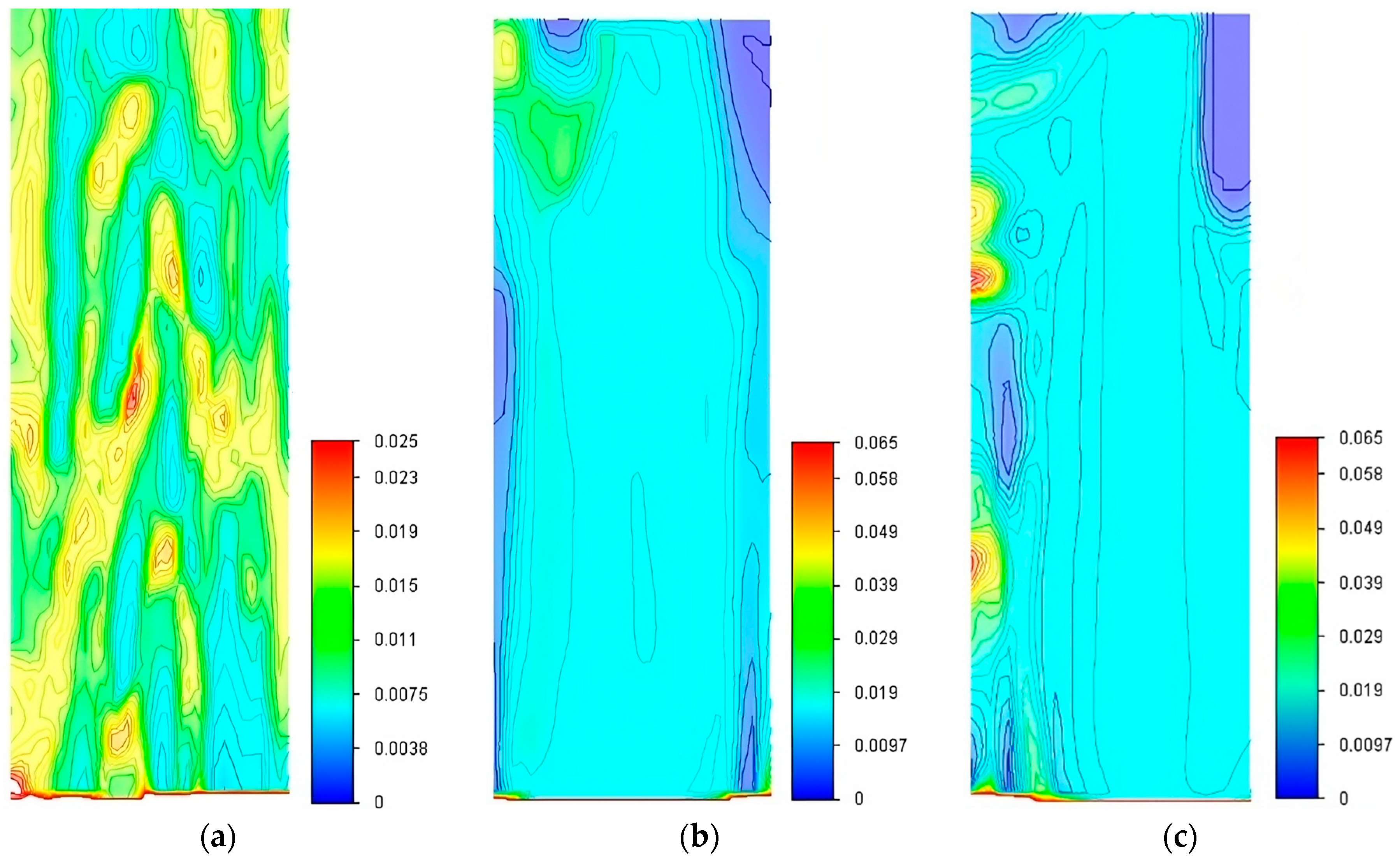
3.2. CFD Simulations
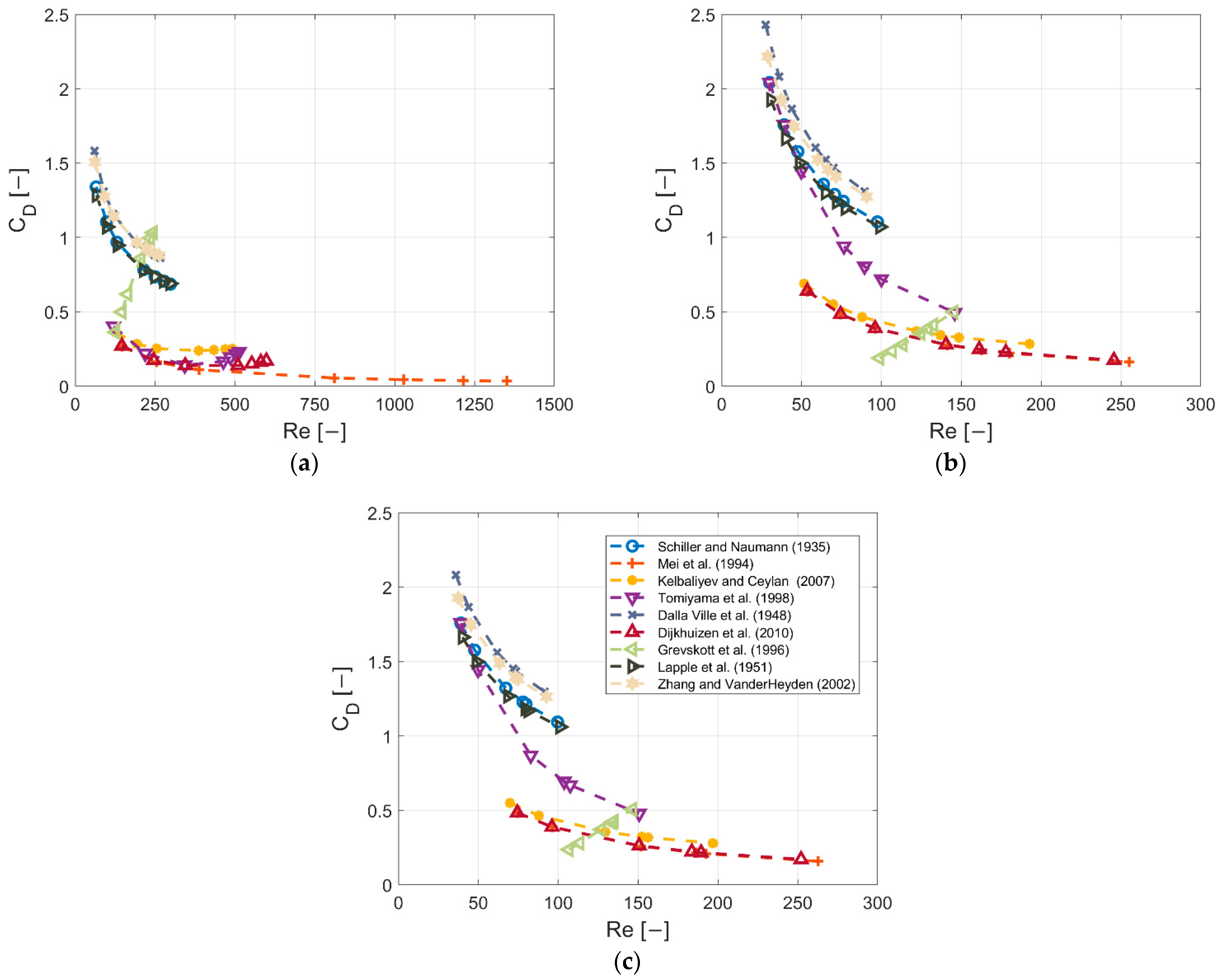
3.3. Correlation of the Drag Coefficient with Re Number
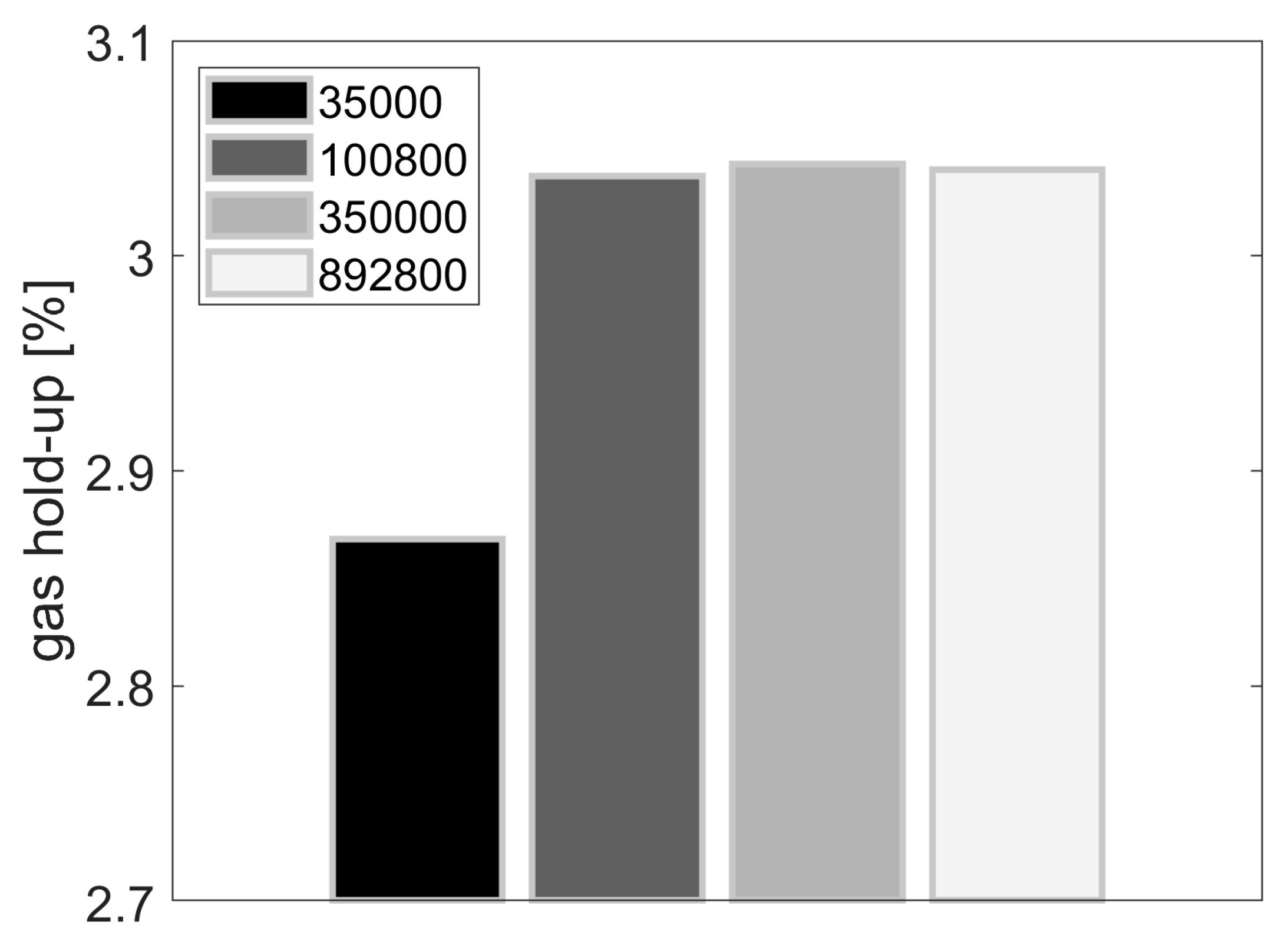
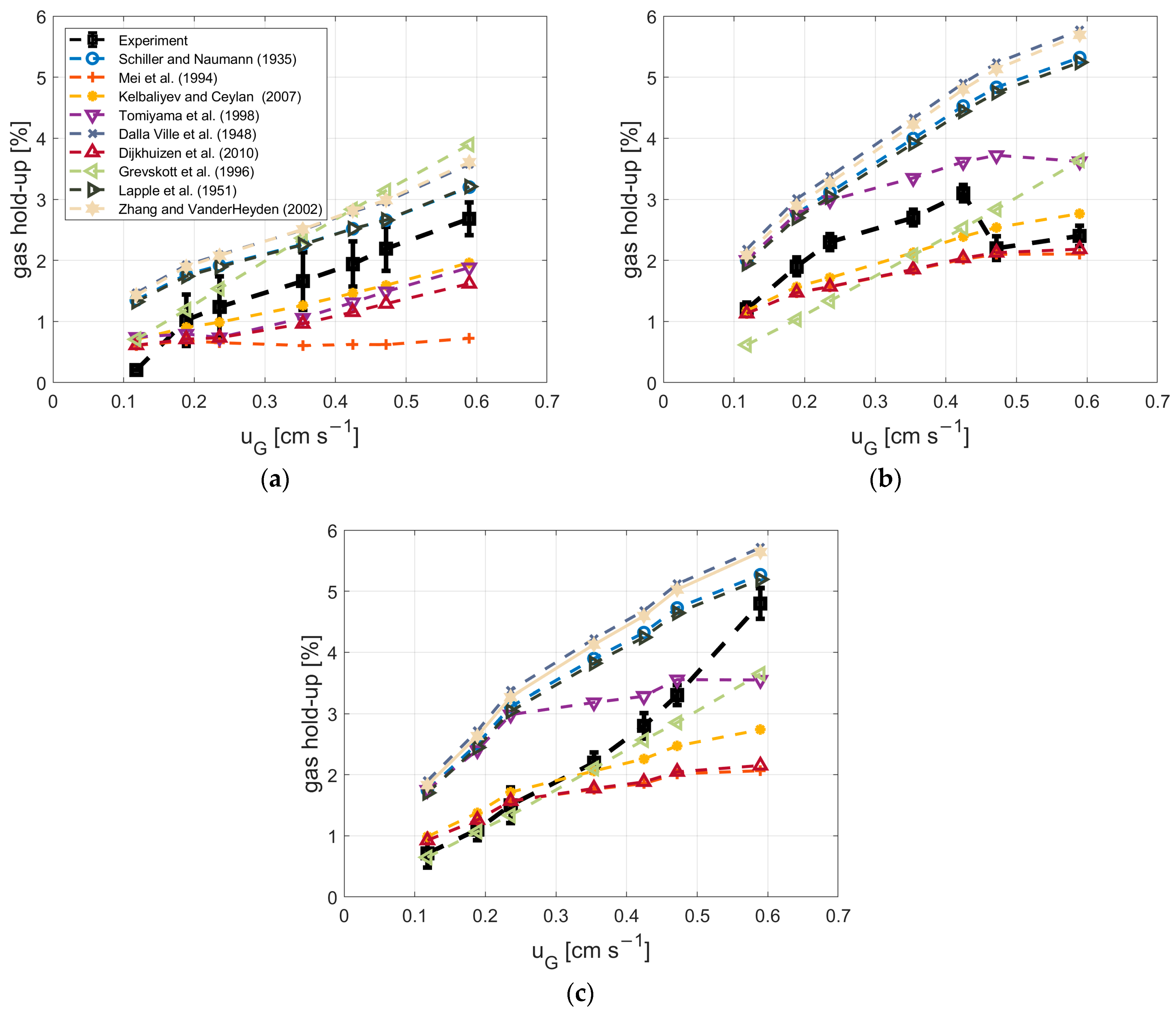
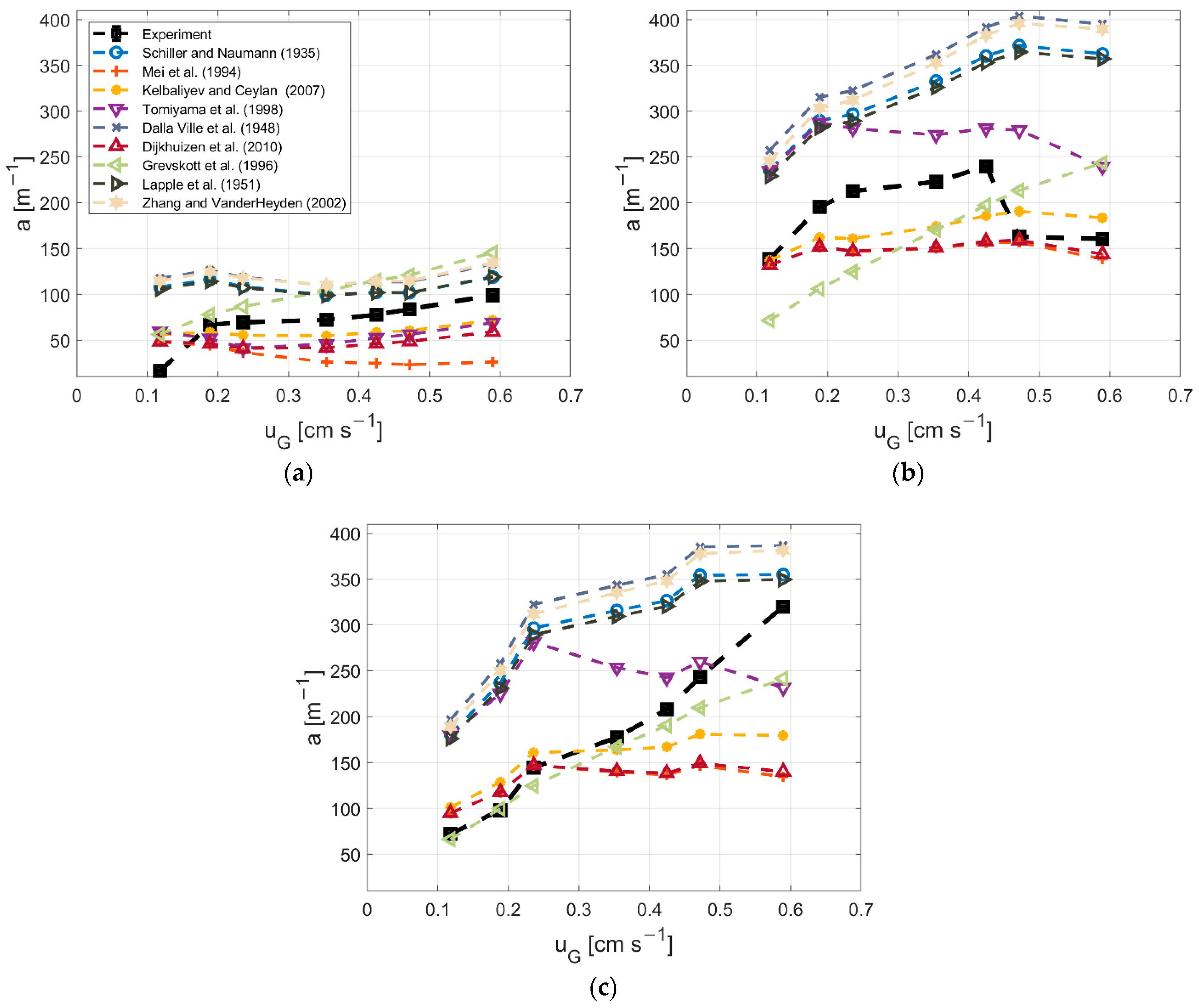
3.4. Dependency of Gas Hold-Up and a on the Drag Model
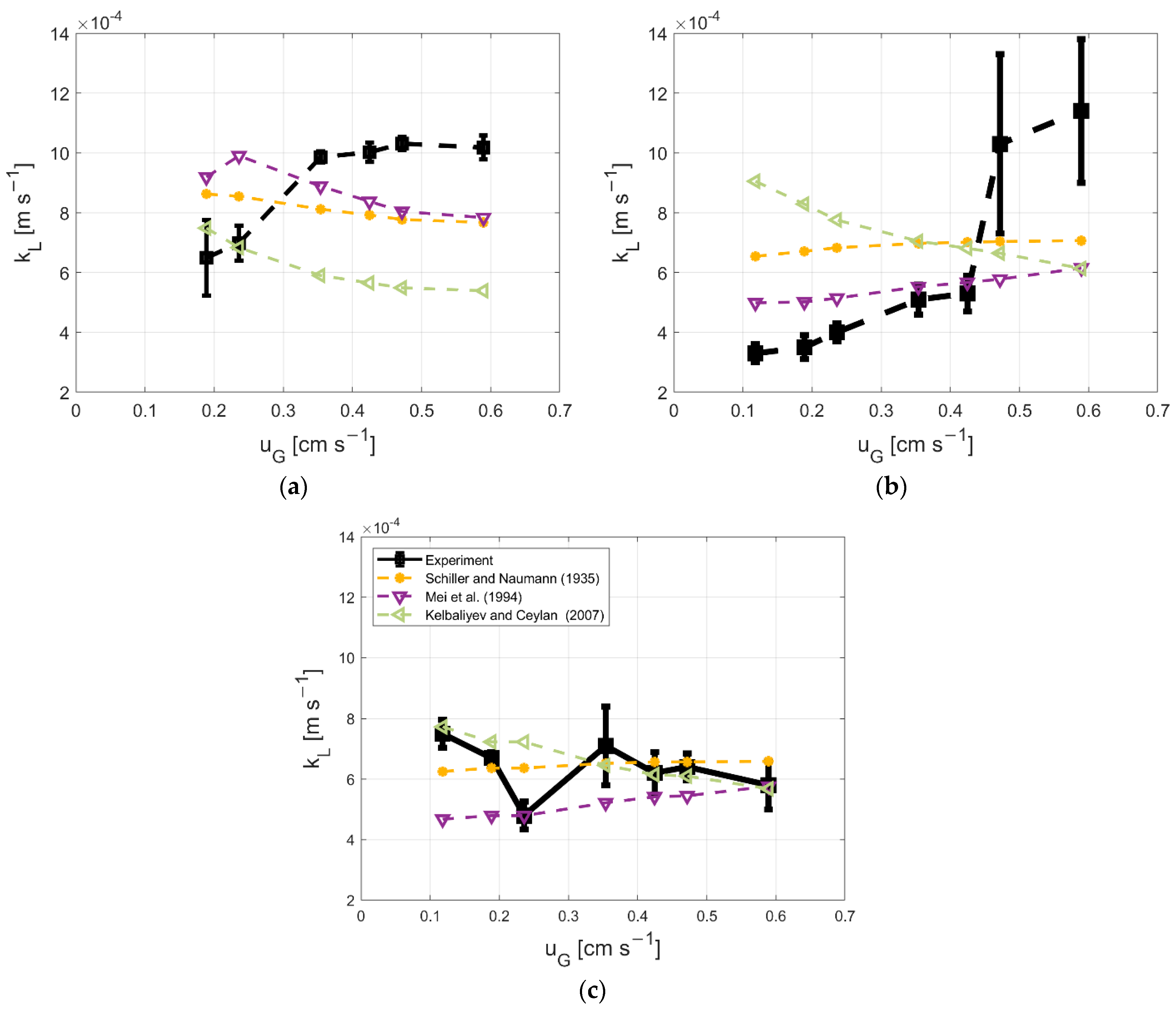
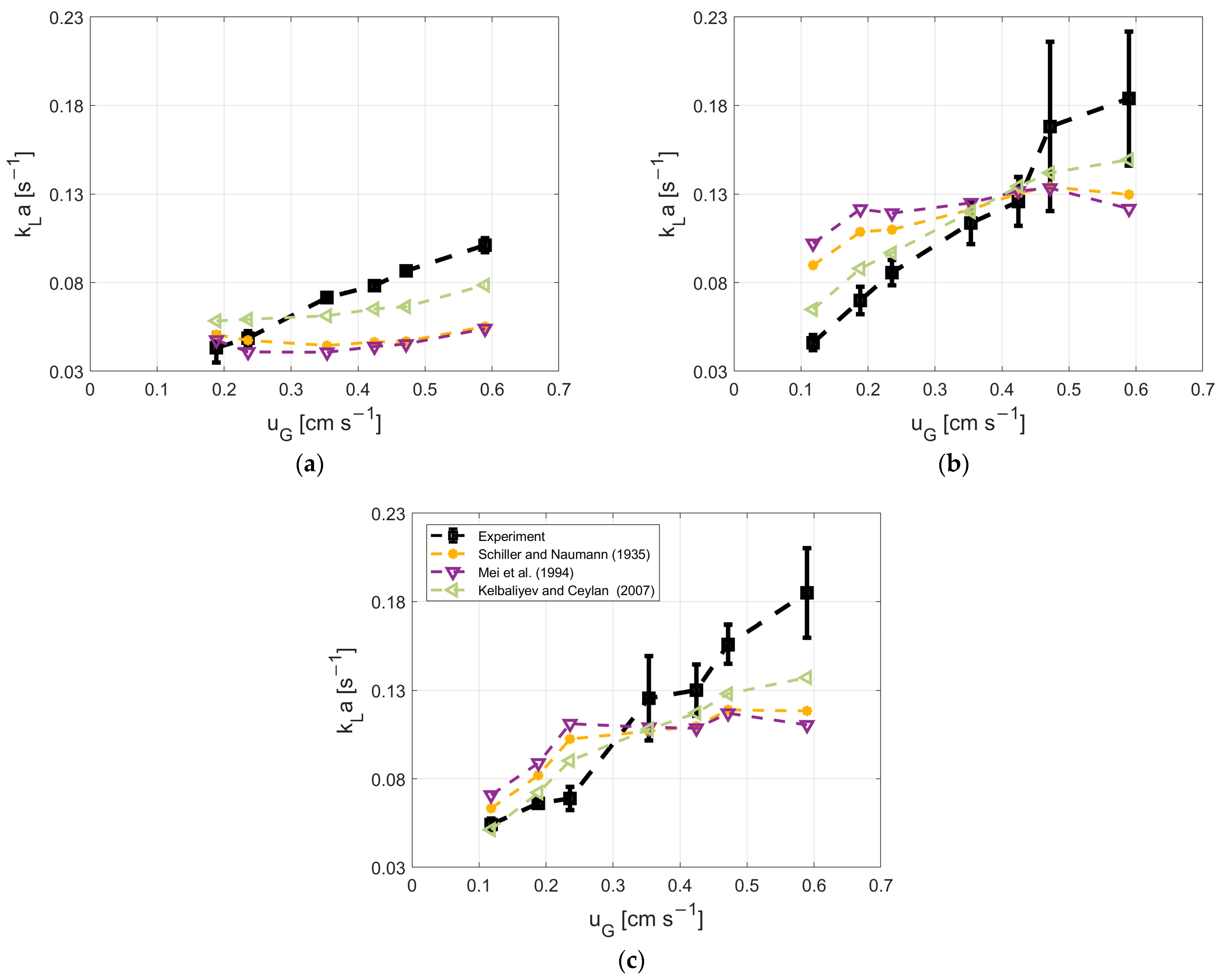
3.5. Model Description for kL and kLa
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | volume-specific surface area | m−1 |
| CD | drag coefficient | - |
| oxygen concentration in liquid | mmol L−1 | |
| diffusion coefficient of oxygen in liquid phase | m2 s−1 | |
| d32 | Sauter mean diameter | m |
| fi | internal friction factor | - |
| g | gravity constant | m s−2 |
| HR | reactor height | m |
| kLa | volumetric oxygen transfer coefficient | s−1 |
| kL | mass transfer coefficient | kg m−1 s−1 |
| s’ | renewal rate of liquid elements at the gas–liquid interface | s−1 |
| t | time | s |
| tmean | mean residence time | s |
| Ui | interfacial momentum transfer velocity | m s−1 |
| uG | gas velocity | m s−1 |
| uL | liquid velocity | m s−1 |
| uB | averaged bubble rising velocity | m s−1 |
| VG | volume of the gas phase | m3 |
| VL | volume of the liquid phase | m3 |
| volume flow rate air | m3 s−1 | |
| Greek Symbols | ||
| gas hold-up | - | |
| Ε | characteristic scales of velocity and length | s−1 |
| kinematic viscosity of the liquid phase | m2 s−1 | |
| µL | dynamic viscosity of the liquid phase | m2 s−1 |
| ρL | density of the liquid phase | kg m−3 |
| ρG | density of the gas phase | kg m−3 |
| surface tension | kg s−2 | |
| τi | interfacial momentum transfer stress | kg m−1 s−2 |
| Abbreviations | ||
| AF | antifoam | |
| BSD | bubble size distribution | |
| CFD | computational fluid dynamics | |
| Eo | Eötvös number | |
| MM | minimal medium | |
| Mo | Morton number | |
| PBS | phosphate buffer solution | |
| Re | Reynolds number | |
| Sc | Schmidt number | |
| 0-D | zero-dimension | |
Appendix A
Appendix B
| uG in cm s−1 | in mm | in mm | d32 in mm |
|---|---|---|---|
| 0.12 | 0.16 | 2.97 | 0.76 |
| 0.19 | 0.16 | 3.51 | 0.93 |
| 0.24 | 0.16 | 3.88 | 1.08 |
| 0.35 | 0.16 | 3.88 | 1.40 |
| 0.42 | 0.15 | 3.88 | 1.52 |
| 0.47 | 0.15 | 4.03 | 1.61 |
| 0.59 | 0.15 | 4.09 | 1.67 |
Appendix C


References
- Ngu, V.; Morchain, J.; Cockx, A. Spatio-temporal 1D gas–liquid model for biological methanation in lab scale and industrial bubble column. Chem. Eng. Sci. 2022, 251, 117478. [Google Scholar] [CrossRef]
- Frey, L.J.; Vorländer, D.; Ostsieker, H.; Rasch, D.; Lohse, J.-L.; Breitfeld, M.; Grosch, J.-H.; Wehinger, G.D.; Bahnemann, J.; Krull, R. 3D-printed micro bubble column reactor with integrated microsensors for biotechnological applications: From design to evaluation. Sci. Rep. 2021, 11, 7276. [Google Scholar] [CrossRef] [PubMed]
- Siebler, F.; Lapin, A.; Takors, R. Synergistically applying 1-D modeling and CFD for designing industrial scale bubble column syngas bioreactors. Eng. Life Sci. 2020, 20, 239–251. [Google Scholar] [CrossRef] [PubMed]
- Siebler, F.; Lapin, A.; Hermann, M.; Takors, R. The impact of CO gradients on C. ljungdahlii in a 125 m3 bubble column: Mass transfer, circulation time and lifeline analysis. Chem. Eng. Sci. 2019, 207, 410–423. [Google Scholar] [CrossRef]
- Gradov, D.V.; Laari, A.; Turunen, I.; Koiranen, T. Experimentally validated CFD model for gas–liquid flow in a round-bottom stirred tank equipped with Rushton turbine. Int. J. Chem. React. Eng. 2017, 15, 20150215. [Google Scholar] [CrossRef]
- Lou, W.; Zhu, M. Numerical simulation of gas and liquid two-phase flow in gas-stirred systems based on Euler–Euler approach. Metall. Mater. Trans. B 2013, 44, 1251–1263. [Google Scholar] [CrossRef]
- Ruthiya, K.C.; van der Schaaf, J.; Kuster, B.F.M.; Schouten, J.C. Influence of particles and electrolyte on gas hold-up and mass transfer in a slurry bubble column. Int. J. Chem. React. Eng. 2006, 4. [Google Scholar] [CrossRef]
- Hikita, H.; Asai, S.; Tanigawa, K.; Segawa, K.; Kitao, M. Gas hold-up in bubble columns. Chem. Eng. J. 1980, 20, 59–67. [Google Scholar] [CrossRef]
- Kellermann, H.; Jüttner, K.; Kreysa, G. Dynamic modelling of gas hold-up in different electrolyte systems. J. Appl. Electrochem. 1998, 28, 311–319. [Google Scholar] [CrossRef]
- Tomiyama, A.; Kataoka, I.; Zun, I.; Sakaguchi, T. Drag coefficients of single bubbles under normal and micro gravity conditions. JSME Int. J. Ser. B 1998, 41, 472–479. [Google Scholar] [CrossRef]
- Dijkhuizen, W.; Roghair, I.; van Sint Annaland, M.; Kuipers, J. DNS of gas bubbles behaviour using an improved 3D front tracking model—Drag force on isolated bubbles and comparison with experiments. Chem. Eng. Sci. 2010, 65, 1415–1426. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A.; Drag, A. Coefficient Correlation. Z. Vereines Dtsch. Ingenieure 1935, 77, 318–320. [Google Scholar]
- Kakulvand, R. Review of drag coefficients on gas–liquid tower: The drag coefficient independent and dependent on bubble diameter in bubble column experiment. Chem. Rev. Lett. 2019, 2, 48–58. [Google Scholar] [CrossRef]
- Pang, M.J.; Wei, J.J. Analysis of drag and lift coefficient expressions of bubbly flow system for low to medium Reynolds number. Nucl. Eng. Des. 2011, 241, 2204–2213. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, C.; Bo, H. Analyses and modified models for bubble shape and drag coefficient covering a wide range of working conditions. Int. J. Multiph. Flow 2020, 127, 103265. [Google Scholar] [CrossRef]
- Celata, G.P.; D’Annibale, F.; Di Marco, P.; Memoli, G.; Tomiyama, A. Measurements of rising velocity of a small bubble in a stagnant fluid in one- and two-component systems. Exp. Therm. Fluid Sci. 2007, 31, 609–623. [Google Scholar] [CrossRef]
- Fan, L.-S.; Tsuchiya, K. Bubble Wake Dynamics in Liquids and Liquid–Solid Suspensions; Elsevier: Amsterdam, The Netherlands, 1990; ISBN 9780409902860. [Google Scholar]
- Saffman, P.G. On the rise of small air bubbles in water. J. Fluid Mech. 1956, 1, 249–275. [Google Scholar] [CrossRef]
- Lewis, W.K.; Whitman, W.G. Principles of gas absorption. Ind. Eng. Chem. 1924, 16, 1215–1220. [Google Scholar] [CrossRef]
- Frössling, N.M. The evaporation of falling drops. Gerlands Beiträge Zur Geophys. 1938, 52, 170–216. [Google Scholar]
- Higbie, R. The Rate of Absorption of a Pure Gas into a Still Liquid during Short Periods of Exposure. Trans. AIChE 1935, 31, 365–389. [Google Scholar]
- Danckwerts, P.V. Significance of liquid-film coefficients in gas absorption. Ind. Eng. Chem. 1951, 43, 1460–1467. [Google Scholar] [CrossRef]
- Alves, S.S.; Vasconcelos, J.M.T.; Orvalho, S.P. Mass transfer to clean bubbles at low turbulent energy dissipation. Chem. Eng. Sci. 2006, 61, 1334–1337. [Google Scholar] [CrossRef]
- Raymond, D.R.; Zieminski, S.A. Mass transfer and drag coefficients of bubbles rising in dilute aqueous solutions. AIChE J. 1971, 17, 57–65. [Google Scholar] [CrossRef]
- Francois, J.; Dietrich, N.; Guiraud, P.; Cockx, A. Direct measurement of mass transfer around a single bubble by micro-PLIFI. Chem. Eng. Sci. 2011, 66, 3328–3338. [Google Scholar] [CrossRef]
- Jimenez, M.; Dietrich, N.; Grace, J.R.; Hébrard, G. Oxygen mass transfer and hydrodynamic behaviour in wastewater: Determination of local impact of surfactants by visualization techniques. Water Res. 2014, 58, 111–121. [Google Scholar] [CrossRef] [PubMed]
- Wild, M.; Mast, Y.; Takors, R. Revisiting basics of kLa dependency on aeration in bubble columns: A is surprisingly stable. Chem. Ing. Tech. 2023, 95, 511–517. [Google Scholar] [CrossRef]
- Jamnongwong, M.; Loubiere, K.; Dietrich, N.; Hébrard, G. Experimental study of oxygen diffusion coefficients in clean water containing salt, glucose or surfactant: Consequences on the liquid-side mass transfer coefficients. Chem. Eng. J. 2010, 165, 758–768. [Google Scholar] [CrossRef]
- Hebrard, G.; Zeng, J.; Loubiere, K. Effect of surfactants on liquid side mass transfer coefficients: A new insight. Chem. Eng. J. 2009, 148, 132–138. [Google Scholar] [CrossRef]
- VDI-Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-19982-0.
- Han, P.; Bartels, D.M. Temperature dependence of oxygen diffusion in H2O and D2O. J. Phys. Chem. 1996, 100, 5597–5602. [Google Scholar] [CrossRef]
- Dalla Valle, J.M. Micromeritics the Technology of Fine Particles; Pitman: New York, NY, USA, 1948; ISBN 9780598902719. [Google Scholar]
- Lapple, C.E. Particle Dynamics; EI du Pont de Nemours and Co., Inc.: Wilmington, Delaware, 1951. [Google Scholar]
- Mei, R.; Klausner, J.F. Shear lift force on spherical bubbles. Int. J. Heat Fluid Flow 1994, 15, 62–65. [Google Scholar] [CrossRef]
- Zhang, D.Z.; VanderHeyden, W.B. The effects of mesoscale structures on the macroscopic momentum equations for two-phase flows. Int. J. Multiph. Flow 2002, 28, 805–822. [Google Scholar] [CrossRef]
- Grevskott, S.; Sannæs, B.H.; Duduković, M.P.; Hjarbo, K.W.; Svendsen, H.F. Liquid circulation, bubble size distributions, and solids movement in two- and three-phase bubble columns. Chem. Eng. Sci. 1996, 51, 1703–1713. [Google Scholar] [CrossRef]
- Kelbaliyev, G.; Ceylan, K. Development of new empirical equations for estimation of drag coefficient, shape deformation, and rising velocity of gas bubbles or liquid drops. Chem. Eng. Commun. 2007, 194, 1623–1637. [Google Scholar] [CrossRef]
- McClure, D.D.; Kavanagh, J.M.; Fletcher, D.F.; Barton, G.W. Oxygen transfer in bubble columns at industrially relevant superficial velocities: Experimental work and CFD modelling. Chem. Eng. J. 2015, 280, 138–146. [Google Scholar] [CrossRef]
- Kheradmandnia, S.; Hashemi-Najafabadi, S.; Shojaosadati, S.A.; Mousavi, S.M.; Malek Khosravi, K. Development of parallel miniature bubble column bioreactors for fermentation process. J. Chem. Technol. Biotechnol. 2015, 90, 1051–1061. [Google Scholar] [CrossRef]
- Anastasiou, A.D.; Passos, A.D.; Mouza, A.A. Bubble columns with fine pore sparger and non-Newtonian liquid phase: Prediction of gas holdup. Chem. Eng. Sci. 2013, 98, 331–338. [Google Scholar] [CrossRef]
- Rampure, M.R.; Kulkarni, A.A.; Ranade, V.V. Hydrodynamics of bubble column reactors at high gas velocity: Experiments and computational fluid dynamics (CFD) simulations. Ind. Eng. Chem. Res. 2007, 46, 8431–8447. [Google Scholar] [CrossRef]
- Leonard, B.; Mokhtari, S. ULTRA-SHARP Nonoscillatory Convection Schemes for High-Speed Steady Multidimensional Flow; NASA: Washington, DC, USA, 1990.
- van Doormaal, J.P.; Raithby, G.D. Enhancements of the simple method for predicting incompressible fluid flows. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar] [CrossRef]
- Hung, G.W.; Dinius, R.H. Diffusivity of oxygen in electrolyte solutions. J. Chem. Eng. Data 1972, 17, 449–451. [Google Scholar] [CrossRef]
- van Stroe-Biezen, S.; Janssen, A.; Janssen, L. Solubility of oxygen in glucose solutions. Anal. Chim. Acta 1993, 280, 217–222. [Google Scholar] [CrossRef][Green Version]
- Sangani, A.S.; Didwania, A.K. Dynamic simulations of flows of bubbly liquids at large Reynolds numbers. J. Fluid Mech. 1993, 250, 307–337. [Google Scholar] [CrossRef]
- Mei, R.; Klausner, J.F.; Lawrence, C.J. A note on the history force on a spherical bubble at finite Reynolds number. Phys. Fluids 1994, 6, 418–420. [Google Scholar] [CrossRef]
- Bayareh, M.; Doostmohammadi, A.; Dabiri, S.; Ardekani, A.M. On the rising motion of a drop in stratified fluids. Phys. Fluids 2013, 25, 103302. [Google Scholar] [CrossRef]
- Nalajala, V.S.; Kishore, N. Drag of contaminated bubbles in power-law fluids. Colloids Surf. A Physicochem. Eng. Asp. 2014, 443, 240–248. [Google Scholar] [CrossRef]
- Tzounakos, A.; Karamanev, D.G.; Margaritis, A.; Bergougnou, M.A. Effect of the surfactant concentration on the rise of gas bubbles in power-law non-Newtonian liquids. Ind. Eng. Chem. Res. 2004, 43, 5790–5795. [Google Scholar] [CrossRef]
- Kulkarni, A.A. Mass transfer in bubble column reactors: Effect of bubble size distribution. Ind. Eng. Chem. Res. 2007, 46, 2205–2211. [Google Scholar] [CrossRef]
- Vasconcelos, J.; Orvalho, S.; Alves, S. Gas–liquid mass transfer to single bubbles: Effect of surface contamination. AIChE J. 2002, 48, 1145–1154. [Google Scholar] [CrossRef]
- Schulze, G.; Schlünder, E. Physical absorption of single gas bubbles in degassed and preloaded water. Chem. Eng. Process. 1985, 53, 755–759. [Google Scholar] [CrossRef]
- Alves, S.S.; Orvalho, S.P.; Vasconcelos, J.M.T. Effect of bubble contamination on rise velocity and mass transfer. Chem. Eng. Sci. 2005, 60, 1–9. [Google Scholar] [CrossRef]
- Fortescue, G.E.; Pearson, J. On gas absorption into a turbulent liquid. Chem. Eng. Sci. 1967, 22, 1163–1176. [Google Scholar] [CrossRef]

| 1 × PBS | |
| NaCl | 8.0 [g L−1] |
| KCl | 0.2 [g L−1] |
| Na2HPO4 | 1.42 [g L−1] |
| KH2PO4 | 0.27 [g L−1] |
| Minimal Media | |
| Glucose × H2O | 14.5 [g L−1] |
| K2HPO4 | 2.6 [g L−1] |
| NaH2HPO4 | 1.0 [g L−1] |
| (NH4)2SO4 | 9.0 [g L−1] |
| MOPS | 20.0 [g L−1] |
| Trace Elements | |
| Na3C6H5O7 × 2 H2O | 110.0 [mg L−1] |
| FeCl3 × 6 H2O | 8.3 [mg L−1] |
| ZnSO4 × 7 H2O | 0.09 [mg L−1] |
| MnSO4 × H2O | 0.05 [mg L−1] |
| CuSO4 × 5 H2O | 0.8 [mg L−1] |
| CoCl2 × 6 H2O | 0.09 [mg L−1] |
| CaCl2 × 2 H2O | 44.0 [mg L−1] |
| MgSO4 × 7 H2O | 100.0 [mg L−1] |
| Medium | |
| Deionized water (Daq) | |
| 1 × PBS (DPBS) | |
| Minimal media (DMM) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mast, Y.; Wild, M.; Takors, R. Optimizing Mass Transfer in Multiphase Fermentation: The Role of Drag Models and Physical Conditions. Processes 2024, 12, 45. https://doi.org/10.3390/pr12010045
Mast Y, Wild M, Takors R. Optimizing Mass Transfer in Multiphase Fermentation: The Role of Drag Models and Physical Conditions. Processes. 2024; 12(1):45. https://doi.org/10.3390/pr12010045
Chicago/Turabian StyleMast, Yannic, Moritz Wild, and Ralf Takors. 2024. "Optimizing Mass Transfer in Multiphase Fermentation: The Role of Drag Models and Physical Conditions" Processes 12, no. 1: 45. https://doi.org/10.3390/pr12010045
APA StyleMast, Y., Wild, M., & Takors, R. (2024). Optimizing Mass Transfer in Multiphase Fermentation: The Role of Drag Models and Physical Conditions. Processes, 12(1), 45. https://doi.org/10.3390/pr12010045









