Study on Sublimation Drying of Carrot and Simulation by Using Cellular Automata
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
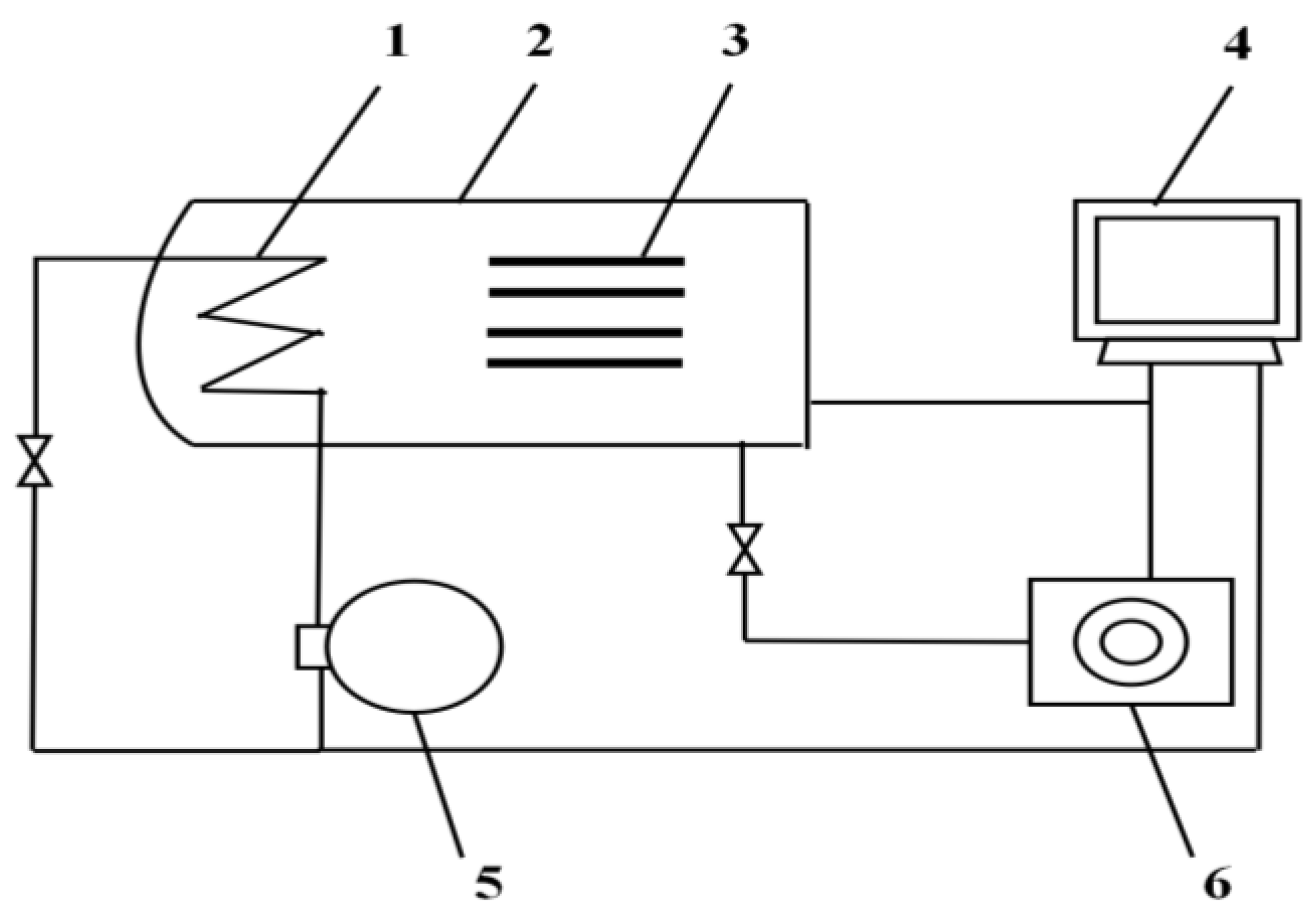
2.2. Experimental Procedure
2.3. Model of Sublimation Drying
- The material itself is isotropic, featuring uniform heat and mass transfer in the frozen region.
- The change in the volume of the material during sublimation is ignored.
- The sublimation interface exists between the dried region and the frozen region, which is continuous and infinitesimal in thickness.
- The concentration of water vapor is in equilibrium with ice at the sublimation interface.
- The porous matrix formed by ice sublimation is rigid in structure, and the matrix is permeable, which enables the vapor flux to circulate.
2.3.1. Governing Equations
2.3.2. The Initial and Boundary Conditions
2.4. Cellular Automata Model
3. Results and Discussion
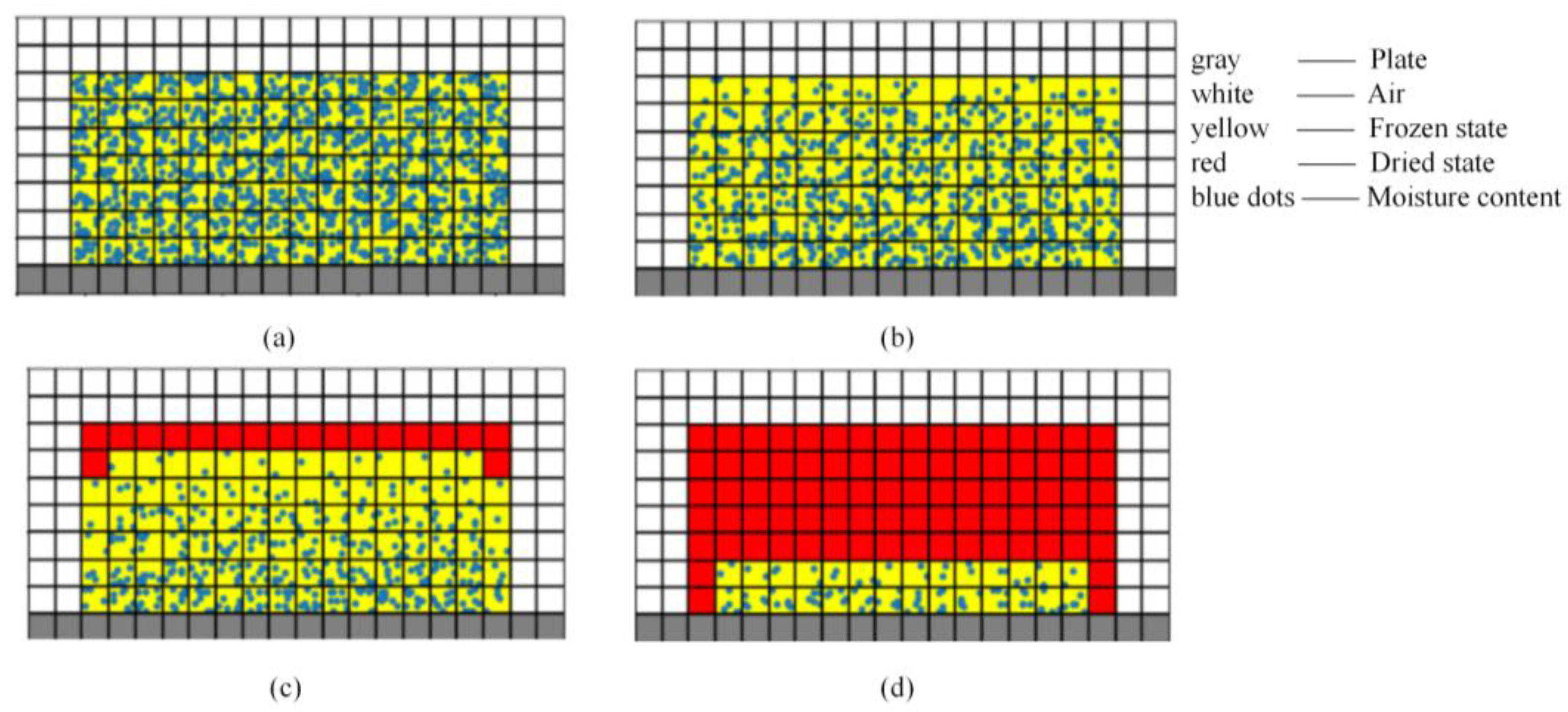
3.1. Simulation Results
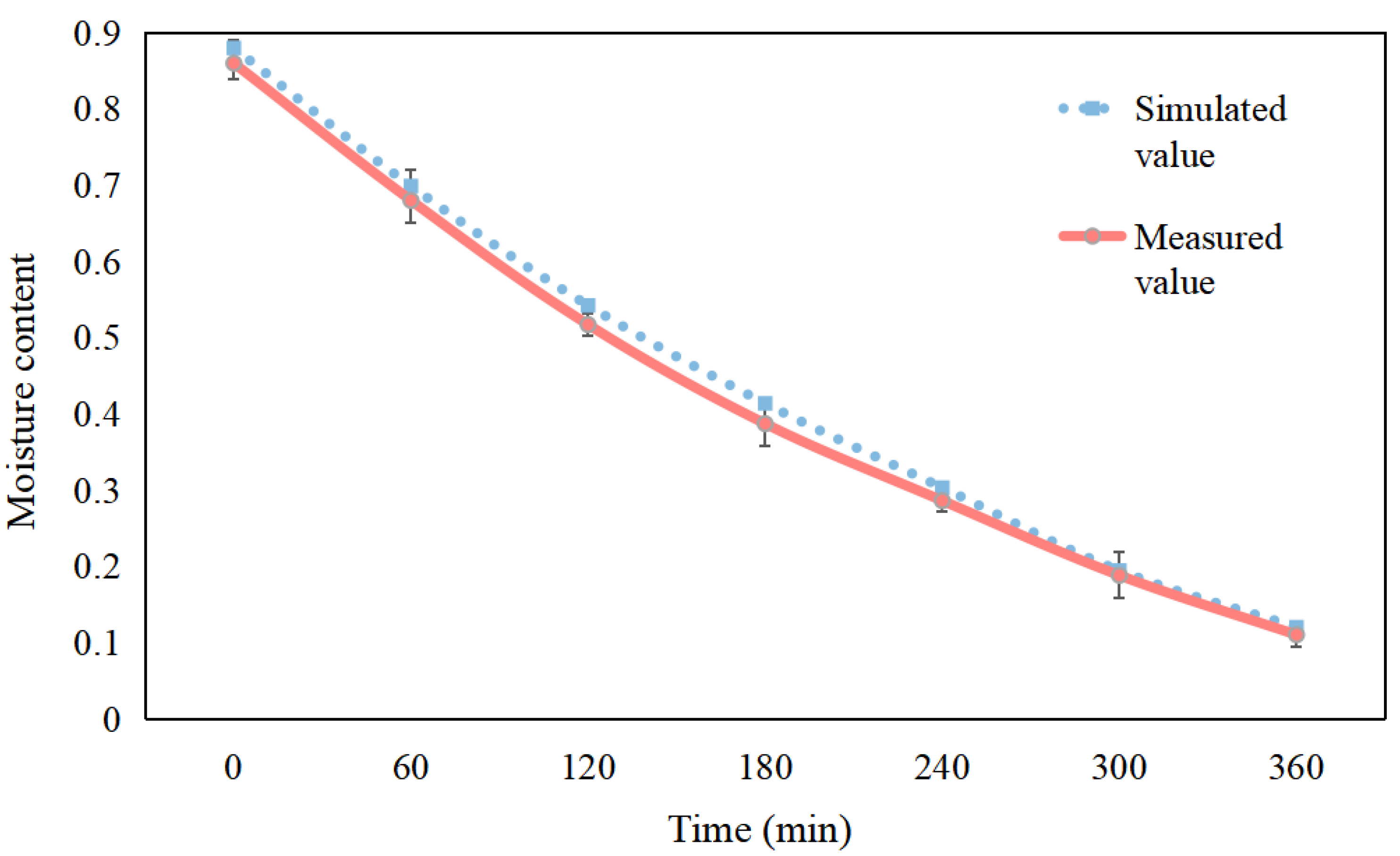
3.2. Comparison of Moisture Content Curve
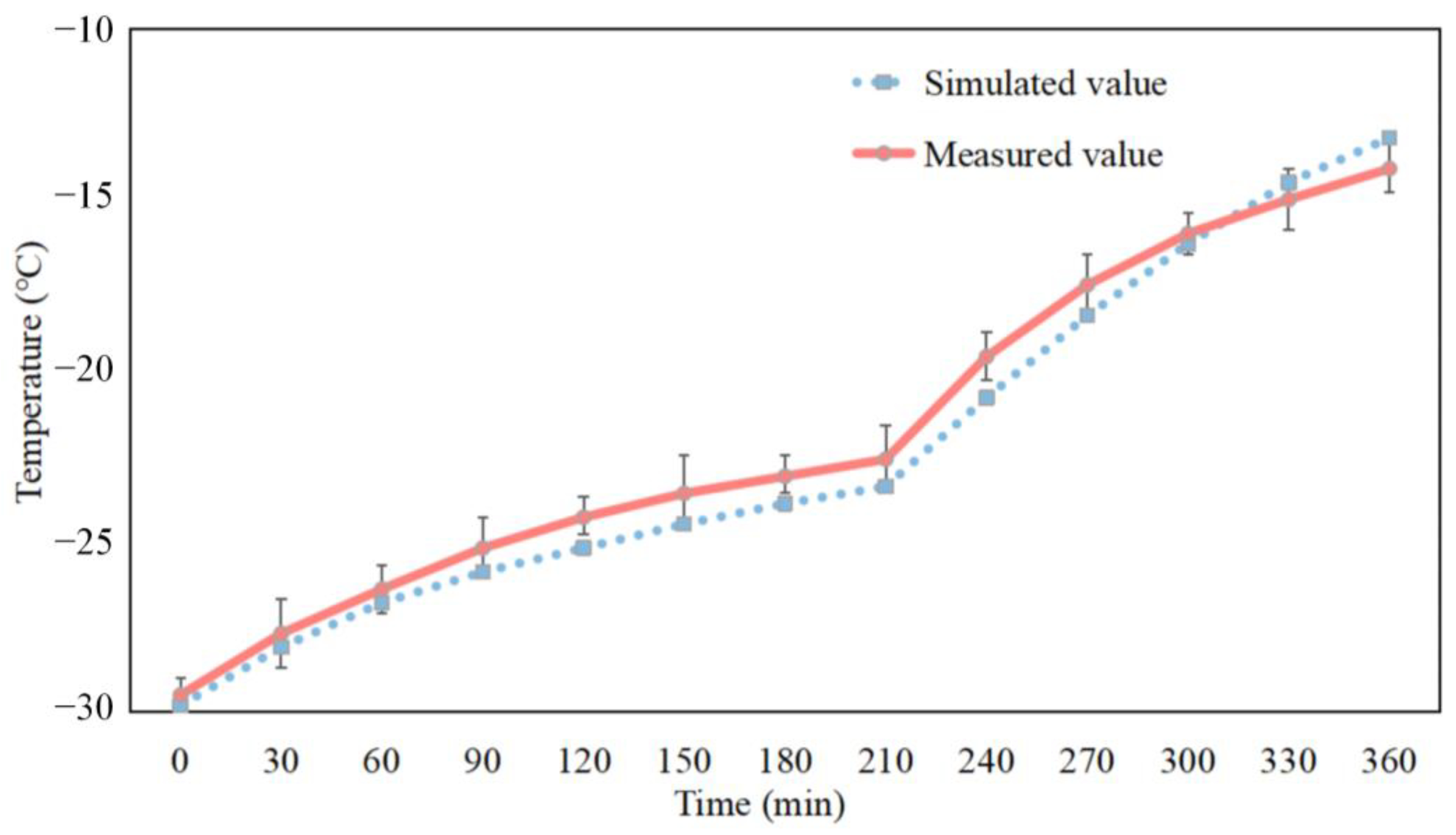
3.3. Comparison of Temperature Curve
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| constant dependent only upon the structure of the porous medium and giving relative D’Arcy flow permeability | |
| constant dependent only upon the structure of the porous medium and giving relative Knudsen flow permeability | |
| constant dependent only upon the structure of the porous medium and giving the ratio of bulk diffusivity within the porous medium to the free gas bulk diffusivity | |
| specific heat capacity at constant pressure | |
| free gas mutual diffusivity in a binary mixture of water vapor and inert gas | |
| F | view factor for radiative heat transfer |
| geometric shape of the moving interface, a function of time and radial distance | |
| convective heat transfer coefficient | |
| k | thermal conductivity |
| bulk diffusivity constant | |
| self-diffusivity constant | |
| knudsen diffusivity for inert gas | |
| mean Knudsen diffusivity for binary gas mixture | |
| knudsen diffusivity for water vapor | |
| L | thickness of sample |
| M | molecular weight |
| N | mass flux |
| P | partial pressure in the dried layer |
| Q | heat flux |
| r | space coordinate of radial distance |
| R | radius of sample |
| ideal gas constant | |
| t | drying time |
| T | temperature |
| v | velocity of moving interface |
| z | space coordinate of distance along the thickness of the sample |
| Z | value of z at the moving interface |
| Greek letters | |
| thermal diffusivity | |
| heat of sublimation of ice (J/kg) | |
| emissivity of the material surface. | |
| porosity of sample | |
| viscosity of vapor phase in pores of the dried layer | |
| density | |
| Stefan–Boltzmann constant | |
| Subscripts | |
| e | effective |
| I | frozen region |
| II | dried region |
| in | inert gas |
| lp | lower heating plate |
| r | r direction |
| up | upper heating plate |
| w | water vapor |
| z | z direction |
References
- Ding, C.J.; Lu, J.; Song, Z.Q. Electrohydrodynamic Drying of Carrot Slices. PLoS ONE 2015, 10, e0124077. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.G.; Guo, X.Y.; Wu, T. A novel dehydration technique for carrot slices implementing ultrasound and vacuum drying methods. Ultrason. Sonochem. 2016, 30, 28–34. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Liu, F.; Wu, M.; Li, Y.; Song, X.; Yin, J. Effects of Drying Treatments on Nutritional Compositions, Volatile Flavor Compounds, and Bioactive Substances of Broad Beans. Foods 2023, 12, 2160. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.M.; Durance, T.D.; Scaman, C.H. Characterization of vacuum microwave, air and freeze dried carrot slices. Food Res. Int. 1998, 31, 111–117. [Google Scholar] [CrossRef]
- Bano, G.; De-Luca, R.; Tomba, E.; Marcelli, A.; Bezzo, F.; Barolo, M.J.I.; Research, E.C. Primary Drying Optimization in Pharmaceutical Freeze-Drying: A Multivial Stochastic Modeling Framework. Ind. Eng. Chem. Res. 2020, 59, 5056–5071. [Google Scholar] [CrossRef]
- Ratti, C. Hot air and freeze-drying of high-value foods: A review. J. Food Eng. 2001, 49, 311–319. [Google Scholar] [CrossRef]
- Niu, J.Z.; Zhao, B.F.; Guo, X.J.; Yin, T. Effects of Vacuum Freeze-Drying and Vacuum Spray-Drying on Biochemical Properties and Functionalities of Myofibrillar Proteins from Silver Carp. J. Food Qual. 2019, 2019, 9457835. [Google Scholar] [CrossRef]
- Cardenas-Bailon, F.; Perez-Vazquez, C.; Osorio-Revilla, G.; Gallardo-Velazquez, T. Shrinkage modeling, drying kinetics and quality assessment of carrot cubes dried in a two stage spouted bed drying process. Emir. J. Food Agric. 2019, 31, 654–665. [Google Scholar] [CrossRef]
- Luo, R.; Zhou, G.; Qiao, X. Dynamic study on operation conditions for the higher sublimation rate during freezing drying of cooked beef slice. Trans. Chin. Soc. Agric. Eng. 2008, 24, 226–231. [Google Scholar]
- Bhatta, S.; Stevanovic Janezic, T.; Ratti, C. Freeze-Drying of Plant-Based Foods. Foods 2020, 9, 87. [Google Scholar] [CrossRef]
- Chen, J.; Venkitasamy, C.; Shen, Q.; McHugh, T.H.; Zhang, R.H.; Pan, Z.L. Development of healthy crispy carrot snacks using sequential infrared blanching and hot air drying method. Lwt-Food Sci. Technol. 2018, 97, 469–475. [Google Scholar] [CrossRef]
- Fratianni, A.; Niro, S.; Messia, M.C.; Panfili, G.; Marra, F.; Cinquanta, L. Evaluation of carotenoids and furosine content in air dried carrots and parsnips pre-treated with pulsed electric field (PEF). Eur. Food Res. Technol. 2019, 245, 2529–2537. [Google Scholar] [CrossRef]
- Munzenmayer, P.; Ulloa, J.; Pinto, M.; Ramirez, C.; Valencia, P.; Simpson, R.; Almonacid, S. Freeze-Drying of Blueberries: Effects of Carbon Dioxide (CO2) Laser Perforation as Skin Pretreatment to Improve Mass Transfer, Primary Drying Time, and Quality. Foods 2020, 9, 211. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, M.; Mujumdar, A.S.; Sun, J.C. Microwave Freeze-Drying Characteristics and Sensory Quality of Instant Vegetable Soup. Dry. Technol. 2009, 27, 962–968. [Google Scholar] [CrossRef]
- Izkara, J.I.L.; Technology, J.J.D. Experimental Estimation of Effective Transport Coefficients in Freeze Drying for Simulaton and Optimization Purposes. Dry. Technol. 1996, 14, 743–763. [Google Scholar]
- Curcio, S.; Aversa, M. Influence of shrinkage on convective drying of fresh vegetables: A theoretical model. J. Food Eng. 2014, 123, 36–49. [Google Scholar] [CrossRef]
- El-Maghlany, W.M.; Bedir, A.E.; Elhelw, M.; Attia, A. Freeze-drying modeling via multi-phase porous media transport model. Int. J. Therm. Sci. 2019, 135, 509–522. [Google Scholar] [CrossRef]
- Capozzi, L.C.; Barresi, A.A.; Pisano, R. A multi-scale computational framework for modeling the freeze-drying of microparticles in packed-beds. Powder Technol. 2019, 343, 834–846. [Google Scholar] [CrossRef]
- Xia, B.; Sun, D.W. Applications of computational fluid dynamics (CFD) in the food industry: A review. Comput. Electron. Agric. 2002, 34, 5–24. [Google Scholar] [CrossRef]
- Ivanov, S.; Troyankin, A.; Gurikov, P.; Kolnoochenko, A.; Menshutina, N. 3D Cellular automata for modeling of spray freeze drying process. In Proceedings of the 21st European Symposium on Computer Aided Process Engineering (ESCAPE-21), Chalkidiki, Greece, 29 May–1 June 2010; pp. 136–140. [Google Scholar]
- Engelbrecht, A.M. Modelling of Mass Transfer in Packing Materials with Cellular Automata; Stellenbosch Stellenbosch University: Stellenbosch, South Africa, 2008. [Google Scholar]
- Gui, C.; Tao, L.R.; Zhang, Y.Q. Experimental study on improvement of freeze-drying process for porcine aorta. Dry. Technol. 2022, 40, 401–415. [Google Scholar] [CrossRef]
- Gan, K.H.; Bruttini, R.; Crosser, O.K.; Liapis, A.I. Freeze-drying of pharmaceuticals in vials on trays: Effects of drying chamber wall temperature and tray side on lyophilization performance. Int. J. Heat Mass Transf. 2005, 48, 1675–1687. [Google Scholar] [CrossRef]
- Mascarenhas, W.J.; Akay, H.U.; Pikal, M.J. A computational model for finite element analysis of the freeze-drying process. Comput. Methods Appl. Mech. Eng. 1997, 148, 105–124. [Google Scholar] [CrossRef]
- da Silva, W.P.; de Souto, L.M.; Ferreira, J.P.D.; Gomes, J.P.; de Lima, A.G.B.; Queiroz, A.J.D.; de Figueiredo, R.M.F.; Santos, D.D.; de Santana, M.D.S.; dos Santos, F.S.; et al. Use of Inverse Method to Determine Thermophysical Properties of Minimally Processed Carrots during Chilling under Natural Convection. Foods 2023, 12, 2084. [Google Scholar] [CrossRef] [PubMed]
- Aydin, E.S.; Yucel, O.; Sadikoglu, H. Modelling and simulation of a moving interface problem: Freeze drying of black tea extract. Heat Mass Transf. 2017, 53, 2143–2154. [Google Scholar] [CrossRef]
- Srinivasan, G.; Muneeshwaran, M.; Raja, B. Numerical investigation of heat and mass transfer behavior of freeze drying of milk in vial. Heat Mass Transf. 2019, 55, 2073–2081. [Google Scholar] [CrossRef]
- Sheehan, P.; Liapis, A.I. Modeling of the primary and secondary drying stages of the freeze drying of pharmaceutical products in vials: Numerical results obtained from the solution of a dynamic and spatially multi-dimensional lyophilization model for different operational policies. Biotechnol. Bioeng. 1998, 60, 712–728. [Google Scholar] [CrossRef]
- Sadikoglu, H.; Liapis, A.I. Mathematical modelling of the primary and secondary drying stages of bulk solution freeze-drying in trays: Parameter estimation and model discrimination by comparison of theoretical results with experimental data. Dry. Technol. 1997, 15, 791–810. [Google Scholar] [CrossRef]
- Levin, P.; Buchholz, M.; Meunier, V.; Kessler, U.; Palzer, S.; Heinrich, S. Comparison of Knudsen Diffusion and the Dusty Gas Approach for the Modeling of the Freeze-Drying Process of Bulk Food Products. Processes 2022, 10, 548. [Google Scholar] [CrossRef]
- Ramsak, M.; Ravnik, J.; Zadravec, M.; Hribersek, M.; Iljaz, J. Freeze-drying modeling of vial using BEM. Eng. Anal. Bound. Elem. 2017, 77, 145–156. [Google Scholar] [CrossRef]
- Millman, M.J.; Liapis, A.I.; Marchello, J.M. An analysis of the lyophilization process using a sorption-sublimation model and various operational policies. AIChE J. 1985, 31, 1594–1604. [Google Scholar] [CrossRef]
- Guo, S.S. Experimental and Numerical Simulation Study on Heat and Mass Transfer Process in Freeze Drying. Master’s Thesis, Qingdao University, Qingdao, China, 2021. [Google Scholar]
- Wolnik, B.; Dzedzej, A.; Baetens, J.M.; De Baets, B. Number-conserving cellular automata with a von Neumann neighborhood of range one. J. Phys. Math. Theor. 2017, 50, 435101. [Google Scholar] [CrossRef][Green Version]
- Farhaninejad, Z.; Fathi, M.; Shahedi, M. Modelling Mass Transfer during Hot Air Drying of Banana Using Cellular Automaton. J. Agric. Sci. Technol. 2019, 21, 89–100. [Google Scholar]
- Muzzio, C.R.; Dini, N.G. Simulation of freezing step in vial lyophilization using finite element method. Comput. Educ. 2011, 35, 2274–2283. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, K.; Zhang, D. Simulation Analysis and Experimental Research on Vacuum Freeze-drying of Pitaya. J. Refrig. 2022, 43, 142–150. [Google Scholar]
- Xanthopoulos, G.; Athanasiou, A.; Sempou, A.; Lentzou, D.; Templalexis, C.; Boudouvis, A.G. Study of the Drying Rate and Colour Kinetics during Stepwise Air-Drying of Apricot Halves. Int. J. Food Eng. 2019, 15, 20180372. [Google Scholar] [CrossRef]
- Thamkaew, G.; Sjoholm, I.; Galindo, F.G. A review of drying methods for improving the quality of dried herbs. Crit. Rev. Food Sci. Nutr. 2021, 61, 1763–1786. [Google Scholar] [CrossRef]
- Zhu, L.C.; Li, M.Q.; Yang, W.X.; Zhang, J.Y.; Yang, X.H.; Zhang, Q.; Wang, H.T. Effects of Different Drying Methods on Drying Characteristics and Quality of Glycyrrhiza uralensis (Licorice). Foods 2023, 12, 1652. [Google Scholar] [CrossRef] [PubMed]
- Arevalo-Pinedo, A.; Murr, F.E.X.; Arevalo, Z.D.S.; Giraldo-Zuniga, A.D. Modeling with shrinkage during the vacuum drying of carrot (daucus carota). J. Food Process. Preserv. 2010, 34, 611–621. [Google Scholar] [CrossRef]
- Khalloufi, S.; Robert, J.L.; Ratti, C. Solid foods freeze-drying simulation and experimental data. J. Food Process Eng. 2005, 28, 107–132. [Google Scholar] [CrossRef]

| Parameters | Value | Unit |
|---|---|---|
| 7.219 × 10−15 | m2 | |
| 3.85583 × 10−4 | m | |
| 0.921 | – | |
| m2/s | ||
| ) | m4/N·s | |
| m2/s | ||
| 8.729 × 10−7(T0 + Tint)2.334 | kg/ms3 | |
| m2/s | ||
| m2/s | ||
| m2/s | ||
| [18.4858(T1.5/(T + 650))] | kg/ms | |
| L | 10 | mm |
| R | 40 | mm |
| 243.15 | K | |
| 303.15 | K | |
| 263.15 | K | |
| 303.15 | K | |
| 1000 | kg/m3 | |
| 236 | kg/m3 | |
| 388 | kg/m3 | |
| 1616.6 | J/(kg∙K) | |
| 2590 | J/(kg∙K) | |
| 1930 | J/(kg∙K) | |
| 2.68 | W/(m∙K) | |
| 0.18 | W/(m∙K) | |
| 680[12.98 × 10−8P + 39.806 × 10−6] | W/(m∙K) | |
| 0.581 | – | |
| 18 | g/mol | |
| 28 | g/mol | |
| 1.07 | Pa | |
| 24 | Pa | |
| 2.7912 × 103 | kJ/kg | |
| 8.314 | J/(mol∙K) | |
| 5.67 × 10−8 | W/(m2∙K4) | |
| 0.85 | – | |
| 0.75 | – | |
| 0.795 | – | |
| 0.00809 | – | |
| 26 | W/(m2∙K) |
| Cell Status | Symbols | Description |
|---|---|---|
| Plate | P (gray) | For fixed cells, heat exchange occurs only with the bottom layer of the carrot. |
| Frozen State | FS (yellow) | The initial state of the carrot cells, with the level of water content indicated by the number of blue dots. |
| Dried State | DS (red) | As the moisture content decreases below a certain threshold, the cell transitions into a dried state, and at this point, the number of blue dots in the cell is 0. |
| Air | Air (white) | Referring to the air within the drying chamber, heat exchange transpires between the air and the material through radiation and convective mechanisms. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, J.; Jiao, F.; Nie, L.; Wang, Y.; Du, Y.; Liu, Z. Study on Sublimation Drying of Carrot and Simulation by Using Cellular Automata. Processes 2023, 11, 2507. https://doi.org/10.3390/pr11082507
Shao J, Jiao F, Nie L, Wang Y, Du Y, Liu Z. Study on Sublimation Drying of Carrot and Simulation by Using Cellular Automata. Processes. 2023; 11(8):2507. https://doi.org/10.3390/pr11082507
Chicago/Turabian StyleShao, Jiayuan, Fan Jiao, Lili Nie, Ying Wang, Yihan Du, and Zhenyu Liu. 2023. "Study on Sublimation Drying of Carrot and Simulation by Using Cellular Automata" Processes 11, no. 8: 2507. https://doi.org/10.3390/pr11082507
APA StyleShao, J., Jiao, F., Nie, L., Wang, Y., Du, Y., & Liu, Z. (2023). Study on Sublimation Drying of Carrot and Simulation by Using Cellular Automata. Processes, 11(8), 2507. https://doi.org/10.3390/pr11082507










