3.1. Overall Process Design
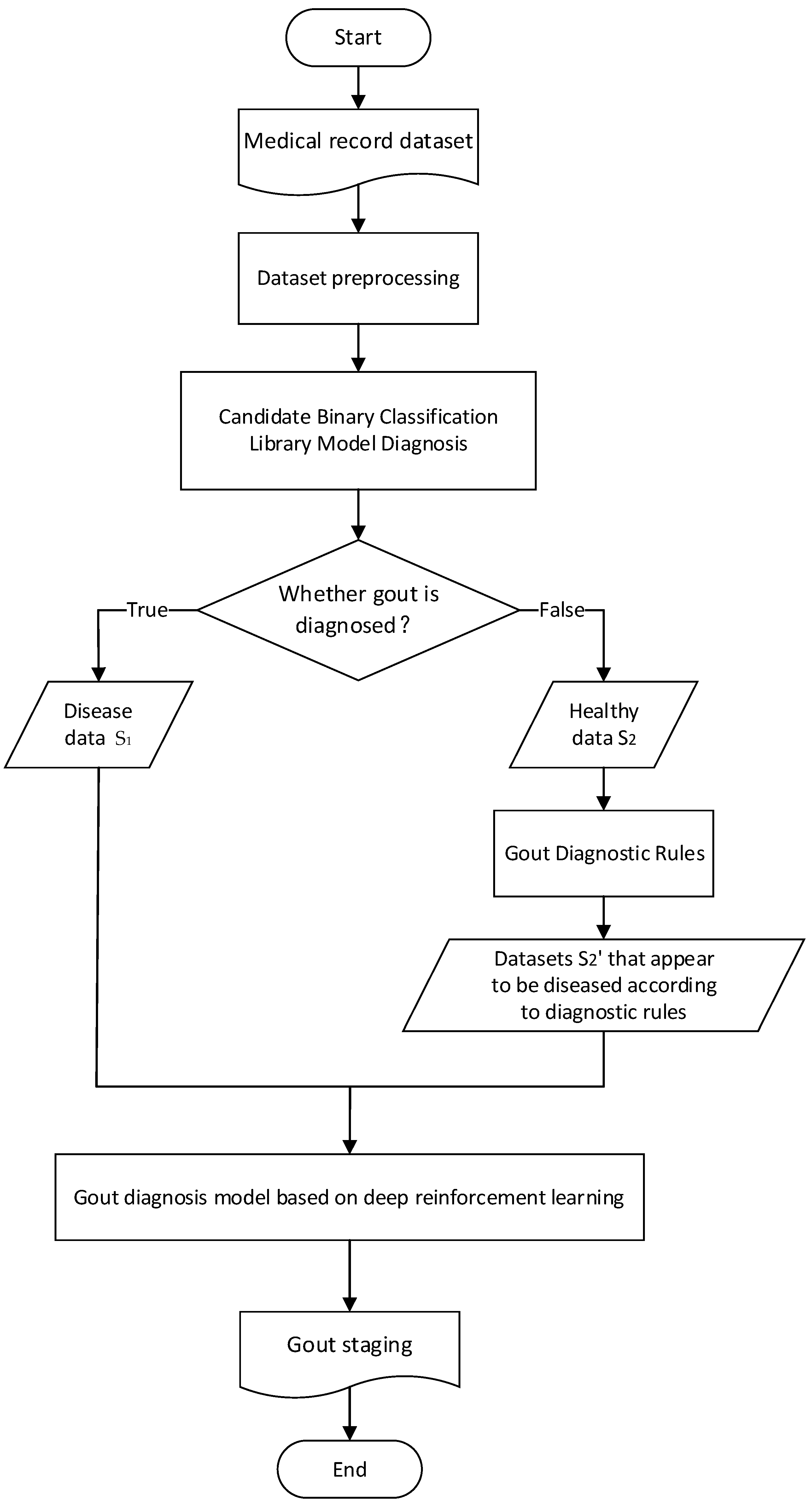
In view of the problem background and related work introduced above, the flow chart of the gout staging diagnosis method designed in this paper is shown in
Figure 2.
The patient’s electronic medical record is derived from the hospital’s electronic medical record system, and the physical examination data such as pain degree, height and weight and biochemical test results such as hematuria in the electronic medical record are used as an eigenvalue set. Firstly, the medical record data are preprocessed.
Then, the multiple diseases diagnosed by doctors are simplified into two categories, confirmed or “healthy”, and the “candidate binary classification model library” on the predicted medical records is used to predict whether to diagnose gout. The samples diagnosed as “disease” in the binary classification are
, and the samples diagnosed as “healthy” are
. The gout diagnosis rules provided by the doctor are used to screen the characteristic values that have a decisive impact on the diagnosis of gout. The set of such characteristic values is set as F′, the health samples are
, and the data set
is selected and displayed as gout on F′. Then,
is combined with
to form the samples
for multi-classification. The specific pseudo-code is shown in
Table 1.
The stage of gout is predicted on , and deep reinforcement learning is introduced to solve the parameter adjustment problem of the stage model so as to realize the stage diagnosis of gout.
3.2. Data Preprocessing
Considering that mistakes in the manual entry of electronic medical records may lead to some incorrect data in the patient’s electronic medical record, we set up data cleaning rules based on common sense in the medical field. For example, the patient’s weight range during physical examination should be within the range of 20 kg to 150 kg, to clean the electronic medical records. Afterwards, the eigenvalues of the electronic medical records are processed, including two directions of absence analysis and correlation analysis.
We first obtain the missing degree of each eigenvalue in the existing eigenvalue set through the calculation of the missing degree, and then determine the threshold of the missing degree and use this threshold as the limit to classify the eigenvalues, which are mainly divided into “categories with more missing values” and “Few classes with missing values”. The threshold we set for this experiment is 70%. For eigenvalues with a missing degree greater than 70%, we delete them. For the eigenvalues with a missing degree less than 70%, the missing data can be divided into completely random missing, random missing and non-random missing according to different reasons for missing. The specific complete random missing value means that the missing value of the feature value is not related to other feature values, such as the missing heart rate feature value; random missing means that the missing value is random, and the missing of the data depends on other feature values, such as underage smoking. Most of the time feature values are null, and this feature value is related to the patient’s age. Non-random missing means that the missing values in the data set do not appear randomly, but there is a certain pattern. For example, the number of abortions in young female patients is partially missing. This characteristic value involves patient privacy, and some patients can choose not to fill in. For the eigenvalues of the first two missing cases, we fill them in by estimating them. For non-randomly missing eigenvalues, we use the random-forest-based missing value filling method to fill. The specific pseudo-code is shown in
Table 2.
In order to further improve the accuracy of model prediction, we comprehensively consider the two aspects of the chi-square test and discrete category interaction information to analyze the correlation degree of the feature value set. The eigenvalues with low correlation are deleted to obtain the feature set after preliminary optimization.
The chi-square test method is a hypothesis testing method, which mainly compares the correlation analysis of two or more sample rates and two categorical variables. The test formula is as follows (4):
where
represents the actual value and
represents the expected value.
is the absolute size of the deviation between the actual value and the expected value, and the larger the
, the greater the influence of the characteristic value on the stage of gout. For example, in this topic, the quantitative assignment of gout is one of the characteristic values. We assume that the quantitative assignment of gout has no correlation with the results of gout staging. According to the distribution of sample data, in each category where the rows and columns cross, the expected value is calculated, that is (Sum of this row * Sum of this column)/Total amount of data set. Finally, the expected value and actual value are substituted into the Formula (4) to calculate the chi-square value. The larger the chi-square value, the greater the impact of gout quantification on the results of gout staging, and vice versa, the smaller the impact.
Discrete category interaction information is an indicator used to measure the degree of interaction between features in a classification model. It can help us understand the impact of input features on model prediction and select the most important features to improve the performance of the model. The test formula is shown as (5).
If are mutually independent variables , the above is 0, so the larger the value of becomes, the correlation between the two variables is becoming bigger and bigger.
Considering the chi-square test and the interactive information results of discrete categories, we sort the result values from large to small. The larger the result value, the greater the impact of the feature value on the gout stage, and we reserve the greater influence on the gout stage. By deleting the eigenvalues that have little influence on the gout staging, a further optimized eigenvalue set can be obtained, which is finally used for the diagnosis and prediction of gout staging.
Finally, the gout staging data of the electronic medical records of patients diagnosed in the hospital were counted; a total of 4043 “healthy” patient medical records were obtained, and a total of 20,829 electronic medical records were diagnosed as gout, Among them, 8115 were in the chronic arthritis period, 1800 were in the acute arthritis period, and 10,914 were in the intermittent period., and the distribution of each sample in the specific data set is shown in
Table 3.
3.3. Gout Diagnosis
In order to better predict the stage of gout, we first predict whether gout is diagnosed or not. This is a binary classification problem. The purpose of this is to reduce the interference of “healthy” data sets on the prediction of the gout stage. In order to better predict whether gout is diagnosed or not, the concept of the “candidate binary classification model library” is proposed. Multiple binary classification models are executed at the same time, and then the most suitable binary classification model is selected according to the actual test results. Commonly used binary classification algorithms include logistic regression, K nearest neighbors (KNN), support vector machines (SVM), and more. In addition to the mainstream binary classification algorithm, random forest and XGBoost also perform well in classification problems. This article uses KNN, SVM and XGBoost for the “candidate binary classification model library”.
K nearest neighbor (KNN) is based on the sample set containing eigenvalues and labels, calculates the distance between the eigenvalues of new samples without labels and the eigenvalues of samples with existing labels, and then selects the nearest sample. The corresponding label is used as the label of the new sample. In this paper, Euclidean distance is used to calculate the similarity between eigenvalues; the coordinates of eigenvalue A of the existing label sample on the two-dimensional plane are
and the coordinates of the eigenvalue A of the new sample on the two-dimensional plane are
. The distance between them is calculated as Formula (6).
Support vector machines (SVM) are a class of models that classify data in a supervised learning manner. The basic idea is to map the sample space to the high-dimensional feature space so that the optimal hyperplane can be found in the feature space for classification [
11]. The optimal hyperplane refers to the hyperplane with the largest classification interval. In the sample space, the calculation method of distance l from any point x to the hyperplane is as follows (7):
The linear equation that divides the hyperplane is assumed to be , where is the normal vector, which determines the direction of the hyperplane, and b is the displacement term, which determines the distance between the hyperplane and the source point.
XGBoost is an optimized distributed gradient boosting model. Compared with the gradient boosting framework, the processing speed and efficiency have been greatly improved, and it is suitable for binary or multi-classification problems of large-scale data. The objective function of XGBoost is Formula (8).
where
n is the number of medical record samples,
is the true diagnosis of the
i-th medical record,
is the predicted diagnosis of the
i-th sample by the model,
represents the kth decision tree, each classification process is the process of learning a new
and
l is the loss function. XGBoost is characterized by approximately expressing the loss function through the second-order Taylor expansion to ensure that the
of each decision tree is as close as possible to the real
;
is the regularization item, which is also the complexity of the decision tree [
12]. The specific expression is the Formula (9).
T is the number of leaf nodes,
uses
to prune when there are too many leaf nodes and
controls the overfitting problem that occurs when the cumulative sum is too large. The objective function is Formula (10).
where
is the value of the leaf node where the sample falls into the ith regression tree in the optimal case. The sum of the predicted scores of the corresponding leaf nodes in each decision tree is the predicted value of the sample.
The input variables of the Obj objective function include the medical record data set participating in the training, the number and depth of the decision tree, the minimum value of the leaf node weight and the learning rate.
The decision variable for minimizing the objective function Obj is determined by the split point and split rules of the decision tree. Specifically, at each node, XGBoost needs to select an optimal feature as the basis for splitting. In order to determine the optimal feature, XGBoost calculates the gain of each feature and selects the feature with the largest gain, as the splitting feature is one of the decision variables. After selecting the best features, XGBoost needs to determine how to distribute the samples to the left and right child nodes. The decision variables include the threshold of the split point and the direction of the split. After selecting the best features and splitting rules, XGBoost can construct a subtree with the minimum objective function value on each node, thereby gradually optimizing the structure of the entire decision tree.
The principle of the “candidate binary classification model library” is to use multiple binary classification machine models to train simultaneously on the medical records and use the best performing binary classification model as the final diagnostic model.
On the basis of the binary classification results, the gout diagnostic rules provided by doctors are introduced, and the feature value set and its conditions that have a decisive impact on the prediction results are selected from the feature value set to calibrate the binary classification results. The data set S2 diagnosed as “healthy” after the above two classifications is found, the data S2’ that meets the diagnosis conditions of F1 are found, and then S2’ is added to the data set “diagnosed” as gout to form a data set S3 for multi-classification. For example, the score f1 of the gout quantitative assignment table has a decisive impact on whether gout is diagnosed, and f1 is the set of feature values of the detection fields corresponding to the table. The medical record data that meet the diagnosis conditions in F1 in the “healthy” data set are found, and this part of the data is added to the data set “diagnosed” as gout to form the original data set S3 for further staging.
3.4. Deep Reinforcement Learning Model for Gout Staging Diagnosis
After being diagnosed and calibrated by the “candidate binary classification model library”, the specific stage diagnosis of gout is carried out. In order to realize automatic parameter tuning of multi-classification models, we introduce deep reinforcement learning to solve the problem of parameter tuning of staging models.
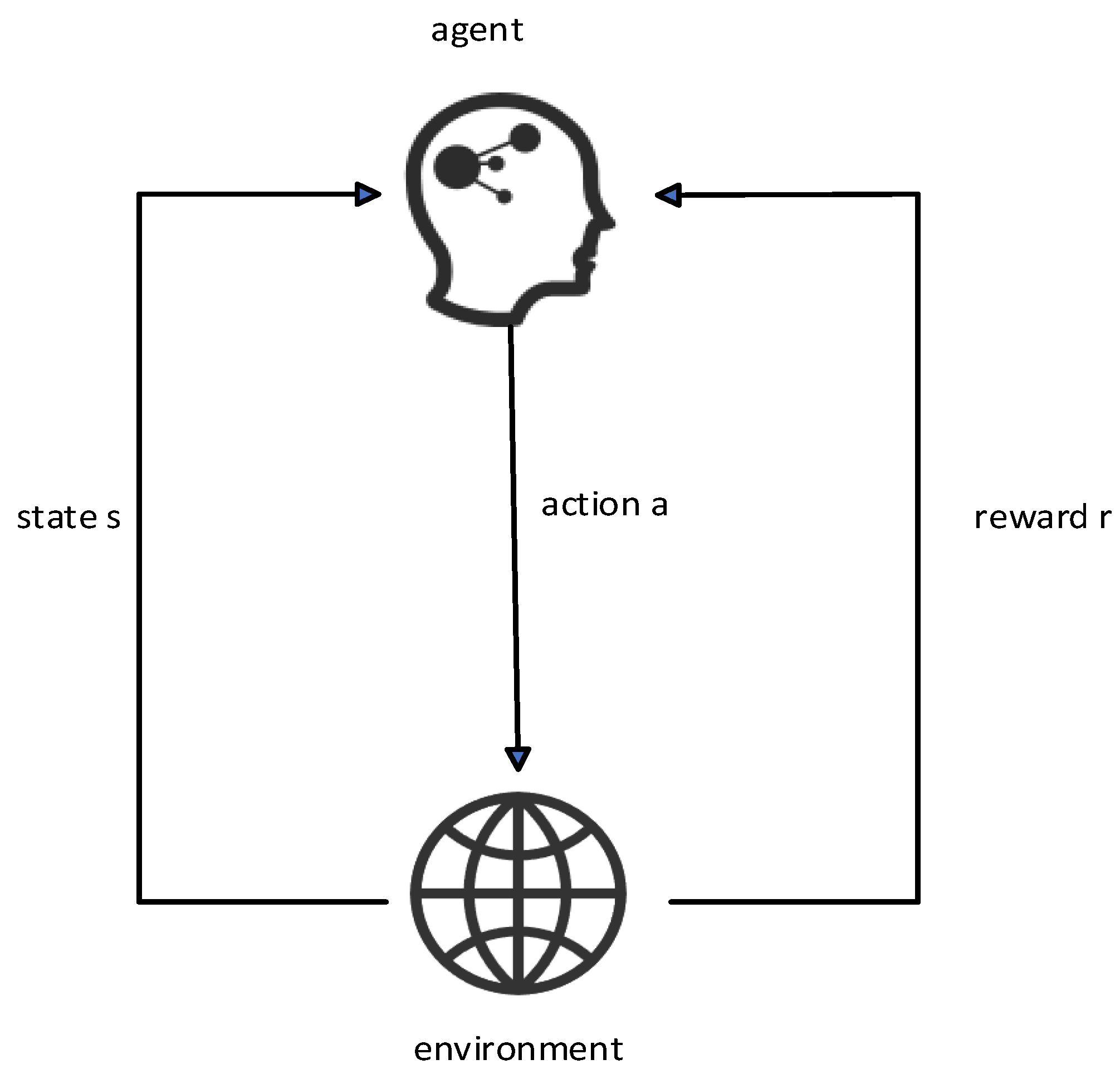
Reinforcement learning is based on the Markov process. In the Markov process, the agent selects an action to execute according to the state of the current environment. After the action is executed, the environment state will change and return the reward value of this action to the agent. The agent will choose the next action according to the reward value. In the hyperparameter tuning problem of the classification model, the mapping between the problem and the Markov process is established. In this paper, the state space is composed of all the hyperparameter configuration spaces contained in the classification model, and the behavior space is the hyperparameter value in the hyperparameter combination of the collection of behaviors.
The Markov process of the specific hyperparameter tuning problem is as follows:
According to the characteristics of the staging diagnosis model currently used, the agent forms a hyperparameter set of all hyperparameter configuration spaces, that is, the current state at time t. Assuming that there are n hyperparameters in the hyperparameter set, the state is .
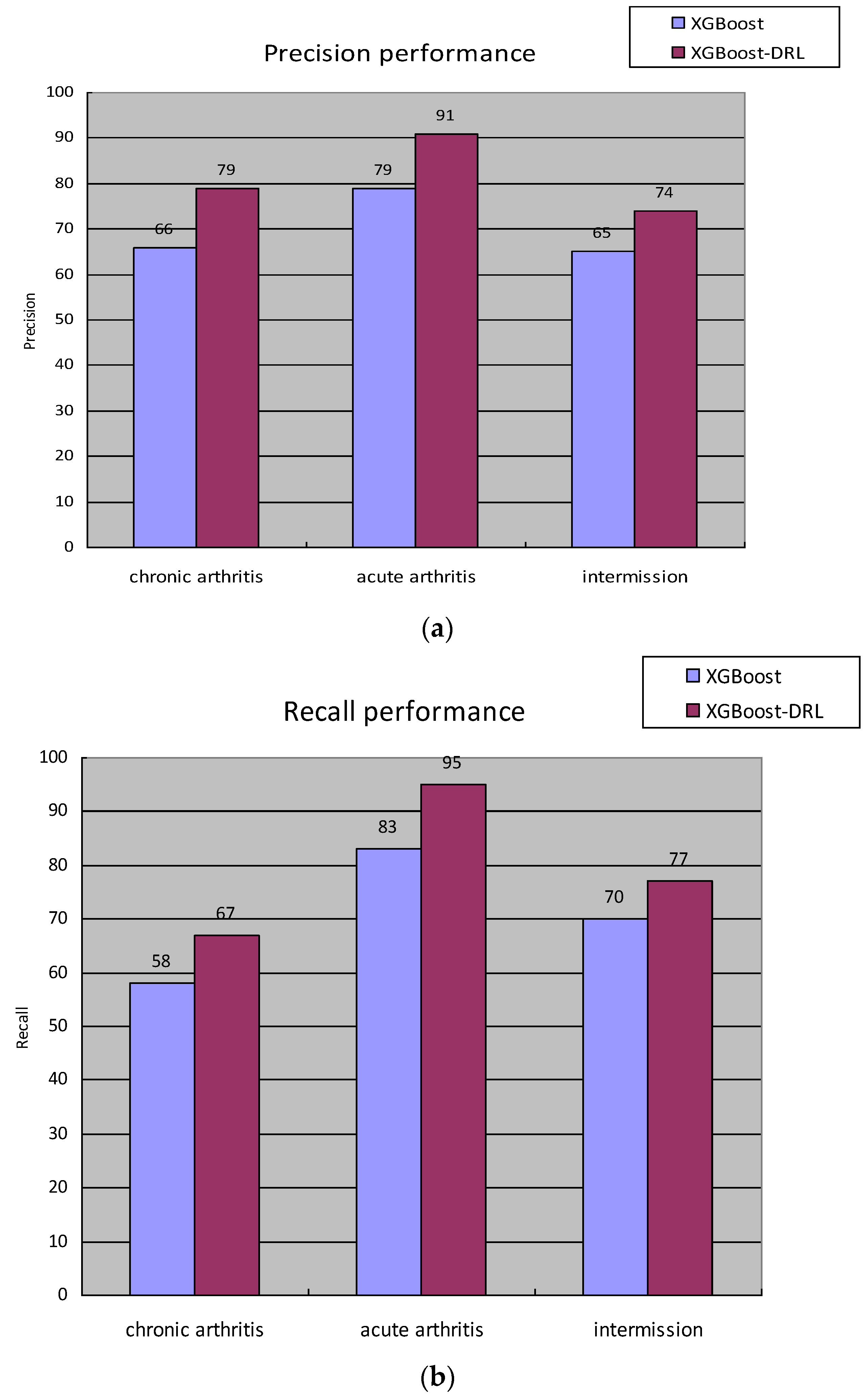
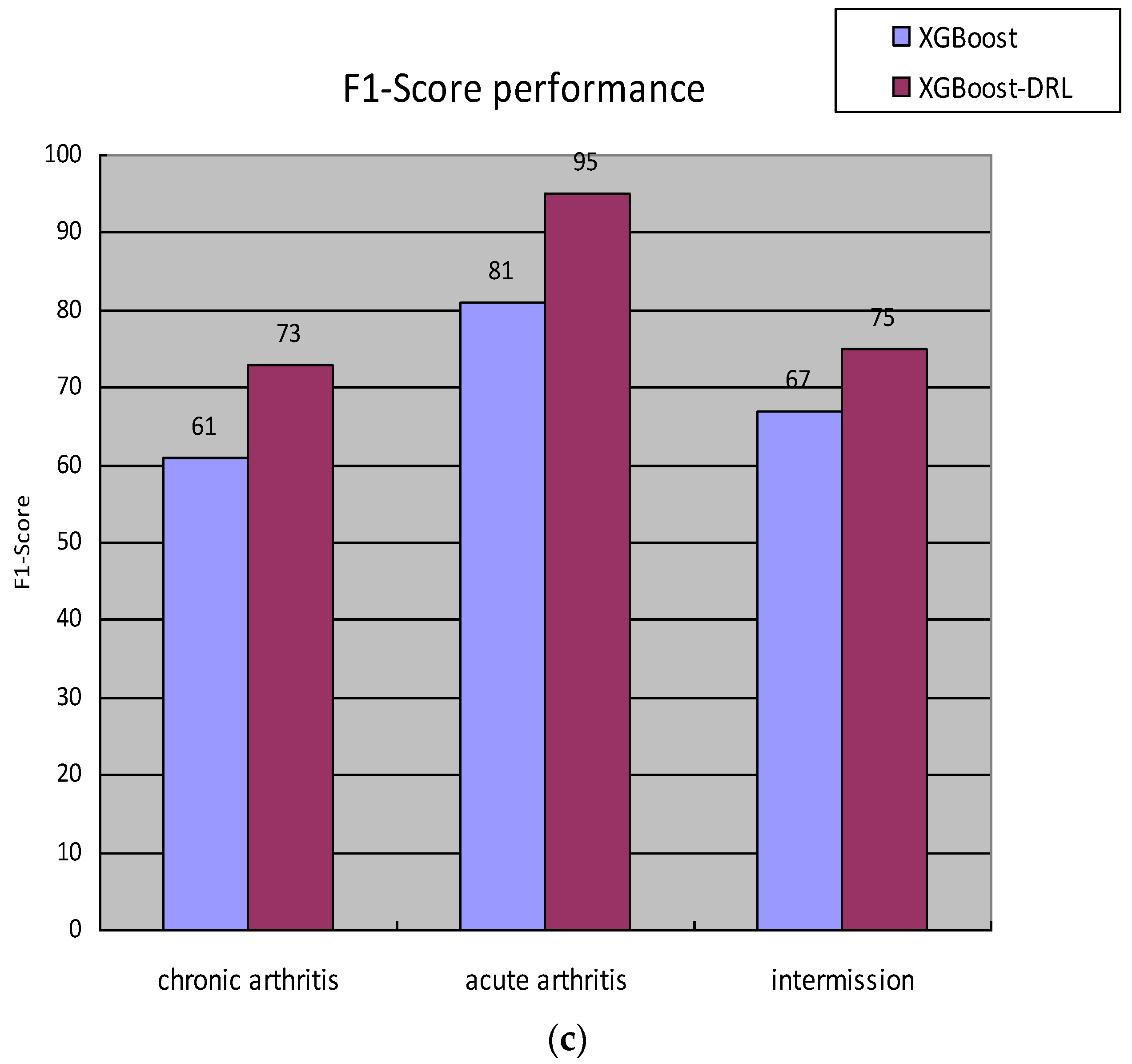
A certain hyperparameter of the hyperparameter space set St is adjusted; that is, use the ε-greedy algorithm to make an action selection and then obtain the F1-Score value of the staging diagnosis model under the hyperparameter combination at this moment, which is recorded as , and set the staging at the previous moment. The F1-Score value of the diagnostic model is , then the reward value generated by the environment at time t is . State transitions to after action is complete.
The above steps are repeated until the cumulative discount reward is the largest.
Every action of the agent will be rewarded by the environment, and the sum of the accumulated discount rewards obtained by the agent after the learning is over satisfies Formula (11) [
13]:
represents the sum of cumulative discounted rewards; is the time step, starting from 0; is the discount factor, ranging from 0 to 1; and rt represents the immediate reward obtained by the agent at time step t. The sum of cumulative discounted rewards in the formula represents the sum of rewards obtained by the agent from the initial state, performing a series of actions until the end. The immediate reward at each time step is multiplied by the discount factor ; represents the attenuation of future rewards, because the reward after each new action is executed cannot be determined. If the reward is not discounted for each time, the total reward sum will approach infinity with the increase in time, making learning enter an endless loop.
The accumulation process of the maximum reward sum is inseparable from the value of each moment of behavior. The mapping of the agent from the environment state to the behavior at each moment is called the strategy function
, and the optimal strategy
satisfies Formula (12):
The process of obtaining the optimal policy can be recorded through the action value function. The action value function, denoted as
, represents the cumulative reward expectation obtained after taking an action a under a certain state
s using the policy function
. The value function of the optimal action needs to satisfy Formula (13):
The process of the agent finding the optimal strategy is the process of optimizing the action value function. In order to obtain the optimal action value function, we use the deep Q-network (DQN for short) [
14]. The classic Q-learning algorithm is usually only suitable for situations where the state space is relatively simple, and its performance may be poor in scenarios where the state space is relatively complex, mainly because in complex state spaces, Q-learning produces Q. The number of tables will be very large, resulting in very slow convergence of the algorithm, and it is difficult to find the optimal solution. Deep neural networks can better handle high-dimensional state spaces by learning hierarchical representations of state features. DQN is like the Q-learning algorithm, which requires a Q table to record the learning process. DQN uses the neural network
instead of
, where
is the weight of the network, and implements the update according to Formula (14)
In the hyperparameter tuning problem, in order to prevent the waste of learning resources caused by choosing the same behavior every time, this paper uses “exploration” in the selection of behavior. Exploration means that the agent will first think about the environment and then take actions, so as to avoid repeated action choices. In this paper, the ε-greedy algorithm is used to realize the exploration. The ε-greedy greedy algorithm is defined as Formula (15):
In Formula (15), is a very small value, and the value of will decrease with time. Therefore, according to the ε-greedy algorithm, actions will be randomly selected at the initial stage of training. When the number of trainings increases, the Q network can already reflect the expected value of the action, so the action will be determined by the Q network. The ε-greedy algorithm can ensure that the large action of the value function is selected first and avoid the occurrence of repeated actions.
In order to better train the Q network, this paper uses the memory pool D to save the path of each exploration and updates the Q network after reaching the specified number of steps. According to the above process, the pseudo-code of the staged diagnosis model algorithm based on deep reinforcement learning designed in this paper is shown in
Table 4: