Water Vapor Adsorption on Desiccant Materials for Rotary Desiccant Air Conditioning Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structural Characterization
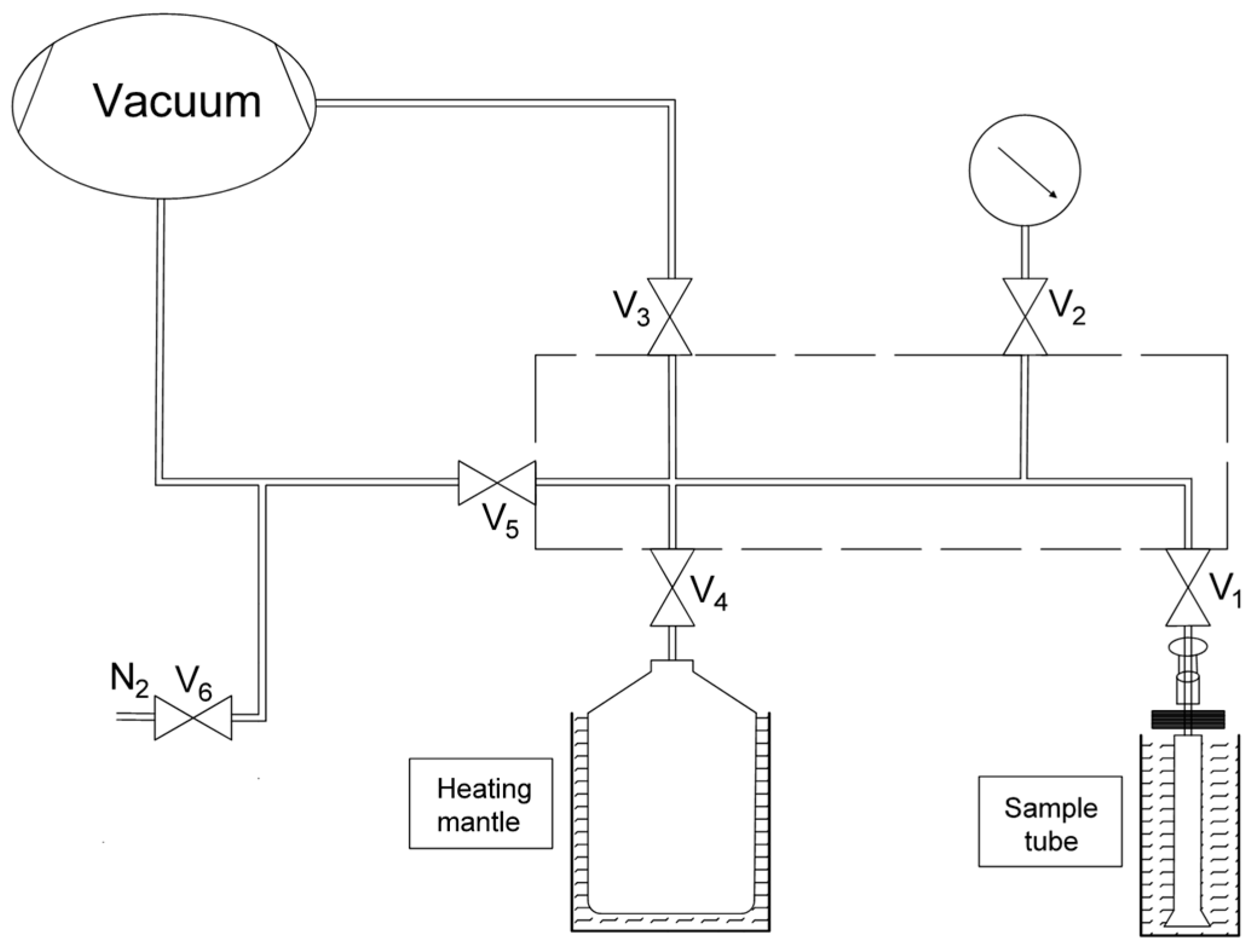
2.2. Adsorption Measurements
2.3. Classical Density Functional Theory
2.3.1. Solid–Fluid Interaction Parameters
2.3.2. PC-SAFT
2.3.3. Numerical Procedure
3. Results and Discussion
3.1. Adsorption in Cylindrical Pore
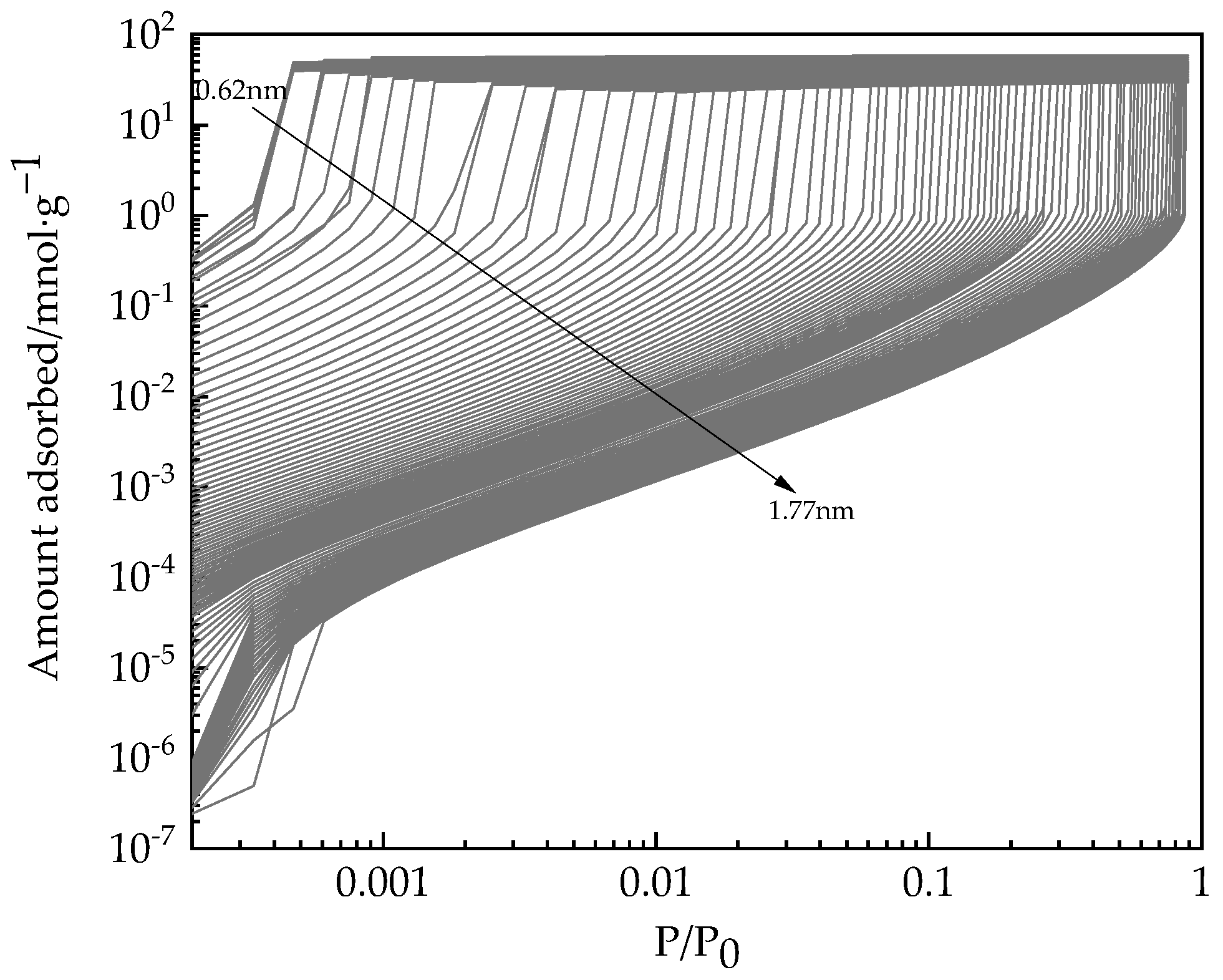
3.2. Application of PC-SAFT for PSD Analysis of Desiccant Materials
4. Conclusions
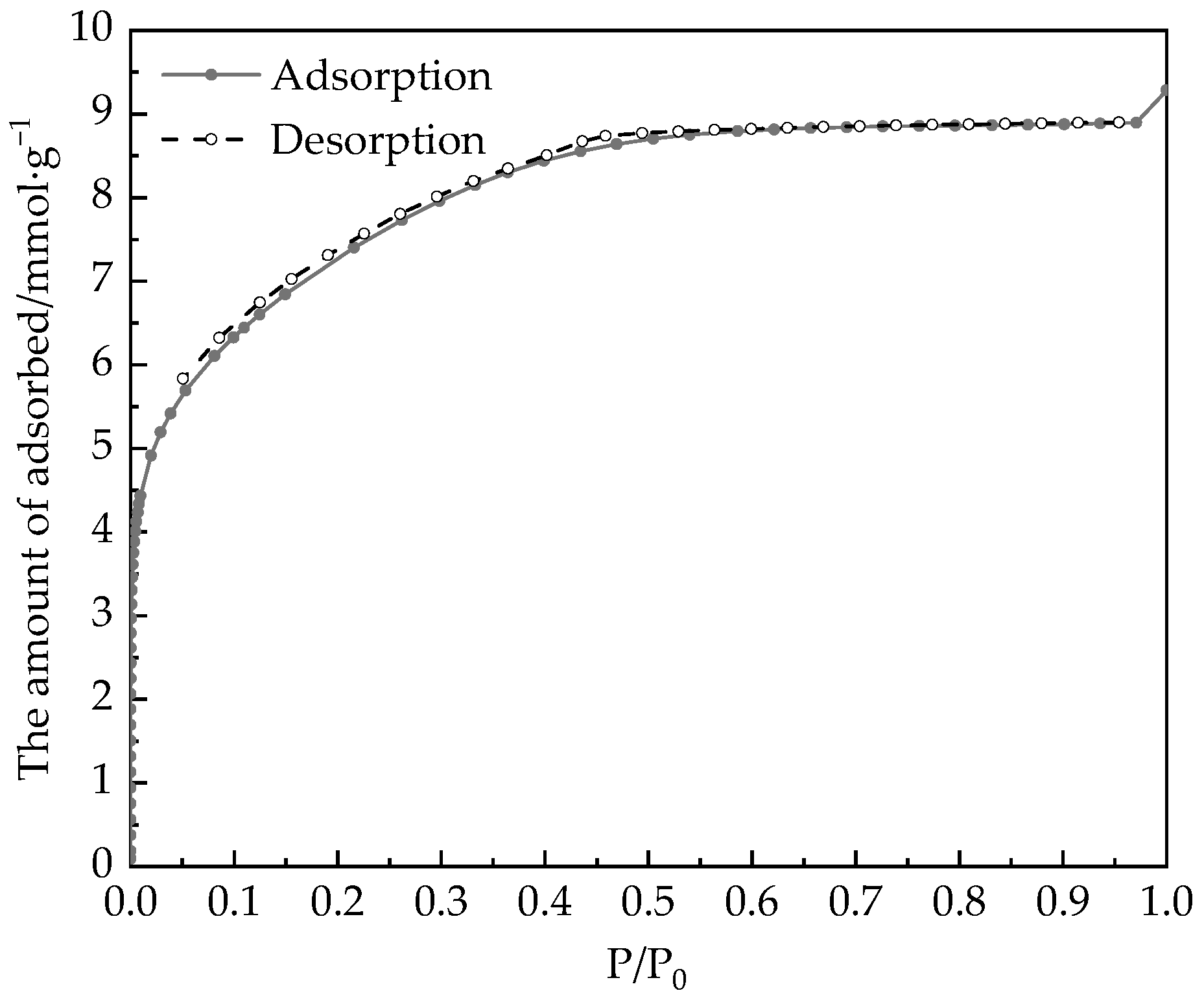
- The main component of desiccant material in this paper is silica gel, and water vapor adsorption on desiccant materials is basically saturated after P/P0 = 0.6, reaching 15.8 mmol·g−1, which is about 0.285 g of water per gram of desiccant;
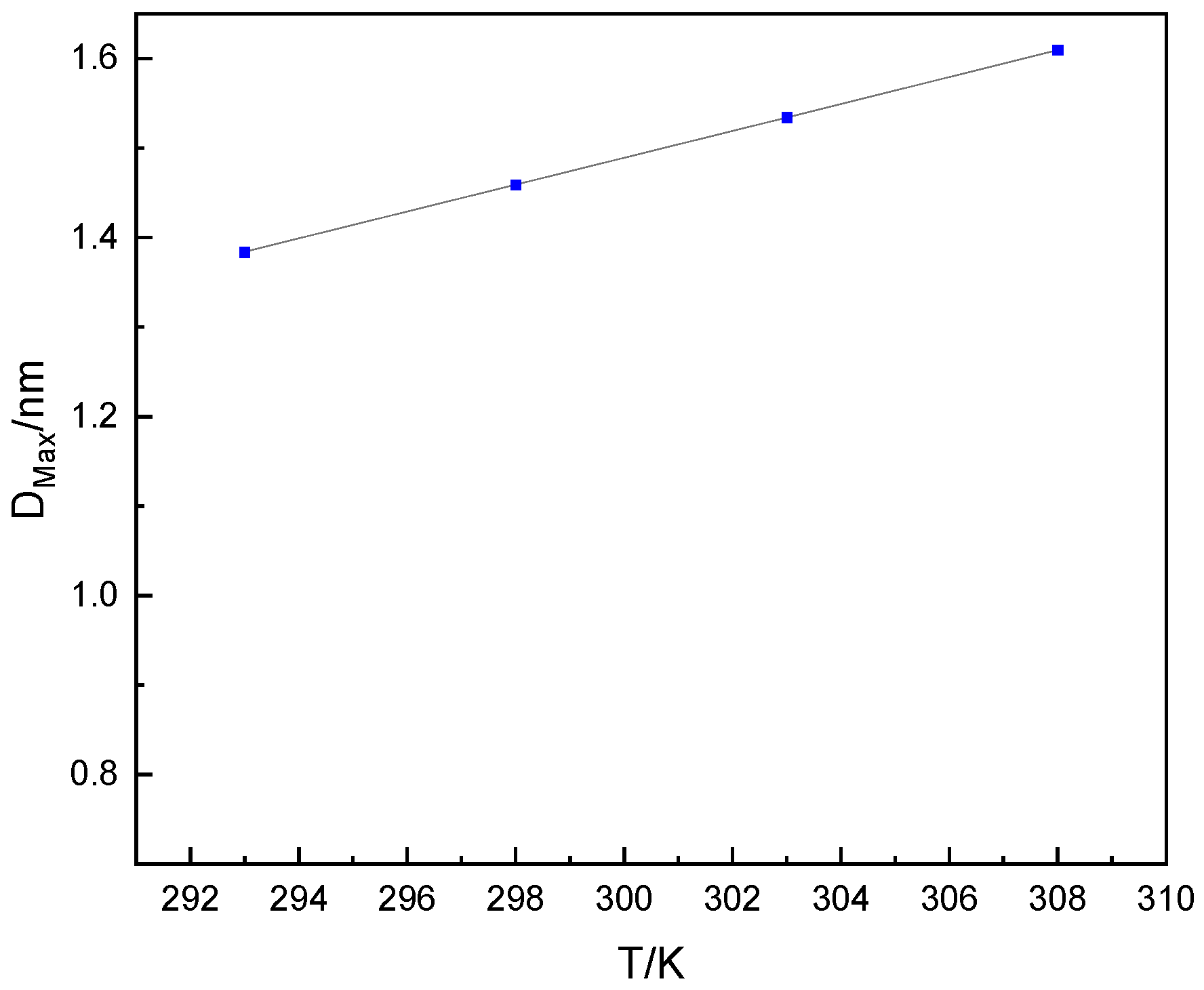
- The optimal PSD range of desiccant material for rotary desiccant air conditioning was determined by CDFT established from PC-SAFT. As the temperature increases, the pore width increases when the condensation pressure Pcond/P0 of different pore widths reaches the saturated steam pressure P0 of water. When the working temperature range of the intake air of the rotary desiccant air conditioning is 293–308 K and the relative humidity is 60–90%, the optimal PSD range of dehumidification is 1.09–1.53 nm;
- The CDFT established from PC-SAFT can characterize the PSD of the desiccant material by water adsorption isotherm. The rotary desiccant materials contain a large number of micropores with a volume of 0.3669 cm3/g. Among them, there are characteristic pore widths at 0.8 nm and 1.25 nm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Greek symbols | ||
| the compressibility of the hard-chain fluid | the fraction of non-bonded particles | ||
| diameter (nm) | the association strength (nm) | ||
| Helmholtz free energy (J) | energy well-depth for L-J fluid and solid (J) | ||
| the universal integral | the weighted packing fraction profile | ||
| Boltzmann constant (J·K−1) | chemical potential (J) | ||
| the association volume | density (nm−3) | ||
| segment number | size well-depth for L-J fluid and solid (J) (nm) | ||
| weighted densities (nm−3) | weighting function | ||
| N | the amount of adsorption (mmol·g−1) | the weighted quantities | |
| the position of and fluid molecules in space (nm) | grand potential (J) | ||
| radius (nm) | Subscripts and superscripts | ||
| external potential (J) | Number of states | ||
| pore width (nm) | assoc | association contribution | |
| the cavity correlation function | avg | Average | |
| Abbreviations | bulk | bulk density of fluid | |
| CDFT | Classical Density Functional Theory | chain | chain contribution |
| EDS | Energy Dispersive Spectrum | disp | dispersion contribution |
| GCMC | Grand Canonical Monte Carlo | ex | excess |
| MD | Molecular Dynamics | ff | fluid-fluid |
| MFMT | Modified Fundamental Measure Theory | HB | the hydrogen bonding |
| PSD | Pore Size Distribution | hs | hard-sphere contribution |
| PC-SAFT | Perturbated Chain Statistical Associating Fluid Theory | id | the intrinsic Helmholtz free energy from ideal gas functional |
| SEM | Scanning Electron Microscopy | int | the intrinsic Helmholtz free energy |
| WDA | Weighed Density Approximation | ss, sf | sloid-sloid, sloid-fluid |
References
- Arsiwala, A.; Elghaish, F.; Zoher, M. Digital twin with Machine learning for predictive monitoring of CO2 equivalent from existing buildings. Energy Build. 2023, 284, 112851. [Google Scholar] [CrossRef]
- Wrobel, J.; Walter, P.S.; Schmitz, G. Performance of a solar assisted air conditioning system at different locations. Sol. Energy 2013, 92, 69–83. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Wang, D.; Liu, J.; Li, L.; Luo, X.; Wang, Y.; Liu, J. Performance evaluation of a hybrid solar powered rotary desiccant wheel air conditioning system for low latitude isolated islands. Energy Build. 2020, 224, 110208. [Google Scholar] [CrossRef]
- Tian, S.; Su, X.; Geng, Y. Review on heat pump coupled desiccant wheel dehumidification and air conditioning systems in buildings. J. Build. Eng. 2022, 54, 104655. [Google Scholar] [CrossRef]
- Zheng, G.; Zheng, C.; Yang, G.; Chen, W. Development of a New Marine Rotary Desiccant Airconditioning System and its Energy Consumption Analysis. Energy Procedia 2012, 16, 1095–1101. [Google Scholar]
- Zhu, J.; Chen, W. Energy and exergy performance analysis of a marine rotary desiccant air-conditioning system based on orthogonal experiment. Energy 2014, 77, 953–962. [Google Scholar] [CrossRef]
- Zheng, C.Y.; Zheng, G.J.; Yu, W.S.; Chen, W. Study on the marine ejector refrigeration-rotary desiccant air-conditioning system. In Proceedings of the 2nd International Conference on Materials Science, Energy Technology and Environmental Engineering (MSETEE), Zhuhai, China, 28–30 April 2017. [Google Scholar]
- Abdelgaied, M.; Saber, M.A.; Bassuoni, M.M.; Khaira, A.M. Comparative analysis of a new desiccant dehumidifier design with a traditional rotary desiccant wheel for air conditioning purpose. Appl. Therm. Eng. 2023, 222, 119945. [Google Scholar] [CrossRef]
- Singh, R.P.; Das, R.K. Progressive Development and Challenges Faced by Solar Rotary Desiccant-Based Air-Conditioning Systems: A Review. Processes 2021, 9, 1785. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, R.; Xia, Z. Experimental analysis of an adsorption air conditioning with micro-porous silica gel–water. Appl. Therm. Eng. 2013, 50, 1015–1020. [Google Scholar] [CrossRef]
- Alyousef, H.; Ben Yahia, M.B.; Aouaini, F. Statistical physics modeling of water vapor adsorption isotherm into kernels of dates: Experiments, microscopic interpretation and thermodynamic functions evaluation. Arab. J. Chem. 2020, 13, 4691–4702. [Google Scholar] [CrossRef]
- Tan, J.-X.; Chen, Z.-Y.; Chen, C.H.; Hsieh, M.-F.; Lin, A.Y.-C.; Chen, S.S.; Wu, K.C.-W. Efficient adsorption and photocatalytic degradation of water emerging contaminants through nanoarchitectonics of pore sizes and optical properties of zirconium-based MOFs. J. Hazard. Mater. 2023, 451, 131113. [Google Scholar] [CrossRef] [PubMed]
- Jagiello, J.; Kenvin, J.; Celzard, A.; Fierro, V. Enhanced resolution of ultra micropore size determination of biochars and activated carbons by dual gas analysis using N2 and CO2 with 2D-NLDFT adsorption models. Carbon 2019, 144, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Li, Z.; Zhao, H.; Zhang, T.; Yan, N.; Li, J. Understanding the Water Effect for Selective Catalytic Reduction of NOx with NH3 over Cu-SSZ-13 Catalysts. ACS EST Eng. 2022, 2, 1684–1696. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Q.; Wang, Q. Energy Storage Analysis of UIO-66 and Water Mixed Nanofluids: An Experimental and Theoretical Study. Energies 2019, 12, 2521. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Le, X.; Wang, X.; Liu, W.; Wang, Z. Molecular Dynamics Simulation of the Synergistic Effect of Alka-li/Surfactant/Polymer on the Formation and Stabilization of Water-Based Foam Systems. Polymers 2023, 15, 584. [Google Scholar] [CrossRef]
- Landers, J.; Gor, G.Y.; Neimark, A.V. Density functional theory methods for characterization of porous materials. Colloids Surf. A Physicochem. Eng. Asp. 2013, 437, 3–32. [Google Scholar] [CrossRef]
- Lucena, S.M.P.; Oliveira, J.C.A.; Gonçalves, D.; Silvino, P.; Dantas, S.; Neimark, A. Pore size analysis of carbons with heterogeneous kernels from reactive molecular dynamics model and quenched solid density functional theory. Carbon 2021, 183, 672–684. [Google Scholar] [CrossRef]
- Malheiro, C.; Mendiboure, B.; Plantier, F.; Blas, F.J.; Miqueu, C. Density functional theory for the description of spherical non-associating monomers in confined media using the SAFT-VR equation of state and weighted density approximations. J. Chem. Phys. 2014, 140, 134707. [Google Scholar] [CrossRef] [Green Version]
- Stierle, R.; Sauer, E.; Eller, J.; Theiss, M.; Rehner, P.; Ackermann, P.; Gross, J. Guide to efficient solution of PC-SAFT classical Density Functional Theory in various Co-ordinate Systems using fast Fourier and similar Transforms. Fluid Phase Equilibria 2020, 504, 112306. [Google Scholar] [CrossRef]
- Sauer, E.; Gross, J. Classical Density Functional Theory for Liquid–Fluid Interfaces and Confined Systems: A Functional for the Perturbed-Chain Polar Statistical Associating Fluid Theory Equation of State. Ind. Eng. Chem. Res. 2017, 56, 4119–4135. [Google Scholar] [CrossRef]
- Xi, S.; Liu, J.; Parambathu, A.V.; Zhang, Y.; Chapman, W.G. An Efficient Algorithm for Molecular Density Functional Theory in Cylindrical Ge-ometry: Application to Interfacial Statistical Associating Fluid Theory (iSAFT). Ind. Eng. Chem. Res. 2020, 59, 6716–6728. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; Domhnaill, S.C.O.; Neimark, A.V.; Schueth, F.; Unger, K.K. Capillary Hysteresis in Nanopores: Theoretical and Experimental Studies of Nitrogen Adsorption on MCM-41. Langmuir 1995, 11, 4765–4772. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; Neimark, A.V. Density Functional Theory Model of Adsorption on Amorphous and Microporous Silica Materials. Langmuir 2006, 22, 11171–11179. [Google Scholar] [CrossRef] [PubMed]
- Miyasaka, K.; Neimark, A.V.; Terasaki, O. Density Functional Theory of in Situ Synchrotron Powder X-ray Diffraction on Mesoporous Crystals: Argon Adsorption on MCM-41. J. Phys. Chem. C 2009, 113, 791–794. [Google Scholar] [CrossRef]
- Guo, P.; Micromeritics Instrumentation Corporation. Water Vapor Sorption in Metal-Organic Frameworks Characterized by Micromeritics 3Flex Gas Sorption Analyzer. Available online: https://www.micromeritics.com/Repository/Files/Application_Note_175_V6.pdf (accessed on 20 June 2023).
- Jahan, I.; Islam, M.A.; Rupam, T.H.; Palash, M.L.; Saha, B.B. Water adsorption characterization of bivalent metal doped HKUST-1. Therm. Sci. Eng. Prog. 2022, 35, 101453. [Google Scholar] [CrossRef]
- Roth, R. Fundamental measure theory for hard-sphere mixtures: A review. J. Physics Condens. Matter 2010, 22, 063102. [Google Scholar] [CrossRef] [Green Version]
- Daniel, D.W.; Gelb, L.D. Extension of the Steele 10-4-3 potential for adsorption calculations in cylindrical, spherical, and other pore geometries. J. Chem. Phys. 2011, 135, 84703. [Google Scholar]
- An, R.; Huang, L.; Long, Y.; Kalanyan, B.; Lu, X.; Gubbins, K.E. Liquid–Solid Nanofriction and Interfacial Wetting. Langmuir 2016, 32, 743–750. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules. Ind. Eng. Chem. Res. 2016, 40, 1244–1260. [Google Scholar] [CrossRef]
- Yu, Y.-X.; Wu, J. Structures of hard-sphere fluids from a modified fundamental-measure theory. J. Chem. Phys. 2002, 117, 10156–10164. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.W.; Zheng, Q.R.; Wang, Z.; Tang, Z.; Chen, W. Hydrogen adsorption on graphene sheets and nonporous graphitized thermal carbon black at low surface coverage. Int. J. Hydrogen Energy 2017, 42, 18465–18472. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Application of the Perturbed-Chain SAFT Equation of State to Associating Systems. Ind. Eng. Chem. Res. 2002, 41, 5510–5515. [Google Scholar] [CrossRef]
- Vergara, E.L.C.; Kontogeorgis, G.M.; Liang, X. A new study of associating inhomogeneous fluids with classical density functional theory. Mol. Phys. 2020, 118, e1725668. [Google Scholar] [CrossRef]
- Vergara, E.L.C.; Kontogeorgis, G.M.; Liang, X. On the study of the vapor-liquid interface of associating fluids with classical density functional theory. Fluid Phase Equilibria 2020, 522, 112744. [Google Scholar] [CrossRef]
- Hughes, J.; Krebs, E.J.; Roundy, D. A classical density-functional theory for describing water interfaces. J. Chem. Phys. 2013, 138, 024509. [Google Scholar] [CrossRef] [Green Version]
- Tripathi, S.; Chapman, W.G. Microstructure and Thermodynamics of Inhomogeneous Polymer Blends and Solutions. Phys. Rev. Lett. 2005, 94, 087801. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, S.; Chapman, W.G. Microstructure of inhomogeneous polyatomic mixtures from a density functional formalism for atomic mixtures. J. Chem. Phys. 2005, 122, 094506. [Google Scholar] [CrossRef]
- Linstrom, P.J.; Mallard, W.G. (Eds.) NIST Chemistry WebBook; NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022; p. 20899. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; Wei, D.; Chueh, W.T.; Haller, G.L.; Neimark, A.V. Evaluation of Pore Structure Parameters of MCM-41 Catalyst Supports and Catalysts by Means of Nitrogen and Argon Adsorption. Cheminform 1997, 28, 3671–3679. [Google Scholar] [CrossRef]
- Jagiello, J. Stable Numerical Solution of the Adsorption Integral Equation Using Splines. Langmuir 1994, 10, 2778–2785. [Google Scholar] [CrossRef]
- Ustinov, E.A.; Do, D.D. Application of density functional theory to analysis of energetic heterogeneity and pore size distribution of activated carbons. Langmuir 2004, 20, 3791–3797. [Google Scholar] [CrossRef]
- Jagiello, J.; Thommes, M. Comparison of DFT characterization methods based on N2, Ar, CO2, and H2 adsorption applied to carbons with various pore size distributions. Carbon 2004, 42, 1227–1232. [Google Scholar] [CrossRef]
- Jagiello, J.; Kenvin, J.; Ania, C.O.; Parra, J.B.; Celzard, A.; Fierro, V. Exploiting the adsorption of simple gases O2 and H2 with minimal quadrupole moments for the dual gas characterization of nanoporous carbons using 2D-NLDFT models. Carbon 2020, 160, 164–175. [Google Scholar] [CrossRef]






| Element | Atom Concentration/% |
|---|---|
| O | 62.07 |
| Si | 20.22 |
| Al | 1.74 |
| Ca | 0.80 |
| C | 15.18 |
| Al | 1.74 |
| Ca | 0.80 |
| Scheme | (nm) | /kB (K) | /kB (K) | ||
|---|---|---|---|---|---|
| 2B | 0.3007 | 366.51 | 1.0655 | 2501 | 0.06659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Zhang, M. Water Vapor Adsorption on Desiccant Materials for Rotary Desiccant Air Conditioning Systems. Processes 2023, 11, 2166. https://doi.org/10.3390/pr11072166
Zhu Z, Zhang M. Water Vapor Adsorption on Desiccant Materials for Rotary Desiccant Air Conditioning Systems. Processes. 2023; 11(7):2166. https://doi.org/10.3390/pr11072166
Chicago/Turabian StyleZhu, Ziwen, and Muyuan Zhang. 2023. "Water Vapor Adsorption on Desiccant Materials for Rotary Desiccant Air Conditioning Systems" Processes 11, no. 7: 2166. https://doi.org/10.3390/pr11072166
APA StyleZhu, Z., & Zhang, M. (2023). Water Vapor Adsorption on Desiccant Materials for Rotary Desiccant Air Conditioning Systems. Processes, 11(7), 2166. https://doi.org/10.3390/pr11072166







