Effect of Al₂O₃, SiO₂, and ZnO Nanoparticle Concentrations Mixed with EG–Water on the Heat Transfer Characteristics through a Microchannel

Abstract

Nanofluids have gained attention for their potential to solve overheating problems in various industries. They are a mixture of a base fluid and nanoparticles dispersed on the nanoscale. The nanoparticles can be metallic, ceramic, or carbon based, depending on the desired properties. While nanofluids offer advantages, challenges such as nanoparticle agglomeration, stability, and cost effectiveness remain. Nonetheless, ongoing research aims to fully harness the potential of nanofluids in addressing overheating issues and improving thermal management in different applications. The current study is concerned with the fluid flow and heat transfer characteristics of different nanofluids using different types of nanoparticles such as Al₂O₃, SiO₂, and ZnO mixed with different base fluids. Pure water and ethylene glycol–water (EG–H₂O) mixtures at different EG–H₂O ratios (ψ = 0%, 10%, 30%, 40%) are used as the base fluid. Furthermore, a rectangular microchannel heat sink is used. Mesh independent study and validation are performed to investigate the current model, and a good agreement is achieved. The numerical analysis evaluates the influence on the heat transfer coefficient and flow characteristics of nanofluids for Reynolds numbers 500 to 1200 at a 288 K inlet flow temperature. The results show that ZnO nanofluid and 40% EG–H₂O increase the heat transfer coefficient by 63% compared to ZnO–H₂O nanofluid obtained at Re = 1200 and φ = 5%. Conversely, the pressure drop by ZnO is nearly double that obtained by Al₂O₃ and SiO_2.

1. Introduction

In recent years, the advancement of electronic devices has led to their smaller size, necessitating an effective thermal management system. However, this poses challenges for cooling technologies within a limited space. The excess heat generated by these smaller devices can damage electrical chips, making efficient heat removal crucial for optimal operation and maximum efficiency. One cooling method involves using a micro-channel heat sink with a single-phase coolant. However, traditional heat transfer fluids such as water, thermal oils, and ethylene glycol/water mixtures have limitations due to their inferior thermal characteristics compared to metals and metal oxides. Therefore, it is crucial to explore methods to enhance the thermal conductivity of these cooling fluids, enabling better heat dissipation to keep up with technology advancements and device miniaturization.

A new coolant fluid called a nanofluid is used in the cooling process. A nanofluid is a liquid suspension containing tiny particles, typically in the range of 1 to 100 nanometers, dispersed in a base fluid. These nanoparticles can be metallic, ceramic, or carbon based. Nanofluids are used in various applications, including cooling processes, due to their enhanced thermal properties. They offer improved heat transfer efficiency compared to pure base fluids, thanks to the nanoparticles’ small size and high surface area. By incorporating nanofluids into cooling systems, the heat dissipation by the heat-generating components is enhanced, resulting in lower operating temperatures, improved cooling performance, and increased system reliability [1,2,3].

One of the primary advantages of nanofluids is their significantly enhanced thermal conductivity compared to conventional fluids. Various studies have reported substantial improvements in thermal conductivity when nanoparticles such as copper oxide (CuO), aluminum oxide (Al₂O₃), and titanium oxide (TiO₂) are dispersed in the base fluids (e.g., water, ethylene glycol, or oil). For example, Li et al. [4] conducted an experimental investigation of CuO–water nanofluids and found a nearly 20% increase in thermal conductivity compared to pure water.

Ali and Salam [5] and Escher et al. [6] suggest that the insertion of nanometer-sized metal or metal oxide particles into a base fluid improves the thermal properties of the coolant. For example, the enhanced thermal conductivity of nanofluids translates into improved heat transfer performance in cooling applications. Several studies have demonstrated the potential of nanofluids to enhance convective heat transfer coefficients and reduce heat transfer resistance. For instance, Zhang et al. [7] conducted numerical simulations and experimental studies on the use of Al₂O₃–water nanofluids in a heat exchanger and observed a 15% increase in the overall heat transfer coefficient compared to pure water. The inclusion of these solid particles in the base fluid enhances energy transmission within the fluid. Consequently, nanofluids exhibit remarkable thermophysical properties compared to base fluids such as oil or water, with substantially higher thermal conductivity, specific heat, dynamic viscosity, and density.

The use of nanofluids as coolants could potentially allow for smaller and better-positioned cooling systems in electronic devices. With increased efficiency, there would be less coolant required, downsizing the fluid pumps and allowing devices to operate at higher temperatures. Mutuku [8] investigated the cooling properties of nanofluids with an ethylene glycol fluid base comprising three types of nanoparticles—titanium dioxide, aluminum oxide, and copper oxide—considering a laminar, incompressible, steady, 2D (x, y) flow of an electrically-conducting EG fluid-based nanofluid across a convectively heated horizontal semi-infinite flat plate. They also considered the occurrence of a transversely imposed magnetic field. The entire flow regime was parametrically studied to demonstrate the impacts of the relevant parameters on temperature, velocity, local Nusselt number, and skin friction coefficient. Furthermore, Mutuku explained that the inclusion of nanoparticles increases the viscosity of the base fluid, causing the fluid flow to be hampered and thus increasing the friction at the plate surface. The results show that CuO–EG has the highest skin friction, while TiO₂–EG nanofluid has the least skin friction. Hence CuO–EG nanofluid has the slowest heat transfer rate, and TiO₂–EG has the greatest rate of heat transfer. However, increasing the magnetic strength improves skin friction but decreases the heat transfer rate. It is also noted that the Brownian motion and the thermophoresis effect cause the nanoparticles to have continual collisions in the base fluid, increasing the fluid temperature. Consequently, increasing the nanoparticle volume fraction raises the fluid temperature.

Elbadawy and Fayed [9] numerically investigated the effect of using nanofluids on heat transfer enhancement and fluid flow characteristics in rectangular cross-sectional microchannel heat sinks (MCHS) explored for single- and double-stack microchannels at a constant heat flux of q = 100 W/cm² and Reynolds numbers spanning from 200 to 1500. Alumina–water nanofluid with varied nanoparticle volume concentrations ranging from 1% to 5% was used as a coolant for the MCHS in this study. When nanoparticles are added, the heat transfer coefficient improves marginally by 13.12%, but the MCHS temperature lowers significantly when compared to pure water. The results by Elbadawy and Fayed demonstrate that increasing the concentration of nanoparticles improves the cooling process. In this study, a reduction in channel volume was considered a crucial metric. By adding 5% Al₂O₃ at Re = 1500 for the same cooling rate and temperature difference, the alumina–water nanofluid reduced the channel volume by 62.6%.

In the study by Mazlam et al. [10], a carbon nanotube (CNT) nanofluid with a volume concentration of 0.1% was used and showed optimal results compared to pure water. The carbon nanotubes in the nanofluid had a diameter of 9.2 nm and a length of 1.5 µm. The density of the nanofluid was measured to be 1800 kg/m³, and the carbon purity was 90%. Lignin was used as a surfactant in the nanofluid. To evaluate the optimization process, Mazlam et al. treated the system as a non-dominated sorting multi-objective function with two objective functions. These objective functions were related to the total thermal resistance and the hydrodynamic performance. The researchers compared their findings at three different operating temperatures, which were based on a previous study conducted by Halelfadl et al., 2014. The optimized results indicated that using the CNT nanofluid at a higher operating temperature of 40 °C reduced the overall thermal resistance by 3% compared to the lower temperature of 20 °C. This improvement in thermal performance suggests that the CNT nanofluid is more effective for heat transfer at higher temperatures. Regarding the hydrodynamic performance, the pumping power required at 40 °C was found to be 35% lower compared to the power required at the lower temperature. This indicates that the CNT nanofluid exhibits improved fluid flow characteristics and reduced energy consumption at higher operating temperatures. It is worth noting that the information provided is based on [10,11].

In 2023, Elbadawy et al. [12] conducted a numerical investigation to analyze the characteristics of fluid flow and heat transfer using different nanoparticles (Al₂O₃, TiO₂, and SiO₂) in various configurations of micro-channel heat sinks (MCHS) such as Rectangular, Triangular, Trapezoidal, and Circular shapes. The study focused on the effects of Reynolds number (Re) ranging from 890 to 1500 and nanoparticle concentration ranging from 1% to 7% while maintaining a constant heat flux (q) of 10⁶ W/m² and fluid inlet temperature of 288 K. The research assessed the average heat transfer coefficient (h) and pressure drop (∆p) as indicators of fluid flow and heat transfer characteristics for each MCHS configuration and nanoparticle concentration. Their findings revealed that Al₂O₃–H₂O nanofluid exhibited a higher heat transfer coefficient compared to other nanoparticle types and pure water, with an 8.58% improvement observed at Re = 1500 and φ = 7% compared to pure water. Additionally, it was found that the triangular MCHS achieved the maximum heat transfer coefficient, although it also resulted in the highest pressure drop due to its lower hydraulic diameter.

Achieving and maintaining a stable nanoparticle dispersion within the base fluid is crucial for the successful application of nanofluids in cooling processes. Researchers have explored various techniques to enhance nanoparticle stability and prevent agglomeration, including the use of surfactants, ultrasonication, and surface modification. Recent studies have focused on developing new approaches to improve the stability and dispersion of nanoparticles in nanofluids, such as the utilization of hybrid nanoparticles and functionalized surfactants [13]. Furthermore, it is important to note that extensive research has been conducted on nanofluids and hybrid nanofluids, exploring their behavior in various geometries and considering the influence of different physical parameters. These investigations have encompassed areas such as porous media effects, rarefied flows, and magnetohydrodynamics [14,15,16,17,18,19,20,21,22,23].

The existing literature emphasizes the necessity for a novel investigation focusing on the thermal performance of a nanofluid coolant utilizing an ethylene glycol–water mixture as the base fluid. To address this research gap, the proposed study aims to provide a comprehensive understanding of three distinct nanoparticles (Al₂O₃, SiO₂, and ZnO) within a micro-channel heat sink (MCHS) featuring a rectangular cross-section. By considering a range of volume concentrations (1% to 5%) and Reynolds numbers (500 to 1200), the study explores the heat transfer enhancement of nanofluids compared to base fluids containing various nanoparticles. Importantly, unlike prior research that predominantly employed water as the base fluid, this study stands out by employing an ethylene glycol–water mixture. The investigation aims to shed light on the thermal performance of the three specified nanoparticles within a rectangular MCHS, examining crucial parameters, such as heat transfer, pressure drop in the channel, and thermal efficiency. To accomplish these goals, the study employs the commercial CFD software Fluent 2022 for rigorous analysis and evaluation. Overall, this research offers a unique perspective and contributes to the existing knowledge on nanofluid thermal performance in micro-channel heat sinks with a specific focus on an ethylene glycol–water mixture and the three chosen nanoparticles.

2. Mathematical Modeling

The use of a rectangular microchannel heat sink (MCHS) can help eliminate the heat flux applied to the bottom surface of the heat sink. This was achieved by circulating nanofluids with different concentrations of ethylene glycol (EG) in water as the base fluid. To provide a visual representation of the MCHS, Figure 1 depicts a schematic geometry of the rectangular microchannel heat sink. The specific dimensions of this geometry are presented in

Table 1. MCHS dimensions for the rectangular configuration [24].

Parameters	Values (mm)
Channel width (W_ch)	0.231
Channel height (H_ch)	0.713
Channel length (L)	44.764
Unit cell width (Wu)	0.467
Half-width of wall separating channels (Ws)	0.118
Unit cell height (H)	19.05
Rectangular Microchannel tip thickness (Ht)	13.700
Unit cell bottom wall to channel bottom wall thickness (HB)	4.637
Thermocouple plane height (Hth)	3.175

.

2.1. Governing Equations

ANSYS Fluent was used in the current study to solve the flow governing equations. It is a widely used commercial computational fluid dynamics (CFD) software that provides a comprehensive platform for analyzing and simulating fluid flow and heat transfer phenomena. Fluent employs numerical methods to solve a set of governing equations that describe fluid flow and the associated transport processes.

The governing equations solved by Fluent are based on the fundamental principles of conservation of mass (Equation (1)), momentum (Equation (2)), and energy (Equation (3)). The assumptions listed in Table 2 are used to solve the mass, momentum, and energy conservation equations [25],

Continuity [25,26]:

$$\nabla .\mathbf{v}=0$$

(1)

where V is the flow velocity vector (m/s),

Momentum [25,26]:

$${\mathsf{\rho }}_{\mathrm{n}\mathrm{f}}\left(\nabla .\mathbf{v}\right).\mathbf{v}=-\nabla .\mathrm{p}+{\nabla }^2.\mathbf{v}$$

(2)

ρ_nf corresponds to the nanofluid density (kg/m³), P stands for pressure (Pa), and µ_nf is the nanofluid dynamic viscosity (kg/m.s).

Energy [25,26]:

$${\mathsf{\rho }}_{\mathrm{n}\mathrm{f}}{{\mathrm{c}}_{\mathrm{p}}}_{\mathrm{n}\mathrm{f}}\left(\mathbf{\nabla }.\mathbf{v}\right)\mathrm{T}={\mathbf{\nabla }}^2.\mathrm{T}$$

(3)

C_pnf is the specific heat of the nanofluid (nf) in (J/kg. K), k_nf is the nanofluid thermal conductivity (W/m.K), and T is the flow temperature (K).

Table 2. Assumptions [27].

Parameters	Assumptions
Flow characteristics	3-D, steady, laminar, incompressible, and single phase
Body force	Neglected
Radiation heat transfer	Neglected
No slip boundary condition	u = v = w = 0 at solid wall [28,29]
Inlet velocity	Uniform [28,29]
No. of Microchannels	One channel is examined since all microchannels have equivalent heat transfer and flow properties [30]

Table 2. Assumptions [27].

Parameters	Assumptions
Flow characteristics	3-D, steady, laminar, incompressible, and single phase
Body force	Neglected
Radiation heat transfer	Neglected
No slip boundary condition	u = v = w = 0 at solid wall [28,29]
Inlet velocity	Uniform [28,29]
No. of Microchannels	One channel is examined since all microchannels have equivalent heat transfer and flow properties [30]

To achieve a numerical solution, a finite volume method was utilized. The convective terms in the governing equations were discretized using a second-order hybrid accuracy scheme that combines upwind and central differences. For the simulations, a mesh with cell volumes of 20 μm³ was employed after confirming its independence through a grid test. The pressure field was determined using the PRESTO algorithm, implemented with the SIMPLE algorithm described in reference [25]. Convergence of the solution was considered achieved when the maximum normalized absolute residual across all nodes fell below 10⁻⁶.

2.2. Thermophysical Properties of Nanofluids

In this study, the temperature of the fluid within the channel exhibited slight variations. However, the thermophysical properties of the nanofluids were assumed to remain constant and independent of temperature. This assumption allows for simplified calculations and analysis.

In this study, different percentages of ethylene glycol in water mixtures were utilized as the base fluid. Additionally, solid particles such as Al₂O₃, SiO₂, and ZnO were incorporated into the mixtures at varying volume concentrations. It was expected that these nanoparticles would significantly influence the thermophysical characteristics of the nanofluids.

To determine the new thermal properties of the nanofluids, the study employed specific correlations numbered 4–12. These correlations were utilized for calculating the altered thermal properties of the nanofluids, considering the presence of the nanoparticles and the varying volume concentrations.

Thermal conductivity for:

Al₂O₃, SiO₂ (Hussein et al., 2013 [31])

$${\mathrm{k}}_{nf}=(1+3\phi )k_{bf}$$

(4)

ZnO (Vajjha and Das, 2009 [32])

$${\mathrm{k}}_{nf}=\frac{{\mathrm{k}}_p+2{\mathrm{k}}_{bf}-2({\mathrm{k}}_{bf}-{\mathrm{k}}_p)\mathsf{\phi }}{{\mathrm{k}}_p+2{\mathrm{k}}_{bf}+({\mathrm{k}}_{bf}-{\mathrm{k}}_p)\mathsf{\phi }}+5\times {10}^4\beta \phi {\rho }_{bf}{C}_{pbf}\sqrt{\frac{kT}{{\rho }_p{d}_p}}f(T,\phi )$$

(5)

$$f\left(T,\phi \right)=\left(2.8217\times {10}^{-2}\phi +3.917\times {10}^{-3}\right)\left(\frac{T}{T_0}\right)+(-3.0669\times {10}^{-2}\phi -3.91123\times {10}^{-3})$$

(6)

where β is the fraction of the liquid volume traveling with a particle. For ZnO, the relation used was with the temperature ranging from 288 k to 363 k, particle volumetric concentration range (1% ≤ φ ≤ 7%), and spherical particle size of 29 mm.

Dynamic viscosity:

Al₂O₃, SiO₂ (Hussein et al., 2013 [31])

$${\mu }_{nf}=(1+2.5\phi ){\mu }_{bf}$$

(7)

ZnO (Vajjha and Das, 2009 [32])

$${\mu }_{nf}=(1+7.3\phi +123{\phi }^2){\mu }_{bf}$$

(8)

Density:

Al₂O₃, SiO₂ [31]

$${\rho }_{nf}=\left(\frac{\mathsf{\phi }}{100}\right){\rho }_p+(1-\frac{\mathsf{\phi }}{100}){\rho }_{bf}$$

(9)

ZnO [32]

$${\rho }_{nf}=\left(1-\phi \right){\rho }_{bf}+\phi {\rho }_p$$

(10)

Heat capacity:

Al₂O₃, SiO₂ [31]

$$c_{pnf}=\frac{\frac{\phi }{100}\left({\rho }_p{c}_{pp}\right)+(1-\frac{\phi }{100}){\rho }_{bf}{c}_{pbf}}{{\rho }_{nf}}$$

(11)

ZnO [32]

$$c_{pnf}=\frac{\phi {\rho }_p{c}_{pp}+(1-\phi ){\rho }_{bf}{c}_{pbf}}{{\rho }_{nf}}$$

(12)

where φ represents the nanoparticle volume concentration, the subscript “bf” refers to the base fluid, “nf” refers to the nanofluids, and “p” refers to the particles.

Table 3. Properties of alumina, silica, and zinc oxide nanoparticles [33].

Properties	Nanoparticle (Al2O3)	Nanoparticle (SiO2)	Nanoparticle (ZnO)
ρ (kg/m3)	3970	2220	5600
cp (J/kg·k)	765	745	40.3
κ (W/m·K)	36	1.4	13

and

Table 4. Properties of base fluids [8].

Properties	Base Fluid (H2O)	Base Fluid (ψ = 10% EG–H2O)	Base Fluid (ψ = 30% EG–H2O)	Base Fluid (ψ = 40% EG–H2O)
ρ (kg/m3)	997	1008.74	1032.22	1043.96
cp (J/kg·k)	4185	4002.6	3649.8	3473.4
κ (W/m·K)	0.613	0.5769	0.5047	0.4686
µ (kg/m·s)	0.000855	0.00234	00.00531	0.00679

provide information on the thermophysical properties of various nanoparticles and different base fluids, respectively, at a temperature of 288 K.

2.3. Numerical Calculations

The average heat transfer coefficient, denoted “h”, was calculated using Equation (13). Equation (13) applies Newton’s cooling law to determine the total heat transfer rate, considering the total microchannel surface area (A_s), the average fluid bulk temperature (T_b) (calculated using Equation (14)), and the average microchannel temperature (T_s) obtained from post-processing of the CFD simulation.

$$\mathit{Q}=\mathit{h}{\mathit{A}}_{\mathit{s}}∆\mathit{T}=\mathit{h}{\mathit{A}}_{\mathit{s}}\left({\mathit{T}}_{\mathit{b}}-{\mathit{T}}_{\mathit{s}}\right)$$

(13)

Equation (14) defines the average fluid bulk temperature (T_b) as the mean temperature between the inlet fluid temperature (T_in) and the outlet fluid temperature (T_out).

$$T_b=\frac{T_{in}+T_{out}}{2}$$

(14)

To obtain the average heat transfer coefficient (h), Equation (15) was utilized.

$$\mathit{h}=\frac{\mathit{q}}{{\mathit{A}}_{\mathit{s}}\left({\mathit{T}}_{\mathit{b}}-{\mathit{T}}_{\mathit{s}}\right)}$$

(15)

The average Nusselt number can be determined by:

$$\mathit{N}\mathit{u}=\frac{\mathit{h}{\mathit{D}}_{\mathit{h}}}{\mathit{k}}$$

(16)

where the hydraulic diameter D_h can be calculated by:

$${\mathit{D}}_{\mathit{h}}=\frac{4\mathit{A}}{\mathit{p}}$$

(17)

where A represents the channel cross-sectional flow area and p is the channel wet perimeter.

2.4. Parameters Conditions

To examine the impact of various nanoparticle concentrations combined with different mixtures of base fluid, a study was conducted on the different parameters listed in

Table 5. Parameters under study.

Variables	Study the Variable’s Effect On
Re = 500 to 1200	T: MCHS temperature (k)
Ethylene glycol percentage in water (ψ = 0%, 10%, 30%, and 40%)	h: Heat transfer coefficient (W/m2k)
Nanoparticles volume fraction: (1 to 5% for Al2O3, SiO2, and ZnO)	Nu: Nusselt number
Geometry: (single-stack Rectangle)	∆p: Pressure drop (Pa)
	P: Power (W)

and their influence on the corresponding variables.

2.5. Boundary Conditions

The objective of the current study was to determine the optimal nanoparticle concentration and type for achieving the best heat transfer to power consumption ratio in nanofluids. The study focuses on three types of nanoparticles: Al₂O₃, SiO₂, and ZnO. The volume concentrations of the nanoparticles range from 1% to 5%. Additionally, different ratios (ψ) of the EG–H₂O mixture as the base fluid, including 0%, 10%, 30%, and 40%, were investigated. The study was conducted within the laminar range of Reynolds numbers, specifically from 500 to 1200.

In order to introduce variations, the inlet velocity boundary condition at x = 0 was assigned different values. Equation (18) was utilized to estimate the inlet velocity. The investigation was carried out under the following conditions: constant heat flux (q) of 100 W/cm², a constant fluid inlet temperature of 288 K, and assuming fully developed flow at both the inlet and outlet.

$$U_{in}=\frac{\mu }{\rho D_h}Re$$

(18)

where Re is the Reynolds number, the dynamic viscosity is μ, the fluid density is ρ, and D_h is the hydraulic diameter and can be estimated with Equation (18). The flowchart in Figure 2 illustrates the procedure and outcomes of the current study.

3. Results and Discussion

In this study, different mesh sizes (Mesh 1, Mesh 2, and Mesh 3) were employed in the computational domain to assess the impact of grid size on the numerical results. The sensitivity of the mesh was evaluated using the centreline temperature as a critical parameter. The boundary conditions for the study included an inlet temperature of T_in = 288 K, fluid velocity v = 4.088 m/s, Reynolds number Re = 890, constant heat flux q = 10⁶ W/m², and pure water as the operating fluid. The channel material was copper.

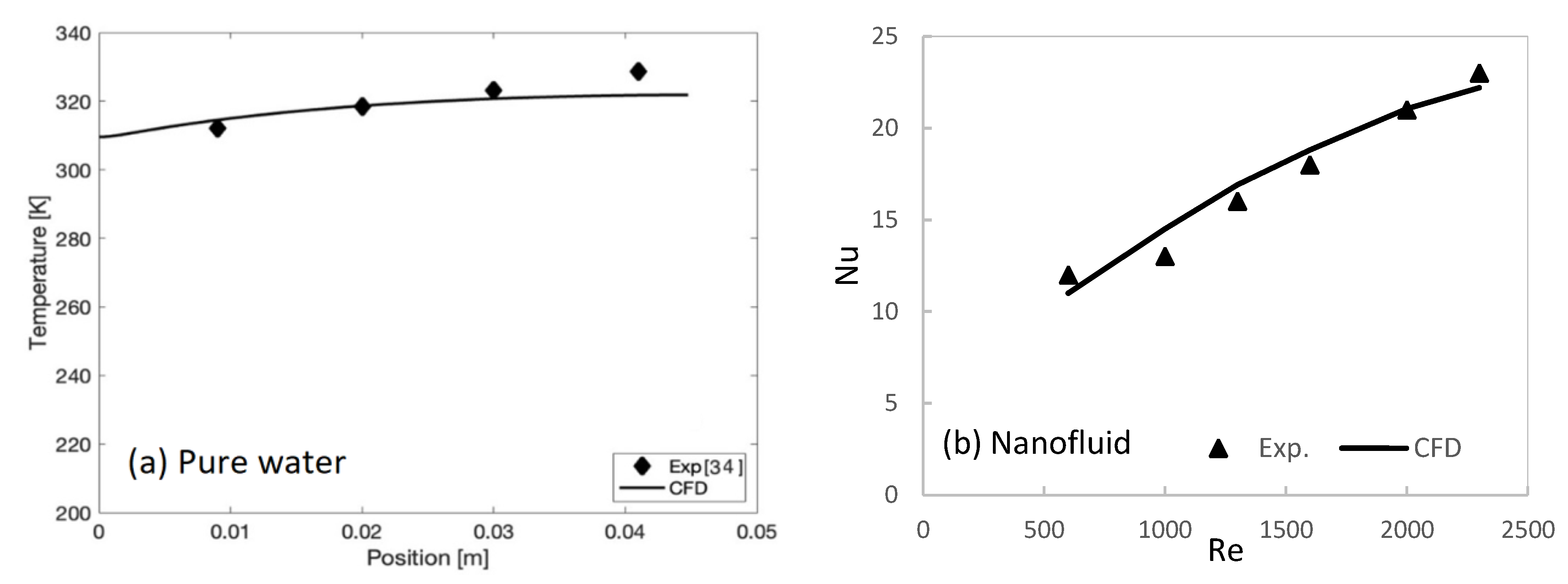
Figure 3 illustrates the grid layout and simulated centreline temperature results, indicating that all three mesh sizes produced comparable results. Although there were minor differences in run time, Mesh 2 (20 μm average cell volume) was selected for the remaining simulations to ensure an adequate level of accuracy. The study concludes that the predicted centreline temperature was independent of the mesh size.

The experimental data [34] are shown in Figure 4a for a temperature measured by thermocouples along the xy-plane and four different locations at 3175 μm height, constant heat flux of q = 10⁶ W/m², Tin = 288 K, and Re = 890. Figure 4 indicates an acceptable agreement between the CFD (current work) and the experimental data [34,35]. Thus, the current model is trusted and can be applied to investigate different nanofluids as a coolant and different microchannel configurations and their effects on the flow and heat transfer characteristics of an MCHS.

3.1. Different Types of Nanofluids

The provided text describes a research study that focuses on the investigation of various nanofluids composed of ZnO, Al₂O₃, and SiO₂ nanoparticles dispersed in different base fluids. The base fluids considered in this study include pure water (H₂O) as well as a mixture of ethylene glycol and water (EG–H₂O). The research analysis was conducted utilizing a rectangular microchannel heat sink (MCHS).

The primary objective of the study was to examine the thermal performance and heat transfer characteristics of these nanofluids within the MCHS. To achieve this, the researchers varied the volume concentrations of the nanoparticles in the base fluids, ranging from 1% to 5%. Additionally, the Reynolds numbers, which are dimensionless parameters used to describe fluid flow, were varied in the range of 500 to 1200.

By investigating this wide range of nanoparticle concentrations and Reynolds numbers, the study aimed to assess the impact of these factors on the heat transfer and flow characteristics of the nanofluids within the microchannel heat sink. The results of this study have the potential to provide valuable insights into the performance and feasibility of using nanofluids in microchannel cooling systems for applications such as electronic devices, thermal management, and heat exchangers.

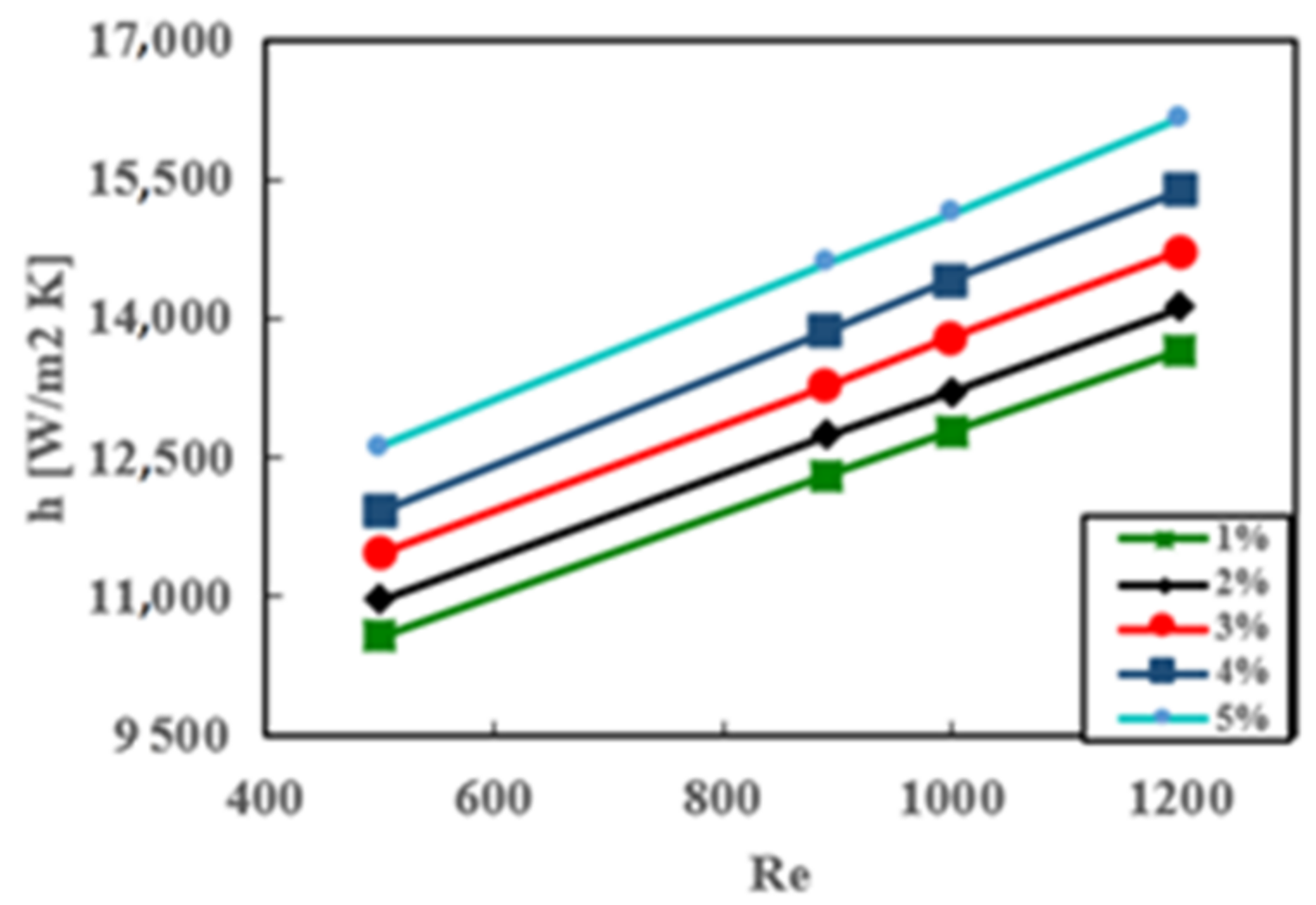
The effect of different types of nanofluids on the heat transfer coefficient, pressure drop, and power was examined in this study. Figure 5 illustrates the impact of nanoparticle volume concentration on the heat transfer coefficient. The findings revealed that the heat transfer coefficient increased as the Reynolds number and nanoparticle volume concentration rose, regardless of the ZnO nanoparticle concentration. The highest heat transfer coefficient was achieved at the maximum nanoparticle concentration. Specifically, at Re = 1200 and φ = 5%, the heat transfer coefficient reached its peak value, exhibiting an 18.39% increase compared to a particle volume concentration of φ = 1%. This outcome supports the prediction that the average heat transfer coefficient would improve with an increased concentration of nanofluid. It suggests that a higher insertion of nanoparticles enhances the cooling process.

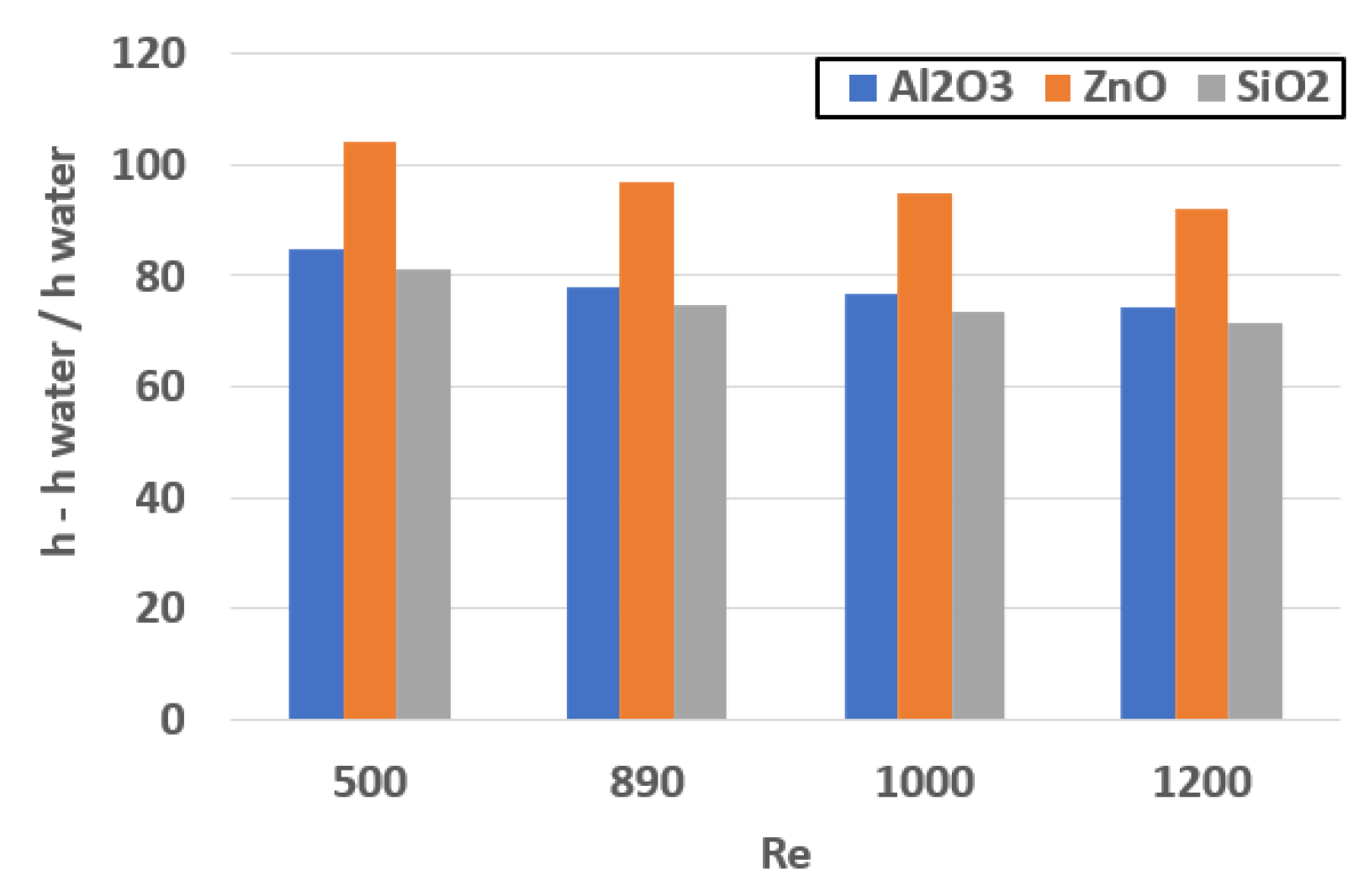
A comparison was conducted to assess various nanofluids using the normalized heat transfer coefficient [(h − h_w)/h_w] plotted against the Reynolds number, as depicted in Figure 6. In this comparison, h represents the average heat transfer coefficient of the nanofluid obtained at a nanoparticle volume concentration of φ = 5%, with pure water as the base fluid (ψ = 0%). On the other hand, h_w denotes the heat transfer coefficient of pure water at the corresponding Reynolds number. Figure 6 visually represents the combined influence of the Reynolds number and different nanoparticles on the normalized heat transfer coefficient. The results indicate that ZnO nanoparticles exhibit the highest normalized heat transfer coefficient, followed by Al₂O₃, and finally SiO₂ at all values of Re. For instance, at Re = 1200, the normalized heat transfer coefficient of ZnO surpassed that of Al₂O₃ by 20% and SiO₂ by 23%.

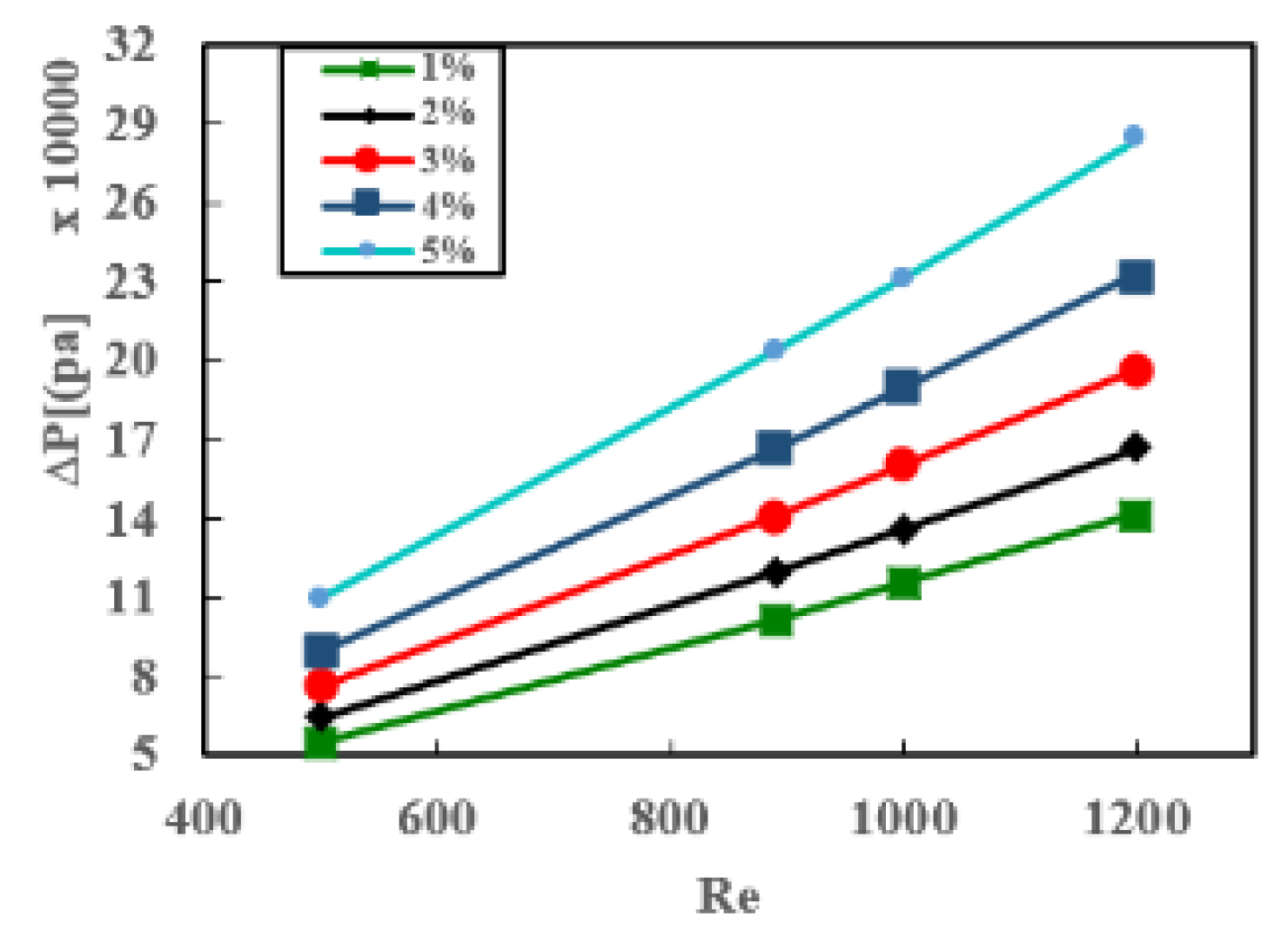
The relationship between the pressure drop profile and Reynolds number for various concentrations of ZnO nanoparticles is depicted in Figure 7. The figure demonstrates a linear increase in pressure drop with the rise in Reynolds number. Likewise, an increase in nanoparticle volume concentration led to an increased pressure drop. Notably, the maximum pressure drop was observed at φ = 5% and Re = 1200, which was 2.5 times higher than that at φ = 1% and 3 times higher than in pure water. This escalation was anticipated due to the significant increase in dynamic viscosity when more nanoparticles were introduced into the nanofluid.

Figure 8 displays a bar chart illustrating the normalized pressure drop quantity, $\frac{∆P-{∆P}_w}{{∆P}_w}$, as a function of Reynolds number. In this chart, ∆P represents the pressure drop between the inlet and outlet pressure of the nanofluid obtained at a nanoparticle volume concentration of φ = 5% and base fluid of pure water (ψ = 0), while ∆P_w represents the pressure drop of pure water at the corresponding Reynolds number. The plot effectively demonstrates the combined impact of the Reynolds number and different nanoparticles on the pressure drop. According to the figure, ZnO nanoparticles exhibit the highest normalized pressure drop, followed by SiO₂ and Al₂O₃. In fact, the normalized pressure drop for ZnO was nearly double the values obtained for both Al₂O₃ and SiO₂, as clearly indicated in the chart.

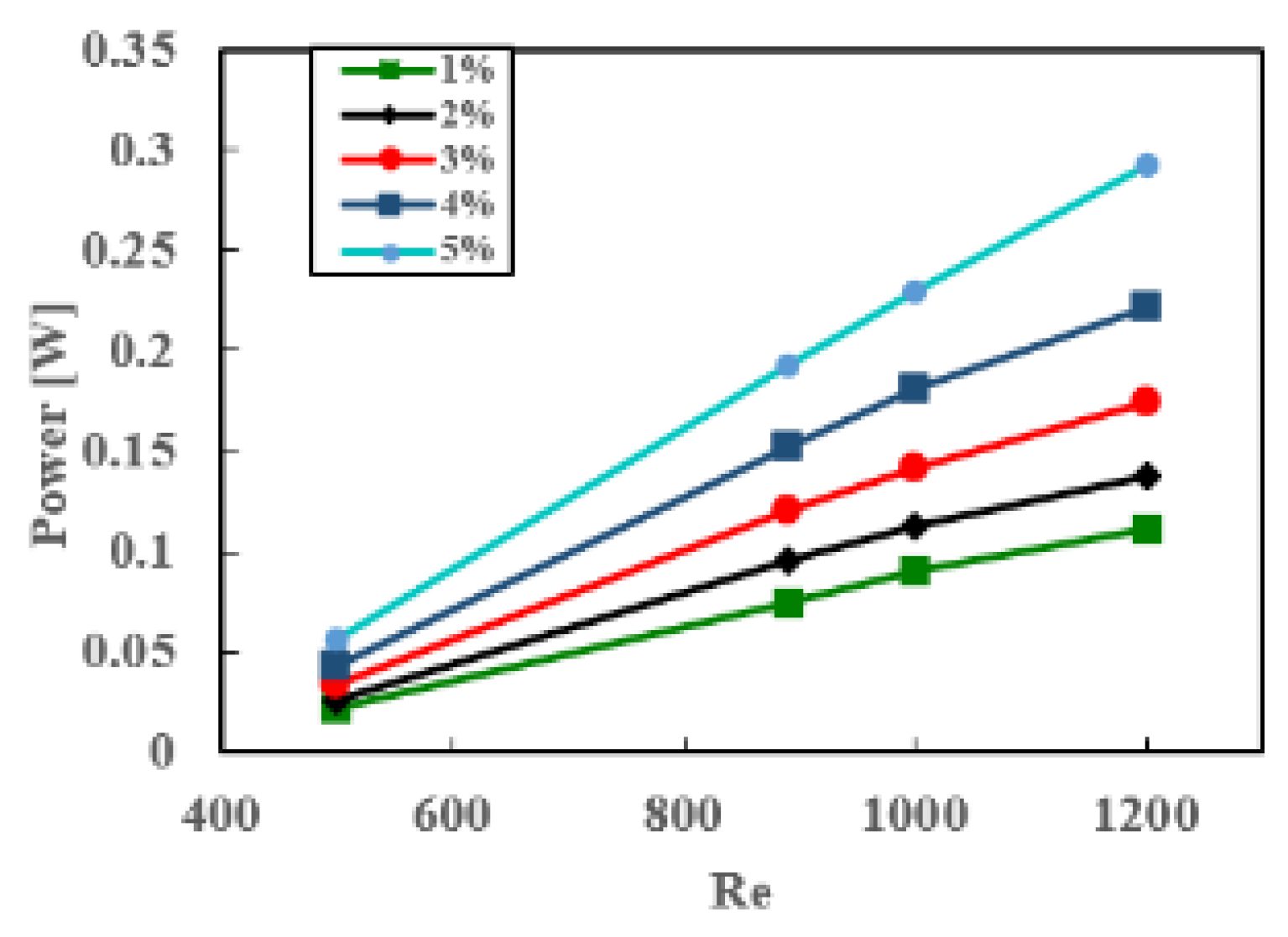
Figure 9 illustrates the variation in pumping power with different Reynolds numbers for ZnO particle concentrations ranging from 1% to 5% in pure water. The results demonstrate that the power demand increases as the volume concentration of nanoparticles increases, specifically between φ = 1% and φ = 5%. Among the three nanoparticles, ZnO required the highest pumping power, followed by SiO₂ and Al₂O₃. This is due to the substantially larger pressure drop associated with ZnO compared to the other two nanoparticles.

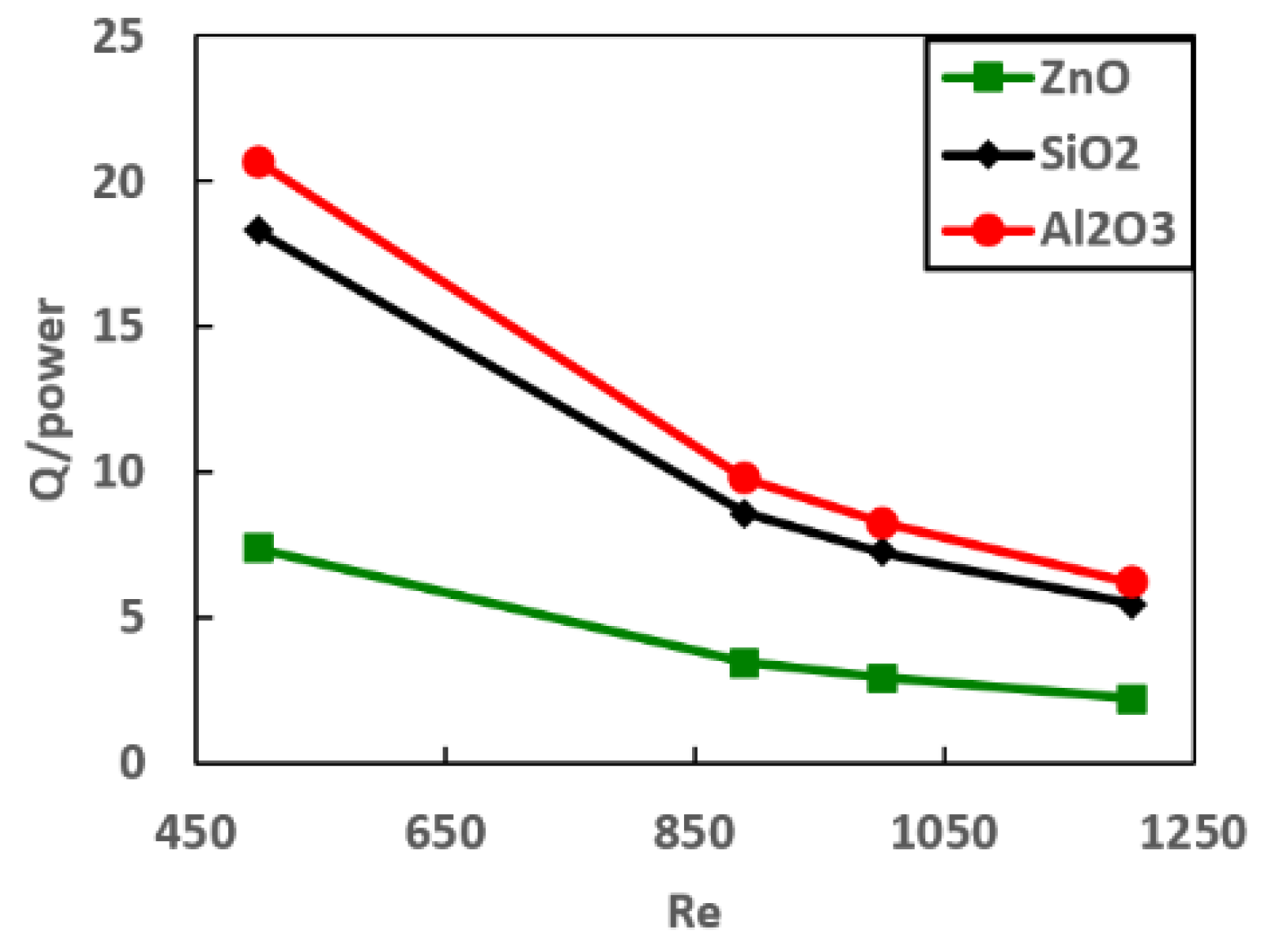
Lastly, Figure 10 depicts the ratio of heat transfer rate to power consumption at a nanoparticle volume concentration of φ = 5% and base fluid of pure water (ψ = 0%) for the three types of nanoparticles. As anticipated, ZnO nanofluids achieved the highest heat transfer coefficient; however, ZnO exhibited the poorest ratio due to their higher power demand. Conversely, Al₂O₃ nanofluids demonstrated the best heat transfer rate to power consumption ratio. The figure clearly illustrates that the maximum ratios were attained at lower Reynolds numbers, as the power consumption increased with higher Reynolds numbers.

3.2. Different EG–H₂O Concentrations

In the study, different ratios of the base fluid EG–H₂O mixture were utilized at various concentrations with different nanoparticles. The analysis of nanofluid performance primarily focused on the volume concentration of φ = 5%, which displayed a higher heat transfer coefficient with the Reynolds number. Subsequent observations were conducted at φ = 5% to evaluate the performance of nanofluids with varying EG–H₂O ratios and different nanoparticles.

Figure 11 illustrates the variation of the heat transfer coefficient for ZnO in EG–H₂O at a volume concentration of φ = 5% and different Reynolds numbers, as well as different EG–H₂O ratios (ψ = 0%, 10%, 30%, and 40%). It can be observed that all nanoparticles exhibited a similar linear increasing trend with Reynolds number across all given ratios. By comparing the heat transfer coefficient of ZnO in different EG–H₂O ratios to the heat transfer coefficient of pure water at Re = 890 and φ = 5%, it is evident that the heat transfer coefficients for ZnO at ψ = 10%, 30%, and 40% were higher. For instance, at Re = 1200 and φ = 5%, the heat transfer coefficient increments for ZnO were 18.78%, 63.22%, and 75.38% for ψ = 10%, 30%, and 40%, respectively. Consequently, the maximum heat transfer coefficient was achieved when using ψ = 40% of EG with φ = 5% of ZnO nanoparticles.

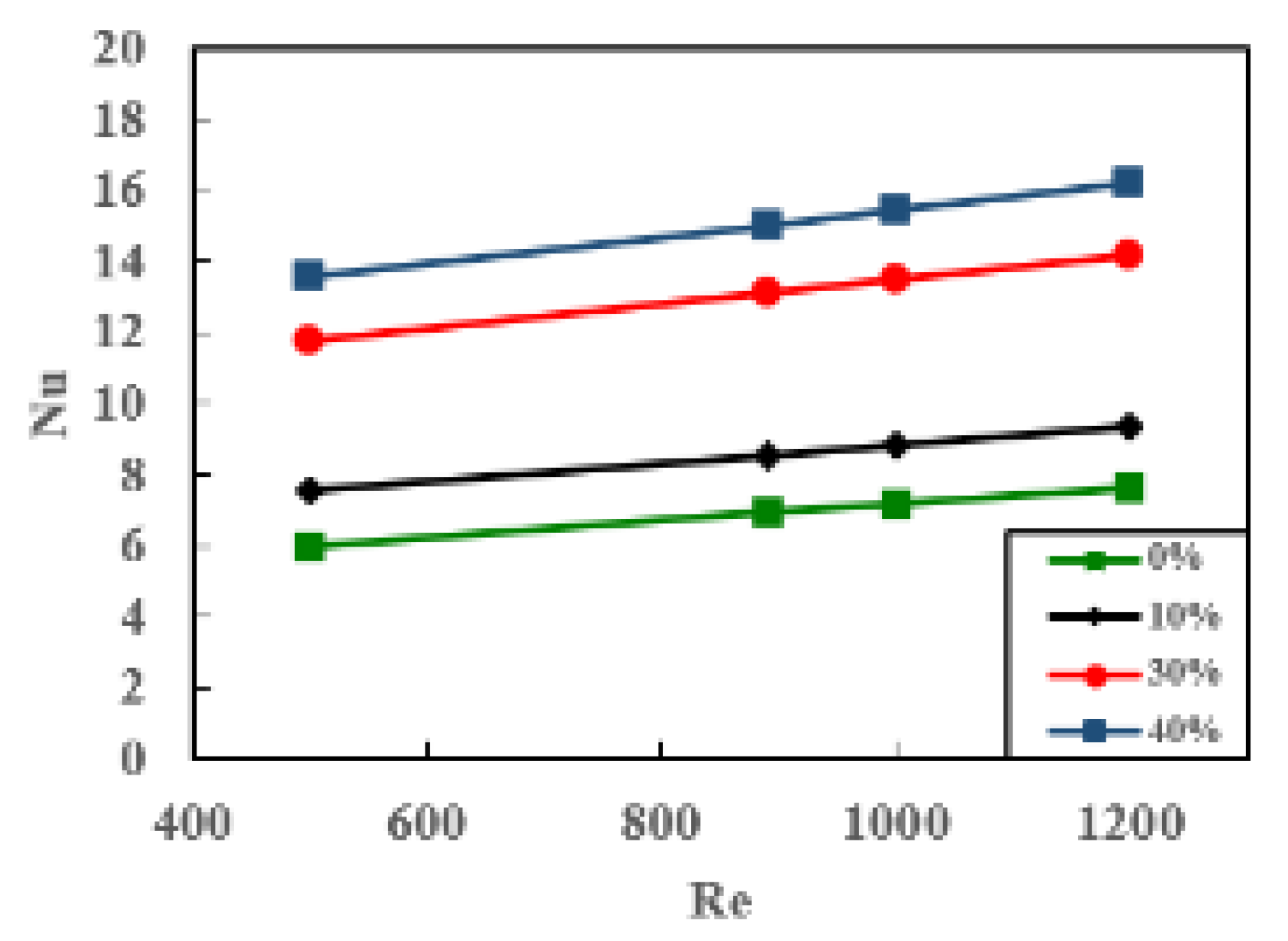
To gain further insights into the influence of EG–H₂O on heat transfer characteristics, the Nusselt number was plotted for different EG–H₂O ratios, as depicted in Figure 12. This figure presents the Nusselt number as a function of the Reynolds number and the EG–H2O ratio while maintaining a constant nanoparticle volume concentration (φ = 5%). The Nusselt number for nanofluids based on EG–H₂O mixtures exhibits a similar increasing trend with the Reynolds number, as observed in pure water-based nanofluids. Remarkably, the graph indicates that the highest Nusselt number was attained at ψ = 40%, surpassing the values obtained by 30%, 10%, and pure water by 16%, 75%, and 130%, respectively. These findings suggest that an increase in the percentage of EG in the base fluid enhances the heat transfer characteristics.

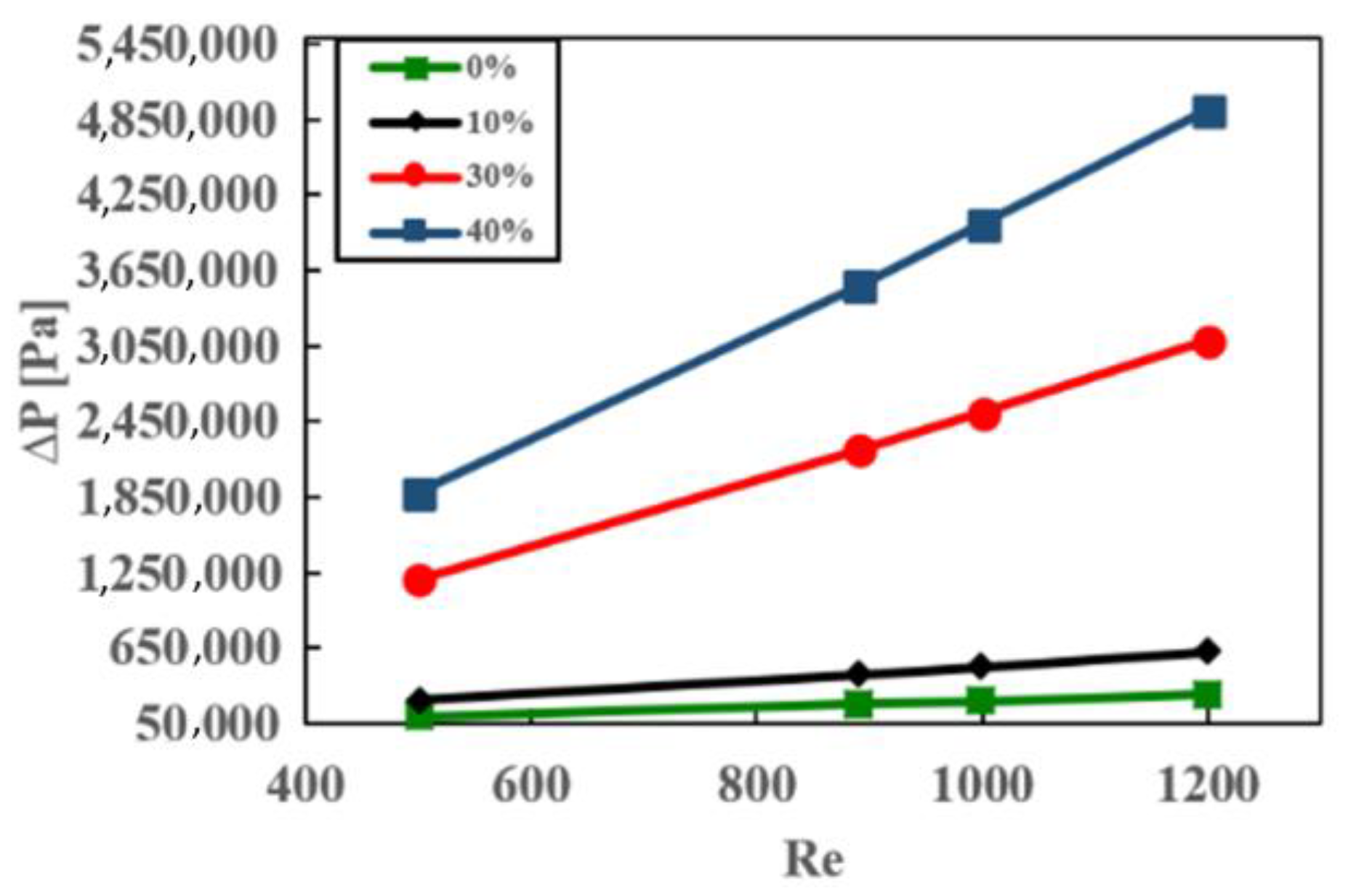
Figure 13 showcases the pressure drop values at various Reynolds numbers for three different EG–H₂O ratios. It is evident that both the Reynolds number and the percentage of EG in the mixture have a significant impact on the pressure drop. As the Reynolds number and percentage of EG increased, the pressure drop experienced a substantial increase. Consequently, the highest pressure drop was observed at ψ = 40% in the EG–H₂O mixture, surpassing the minimum pressure drop obtained with pure water (ψ = 0%). This trend highlights the considerable influence of both the flow conditions and the presence of EG in the fluid mixture on the resulting pressure drop. Further investigation of these factors can provide valuable insights into optimizing the system for desired pressure drop characteristics.

Moreover, to delve deeper into the investigation of pressure drop, a 30% EG–H2O ratio was employed, along with different types of nanoparticles (ZnO, Al₂O₃, and SiO₂) at a volume concentration of 5%. The results are presented in Figure 14. The figure clearly demonstrates that ZnO nanoparticles generated the highest pressure drop, approximately twice the values obtained by SiO₂ and Al₂O₃. On the other hand, SiO₂ and Al₂O₃ exhibited similar magnitudes of pressure drop. These findings highlight the distinctive effects of various nanoparticles on the resulting pressure drop, with ZnO nanoparticles demonstrating the greatest impact in terms of inducing a higher pressure drop.

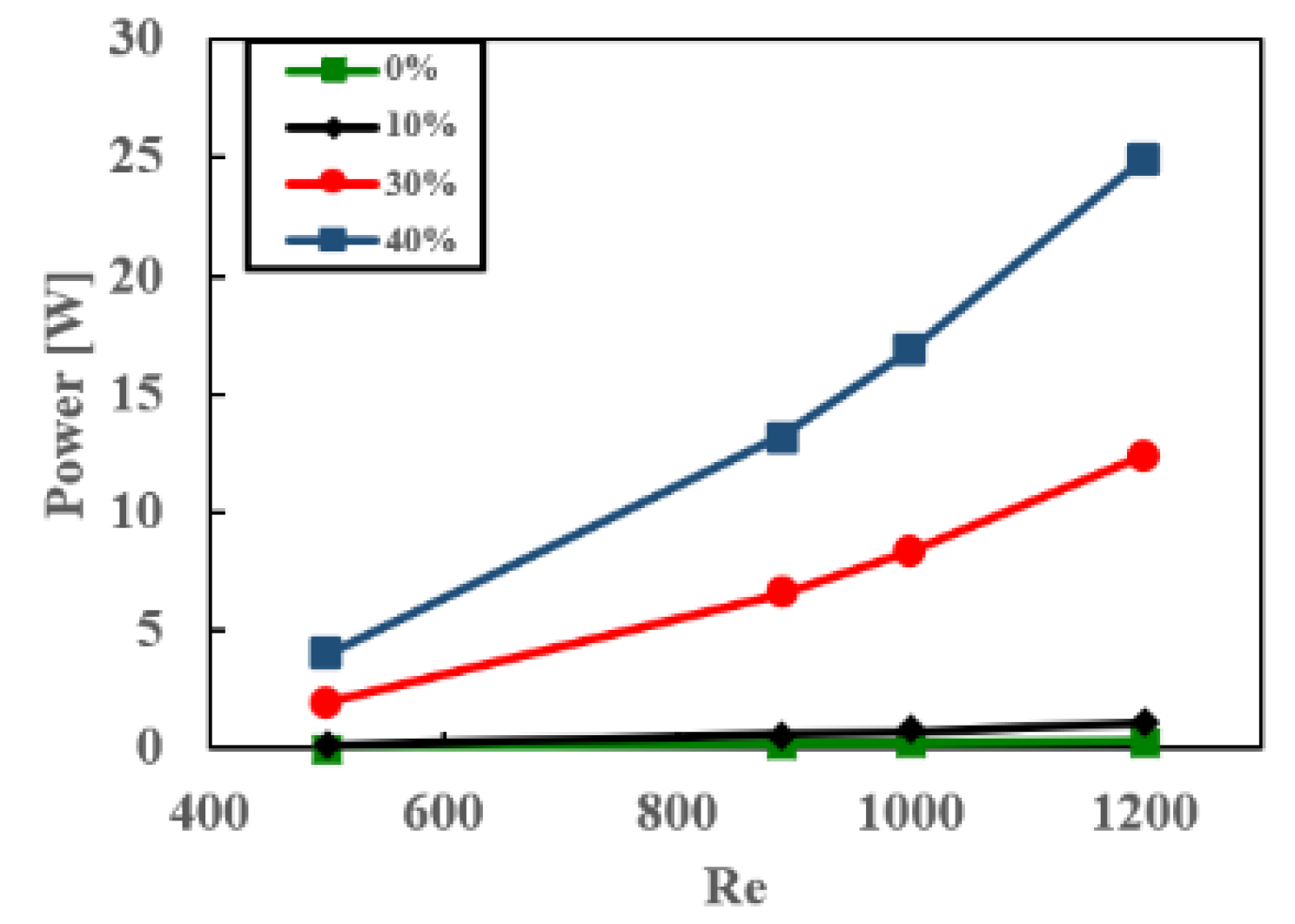
In order to further explore the impact of EG percentage in the base fluid, Figure 15 examines the variations in pumping power requirements at a volume concentration of φ = 5% for different Reynolds numbers and EG percentages (ψ = 0%, 10%, 30%, and 40%), specifically focusing on ZnO nanoparticles. The findings reveal a substantial increase in power requirements over 20 times when transitioning from ψ = 0% to ψ = 40%. Overall, the provided figures offer valuable insights into the performance of nanofluids based on EG–H₂O mixtures, including their heat transfer capabilities, pressure drop characteristics, and the associated pumping power requirements. These observations consider the diverse nanoparticle concentrations, EG percentages, and Reynolds numbers involved in the analysis.

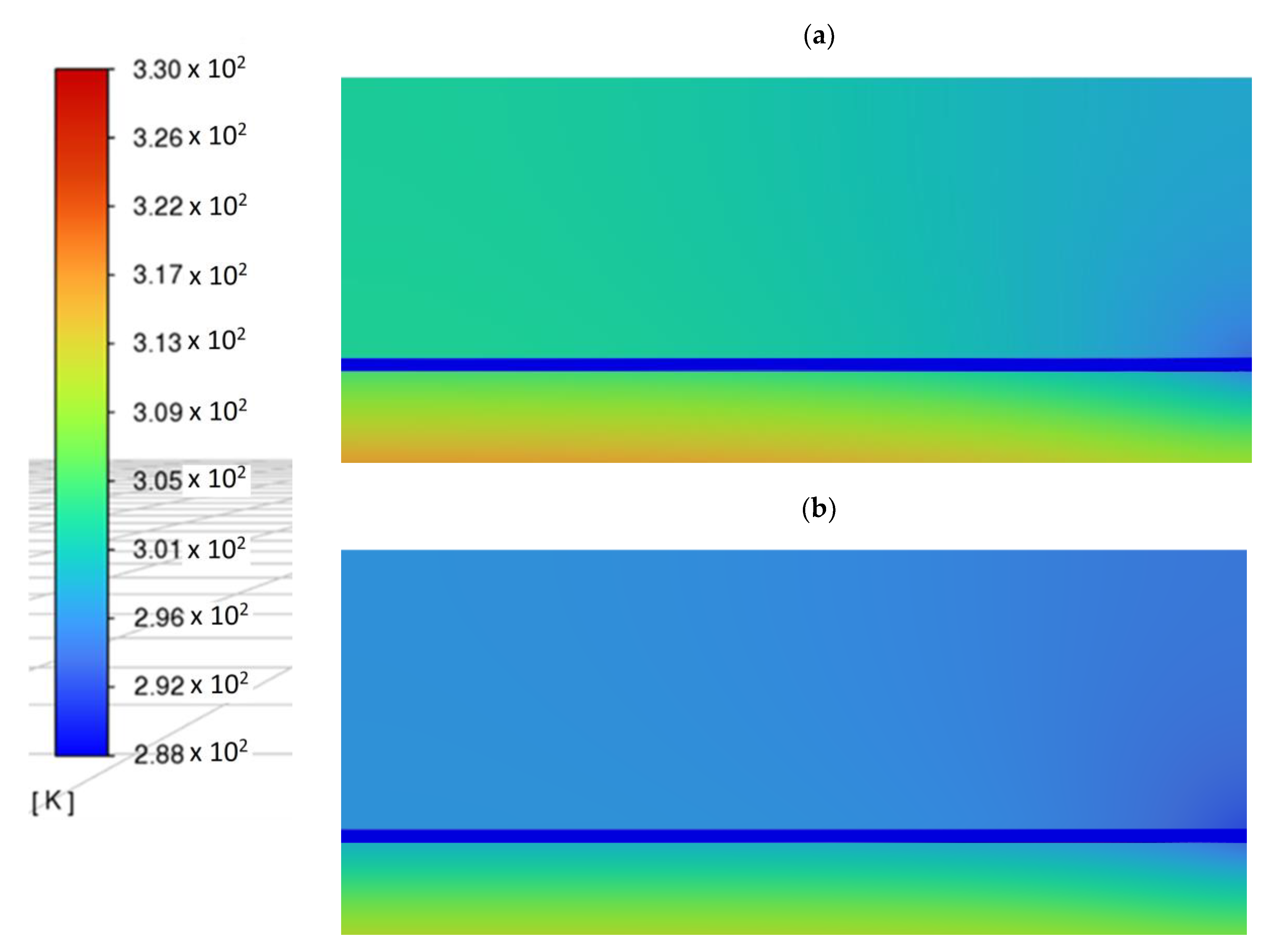
In order to examine the impact of nanoparticle concentration and the proportion of EG in greater detail, contour plots depicting the local temperature distribution in the x–y plane were employed for six distinct scenarios, as denoted in Figure 16 and Figure 17. The selected cases for comparison purposes encompass a Reynolds number of Re = 1200 and a particle concentration of φ = 5% for SiO₂, ZnO, and Al₂O₃, in combination with two different base fluids (ψ = 0% and ψ = 30%). Based on the findings illustrated in the figures, it is evident that the EG–H₂O mixture exhibits a notable cooling effect compared to pure water. This outcome can be attributed to the augmentation of the heat transfer coefficient with an increase in the percentage of EG, as discussed in Figure 10 and Figure 11. Furthermore, the results indicate that the minimum temperature of the heat sink was attained by employing ZnO (Figure 15c and Figure 16c). Consequently, the heat transfer characteristics and cooling process were significantly superior when employing ZnO in comparison to Al₂O₃ and SiO₂.

4. Conclusions

In the present study, 3-D fluid laminar flow and heat transfer in a microchannel were computationally studied. Different nanoparticles (Al₂O₃, SiO₂, and ZnO) and various base fluids (pure water and ethylene glycol–water) were investigated. Based on the simulation results, the following conclusions can be drawn:

• For all values of nanoparticle volume fractions, the temperature of both the coolant fluid and microchannel heat sink (MCHS) increases along the channel axis.
• Increasing the concentration of nanoparticles leads to an increase in the average heat transfer coefficient and significantly reduces the temperature of the MCHS compared to that of pure water. For example, at a volume fraction of 5%, the heat transfer coefficient increased by 18.39% more than that of pure water.
• The maximum average heat transfer coefficient is achieved by using ZnO at a volume fraction of 5%, which is 20% and 23% higher than that of Al₂O₃ and SiO₂, respectively.
• ZnO, at low and high concentrations of nanoparticles, causes the highest pressure drop compared to the corresponding values for Al₂O₃ and SiO₂ at all Reynolds numbers (Re).
• The study of different ratios of ethylene glycol–water shows that a higher ratio leads to a higher heat transfer coefficient at the same Re, same nanoparticles, and same heat flux. The heat transfer coefficient increases by 18.78%, 63.22%, and 75.38%, with a 10%, 30%, and 40% increase in the ethylene glycol ratio, respectively.
• However, increasing the ratio of ethylene glycol leads to a significant increase in pressure drop as well as power consumption.
• The minimum heat sink temperature is achieved by using ZnO at a high volume concentration of 5% mixed with 40% EG–H₂O.