Abstract
The safety of underground engineering projects is significantly influenced by groundwater. One of the key complexities is identifying the primary seepage paths within underground rock formations, understanding the patterns of seepage, and determining the effects of fracture parameters on the fluid movement inside the rock mass. To address these issues, a probabilistic model is constructed for random fractures using the finite element method, reflecting the random nature of fracture distributions in the real world. This model allows for an in-depth examination of the distribution of pore water pressure and Darcy velocity field, revealing the permeability trends in fractured rock masses. A variety of fracture models were devised to understand the relationship between factors such as fracture density, length, length power law, angle, dispersion coefficient, aperture, and power law, and how they affect the overall permeability of rock masses. The study suggests that, in the context of discrete fractured rock masses, there is a linear increase in permeability with an increase in fracture density and aperture. Moreover, fractures of greater length lead to increased permeability, with fractures aligned with the direction of water pressure having the most impact on seepage velocity. A thorough investigation of the factors that affect each fracture parameter was performed, and the permeability of each model was computed. From these findings, a series of predictive equations were suggested for estimating rock permeability based on fracture geometry parameters.
1. Introduction
The ability to predict characteristics of fractured rock masses has critical implications across a variety of domains, such as mining, foundational and underground engineering [1,2,3], storage of oil in underground reservoirs [4,5,6], CO2 sequestration practices [7], and even the transport of contaminants [8]. The permeability of these rock masses is significantly influenced by a broad spectrum of factors. These include matrix porosity, fracture length, pore size, and even the roughness of the fracture surfaces [9,10] to characterize field fractures. In general, fluid flow within these rock masses follows the fundamental principle known as Darcy’s law [11,12]. For the purpose of prediction, several key parameters have been put forth, such as the representative fundamental volume, the fractal dimension of the fracture network, and the distribution of fracture lengths [13,14,15,16,17,18], to simplify the characterization of fractures. However, it is important to note that calculating permeability through fluid flow within the fracture network is a complex process. It can be time-consuming and computationally demanding, potentially exceeding the capabilities of existing computer systems [19]. Therefore, the development of a predictive permeability formula, one that is based on simple fracture statistical parameters, is a necessary step forward. This would ideally simplify the process, making it more feasible and efficient.
Three permeability models for fractured rock include: (1) the stochastic continuous (SC) model, using equivalent homogeneity to represent varying fracture apertures [20,21]; the model may not accurately describe the directionality of the fractures because it assumes that the cracks are evenly distributed in all directions. Because fractures are treated as discrete elements, the model may not accurately describe the interactions between fractures and the surrounding rock; (2) the discrete fracture network (DFN) model, where fluid moves within rock fractures, assuming an impermeable rock matrix [22,23]; and (3) the channel network (CN) model [24,25,26], focusing on the non-uniformity of pore space within each fracture, with fluid primarily moving along the optimal pathway [27,28,29]. The model may place too much emphasis on the connectivity of fractures and neglect the independence of fractures and the interaction of fractures with surrounding rocks. However, these analyses exhibit a certain degree of limitation, primarily due to their lack of systematic investigation into seepage within a discretely fractured rock body. There is a notable absence of quantitative analysis results, which can otherwise contribute significantly to our understanding of this complex process.
Common distribution forms of natural rift parameters include random distribution [30,31], power law distribution, log-normal distribution, and Fisher function distribution [17]. This study focuses on analyzing the most common power law distribution and Fisher function distribution forms and distribution characteristics of fractures in nature. These forms were used to examine the variations in these parameters and their effects on rock permeability.
In the realm of numerical simulation, the boundary element method is renowned for its high accuracy and efficiency as it discretizes only the boundary of the domain of interest and is constructed from the fundamental analytical solution [32]. However, when the fundamental analytical solution does not exist, the boundary element method may no longer be suitable. In such cases, the finite element method becomes a satisfactory choice due to its basis in general physics despite its need for discretization of the entire domain of interest. Moreover, analytical methods, such as fractal theory, can also be used to calculate the equivalent permeability of rock as it offers the highest precision. However, in practical application, determining a system’s fractal dimension or other fractal parameters can be quite complex and challenging. Therefore, fractal theory may not be applicable to all types of problems [33,34].
Finite element methods had been studied for single-phase or multiphase flows [35]. Reddy noted that the finite element method was a powerful computer-oriented approach for solving engineering problems [36]. One primary advantage of this method for rock fracture simulation was that grid points could be discretized, reducing the number of computational steps and individual cells, allowing for rapid computation of accurate results. Many scholars utilize COMSOL Multiphysics software for calculations and have demonstrated the accuracy of calculations performed using this software [37,38,39,40,41]. Consequently, this numerical simulation employs the finite element method to analyze the characteristics and influence the range of seepage and pore water pressure in fractured rock and calculate the magnitude of equivalent permeability.
This paper aims at developing a predictive formulation based on a pore–fracture dual medium that relates equivalent permeability to simple statistical parameters of the fracture network. First, a single-factor model was developed, considering only the influence mechanism of ideal fracture density, length, angle, and opening and the influence effect. Then, a two-dimensional random fracture network was created according to the fracture parameters: fracture mass density (ρ), fracture length (L), power law of length (aL), fracture angle (°), dispersion coefficient (b), aperture (d), and power law of opening (ad). The effects of these parameters on permeability and the interactions of related parameters with permeability were analyzed separately, and, finally, a response surface function equation was proposed to predict permeability.
2. Numerical Modeling
2.1. Theoretical Formula
2.1.1. Equation of Water Flow in Pores
Fluid percolation in a homogeneous matrix block follows Darcy’s law [42] with time by the equation:
where u was the velocity vector in m/s; p was the pore water pressure in Pa; εp was the porosity of the matrix block; S was the matrix block water storage coefficient in 1/Pa; ρ was the density in kg/m3; t was the time.
The linear water storage model is:
where Xf was the fluid compressibility rate, 1/Pa; Xp was the equivalent compressibility of the matrix block, 1/Pa.
Within the block, the built-in velocity variable u provides the Darcy velocity, which was the volume flow rate per unit area of the porous medium.
where k was the permeability of the matrix block, m2; μ was the hydrodynamic viscosity, Pa·s.
2.1.2. Water Flow Equation in Fracture
Although rock fissures in nature had rough surfaces, variable apertures, and different contact ratios, in indoor tests and numerical simulations, generally assume that a single fissure had a constant aperture and that it conforms to the cubic law of seepage [43], which was expressed as:
where q was the flow rate (m2/s); e was the fracture width (m); g was the gravitational acceleration (m/s2); ν was the fluid motion viscosity coefficient (m2/s); and J was the hydraulic gradient (dimensionless).
The fracture density range of natural rocks was huge and different rock types, genesis, degree of metamorphism, and other factors impact fracture density. The fracture density in some rocks could reach about 0.05–0.1 m−2. It should be noted, however, that the exact values need to be determined in conjunction with the specific rock type and field measurements. The fracture density range for this simulation was 0.05–0.45/m2.
According to the field outcrop investigation, the cumulative probability density function of fracture trace length distributed by the power law was provided in the literature [44] by analyzing the geometric features of some larger fractures:
where α was the power law exponent. L represents the fracture length, and Lmin is the shortest fracture length.
The fracture strike follows the Fisher distribution, which was commonly used in the numerical modelling of discrete fracture networks, and the probability density function of the Fisher function demonstrated the angular deviation θ (SI units: rad)
where b was the dispersion coefficient or Fisher’s constant. (The cumulative probability function for Equations (6) and (8) is in supplement Figure S15.)
In general, it was commonly assumed that there was no correlation between aperture and trace length. Therefore, the aperture ground distribution form could be considered as the probability density function of the fracture length:
where β was the power law exponent. d represents the fracture aperture and Lmin is the shortest fracture aperture. (The cumulative probability function for Equations (6) and (8) is in supplement Figure S14.)
The response surface method was the product of a combination of mathematical and statistical methods for modelling and analyzing problems that were influenced by multiple variables. This experiment was designed to analyze the effect of pores and fractures in the rock mass on the permeability of the rock mass. The expression was:
where ε was the observation error or noise of the corresponding y. ρ was the fracture density in/m2; L was the fracture length; aL was the fracture length power law exponent; θ was the fracture angle in °; b was the dispersion coefficient; d was the fracture aperture in cm; and ad was the opening power law exponent.
2.2. Model Building
The methodology commenced by employing COMSOL’s Model Wizard to specify a 2-dimensional model space, wherein the governing physics field was Darcy’s law under the constraints of a steady state study. Our model framework was geometrically defined as a square, each side measuring 20 m, as illustrated in Figure 1.
Figure 1.
Define geometry.
In the materials phase, we were meticulous in specifying our model’s material parameters. These included a fluid density of 1 × 103 kg/m3 within the fractures, a dynamic viscosity of 1 × 10−3 Pa·s, a fluid compressibility of 4.4 × 10−10 Pa−1, a matrix porosity of 0.3, a matrix permeability of 1 × 10−11 m2, and a matrix compressibility of 10−3 Pa−1.
The boundary conditions were set up in the subsequent stage, where the left boundary was defined as a pressure boundary with an initial pressure of 1 × 10⁵ Pa. The top and bottom boundaries were deemed impermeable, while the right side was designated as the outlet.
The determination of fracture attributes was based on a fracture density of 0.25/m2, which equated to 100 fractures for the control group. A random simulator was utilized to generate the coordinates of the 100 fracture centers, as depicted in Figure 2. These coordinates then served as reference points for setting the fracture parameters. After adjusting the fracture length, direction, and aperture according to the fracture parameters, the standard conditions adopted included a fracture length ranging between 25.6 and 38.4 m, a length power law index of 2, an angle of 45°, a dispersion coefficient of 5, a fracture aperture ranging between 0.8 and 1.2 mm, and an aperture power law of 2. The numerical requirements corresponding to these parameters were inputted into the random simulator. The generated values were then substituted into the fracture model, simulating the corresponding fracture conditions, as shown in Figure 3.
Figure 2.
Set point.
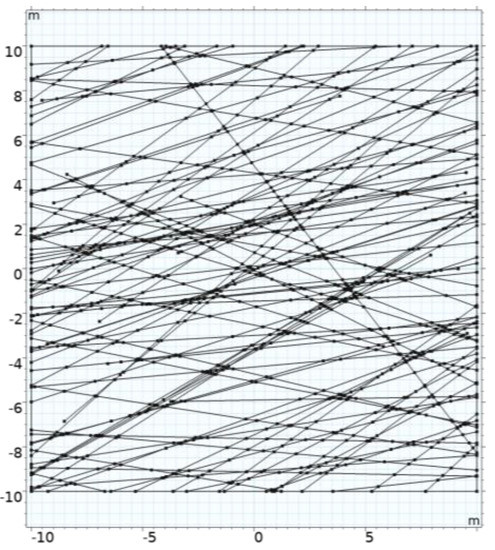
Figure 3.
Set fractures.
Upon completion of the calculations, the model’s right end, representing the simulated outlet end, was selected for data collection. The intersection points between the fractures and the boundaries were identified as data collection points for cumulative summation. The data on the right boundary were added to the fracture seepage data to yield the final total Darcy velocity data.
2.3. Two-Dimensional Finite Element Model
In this experiment, numerical simulation of fracture models necessitated addressing data from three aspects. Firstly, the geometric parameters of simulated fractures were considered, followed by the physical properties of fractures, and, finally, the physical properties of the simulated matrix. Since non-connected fractures only served a water storage function in seepage calculations, they exerted minimal influence on water conductivity. The primary network was one of the key factors affecting the water conductivity of the fracture network.
Matrix flow adhered to Darcy’s law, while flow within fractures conformed to a modified version of Darcy’s law. The flow process encompassed four distinct modes of fluid transport: from the matrix, from the matrix to fractures, from fractures to the matrix, and from one fracture to another.
These processes were sequentially computed in the following steps. Firstly, the entire flow domain was divided into a series of flow units. The flow region was described as an unstructured mesh using a triangulation algorithm, with the center of each mesh serving as a study node. A single fracture was equivalent to an internal boundary, which reduced the overall computational load. This allowed for the description of fracture behavior in the absence of a large number of densely packed, minuscule grids. The unstructured mesh effectively partitioned matrix and fracture units, providing an algorithmic guarantee for accurately calculating the material transfer between any two units. Consequently, the finite element method was chosen to implement the simulation process in this experiment.
The basic model for this experiment was a two-dimensional single-phase flow model. The geometry of the model was a square with a side length of 20 m, with the inlet and outlet ends being the left and right sides, respectively, while the top and bottom ends were impermeable boundaries. The boundary conditions for this model are presented in Table 1.

Table 1.
Numerical simulation parameters.
Figure 4 shows the simulation model. The simulation parameters of a fracture density of 0.25/m2, a fracture length of 25.6–38.4 m, a power law index of length of 2, an angle of 45°, a dispersion coefficient of 5, an aperture of 0.8–1.2 mm, and a power law of opening of 2 were selected as the standard working conditions for this study.
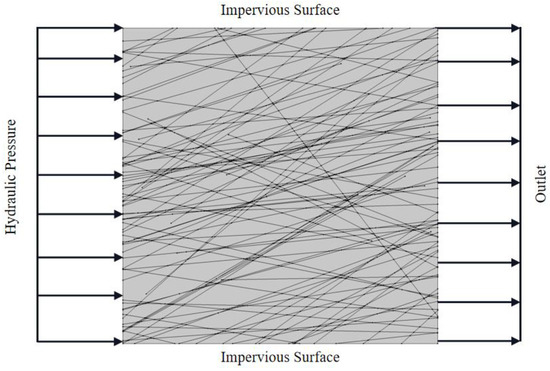
Figure 4.
Schematic of the finite element model.
2.4. Constant Fracture Model
The constant fracture model with fracture density of 0.25 m−2, fracture length of 32 m, fracture angle of 45, and aperture of 1 mm was selected as the control group.
The distribution of fractures had a considerable effect on the seepage movement of fluids in the rock matrix as well as the pore water pressure.
Fracture density increase positively correlates with rock mass equivalent permeability. Figure 5 shows the impact of fracture density on permeability under different fracture apertures. Equivalent permeability increases with fracture density, and the influence of aperture density is evident. For densities less than 0.25 m−2, the order of permeability is 3 mm, 4 mm, 2 mm, 5 mm, and 1 mm. For densities greater than 0.35 m−2, 4 mm and 5 mm apertures have similar permeabilities, with the remaining order being 3 mm, 2 mm, and 1 mm.
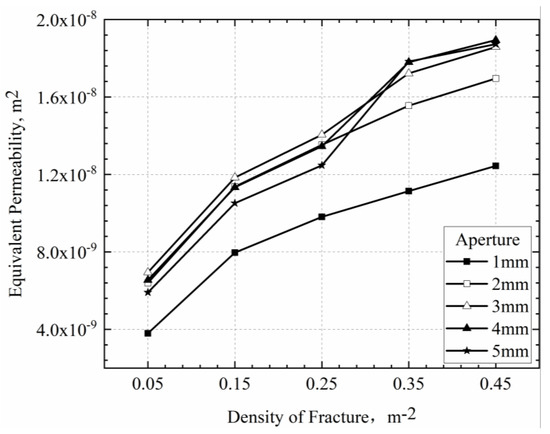
Figure 5.
Effect of fracture density and fracture aperture on permeability.
Fracture angle variations significantly impact Darcy velocity and pore water pressure in the rock mass matrix. Figure 6 shows six models representing the influence of angle variation on permeability. Models a–c demonstrate angle impacts on Darcy velocity, while models d–f show pressure effects. Model a highlights velocity changes at fracture ends and even pressure distribution. Model b exhibits greater flow velocity in connected high hydraulic gradient regions and perpendicular pressure distribution. In Model c (90° fracture angle), fluid seepage effects vanish, with no velocity changes and uniform pressure distribution in matrix seepage direction.
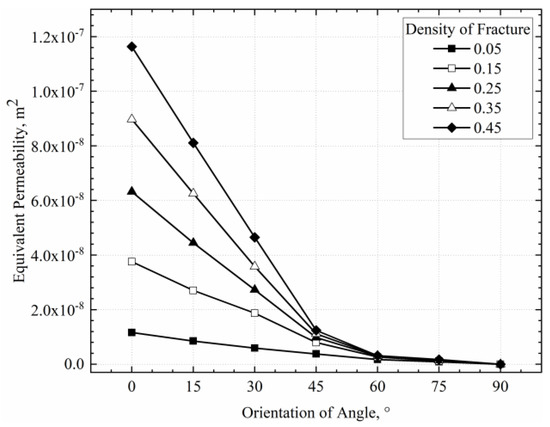
Figure 6.
Effect of fracture angle and fracture density on permeability.
Fracture angle increase negatively correlates with rock mass equivalent permeability. Figure 3 shows the influence of fracture angle on permeability under different fracture densities. Permeability decreases as the angle increases within the 0–90° range. At 60°, various fracture densities have similar permeability values. At 90°, fractures with different apertures reach uniform permeability, corresponding to matrix permeability, and fracture influence vanishes, confirming the negative correlation.
Fracture aperture increase positively correlates with rock mass equivalent permeability. Figure 7 shows the effects of different aperture on equivalent permeability under different angles. Within the 0–30° range, aperture increase significantly impacts permeability. However, within the 45–90° range, aperture influence on permeability is less pronounced due to weakened fluid connectivity and increased storage capacity as fracture angle increases. The impact of fracture aperture on permeability is positively correlated under the same angle conditions but varies at different angles.
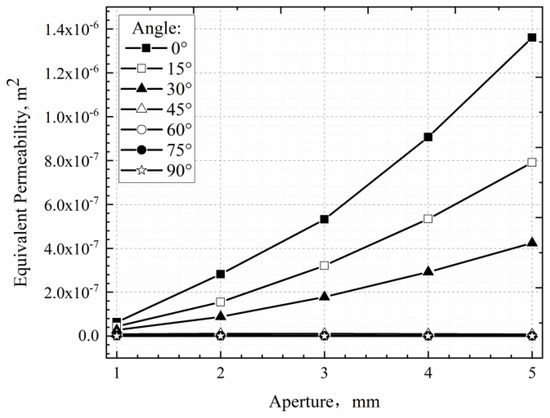
Figure 7.
Effect of aperture and fracture angle on permeability.
Fracture aperture increase positively correlates with rock mass equivalent permeability. Figure 8 displays the impact of different fracture lengths on permeability under varying fracture densities. Under the same fracture density, increased fracture length positively affects permeability, although the growth rate decreases as length increases. When fracture length exceeds 48 m, equivalent permeability stabilizes, and the growth rate diminishes, confirming the positive correlation between fracture length and permeability.
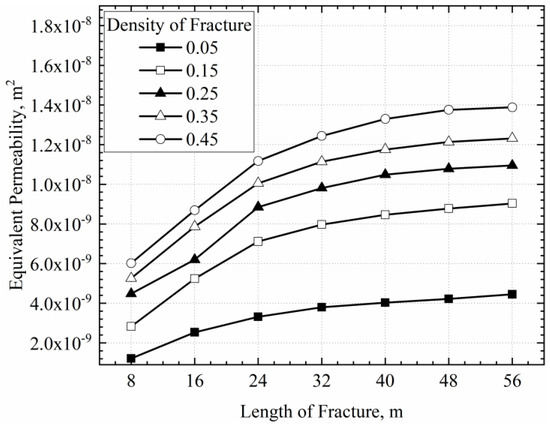
Figure 8.
Effect of fracture length and fracture density on permeability.
2.5. Random Fracture Model
The effect of the street-following fracture parameters on the permeability was studied based on the COMSOL model. To make the study more systematic and comprehensive, it was necessary to start with a single parameter variation and eliminate the interference of fractures intersections. During the single work simulation, we investigated the effects of fracture density, direction, length, and pore size on permeability. The parameters of the experimental model were shown in Supplementary Material Table S1.
Given the strong randomness of discrete fractures in simulating the calculated permeation velocity, as shown in Figure 9, the average value tended to be stable, with a variation of <5% at the simulation result of 20. Therefore, the average value of 20 simulations for a single condition was chosen as the numerical result for this condition.
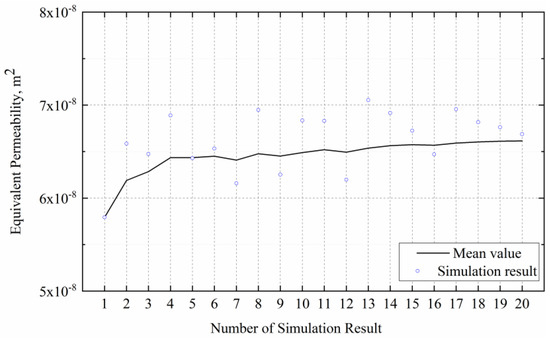
Figure 9.
Analysis of the stability number of random fracture model.
Fracture density increase positively correlates with rock mass equivalent permeability. Figure 10 displays the variation curve of fracture density on equivalent permeability, revealing that numerically simulated equivalent permeability increases linearly with fracture density. This indicates that, as fracture density increases, flow velocity and water pressure in individual fractures decrease, while the overall permeability of a single rock mass increases linearly.
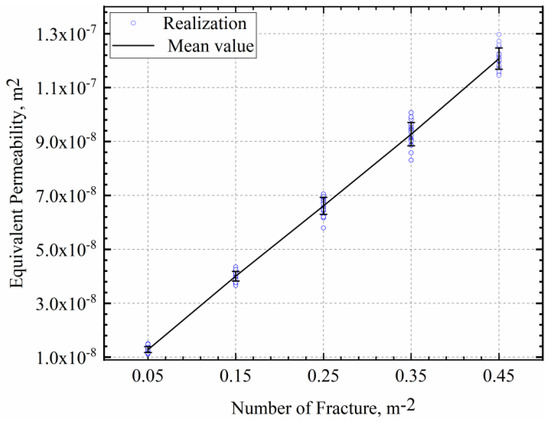
Figure 10.
Effect of fracture density on equivalent permeability.
Fracture length increase positively correlates with equivalent permeability. Figure 11 displays the change curve of fracture length on equivalent permeability, revealing that, as fracture length increases, equivalent permeability also rises, but the increase gradually reduces and stabilizes at a fracture length of 48 m. This phenomenon results from model limitations: as fracture length increases, most fractures penetrate the model directly, and parts sticking out cannot be shown. This connects water pressure and the outlet end, causing the final change curve to show permeability increasing with fracture length but at a decreasing rate.
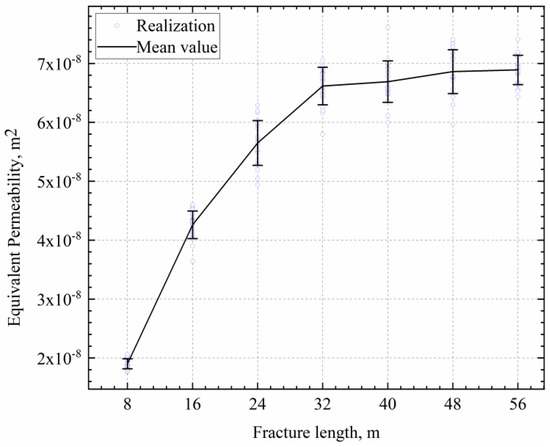
Figure 11.
Effect of fracture length on equivalent permeability.
The effects of increasing the length power law and equivalent permeability are not significant. Figure 9 displays the variation curve of the fracture length power law on equivalent permeability. As the power law index increases, the fracture length distribution shows the Pareto principle characteristic, meaning that shorter fractures account for an increasing proportion within the length interval as the power law index increases. However, Figure 12 reveals that the effect of the fracture length power law on equivalent permeability relative to fracture length is not significant and does not show a clear trend.
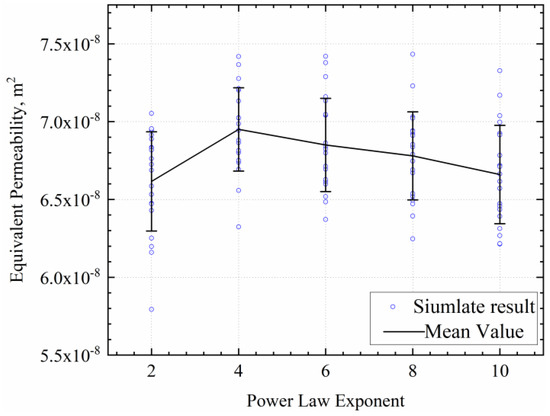
Figure 12.
Effect of random fracture length power law on equivalent permeability.
The effect of increasing fracture angle and dispersion coefficient on the equivalent permeability mostly tends to increase first and then decrease. Figure 13 and Figure 14 show the variation curves of angle and dispersion coefficient on permeability. It can be observed that the equivalent permeability increases with the fracture angle from 0 to 35°, decreases from 35 to 120°, and increases again from 120 to 180°. Due to symmetry, the trend of equivalent permeability from 180 to 360° is consistent with that from 0 to 180°, displaying a distribution similar to a sine function. However, the degree of change in the function is larger near the peak and smaller near the valley. Due to the impact of the deviation angle, the maximum equivalent permeability is not at 0° but at 30°, where most fractures can be in a horizontal state, which is conducive to fluid migration. At 120°, most fractures cannot reach the outlet end, resulting in the lowest equivalent permeability. As the dispersion coefficient increases, the equivalent permeability also first increases and then decreases; the reason was that, in the case of 45° set by the standard condition, the overall deviation angle of fissures was decreasing with the increase in dispersion coefficient; at the dispersion coefficient of 0.1, nearly 50% of fissures deviation angles were between 90° and 180°; at the dispersion coefficient of 13, all fissures deviation angles were within 60°; it could be observed that, as the dispersion coefficient increases, the number of near-horizontal fissures first increases and then decreases. Thus, the equivalent permeability first increases and then decreases.
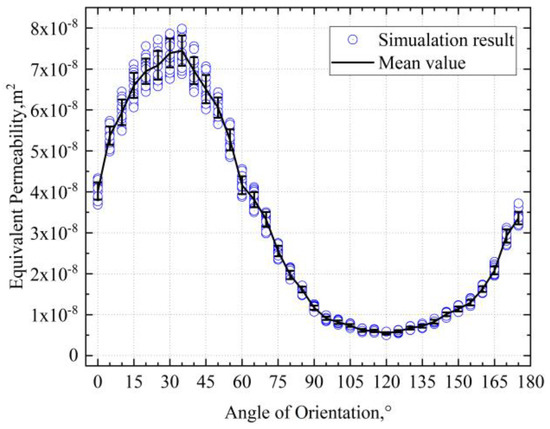
Figure 13.
Effect of fracture angle on equivalent permeability.
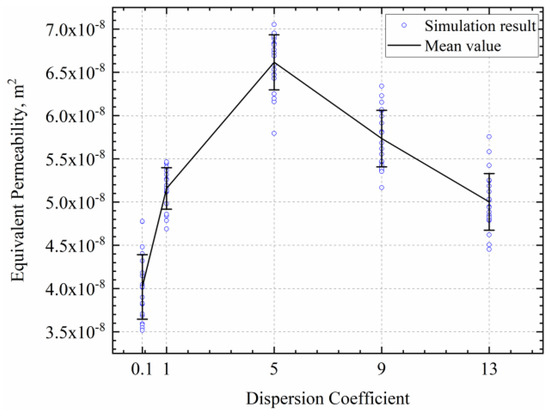
Figure 14.
Effect of dispersion coefficient on equivalent permeability.
The aperture has a significant effect on the equivalent permeability, while the power law of aperture does not. Figure 15 and Figure 16 show the variation curves of aperture and the power law of aperture on permeability, respectively. As the aperture increases, the equivalent permeability also increases significantly. However, the effect of increasing the aperture power law on the equivalent permeability is not significant and does not show a clear trend.
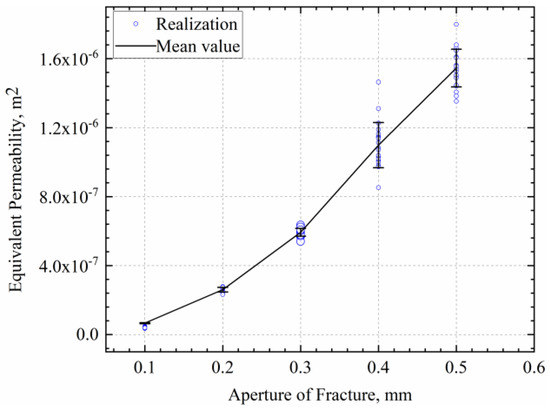
Figure 15.
Effect of fracture aperture on equivalent permeability.
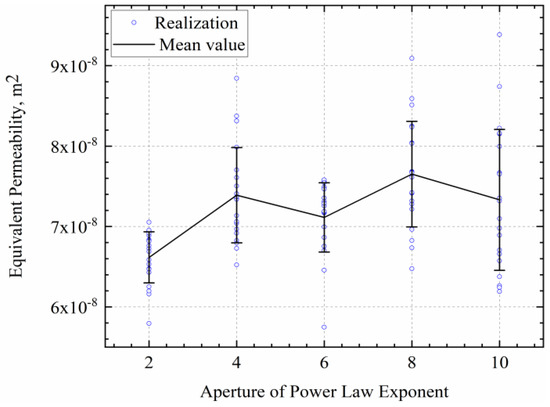
Figure 16.
Effect of aperture power law on equivalent permeability.
2.6. Response Surface Method for Predicting the Permeability Coefficient Based on Fracture Parameters
This research investigated the effects of seven fracture parameters on equivalent permeability. Five parameters—fracture density, fracture length, fracture angle, dispersion coefficient, and aperture—significantly impacted equivalent permeability, while the power law of length and aperture had no notable influence.
Figure 17 shows that effect of length and length power law interaction on permeability and the length power law significantly influences the distribution of fracture length, indirectly affecting permeability. When the length power law was 6, the impact of fracture length on permeability was most pronounced.
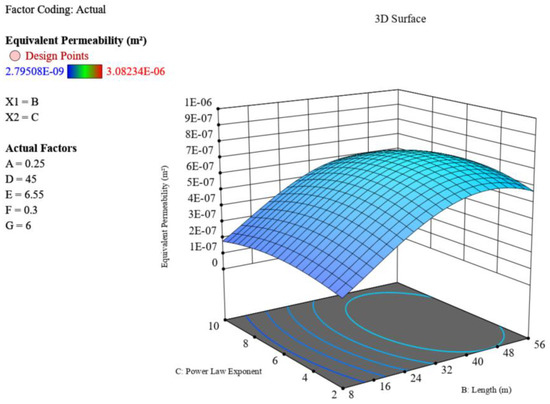
Figure 17.
Effect of length and length power law interaction on permeability.
Figure 18 presents the effect of angle and dispersion coefficient interaction on permeability. Fracture angle negatively correlates with permeability, and the deviation angle between fractures indirectly affects the distribution trend of fracture angles. As the dispersion coefficient increases, the deviation angle decreases, while it increases as the dispersion coefficient decreases. When the parameter angle was small, the dispersion coefficient positively correlated with equivalent permeability; when the parameter angle was large, it negatively correlated with equivalent permeability.
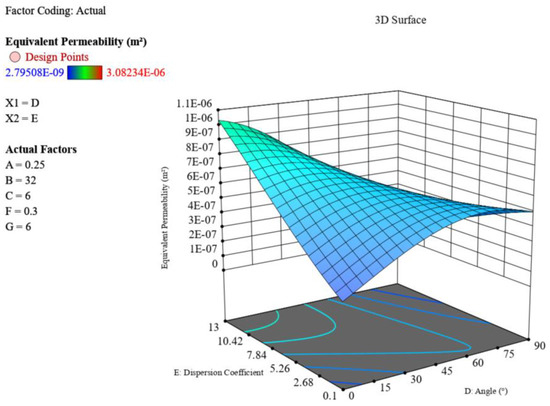
Figure 18.
Effect of angle and dispersion coefficient interaction on permeability.
Figure 19 reveals that aperture power law has an insignificant influence on permeability, while aperture significantly impacts permeability, consistent with previous findings.
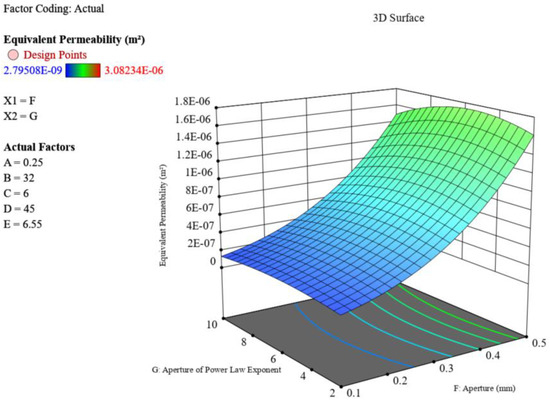
Figure 19.
Effect of aperture and aperture power law interactions on permeability.
Fracture density, length, and aperture showed a positive correlation with equivalent permeability. Fracture angle and dispersion coefficient initially increased permeability before causing a decline. Although variations in length power law and aperture power law were insignificant, they may still influence the numerical distribution of significant parameters governing equivalent permeability.
This section analyzed the interaction of relevant parameters, grouped into three: fracture length–length power law, fracture angle–dispersion coefficient, and fracture aperture–aperture power law.
The correlation between the equivalent permeability and the effective parameters of fracture density, length, length power law, angle, dispersion coefficient, fracture aperture, and aperture power law were investigated using response surface methodology. The model was chosen based on the highest order polynomial regression; in the model, the additional terms were significant and the model had no aliases. A quadratic model was chosen for the inflow rate based on the sum of squares of the serial model proposed by the software. Regression analysis was employed to ascertain the equivalent permeability as a function of the respective fracture density, length, length power law, angle, dispersion coefficient, aperture, and aperture power law.
Equation (1) represents the formula, where variables take their coded values, signifying the square root of equivalent permeability: (i) fracture density (A), (ii) length (B), (iii) power law exponent (C), (iv) angle (D), (v) dispersion coefficient (E), (vi) aperture (F), and (vii) aperture power law exponent (G). The final empirical equation for coded factors was as follows:
Sqrt (Equivalent Permeability) = 7.58579 × 10−4 + 2.79362 × 10−4 × A + 1.66242 × 10−4 × B − 5.64264 × 10−6 × C
−1.09312 × 10−4 × D + 4.60346 × 10−5 × E + 4.49094 × 10−4 × F − 1.36015 × 10−5 × G + 2.11919 × 10−4 × A × F +
1.34111 × 10−4 × B × F − 2.5511 × 10−4 × D × E − 7.31011 × 10−5 × A2 − 1.55212 × 10−4 × B2 − 5.71571 × 10−5 × C2 −
1.42748 × 10−4 × D2 + 7.40294 × 10−5 × F2 − 6.41053 × 10−5 × G2
−1.09312 × 10−4 × D + 4.60346 × 10−5 × E + 4.49094 × 10−4 × F − 1.36015 × 10−5 × G + 2.11919 × 10−4 × A × F +
1.34111 × 10−4 × B × F − 2.5511 × 10−4 × D × E − 7.31011 × 10−5 × A2 − 1.55212 × 10−4 × B2 − 5.71571 × 10−5 × C2 −
1.42748 × 10−4 × D2 + 7.40294 × 10−5 × F2 − 6.41053 × 10−5 × G2
A positive sign in front of a term indicated a synergistic effect on the inflow rate, while a negative sign indicated an antagonistic effect.
The coefficients of the parameters in Equation (1) could be considered to evaluate the effect of each parameter on the equivalent permeability. Seven coefficients were used in this equation, of which four parameters had significant effects, i.e., fracture density, length, angle, aperture, and dispersion coefficient, and the parameters with insignificant effects were length power law exponent and aperture power law exponent. It was difficult for insignificant parameters to independently have significant effects on the equivalent permeability, which was discussed in the previous section, so this was not reiterated here.
Equation (1) also illustrates the weighting factor of each parameter with respect to equivalent permeability. Based on this, aperture was the most significant weighting parameter as its variation substantially impacts equivalent permeability. With the variation in weighted fracture density being the second most important influencing parameter, the remaining angle and length are both significantly influencing parameters and had a considerable effect on permeability. By considering the individual effects and their interactions, the parameters provide clear conclusions about the weighting of the inflow rate, and these results were presented in the previous subsection.
According to Figure 20 and Figure 21, data distribution was mostly concentrated in the predicted range in the residual normal plots and the residual prediction comparison plots of the statistics of the simulation results; i.e., the numerical simulation results meet the statistical requirements.
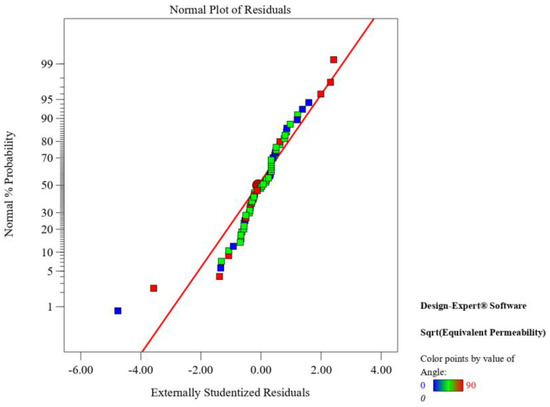
Figure 20.
Statistical residual plot.
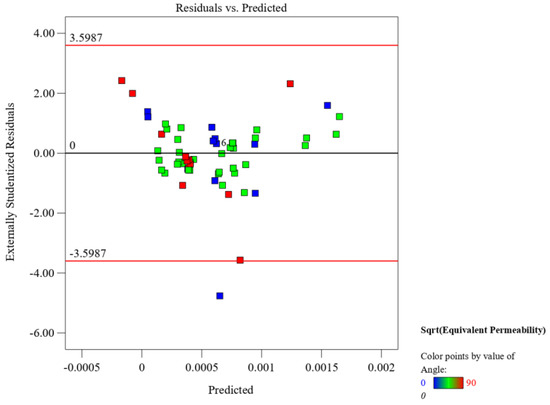
Figure 21.
Figure 21. Comparison of residual predictions.
The reliability of Equation (1) was assessed based on the correlation values. As shown in Table 2, the coefficient of determination (R2) of Equation (1) was 0.9569. Therefore, the total variation in the equivalent permeability was attributed to the experimental variables considered. The values of R2 close to the unit and low standard deviation contribute to the accurate prediction of the model, where the simulated values were close to the actual permeability values of the response.

Table 2.
Analysis of variance (ANOVA) for the reduced quadratic model of the unit inflow rate to the tunnel based on Equation (1).
An analysis of variance was used to demonstrate the adequacy of the model. The ANOVA results of the simplified quadratic model for the equivalent permeability derived from Equation (1) are provided in Table 2. The R2 was 0.9569, which means that 95.69% of the total variation in equivalent permeability was attributed to the experimental variables considered.
In this model, fracture density, length, length power law exponent, angle, dispersion coefficient, pore space, and pore space power law exponent were important model terms. The obtained statistical results show that the proposed model footprint of Equation (1) predicts equivalent permeability under the considered variables.
Utilizing the finite element method, ten sets of random fracture models were generated, and the equivalent permeability coefficients for each model were calculated. Subsequently, the response surface Equation (1), based on fracture parameters for predicting permeability coefficients, was employed to compute the equivalent permeability coefficients for these ten random models. As illustrated in Figure 22, the calculated outcomes for both methods are generally within an acceptable range.
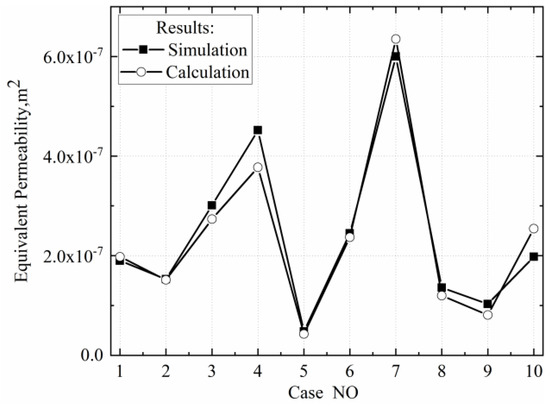
Figure 22.
Comparison of prediction equation and finite element calculation results.
3. Results and Discussion
In this study, the stochastic fracture models were established by the finite element method to describe the fluid flow behavior in natural fractures. The results illustrated the transfer relationship between the matrix and the fracture. This study provides insights for seepage simulation of fractured network and permeability prediction of fractured rock mass. Based on the analysis of numerical simulation results, the following conclusions could be drawn.
(1) This study investigated the impact of fractures on Darcy velocity and pore water pressure in the rock matrix. It also analyzed the influence of natural fracture parameters on the equivalent permeability of the rock mass. The effect of fractures on the Darcy’s velocity and pore water pressure in the rock matrix was investigated. The numerical characteristics of the common distribution forms of natural fissures were also analyzed. The velocity and pressure fields were combined to analyze the flow characteristics of the fluid in the rock matrix.
(2) Darcy’s velocity, pore water pressure in the matrix, and the equivalent permeability of the rock mass were analyzed. Increases in fracture density and length enhance rock permeability. Fractures parallel to the water pressure direction contribute more to flow and significantly alter permeability. In contrast, fractures that were perpendicular to the direction of water pressure had virtually no effect on permeability when they did not intersect with other fractures. When significant major fractures were connected together, permeability would surge, and displacement in the surrounding area decreased significantly. When the sensitivity interval of the aperture was within the range of 1 to 5 mm, permeability increased rapidly with the enlargement of the aperture, enhancing flow from the matrix to the fracture, while fluid flow within the matrix was substantially reduced.
(3) This study examined the influence of random fracture parameters on equivalent permeability. In random fractures, the effects of fracture density, length, and aperture on equivalent permeability are positively correlated, while the impact of fracture angle required analysis in conjunction with the magnitude of the dispersion coefficient. At smaller angles, a larger dispersion coefficient corresponds to greater equivalent permeability, and, at larger angles, a smaller dispersion coefficient results in increased equivalent permeability, and vice versa. The influence of fracture length power law and aperture power law on equivalent permeability was not significant.
(4) Two theoretical numerical equations were proposed for calculating the permeability of discrete fracture. The first equation (Equation (1)) was derived by analyzing the variations in each parameter. Consequently, Equation (1) was conducive to application and evaluation while maintaining precision.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/pr11071962/s1, Figure S1: Darcy velocity contour and Pore water pressure contour; Figure S2: Effect of density Darcy’s velocity and pore water pressure; Figure S3: Effect of fracture direction on flow rate and water pressure; Figure S4: Effect of Aperture on flow rate and water pressure; Figure S5: Effect of fracture length on flow rate and water pressure; Figure S6: Effect of random fracture density on the flow rate and water pressure; Figure S7: Effect of random fracture length on flow rate and water pressure; Figure S8: Effect of discrete fracture angle on flow rate and water pressure; Figure S9: Effect of discrete fracture dispersion coefficient on flow rate and water pressure; Figure S10: Effect of random fracture angle on the flow rate; Figure S11: Effect of length and length power law interaction on permeability; Figure S12: Effect of angle and dispersion coefficient interaction on permeability; Figure S13: Effect of aperture and aperture power law interactions on permeability; Figure S14: Effect of different power law indices on cumulative probability; Figure S15: Effect of different Fisher constants K on the deviation angle θ of the fracture azimuth; Table S1: Random fracture model working condition parameter design.
Author Contributions
Conceptualization, B.Z. and L.W.; methodology, B.Z. and L.W.; software, B.Z. and L.W.; validation, B.Z. and L.W.; formal analysis, B.Z.; investigation, B.Z. and L.W.; resources, B.Z.; data curation, B.Z. and J.L.; writing—original draft preparation, B.Z.; writing—review and editing, B.Z. and J.L.; visualization, B.Z.; supervision, L.W. and J.L.; project administration, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
Bochao Zhang would like to express his sincere appreciation for Inner Mongolia Beifang Shidai Design & Research Institute Co., Ltd.’s technology support and College of Civil Engineering, Tongji University’s scholarship program.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gurocak, Z.; Alemdag, S. Assessment of permeability and injection depth at the Atasu dam site (Turkey) based on experimental and numerical analyses. Bull. Eng. Geol. Environ. 2012, 71, 221–229. [Google Scholar] [CrossRef]
- Alemdag, S. Assessment of bearing capacity and permeability of foundation rocks at the Gumustas waste dam site, (NE Turkey) using empirical and numerical analysis. Arab. J. Geosci. 2015, 8, 1099–1110. [Google Scholar] [CrossRef]
- Li, L.P.; Zhou, Z.Q.; Li, S.C.; Xue, Y.G.; Xu, Z.H.; Shi, S.S. An attribute synthetic evaluation system for risk assessment of floor water inrush in coal mines. Mine Water Environ. 2015, 34, 288–294. [Google Scholar] [CrossRef]
- Van Golf-Racht, T.D. Fundamentals of Fractured Reservoir Engineering; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Cai, J.; Hu, X.; Standnes, D.C.; You, L. An analytical model for spontaneous imbibition in fractal porous media including gravity. Colloids Surf. Physicochem. Eng. Asp. 2012, 414, 228–233. [Google Scholar] [CrossRef]
- Li, X.; Du, C.; Wang, X.; Zhang, J. Quantitative determination of high-order crack fabric in rock plane. Rock Mech. Rock Eng. 2023. [Google Scholar] [CrossRef]
- MacMinn, C.W.; Szulczewski, M.L.; Juanes, R. CO2 migration in saline aquifers. Part 1. Capillary trapping under slope and groundwater flow. J. Fluid Mech. 2010, 662, 329–351. [Google Scholar] [CrossRef]
- Ren, C.; Yu, J.; Liu, S.; Yao, W.; Zhu, Y.; Liu, X. A plastic strain-induced damage model of porous rock suitable for different stress paths. Rock Mech. Rock Eng. 2022, 55, 1887–1906. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y.; Huang, N. Review: Mathematical expressions for estimating equivalent permeability of rock fracture networks. Hydrogeol. J. 2016, 24, 1623–1649. [Google Scholar] [CrossRef]
- Wei, W.; Xia, Y. Geometrical, fractal and hydraulic properties of fractured reservoirs: A mini-review. Adv. Geo-Energy Res. 2017, 1, 31–38. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Hydraulic properties of fractured rock masses with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2007, 44, 704–719. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Stress effects on permeability in a fractured rock mass with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2008, 45, 1320–1334. [Google Scholar] [CrossRef]
- Min, K.B.; Jing, L. Numerical determination of the equivalent elastic compliance tensor for fractured rock masses using the distinct element method. Int. J. Rock Mech. Min. Sci. 2003, 40, 795–816. [Google Scholar] [CrossRef]
- Min, K.B.; Rutqvist, J.; Tsang, C.F.; Jing, L. Stress-dependent permeability of fractured rock masses: A numerical study. Int. J. Rock Mech. Min. Sci. 2004, 41, 1191–1210. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, J.; Feng, Q.; Liu, W.; He, P.; Fu, S. Elastoplastic analytical solution for the stress and deformation of the surrounding rock in cold region tunnels considering the influence of the temperature field. Int. J. Geomech. 2022, 22, 4022118. [Google Scholar] [CrossRef]
- Dai, Z.; Ma, Z.; Zhang, X.; Chen, J.; Ershadnia, R.; Luan, X.; Soltanian, M.R. An integrated experimental design framework for optimizing solute transport monitoring locations in heterogeneous sedimentary media. J. Hydrol. 2022, 614, 128541. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Davy, P.; Bour, O. Hydraulic properties of two dimensional random fracture networks following a power law length distribution: 1. Effective connectivity. Water Resour. Res. 2001, 37, 2065–2078. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Davy, P.; Bour, O. Hydraulic properties of two dimensional random fracture networks following a power law length distribution: 2. Permeability of networks based on lognormal distribution of apertures. Water Resour. Res. 2001, 37, 2079–2095. [Google Scholar] [CrossRef]
- Leung, C.T.O.; Zimmerman, R.W. Estimating the hydraulic conductivity of two-dimensional fracture networks using network geometric properties. Transp. Porous Media 2012, 93, 777–797. [Google Scholar] [CrossRef]
- Selroos, J.O.; Walker, D.D.; Ström, A.; Gylling, B.; Follin, S. Comparison of alternative modelling approaches for groundwater flow in fractured Rock. J. Hydrol. 2002, 257, 174–188. [Google Scholar] [CrossRef]
- Figueiredo, B.; Tsang, C.F.; Niemi, A.; Lindgren, G. Review: The state of-art of sparse channel models and their applicability to performance assessment of radioactive waste repositories in fractured crystalline formations. Hydrogeol. J. 2016. [CrossRef]
- Tsang, Y.W.; Tsang, C.F.; Hale, F.V.; Dverstorp, B. Tracer transport in a stochastic continuum model of fractured media. Water Resour. Res. 1996, 32, 3077–3092. [Google Scholar] [CrossRef]
- Hartley, L.; Hunter, F.; Jackson, P.; McCarthy, R. Regional hydrogeological simulations using connect flow. In Preliminary Site Description–Laxemar Subarea, version 1.2; Report R-06-23; Swedish Nuclear Fuel and Waste Management Co.: Stockholm, Sweden, 2006. [Google Scholar]
- Long, J.C.S.; Remer, J.S.; Wilson, C.R.; Witherspoon, P.A. Porous media equivalents for networks of discontinuous fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef]
- Tsang, C.F. Was current hydrogeologic research addressing long-term predictions? Ground Water 2005, 43, 296–300. [Google Scholar] [CrossRef]
- Hartley, L.; Roberts, D. Summary of Discrete Fracture Network Modelling as Applied to Hydrogeology of the Forsmark and Laxemar Sites; Report R-12-04; Swedish Nuclear Fuel and Waste Management Co.: Stockholm, Sweden, 2012. [Google Scholar]
- Neretnieks, I. Channeling effects in flow and transport in fractured rocks-Some recent observations and models. In Proceedings of GEOVAL-87; International Symposium: Stockholm, Sweden, 1987; pp. 315–335. [Google Scholar]
- Dershowitz, W.S.; Fidelibus, C. Derivation of equivalent pipe network analogues for three-dimensional discrete fracture networks by the boundary element method. Water Resour. Res. 1999, 35, 2685–2691. [Google Scholar] [CrossRef]
- Black, J.H.; Barker, J.A.; Woodman, N.D. An investigation of ‘sparse channel networks’. In Characteristic Behaviours and Their Causes; Report R-07-35; Swedish Nuclear Fuel and Waste Management Co.: Stockholm, Sweden, 2007. [Google Scholar]
- Jafari, A.; Babadagli, T. Relationship between percolation-fractal properties and permeability of 2-D fracture networks. Int. J. Rock Mech. Min. Sci. 2013, 60, 353–362. [Google Scholar] [CrossRef]
- Jafari, A.; Babadagli, T. Estimation of equivalent fracture network permeability using fractal and statistical network properties. J. Pet. Sci. Eng. 2012, 92, 110–123. [Google Scholar] [CrossRef]
- Long, G.; Liu, Y.; Xu, W.; Zhou, P.; Zhou, J.; Xu, G.; Xiao, B. Analysis of crack problems in multilayered elastic medium by a consecutive stiffness method. Mathematics 2022, 10, 4403. [Google Scholar] [CrossRef]
- Liang, M.; Fu, C.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Transf. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Manafi, M.; Kalantariasl, A.; Ghaedi, M. A COMSOL Multiphysics study on block-to-block interactions in naturally fractured reservoirs. J. Pet. Sci. Eng. 2022, 208, 109540. [Google Scholar] [CrossRef]
- Wanniarachchi, W.A.M.; Ranjith, P.G.; Perera, M.S.A.; Rathnaweera, T.D.; Zhang, C.; Zhang, D.C. An integrated approach to simulate fracture permeability and flow characteristics using regenerated rock fracture from 3-D scanning: A numerical study. J. Nat. Gas Sci. Eng. 2018, 53, 249–262. [Google Scholar] [CrossRef]
- Romano-Perez, C.A.; Diaz-Viera, M.A. A comparison of discrete fracture models for single phase flow in porous media by COMSOL Multiphysics® Software. In Proceedings of the 2015 COMSOL Conference in Boston, Boston, MA, USA, 7–9 October 2012; pp. 7–9. [Google Scholar]
- Lepillier, B.; Daniilidis, A.; Gholizadeh, N.D.; Bruna, P.O.; Kummerow, J.; Bruhn, D. A fracture flow permeability and stress dependency simulation applied to multi-reservoirs, multi-production scenarios analysis. Geotherm. Energy 2019, 7, 24. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, G.; Wang, Y.; Zhang, X.; Li, K.; Guo, W.; Du, F. A numerical investigation of hydraulic fracturing on coal seam permeability based on PFC-COMSOL coupling method. Int. J. Coal Sci. Technol. 2022, 9, 10. [Google Scholar] [CrossRef]
- Priest, S.D. Discontinuity Analysis for Rock Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Kim, J.G.; Deo, M.D. Finite element, discrete-fracture model for multiphase flow in porous media. AIChE J. 2000, 46, 1120–1130. [Google Scholar] [CrossRef]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Warren, J.E. The behavior of naturally fractured reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Snow, D.T. Anisotropic permeability of fractured media. Water Resour. Res. 1969, 5, 1273–1289. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).