Fluctuation in the Water Level of the Air Hole of the Gate Shaft in the Pumped Storage Power Station
Abstract
1. Introduction
- Established a platform for a calculation of a simulation of a power station.
- The accuracy of the calculation is proved by comparing the calculated and field test.
- Analyzed the changes in the water level of the gate shaft and air hole based on different gate shaft areas.
- The influence of the gate shaft location on the changes in the water level of the gate shaft and air hole was determined.
2. Literature Review
3. Mathematical Model
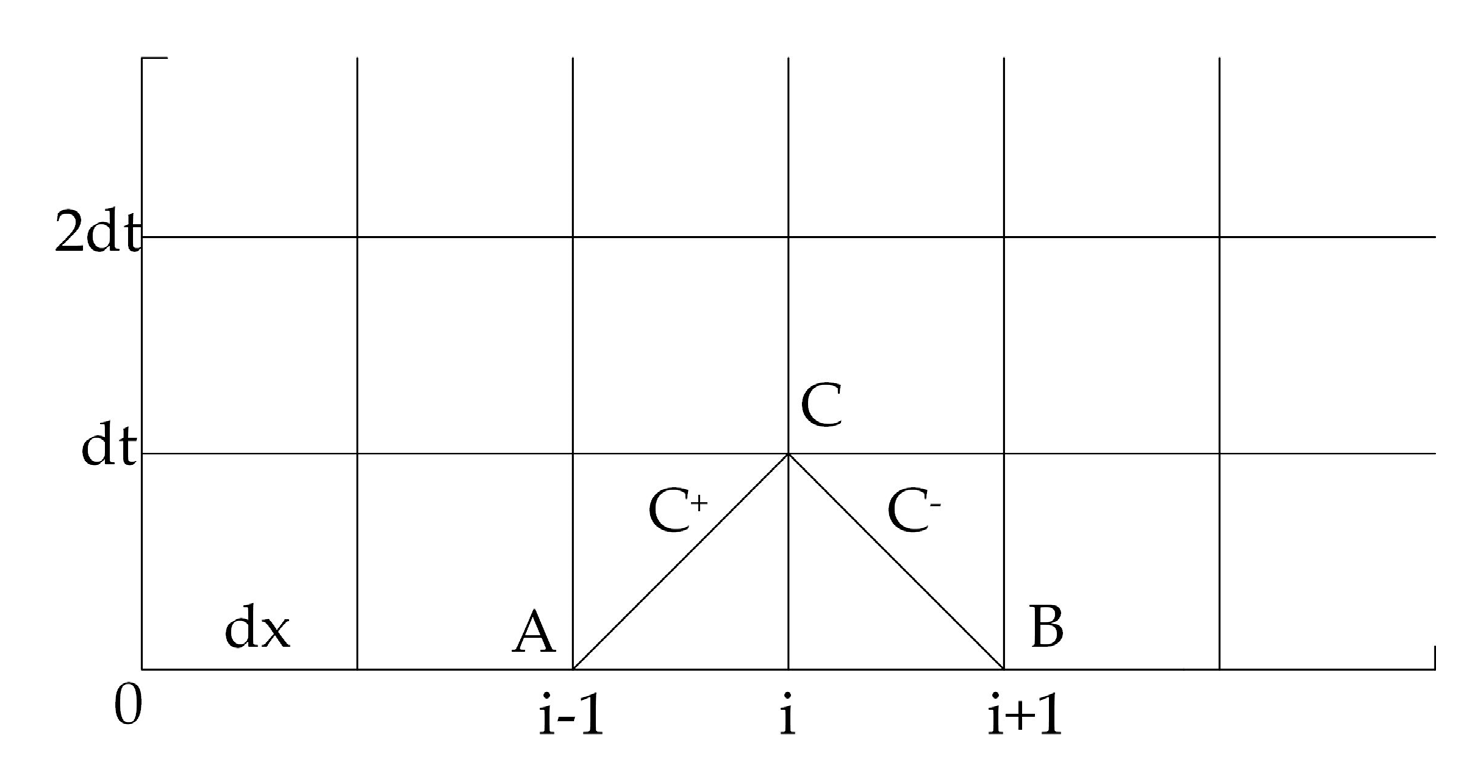
3.1. Pipeline
3.2. Gate Shaft
3.3. Upper and Lower Reservoirs
3.4. Runner
3.5. Governor Model
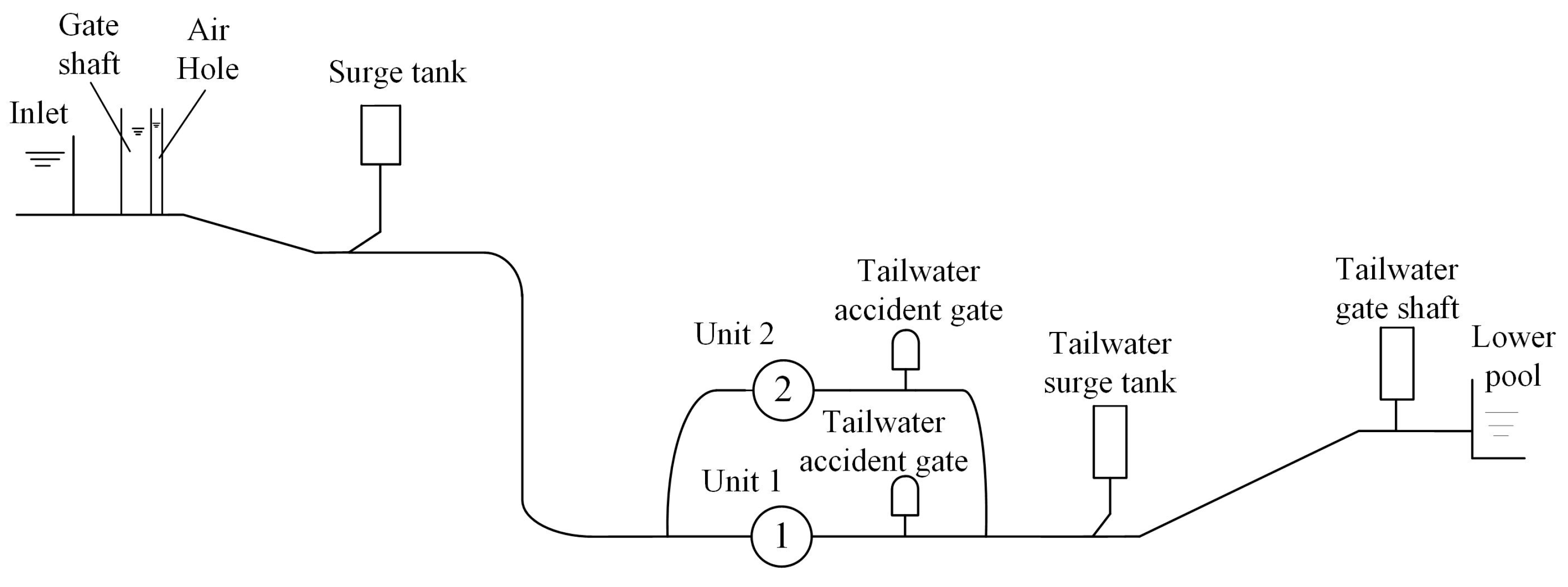
4. Experimental Results and Discussion
4.1. Comparison of Calculated and Field Test Data
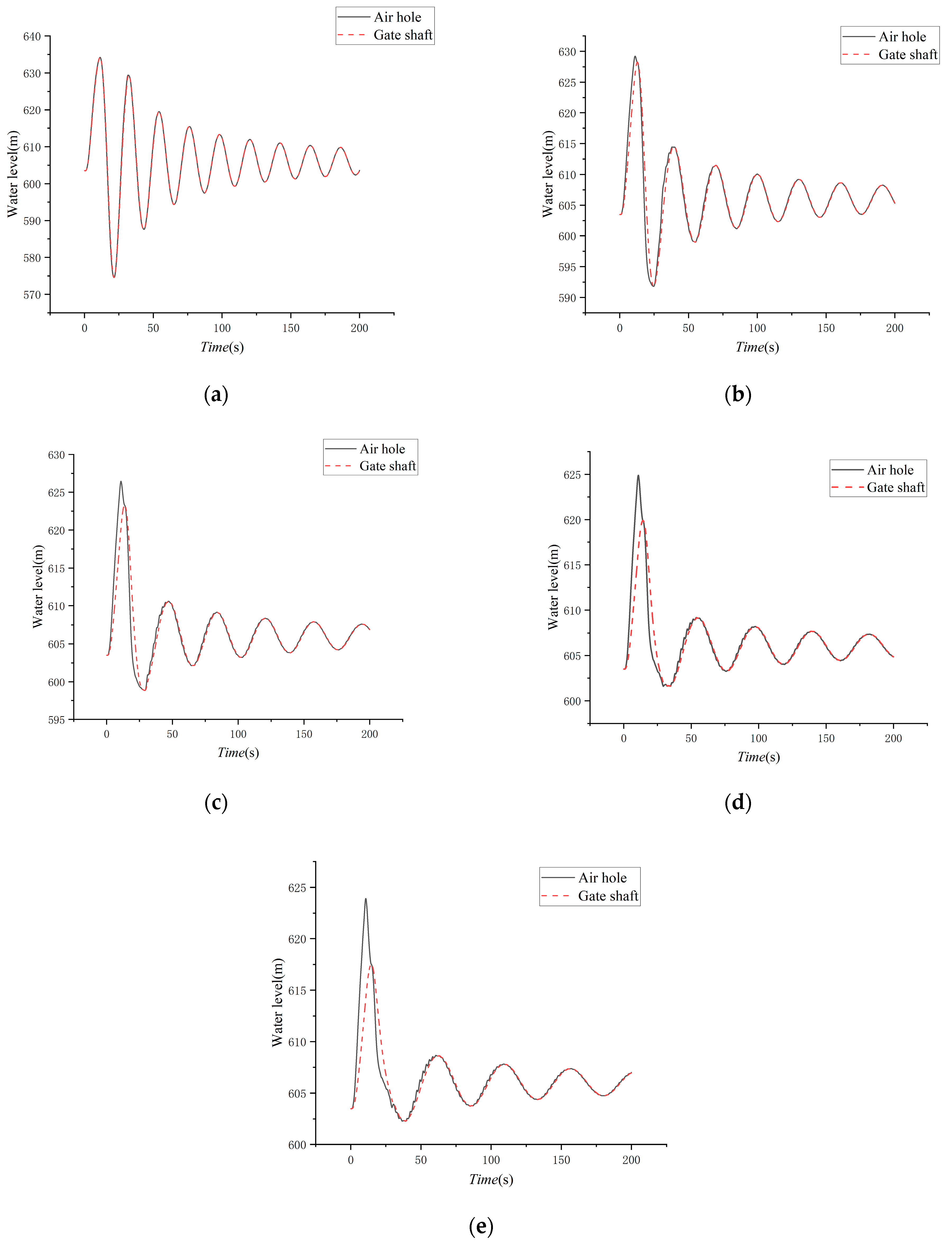
4.2. With Surge Tank
4.3. Without Surge Tank
4.4. Influence of Distance from Gate Shaft to Inlet
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, H.; Chen, C.; Hong, Y.; Li, W. Environmental Benefit Analysis of Pumped Storage Power Station. In Proceedings of the 2017 2nd International Conference on Civil, Transportation and Environmental Engineering (ICCTE 2017), Shenzhen, China, 10–11 May 2017. [Google Scholar]
- Luo, Y.; Sheng, X.; Qiao, Z. Development Situation and Relevant Inspiration of Pumped Storage Power Station in the world. IOP Conf. Ser. Earth Environ. Sci. 2020, 619, 012017. [Google Scholar] [CrossRef]
- Wen, B.; Huang, D.; Yu, L. Functional localization analysis on pumped storage station under the new situation of energy transformation. IOP Conf. Ser. Earth Environ. Sci. 2021, 781, 042056. [Google Scholar] [CrossRef]
- Gabl, R.; Righetti, M. Design criteria for a type of asymmetric orifice in a surge tank using CFD. Eng. Appl. Comput. Fluid Mech. 2018, 12, 397–410. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, J.; Zhou, L. Hydraulic Transients in the Long Diversion-Type Hydropower Station with a Complex Differential Surge Tank. Sci. World J. 2014, 2014, 241868. [Google Scholar] [CrossRef] [PubMed]
- Richter, W.; Zenz, G.; Vereide, K. The Semi-Air-Cushion Surge Tank: Design Principles and Case Study. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012102. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Cai, F.L.; Hua, Y.L.; Cheng, H. Study on the Influence of Tailrace Tunnel Outlet Bottom Slope on Water Level Fluctuation in the Tailrace Surge Tank. Adv. Mater. Res. 2014, 1065–1069, 644–649. [Google Scholar] [CrossRef]
- Li, X.; Brekke, H. Large amplitude water level oscillations in throttled surge tanks. J. Hydraul. Res. 1989, 27, 537–551. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.; Yu, X.; Chen, S.; Shi, L.; Bergant, A.; Zhou, J.F. Study on impedance size optimization of a one-way surge tank in a long-distance water supply system. Water Supply 2020, 21, 868–877. [Google Scholar] [CrossRef]
- Zhu, D.; Guo, W. Setting condition of surge tank based on stability of hydro-turbine governing system considering nonlinear penstock head loss. Int. J. Electr. Power Energy Syst. 2019, 113, 372–382. [Google Scholar] [CrossRef]
- Guo, W.; Zhu, D. A Review of the Transient Process and Control for a Hydropower Station with a Super Long Headrace Tunnel. Energies 2018, 11, 2994. [Google Scholar] [CrossRef]
- Guo, W.; Wang, B.; Yang, J.; Xue, Y. Optimal control of water level oscillations in surge tank of hydropower station with long headrace tunnel under combined operating conditions. Appl. Math. Model. 2017, 47, 260–275. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Cheng, Y.G.; Liu, K.; Wang, Q.; Yang, F. Optimization of surge tank structures in hydropower station based on VOF method. IOP Conf. Ser. Earth Environ. Sci. 2021, 627, 012007. [Google Scholar] [CrossRef]
- Fathi-Moghadam, M.; Haghighipour, S.; Samani, H.M.V. Design-Variable Optimization of Hydropower Tunnels and Surge Tanks Using a Genetic Algorithm. J. Water Resour. Plan. Manag. 2013, 139, 200–208. [Google Scholar] [CrossRef]
- Vereide, K.; Svingen, B.; Nielsen, T.K.; Lia, L. The Effect of Surge Tank Throttling on Governor Stability, Power Control, and Hydraulic Transients in Hydropower Plants. IEEE Trans. Energy Convers. 2017, 32, 91–98. [Google Scholar] [CrossRef]
- Guo, W.; Liu, Y.; Qu, F.; Xu, X. A Review of Critical Stable Sectional Areas for the Surge Tanks of Hydropower Stations. Energies 2020, 13, 6466. [Google Scholar] [CrossRef]
- France, P.W. Surge tank water level variations following rapid valve opening. Adv. Water Resour. 1980, 3, 41–43. [Google Scholar] [CrossRef]
- Yu, X.; Yang, X.; Liu, Z.; Zhang, J. Mechanism and quantified criteria of stability characteristics of hydropower plants with surge tanks during regulation. Int. J. Electr. Power Energy Syst. 2020, 122, 106160. [Google Scholar] [CrossRef]
- Rezghi, A.; Riasi, A.; Tazraei, P. Multi-objective optimization of hydraulic transient condition in a pump-turbine hydropower considering the wicket-gates closing law and the surge tank position. Renew. Energy 2019, 148, 478–491. [Google Scholar] [CrossRef]
- Dhakal, R.; Zhou, J.; Palikhe, S.; Bhattarai, K.P. Hydraulic Optimization of Double Chamber Surge Tank Using NSGA-II. Water 2020, 12, 455. [Google Scholar] [CrossRef]
- Yang, X.L.; Kung, C.S. Nonlinear Stability of Differential Surge Chambers. J. Hydraul. Eng. 1992, 118, 1526–1539. [Google Scholar] [CrossRef]
- Li, X.; Hou, J.; Wu, X.; Li, X. Parameter Optimization on Asymmetry Orifice in a Differential Surge Chamber. Energy Procedia 2012, 16, 730–736. [Google Scholar] [CrossRef]
- Ahmed, T.M. Variation of Pressure Coefficient Along Bottom of Dam Vertical Lift Gates. J. Inst. Eng. Ser. A 2020, 101, 561–570. [Google Scholar] [CrossRef]
- Taher, T.M.; Anwar, A.O. Effects of Gate Lip Orientation on Bottom Pressure Coefficient of Dam Tunnel Gate. Arab. J. Sci. Eng. 2016, 41, 4927–4936. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]






| Project | Number |
|---|---|
| Unit Speed (r/min) | 375 |
| Rated Output of Unit (MW) | 306 |
| Rotational Inertia (t ∗ m2) | 8000 |
| Rated Water Head (m) | 375 |
| Maximum Opening of Guiding Blade | 28 |
| Total Pipe Length (m) | 3324.225 |
| Water Diversion Pipe Length (m) | 1187.385 |
| Gate Shaft Bottom Elevation (m) | 502.2 |
| Gate Shaft Water Level Design Value (m) | 614 |
| Gate Shaft Inflow Coefficient | 1.09 × 10−3 |
| Gate Shaft Outflow Coefficient | 6.13 × 10−4 |
| Air Hole Inflow Coefficient | 8.75 × 10−2 |
| Air Hole Outflow Coefficient | 4.92 × 10−2 |
| Gate Shaft Maximum Water Level (m) | Gate Shaft Minimum Water Level (m) | Tailwater Surge Tank Maximum Water Level (m) | Tailwater Surge Tank Minimum Water Level (m) | ||
|---|---|---|---|---|---|
| Field test Value | Value | 593.126 | 582.901 | 205.438 | 193.244 |
| Time | 11.900 | 31.500 | 104.200 | 35.100 | |
| Calculated Value | Value | 593.473 | 582.368 | 205.298 | 193.269 |
| Time | 20.015 | 29.558 | 105.315 | 35.021 | |
| Project | Number |
|---|---|
| Gate Shaft Bottom Elevation (m) | 524 |
| Gate Shaft Water Level Design Value (m) | 580 |
| Gate Shaft Inflow Coefficient | 3.75 × 10−4 |
| Gate Shaft Outflow Coefficient | 2.11 × 10−4 |
| Air Hole Inflow Coefficient | 3.62 × 10−3 |
| Air Hole Outflow Coefficient | 2.04 × 10−3 |
| Enlarge the Upper Chamber | Air Hole/Gate Shaft Area (m2) | 6.25/52.47–80 | 6.25/52.47–100 | 6.25/52.47–150 |
| Air Hole/Gate Shaft Water Level (m) | 578.104/578.104 | 577.700/577.696 | 577.190/577.101 | |
| Enlarge the Entire Gate Shaft | Air Hole/Gate Shaft Area (m2) | 6.25/80 | 6.25/100 | 6.25/150 |
| Air Hole/Gate Shaft Water Level (m) | 578.104/578.104 | 577.700/577.696 | 577.190/577.101 |
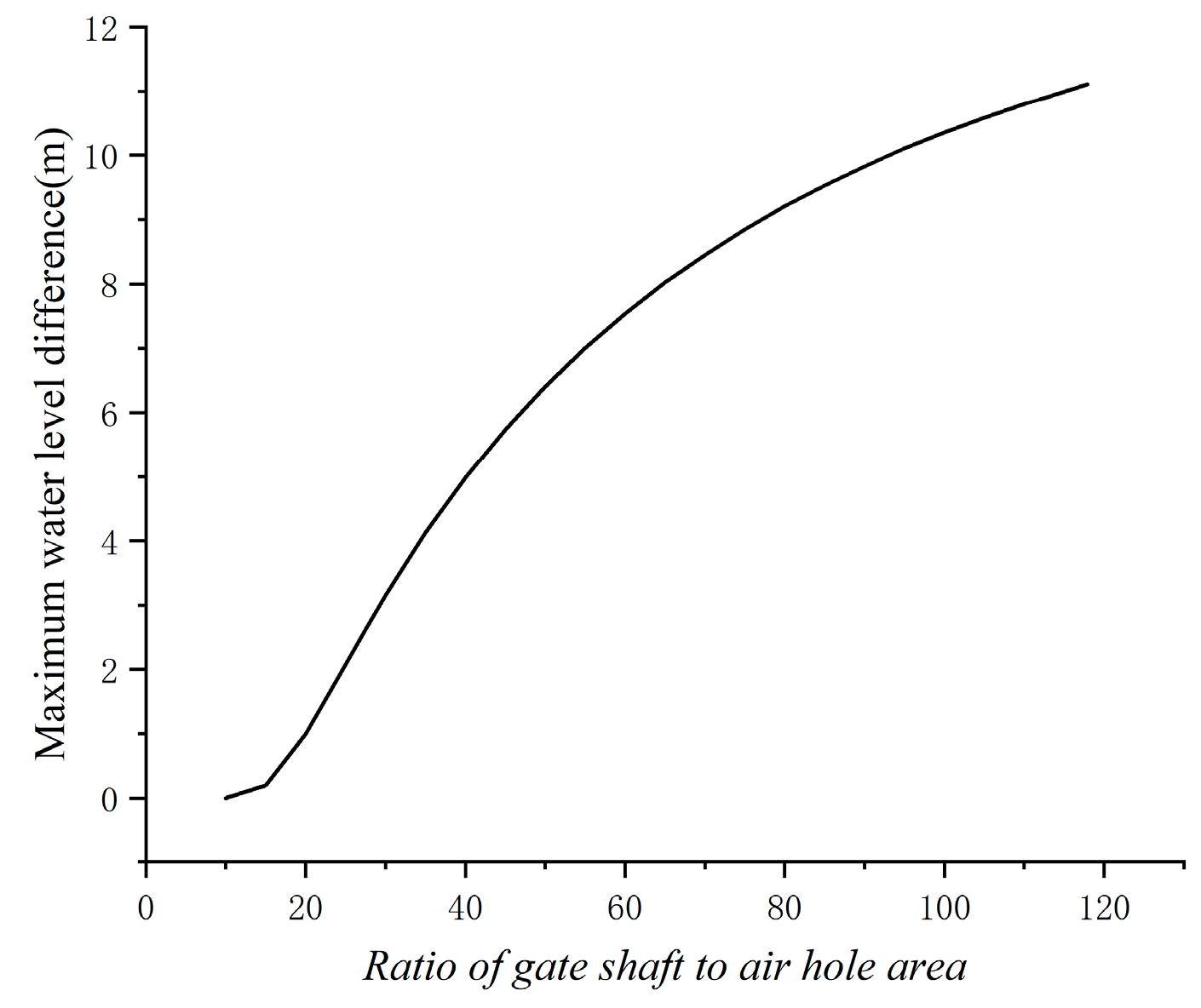
| Air Hole Area (m2) | Gate Shaft Area (m2) | Gate Shaft Upper Chamber Area (m2) | Air Hole Maximum Water Level (m) | Gate Shaft Maximum Water Level (m) | Maximum Water Level Difference (m) |
|---|---|---|---|---|---|
| 1.27 | 6.40 | 6.40 | 640.811 | 640.811 | 0.000 |
| 1.27 | 12.70 | 12.70 | 634.202 | 634.202 | 0.000 |
| 1.27 | 25.40 | 25.40 | 629.201 | 628.201 | 1.000 |
| 1.27 | 35.00 | 38.10 | 626.411 | 623.310 | 3.101 |
| 1.27 | 35.00 | 50.80 | 624.902 | 619.901 | 5.001 |
| 1.27 | 35.00 | 63.50 | 623.912 | 617.510 | 6.402 |
| 1.27 | 35.00 | 127.00 | 621.900 | 611.601 | 10.299 |
| 1.27 | 35.00 | 149.80 | 621.600 | 610.500 | 11.100 |
| Gate Shaft Area (m2) | 12.7 | 25.4 | 38.1 | 50.8 | 63.5 |
| Inflow Volume (m3) | 389.836 | 628.116 | 754.115 | 833.663 | 889.610 |
| Rising Water Level (m) | 30.696 | 24.729 | 19.793 | 16.411 | 14.010 |
| Gate Shaft Area (m2) | 6.40 | 12.70 | 25.40 | 38.10 | 50.80 | 63.50 | 127.00 | 149.80 |
| Maximum Water Level of Air Hole (m) | 640.811 | 634.202 | 629.201 | 626.411 | 624.902 | 623.912 | 621.900 | 621.600 |
| Maximum Water Level of the Gate Shaft (m) | 640.811 | 634.202 | 628.201 | 623.310 | 619.901 | 617.510 | 611.601 | 610.500 |
| Water Level Difference (m) | 0.000 | 0.000 | 1.000 | 3.101 | 5.001 | 6.402 | 10.299 | 11.100 |
| Plan | Raw Data | Closer 50 m | Closer 100 m | Further 50 m | Further 100 m |
|---|---|---|---|---|---|
| Air Hole Maximum Water Level (m) | 621.623 | 620.083 | 618.290 | 622.932 | 624.095 |
| Gate Shaft Maximum Water Level (m) | 610.514 | 610.244 | 609.890 | 610.721 | 610.880 |
| Maximum Water Level Difference (m) | 11.109 | 9.839 | 8.400 | 12.211 | 13.215 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Li, S.; Fan, H.; Wang, L. Fluctuation in the Water Level of the Air Hole of the Gate Shaft in the Pumped Storage Power Station. Processes 2023, 11, 905. https://doi.org/10.3390/pr11030905
Zhao W, Li S, Fan H, Wang L. Fluctuation in the Water Level of the Air Hole of the Gate Shaft in the Pumped Storage Power Station. Processes. 2023; 11(3):905. https://doi.org/10.3390/pr11030905
Chicago/Turabian StyleZhao, Weiguo, Shuo Li, Honggang Fan, and Liying Wang. 2023. "Fluctuation in the Water Level of the Air Hole of the Gate Shaft in the Pumped Storage Power Station" Processes 11, no. 3: 905. https://doi.org/10.3390/pr11030905
APA StyleZhao, W., Li, S., Fan, H., & Wang, L. (2023). Fluctuation in the Water Level of the Air Hole of the Gate Shaft in the Pumped Storage Power Station. Processes, 11(3), 905. https://doi.org/10.3390/pr11030905






