Prediction of the Ultimate Tensile Strength (UTS) of Asymmetric Friction Stir Welding Using Ensemble Machine Learning Methods
Abstract
1. Introduction
- (1)
- The lack of research on the overall number and types of parameters in the previous literature.
- (2)
- Ensemble machine learning has not yet been utilized to predict the UTS of FSW on the basis of a predefined set of parameters.
- (3)
- The heterogeneous ensemble machine learning architecture has not yet been applied to predict the UTS of FSW.
- It is the first time that EML has been used to predict the UTS from eleven controlled parameters.
- We present an effective decision fusion strategy of integrating the unweighted average model and the well-known metaheuristics model (differential evolution algorithm (DE)).
- We develop new datasets for heterogeneous FSW (AA5083 and AA6061).
2. Related Literature
3. Materials and Methods
3.1. Dataset Preparation
3.1.1. Dataset 2PI-V1
3.1.2. Dataset 11PI-V1
3.1.3. Experiment 11PI-V2 Dataset
3.2. Machine Learning Methods
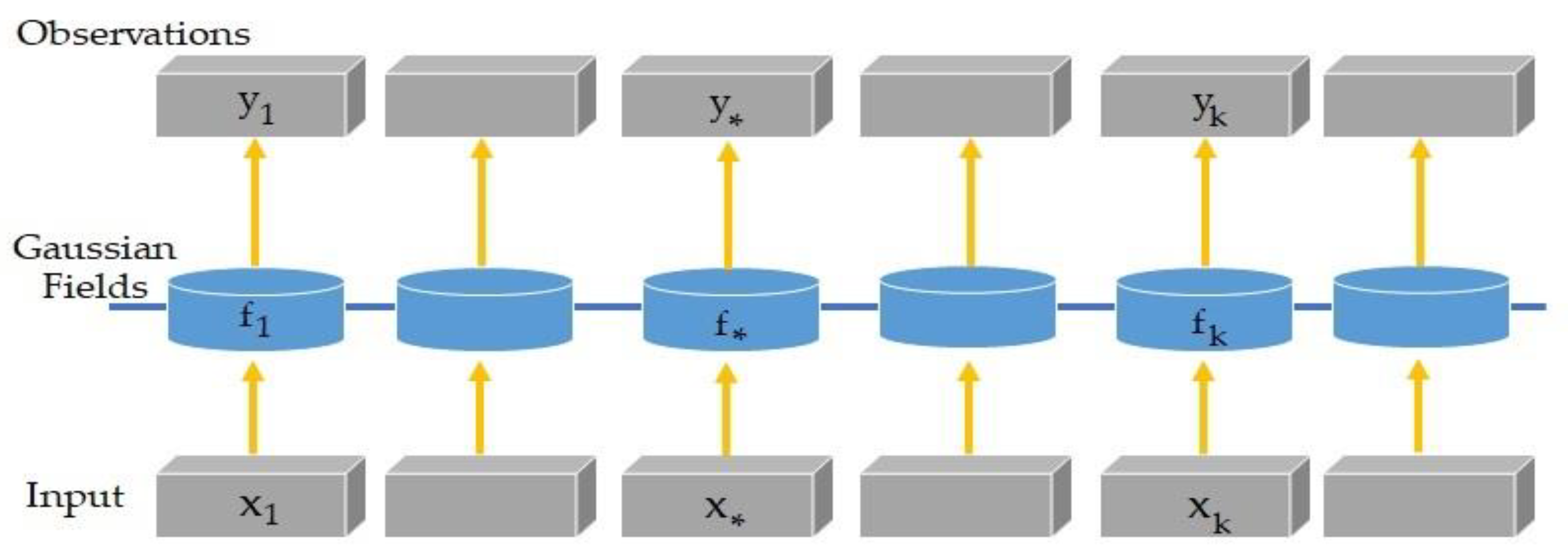
3.2.1. Gaussian Process Regression
3.2.2. Support Vector Machines
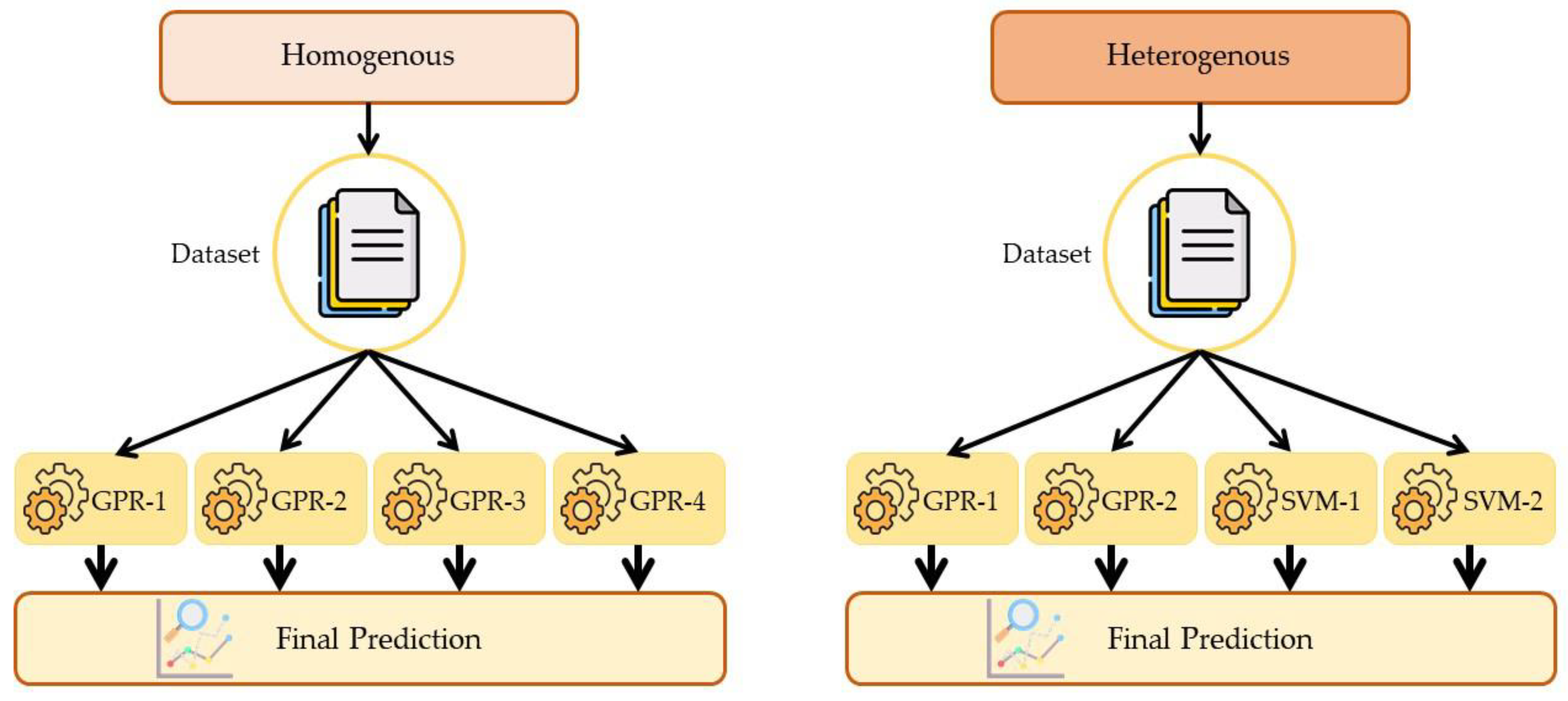
3.2.3. Ensemble Strategy
3.2.4. Decision Fusion Strategy
Unweight Average Ensemble (UAE)
Weighted Ensemble Optimization Using Differential Evolution (WEDE)
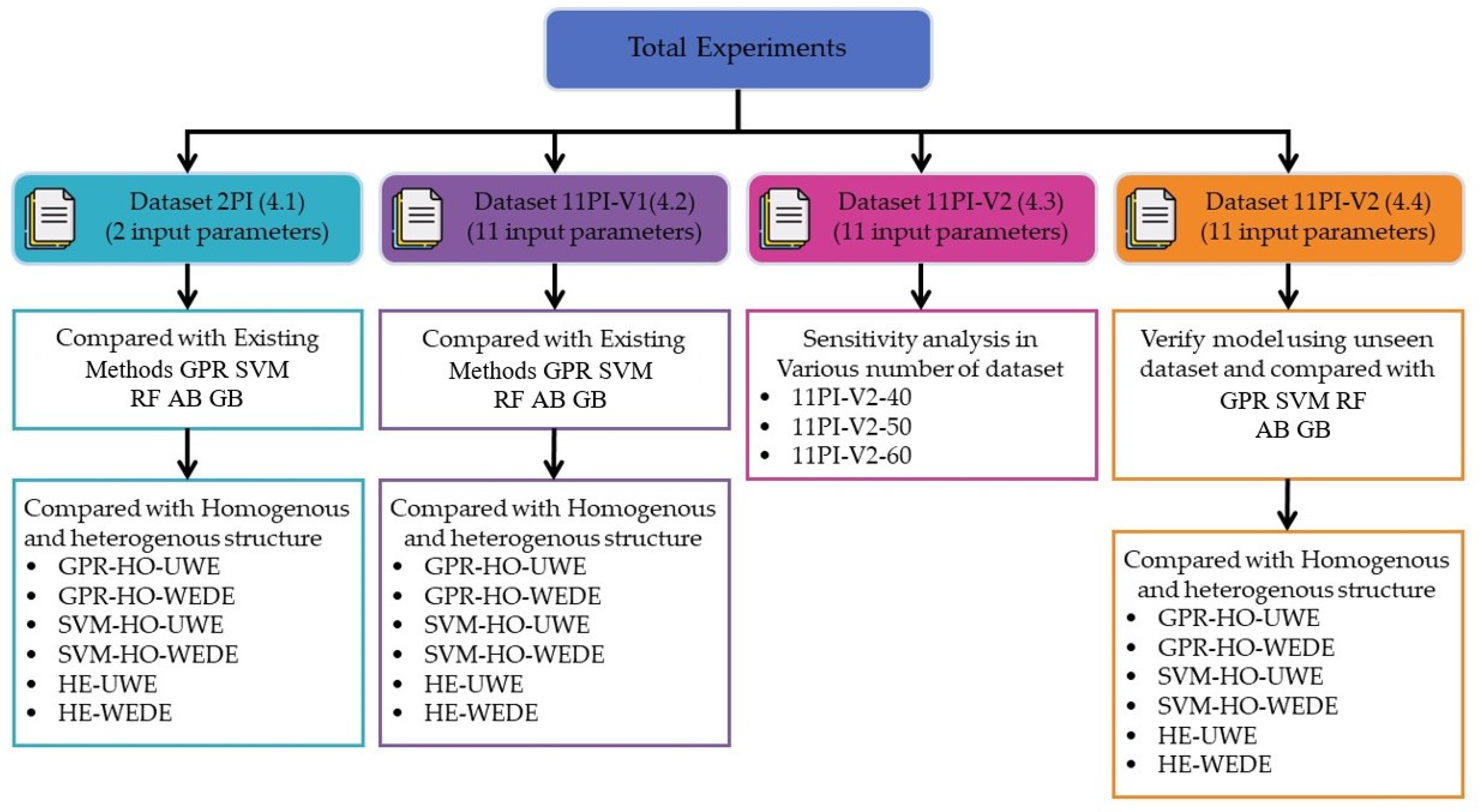
4. Results
4.1. Testing the Proposed Model with the Existing Dataset (Dataset 2PI-V1)
4.2. Testing the Proposed Model with the Newly Built Dataset (Dataset 11PI-V1)
4.3. Sensitivity Analysis on the Changing of Problem Size (Number of Sets of Data in a Dataset)
4.4. Testing the Effectiveness of the Proposed Method with the Unseen Dataset (11PI-V2)
5. Discussion
6. Conclusions
- (1)
- The effective decision fusion methodology, such as artificial multiple intelligence systems (AMISs) or other weight optimization approaches, can be investigated in depth, as can the best decision-making strategy for fusing various ML methods into a single answer;
- (2)
- Increasing the efficiency of the ML method can be accomplished using different approaches to find the optimal ML parameters, such as discovering a more efficient layer of the SVM and GPR;
- (3)
- The online application based on the proposed model can be developed to make it easier for a welder to select the appropriate parameters to achieve the desired UTS;
- (4)
- In the future, new parameters and outcomes can be explored so that the built application can be used with more materials, parameters, and outputs in order to function better.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ogunsemi, B.; Abioye, T.; Ogedengbe, T.; Zuhailawati, H. A review of various improvement strategies for joint quality of AA 6061-T6 friction stir weldments. J. Mater. Res. Technol. 2021, 11, 1061–1089. [Google Scholar] [CrossRef]
- Verma, S.; Kumar, V. Optimization of friction stir welding parameters of dissimilar aluminium alloys 6061 and 5083 by using response surface methodology. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 7009–7020. [Google Scholar] [CrossRef]
- Ramesh, N.; Kumar, V.S. Experimental erosion-corrosion analysis of friction stir welding of AA 5083 and AA 6061 for sub-sea applications. Appl. Ocean Res. 2020, 98, 102121. [Google Scholar] [CrossRef]
- Kumar, A.; Khurana, M.; Singh, G. Modeling and optimization of friction stir welding process parameters for dissimilar aluminium alloys. Mater. Today Proc. 2018, 5, 25440–25449. [Google Scholar] [CrossRef]
- Kumar, K.K.; Kumar, A.; Satyanarayana, M. Effect of friction stir welding parameters on the material flow, mechanical properties and corrosion behavior of dissimilar AA5083-AA6061 joints. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 2901–2917. [Google Scholar] [CrossRef]
- Liyakat, N.A.; Veeman, D. Improvement of mechanical and microstructural properties of AA 5052-H32 TIG weldment using friction stir processing approach. J. Mater. Res. Technol. 2022, 19, 332–344. [Google Scholar] [CrossRef]
- Chadha, U.; Selvaraj, S.K.; Gunreddy, N.; Sanjay Babu, S.; Mishra, S.; Padala, D.; Shashank, M.; Mathew, R.M.; Kishore, S.R.; Panigrahi, S. A Survey of Machine Learning in Friction Stir Welding, including Unresolved Issues and Future Research Directions. Mater. Des. Process. Commun. 2022, 2022, 2568347. [Google Scholar] [CrossRef]
- Banik, A.; Saha, A.; Barma, J.D.; Acharya, U.; Saha, S.C. Determination of best tool geometry for friction stir welding of AA 6061-T6 using hybrid PCA-TOPSIS optimization method. Measurement 2021, 173, 108573. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, R. Influence of Reinforcement with Multi-Pass FSW on the Mechanical and Microstructural Behavior of Dissimilar Weld Joint of AA5083 and AA6061. Silicon 2022, 14, 11219–11233. [Google Scholar] [CrossRef]
- Devaiah, D.; Kishore, K.; Laxminarayana, P. Optimal FSW process parameters for dissimilar aluminium alloys (AA5083 and AA6061) Using Taguchi Technique. Mater. Today Proc. 2018, 5, 4607–4614. [Google Scholar] [CrossRef]
- Huang, L.; Wu, D.; Hua, X.; Liu, S.; Jiang, Z.; Li, F.; Wang, H.; Shi, S. Effect of the welding direction on the microstructural characterization in fiber laser-GMAW hybrid welding of 5083 aluminum alloy. J. Manuf. Process. 2018, 31, 514–522. [Google Scholar] [CrossRef]
- Zhu, C.; Tang, X.; He, Y.; Lu, F.; Cui, H. Characteristics and formation mechanism of sidewall pores in NG-GMAW of 5083 Al-alloy. J. Mater. Process. Technol. 2016, 238, 274–283. [Google Scholar] [CrossRef]
- Kianezhad, M.; Raouf, A.H. Effect of nano-Al2O3 particles and friction stir processing on 5083 TIG welding properties. J. Mater. Process. Technol. 2019, 263, 356–365. [Google Scholar] [CrossRef]
- Anandan, B.; Manikandan, M. Machine learning approach for predicting the peak temperature of dissimilar AA7050-AA2014A friction stir welding butt joint using various regression models. Mater. Lett. 2022, 325, 132879. [Google Scholar] [CrossRef]
- Guan, W.; Zhao, Y.; Liu, Y.; Kang, S.; Wang, D.; Cui, L. Force data-driven machine learning for defects in friction stir welding. Scr. Mater. 2022, 217, 114765. [Google Scholar] [CrossRef]
- Moradi, M.M.; Aval, H.J.; Jamaati, R.; Amirkhanlou, S.; Ji, S. Effect of SiC nanoparticles on the microstructure and texture of friction stir welded AA2024/AA6061. Mater. Charact. 2019, 152, 169–179. [Google Scholar] [CrossRef]
- Moradi, M.M.; Aval, H.J.; Jamaati, R. Effect of pre and post welding heat treatment in SiC-fortified dissimilar AA6061-AA2024 FSW butt joint. J. Manuf. Process. 2017, 30, 97–105. [Google Scholar] [CrossRef]
- Tayebi, P.; Fazli, A.; Asadi, P.; Soltanpour, M. Formability analysis of dissimilar friction stir welded AA 6061 and AA 5083 blanks by SPIF process. CIRP J. Manuf. Sci. Technol. 2019, 25, 50–68. [Google Scholar] [CrossRef]
- Verma, S.; Gupta, M.; Misra, J.P. Optimization of process parameters in friction stir welding of armor-marine grade aluminium alloy using desirability approach. Mater. Res. Express 2018, 6, 026505. [Google Scholar] [CrossRef]
- Rajakumar, S.; Balasubramanian, V. Establishing relationships between mechanical properties of aluminium alloys and optimised friction stir welding process parameters. Mater. Des. 2012, 40, 17–35. [Google Scholar] [CrossRef]
- Gupta, S.K.; Pandey, K.; Kumar, R. Multi-objective optimization of friction stir welding process parameters for joining of dissimilar AA5083/AA6063 aluminum alloys using hybrid approach. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 232, 343–353. [Google Scholar] [CrossRef]
- Kesharwani, R.; Panda, S.; Pal, S. Multi objective optimization of friction stir welding parameters for joining of two dissimilar thin aluminum sheets. Procedia Mater. Sci. 2014, 6, 178–187. [Google Scholar] [CrossRef]
- Chainarong, S.; Pitakaso, R.; Sirirak, W.; Srichok, T.; Khonjun, S.; Sethanan, K.; Sangthean, T. Multi-Objective Variable Neighborhood Strategy Adaptive Search for Tuning Optimal Parameters of SSM-ADC12 Aluminum Friction Stir Welding. J. Manuf. Mater. Process. 2021, 5, 123. [Google Scholar] [CrossRef]
- Khaidem, L.; Saha, S.; Dey, S.R. Predicting the direction of stock market prices using random forest. arXiv 2016, arXiv:1605.00003. [Google Scholar]
- Narayanan, B.; Govindarajan, M. Prediction of stock market using ensemble model. Int. J. Comput. Appl. 2015, 128, 18–21. [Google Scholar] [CrossRef]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Wu, Q.; Chen, Y.; Liu, Z. Ensemble model of intelligent paradigms for stock market forecasting. In Proceedings of the First International Workshop on Knowledge Discovery and Data Mining (WKDD 2008), Adelaide, Australia, 23–24 January 2008; pp. 205–208. [Google Scholar]
- Desai, P.; Granja, V.; Higgs, C., III. Lifetime Prediction Using a Tribology-Aware, Deep Learning-Based Digital Twin of Ball Bearing-Like Tribosystems in Oil and Gas. Processes 2021, 9, 922. [Google Scholar] [CrossRef]
- Schmoeller, M.; Weiss, T.; Goetz, K.; Stadter, C.; Bernauer, C.; Zaeh, M.F. Inline Weld Depth Evaluation and Control Based on OCT Keyhole Depth Measurement and Fuzzy Control. Processes 2022, 10, 1422. [Google Scholar] [CrossRef]
- Shaheen, B.W.; Németh, I. Integration of Maintenance Management System Functions with Industry 4.0 Technologies and Features—A Review. Processes 2022, 10, 2173. [Google Scholar] [CrossRef]
- Okuyucu, H.; Kurt, A.; Arcaklioglu, E. Artificial neural network application to the friction stir welding of aluminum plates. Mater. Des. 2007, 28, 78–84. [Google Scholar] [CrossRef]
- Shojaeefard, M.H.; Khalkhali, A.; Akbari, M.; Asadi, P. Investigation of friction stir welding tool parameters using FEM and neural network. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2015, 229, 209–217. [Google Scholar] [CrossRef]
- Tansel, I.N.; Demetgul, M.; Okuyucu, H.; Yapici, A. Optimizations of friction stir welding of aluminum alloy by using genetically optimized neural network. Int. J. Adv. Manuf. Technol. 2010, 48, 95–101. [Google Scholar] [CrossRef]
- Verma, S.; Gupta, M.; Misra, J.P. Performance evaluation of friction stir welding using machine learning approaches. MethodsX 2018, 5, 1048–1058. [Google Scholar] [CrossRef]
- Vignesh, R.V.; Padmanaban, R. Artificial neural network model for predicting the tensile strength of friction stir welded aluminium alloy AA1100. Mater. Today Proc. 2018, 5, 16716–16723. [Google Scholar] [CrossRef]
- Chainarong, S.; Srichok, T.; Pitakaso, R.; Sirirak, W.; Khonjun, S.; Akararungruangku, R. Variable Neighborhood Strategy Adaptive Search for Optimal Parameters of SSM-ADC 12 Aluminum Friction Stir Welding. Processes 2021, 9, 1805. [Google Scholar] [CrossRef]
- Sefene, E.M.; Tsegaw, A.A.; Mishra, A. Process Parameter Optimization of 6061AA Friction Stir Welded Joints Using Supervised Machine Learning Regression-Based Algorithms. J. Soft Comput. Civ. Eng. 2022, 6, 127–137. [Google Scholar]
- Srichok, T.; Pitakaso, R.; Sethanan, K.; Sirirak, W.; Kwangmuang, P. Combined response surface method and modified differential evolution for parameter optimization of friction stir welding. Processes 2020, 8, 1080. [Google Scholar] [CrossRef]
- Anandan, B.; Manikandan, M. Machine learning approach with various regression models for predicting the ultimate tensile strength of the Friction stir welded AA 2050-T8 joints by the K-Fold Cross-Validation method. Mater. Today Commun. 2022, 34, 105286. [Google Scholar] [CrossRef]
- Prasitpuriprecha, C.; Pitakaso, R.; Gonwirat, S.; Enkvetchakul, P.; Preeprem, T.; Jantama, S.S.; Kaewta, C.; Weerayuth, N.; Srichok, T.; Khonjun, S. Embedded AMIS-Deep Learning with Dialog-Based Object Query System for Multi-Class Tuberculosis Drug Response Classification. Diagnostics 2022, 12, 2980. [Google Scholar] [CrossRef]
- Prasitpuriprecha, C.; Jantama, S.S.; Preeprem, T.; Pitakaso, R.; Srichok, T.; Khonjun, S.; Weerayuth, N.; Gonwirat, S.; Enkvetchakul, P.; Kaewta, C. Drug-Resistant Tuberculosis Treatment Recommendation, and Multi-Class Tuberculosis Detection and Classification Using Ensemble Deep Learning-Based System. Pharmaceuticals 2023, 16, 13. [Google Scholar] [CrossRef]
- Yin, L.; Du, X.; Ma, C.; Gu, H. Virtual Screening of Drug Proteins Based on the Prediction Classification Model of Imbalanced Data Mining. Processes 2022, 10, 1420. [Google Scholar] [CrossRef]
- Karki, M.; Kantipudi, K.; Yang, F.; Yu, H.; Wang, Y.X.J.; Yaniv, Z.; Jaeger, S. Generalization Challenges in Drug-Resistant Tuberculosis Detection from Chest X-rays. Diagnostics 2022, 12, 188. [Google Scholar] [CrossRef]
- Ghetiya, N.; Patel, K.; Kavar, A. Multi-objective optimization of FSW process parameters of aluminium alloy using Taguchi-based grey relational analysis. Trans. Indian Inst. Met. 2016, 69, 917–923. [Google Scholar] [CrossRef]
- Na, M.G.; Kim, J.W.; Lim, D.H.; Kang, Y.-J. Residual stress prediction of dissimilar metals welding at NPPs using support vector regression. Nucl. Eng. Des. 2008, 238, 1503–1510. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Lv, P.; Wang, H. Detection of line weld defects based on multiple thresholds and support vector machine. Ndt E Int. 2008, 41, 517–524. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. Modelling pile capacity using Gaussian process regression. Comput. Geotech. 2010, 37, 942–947. [Google Scholar] [CrossRef]
- Verma, S.; Misra, J. Study on temperature distribution during Friction Stir Welding of 6082 aluminum alloy. Mater. Today Proc. 2017, 4, 1350–1356. [Google Scholar] [CrossRef]
- Manvatkar, V.; Arora, A.; De, A.; DebRoy, T. Neural network models of peak temperature, torque, traverse force, bending stress and maximum shear stress during friction stir welding. Sci. Technol. Weld. Join. 2012, 17, 460–466. [Google Scholar] [CrossRef]
- Yousif, Y.; Daws, K.; Kazem, B. Prediction of friction stir welding characteristic using neural network. Jordan J. Mech. Ind. Eng. 2008, 2, 151–155. [Google Scholar]
- Kshirsagar, R.; Jones, S.; Lawrence, J.; Tabor, J. Prediction of bead geometry using a two-stage SVM–ANN algorithm for automated tungsten inert gas (TIG) welds. J. Manuf. Mater. Process. 2019, 3, 39. [Google Scholar] [CrossRef]
- Liang, R.; Yu, R.; Luo, Y.; Zhang, Y. Machine learning of weld joint penetration from weld pool surface using support vector regression. J. Manuf. Process. 2019, 41, 23–28. [Google Scholar] [CrossRef]
- Britto, A.S.F.; Raj, R.E.; Mabel, M.C. Prediction of shear and tensile strength of the diffusion bonded AA5083 and AA7075 aluminium alloy using ANN. Mater. Sci. Eng. A 2017, 692, 1–8. [Google Scholar] [CrossRef]
- Dehabadi, V.M.; Ghorbanpour, S.; Azimi, G. Application of artificial neural network to predict Vickers microhardness of AA6061 friction stir welded sheets. J. Cent. South Univ. 2016, 23, 2146–2155. [Google Scholar] [CrossRef]
- Verma, S.; Misra, J.P.; Popli, D. Modeling of friction stir welding of aviation grade aluminium alloy using machine learning approaches. Int. J. Model. Simul. 2022, 42, 1–8. [Google Scholar] [CrossRef]
- Syah, A.; Astuti, W.; Saedon, J. Development of prediction system model for mechanical property in friction stir welding using support vector machine (SVM). J. Mech. Eng. 2018, 5, 216–225. [Google Scholar]
- Das, B.; Pal, S.; Bag, S. Weld quality prediction in friction stir welding using wavelet analysis. Int. J. Adv. Manuf. Technol. 2017, 89, 711–725. [Google Scholar] [CrossRef]
- Hartl, R.; Vieltorf, F.; Benker, M.; Zaeh, M.F. Predicting the ultimate tensile strength of friction stir welds using Gaussian process regression. J. Manuf. Mater. Process. 2020, 4, 75. [Google Scholar] [CrossRef]
- Mishra, A. Artificial intelligence algorithms for the analysis of mechanical property of friction stir welded joints by using python programming. Weld. Technol. Rev. 2020, 92, 7–16. [Google Scholar] [CrossRef]
- Upender, K.; Kumar, B.; Rao, M.; Ramana, M.V. Friction Stir Welding of IS: 65032 Aluminum Alloy and Predicting Tensile Strength Using Ensemble Learning. In Proceedings of the International Conference on Advances in Mechanical Engineering and Material Science, Andrha Pradesh, India, 22–24 January 2022; pp. 103–114. [Google Scholar]
- De Filippis, L.A.C.; Serio, L.M.; Facchini, F.; Mummolo, G.; Ludovico, A.D. Prediction of the vickers microhardness and ultimate tensile strength of AA5754 H111 friction stir welding butt joints using artificial neural network. Materials 2016, 9, 915. [Google Scholar] [CrossRef] [PubMed]
- Jenarthanan, M.; Varma, C.V.; Manohar, V.K. Impact of friction stir welding (FSW) process parameters on tensile strength during dissimilar welds of AA2014 and AA6061. Mater. Today Proc. 2018, 5, 14384–14391. [Google Scholar] [CrossRef]
- Mishra, A.; Morisetty, R. Determination of the Ultimate Tensile Strength (UTS) of friction stir welded similar AA6061 joints by using supervised machine learning based algorithms. Manuf. Lett. 2022, 32, 83–86. [Google Scholar] [CrossRef]
- Mishra, A.; Dasgupta, A. Supervised and Unsupervised Machine Learning Algorithms for Forecasting the Fracture Location in Dissimilar Friction-Stir-Welded Joints. Forecasting 2022, 4, 787–797. [Google Scholar] [CrossRef]
- Giraud, L.; Robe, H.; Claudin, C.; Desrayaud, C.; Bocher, P.; Feulvarch, E. Investigation into the dissimilar friction stir welding of AA7020-T651 and AA6060-T6. J. Mater. Process. Technol. 2016, 235, 220–230. [Google Scholar] [CrossRef]
- Guo, J.; Chen, H.; Sun, C.; Bi, G.; Sun, Z.; Wei, J. Friction stir welding of dissimilar materials between AA6061 and AA7075 Al alloys effects of process parameters. Mater. Des. 2014, 56, 185–192. [Google Scholar] [CrossRef]
- Maeda, M.; Liu, H.; Fujii, H.; Shibayanagi, T. Temperature field in the vicinity of FSW-tool during friction stir welding of aluminium alloys. Weld. World 2005, 49, 69–75. [Google Scholar] [CrossRef]
- Elangovan, K.; Balasubramanian, V.; Babu, S. Predicting tensile strength of friction stir welded AA6061 aluminium alloy joints by a mathematical model. Mater. Des. 2009, 30, 188–193. [Google Scholar] [CrossRef]
- Ghetiya, N.; Patel, K. Prediction of tensile strength in friction stir welded aluminium alloy using artificial neural network. Procedia Technol. 2014, 14, 274–281. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. In Proceedings of the Summer School on Machine Learning, Tübingen, Germany, 4–16 August 2003; pp. 63–71. [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Gonwirat, S.; Surinta, O. Optimal weighted parameters of ensemble convolutional neural networks based on a differential evolution algorithm for enhancing pornographic image classification. Eng. Appl. Sci. Res. 2021, 48, 560–569. [Google Scholar]
- Sethanan, K.; Pitakaso, R. Improved differential evolution algorithms for solving generalized assignment problem. Expert Syst. Appl. 2016, 45, 450–459. [Google Scholar] [CrossRef]
- Gonwirat, S.; Surinta, O. DeblurGAN-CNN: Effective Image Denoising and Recognition for Noisy Handwritten Characters. IEEE Access 2022, 10, 90133–90148. [Google Scholar] [CrossRef]
- Noppitak, S.; Surinta, O. dropCyclic: Snapshot Ensemble Convolutional Neural Network Based on a New Learning Rate Schedule for Land Use Classification. IEEE Access 2022, 10, 60725–60737. [Google Scholar] [CrossRef]

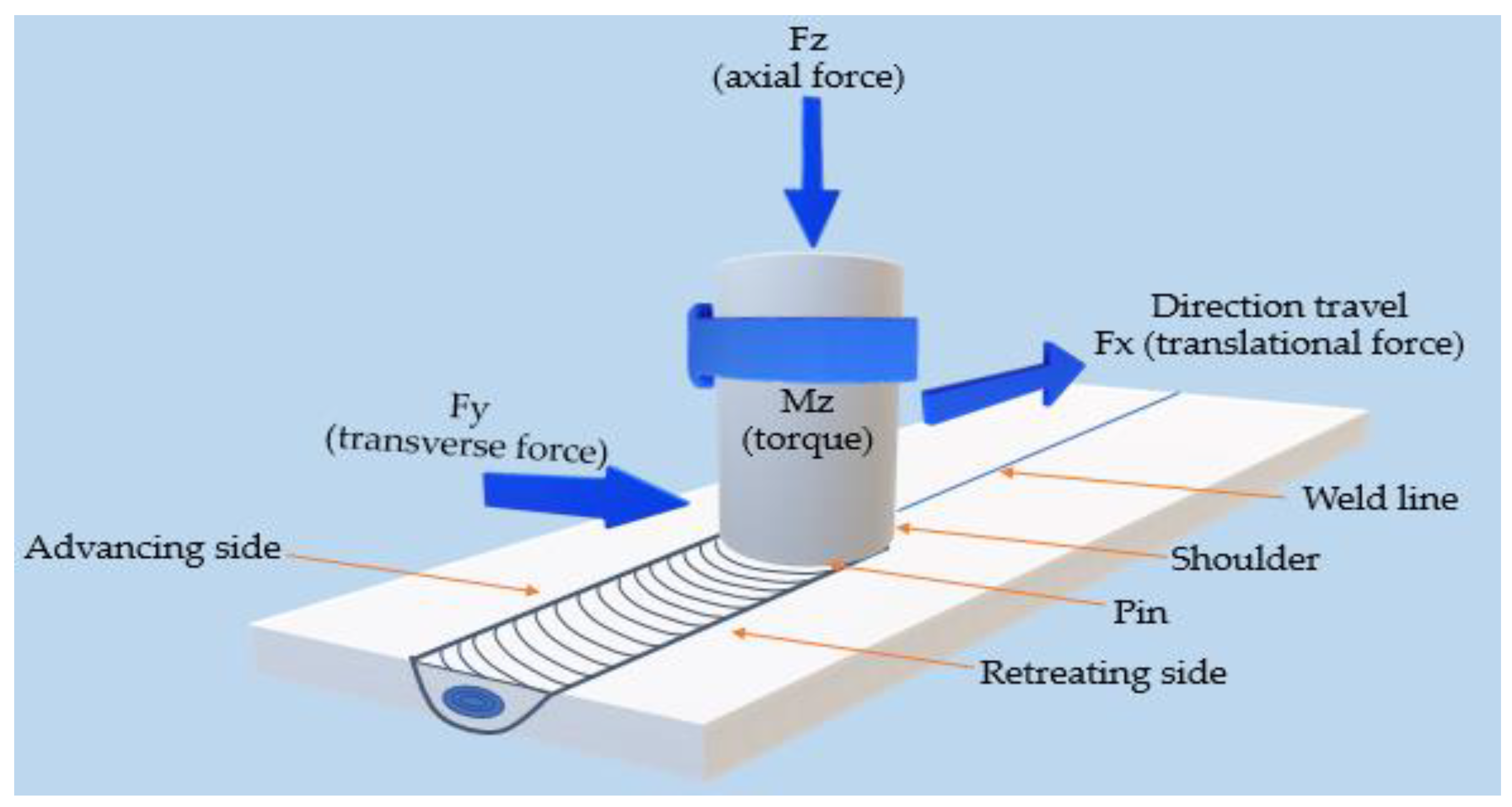
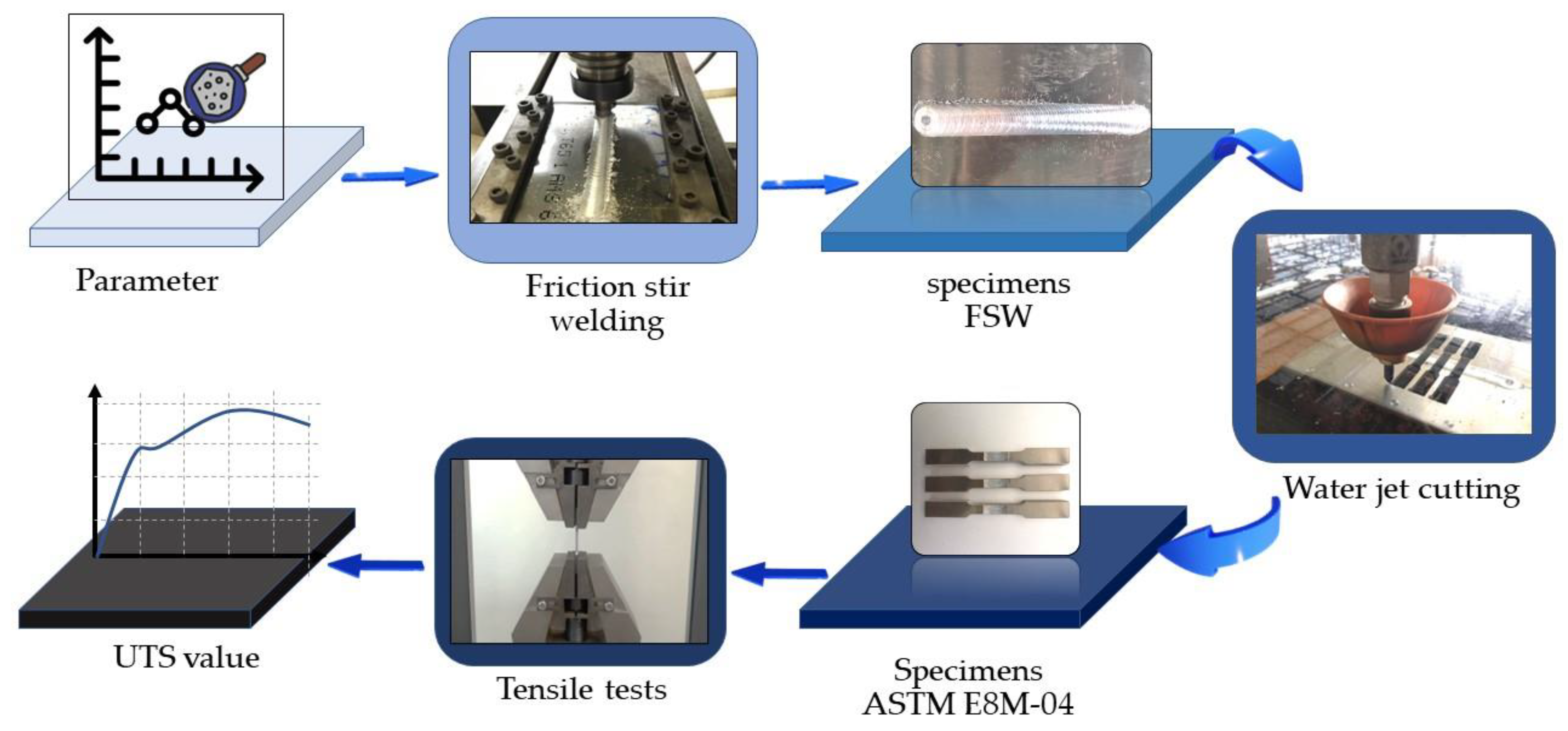

| Ref. | Input | Output | Method | Type of Material | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TD - | TAD - | RS) (rpm) | WS (mm/min) | SD (mm) | PT - | PL (mm) | PD (mm) | PN (mm) | TT - | TA (Degrees) | Other - | UTS (mPa) | Other | ML | EML | Other | Similar | Dissimilar | |
| [4] | - | - | √ | √ | - | - | - | - | - | - | - | √ -axial forces | √ | - | √ | - | - | - | √ AA6061 AA2024 |
| [34] | - | - | √ | √ | - | - | - | - | - | - | - | - | √ | - | √ | - | - | √ AA6082 | |
| [35] | - | - | √ | √ | √ | √ | - | - | - | - | √ | - | √ | - | - | √ AA1100 | - | ||
| [37] | - | - | √ | √ | - | - | - | - | - | - | - | √ -axial forces | √ | - | - | √ | - | √ AA6061 | - |
| [51] | - | - | - | - | - | - | - | - | - | - | - | - | - | - | √ | - | - | - | - |
| [52] | - | - | - | - | - | - | - | - | - | - | - | - | - | √ Backside bead width | √ | - | - | - | - |
| [53] | - | - | - | - | - | - | - | - | - | - | - | - | √ | √ Shear strength | √ | - | - | - | √ AA5083 AA7075 |
| [54] | - | - | - | - | - | - | - | - | - | - | - | - | √ | - | - | √ AA6061 | |||
| [55] | - | - | √ | √ | - | - | - | - | - | - | - | - | √ | - | √ | √ | √ AA6082. | - | |
| [56] | - | - | √ | √ | - | - | - | - | - | - | - | - | √ | - | √ | - | - | √ AA6061 | - |
| [57] | - | - | √ | √ | √ | √ | - | √ | - | - | √ AA1100 | - | |||||||
| [58] | - | - | √ | √ | - | - | - | - | - | - | - | - | √ | - | √ | - | - | √ ENAW-6082-T6 | - |
| [59] | - | - | √ | √ | - | - | - | - | - | - | - | - | √ | - | √ | √ | √ AA6061-T6 | - | |
| [60] | - | - | √ | √ | √ | - | - | - | - | - | √ | √ | - | √ | √ IS:65032 | - | |||
| [61] | - | - | √ | √ | - | - | - | - | - | - | - | - | √ | √ Vickers hardness | √ | - | - | √ AA5754 H111 | - |
| [62] | - | - | √ | √ | - | - | - | - | √ | - | - | - | √ | - | - | - | √ applying RSM | - | √ AA6061 AA2014 |
| [63] | - | - | √ | √ | - | - | - | - | - | - | - | √ -axial forces | √ | - | - | √ | √ AA6061 | - | |
| [64] | - | - | √ | √ | √ | - | - | - | - | - | - | - | √ | - | √ | - | - | - | √ AA5754 C11000 |
| Our | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | - | √ | - | - | √ | - | - | √ AA5083 AA6061 |
| Alloy | Ultimate Tensile Strength (mPa) |
|---|---|
| AA5083 | 276.47 |
| AA6061 | 286.82 |
| Continuous Variable | |||
| Parameter | Levels | ||
| Min | Max | ||
| Pin length (mm) | 4.8 | 5.5 | |
| Shoulder diameter (mm) | 18 | 25 | |
| Pin diameter (mm) | 6 | 8 | |
| Tilt angle (degrees) | 0 | 3 | |
| Rotation speed (rpm) | 150 | 1500 | |
| welding speed (mm/min) | 15 | 135 | |
| Penetration (mm) | 0.3 | 0.5 | |
| Categorical Variable | |||
| Parameter | Levels | ||
| Pin Type | Straight Cylindrical | Hexagonal Cylindrical | Threaded Cylindrical |
| Additive | Silicon Carbide | Aluminum Oxide | - |
| Technique for additive | Drill | Groove | - |
| Traveling method | Straight | Zig Zag | Circles |
| Continuous Variable | |||
| Parameter | Levels | ||
| Min | Max | ||
| Pin length (mm) | 4.8 | 5.5 | |
| Shoulder diameter (mm) | 18 | 25 | |
| Pin diameter (mm) | 6 | 8 | |
| Tilt angle (degrees) | 0 | 3 | |
| Rotation speed (rpm) | 800 | 1500 | |
| Welding speed (mm/min) | 15 | 75 | |
| Penetration (mm) | 0.3 | 0.5 | |
| Categorical Variable | |||
| Parameter | Levels | ||
| Pin type | Straight Cylindrical | Hexagonal Cylindrical | Threaded Cylindrical |
| Additive | Silicon Carbide | Aluminum Oxide | - |
| Technique for additive | Drill | Groove | - |
| Traveling method | Straight | Zig Zag | Circles |
| Type of Dataset | 2PI-V1 | 11PI-V1 | 11PI-V2 |
|---|---|---|---|
| Train dataset | 19 | 48 | - |
| Test dataset | 6 | 12 | 36 |
| Total dataset | 25 | 60 | 36 |
| NP\Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | . | . | 99 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NP1 ( | 0.48 | 0.76 | 0.32 | 0.87 | 0.94 | 0.53 | 0.76 | . | . | . | 0.47 | 0.69 |
| NP2 ( | 0.72 | 0.51 | 0.92 | 0.40 | 0.89 | 0.74 | 0.90 | . | . | . | 0.65 | 0.95 |
| Regressor | User Defined Parameters |
|---|---|
| Gaussian process regression [34] | Kernel = ‘rbf’, gamma = 7, noise = 0.2 |
| Support Vector Machine [34] | Kernel = ‘rbf’, gamma = 7, C = 0.2 |
| Random Forest [55] | learner = 100, max leaf = 1 |
| Ada boosting [63] | learner = 100, max leaf = 5 |
| Gradient boosting [37] | learner = 100, max leaf = 5, learning rate = 0.001 |
| Our proposed ensemble learning (HO-UWE, HE-UWE, HO-WEDE, and HE-UWE) | learner = 100 |
| Machine Learning and Ensemble Machine Learning Approach | Training Dataset | Testing Dataset | ||
|---|---|---|---|---|
| CC | RMSE (mPa) | CC | RMSE (mPa) | |
| GPR [34] | 0.995 | 1.69 | 0.970 | 5.94 |
| SVM [34] | 0.983 | 10.63 | 0.950 | 6.19 |
| RF [55] | 0.996 | 7.89 | 0.930 | 6.72 |
| AB [63] | 0.964 | 8.57 | 0.762 | 14.10 |
| GB [37] | 0.996 | 2.98 | 0.713 | 15.49 |
| GPR-HO-UWE | 0.975 | 7.14 | 0.982 | 4.30 |
| GPR-HO-WEDE | 0.981 | 6.78 | 0.989 | 3.87 |
| SVM-HO-UWE | 0.991 | 4.27 | 0.977 | 4.38 |
| SVM-HO-WEDE | 0.966 | 5.85 | 0.99 | 4.02 |
| HE-UWE | 0.974 | 6.78 | 0.989 | 4.24 |
| HE-WEDE | 0.976 | 6.68 | 0.995 | 3.18 |
| Machine Learning and Ensemble Machine Learning Approach | RMSE (mPa) | ||
|---|---|---|---|
| 2-cv | 3-cv | 5-cv | |
| GPR [34] | 7.39 ± 0.48 | 7.67 ± 0.48 | 6.14 ± 0.48 |
| SVM [34] | 8.83 ± 0.28 | 9.85 ± 0.28 | 9.22 ± 0.28 |
| RF [55] | 9.02 ± 0.52 | 8.25 ± 0.52 | 7.98 ± 0.52 |
| AB [63] | 14.79 ± 0.36 | 13.86 ± 0.36 | 13.09 ± 0.36 |
| GB [37] | 13.16 ± 0.44 | 13.6 ± 0.44 | 12.45 ± 0.44 |
| GPR-HO-UWE | 6.73 ± 0.74 | 7.51 ± 0.74 | 5.8 ± 0.74 |
| GPR-HO-WEDE | 6.05 ± 0.67 | 7.27 ± 0.67 | 5.99 ± 0.67 |
| SVM-HO-UWE | 5.35 ± 0.6 | 6.17 ± 0.6 | 5.59 ± 0.6 |
| SVM-HO-WEDE | 7.84 ± 0.47 | 6.32 ± 0.47 | 5.29 ± 0.47 |
| HE-UWE | 5.58 ± 0.61 | 5.81 ± 0.61 | 5.91 ± 0.61 |
| HE-WEDE | 5.94 ± 0.74 | 5.36 ± 0.74 | 4.98 ± 0.74 |
| Dataset | TD | TAD | RS | WS | SD | PT | PL | PD | PN | TT | TA | UTS (mPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | SiC | Drill | 865 | 15 | 25 | SC | 5.5 | 6 | 0.5 | ST | 3 | 232.07 |
| 2 | SiC | Drill | 150 | 15 | 18 | SC | 4.8 | 6 | 0.5 | ZZ | 0 | 135.74 |
| 3 | SiC | Groove | 150 | 15 | 18 | TC | 4.8 | 6 | 0.5 | ST | 2 | 150.81 |
| 4 | Al2O3 | Drill | 1500 | 15 | 25 | SC | 4.8 | 8 | 0.5 | ST | 3 | 225.70 |
| 5 | Al2O3 | Drill | 150 | 135 | 25 | SC | 5 | 8 | 0.5 | CC | 3 | 145.20 |
| 6 | SiC | Groove | 150 | 135 | 18 | HC | 4.8 | 6 | 0.5 | CC | 0 | 158.10 |
| 7 | Al2O3 | Drill | 150 | 135 | 20 | TC | 5.5 | 7.5 | 0.3 | ST | 0 | 165.50 |
| 8 | SiC | Groove | 1500 | 15 | 18 | SC | 4.8 | 7.5 | 0.5 | ST | 0 | 197.43 |
| 9 | SiC | Groove | 150 | 135 | 25 | SC | 4.8 | 8 | 0.3 | CC | 0 | 120.52 |
| 10 | SiC | Groove | 1150 | 135 | 18 | SC | 4.8 | 6.5 | 0.4 | ST | 1.5 | 237.54 |
| 11 | SiC | Groove | 150 | 135 | 25 | SC | 4.8 | 6 | 0.3 | ZZ | 0.5 | 115.68 |
| 12 | Al2O3 | Groove | 150 | 100 | 25 | SC | 4.8 | 8 | 0.3 | ZZ | 3 | 118.00 |
| 13 | Al2O3 | Groove | 1500 | 135 | 18 | TC | 4.8 | 6 | 0.3 | CC | 2.5 | 231.65 |
| 14 | Al2O3 | Groove | 150 | 15 | 21 | SC | 4.8 | 6 | 0.5 | CC | 3 | 116.50 |
| 15 | SiC | Drill | 150 | 15 | 18 | SC | 5.5 | 8 | 0.3 | ZZ | 3 | 121.20 |
| 16 | SiC | Groove | 1500 | 15 | 18 | TC | 4.8 | 7.5 | 0.5 | CC | 0 | 236.32 |
| 17 | Al2O3 | Drill | 1500 | 15 | 18 | TC | 5 | 8 | 0.3 | CC | 0 | 238.89 |
| 18 | SiC | Drill | 1185 | 135 | 25 | HC | 5.5 | 8 | 0.5 | CC | 1 | 242.76 |
| 19 | SiC | Groove | 150 | 120 | 25 | SC | 5.5 | 8 | 0.5 | ST | 0 | 115.20 |
| 20 | Al2O3 | Groove | 150 | 30 | 25 | TC | 5.5 | 8 | 0.5 | CC | 3 | 125.84 |
| 21 | Al2O3 | Drill | 1500 | 135 | 25 | SC | 5.5 | 7.5 | 0.3 | CC | 3 | 201.65 |
| 22 | Al2O3 | Groove | 1500 | 15 | 18 | HC | 4.8 | 8 | 0.3 | CC | 3 | 232.67 |
| 23 | Al2O3 | Drill | 150 | 15 | 22 | TC | 4.8 | 8 | 0.3 | ST | 3 | 139.00 |
| 24 | SiC | Drill | 1500 | 135 | 21 | SC | 5.5 | 6 | 0.3 | CC | 0 | 222.76 |
| 25 | Al2O3 | Groove | 150 | 15 | 18 | HC | 4.8 | 8 | 0.3 | ST | 0 | 132.40 |
| 26 | SiC | Groove | 150 | 15 | 18 | TC | 5 | 8 | 0.4 | ST | 0 | 144.50 |
| 27 | Al2O3 | Groove | 1500 | 135 | 25 | SC | 4.8 | 8 | 0.5 | CC | 0 | 217.67 |
| 28 | SiC | Drill | 1500 | 55 | 18 | HC | 4.8 | 6 | 0.3 | CC | 0 | 226.56 |
| 29 | SiC | Groove | 335 | 15 | 25 | HC | 5.5 | 6.5 | 0.5 | ZZ | 3 | 222.24 |
| 30 | Al2O3 | Drill | 1500 | 135 | 18 | TC | 5.5 | 6 | 0.5 | CC | 0 | 232.76 |
| 31 | SiC | Groove | 1500 | 15 | 25 | SC | 4.8 | 8 | 0.3 | ZZ | 0 | 238.87 |
| 32 | Al2O3 | Groove | 1500 | 15 | 25 | SC | 4.9 | 6 | 0.3 | ST | 3 | 227.90 |
| 33 | SiC | Groove | 1500 | 135 | 25 | HC | 4.8 | 7.5 | 0.3 | ST | 3 | 236.89 |
| 34 | Al2O3 | Groove | 1500 | 15 | 18 | HC | 5.5 | 6 | 0.4 | CC | 0 | 231.62 |
| 35 | Al2O3 | Drill | 1165 | 15 | 18 | SC | 5.2 | 7.5 | 0.5 | CC | 0 | 238.90 |
| 36 | Al2O3 | Groove | 150 | 30 | 25 | TC | 5.5 | 8 | 0.5 | CC | 3 | 140.00 |
| 37 | SiC | Drill | 1500 | 15 | 25 | HC | 5.5 | 8 | 0.3 | ST | 1.5 | 239.69 |
| 38 | SiC | Drill | 150 | 51 | 18 | HC | 4.8 | 6.8 | 0.3 | ST | 2 | 121.48 |
| 39 | Al2O3 | Groove | 150 | 15 | 20 | HC | 4.8 | 8 | 0.5 | ZZ | 2.5 | 130.40 |
| 40 | SiC | Groove | 150 | 135 | 18 | SC | 5.5 | 6 | 0.3 | CC | 3 | 110.00 |
| 41 | SiC | Drill | 150 | 15 | 25 | SC | 5.3 | 8 | 0.3 | ZZ | 3 | 135.80 |
| 42 | SiC | Drill | 1500 | 15 | 18 | TC | 4.8 | 6 | 0.3 | ST | 0 | 246.32 |
| 43 | SiC | Groove | 150 | 15 | 18 | SC | 5.5 | 6 | 0.3 | ST | 0 | 142.00 |
| 44 | Al2O3 | Drill | 1500 | 135 | 25 | SC | 4.8 | 6 | 0.3 | ZZ | 3 | 227.50 |
| 45 | Al2O3 | Groove | 1295 | 90 | 25 | HC | 5.5 | 8 | 0.5 | ST | 0 | 240.34 |
| 46 | Al2O3 | Groove | 150 | 135 | 25 | TC | 4.8 | 6.5 | 0.5 | ST | 3 | 138.00 |
| 47 | Al2O3 | Drill | 150 | 135 | 22 | SC | 4.8 | 6 | 0.3 | ST | 3 | 121.00 |
| 48 | Al2O3 | Groove | 150 | 15 | 20 | HC | 5.5 | 6 | 0.3 | ST | 3 | 140.02 |
| 49 | Al2O3 | Drill | 1500 | 135 | 21 | HC | 4.8 | 6 | 0.3 | ST | 0 | 236.89 |
| 50 | SiC | Groove | 1500 | 135 | 18 | TC | 5.5 | 6 | 0.5 | ST | 0.5 | 221.6 |
| 51 | SiC | Drill | 1500 | 95 | 23 | TC | 4.8 | 6 | 0.5 | CC | 3 | 210.94 |
| 52 | Al2O3 | Groove | 1500 | 15 | 18 | TC | 5.5 | 6.5 | 0.3 | ZZ | 2.5 | 237.8 |
| 53 | Al2O3 | Drill | 895 | 15 | 25 | TC | 4.8 | 6 | 0.4 | ZZ | 3 | 241.56 |
| 54 | Al2O3 | Drill | 525 | 135 | 22 | TC | 4.8 | 8 | 0.5 | ST | 0 | 233.43 |
| 55 | SiC | Drill | 1500 | 15 | 25 | TC | 4.8 | 8 | 0.5 | ZZ | 1.5 | 241.00 |
| 56 | SiC | Groove | 150 | 15 | 25 | TC | 4.8 | 6 | 0.5 | ST | 2 | 115.00 |
| 57 | Al2O3 | Groove | 150 | 15 | 25 | TC | 4.8 | 6 | 0.3 | CC | 0 | 112.00 |
| 58 | SiC | Drill | 795 | 135 | 21 | SC | 5.5 | 8 | 0.4 | ZZ | 0 | 226.90 |
| 59 | Al2O3 | Drill | 150 | 135 | 18 | HC | 4.8 | 6 | 0.5 | CC | 3 | 112.50 |
| 60 | Al2O3 | Drill | 150 | 55 | 18 | HC | 4.8 | 8 | 0.4 | CC | 0 | 110.78 |
| Machine Learning and Ensemble Machine Learning Approach | Training Dataset with 5-cv | Testing Dataset | ||
|---|---|---|---|---|
| CC | RMSE (mPa) | CC | RMSE (mPa) | |
| GPR [34] | 0.983 ± 0.007 | 5.33 ± 0.11 | 0.990 | 3.73 |
| SVM [34] | 0.981 ± 0.033 | 5.72 ± 0.37 | 0.989 | 4.52 |
| RF [55] | 0.975 ± 0.023 | 5.69 ± 0.18 | 0.990 | 4.23 |
| AB [63] | 0.981 ± 0.029 | 5.05 ± 0.34 | 0.989 | 4.63 |
| GB [37] | 0.984 ± 0.035 | 4.09 ± 0.20 | 0.988 | 4.67 |
| GPR-HO-UWE | 0.989 ± 0.037 | 3.91 ± 0.15 | 0.993 | 3.62 |
| GPR-HO-WEDE | 0.990 ± 0.036 | 3.81 ± 0.16 | 0.992 | 3.67 |
| SVM-HO-UWE | 0.985 ± 0.016 | 4.67 ± 0.18 | 0.990 | 4.23 |
| SVM-HO-WEDE | 0.991 ± 0.038 | 4.21 ± 0.30 | 0.994 | 4.02 |
| HE-UWE | 0.992 ± 0.013 | 3.73 ± 0.15 | 0.993 | 3.53 |
| HE-WEDE | 0.992 ± 0.008 | 3.74 ± 0.16 | 0.995 | 3.46 |
| Machine Learning and Ensemble Machine Learning Approach | 11PI-V1-40 | 11PI-V1-50 | 11PI-V1-60 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train Dataset | Test Dataset | Train Dataset | Test Dataset | Train Dataset | Test Dataset | |||||||
| CC | RSME | CC | RSME | CC | RSME | CC | RSME | CC | RSME | CC | RSME | |
| GPR [34] | 0.975 ± 0.014 | 6.03 ± 0.34 | 0.989 | 4.21 | 0.985 ± 0.027 | 4.67 ± 0.28 | 0.985 | 4.29 | 0.983 ± 0.007 | 5.33 ± 0.11 | 0.990 | 3.73 |
| SVM [34] | 0.972 ± 0.015 | 6.35 ± 0.37 | 0.980 | 4.98 | 0.983 ± 0.008 | 5.25 ± 0.30 | 0.983 | 4.78 | 0.981 ± 0.033 | 5.72 ± 0.37 | 0.989 | 4.52 |
| RF [55] | 0.970 ± 0.011 | 6.68 ± 0.40 | 0.979 | 4.90 | 0.981 ± 0.008 | 5.29 ± 0.38 | 0.983 | 4.78 | 0.975 ± 0.023 | 5.69 ± 0.18 | 0.990 | 4.23 |
| AB [63] | 0.985 ± 0.018 | 5.04 ± 0.20 | 0.984 | 4.48 | 0.983 ± 0.018 | 4.82 ± 0.42 | 0.982 | 4.72 | 0.981 ± 0.029 | 5.05 ± 0.34 | 0.989 | 4.63 |
| GB [37] | 0.986 ± 0.004 | 4.93 ± 0.21 | 0.981 | 4.80 | 0.987 ± 0.009 | 4.35 ± 0.18 | 0.981 | 4.50 | 0.984 ± 0.035 | 4.09 ± 0.20 | 0.988 | 4.67 |
| GPR-HO-UWE | 0.987 ± 0.012 | 4.89 ± 0.48 | 0.990 | 4.10 | 0.991 ± 0.015 | 3.81 ± 0.41 | 0.993 | 3.63 | 0.989 ± 0.037 | 3.91 ± 0.15 | 0.993 | 3.62 |
| GPR-HO-WEDE | 0.984 ± 0.012 | 5.11 ± 0.40 | 0.986 | 4.39 | 0.987 ± 0.009 | 4.03 ± 0.31 | 0.991 | 3.87 | 0.990 ± 0.036 | 3.81 ± 0.16 | 0.992 | 3.67 |
| SVM-HO-UWE | 0.981 ± 0.025 | 5.31 ± 0.37 | 0.984 | 4.65 | 0.983 ± 0.004 | 4.71 ± 0.29 | 0.984 | 4.82 | 0.985 ± 0.016 | 4.67 ± 0.18 | 0.990 | 4.23 |
| SVM-HO-WEDE | 0.984 ± 0.027 | 5.12 ± 0.39 | 0.989 | 4.20 | 0.984 ± 0.027 | 4.77 ± 0.24 | 0.990 | 3.92 | 0.991 ± 0.038 | 4.21 ± 0.30 | 0.994 | 4.02 |
| HE-UWE | 0.983 ± 0.008 | 5.29 ± 0.43 | 0.990 | 3.90 | 0.988 ± 0.012 | 4.39 ± 0.30 | 0.992 | 3.71 | 0.992 ± 0.013 | 3.73 ± 0.15 | 0.993 | 3.53 |
| HE-WEDE | 0.985 ± 0.011 | 5.07 ± 0.24 | 0.992 | 3.67 | 0.990 ± 0.012 | 4.29 ± 0.23 | 0.993 | 3.63 | 0.992 ± 0.008 | 3.74 ± 0.16 | 0.995 | 3.46 |
| Training time (s) | 5.8 | 6.4 | 6.7 | |||||||||
| Testing time (s/set of data) | 0.42 | 0.50 | 0.54 | |||||||||
| Dataset | TD | TAD | RS | WS | SD | PT | PL | PD | PN | TT | TA | UTS (mPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Al2O3 | Drill | 800 | 15 | 18 | HC | 4.8 | 6 | 0.3 | CC | 0 | 224.45 |
| 2 | Al2O3 | Drill | 1200 | 50 | 22 | SC | 5.2 | 7 | 0.4 | ST | 1.5 | 225.00 |
| 3 | Al2O3 | Drill | 1500 | 75 | 25 | TC | 5.5 | 8 | 0.5 | ZZ | 3 | 233.12 |
| 4 | Al2O3 | Drill | 1200 | 50 | 18 | SC | 4.8 | 6 | 0.4 | ZZ | 0 | 228.78 |
| 5 | Al2O3 | Drill | 1500 | 75 | 22 | TC | 5.2 | 7 | 0.5 | CC | 1.5 | 230.23 |
| 6 | Al2O3 | Drill | 800 | 15 | 25 | HC | 5.5 | 8 | 0.3 | ST | 3 | 236.90 |
| 7 | Al2O3 | Drill | 800 | 50 | 18 | TC | 4.8 | 7 | 0.5 | CC | 3 | 227.00 |
| 8 | Al2O3 | Drill | 1200 | 75 | 22 | HC | 5.2 | 8 | 0.3 | ST | 0 | 232.97 |
| 9 | Al2O3 | Drill | 1500 | 15 | 25 | SC | 5.5 | 6 | 0.4 | ZZ | 1.5 | 234.34 |
| 10 | Al2O3 | Groove | 800 | 75 | 18 | TC | 4.8 | 8 | 0.4 | ST | 1.5 | 236.13 |
| 11 | Al2O3 | Groove | 1200 | 15 | 22 | HC | 5.2 | 6 | 0.5 | ZZ | 3 | 228.45 |
| 12 | Al2O3 | Groove | 1500 | 50 | 25 | SC | 5.5 | 7 | 0.3 | CC | 0 | 221.78 |
| 13 | Al2O3 | Groove | 1500 | 50 | 22 | TC | 4.8 | 8 | 0.3 | ZZ | 0 | 235.46 |
| 14 | Al2O3 | Groove | 800 | 75 | 25 | HC | 5.2 | 6 | 0.4 | CC | 1.5 | 220.34 |
| 15 | Al2O3 | Groove | 1200 | 15 | 18 | SC | 5.5 | 7 | 0.5 | ST | 3 | 227.56 |
| 16 | Al2O3 | Groove | 800 | 15 | 22 | SC | 4.8 | 8 | 0.5 | ZZ | 1.5 | 230.82 |
| 17 | Al2O3 | Groove | 1200 | 50 | 25 | TC | 5.2 | 6 | 0.3 | CC | 3 | 225.08 |
| 18 | Al2O3 | Groove | 1500 | 75 | 18 | HC | 5.5 | 7 | 0.4 | ST | 0 | 234.14 |
| 19 | SiC | Drill | 1500 | 75 | 22 | SC | 4.8 | 6 | 0.3 | ST | 3 | 226.46 |
| 20 | SiC | Drill | 800 | 15 | 25 | TC | 5.2 | 7 | 0.4 | ZZ | 0 | 233.00 |
| 21 | SiC | Drill | 1200 | 50 | 18 | HC | 5.5 | 8 | 0.5 | CC | 1.5 | 229.05 |
| 22 | SiC | Drill | 1500 | 15 | 22 | HC | 4.8 | 7 | 0.4 | CC | 3 | 221.48 |
| 23 | SiC | Drill | 800 | 50 | 25 | SC | 5.2 | 8 | 0.5 | ST | 0 | 237.35 |
| 24 | SiC | Drill | 1200 | 75 | 18 | TC | 5.5 | 6 | 0.3 | ZZ | 1.5 | 234.67 |
| 25 | SiC | Drill | 1200 | 75 | 25 | HC | 4.8 | 7 | 0.5 | ZZ | 0 | 227.27 |
| 26 | SiC | Drill | 1500 | 15 | 18 | SC | 5.2 | 8 | 0.3 | CC | 1.5 | 220.60 |
| 27 | SiC | Drill | 800 | 50 | 22 | TC | 5.5 | 6 | 0.4 | ST | 3 | 247.10 |
| 28 | SiC | Groove | 1200 | 15 | 25 | TC | 4.8 | 7 | 0.3 | ST | 1.5 | 242.07 |
| 29 | SiC | Groove | 1500 | 50 | 18 | HC | 5.2 | 8 | 0.4 | ZZ | 3 | 232.55 |
| 30 | SiC | Groove | 800 | 75 | 22 | SC | 5.5 | 6 | 0.5 | CC | 0 | 224.52 |
| 31 | SiC | Groove | 1200 | 75 | 25 | SC | 4.8 | 8 | 0.4 | CC | 3 | 220.84 |
| 32 | SiC | Groove | 1500 | 15 | 18 | TC | 5.2 | 6 | 0.5 | ST | 0 | 238.45 |
| 33 | SiC | Groove | 800 | 50 | 22 | HC | 5.5 | 7 | 0.3 | ZZ | 1.5 | 222.72 |
| 34 | SiC | Groove | 1500 | 50 | 25 | HC | 4.8 | 6 | 0.5 | ST | 1.5 | 228.00 |
| 35 | SiC | Groove | 800 | 75 | 18 | SC | 5.2 | 7 | 0.3 | ZZ | 3 | 223.95 |
| 36 | SiC | Groove | 1200 | 15 | 22 | TC | 5.5 | 8 | 0.4 | CC | 0 | 220.48 |
| Machine Learning and Ensemble Machine Learning Approach | Test Dataset | |
|---|---|---|
| CC | RMSE (mPa) | |
| GPR [34] | 0.995 | 6.69 |
| SVM [34] | 0.983 | 6.63 |
| RF [55] | 0.996 | 4.89 |
| AB [63] | 0.9769 | 4.06 |
| GB [37] | 0.9748 | 6.67 |
| GPR-HO-UWE | 0.9890 | 5.72 |
| GPR-HO-WEDE | 0.9944 | 4.09 |
| SVM-HO-UWE | 0.9946 | 4.00 |
| SVM-HO-WEDE | 0.9890 | 3.90 |
| HE-UWE | 0.9946 | 3.78 |
| HE-WEDE | 0.9965 | 3.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matitopanum, S.; Pitakaso, R.; Sethanan, K.; Srichok, T.; Chokanat, P. Prediction of the Ultimate Tensile Strength (UTS) of Asymmetric Friction Stir Welding Using Ensemble Machine Learning Methods. Processes 2023, 11, 391. https://doi.org/10.3390/pr11020391
Matitopanum S, Pitakaso R, Sethanan K, Srichok T, Chokanat P. Prediction of the Ultimate Tensile Strength (UTS) of Asymmetric Friction Stir Welding Using Ensemble Machine Learning Methods. Processes. 2023; 11(2):391. https://doi.org/10.3390/pr11020391
Chicago/Turabian StyleMatitopanum, Surasak, Rapeepan Pitakaso, Kanchana Sethanan, Thanatkij Srichok, and Peerawat Chokanat. 2023. "Prediction of the Ultimate Tensile Strength (UTS) of Asymmetric Friction Stir Welding Using Ensemble Machine Learning Methods" Processes 11, no. 2: 391. https://doi.org/10.3390/pr11020391
APA StyleMatitopanum, S., Pitakaso, R., Sethanan, K., Srichok, T., & Chokanat, P. (2023). Prediction of the Ultimate Tensile Strength (UTS) of Asymmetric Friction Stir Welding Using Ensemble Machine Learning Methods. Processes, 11(2), 391. https://doi.org/10.3390/pr11020391









