Modeling Microscale Foam Propagation in a Heterogeneous Grain-Based Pore Network with the Pore-Filling Event Network Method
Abstract
1. Introduction
2. Method
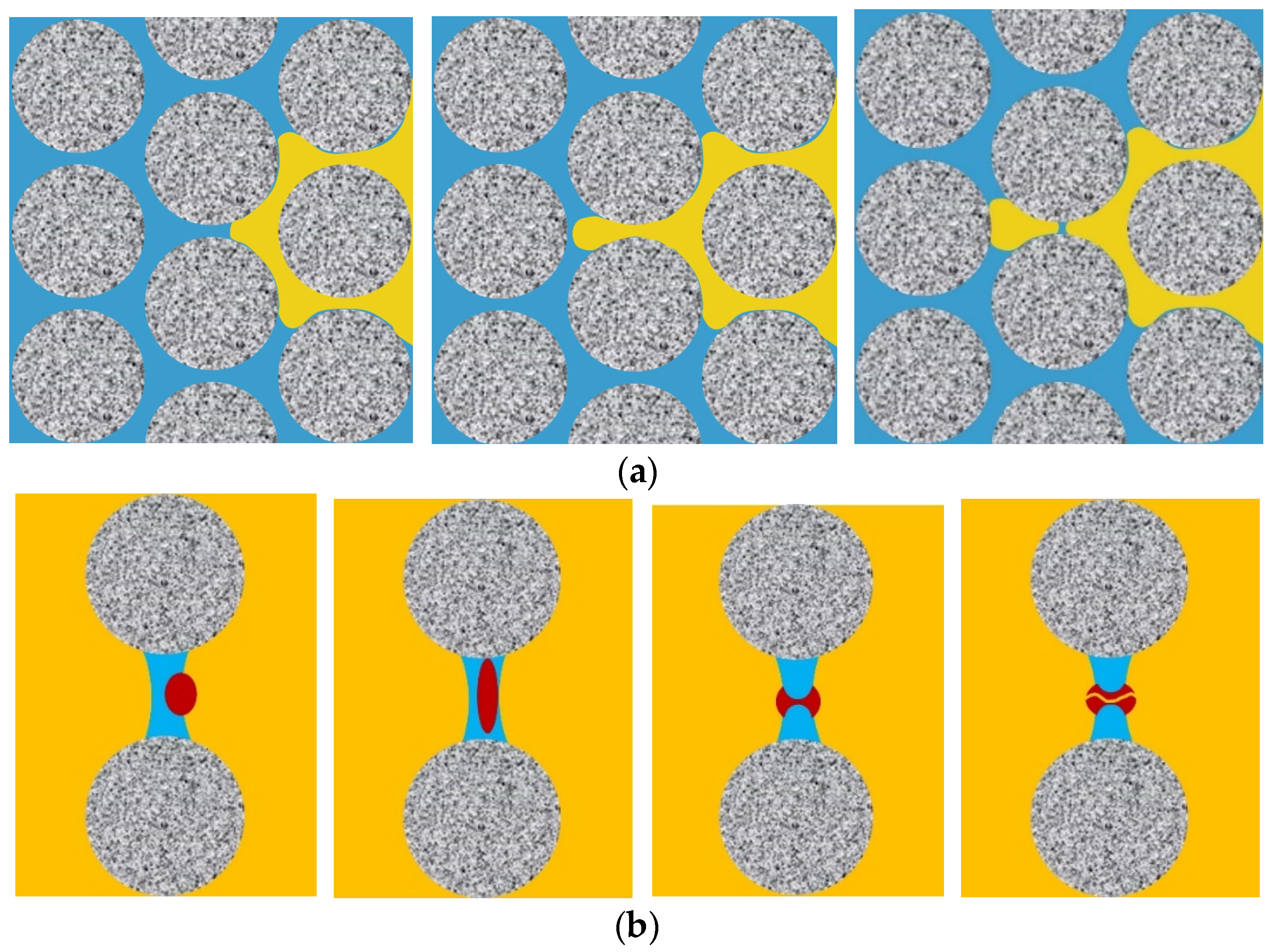
2.1. Category of Invasion Events
2.2. Coupling of Foaming and Defoaming Events
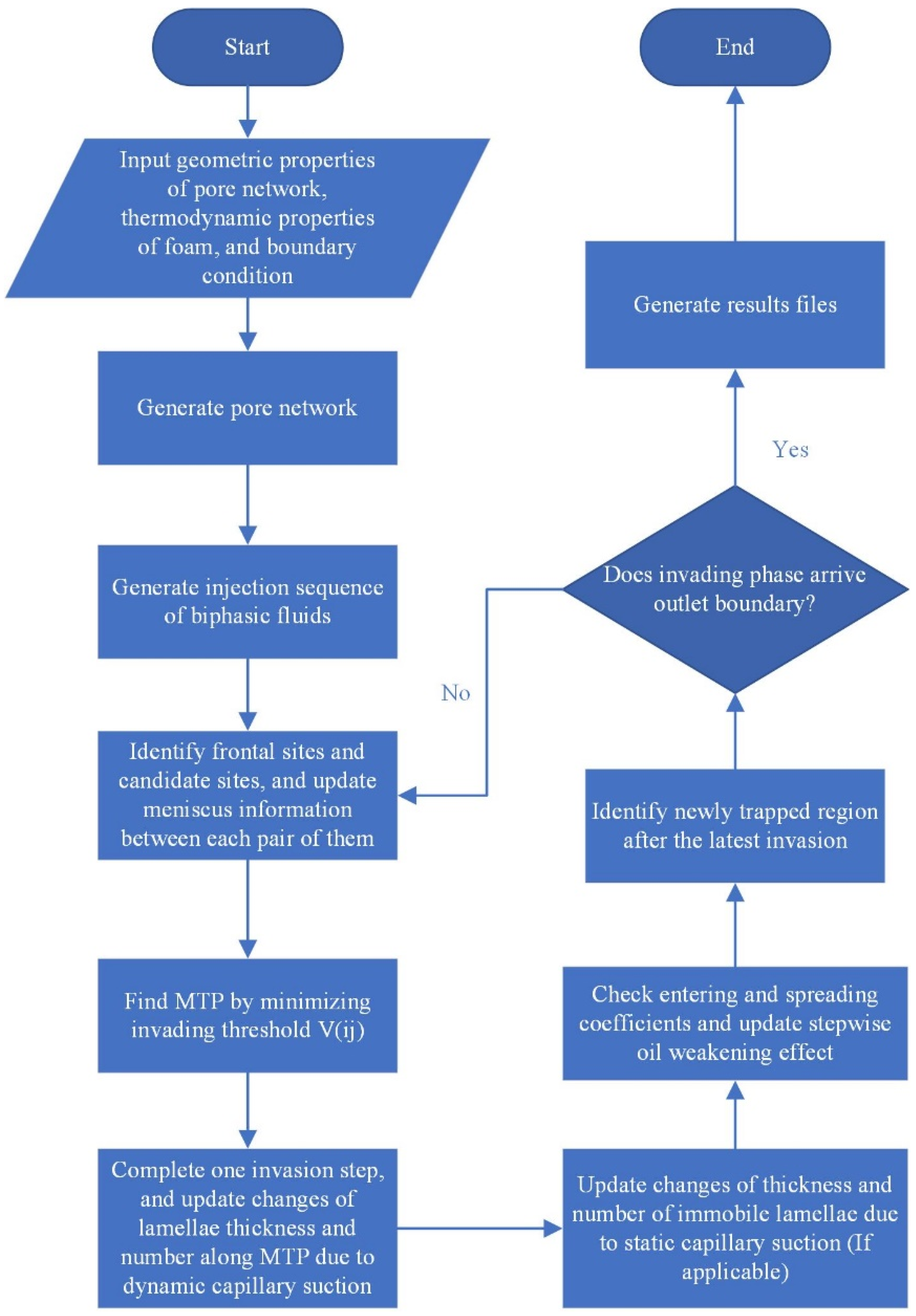
2.3. Algorithm of Foam Propagation
3. Results and Discussion
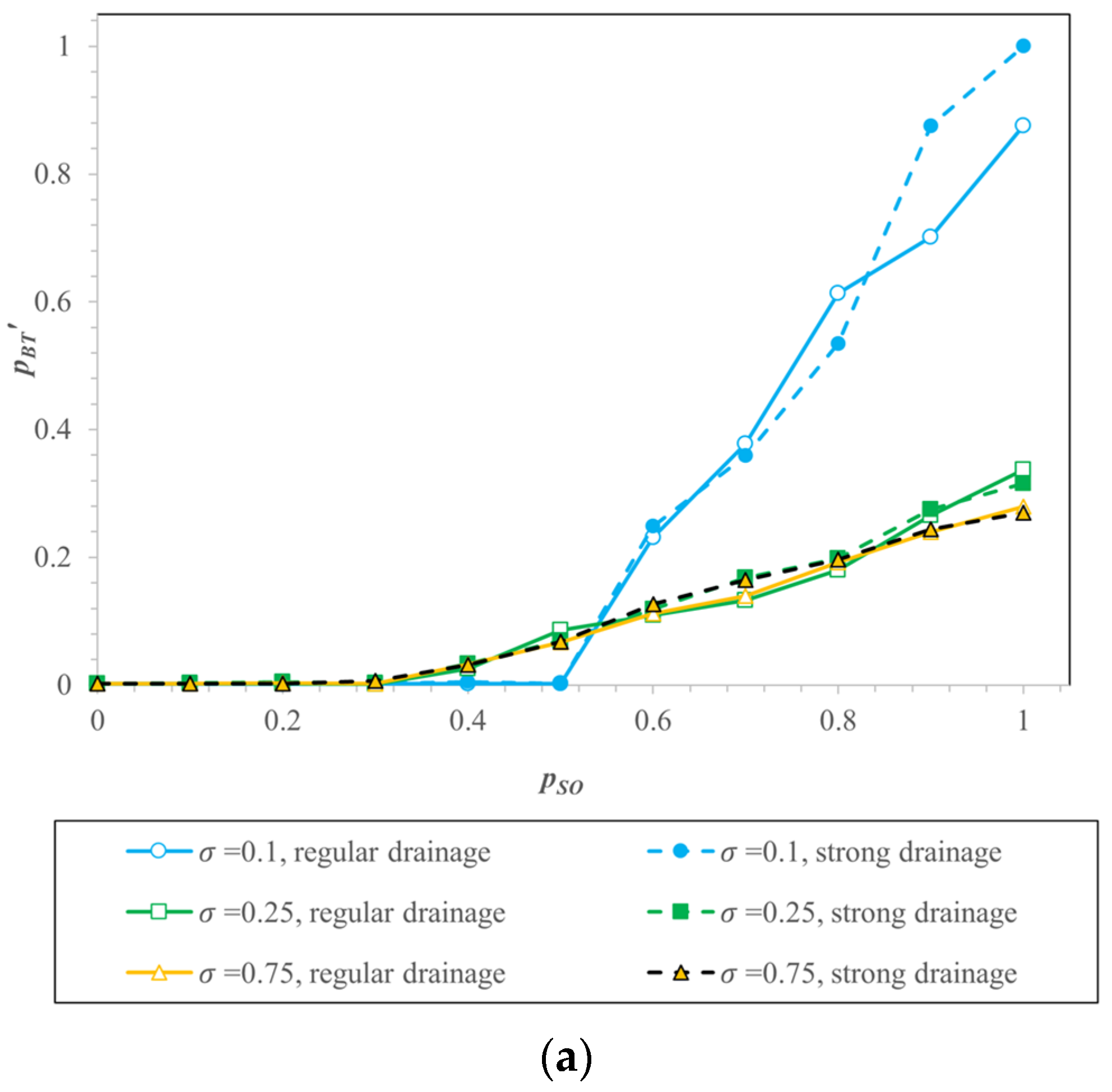
3.1. Oil-Free Foam Propagation
- (1)
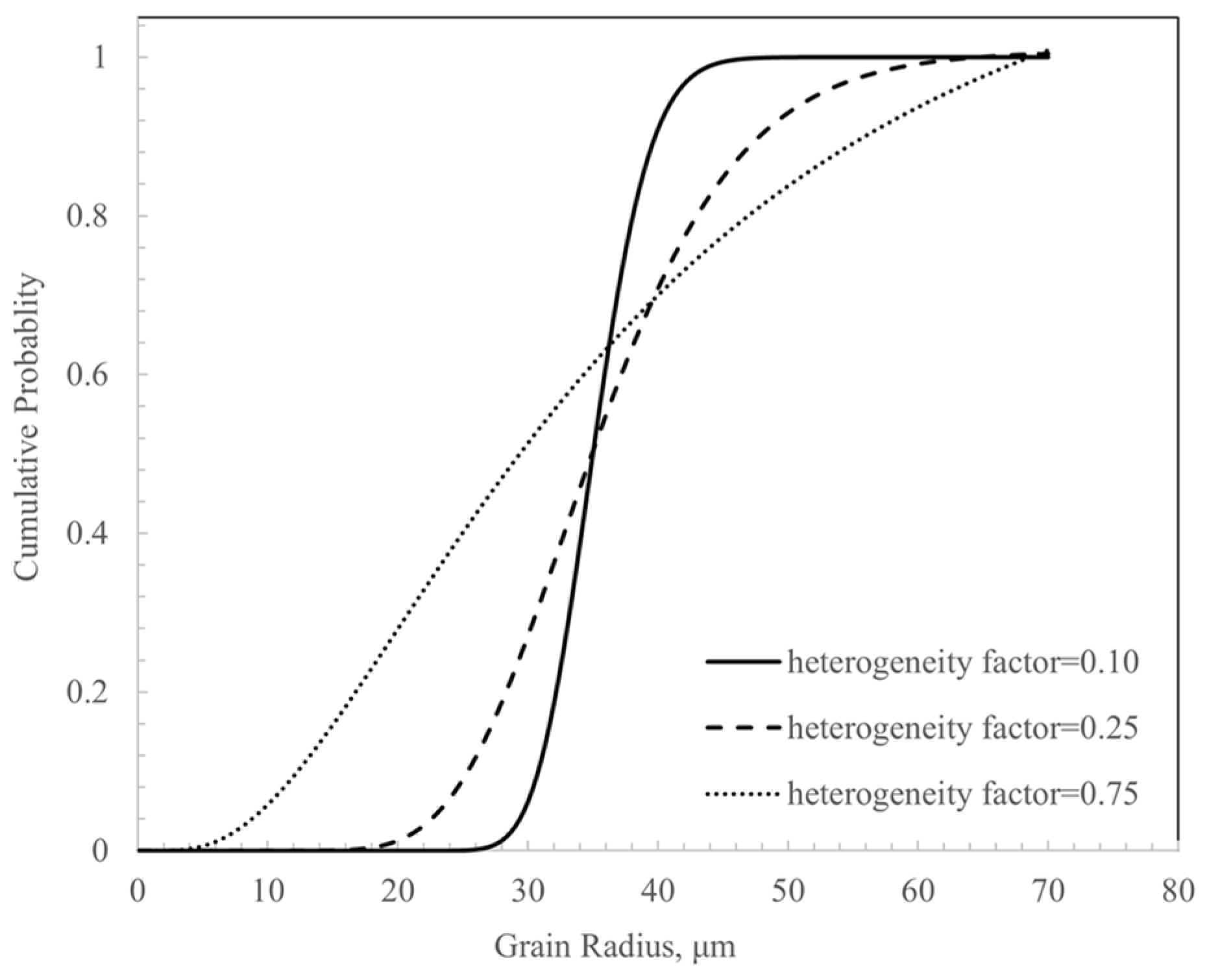
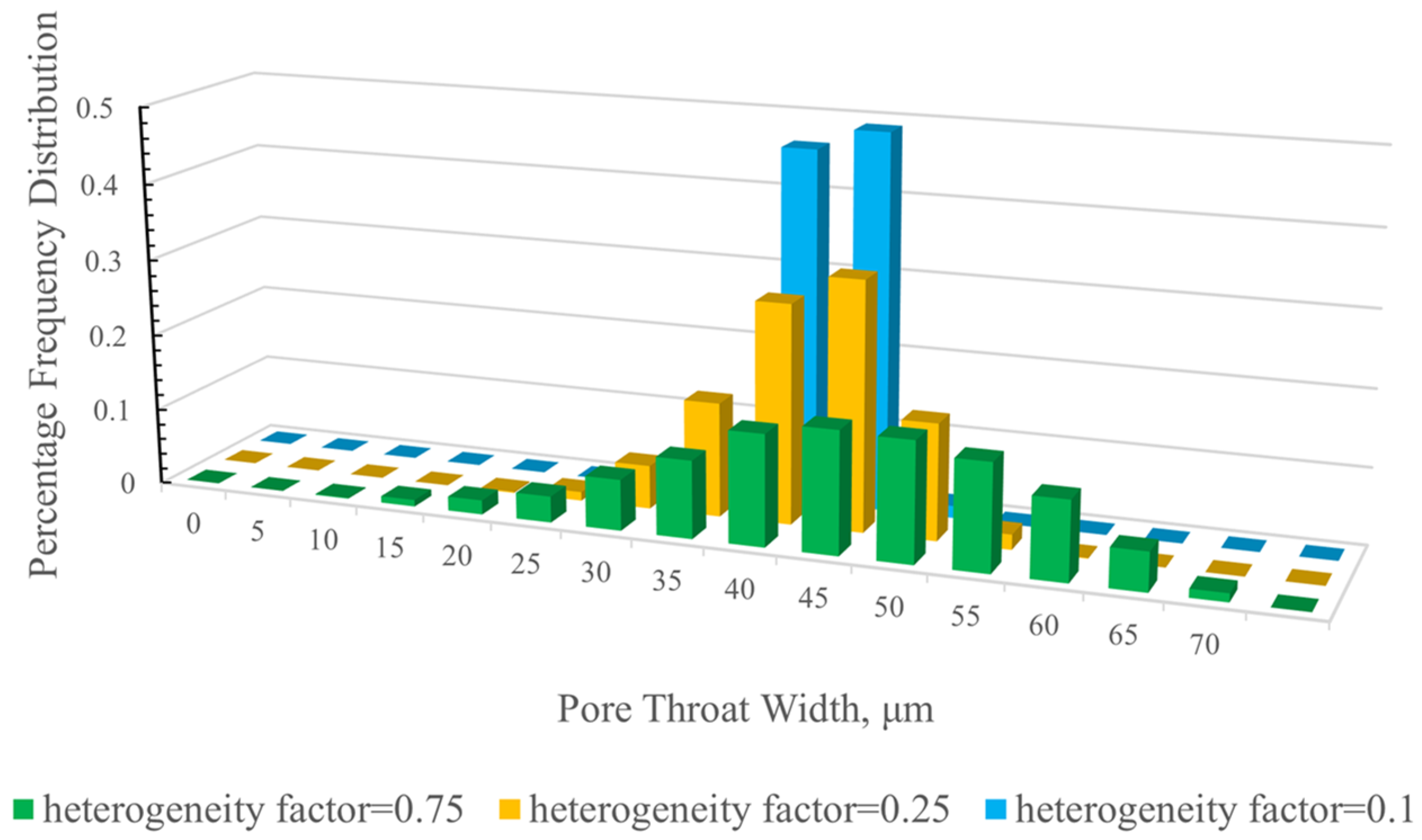
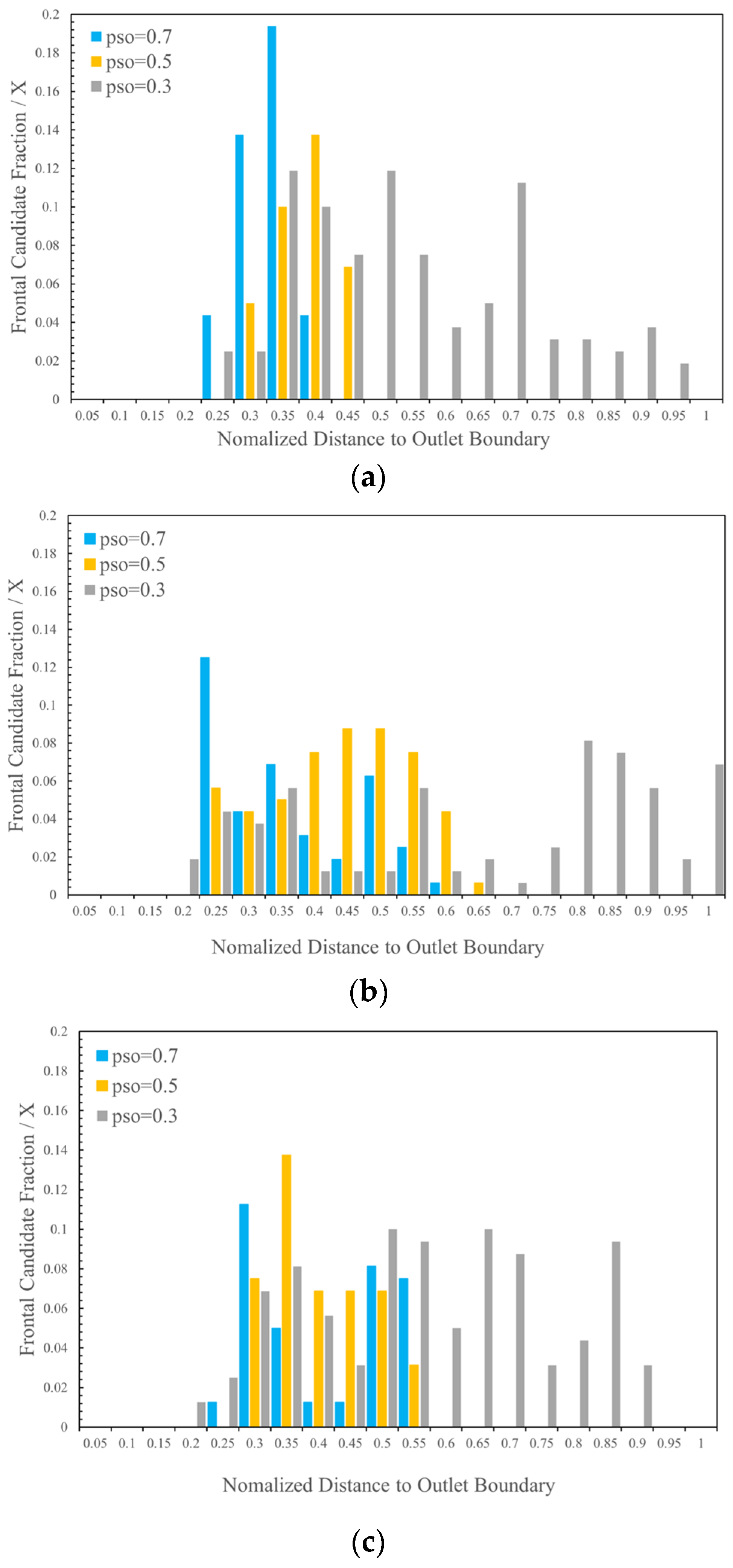
- Heterogeneity factor
- (2)
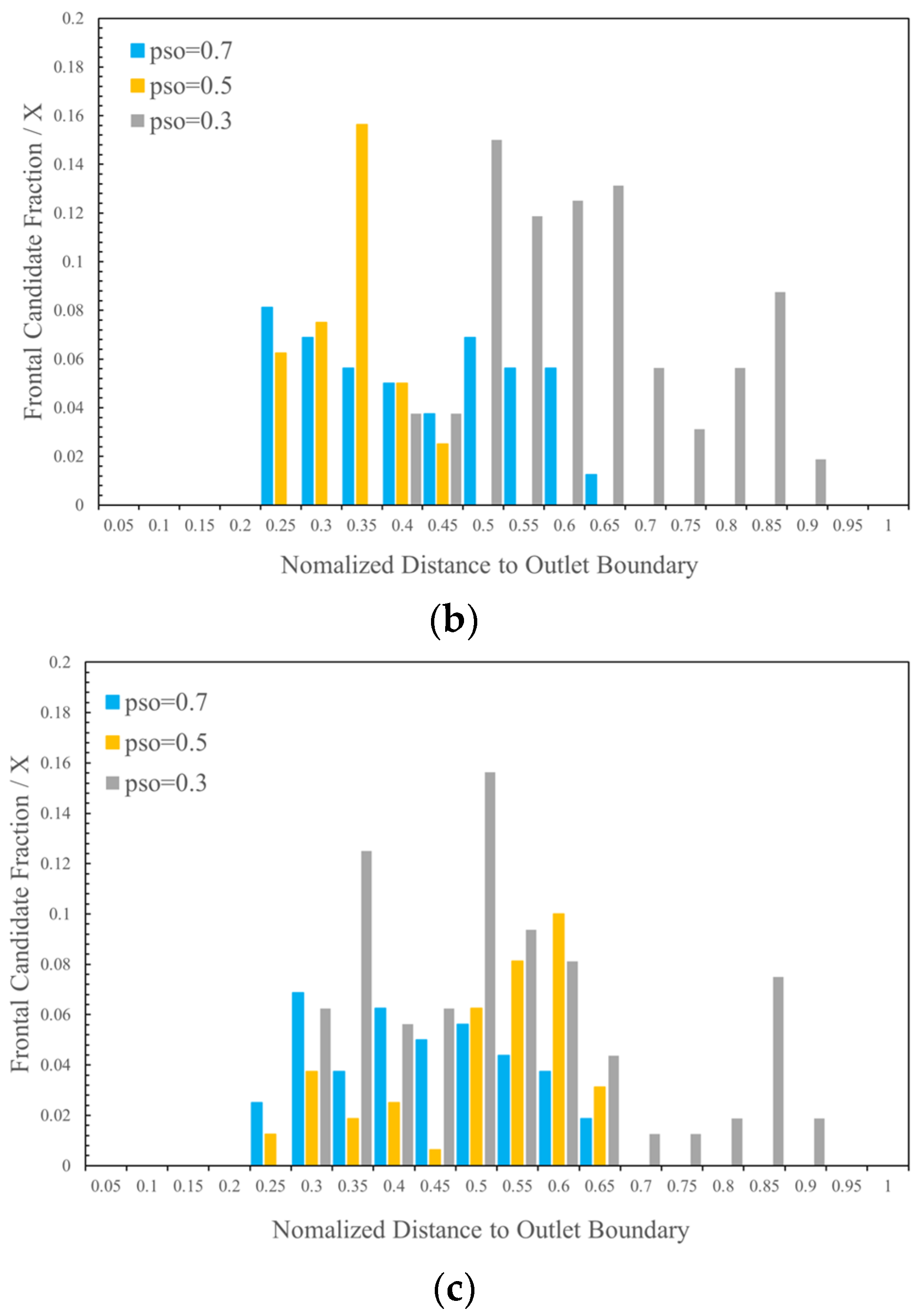
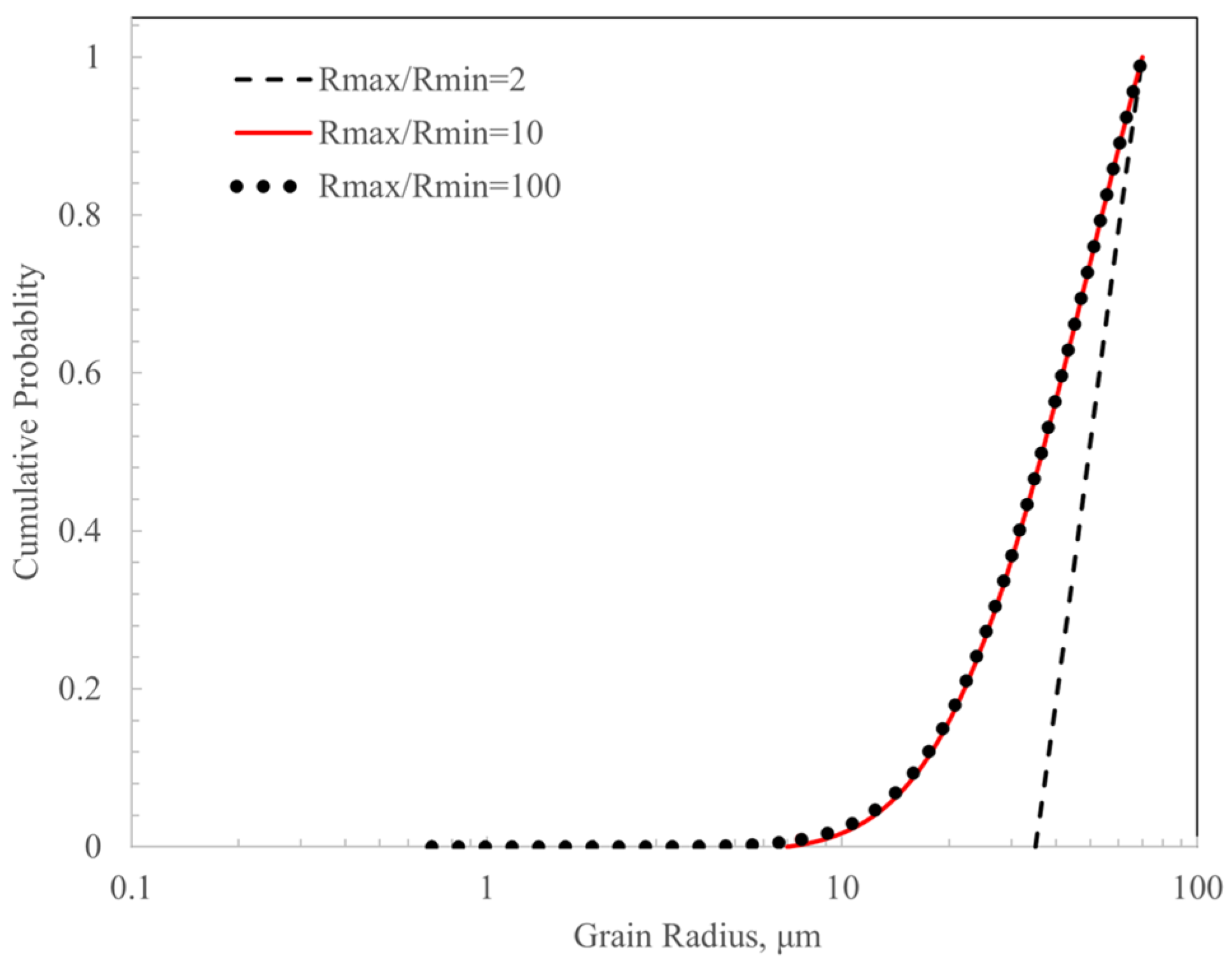
- Grain size range
3.2. Foam Propagation with Oil-Weakening Effect
3.3. Comparative Experimental Investigation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
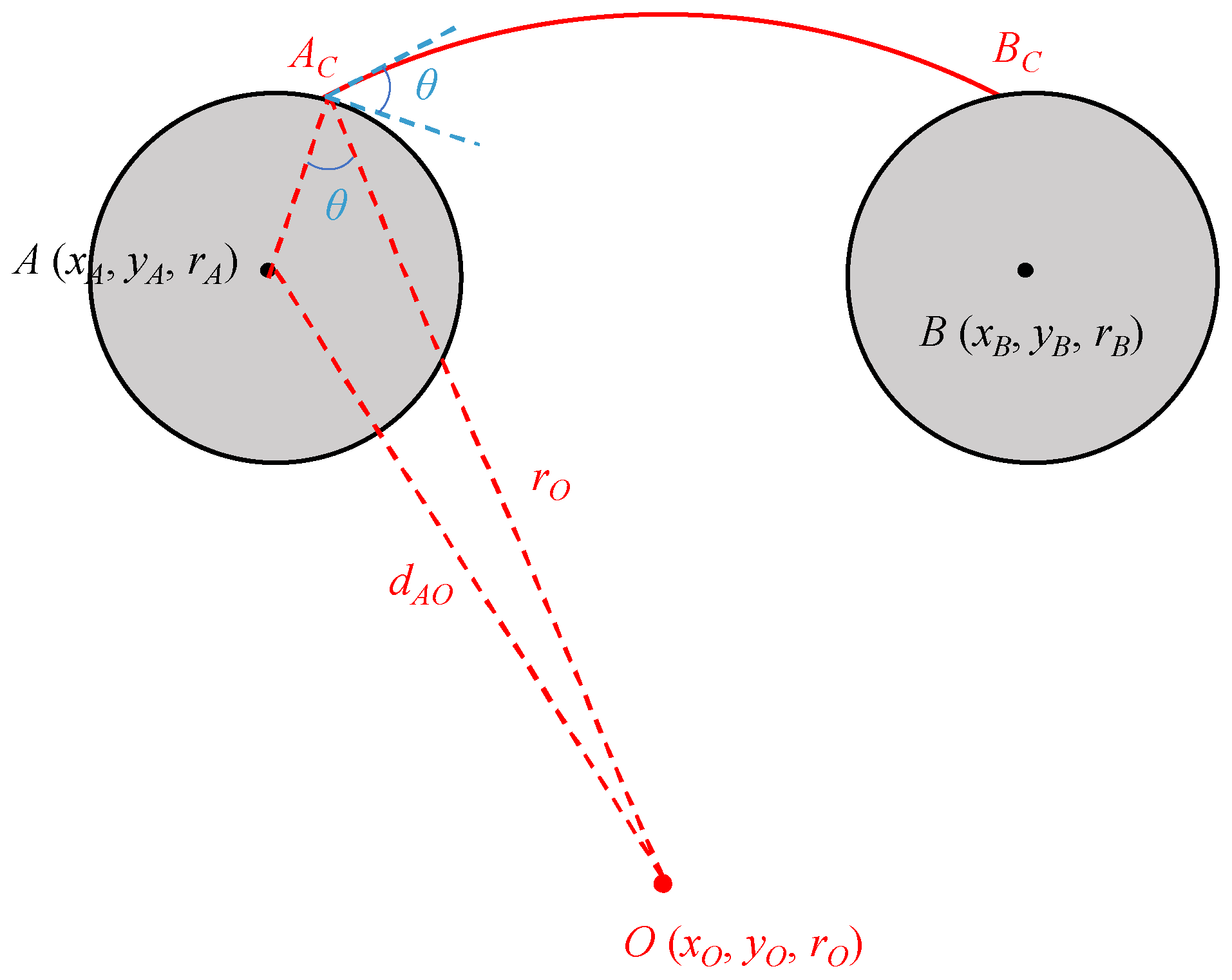
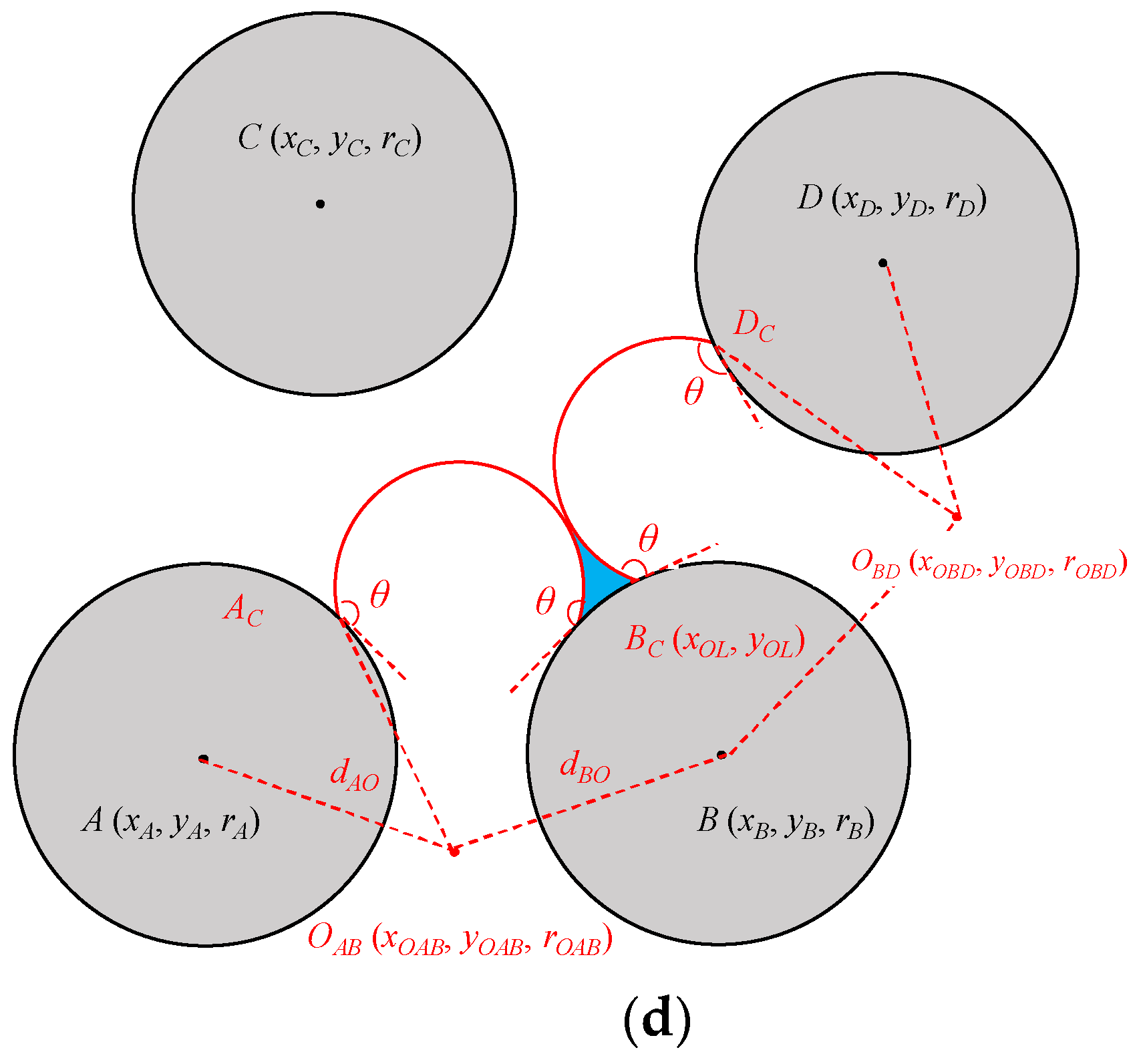
| dOA | Distance between the center of grain circle A and the center of arc ACBC. |
| pi | Stochastic model parameter controls fluid type injected during a co-injection foaming process. |
| rA | Radius of grain A, μm |
| rO | Radius of curvature of the meniscus ACBC, μm |
| Smin | The minimum fluid segment size during a co-injection foaming process |
| Γ | Foam quality, the gas fraction in foam flow |
| θ | Contact angle, ° |
| γ | Interfacial tension between invading and defending fluids, mN/m |
| p | Sitewise probability |
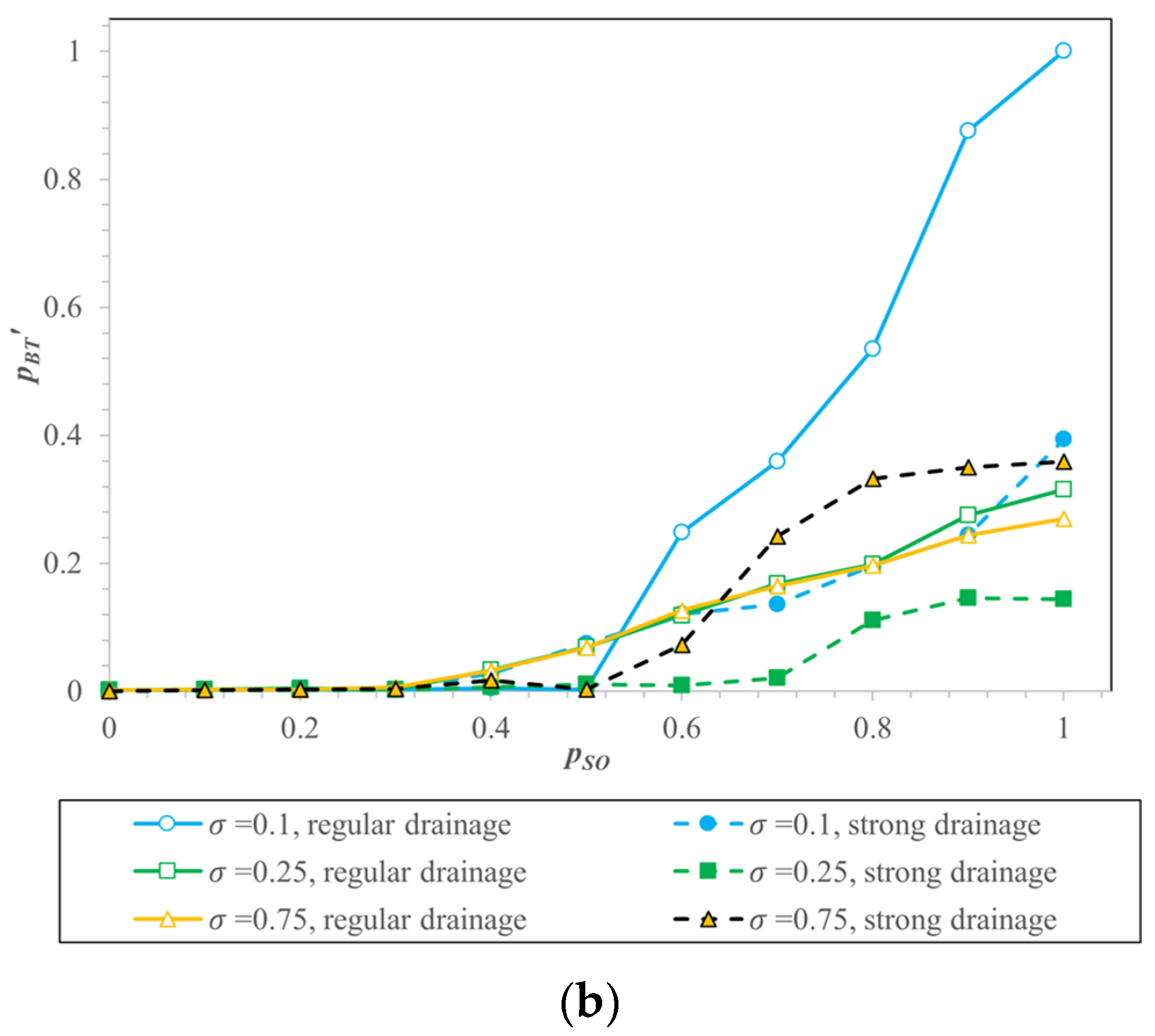
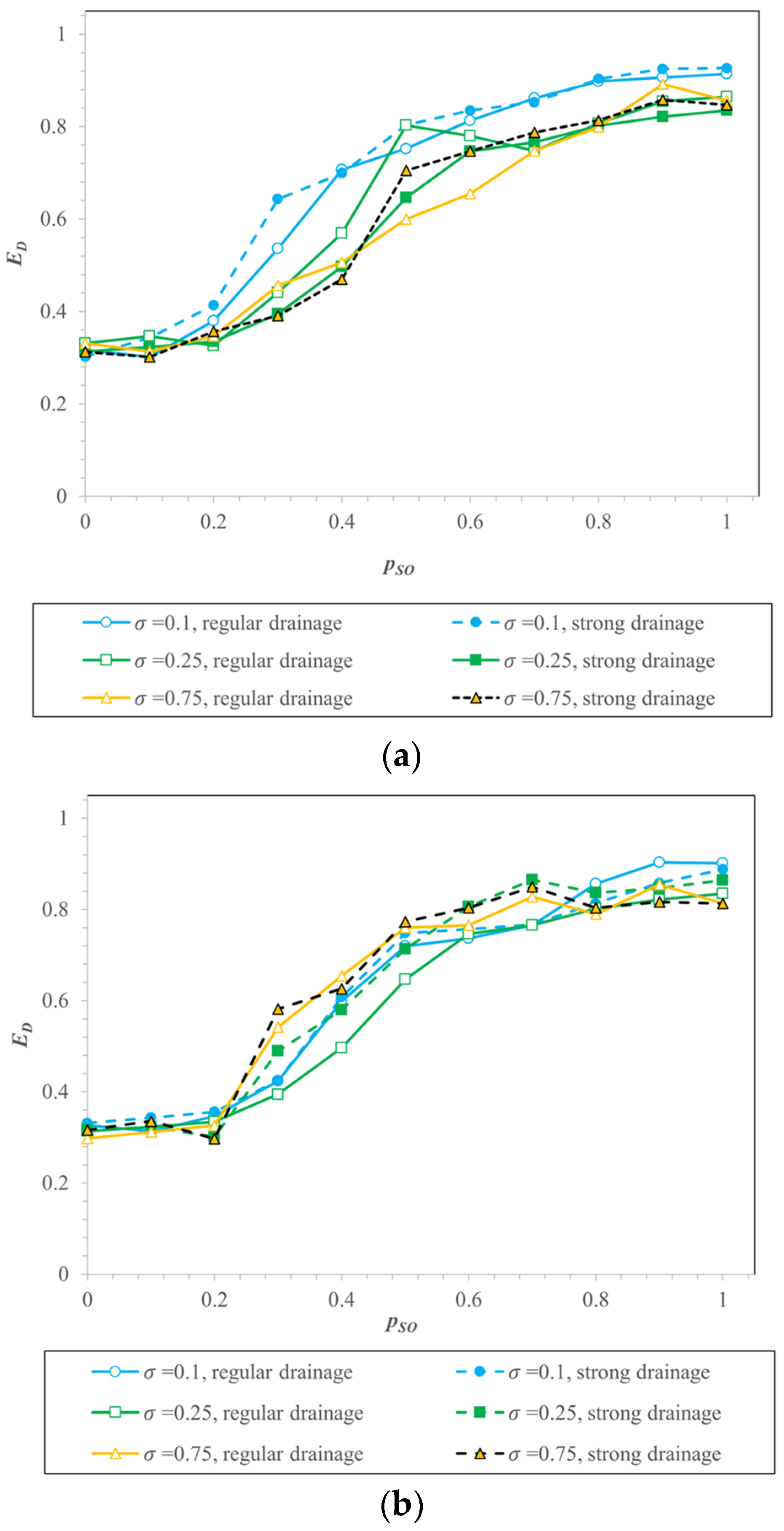
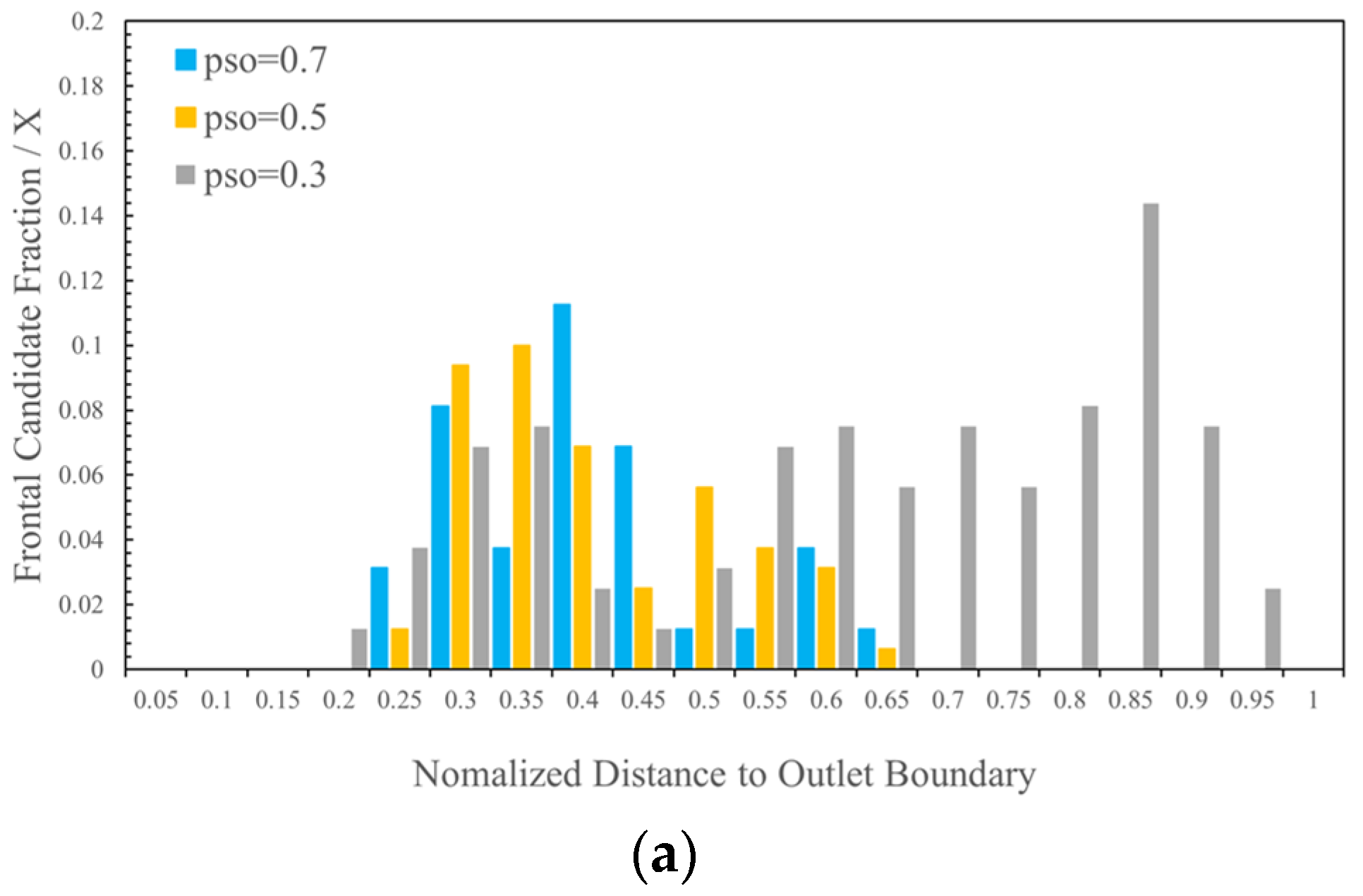
| pSO | Snap-off probability |
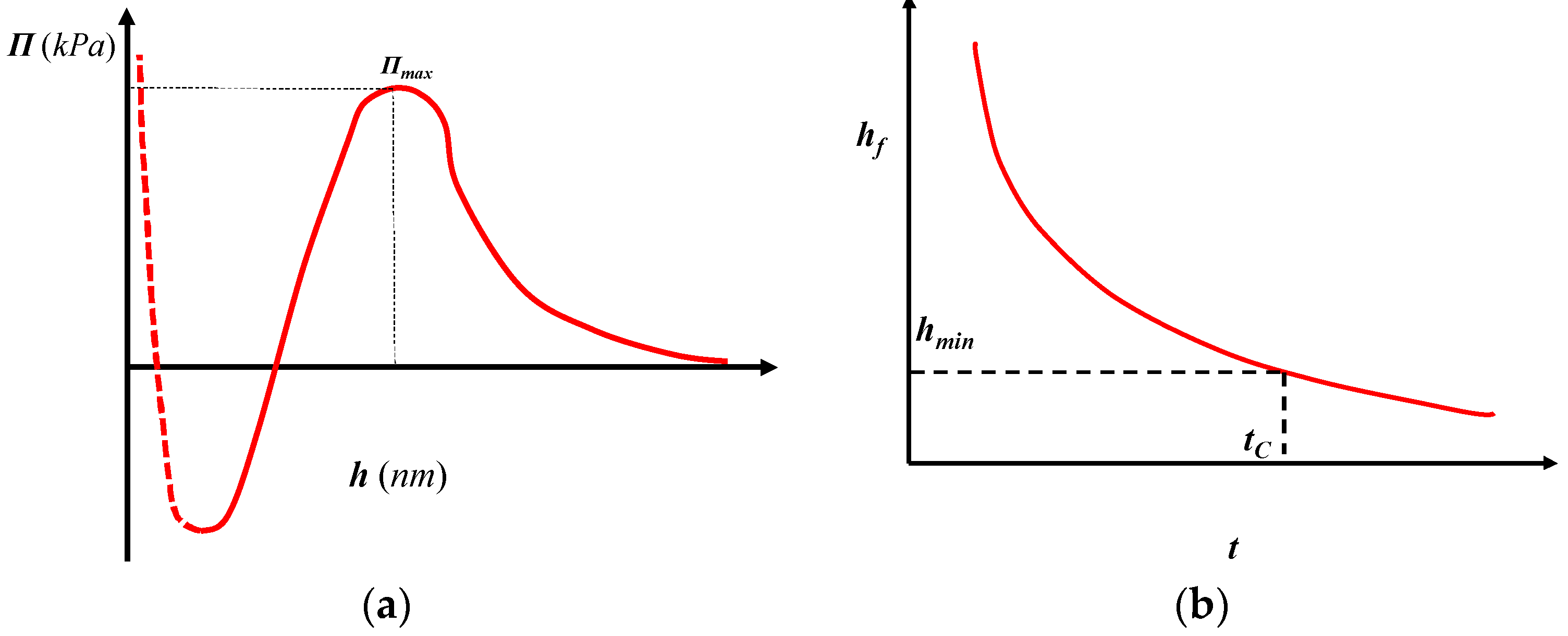
| Π | Disjoining pressure, kPa |
| Πmax | Maximum disjoining pressure, kPa |
| tc | Time for foam film thinning to critical film thickness, ms |
| h | Foam film thicnkness, nm |
| μL | Viscosity of foaming surfactant solution, mPa·s |
| RF | Equivalent radius of lamella structure |
| pCA | Local capillary pressure at the constricting part of the grain-based pore space, kPa |
| tF | Elapsed time of the invasion step, ms |
| hFO | Lamella thickness at the beginning of the corresponding invasion step, nm |
| hF | Dynamic film thickness of the foam lamella after tf, nm |
| FD | Coefficient representing additional thinning effect due to oil, nm |
| V | Minimum pressure threshold, kPa |
| σ | Heterogeneity factor |
| Rg | Grain size, µm |
| Rmax | Maximum grain size, µm |
| Rmin | Minimum grain size, µm |
| ED | Displacement efficiency, % |
| pBT’ | Pressure threshold at breakthrough, kPa |
| Xf | Flowing foam fraction |
| S | Saturation, % |
| X | Normalized distance from the outlet boundary |
References
- Tang, J.; Castañeda, P.; Marchesin, D.; Rossen, W.R. Three-Phase Fractional-Flow Theory of Foam-Oil Displacement in Porous Media with Multiple Steady States. Water Resour. Res. 2019, 55, 10319–10339. [Google Scholar] [CrossRef]
- Sochi, T. Modelling the Flow of Yield-Stress Fluids in Porous Media. Transp. Porous Media 2010, 85, 489–503. [Google Scholar] [CrossRef]
- Costantini, M.; Colosi, C.; Jaroszewicz, J.; Tosato, A.; Święszkowski, W.; Dentini, M.; Garstecki, P.; Barbetta, A. Microfluidic Foaming: A Powerful Tool for Tailoring the Morphological and Permeability Properties of Sponge-like Biopolymeric Scaffolds. ACS Appl. Mater. Interfaces 2015, 7, 23660–23671. [Google Scholar] [CrossRef] [PubMed]
- Ettinger, R.A.; Radke, C.J. Influence of foam texture on steady foam flow in Berea sandstone. Soc. Pet. Res. Eng. 1992, 7, 83–90. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, C.; Lei, Z.; Yin, X.; Kazemi, H.; Wu, Y.S. An improved multicomponent diffusion model for compositional simulation of fractured unconventional reservoirs. SPE J. 2021, 26, 3316–3341. [Google Scholar] [CrossRef]
- Su, Y.; Sun, Q.; Wang, W.; Guo, X.; Xu, J.; Li, G.; Pu, X.; Han, W.; Shi, Z. Spontaneous imbibition characteristics of shale oil reservoir under the influence of osmosis. Int. J. Coal Sci. Technol. 2022, 9, 69. [Google Scholar] [CrossRef]
- Zhao, J.; Torabi, F.; Yang, J. The role of emulsification and IFT reduction in recovering heavy oil during alkaline-surfactant-assisted CO2 foam flooding: An experimental study. Fuel 2022, 313, 122942. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Wu, W.; Liang, Y.; Wang, F. Coupled pressure-driven flow and spontaneous imbibition in shale oil reservoirs. Phys. Fluids 2023, 35, 042104. [Google Scholar]
- Szlendak, S.M.; Nguyen, N.M.; Nguyen, Q.P. Laboratory investigation of low-tension-gas flooding for improved oil recovery in tight formations. SPE J. 2013, 18, 851–866. [Google Scholar] [CrossRef]
- Yu, H.; Yang, B.; Xu, G.; Wang, J.; Ren, S.; Lin, W.; Gao, H. Air Foam Injection for IOR: From Laboratory to Field Implementation in Zhongyuan Oilfield China. In Proceedings of the SPE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 20–23 April 2008. [Google Scholar]
- Zou, G.; Zhang, Q.; Peng, S.; She, J.; Teng, D.; Jin, C.; Che, Y. Influence of geological factors on coal permeability in the Sihe coal mine. Int. J. Coal Sci. Technol. 2022, 9, 6. [Google Scholar] [CrossRef]
- Rossen, W.R. Foams in enhanced oil recovery. In Foams: Theory, Measurements and Applications; Surfactant Science Series; Prud’homme, R.K., Khan, S., Eds.; Marcel Dekker: New York, NY, USA, 1994; pp. 413–462. [Google Scholar]
- Rossen, W.R.; Gauglitz, P.A. Percolation theory of creation and mobilization of foams in porous media. AIChE J. 1990, 36, 1176–1188. [Google Scholar] [CrossRef]
- Rossen, W.R.; Zeilinger, S.C.; Shi, J.X.; Lim, M.T. Simplified Mechanistic Simulation of Foam Processes in Porous Media. SPE J. 1999, 4, 279–287. [Google Scholar] [CrossRef]
- Simjoo, M.; Nguyen, Q.P.; Zitha, P.L.J. Rheological transition during foam flow in porous media. Ind. Eng. Chem. Res. 2012, 51, 10225–10231. [Google Scholar] [CrossRef]
- Friedmann, F.; Chen, W.H.; Gauglitz, P.A. Experimental and simulation study of high-temperature foam displacement in porous media. SPE Reserv. Eng. 1991, 6, 37–45. [Google Scholar] [CrossRef]
- Osei-Bonsu, K.; Grassia, P.; Shokri, N. Investigation of foam flow in a 3D printed porous medium in the presence of oil. J. Colloid Interface Sci. 2017, 490, 850–858. [Google Scholar] [CrossRef] [PubMed]
- Kovscek, A.R.; Bertin, H.J. Foam mobility in heterogeneous porous media. Transp. Porous Med. 2003, 52, 17–35. [Google Scholar] [CrossRef]
- Wang, X.; Wu, W. Numerical Comparison of Hydrogen and CO2 Storage in Deep Saline Aquifers from Pore Scale to Field Scale. J. Energy Eng. 2023, 149, 04023038. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Rossen, W.R. Applying Fractional-Flow Theory to Foams for Diversion in Matrix Acidization. SPE Prod. Fac. 1994, 9, 29–35. [Google Scholar] [CrossRef]
- Braconnier, B.; Flauraud, E.; Nguyen, Q.L. Efficient scheme for chemical flooding. Oil Gas Sci. Technol.—Rev. IFP Energ. Nouv. 2014, 69, 585–601. [Google Scholar] [CrossRef][Green Version]
- Friedmann, F.; Jensen, J.A. Some Parameters Influencing the Formation and Propagation of Foams in Porous Media. In Proceedings of the SPE California Regional Meeting, Oakland, CA, USA, 2–4 April 1986. [Google Scholar]
- Gassara, O.; Douarche, F.; Braconnier, B.; Bourbiaux, B. Equivalence Between Semi-empirical and Population-Balance Foam Models. Transp. Porous Media 2017, 120, 473–493. [Google Scholar] [CrossRef]
- Vries, A.S.d.; Wit, K. Rheology of Gas/Water Foam in the Quality Range Relevant to Steam Foam. SPE Res. Eng. 1990, 5, 185–192. [Google Scholar] [CrossRef]
- Persoff, P.; Radke, C.J.; Pruess, K.; Benson, S.M.; Witherspoon, P.A. A laboratory investigation of foam flow in sandstone at elevated pressure. SPE Reserv. Eng. 1991, 6, 365–372. [Google Scholar] [CrossRef]
- Ashoori, E.; van der Heijden, T.; Rossen, W. Fractional-flow theory of foam displacements with oil. SPE J. 2010, 15, 20–22. [Google Scholar] [CrossRef]
- Kharabaf, H.; Yortsos, Y.C. Pore network model for foam formation and propagation in porous media. SPE J. 1998, 3, 42–53. [Google Scholar] [CrossRef]
- Chen, M.; Yortsos, Y.C.; Rossen, W.R. Pore-network study of the mechanisms of foam generation in porous media. Phys. Rev. E 2006, 73, 036304. [Google Scholar] [CrossRef]
- Almajid, M.M.; Kovscek, A.R. Pore Network Investigation of Trapped Gas and Foam Generation Mechanisms. Transp. Porous Media 2019, 131, 289–313. [Google Scholar] [CrossRef]
- Zhao, J.; Torabi, F.; Yang, J. Pore Network Investigation of Gas Trapping and Mobility During Foam Propagation Using Invasion Percolation with Memory. Transp. Porous Media 2020, 134, 195–230. [Google Scholar] [CrossRef]
- Zhao, J.; Torabi, F.; Yang, J. Role of Viscous Forces in Foam Flow in Porous Media at the Pore Level. Ind. Eng. Chem. Res. 2021, 60, 3156–3173. [Google Scholar] [CrossRef]
- Kharabaf, H.; Yortsos, Y.C. Invasion percolation with memory. Phys. Rev. E 1997, 55, 7177–7191. [Google Scholar] [CrossRef]
- Chen, M.; Rossen, W.; Yortsos, Y.C. The flow and displacement in porous media of fluids with yield stress. Chem. Eng. Sci. 2005, 60, 4183–4202. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, J.; Zeng, F. Complex displacement behavior during foaming gas drainage in 2D microfluidic networks. Fuel 2023, 344, 128071. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, J.; Zeng, F. Modeling foam propagation in pore network with designated pressure constraints. Fuel 2023, 331, 125772. [Google Scholar] [CrossRef]
- David, A.; Marsden, S.S. The Rheology of Foam. In Proceedings of the SPE 2544 Presented at the 1969 SPE Annual Meeting, Denver, CO, USA, 28 September–1 October 1969. [Google Scholar]
- Hirasaki, G.J.; Lawson, J.B. Mechanisms of foam flow in porous media: Apparent viscosity in smooth capillaries. SPE J. 1985, 25, 176–190. [Google Scholar] [CrossRef]
- Ransohoff, T.C.; Radke, C.T. Mechanisms of foam generation in glass-bead packs. J. Reserv. Eng. Soc. Petrol. Eng. 1988, 3, 573–585. [Google Scholar] [CrossRef]
- Kahrobaei, S.; Vincent-Bonnieu, S.; Farajzadeh, R. Experimental Study of Hysteresis behavior of Foam Generation in Porous Media. Sci. Rep. 2017, 7, 8986. [Google Scholar] [CrossRef] [PubMed]
- Osterloh, W.T.; Jante, M.J., Jr. Effects of Gas and Liquid Velocity on Steady-State Foam Flow at High Temperatures. In Proceedings of the Paper SPE/DOE 24179 Presented at the 1992 SPE/DOE Symposium on Enhanced Oil Recovery, Tulsa, OK, USA, 22–24 April 1992. [Google Scholar]
- Rossen, W.R.; Wang, M.W. Modeling Foams for Acid Diversion. SPE J. 1999, 4, 92–100. [Google Scholar] [CrossRef]
- Shan, D.; Rossen, W.R. Optimal injection strategies for foam IOR. SPE J. 2004, 9, 132–150. [Google Scholar] [CrossRef]
- Zhao, J.; Torabi, F.; Yang, J. The synergistic role of silica nanoparticle and anionic surfactant on the static and dynamic CO2 foam stability for enhanced heavy oil recovery: An experimental study. Fuel 2021, 287, 119443. [Google Scholar] [CrossRef]
- Koczo, K.; Lobo, L.A.; Wasan, D.T. Effect of oil on foam stability: Aqueous foams stabilized by emulsions. J. Colloid Interface Sci. 1992, 150, 492–506. [Google Scholar] [CrossRef]
- Frye, G.C.; Berg, J.C. Antifoam Action by Solid Particles. J. Colloid Interface Sci. 1989, 127, 222. [Google Scholar] [CrossRef]
- Cieplak, M.; Robbins, M.O. Influence of contact angle on quasistatic fluid invasion of porous media. Phys. Rev. B 1990, 41, 11508–11521. [Google Scholar] [CrossRef] [PubMed]
- Berg, S.; Ott, H.; Klapp, S.A.; Schwing, A.; Neiteler, R.; Brussee, N.; Makurat, A.; Leu, L.; Enzmann, F.; Schwarz, J.O.; et al. Real-time 3D imaging of Haines jumps in porous media flow. Proc. Natl. Acad. Sci. USA 2013, 110, 3755–3759. [Google Scholar] [CrossRef] [PubMed]
- Primkulov, B.K.; Talman, S.; Khaleghi, K.; Rangriz Shokri, A.; Chalaturnyk, R.; Zhao, B.; Macminn, C.W.; Juanes, R. Quasistatic fluid-fluid displacement in porous media: Invasion-percolation through a wetting transition. Phys. Rev. Fluids 2018, 3, 104001. [Google Scholar] [CrossRef]
- Liu, Y.; Block, E.; Squier, J.; Oakey, J. Investigating low salinity waterflooding via glass micromodels with triangular pore-throat architectures. Fuel 2021, 283, 119264. [Google Scholar] [CrossRef]
- Joekar-Niasar, V.; Hassanizadeh, S.M.; Dahle, H.K. Non-equilibrium effects in capillarity and interfacial area in two-phase flow: Dynamic pore-network modelling. J. Fluid Mech. 2010, 655, 38–71. [Google Scholar] [CrossRef]
- Wang, X.; Sheng, J.J. Multi-scaled pore network modeling of gas-water flow in shale formations. J. Petrol. Sci. Eng. 2019, 177, 899–908. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, J.; He, Y.; Zeng, F. Microscale Evaluation on the Feasibility of Foam-Assisted CO2 Sequestration in the Absence and Presence of Oleic Phase: An Integrated Microfluidic Experimental and Pore Network Modeling Study. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 16–18 October 2023. [Google Scholar]
















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Lu, N.; Lin, Z.; Zhang, B.; Zhang, Y.; He, Y.; Zhao, J. Modeling Microscale Foam Propagation in a Heterogeneous Grain-Based Pore Network with the Pore-Filling Event Network Method. Processes 2023, 11, 3322. https://doi.org/10.3390/pr11123322
Yang J, Lu N, Lin Z, Zhang B, Zhang Y, He Y, Zhao J. Modeling Microscale Foam Propagation in a Heterogeneous Grain-Based Pore Network with the Pore-Filling Event Network Method. Processes. 2023; 11(12):3322. https://doi.org/10.3390/pr11123322
Chicago/Turabian StyleYang, Jun, Nu Lu, Zeyu Lin, Bo Zhang, Yizhong Zhang, Yanfeng He, and Jing Zhao. 2023. "Modeling Microscale Foam Propagation in a Heterogeneous Grain-Based Pore Network with the Pore-Filling Event Network Method" Processes 11, no. 12: 3322. https://doi.org/10.3390/pr11123322
APA StyleYang, J., Lu, N., Lin, Z., Zhang, B., Zhang, Y., He, Y., & Zhao, J. (2023). Modeling Microscale Foam Propagation in a Heterogeneous Grain-Based Pore Network with the Pore-Filling Event Network Method. Processes, 11(12), 3322. https://doi.org/10.3390/pr11123322






